弁言
教程资源
- ZJU 数据结构
- ZJU Advanced Data Structures and Algorithm Analysis
- UCB CS61B: Data Structures and Algorithms
- Coursera: Algorithms I & II
- MIT 6.006: Introduction to Algorithms
- MIT 6.046: Design and Analysis of Algorithms
- UCB CS170: Efficient Algorithms and Intractable Problems
Leetcode刷题指南
代码随想录
很多刚开始刷题的同学都有一个困惑:面对leetcode上近两千道题目,从何刷起。
大家平时刷题感觉效率低,浪费的时间主要在三点:
- 找题
- 找到了不应该现阶段做的题
- 没有全套的优质题解可以参考
其实我之前在知乎上回答过这个问题,回答内容大概是按照如下类型来刷数组-> 链表-> 哈希表->字符串->栈与队列->树->回溯->贪心->动态规划->图论->高级数据结构,再从简单刷起,做了几个类型题目之后,再慢慢做中等题目、困难题目。
即使有这样一个整体规划,对于一位初学者甚至算法老手寻找合适自己的题目也是很困难,时间成本很高,而且题目还不一定就是经典题目。
对于刷题,我们都是想用最短的时间按照循序渐进的难度顺序把经典题目都做一遍,这样效率才是最高的!
而且一个正确的刷题顺序对算法学习是非常重要的!
所以我整理了leetcode刷题攻略:一个超级详细的刷题顺序,每道题目都是我精心筛选,都是经典题目高频面试题,大家只要按照这个顺序刷就可以了,你没看错,左面的菜单栏就是刷题顺序,每一个专题,挨个刷就可以,不用自己再去题海里选题了!
而且每道题目我都写了的详细题解(图文并茂,难点配有视频),我的题解已经陪伴了几万录友渡过了算法学习旅程,质量是有目共睹的。
那么现在我把刷题顺序都整理出来,是为了帮助更多的学习算法的同学少走弯路!
如果你在刷leetcode,强烈建议先按照本站的题目顺序来刷,刷完了你会发现对整个知识体系有一个质的飞跃,不用在题海茫然的寻找方向。
吴师兄学算法
大家好,我是吴师兄。
1、LeetCode 题目太多,全部刷完肯定不是最好最有效的方式,其中涉及到的基本知识点来来回回就那些,同时有非常多的类似题,所以刷经典题,掌握这些经典题是最有效的学习方式。
2、从算法训练营第一期开始到现在的第十二期,吴师兄整理和迭代了非常多的刷题顺序,经过这两年的同学们的反馈,终于整理出一份我认为是最适合新手小白转码同学的 LeetCode 刷题顺序。
3、本刷题顺序涵盖了 205 道算法题,如果你的自学能力强,每天能够投入 2 小时的刷题时间,两个月左右是可以做到完完整整的全部刷完。
4、所有题目均来源于算法训练营的内容,以动画和视频的形式讲解,弱化了文字讲解部分,所以很多题目没有提供题目解析部分,而是以代码注释的形式进行讲解。
5、每道题目的文字解析部分会逐步补充好,为后续实体书的出版提供物料。
6、添加吴师兄的微信 algomooc555 ,后期将会在朋友圈赠送 205 道题目的 PDF 版题解。
如何高效学习数据结构与算法
原作者:三钻
前言
本文是个人基于覃超老师的《算法训练营》的学习笔记,此笔记的内容都是学习后的个人记录、个人总结、理解和思想。仅供参考学习。
很多同学在大学的时候会觉得数据结构与算法很枯燥,很多小伙伴都不愿意听这门课程。甚至以前还觉得能开发一个项目就能成为一个合格的程序员。但是学会算法,或者接触过数据结构与算法后,发现懂这门知识的程序员编写出来的代码相对有更高的质量。代码的性能、写法、底层逻辑和解决问题的能力都会高于不懂数据结构与算法的程序员。
到了如今,如果想成为一个高级开发工程师或者进入大厂,不论岗位是前端、后端还是AI,算法都是重中之重。也无论我们需要进入的公司的岗位是否最后是做算法工程师,前提面试就需要考算法。所以小时不学算法,长大掉头发。
这系列的《算法学习笔记》,与大家一起重温或者学习数据结构与算法。
这里也赠送大家一句话: "好记性不如烂笔头,好记性更不如好笔记"
愿大家在技术银河中终身漂泊学习时,习惯编写自己的笔记,以后这些笔记必定成为我们最珍贵的宝藏!✨
如何系统化学习算法
深入到精通一门知识的我们都需要一个系统化的学习方法,如果这门知识越是有难度,前期就越是枯燥无味,或者甚至觉得很困难。所以学习算法也是一样的:
-
枯燥无味
- 所以需要系统化学习;
- 小步快跑的方式进行学习;
- 不懂就找答案不要埋头苦学;
-
不牢固
- 越是庞大的知识,越学就会越觉得之前学到的知识忘的差不多了;
- 其实就是缺乏知识的稳固性;
-
预习
- 学习任何一门知识,都要先了解和预习这门知识;
- 同理,在学习一门新的开发语言时,我们都会先来一个
hello world;
-
坚持leetcode刷题
- 要学会算法,并且稳固这一门知识,不断的刻意练习是重中之重;

系统化的效果
系统化学习和拿起一本书最终的效果是不一样的。很多时候我们开始学习一门知识,我们都会看:《xxx深入浅出》、《xxx指南》和《从0到1学会xxx》,其实里面的知识是很庞大的。只靠知识是无法支撑我们的实战和经验的,所以我们需要系统化的学习方法最终达到的目标也是不一样的,例如:
- 提升到职业顶尖水平
- 通过一线互联网大厂的面试
- 要有Leetcode 300+ 刷题量
推荐阅读《Outliner》这本书中的学习方法

精通一个领域
前面说到,任何一个领域的知识都是很庞大的。而且只靠看书,看文章学习都是不够的。所以一套好的学习方法,可以为我们打开一扇大门。而且在打开这扇大门的同时不会因为艰苦、困难、煎熬或者是枯燥而最后放弃。
- 切碎知识点 Chunk it up
- 庖丁解牛
- 脉络相连 - 从根部开始学习,到分支,再到树叶。让每一个知识点都有关联关系
- 刻意练习 Deliberate Practicing
- 反馈 Feedback

数据结构有什么?
-
一维:
-
基础: 数组 array (string),链表 linked list
-
高级:栈 stack,队列 queue, 双端队列 duque,集合 set,映射 map (hash or map),等等
-
二维:
-
基础:树 tree, 图 graph
-
高级:二叉搜索树 binary search tree(红黑树 red-black tree, AVL),堆 heap,并查集 disjoint set,字典树 Trie
-
特殊:
-
位运算 Bitwise,步隆过滤器 BloomFilter
-
LRU Cache (缓存)
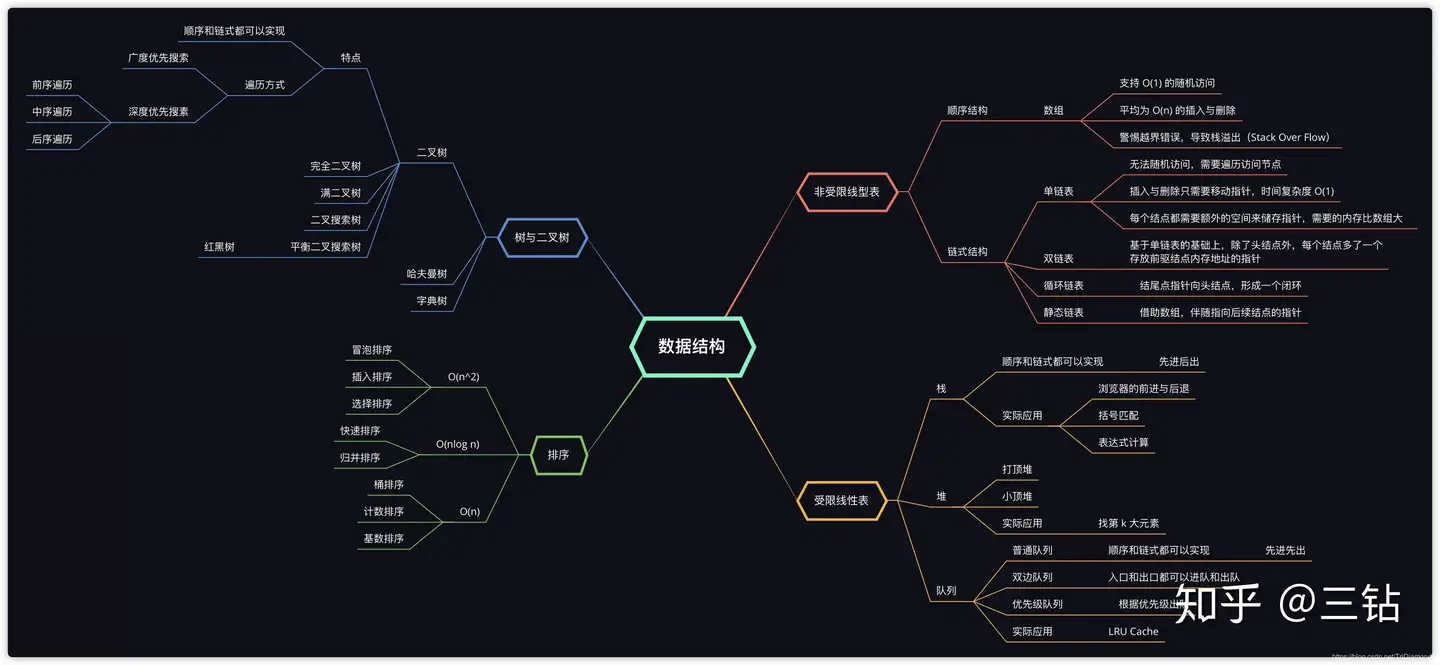
参考:覃超老师的《数据库脑图》

算法有什么?
任何的高级算法与数据结构都会转换成If Else,for循环,其实也是最朴素的计算机的知识,没有什么AI,人工智能的知识。高级算法重点是找到重复单元。
- 跳转语句 (Branch) :If-else,switch
- 循环 (Iteration) :for, which,while loop
- 递归 (Recursion) : Divide & Conquer, Backtrace
- 搜索 (Search) :深度优先搜索 Depth first search,广度优先搜索 Breadth first search,启发式搜索 A*
- 动态规划 (Dynamic Programming)
- 二分查找 (Binary Search)
- 贪心 (Greedy)
- 数学 (Math),几何 (Geometry)
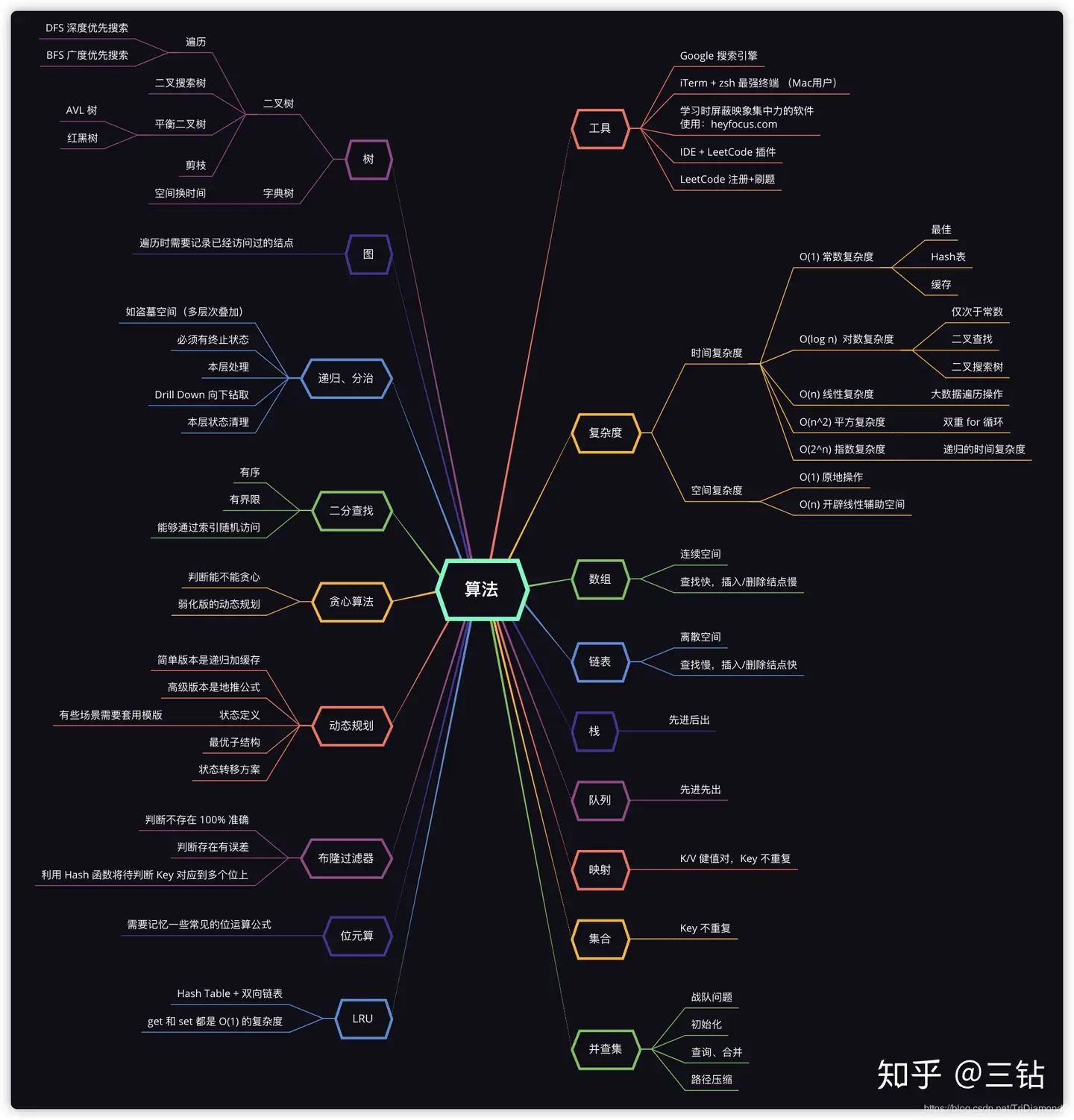
参考:覃超老师的《算法脑图》

刻意练习 - Deliberate practice
无论是科学家、国家运动员、技术专家还是游戏职业选手,他们的优秀的背后都有一个共同点:刻意练习。
什么是刻意练习?
- 刻意练习 - 过遍数,持续多边形的练习,用数遍达到质变!(五毒神掌);
- 练习不擅长的地方;
- 如果感到不舒服、不爽、枯燥的话,那证明我们正在爬坡,正在提升!

反馈 - Feedback
很多时候在学习中,特别是在自学的过程,我们永远不知道自己的学习的成果是怎么样的。或者我们有时候会遇到难点但是无法突破,甚至有时候我们以为自己很努力,或者已经很强了。但是其实还只是坐井观天而已。所以我们在学习的时候需要反馈。所谓的反馈有几种:
- 即时反馈
- 学会使用一门语言;
- 能写出能执行的代码;
- 能写出一个项目;
- 能实现一个功能;
- 主动型反馈
- 高手代码(Github、LeetCode);
- 第一视角止步(看视频,看高手写的代码,学习思路);
- 被动式反馈(高手指点)
- 代码审查 code review;
- 例如:教练看你打,给你反馈;

切题四件套
我个人认为也可以叫解题四大法则:
-
理解题目(Clarification)
- 在LeetCode看题后,先思考,认真确认和理解题目;
- 避免忽略了一些条件或者是误解题目;
- 面试的时候更加应该跟面试官确认清楚题目、条件、场景等;
-
多种解题方案(Possible solutions)
- 对比时间和空间复杂度 compare (time/space)
- 最优解 optimal (加强)
-
多编写(Coding)
- 代码反复练习和编写;
- 每一种解法都反复练习和编写;
-
多测试案例(Test cases)
- 在LeetCode上可以改变测试案例;
- 多测试几种案例,确保自己的代码可以适应各种特殊情况;

刷题方式(五毒神掌)
第一遍
- 5分钟:读题 + 思考;
- 5分钟过后,没有思路就直接看解法;
- 记录多个解题方法,比较解题方法的优弊;
- 尝试默写代码,训练刻意手写代码;
第二遍
- 自己编写,这时候就不要再看题解了;
- LeetCode提交代码,确保能通过;
- 有Bug没有关系,重复debug到通过为止;
- 编写出多种解题方法;
- 持续优化 - 重点是
执行时间(可参考LeetCode中打败了多少的人,也可以点击比较优秀的人,学习更好的写法);
第三遍
- 过了一天后,再重复做题;
- 根据自己不熟悉的题目与程度做专项练习;
- 专项练习就是针对自己不熟悉的种类的题,从而刻意练习哪一种题;
第四遍
- 过了一周后,再反复练习;
第五遍
- 面试前,提前2-3周开始重复练习;

总结
这篇笔记中,我们记录了一下关键知识重点点:
-
如何深入学习一门知识
- 通过系统化学习一门知识;
- 最高效和持续的学习算法就是通过系统化的学习;
- 这里推荐大家,真的想学好一个技术,最好的方法就是找对老师,找对课程,找对人;
-
如何攻破庞大的知识体系变成编程职业高手
- 切碎知识点与建立脉络
- 刻意练习
- 反馈
-
数据结构中有什么? - 看脑图
-
算法中有什么?- 看脑图
-
算法练习方法
- 切题四件套
- 五毒神掌
数据结构与算法概论
数据结构绪论
数据结构是相互之间存在一种或多种特定关系的数据元素的集合。
逻辑结构和物理结构
按照视点的不同,我们把数据结构分为逻辑结构和物理结构。
逻辑结构
逻辑结构是指数据对象中数据元素之间的相互关系。其实这也是我们今后最需要关心的问题。逻辑结构分为以下四种。
(1)集合结构
集合结构中的数据元素除了同属于一个集合外,它们之间没有其他关系。数据结构中的集合关系就类似于数学中的集合。
(2)线性结构
线性结构中的数据元素之间是一对一的关系。
(3)树形结构
树型结构中的数据元素之间存在一种一对多的层次关系。
(4)图形结构
图形结构的数据元素是多对多的关系。
从之前的例子也可以看出,逻辑结构是针对具体问题的,是为了解决某个问题,在对问题理解的基础上,选择一个合适的数据结构表示数据元素之间的逻辑关系。
物理结构
物理结构(存储结构)是指数据的逻辑结构在计算机中的存储形式。
数据的存储结构应正确反映数据元素之间的逻辑关系,这才是最为关键的,如何存储数据元素之间的逻辑关系,是实现物理结构的重点和难点。
数据元素的存储结构形式有两种:顺序存储和链式存储。
(1)顺序存储结构
顺序存储结构是把数据元素存放在地址连续的存储单元里,其数据间的逻辑关系和物理关系是一致的。 典型的顺序存储结构就是数组。
(2)链式存储结构
链式存储结构是把数据元素存放在任意的存储单元里,这组存储单元可以是连续的,也可以是不连续的。数据元素的存储关系并不能反映其逻辑关系,因此需要用一个指针存放数据元素的地址,这样通过地址就可以找到相关联数据元素的位置。
显然链式存储就灵活多了,数据存在哪里不重要,只要有一个指针存放了相应的地址就能找到它了。
数据类型
数据类型是指一组性质相同的值的集合及定义在此集合上的一些操作的总称。
在C语言中,按照取值的不同,数据类型可以分为两类:
- 原子类型:不可再分解的类型,包括整型、实型、字符型等。
- 结构类型:由若干个类型组合而成,是可以再分解的。例如整型数组是由若干整型数据组成的。
抽象是指抽取出事物具有的普遍性的本质。它是抽出问题的特征而忽略非本质的细节,是对具体事物的一个概括。抽象是一种思考问题的方式,它隐藏了繁杂的细节,只保留实现目标所必需的信息。
抽象数据类型(Abstract Data Type,ADT):一个数学模型及定义在该模型上的一组操作。抽象数据类型的定义仅取决于它的一组逻辑特性,而与其在计算机内部如何表示和实现无关。

实际上,抽象数据类型体现了程序设计中问题分解、抽象和信息隐藏的特性。抽象数据类型把实际生活中的问题分解为多个小规模且容易处理的问题,然后建立一个计算机能处理的数据类型,并把每个功能模块的实现细节作为一个独立的单元,从而使具体实现过程隐藏起来。
为了便于在之后的讲解中对抽象数据类型进行规范的描述,我们给出了抽象数据类型的标准格式:
ADT 抽象数据类型名
Data
数据元素之间逻辑关系的定义
Operation
操作1
初始条件
操作结构描述
操作2
...
操作3
...
endADT
算法绪论
算法是解决特定问题求解步骤的描述,在计算机中表现为指令的有限序列,并且每条指令表示一个或多个操作。
算法特性

算法具有五个基本特性:输入、输出、有穷性、确定性和可行性
算法具有零个或多个输入,有一个或多个输出。
有穷性只算法在执行有限的步骤之后,自动结束而不会出现无限循环,并且一个步骤在可接受的时间内完成。
确定性:算法的每一步骤都要具有确定的含义,不会出现二义性。算法在一定条件下,只有一条执行路径,相同的输入只能有唯一的输出结果。算法的每个步骤被精确定义而无歧义。
可行性:算法的每一步都必须是可行的,也就是说,每一步都能够通过执行有限次数完成。可行性意味着算法可以转换为程序上机运行,并得到正确的结果。
算法设计的要求
正确性
算法的正确性是指算法至少应该具有输入、输出和加工处理无歧义性,能正确反映问题得需求,能够得到问题的正确答案。
但是算法得”正确“通常在用法上有很大的差别,大体上分为以下四个层次。
(1)算法程序没有语法错误。
(2)算法程序对于合法的输入数据能够产生满足要求的输出结果。
(3)算法程序对于非法的输入数据能够得出满足规格说明的结果。
(4)算法程序对于精心选择的,甚至刁难的测试数据都有满足要求的输出结果。
一般情况下,我们把层次(3)作为一个算法是否正确的标准。
可读性
算法设计的另一目的是为了便于阅读、理解和交流。
健壮性
当输入数据不合法时,算法也能做出相关处理,而不是产生异常或莫名其妙的结果。
时间效率高和存储量低
设计算法应该尽量满足时间效率高和存储量低的需求。

算法效率的度量方法
事后统计方法
这种方法主要是通过设计好的测试程序和数据,利用计算机计时器对不同算法编写的程序的运行时间进行比较,从而确定算法效率的高低。
这种方法有多种缺陷,我们考虑不予采纳。
事前分析估算方法
事前分析估算方法:在计算机程序编制前,依据统计方法对算法进行统计。
一个程序的运行时间,依赖于算法的好坏和问题的输入规模。所谓问题输入规模是指输入量的多少。
最终,在分析程序的运行时间时,最重要的是把程序看成是独立于程序设计语言的算法或一系列步骤。
函数的渐近增长
函数的渐近增长:给定两个函数f(n)和g(n),如果存在一个整数N,使得对于所有的n>N,f(n)总是比g(n)大,那么我们说f(n)的增长渐近快于g(n)。
判断一个算法的效率时,函数中的常数和其他次要项常常可以忽略,而更应该关注主项(最高阶项)的阶数。

算法时间复杂度
算法时间复杂度定义
在进行算法分析时,语句总的执行次数T(n)是关于问题规模的函数,进而分析T(n)随n的变化情况并确定T(n)的数量级。算法的时间复杂度,也就是算法的时间度量,记作T(n)=O(f(n))。它表示随问题规模n的增大,算法执行时间的增长率和f(n)的增长率相同,称作算法的渐近时间复杂度,简称为时间复杂度。其中f(n)是问题规模n的函数。
这样用大写O()来体现算法时间复杂度的记法,我们称之为大O记法。
一般情况下,随着n的增大,T(n)增长最慢的算法为最优算法。

if ( A > B ) {
for ( i=0; i<N; i++ )
for ( j=N*N; j>i; j-- )
A += B;
}
else {
for ( i=0; i<N*2; i++ )
for ( j=N*2; j>i; j-- )
A += B;
}
这段代码时间复杂度为
推导大O阶方法
(1)用常数1取代运行时间中的所有加法常数。
(2)在修改后的运行次数函数中,只保留最高阶项。
(3)如果最高阶项存在且其系数不是1,则去除与这个项相乘的系数。得到的结果就是大O阶。
常数阶O(1)
不管算法运行次数常数是多少,我们都记作O(1),而不能是O(3)、O(12)等其他任何数字。
线性阶O(n)
要分析算法的复杂度,关键就是要分析循环结构的运行情况。
int i,sum;
sum=0;
for(i=0;i<n;i++)
sum+=i;
对数阶O(logn)
int count=1;
while(count<n)
count=count*2;
平方阶O(n^2)
循环的时间复杂度等于循环体的复杂度乘以该循环运行的次数。
下面这个程序的时间复杂度为O(m*n)
int i,j;
for(i=0;i<m;i++)
{
for(j=0;j<n;j++)
{
/*时间复杂度为O(1)的程序步骤序列*/
}
}
下面这个程序的时间复杂度为O(n^2)
int i,j;
for(i=0;i<n;i++)
{
for(j=i;j<n;j++)
{
/*时间复杂度为O(1)的程序步骤序列*/
}
}
常见的时间复杂度
O(1)<O(logn)<O(n)<O(nlogn)<O(n^2)<O(n^3)<O(2^n)<O(n!)<O(n^n)
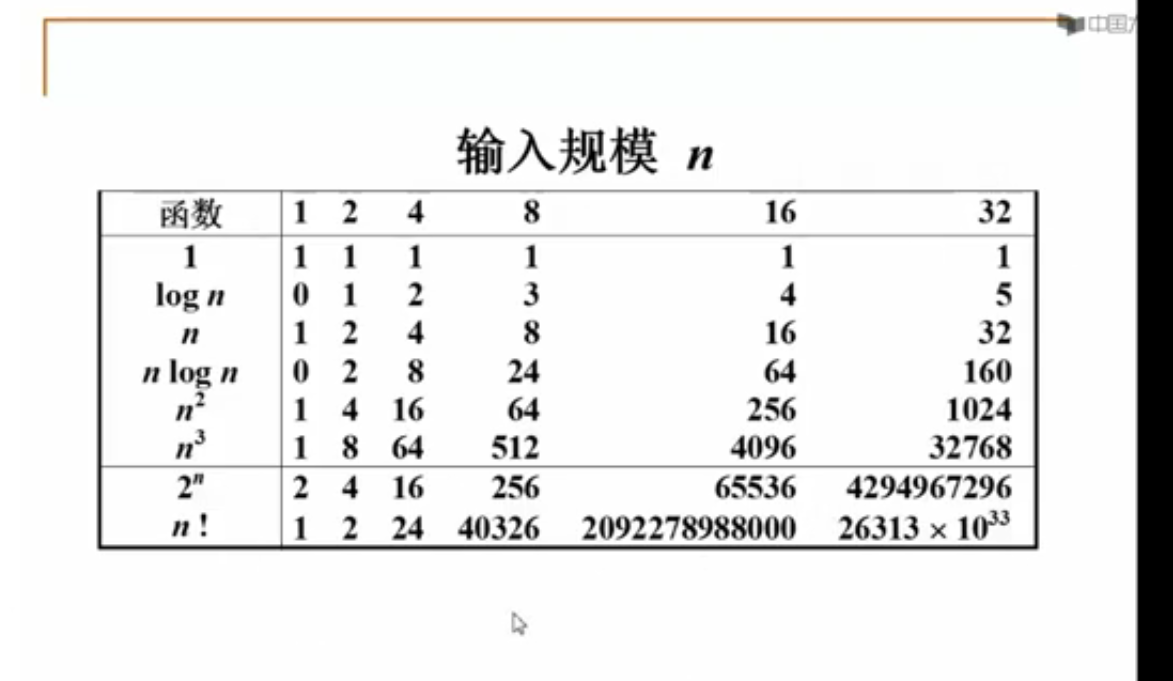
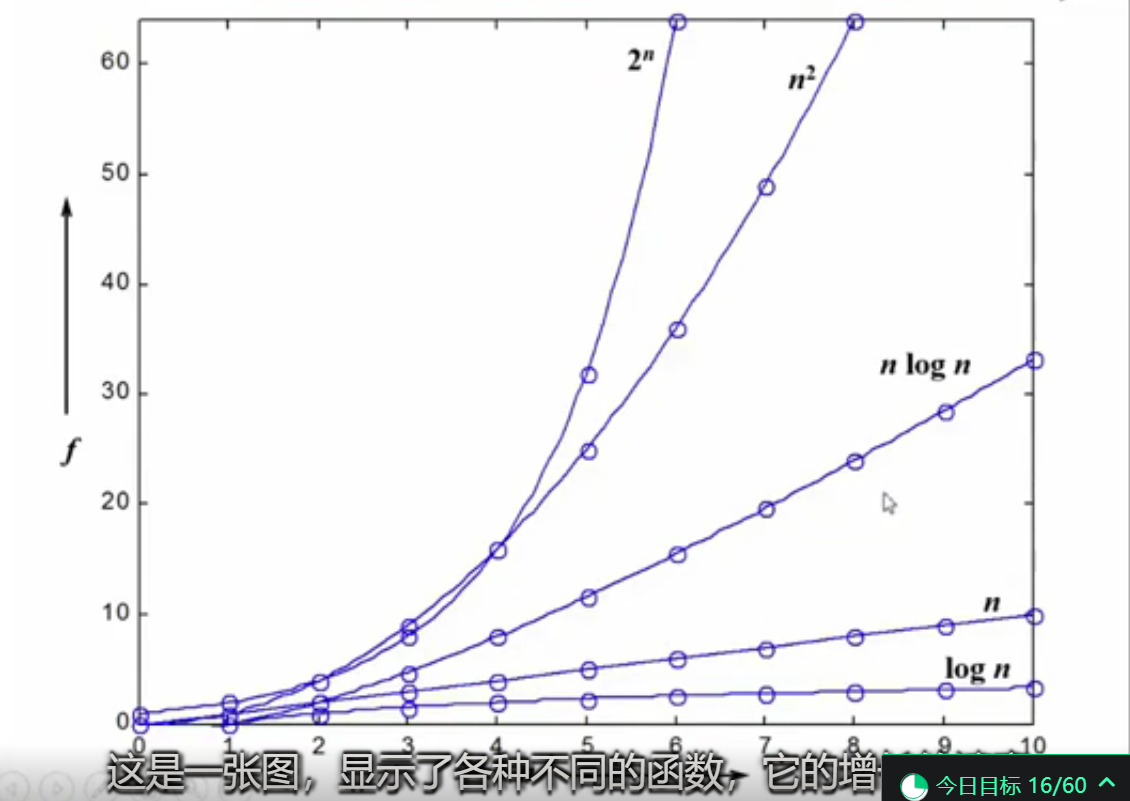
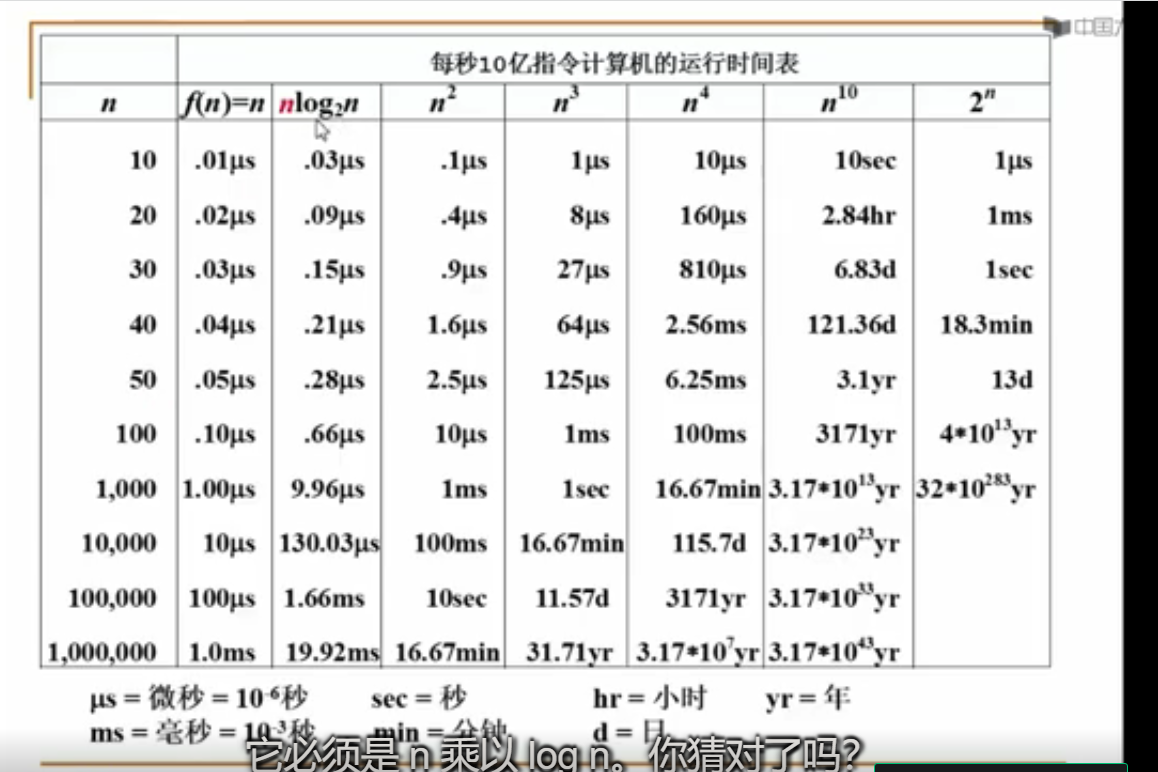
最坏情况和平均情况
平均运行时间是所有情况中最有意义的,因为它是期望的运行时间。也就是说,我们运行一段程序代码时,是希望看到平均运行时间的。可现实中,平均运行时间很难通过分析得到,一般都是通过一定数量的实验数据后估算出来的。
对于算法的分析,一种方法是计算所有情况的平均值,这种时间复杂度的计算方法被称为平均时间复杂度。另一种方法是计算最坏情况下的时间复杂度,这种方法被称为最坏时间复杂度。一般在没有特殊说明的情况下,都是指最坏时间复杂度。
算法空间复杂度
算法的空间复杂度通过计算算法所需的存储空间实现,算法空间复杂度的计算公式记作:S(n)=O(f(n)),其中n为问题的规模,f(n)为语句关于n所占存储空间的函数。
数据结构和算法的联系
由放书问题得出了下面的结论:

打印1-N这N个数的循环写法和递归写法运行结果不同,得出了下面的结论:

计算多项式,普通写法和秦久韶算法有着明显的区别。
计时的基本程序如下:
#include <stdio.h>
#include <time.h>
clock_t start,stop;
//clock_t是clock()函数返回的变量类型
double duration;
//记录被调函数运行时间——以秒为单位
void MyFunction()
{
}
int main()
{
printf("%d\n",CLK_TCK);//本机每秒所走的时钟打点数为1000
start = clock();
MyFunction();
stop = clock();
duration = ((double)(stop-start))/CLK_TCK;
printf("%f\n",duration);
}
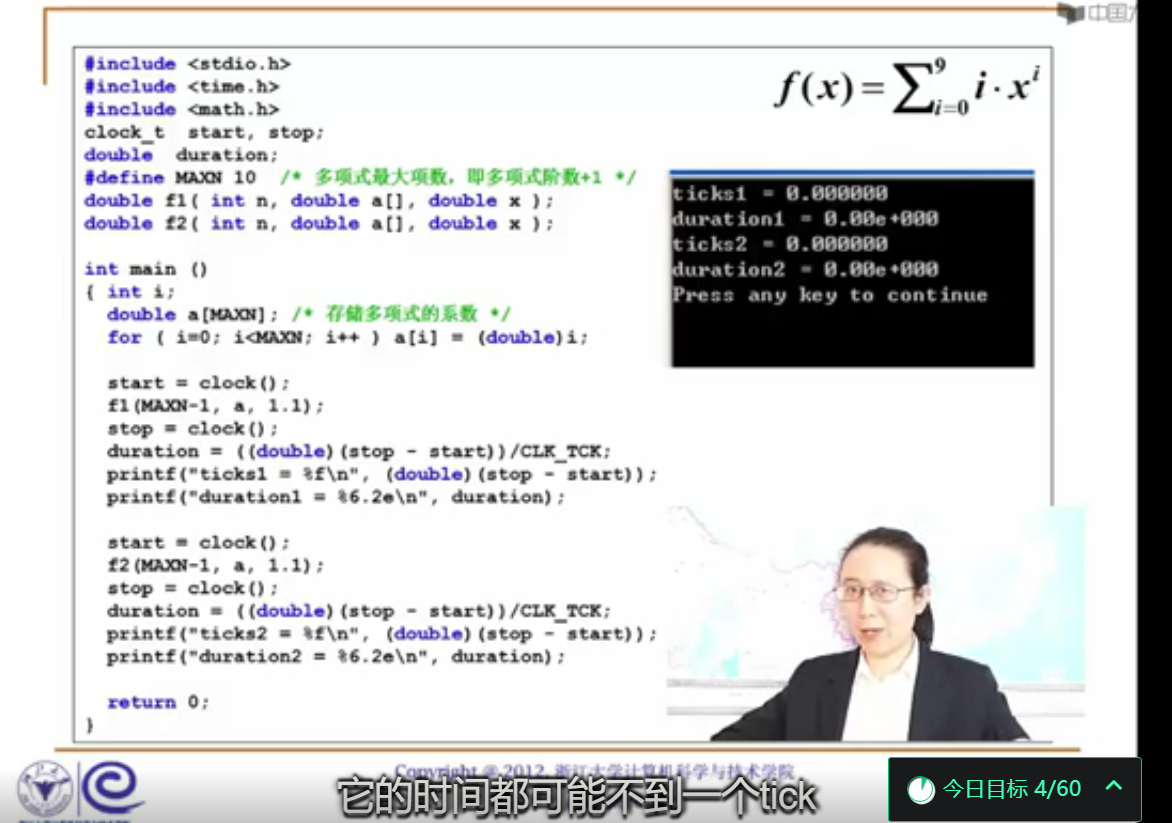
#include <stdio.h>
#include <math.h>
#include <time.h>
clock_t start,stop;
//clock_t是clock()函数返回的变量类型
double duration;
//记录被调函数运行时间——以秒为单位
#define MAXN 10 //多项式最大项数,即多项式阶数+1
double f1(int n,double a[],double x);
double f2(int n,double a[],double x);
int main()
{
int i;
double a[MAXN]; //存储多项式的系数
for(i=0;i<MAXN;i++) a[i] = double(i);
return 0;
}
这个程序第18行为何会报错error: expected expression before 'double'?
double(i)应该写成(double)i。。。。。
此外在C语言中,CLK_TCK 是一个过时的宏定义,代表每秒的时钟计时单元数。在新的标准中,该宏定义已被废弃。可以直接使用 CLOCKS_PER_SEC 来代替 CLK_TCK。
所以,将计算duration的代码修改为以下形式:
duration = ((double)(stop - start))/CLOCKS_PER_SEC;
单次运行代码如下:
#include <stdio.h>
#include <math.h>
#include <time.h>
clock_t start,stop;
//clock_t是clock()函数返回的变量类型
double duration;
//记录被调函数运行时间——以秒为单位
#define MAXN 10 //多项式最大项数,即多项式阶数+1
double f1(int n,double a[],double x);
double f2(int n,double a[],double x);
int main()
{
int i;
double a[MAXN]; //存储多项式的系数
for(i=0;i<MAXN;i++)
a[i] = (double)i;
start = clock();
f1(MAXN,a,1.1);
stop = clock();
//duration = ((double)(stop-start))/CLK_TCK;
duration = ((double)(stop - start))/CLOCKS_PER_SEC;
printf("ticks1 = %f\n",(double)(stop - start));
printf("duration1 = %6.2e\n", duration);
start = clock();
f2(MAXN,a,1.1);
stop = clock();
duration = ((double)(stop - start))/CLOCKS_PER_SEC;
//duration = ((double)(stop-start))/CLK_TCK;
printf("ticks1 = %f\n",(double)(stop - start));
printf("duration1 = %6.2e\n", duration);
return 0;
}
double f1(int n,double a[], double x)
{
int i;
double p = a[0];
for(i=1;i<=n;i++)
p+=(a[i]*pow(x,i));
return p;
}
double f2(int n,double a[], double x)
{
int i;
double p = a[n];
for(i=n;i>0;i--)
p+=(a[i-1]+x*p);
return p;
}
ticks1 = 0.000000
duration1 = 0.00e+000
ticks1 = 0.000000
duration1 = 0.00e+000
多项式阶数太低,两个程序运行时间都不到一个tick,几乎没有差别。
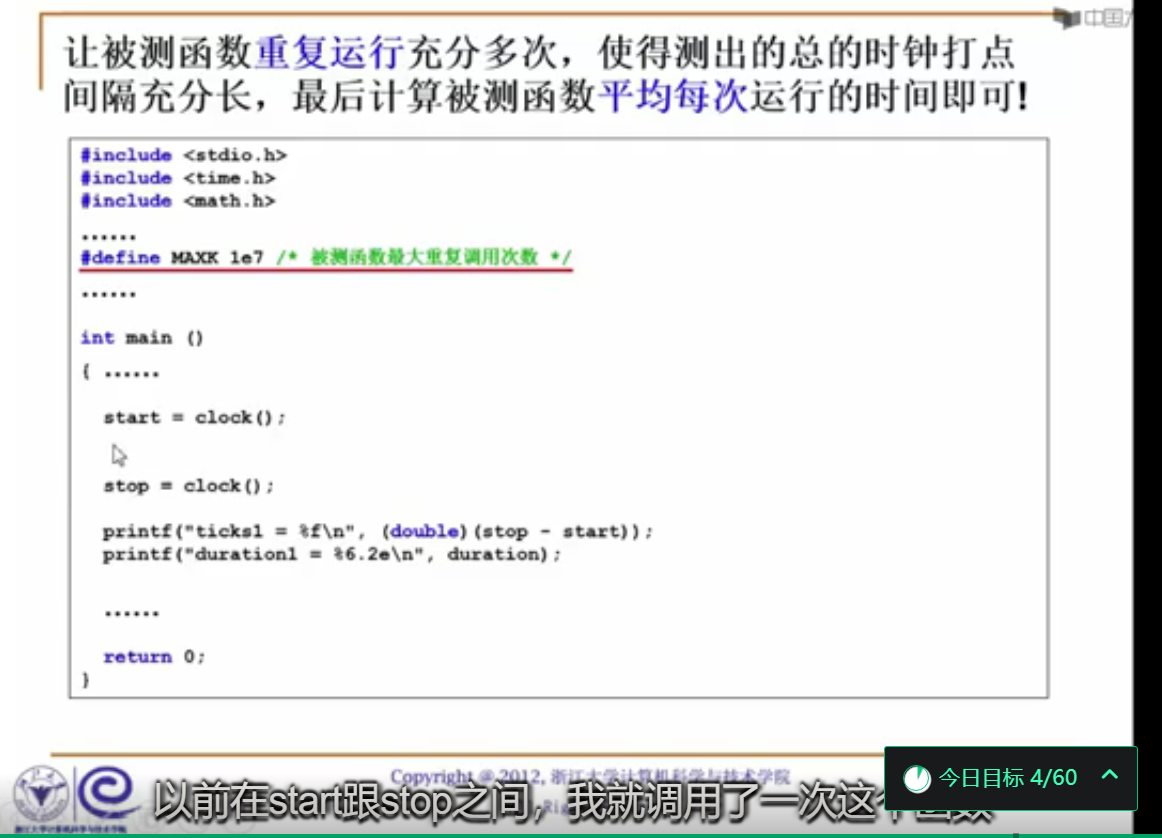
多次重复运行代码如下:
#include <stdio.h>
#include <math.h>
#include <time.h>
clock_t start,stop;
//clock_t是clock()函数返回的变量类型
double duration;
//记录被调函数运行时间——以秒为单位
#define MAXN 10 //多项式最大项数,即多项式阶数+1
#define MAXK 1e7 //被测函数最大重复调用次数
double f1(int n,double a[],double x);
double f2(int n,double a[],double x);
int main()
{
int i;
double a[MAXN]; //存储多项式的系数
for(i=0;i<MAXN;i++)
a[i] = (double)i;
start = clock();
for(i=1;i<MAXK;i++) //重复调用函数以获得充分多的时钟打点数
f1(MAXN,a,1.1);
stop = clock();
//duration = ((double)(stop-start))/CLK_TCK;
duration = ((double)(stop - start))/CLOCKS_PER_SEC/MAXK; //计算函数单次运行的时间
printf("ticks1 = %f\n",(double)(stop - start));
printf("duration1 = %6.2e\n", duration);
start = clock();
for(i=1;i<MAXK;i++) //重复调用函数以获得充分多的时钟打点数
f2(MAXN,a,1.1);
stop = clock();
//duration = ((double)(stop-start))/CLK_TCK;
duration = ((double)(stop - start))/CLOCKS_PER_SEC/MAXK; //计算函数单次运行的时间
printf("ticks1 = %f\n",(double)(stop - start));
printf("duration1 = %6.2e\n", duration);
return 0;
}
double f1(int n,double a[], double x)
{
int i;
double p = a[0];
for(i=1;i<=n;i++)
p+=(a[i]*pow(x,i));
return p;
}
double f2(int n,double a[], double x)
{
int i;
double p = a[n];
for(i=n;i>0;i--)
p+=(a[i-1]+x*p);
return p;
}
ticks1 = 2092.000000
duration1 = 2.09e-007
ticks1 = 443.000000
duration1 = 4.43e-008
两个程序运行时间差了一个数量级!由此可见:

主定理
MOOC-PTA复杂度题目
PTA 01-复杂度1 最大子列和问题
给定K个整数组成的序列{ N1, N2, ..., NK },“连续子列”被定义为{ Ni, Ni+1, ..., Nj },其中 1≤i≤j≤K。“最大子列和”则被定义为所有连续子列元素的和中最大者。例如给定序列{ -2, 11, -4, 13, -5, -2 },其连续子列{ 11, -4, 13 }有最大的和20。现要求你编写程序,计算给定整数序列的最大子列和。
本题旨在测试各种不同的算法在各种数据情况下的表现。各组测试数据特点如下:
- 数据1:与样例等价,测试基本正确性;
- 数据2:102个随机整数;
- 数据3:103个随机整数;
- 数据4:104个随机整数;
- 数据5:105个随机整数;
输入格式:
输入第1行给出正整数K (≤100000);第2行给出K个整数,其间以空格分隔。
输出格式:
在一行中输出最大子列和。如果序列中所有整数皆为负数,则输出0。
输入样例:
6
-2 11 -4 13 -5 -2
输出样例:
20
三重循环求解

#include <stdio.h>
int MaxSubSeq(int A[], int N)
{
int ThisSum = 0,MaxSum = 0;
for(int i=0;i < N;i++)
{
for(int j = i;j < N;j++)
{
ThisSum = 0;
for(int k=i;k<=j;k++)
ThisSum += A[k];
if(ThisSum>MaxSum)
MaxSum = ThisSum;
}
}
return MaxSum;
}
int main()
{
int arr[100];
int n;
scanf("%d",&n);
for(int i=0;i<n;i++)
scanf("%d",&arr[i]);
printf("%d",MaxSubSeq(arr,n));
return 0;
}
二重循环求解

#include <stdio.h>
int MaxSubSeq(int A[], int N)
{
int ThisSum = 0,MaxSum = 0;
for(int i=0;i < N;i++)
{
ThisSum = 0;
for(int j = i;j < N;j++)
{
ThisSum += A[j];
if(ThisSum>MaxSum)
MaxSum = ThisSum;
}
}
return MaxSum;
}
int main()
{
int arr[100];
int n;
scanf("%d",&n);
for(int i=0;i<n;i++)
scanf("%d",&arr[i]);
printf("%d",MaxSubSeq(arr,n));
return 0;
}
分治算法
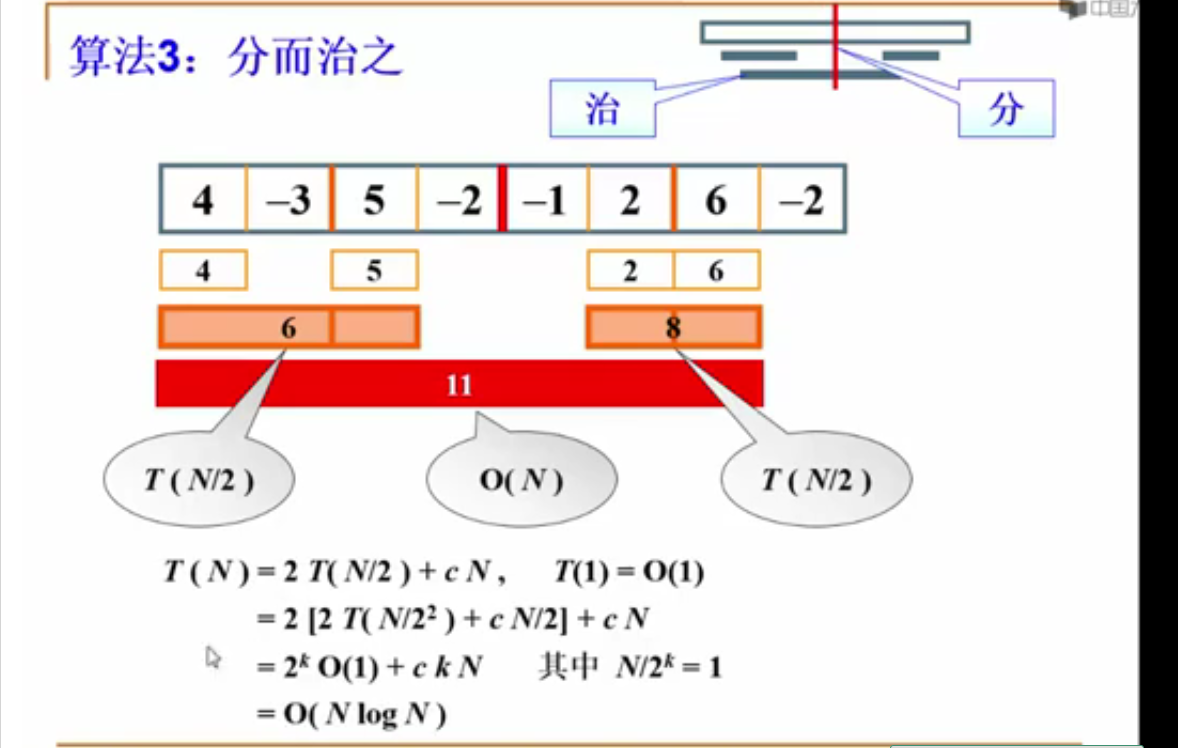
#include <stdio.h>
int Max3( int A, int B, int C )
{ /* 返回3个整数中的最大值 */
return A > B ? A > C ? A : C : B > C ? B : C;
}
int DivideAndConquer( int List[], int left, int right )
{ /* 分治法求List[left]到List[right]的最大子列和 */
int MaxLeftSum, MaxRightSum; /* 存放左右子问题的解 */
int MaxLeftBorderSum, MaxRightBorderSum; /*存放跨分界线的结果*/
int LeftBorderSum, RightBorderSum;
int center, i;
if( left == right ) { /* 递归的终止条件,子列只有1个数字 */
if( List[left] > 0 ) return List[left];
else return 0;
}
/* 下面是"分"的过程 */
center = ( left + right ) / 2; /* 找到中分点 */
/* 递归求得两边子列的最大和 */
MaxLeftSum = DivideAndConquer( List, left, center );
MaxRightSum = DivideAndConquer( List, center+1, right );
/* 下面求跨分界线的最大子列和 */
MaxLeftBorderSum = 0; LeftBorderSum = 0;
for( i=center; i>=left; i-- ) { /* 从中线向左扫描 */
LeftBorderSum += List[i];
if( LeftBorderSum > MaxLeftBorderSum )
MaxLeftBorderSum = LeftBorderSum;
} /* 左边扫描结束 */
MaxRightBorderSum = 0; RightBorderSum = 0;
for( i=center+1; i<=right; i++ ) { /* 从中线向右扫描 */
RightBorderSum += List[i];
if( RightBorderSum > MaxRightBorderSum )
MaxRightBorderSum = RightBorderSum;
} /* 右边扫描结束 */
/* 下面返回"治"的结果 */
return Max3( MaxLeftSum, MaxRightSum, MaxLeftBorderSum + MaxRightBorderSum );
}
int MaxSubseqSum3( int List[], int N )
{ /* 保持与前2种算法相同的函数接口 */
return DivideAndConquer( List, 0, N-1 );
}
int main()
{
int arr[100];
int n;
scanf("%d",&n);
for(int i=0;i<n;i++)
scanf("%d",&arr[i]);
printf("%d",MaxSubseqSum3(arr,n));
return 0;
}
在线处理(动态规划)

#include <stdio.h>
int MaxSubSeq(int A[], int N)
{
int i;
int ThisSum,MaxSum;
ThisSum = 0,MaxSum = 0;
for(i=0;i < N;i++)
{
ThisSum += A[i];
if(ThisSum > MaxSum)
MaxSum = ThisSum;
else if(ThisSum < 0)
ThisSum = 0;
}
return MaxSum;
}
int main()
{
int arr[100];
int n;
scanf("%d",&n);
for(int i=0;i<n;i++)
scanf("%d",&arr[i]);
printf("%d",MaxSubSeq(arr,n));
return 0;
}
PTA 01-复杂度2 Maximum Subsequence Sum
Given a sequence of K integers { N1, N2, ..., NK }. A continuous subsequence is defined to be { Ni, Ni+1, ..., Nj } where 1≤i≤j≤K. The Maximum Subsequence is the continuous subsequence which has the largest sum of its elements. For example, given sequence { -2, 11, -4, 13, -5, -2 }, its maximum subsequence is { 11, -4, 13 } with the largest sum being 20.
Now you are supposed to find the largest sum, together with the first and the last numbers of the maximum subsequence.
Input Specification:
Each input file contains one test case. Each case occupies two lines. The first line contains a positive integer K (≤10000). The second line contains K numbers, separated by a space.
Output Specification:
For each test case, output in one line the largest sum, together with the first and the last numbers of the maximum subsequence. The numbers must be separated by one space, but there must be no extra space at the end of a line. In case that the maximum subsequence is not unique, output the one with the smallest indices i and j (as shown by the sample case). If all the K numbers are negative, then its maximum sum is defined to be 0, and you are supposed to output the first and the last numbers of the whole sequence.
Sample Input:
10
-10 1 2 3 4 -5 -23 3 7 -21
Sample Output:
10 1 4
注意:这里需特别注意输出部分,因为题目中说“If all the K numbers are negative, then its maximum sum is defined to be 0, and you are supposed to output the first and the last numbers of the whole sequence.”(当输入的这K个数全为负时,输出的最大子列和应为0,并输出整个输入序列的首尾两个数)。那就需要对应MaxSum >= 0和MaxSum < 0的情况,之所以要把 = 0的情况放到前者,是因为 = 0可能是输入序列中有0有负的结果,比如输入6个数-2,0,-1,0,0,0。那最大子列和也是0但是显然不应输出题意要求的全为负情况下的首末两个数(-2和0)而是输出正常比较后的0和0(对应下标都为1)。
这也涉及到和前一题不同的MaxSum初值问题,因为输入全为负的情况下,累加时ThisSum不断重置为0,MaxSum保持不变,最后直接进入输出的else情况,符合题意。
6
-2 0 -1 0 0 0
ThisSum=0, MaxSum=-1, MaxIndex=0, MinIndex=0, tmpMinIndex=1
ThisSum=0, MaxSum=0, MaxIndex=1, MinIndex=1, tmpMinIndex=1
ThisSum=0, MaxSum=0, MaxIndex=1, MinIndex=1, tmpMinIndex=3
ThisSum=0, MaxSum=0, MaxIndex=1, MinIndex=1, tmpMinIndex=3
ThisSum=0, MaxSum=0, MaxIndex=1, MinIndex=1, tmpMinIndex=3
ThisSum=0, MaxSum=0, MaxIndex=1, MinIndex=1, tmpMinIndex=3
0 0 0
#include <stdio.h>
void MaxSubSumWithIndex(int List[], int K)
{
int i;
int MaxIndex = 0, MinIndex = 0, tmpMinIndex = 0;
int ThisSum = 0, MaxSum = -1; //这里MaxSum不能改成0
for(i = 0; i < K; i++)
{
ThisSum += List[i];
if (ThisSum > MaxSum)
{
MaxSum = ThisSum;
MaxIndex = i;
MinIndex = tmpMinIndex;
}else if(ThisSum < 0)
{
ThisSum = 0;
tmpMinIndex = i + 1;
}
printf("ThisSum=%d, MaxSum=%d, MaxIndex=%d, MinIndex=%d, tmpMinIndex=%d\n",ThisSum, MaxSum, MaxIndex, MinIndex, tmpMinIndex);
}
if(MaxSum >= 0)
printf("%d %d %d\n", MaxSum, List[MinIndex], List[MaxIndex]);
else
printf("0 %d %d\n", List[0], List[K - 1]);
}
int main()
{
int n;
scanf("%d",&n);
int arr[n];
for(int i = 0; i<n; i++)
scanf("%d",&arr[i]);
MaxSubSumWithIndex(arr, n);
return 0;
}
PTA 01-复杂度3 二分查找
本题要求实现二分查找算法。
函数接口定义:
Position BinarySearch( List L, ElementType X );
其中List结构定义如下:
typedef int Position;
typedef struct LNode *List;
struct LNode {
ElementType Data[MAXSIZE];
Position Last; /* 保存线性表中最后一个元素的位置 */
};
L是用户传入的一个线性表,其中ElementType元素可以通过>、==、<进行比较,并且题目保证传入的数据是递增有序的。函数BinarySearch要查找X在Data中的位置,即数组下标(注意:元素从下标1开始存储)。找到则返回下标,否则返回一个特殊的失败标记NotFound。
裁判测试程序样例:
#include <stdio.h>
#include <stdlib.h>
#define MAXSIZE 10
#define NotFound 0
typedef int ElementType;
typedef int Position;
typedef struct LNode *List;
struct LNode {
ElementType Data[MAXSIZE];
Position Last; /* 保存线性表中最后一个元素的位置 */
};
List ReadInput(); /* 裁判实现,细节不表。元素从下标1开始存储 */
Position BinarySearch( List L, ElementType X );
int main()
{
List L;
ElementType X;
Position P;
L = ReadInput();
scanf("%d", &X);
P = BinarySearch( L, X );
printf("%d\n", P);
return 0;
}
/* 你的代码将被嵌在这里 */
\输入样例1:
5
12 31 55 89 101
31
输出样例1:
2
输入样例2:
3
26 78 233
31
输出样例2:
0
Position BinarySearch( List L, ElementType X )
{
Position left = 1;
Position right = L->Last;
Position mid;
while(left <= right)
{
mid = (left + right) / 2;
if(L->Data[mid] < X)
left = mid + 1;
else if(L->Data[mid] > X)
right = mid - 1;
else
return mid;
}
return NotFound;
}
线性结构
线性结构主要包括线性表、栈和队列。
线性表可以分成由数组实现的顺序表和由指针实现的链式表。
- 线性表: 逻辑结构, 就是对外暴露数据之间的关系,不关心底层如何实现,数据结构的逻辑结构大分类就是线性结构和非线性结构而顺序表、链表都是一种线性表。
- 顺序表、链表: 物理结构,他是实现一个结构实际物理地址上的结构。比如顺序表就是用数组实现。而链表用指针完成主要工作。不同的结构在不同的场景有不同的区别。
链表
单链表功能实现详细版
创建、插入、删除
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
typedef int ElementType;
typedef struct Node
{
ElementType Data;
struct Node *Next;
}NODE,*LIST,*LPNODE;
LIST createHead();
LPNODE createNode(ElementType X);
void insertByHead(LIST headNode, ElementType X);
void insertByBack(LIST headNode, ElementType X);
void insertByAppoin(LIST headNode, ElementType X, int posData);
void deleteByHead(LIST headNode);
void deleteByBack(LIST headNode);
void deleteByAppoin(LIST headNode, int posData);
void printList(LIST headNode);
void freeList(LIST* headNode);
LIST createHead()
{
LIST headNode = (LIST)malloc(sizeof(struct Node));
assert(headNode);
headNode->Next = NULL;
return headNode;
}
LPNODE createNode(ElementType X)
{
LPNODE newNode = (LPNODE)malloc(sizeof(NODE));
assert(newNode);
newNode->Data = X;
newNode->Next = NULL;
return newNode;
}
void InsertByHead(LIST headNode, ElementType X)
{
LPNODE newNode = createNode(X);
newNode->Next = headNode->Next;
headNode->Next = newNode;
}
void insertByBack(LIST headNode, ElementType X)
{
LPNODE pMove = headNode;
while(pMove->Next)
pMove = pMove->Next;
LPNODE newNode = createNode(X);
pMove->Next = newNode;
}
void insertByAppoin(LIST headNode, ElementType X, int posData)
{
LPNODE posLeftNode = headNode;
LPNODE posNode = headNode->Next;
while(posNode != NULL && posData != posNode->Data)
{
posLeftNode = posNode;
posNode = posNode->Next;
}
if(!posNode)
printf("未找到,无法做指定数据所在的位置插入!\n");
else
{
LPNODE newNode = createNode(X);
newNode->Next = posNode;
posLeftNode->Next = newNode;
//这里可以不考虑顺序
}
}
void deleteByHead(LIST headNode)
{
LPNODE temp = headNode->Next;
if(!temp)
printf("链表为空,无法删除!\n");
else
{
headNode->Next = temp->Next;
free(temp);
}
}
void deleteByBack(LIST headNode)
{
LPNODE pTailLeft = headNode;
LPNODE pTail = headNode->Next;
while(pTail != NULL && pTail->Next != NULL)
{
pTailLeft = pTail;
pTail = pTail->Next;
}
if(pTail == NULL)
printf("链表为空,无法删除!\n");
else
{
free(pTail);
pTailLeft->Next = NULL;
}
}
void deleteByAppoin(LIST headNode, int posData)
{
LPNODE posLeftNode = headNode;
LPNODE posNode = headNode->Next;
while(posNode && posNode->Data != posData)
{
posLeftNode = posNode;
posNode = posNode->Next;
}
if(!posNode)
printf("无法删除指定数据!\n");
else
{
posLeftNode->Next = posNode->Next;
free(posNode);
posNode = NULL;
}
}
void printList(LIST headNode)
{
if(headNode == NULL)
{
printf("无法打印链表,链表为空!\n");
return;
}
LPNODE pMove = headNode->Next;
while(pMove != NULL)
{
printf("%d ",pMove->Data);
pMove = pMove->Next;
}
printf("\n");
}
void freeList(LIST* headNode)
{
if(headNode == NULL) //写成if((*headNode) == NULL)也行
return;
LPNODE nextNode = NULL;
while((*headNode) != NULL)
{
nextNode = (*headNode)->Next;
free(*headNode);
*headNode = nextNode;
}
}
int main()
{
LIST list = createHead();
InsertByHead(list,1);
InsertByHead(list,2);
InsertByHead(list,3);
InsertByHead(list,4);
InsertByHead(list,5);
printList(list);
insertByBack(list,5);
insertByBack(list,4);
insertByBack(list,3);
printList(list);
insertByAppoin(list,6,2);
insertByAppoin(list,7,2);
printList(list);
deleteByHead(list);
deleteByBack(list);
deleteByAppoin(list,2);
printList(list);
freeList(&list);
printList(list);
return 0;
}
5 4 3 2 1
5 4 3 2 1 5 4 3
5 4 3 6 7 2 1 5 4 3
4 3 6 7 1 5 4
无法打印链表,链表为空!
合并、反转
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
typedef int ElementType;
typedef struct Node
{
ElementType Data;
struct Node *Next;
}NODE,*LIST,*LPNODE;
LIST createHead();
LPNODE createNode(ElementType X);
void insertByHead(LIST headNode, ElementType X);
void insertByBack(LIST headNode, ElementType X);
void printList(LIST headNode);
LIST createHead()
{
LIST headNode = (LIST)malloc(sizeof(struct Node));
assert(headNode);
headNode->Next = NULL;
return headNode;
}
LPNODE createNode(ElementType X)
{
LPNODE newNode = (LPNODE)malloc(sizeof(NODE));
assert(newNode);
newNode->Data = X;
newNode->Next = NULL;
return newNode;
}
void InsertByHead(LIST headNode, ElementType X)
{
LPNODE newNode = createNode(X);
newNode->Next = headNode->Next;
headNode->Next = newNode;
}
void insertByBack(LIST headNode, ElementType X)
{
LPNODE pMove = headNode;
while(pMove->Next)
pMove = pMove->Next;
LPNODE newNode = createNode(X);
pMove->Next = newNode;
}
void printList(LIST headNode)
{
if(headNode == NULL)
{
printf("无法打印链表,链表为空!\n");
return;
}
LPNODE pMove = headNode->Next;
while(pMove != NULL)
{
printf("%d ",pMove->Data);
pMove = pMove->Next;
}
printf("\n");
}
void freeList(LIST* headNode)
{
if(headNode == NULL) //写成if((*headNode) == NULL)也行
return;
LPNODE nextNode = NULL;
while((*headNode) != NULL)
{
nextNode = (*headNode)->Next;
free(*headNode);
*headNode = nextNode;
}
}
LIST listCat(LIST list1, LIST list2) //把list2加到list1的末尾。
{
if(list1->Next == NULL || list2->Next == NULL)
return (list1->Next == NULL) ? list2 : list1;
LPNODE pMove = list1;
while(pMove->Next)
{
pMove = pMove->Next;
}
pMove->Next = list2->Next;
return list1;
}
LIST listCatByBack(LIST list1, LIST list2) //把list2加到list1的末尾。这里使用尾插法
{
LPNODE pMove = list2->Next;
while(pMove != NULL)
{
insertByBack(list1,pMove->Data);
pMove = pMove->Next;
}
return list1;
}
LIST listCatByValue(LIST list1, LIST list2)
{
LIST list3 = createHead();
LPNODE pFirst = list1->Next;
while(pFirst)
{
LPNODE pSecond = list2->Next;
while(pSecond)
{
if(pFirst->Data == pSecond->Data)
{
insertByBack(list3,pFirst->Data);
break;
}
pSecond = pSecond->Next;
}
pFirst = pFirst->Next;
}
return list3;
}
void ListReverseFirst(LIST* list)
{
LIST new_list = createHead();
LPNODE pMove = (*list)->Next;
while(pMove)
{
InsertByHead(new_list, pMove->Data);
pMove = pMove->Next;
}
freeList(list);
*list = new_list;
}
LIST ListReverse1(LIST list)
{
LIST new_list = createHead();
LPNODE pMove = list->Next;
while(pMove)
{
InsertByHead(new_list, pMove->Data);
pMove = pMove->Next;
}
return new_list;
}
void ListReverse2(LIST list)
{
LPNODE pre = NULL;
LPNODE cur = list->Next;
LPNODE nextNode = list->Next;
while(cur)
{
//先存储下一个,再反转
nextNode = cur->Next;
cur->Next = pre;
pre = cur;
cur = nextNode;
}
list->Next = pre;
}
int main()
{
LIST list1 = createHead();
InsertByHead(list1,4);
InsertByHead(list1,2);
InsertByHead(list1,1);
printList(list1);
LIST list2 =createHead();
InsertByHead(list2,4);
InsertByHead(list2,2);
printList(list2);
//LIST list3 = listCat(list1,list2);
//printList(list3);
//ListReverseFirst(&list1);
//printList(list1);
ListReverse2(list1);
printList(list1);
return 0;
}
1 2 4
2 4
4 2 1
有序链表
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
typedef int ElementType;
typedef struct Node
{
ElementType Data;
struct Node *Next;
}NODE,*LIST,*LPNODE;
LIST createHead()
{
LIST headNode = (LIST)malloc(sizeof(struct Node));
assert(headNode);
headNode->Next = NULL;
return headNode;
}
LPNODE createNode(ElementType X)
{
LPNODE newNode = (LPNODE)malloc(sizeof(NODE));
assert(newNode);
newNode->Data = X;
newNode->Next = NULL;
return newNode;
}
void InsertBySort(LIST headNode, ElementType X)
{
LPNODE newNode = createNode(X);
LPNODE preNode = headNode;
LPNODE posNode = headNode->Next;
while(posNode != NULL && posNode->Data < X)
{
preNode = posNode;
posNode = posNode->Next;
}
if(posNode == NULL)
{
preNode->Next = newNode;
}
else
{
preNode->Next = newNode;
newNode->Next = posNode;
}
}
void printList(LIST headNode)
{
if(headNode == NULL)
{
printf("无法打印链表,链表为空!\n");
return;
}
LPNODE pMove = headNode->Next;
while(pMove != NULL)
{
printf("%d ",pMove->Data);
pMove = pMove->Next;
}
printf("\n");
}
int main()
{
LIST list3 = createHead();
InsertBySort(list3,4);
InsertBySort(list3,5);
InsertBySort(list3,1);
InsertBySort(list3,40);
InsertBySort(list3,53);
InsertBySort(list3,12);
InsertBySort(list3,49);
InsertBySort(list3,25);
InsertBySort(list3,19);
printList(list3);
return 0;
}
1 2 4
2 4
1 4 5 12 19 25 40 49 53
无头单链表
核心在于表头的处理,插入操作需要使用二级指针来修改头指针。要考虑链表为空的状态。
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
typedef int ElementType;
struct Node
{
ElementType Data;
struct Node *Next;
};
struct Node* createNode(ElementType X)
{
struct Node* newNode = (struct Node*)malloc(sizeof(struct Node));
assert(newNode);
newNode->Data = X;
newNode->Next = NULL;
return newNode;
}
void InsertByHead(struct Node** headNode, ElementType X)
{
struct Node* newNode = createNode(X);
newNode->Next = *headNode;
*headNode = newNode;
}
void InsertByBack(struct Node** headNode, ElementType X)
{
if(headNode == NULL)
{
InsertByHead(headNode,X);
}
else
{
struct Node* pMove = *headNode;
while(pMove->Next)
{
pMove = pMove->Next;
}
struct Node* newNode = createNode(X);
pMove->Next = newNode;
}
}
void printList(struct Node* headNode)
{
struct Node* pMove = headNode;
while(pMove != NULL)
{
printf("%d ",pMove->Data);
pMove = pMove->Next;
}
printf("\n");
}
int main()
{
struct Node* list3 = NULL;
InsertByHead(&list3,4);
InsertByHead(&list3,5);
InsertByHead(&list3,1);
InsertByHead(&list3,40);
printList(list3);
printf("\n");
InsertByBack(&list3,53);
InsertByBack(&list3,12);
InsertByBack(&list3,49);
InsertByBack(&list3,25);
InsertByBack(&list3,19);
printList(list3);
return 0;
}
40 1 5 4
40 1 5 4 53 12 49 25 19
双向链表
普通双向链表
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
typedef struct Node *LPNODE;
typedef int ElementType;
struct Node
{
LPNODE prev;
LPNODE next;
ElementType data;
};
LPNODE createNode(ElementType data)
{
LPNODE newNode = (LPNODE)malloc((sizeof(struct Node)));
assert(newNode);
newNode->prev = NULL;
newNode->next = NULL;
newNode->data = data;
return newNode;
}
//再封装的方式描述链表特性
struct List
{
LPNODE firstNode;
LPNODE lastNode;
int listSize;
};
//创建链表,描述链表的初始状态
struct List* creatList()
{
struct List* list = (struct List*)malloc(sizeof(struct List));
//assert(list);
//这里也可以写成if语句形式
if(list == NULL)
return NULL;
list->firstNode = NULL;
list->lastNode = NULL;
list->listSize = 0;
return list;
}
//表头插入
void InsertByHead(struct List* list, ElementType data)
{
LPNODE newNode = createNode(data);
if(list->listSize == 0)
{
//第一次插入
list->firstNode = newNode;
list->lastNode = newNode;
list->listSize++;
}
else
{
newNode->next = list->firstNode;
list->firstNode->prev = newNode;
list->firstNode = newNode;
list->listSize++;
}
}
void printListByHead(struct List* list)
{
LPNODE pMove = list->firstNode;
while(pMove)
{
printf("%d\t",pMove->data);
pMove = pMove->next;
}
printf("\n");
}
void printListByRear(struct List* list)
{
LPNODE pMove = list->lastNode;
while(pMove)
{
printf("%d\t",pMove->data);
pMove = pMove->prev;
}
printf("\n");
}
int main()
{
struct List* list = creatList();
for(int i=0; i<5; i++)
InsertByHead(list, i);
printListByHead(list);
printListByRear(list);
}
4 3 2 1 0
0 1 2 3 4
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
typedef struct Node *LPNODE;
typedef int ElementType;
struct Node
{
LPNODE prev;
LPNODE next;
ElementType data;
};
LPNODE createNode(ElementType data)
{
LPNODE newNode = (LPNODE)malloc((sizeof(struct Node)));
assert(newNode);
newNode->prev = NULL;
newNode->next = NULL;
newNode->data = data;
return newNode;
}
//再封装的方式描述链表特性
struct List
{
LPNODE firstNode;
LPNODE lastNode;
int listSize;
};
//创建链表,描述链表的初始状态
struct List* creatList()
{
struct List* list = (struct List*)malloc(sizeof(struct List));
//assert(list);
//这里也可以写成if语句形式
if(list == NULL)
return NULL;
list->firstNode = NULL;
list->lastNode = NULL;
list->listSize = 0;
return list;
}
//表头插入
void InsertByHead(struct List* list, ElementType data)
{
LPNODE newNode = createNode(data);
if(list->listSize == 0)
{
list->firstNode = newNode;
list->lastNode = newNode;
list->listSize++;
}
else
{
newNode->next = list->firstNode;
list->firstNode->prev = newNode;
list->firstNode = newNode;
list->listSize++;
}
}
//表尾插入
void InsertByTail(struct List* list, ElementType data)
{
LPNODE newNode = createNode(data);
if(list->listSize == 0)
{
list->firstNode = newNode;
list->lastNode = newNode;
list->listSize++;
}
else
{
newNode->prev = list->lastNode;
list->lastNode->next = newNode;
list->lastNode = newNode;
list->listSize++;
}
}
//指定数据处插入方式1
void InsertByAppointment(struct List* list, ElementType data, ElementType posData)
{
LPNODE pos = list->firstNode;
LPNODE preNode = NULL;
while(pos != NULL && pos->data != posData)
{
preNode = pos;
pos = pos->next;
}
if(pos == NULL)
{
printf("Failed! There is no posData in this linked list!\n");
}
else if(pos == list->firstNode)
{
//指定位置为第一个结点,这时使用头插法
InsertByHead(list,data);
}
else
{
LPNODE newNode = createNode(data);
preNode->next = newNode;
newNode->prev = preNode;
newNode->next = pos;
pos->prev = newNode;
list->listSize++;
}
}
void DeleteByHead(struct List* list)
{
if(list->listSize == 0)
{
printf("The linked list is empty!\n");
return;
}
LPNODE nextNode = list->firstNode->next;
free(list->firstNode);
list->firstNode = nextNode;
if(list->listSize == 1)
list->lastNode = NULL;
else
nextNode->prev = NULL;
list->listSize--;
}
void DeleteByTail(struct List* list)
{
if(list->listSize == 0)
{
printf("The linked list is empty!\n");
return;
}
LPNODE prevNode = list->lastNode->prev;
free(list->lastNode);
list->lastNode = prevNode;
if(list->listSize == 1)
list->firstNode = NULL;
else
prevNode->next = NULL;
list->listSize--;
}
int IsEmpty(struct List* list)
{
return list->listSize == 0;
}
void printListByHead(struct List* list)
{
LPNODE pMove = list->firstNode;
while(pMove)
{
printf("%d\t",pMove->data);
pMove = pMove->next;
}
printf("\n");
}
void printListByRear(struct List* list)
{
LPNODE pMove = list->lastNode;
while(pMove)
{
printf("%d\t",pMove->data);
pMove = pMove->prev;
}
printf("\n");
}
int main()
{
struct List* list = creatList();
for(int i=0; i<5; i++)
InsertByHead(list, i);
printListByHead(list);
printListByRear(list);
DeleteByHead(list);
printListByHead(list);
printListByRear(list);
for(int i=0; i<5; i++)
InsertByTail(list, i);
printListByHead(list);
printListByRear(list);
InsertByAppointment(list,100,4);
printListByRear(list);
InsertByAppointment(list,100,2);
InsertByTail(list,30);
printListByRear(list);
InsertByAppointment(list,200,30);
printListByHead(list);
printListByRear(list);
while(!IsEmpty(list))
{
DeleteByTail(list);
printListByHead(list);
printListByRear(list);
}
}
4 3 2 1 0
0 1 2 3 4
3 2 1 0
0 1 2 3
3 2 1 0 0 1 2 3 4
4 3 2 1 0 0 1 2 3
4 100 3 2 1 0 0 1 2 3
30 4 100 3 2 1 0 0 1 2 100 3
3 100 2 1 0 0 1 2 3 100 4 200 30
30 200 4 100 3 2 1 0 0 1 2 100 3
3 100 2 1 0 0 1 2 3 100 4 200
200 4 100 3 2 1 0 0 1 2 100 3
3 100 2 1 0 0 1 2 3 100 4
4 100 3 2 1 0 0 1 2 100 3
3 100 2 1 0 0 1 2 3 100
100 3 2 1 0 0 1 2 100 3
3 100 2 1 0 0 1 2 3
3 2 1 0 0 1 2 100 3
3 100 2 1 0 0 1 2
2 1 0 0 1 2 100 3
3 100 2 1 0 0 1
1 0 0 1 2 100 3
3 100 2 1 0 0
0 0 1 2 100 3
3 100 2 1 0
0 1 2 100 3
3 100 2 1
1 2 100 3
3 100 2
2 100 3
3 100
100 3
3
3
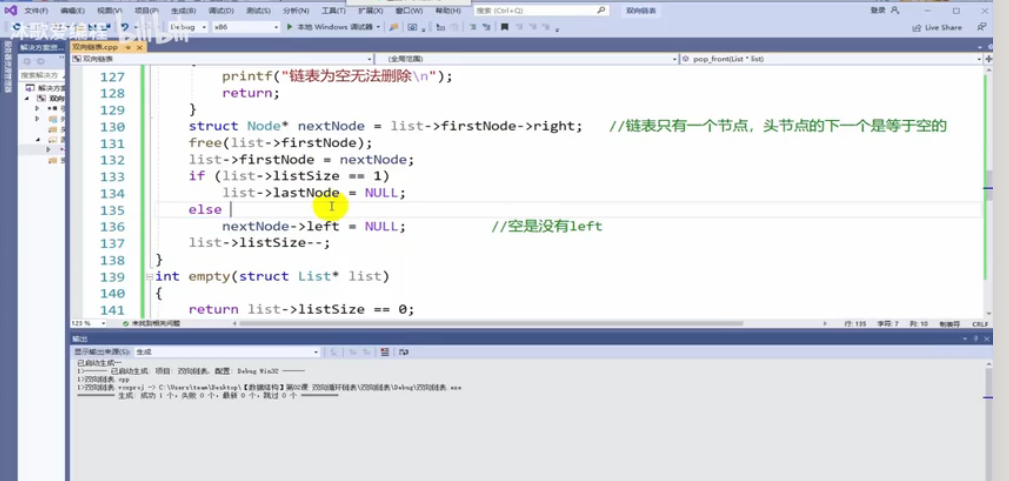
指定位置删除需要特殊处理头和尾。。。
双向循环链表
注意:这里最好写有头(头节点不存数据即可)的双向循环链表。。
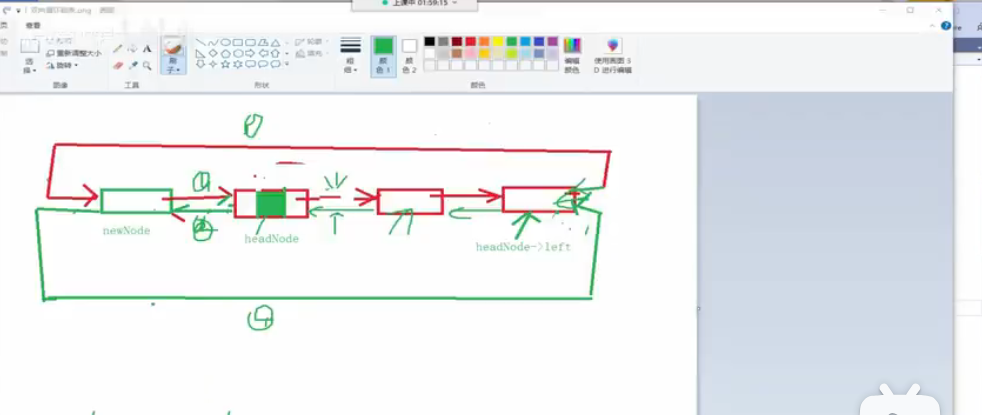
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
typedef struct Node *LPNODE;
typedef int ElementType;
struct Node
{
LPNODE prev;
LPNODE next;
ElementType data;
};
LPNODE createNode(ElementType data)
{
//新节点不需要是环形
LPNODE newNode = (LPNODE)malloc((sizeof(struct Node)));
assert(newNode);
newNode->prev = NULL;
newNode->next = NULL;
newNode->data = data;
return newNode;
}
//创建链表,描述链表的初始状态
struct Node* creatList()
{
//单个节点指向自身,形成环形
struct Node* headNode = (struct Node*)malloc(sizeof(struct Node));
//assert(list);
//这里也可以写成if语句形式
if(headNode == NULL)
return NULL;
headNode->prev = headNode;
headNode->next = headNode;
return headNode;
}
//表尾插入
void InsertByTail(struct Node* headNode, ElementType data)
{
LPNODE newNode = createNode(data);
LPNODE temp = headNode->prev;
//headNode->prev是最后一个结点
newNode->next = headNode;
headNode->prev = newNode;
temp->next = newNode;
newNode->prev = temp;
}
void InsertByAppointment(struct Node* headNode, ElementType data, ElementType posData)
{
LPNODE preNode = headNode;
LPNODE posNode = headNode->next;
while(headNode != posNode && posData != posNode->data)
{
preNode = posNode;
posNode = posNode->next;
}
if(headNode == posNode)
{
printf("The posData is not in this linked list!\n");
return;
}
else
{
LPNODE newNode = createNode(data);
newNode->next = posNode;
posNode->prev = newNode;
preNode->next = newNode;
newNode->prev = preNode;
}
}
void printListByHead(struct Node* headNode)
{
LPNODE pMove = headNode->next;
while(pMove != headNode)
{
printf("%d\t",pMove->data);
pMove = pMove->next;
}
printf("\n");
}
void printListByTail(struct Node* headNode)
{
LPNODE pMove = headNode->prev;
while(pMove != headNode)
{
printf("%d\t",pMove->data);
pMove = pMove->prev;
}
printf("\n");
}
int main()
{
struct Node* list = creatList();
for(int i=0; i<5; i++)
InsertByTail(list, i);
printListByHead(list);
printListByTail(list);
InsertByAppointment(list, 100, 2);
printListByHead(list);
printListByTail(list);
return 0;
}
0 1 2 3 4
4 3 2 1 0
0 1 100 2 3 4
4 3 2 100 1 0
单链表题目
PTA6-1 单链表逆转
本题要求实现一个函数,将给定的单链表逆转。
函数接口定义:
List Reverse( List L );
其中List结构定义如下:
typedef struct Node *PtrToNode;
struct Node {
ElementType Data; /* 存储结点数据 */
PtrToNode Next; /* 指向下一个结点的指针 */
};
typedef PtrToNode List; /* 定义单链表类型 */
L是给定单链表,函数Reverse要返回被逆转后的链表。
裁判测试程序样例:
#include <stdio.h>
#include <stdlib.h>
typedef int ElementType;
typedef struct Node *PtrToNode;
struct Node {
ElementType Data;
PtrToNode Next;
};
typedef PtrToNode List;
List Read(); /* 细节在此不表 */
void Print( List L ); /* 细节在此不表 */
List Reverse( List L );
int main()
{
List L1, L2;
L1 = Read();
L2 = Reverse(L1);
Print(L1);
Print(L2);
return 0;
}
/* 你的代码将被嵌在这里 */
输入样例:
5
1 3 4 5 2
输出样例:
1
2 5 4 3 1
双指针解法:
List Reverse( List L )
{
List cur = L;
List pre = NULL;
while(cur!=NULL)
{
List temp = cur->Next;
cur->Next = pre;
pre = cur;
cur = temp;
}
return pre;
}
递归解法:
List Reverse( List L )
{
if(L==NULL||L->Next==NULL)
return L;
List cur = Reverse(L->Next);
L->Next->Next=L;
L->Next=NULL;
return cur;
}
PTA 6-2 顺序表操作集
本题要求实现顺序表的操作集。
函数接口定义:
List MakeEmpty();
Position Find( List L, ElementType X );
bool Insert( List L, ElementType X, Position P );
bool Delete( List L, Position P );
其中List结构定义如下:
typedef int Position;
typedef struct LNode *List;
struct LNode {
ElementType Data[MAXSIZE];
Position Last; /* 保存线性表中最后一个元素的位置 */
};
各个操作函数的定义为:
List MakeEmpty():创建并返回一个空的线性表;
Position Find( List L, ElementType X ):返回线性表中X的位置。若找不到则返回ERROR;
bool Insert( List L, ElementType X, Position P ):将X插入在位置P并返回true。若空间已满,则打印“FULL”并返回false;如果参数P指向非法位置,则打印“ILLEGAL POSITION”并返回false;
bool Delete( List L, Position P ):将位置P的元素删除并返回true。若参数P指向非法位置,则打印“POSITION P EMPTY”(其中P是参数值)并返回false。
裁判测试程序样例:
#include <stdio.h>
#include <stdlib.h>
#define MAXSIZE 5
#define ERROR -1
typedef enum {false, true} bool;
typedef int ElementType;
typedef int Position;
typedef struct LNode *List;
struct LNode {
ElementType Data[MAXSIZE];
Position Last; /* 保存线性表中最后一个元素的位置 */
};
List MakeEmpty();
Position Find( List L, ElementType X );
bool Insert( List L, ElementType X, Position P );
bool Delete( List L, Position P );
int main()
{
List L;
ElementType X;
Position P;
int N;
L = MakeEmpty();
scanf("%d", &N);
while ( N-- ) {
scanf("%d", &X);
if ( Insert(L, X, 0)==false )
printf(" Insertion Error: %d is not in.\n", X);
}
scanf("%d", &N);
while ( N-- ) {
scanf("%d", &X);
P = Find(L, X);
if ( P == ERROR )
printf("Finding Error: %d is not in.\n", X);
else
printf("%d is at position %d.\n", X, P);
}
scanf("%d", &N);
while ( N-- ) {
scanf("%d", &P);
if ( Delete(L, P)==false )
printf(" Deletion Error.\n");
if ( Insert(L, 0, P)==false )
printf(" Insertion Error: 0 is not in.\n");
}
return 0;
}
/* 你的代码将被嵌在这里 */
输入样例:
6
1 2 3 4 5 6
3
6 5 1
2
-1 6
输出样例:
FULL Insertion Error: 6 is not in.
Finding Error: 6 is not in.
5 is at position 0.
1 is at position 4.
POSITION -1 EMPTY Deletion Error.
FULL Insertion Error: 0 is not in.
POSITION 6 EMPTY Deletion Error.
FULL Insertion Error: 0 is not in.
List MakeEmpty()
{
List PtrL;
PtrL=(List)malloc(sizeof(struct LNode));
PtrL->Last=-1;
return PtrL;
}
Position Find( List L, ElementType X )
{
for(Position i=0;i<=L->Last+1;i++)
{
if(L->Data[i]==X)
return i;
}
return ERROR;
/*int i=0;
while(i<L->Last&&L->Data[i]!=X)
i++;
if(i>L->Last) return ERROR;//如果没找到,返回ERROR
else return i;//找到后返回的是存储位置*/
}
bool Insert( List L, ElementType X, Position P )
{
if(L->Last==MAXSIZE-1)
{
printf("FULL");
return false;
}
if(P<0||P>L->Last+1||P>=MAXSIZE)
{
printf("ILLEGAL POSITION");
return false;
}
for(int j=L->Last;j>=P;j--)
{
L->Data[j+1]=L->Data[j];
}
L->Data[P]=X;
L->Last++;
return true;
}
bool Delete( List L, Position P )
{
if(P<0||P>L->Last)
{
printf("POSITION %d EMPTY",P);
return false;
}
if(P!=L->Last)
{
for(int j=P;j<L->Last;j++)
L->Data[j]=L->Data[j+1];
}
L->Last--;
return true;
}
PTA 6-3 求链式表的表长
本题要求实现一个函数,求链式表的表长。
函数接口定义:
int Length( List L );
其中List结构定义如下:
typedef struct LNode *PtrToLNode;
struct LNode {
ElementType Data;
PtrToLNode Next;
};
typedef PtrToLNode List;
L是给定单链表,函数Length要返回链式表的长度。
裁判测试程序样例:
#include <stdio.h>
#include <stdlib.h>
typedef int ElementType;
typedef struct LNode *PtrToLNode;
struct LNode {
ElementType Data;
PtrToLNode Next;
};
typedef PtrToLNode List;
List Read(); /* 细节在此不表 */
int Length( List L );
int main()
{
List L = Read();
printf("%d\n", Length(L));
return 0;
}
/* 你的代码将被嵌在这里 */
输入样例:
1 3 4 5 2 -1
输出样例:
5
int Length( List L )
{
List head=L;
int length=0;
while(head!=NULL)
{
length++;
head=head->Next;
}
return length;
}
PTA 6-4 链式表的按序号查找
本题要求实现一个函数,找到并返回链式表的第K个元素。
函数接口定义:
ElementType FindKth( List L, int K );
其中List结构定义如下:
typedef struct LNode *PtrToLNode;
struct LNode {
ElementType Data;
PtrToLNode Next;
};
typedef PtrToLNode List;
L是给定单链表,函数FindKth要返回链式表的第K个元素。如果该元素不存在,则返回ERROR。
裁判测试程序样例:
#include <stdio.h>
#include <stdlib.h>
#define ERROR -1
typedef int ElementType;
typedef struct LNode *PtrToLNode;
struct LNode {
ElementType Data;
PtrToLNode Next;
};
typedef PtrToLNode List;
List Read(); /* 细节在此不表 */
ElementType FindKth( List L, int K );
int main()
{
int N, K;
ElementType X;
List L = Read();
scanf("%d", &N);
while ( N-- ) {
scanf("%d", &K);
X = FindKth(L, K);
if ( X!= ERROR )
printf("%d ", X);
else
printf("NA ");
}
return 0;
}
/* 你的代码将被嵌在这里 */
输入样例:
1 3 4 5 2 -1
6
3 6 1 5 4 2
输出样例:
4 NA 1 2 5 3
ElementType FindKth( List L, int K )
{
List p = L;
if(p==NULL)
return ERROR;
int i = 1;
while(p!=NULL && i<K)
{
p=p->Next;
i++;
}
if(i==K)
return p->Data;
else return ERROR;
}
这样写会在测试题中数据时报错段错误,这是if(i==K)这个判断条件不严谨导致的。
设想一下K=2; L的长度仅为1,这个程序会进入while循环,然后i=2,但此时p结点对应的Data不存在。这时输出会报错段错误。修改后能AC的代码如下:
ElementType FindKth( List L, int K )
{
List p = L;
int i = 1;
if(p==NULL)
return ERROR;
else
{
while(p!=NULL && i<K)
{
p=p->Next;
i++;
}
if(p!=NULL && i==K)
return p->Data;
else return ERROR;
}
}
下面是另一种能AC的代码:
ElementType FindKth( List L, int K )
{
int i = 1;
while(L)
{
if(i==K)
return L->Data;
i++;
L=L->Next;
}
return ERROR;
}
这里的if语句要放在链表后移操作之前,因为要判断当前结点是否满足条件,如果放在后面就会漏掉第一个值。
若能找到符合要求的值,则在while循环中就会返回内容;如果while循环结束也没找到,程序会直接返回ERROR。
补全的Read()函数代码如下:
List Read()
{
List L,p,r;
int num = 0;
L = (List)malloc(sizeof(List));
r = L;
do
{
scanf("%d",&num);
p=(List)malloc(sizeof(List));
p->Data = num;
r->Next = p;
r = p;
}while(getchar()!='\n');
r->Next = NULL;
return L->Next;
}
PTA 6-5 链式表操作集
本题要求实现链式表的操作集。
函数接口定义:
Position Find( List L, ElementType X );
List Insert( List L, ElementType X, Position P );
List Delete( List L, Position P );
其中List结构定义如下:
typedef struct LNode *PtrToLNode;
struct LNode {
ElementType Data;
PtrToLNode Next;
};
typedef PtrToLNode Position;
typedef PtrToLNode List;
各个操作函数的定义为:
Position Find( List L, ElementType X ):返回线性表中首次出现X的位置。若找不到则返回ERROR;
List Insert( List L, ElementType X, Position P ):将X插入在位置P指向的结点之前,返回链表的表头。如果参数P指向非法位置,则打印“Wrong Position for Insertion”,返回ERROR;
List Delete( List L, Position P ):将位置P的元素删除并返回链表的表头。若参数P指向非法位置,则打印“Wrong Position for Deletion”并返回ERROR。
裁判测试程序样例:
#include <stdio.h>
#include <stdlib.h>
#define ERROR NULL
typedef int ElementType;
typedef struct LNode *PtrToLNode;
struct LNode {
ElementType Data;
PtrToLNode Next;
};
typedef PtrToLNode Position;
typedef PtrToLNode List;
Position Find( List L, ElementType X );
List Insert( List L, ElementType X, Position P );
List Delete( List L, Position P );
int main()
{
List L;
ElementType X;
Position P, tmp;
int N;
L = NULL;
scanf("%d", &N);
while ( N-- ) {
scanf("%d", &X);
L = Insert(L, X, L);
if ( L==ERROR ) printf("Wrong Answer\n");
}
scanf("%d", &N);
while ( N-- ) {
scanf("%d", &X);
P = Find(L, X);
if ( P == ERROR )
printf("Finding Error: %d is not in.\n", X);
else {
L = Delete(L, P);
printf("%d is found and deleted.\n", X);
if ( L==ERROR )
printf("Wrong Answer or Empty List.\n");
}
}
L = Insert(L, X, NULL);
if ( L==ERROR ) printf("Wrong Answer\n");
else
printf("%d is inserted as the last element.\n", X);
P = (Position)malloc(sizeof(struct LNode));
tmp = Insert(L, X, P);
if ( tmp!=ERROR ) printf("Wrong Answer\n");
tmp = Delete(L, P);
if ( tmp!=ERROR ) printf("Wrong Answer\n");
for ( P=L; P; P = P->Next ) printf("%d ", P->Data);
return 0;
}
/* 你的代码将被嵌在这里 */
输入样例:
6
12 2 4 87 10 2
4
2 12 87 5
输出样例:
2 is found and deleted.
12 is found and deleted.
87 is found and deleted.
Finding Error: 5 is not in.
5 is inserted as the last element.
Wrong Position for Insertion
Wrong Position for Deletion
10 4 2 5
根据课堂代码改写的代码如下:
Position Find( List L, ElementType X )
{
List p = L;
while(p!=NULL && p->Data!=X)
p=p->Next;
return p;
}
另一种能AC的代码如下:
Position Find( List L, ElementType X )
{
while(L)
{
if(L->Data==X)
return L;
L = L->Next;
}
return ERROR;
}
List Insert( List L, ElementType X, Position P )
{
List head = L;
List p = (List)malloc(sizeof(List));
p->Data = X;
p->Next = NULL;
if(L==P)
{
p->Next = L;
return p;
}
while(L)
{
if(P==L->Next)
{
p->Next = L->Next;
L->Next = p;
return head;
}
L=L->Next;
}
printf("Wrong Position for Insertion\n");
return ERROR;
}
List Delete( List L, Position P )
{
if(L==P)
{
L = L->Next;
return L;
}
List head = L;
while(L)
{
if(L->Next==P)
{
L->Next=P->Next;
return head;
}
L=L->Next;
}
printf("Wrong Position for Deletion\n");
return ERROR;
}
线性表Linear List
引子:多项式表示
一元多项式及其运算:
主要运算:多项式相加、相减、相乘等
分析:如何表示多项式?
(1)顺序存储结构直接表示
数组各分量对应多项式各项,a[i]:项的系数
两个多项式相加:两个数组对应分量相加
问题:如何表示多项式?
空间利用率较低
(2)顺序存储结构表示非零项
每个非零项涉及两个信息:系数和指数i
可以将一个多项式看成是一个二元组的集合。
用结构数组表示:数组分量是由系数、指数i组成的结构,对应一个非零项
例如:
为了方便相加可以按指数大小存储!
相加过程:从头开始,比较两个多项式当前对应项的指数
(3)链表结构存储非零项
链表中每个节点存储多项式中的一个非零项,包括系数和指数两个数据域以及一个指针域
| coef | expon | link |
|---|
typedef struct PolyNode *Polynomial;
struct PolyNode
{
int coef;
int expon;
Polynomial link;
};
线性表定义
多项式表示问题的启示:
1.同一个问题可以有不同的表示(存储)方法
2.有一类共性问题:有序线性序列的组织和管理
线性表:0个或多个同类型数据元素的有限序列。
班级同学的花名册是线性表,因为这是有限序列。在较复杂的线性表中,一个数据元素可以由若干个数据项组成。
线性表的抽象数据类型定义
线性表的抽象数据类型定义如下:
ADT 线性表(List)
Data
线性表的数据对象集合为{a1,a2,...,an},每个元素的类型均为DataType。其中,除第一个元素a1外,每一个元素有且只有一个直接前驱元素,除了最后一个元素an,每一个元素有且只有一个直接后继元素。数据元素之间的关系是一对一的关系。
Operation
InitList(*L):初始化操作,建立一个空的线性表L。
ListEmpty(L):若线性表为空,返回true,否则返回false。
ClearList(*L):将线性表清空。
GetElem(L,i,*e):将线性表L中的第i个未知元素值返回给e。
LocateElem(L,e):在线性表L中查找与给定值e相等的元素,如果查找成功,返回该元素在表中序号表示成功;否则,返回0表示失败。
ListInsert(*L,i,e):在线性表L中的第i个位置插入新元素e。
ListDelete(*L,i,*e):删除线性表L中第i个位置元素,并用e返回其值。
ListLength(L):返回线性表L的元素个数。
endADT
线性表的顺序存储实现
利用数组的连续存储空间顺序存放线性表的各元素
typedef struct LNode* List;
struct LNode
{
ElementType Data[MAXSIZE];
int Last;//记录最后一位有效位
};
struct LNode L;
List PtrL;
访问下标为i的元素:L.Data[i]或PtrL->Data[i]
线性表的长度:L.Last+1或PtrL->Last+1
陈越姥姥《数据结构》课程实现版本:
#define MAXSIZE 20 /*存储空间初始分配量*/
typedef struct LNode* List;
struct LNode
{
ElementType Data[MAXSIZE];
int Last;//记录最后一位有效位
};
struct LNode L;
List PtrL;
List MakeEmpty()
{
List PtrL;
PtrL=(List)malloc(sizeof(struct LNode));
PtrL->Last=-1;
return PtrL;
}
int Find(ElementType X,List PtrL)
{
int i=0;
while(i<=PtrL->Last&&PtrL->Data[i]!=X)
i++;
if(i>PtrL->Last) return -1;//如果没找到,返回-1
else return i;//找到后返回的是存储位置(下标)
}
/*插入(第i(1<=i<=n+1)个位置上插入一个值为X的新元素*/
void Insert(ElementType X,int i,List PtrL) /*i是序数,为下标+1,不是下标*/
{
int j;
if(PtrL->Last==MAXSIZE-1) /*表空间已满,不能插入*/
{
printf("表满");
return;
}
if(i<1||i>PtrL->Last+2) /*检查插入位置的合法性*/
{
printf("位置不合法");
return;
}
for(j=PtrL->Last;j>=i-1;j--)
PtrL->Data[j+1]=PtrL->Data[j]; /*将ai~an倒序向后移动*/
PtrL->Data[i-1]=X; /*新元素插入*/
PtrL->Last++; /*Last仍指向最后一个元素*/
return;
}
/*删除:删除表的第i(1<=i<=n)个位置上的元素*/
void Delete(int i,List PtrL)
{
int j;
if(i<1||i>PtrL->Last+1) /*检查是否为空表及删除位置的合法性*/
{
printf("不存在第%d个元素",i);
return;
}
for(j=i;j<=PtrL->Last;j++)
PtrL->Data[j-1]=PtrL->Data[j]; /*将a(i+1)~an顺序向前移动*/
PtrL->Last--; /*Last仍指向最后一个元素*/
return;
}
《大话数据结构》给出的顺序存储的链表实例:
#include <bits/stdc++.h>
using namespace std;
#define MAXSIZE 100
#define OK 1
#define ERROR 0
#define OVERFLOW -2 //这样就为 `OVERFLOW` 定义了一个值为 `-2` 的常量。
typedef int ElemType;
typedef int Status;
typedef struct
{
ElemType *elem;
int length;
}SqList;
//线性表的初始化
Status InitList(SqList &L)
{
L.elem=new ElemType[MAXSIZE];
if(!L.elem)
exit(OVERFLOW);
L.length=0;
return OK;
}
//线性表的取值
Status GetElem(SqList L,int i,ElemType &e)
{
if(i<1||i>L.length)
return ERROR;
e=L.elem[i-1];
return OK;
}
//查找元素
int LocateElem(SqList L,ElemType e)
{
for(int i=0;i<L.length;i++)
{
if(L.elem[i]==e)
return i+1;
}
return 0;
}
//线性表插入元素
Status ListInsert(SqList &L,int i,ElemType e)
{
if(i<1||i>L.length+1)
return ERROR;
if(L.length==MAXSIZE)
return ERROR;
for(int j=L.length-1;j>=i-1;j--)
{
L.elem[j+1]=L.elem[j];
}
L.elem[i-1]=e;
L.length++;
return OK;
}
//线性表删除元素
Status ListDelete(SqList &L,int i)
{
if(i<1||i>L.length)
return ERROR;
for(int j=i;j<=L.length-1;j++)
L.elem[j-1]=L.elem[j];
L.length--;
return OK;
}
//打印线性表
Status Display(SqList &L)
{
for(int i=0;i<L.length;i++)
printf("%d ",L.elem[i]);
printf("\n");
return 0;
}
int main()
{
SqList L;
int v,k,opt;
InitList(L);
printf("1:在线性表中存入5个值\n");
printf("2:查找线性表中的元素\n");
printf("3:向线性表中插入一个元素\n");
printf("4:从线性表中删除一个元素\n");
printf("5:退出\n");
while(1)
{
printf("输入你的选择:");
cin>>opt;
if(opt==1)
{
printf("请输入要插入的5个值:");
for(int i=1;i<=5;i++)
{
cin>>v;
ListInsert(L,i,v);
}
printf("当前线性表为:");
Display(L);
}
else if(opt==2)
{
printf("请输入要查找的元素:");
cin>>v;
k=LocateElem(L,v);
printf("要查找的元素的所在的位置为:%d\n",k);
}
else if(opt==3)
{
printf("请输入要插入的元素及插入的位置:");
cin>>v>>k;
ListInsert(L,k,v);
printf("插入元素后的线性表为:");
Display(L);
}
else if(opt==4)
{
printf("输入要删除的元素的序数:");
cin>>v;
ListDelete(L,v);
printf("删除后的线性表为:");
Display(L);
}
else if(opt==5)
{
printf("退出成功!");
break;
}
}
return 0;
}
1:在线性表中存入5个值
2:查找线性表中的元素
3:向线性表中插入一个元素
4:从线性表中删除一个元素
5:退出
输入你的选择:1
请输入要插入的5个值:9 4 2 1 0
当前线性表为:9 4 2 1 0
输入你的选择:2
请输入要查找的元素:4
要查找的元素的所在的位置为:2
输入你的选择:3
请输入要插入的元素及插入的位置:5 3
插入元素后的线性表为:9 4 5 2 1 0
输入你的选择:4
输入要删除的元素的序数:6
删除后的线性表为:9 4 5 2 1
输入你的选择:5
退出成功!
线性表的链式存储实现
不要求逻辑上相邻的两个元素物理上也相邻;通过”链“建立起数据元素之间的逻辑关系。
插入、删除元素不需要移动数据元素,只需要修改”链“。
如果只知道链表头,该怎么访问序号为i的元素?以及怎么求线性表的长度?
建立结构体和结构体指针:
typedef struct LNode *List;
struct LNode
{
ElementType Data;
List Next;
};
struct LNode L;
List PtrL;
展示链表结构:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
struct list_node
{
int data ;
struct list_node *next ;
};
typedef struct list_node list_single ;
list_single *create_list_node(int data)
{
list_single *node = NULL ;
node = (list_single *)malloc(sizeof(list_single));
if(node == NULL){
printf("malloc fair!\n");
}
memset(node,0,sizeof(list_single));
node->data = data;
node->next = NULL ;
return node ;
}
int main(void)
{
int data = 100 ;
list_single *node_ptr = create_list_node(data); //创建一个节点
printf("node_ptr->data=%d\n",node_ptr->data); //打印节点里的数据
printf("node_ptr->next=%d\n",node_ptr->next);
free(node_ptr);
return 0 ;
}
node_ptr->data=100
node_ptr->next=0
1.求链表的长度
int Length(List Ptrl)
{
List p=Ptrl; //p指向表的第一个结点
int j=0;
while(p)
{
p=p->Next;
j++; //当前p指向的是第j个结点
}
return j;
}
2.查找(1)按序号(不是下标)查找:FindKth
List FindKth(int K,List PtrL)
{
List p=PtrL;
int i=1;
while(p!=NULL&&i<K)
{
p=p->Next;
i++;
}
if(i==K)
return p; //找到第K个,返回指针
else
return NULL; //否则返回空
}
(2)按值查找
List Find(ElementType X,List PtrL)
{
List p=PtrL;
while(p!=NULL && p->Data!=X)
{
p=p->Next;
}
return p;
}
3.插入(在个结点后插入一个值为X的新结点
这个结点是第i个结点。
步骤(1)先构造一个新结点,用s指向;(2)再找到链表的第i-1个结点,用p指向;(3)然后修改指针,插入结点(p之后插入的新结点是s)。
链表要先断再接,顺序不能更改!!
链表要先断再接,顺序不能更改!!
链表要先断再接,顺序不能更改!!
List Insert(ElementType X,int i,List PtrL)
{
List p,s;
if(i==1) //新节点插在表头
{
s=(List)malloc(sizeof(struct LNode)); //申请、填装结点
s->Data=X;
s->Next=Ptrl;
return s; //返回新表头指针
}
p=FindKth(i-1;PtrL); //查找第i-1个结点
if(p==NULL) //第i-1个不存在,不能插入
{
printf("参数i错");
return NULL;
}
else
{
s=(List)malloc(sizeof(struct LNode)); //申请、填装结点
s.Data=X;
s->Next=p->Next; //新节点插在第i-1个结点的后面
p->Next=s;
return PtrL;
}
}
4.删除(删除链表的个位置上的的结点
步骤:(1)先找到链表的第i-1个结点,用p指向;(2)再用指针s指向要被删除的结点(p的下一个结点);(3)然后修改指针,删除s所指结点;(4)最后释放s所指结点的空间。
步骤不能更改!!!
步骤不能更改!!!
步骤不能更改!!!
List Delete(int i,List PtrL)
{
List p,s;
if(i==1) //若要删除的是表的第一个结点
{
s=PtrL; //s指向第一个结点
if(PtrL!=NULL)
PtrL=PtrL->Next; //从链表中删除
else
return NULL;
free(s); //释放被删除结点
return PtrL; //返回新表头指针
}
p=FindKth(i-1;PtrL); //查找第i-1个结点
if(p==NULL)
{
printf("第%d个结点不存在",i-1);
return NULL;
}
else if(p->Next==NULL)
{
printf("第%d个结点不存在",i);
return NULL;
}
else
{
s=p->Next; //s指向第i个结点
p->Next=s->Next; //从链表中删除
free(s); //释放被删除结点
return PtrL;
}
}
陈越姥姥《数据结构》课程给出的完整代码如下:
typedef struct LNode *List;
struct LNode
{
ElementType Data;
List Next;
};
struct LNode L;
List PtrL;
int Length(List Ptrl)
{
List p=Ptrl; //p指向表的第一个结点
int j=0;
while(p)
{
p=p->Next;
j++; //当前p指向的是第j个结点
}
return j;
}
List FindKth(int K,List PtrL)
{
List p=PtrL;
int i=1;
while(p!=NULL&&i<K)
{
p=p->Next;
i++;
}
if(i==K)
return p; //找到第K个,返回指针
else
return NULL; //否则返回空
}
List Find(ElementType X,List PtrL)
{
List p=PtrL;
while(p!=NULL && p->Data!=X)
{
p=p->Next;
}
return p;
}
List Insert(ElementType X,int i,List PtrL)
{
List p,s;
if(i==1) //新节点插在表头
{
s=(List)malloc(sizeof(struct LNode)); //申请、填装结点
s->Data=X;
s->Next=Ptrl;
return s; //返回新表头指针
}
p=FindKth(i-1;PtrL); //查找第i-1个结点
if(p==NULL) //第i-1个不存在,不能插入
{
printf("参数i错");
return NULL;
}
else
{
s=(List)malloc(sizeof(struct LNode)); //申请、填装结点
s.Data=X;
s->Next=p->Next; //新节点插在第i-1个结点的后面
p->Next=s;
return PtrL;
}
}
List Delete(int i,List PtrL)
{
List p,s;
if(i==1) //若要删除的是表的第一个结点
{
s=PtrL; //s指向第一个结点
if(PtrL!=NULL)
PtrL=PtrL->Next; //从链表中删除
else
return NULL;
free(s); //释放被删除结点
return PtrL; //返回新表头指针
}
p=FindKth(i-1;PtrL); //查找第i-1个结点
if(p==NULL)
{
printf("第%d个结点不存在",i-1);
return NULL;
}
else if(p->Next==NULL)
{
printf("第%d个结点不存在",i);
return NULL;
}
else
{
s=p->Next; //s指向第i个结点
p->Next=s->Next; //从链表中删除
free(s); //释放被删除结点
return PtrL;
}
}
《大话数据结构》中链式存储的链表实例:
#include <stdio.h>
#include <stdlib.h>
#define ERROR 0
#define OK 1
typedef int Status;
typedef int ElementType;
typedef struct LNode *List;
struct LNode
{
ElementType Data;
List Next;
};
struct LNode L;
List PtrL;
//表的创建(头插法)
void CreateListHead(List *L,int m[],int n)
{
List p;
int i;
*L=(List)malloc(sizeof(struct LNode));
(*L)->Next=NULL;
for(i=0;i<n;i++)
{
p=(List)malloc(sizeof(struct LNode));
p->Data=m[i];
p->Next=(*L)->Next;
(*L)->Next=p;
}
}
//表的创建(尾插法)
void CreateListTail(List *L,int m[],int n)
{
List p,r;
int i;
*L=(List)malloc(sizeof(struct LNode));
r=*L;
for(i=0;i<n;i++)
{
p=(List)malloc(sizeof(struct LNode));
p->Data=m[i];
r->Next=p;
r=p;
}
r->Next=NULL;
}
Status GetElem(List L,int i,ElementType *e)
{
int j;
List p;
p=L->Next;
j=1;
while(p&&j<i)
{
p=p->Next;
j++;
}
if(!p||j>i)
return ERROR;
*e=p->Data;
return OK;
}
Status ListInsert(List *L,int i,ElementType e)
{
int j;
List p,s;
p=*L;
j=1;
while(p&&j<i)
{
p=p->Next;
j++;
}
if(!p||j>i)
return ERROR;
s=(List)malloc(sizeof(struct LNode));
s->Data=e;
s->Next=p->Next;
p->Next=s;
return OK;
}
Status ListDelete(List *L,int i)
{
int j;
List p,q;
p=*L;
j=1;
while(p->Next&&j<i)
{
p=p->Next;
j++;
}
if(!(p->Next)||j>i)
return ERROR;
q=p->Next;
p->Next=q->Next;
free(q);
return OK;
}
Status Output(List L)
{
List p;
p=L->Next;
while(p)
{
printf("%d",p->Data);
p=p->Next;
}
printf("\n");
}
int main()
{
List L;
int i,j,k,n,e,m[100];
printf("请输入要存储元素的总个数:");
scanf("%d",&n);
printf("请输入各个元素的值:");
for(i=0;i<n;i++)
scanf("%d",&m[i]);
CreateListHead(&L,m,n);
printf("此时链表的元素如下所示:\n");
Output(L);
printf("请输入要获取的第j个元素并返回到e值中(输入j的值):");
scanf("%d",&j);
GetElem(L,j,&e);
printf("此时e的值为第j个元素值:%d\n",e);
printf("请输入在第k个元素前插入一个元素e1:");
int e1;
scanf("%d%d",&k,&e1);
ListInsert(&L,k,e1);
printf("此时链表的个元素如下:\n");
Output(L);
printf("请输入要删除元素的序号:");
int l;
scanf("%d",&l);
ListDelete(&L,l);
printf("此时链表的各元素如下:\n");
Output(L);
return 0;
}
请输入要存储元素的总个数:5
请输入各个元素的值:1 2 3 4 5
此时链表的元素如下所示:
54321
请输入要获取的第j个元素并返回到e值中(输入j的值):2
此时e的值为第j个元素值:4
请输入在第k个元素前插入一个元素e1:1 2
此时链表的个元素如下:
254321
请输入要删除元素的序号:2
此时链表的各元素如下:
24321
广义表和多重链表
我们知道了一元多项式的表示,那么二元多项式又该如何表示呢?比如给定二元多项式:


广义表(Generalized List)
- 广义表是线性表的推广;
- 对于线性表而言,n个元素都是基本的单元素;
- 广义表中,这些元素不仅可以是单元素也可以是另一个广义表。
typedef struct GNode *Glist;
struct GNode
{
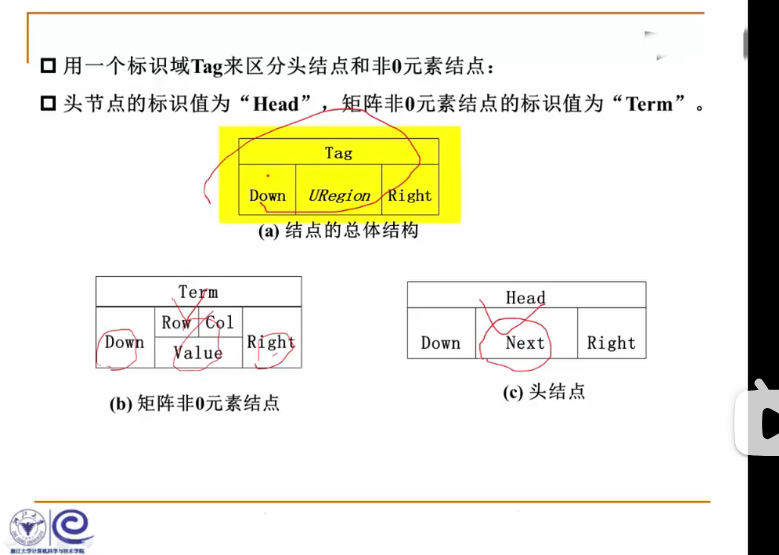
int Tag; //标志域:0表示结点是单元素,1表示结点是广义表
union
{
ElementType Data; //子表指针域SubList与单元素数据域Data复用,即共用存储空间
GList SubList;
}URegion;
GList Next; //指向后继结点
};
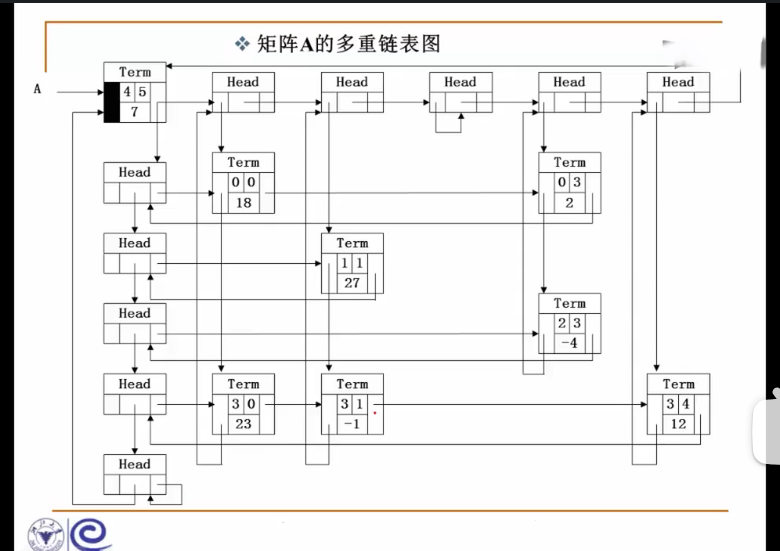
多重链表:链表中的结点可能同时隶属于多个链
- 多重链表中结点的指针域会有多个,如前面例子包含了Next和SubList两个指针域
- 但包含两个指针域的链表并不一定是多重链表,比如双向链表不是多重链表
多重链表有广泛的用途:基本上如树、图这样相对复杂的数据结构都可以采用多重链表的方式存储。

栈Stack
定义


还有一种表达式叫“前缀表达式”,即运算符号位于运算数之前,比如a+b*c的前缀表达式是+a*bc。
你能写出a+b*c-d/e的前缀表达式吗?-+a*bc/de



栈的顺序存储实现


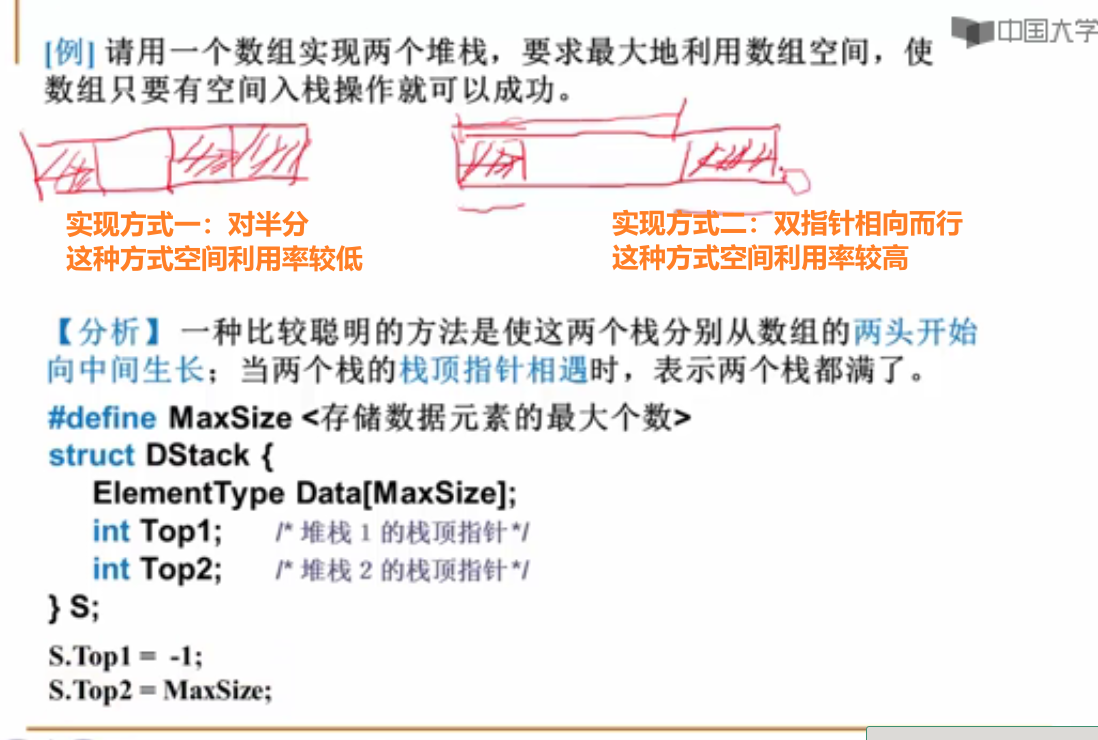
根据刚才讲的方法,用一个数组来表示双堆栈,如果这两个堆栈的栈顶位置分别是top1和top2,那么可以用top1+top2==MaxSize(数组大小)来判别堆栈是否满?
不可以!!!
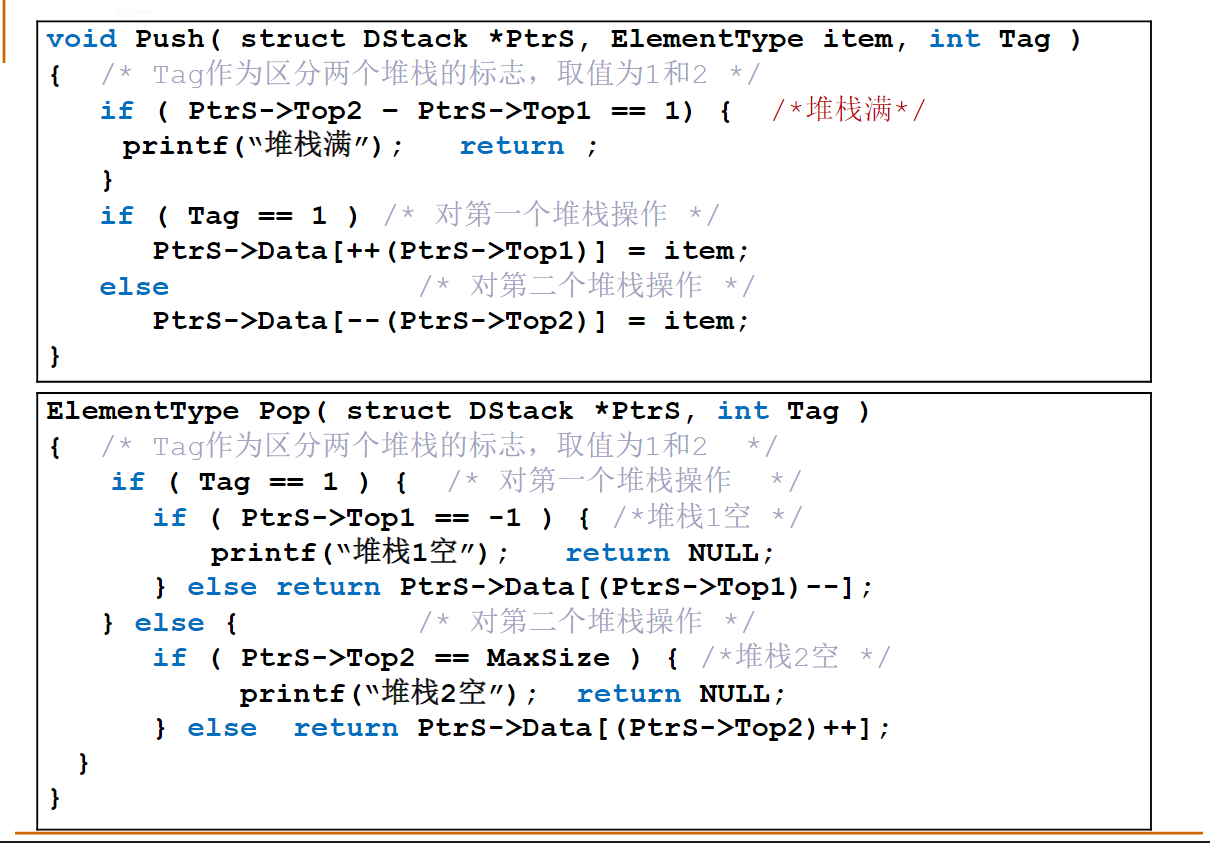
《数据结构》课程给出的代码如下:
typedef int Position;
struct SNode {
ElementType *Data; /* 存储元素的数组 */
Position Top; /* 栈顶指针 */
int MaxSize; /* 堆栈最大容量 */
};
typedef struct SNode *Stack;
Stack CreateStack( int MaxSize )
{
Stack S = (Stack)malloc(sizeof(struct SNode));
S->Data = (ElementType *)malloc(MaxSize * sizeof(ElementType));
S->Top = -1;
S->MaxSize = MaxSize;
return S;
}
bool IsFull( Stack S )
{
return (S->Top == S->MaxSize-1);
}
bool Push( Stack S, ElementType X )
{
if ( IsFull(S) ) {
printf("堆栈满");
return false;
}
else {
S->Data[++(S->Top)] = X;
return true;
}
}
bool IsEmpty( Stack S )
{
return (S->Top == -1);
}
ElementType Pop( Stack S )
{
if ( IsEmpty(S) ) {
printf("堆栈空");
return ERROR; /* ERROR是ElementType的特殊值,标志错误 */
}
else
return ( S->Data[(S->Top)--] );
}
测试程序如下:
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#define ElementType int
#define ERROR -1
#define OK 0
typedef int Position;
typedef struct SNode *Stack;
struct SNode
{
ElementType *Data;
Position Top;
int MaxSize;
};
Stack CreateStack(int MaxSize)
{
Stack S = (Stack)malloc(sizeof(struct SNode));
S->Data = (ElementType*)malloc(MaxSize * sizeof(ElementType));
S->Top = -1;
S->MaxSize = MaxSize;
return S;
}
bool IsFull(Stack S)
{
return (S->Top == S->MaxSize-1);
}
bool Push(Stack PtrS,ElementType X)
{
if(IsFull(PtrS))
return false;
else
{
PtrS->Data[++(PtrS->Top)] = X;
return true;
}
}
bool IsEmpty(Stack S)
{
return (S->Top == -1);
}
ElementType Pop(Stack PtrS)
{
if(IsEmpty(PtrS))
{
printf("栈已空!");
return ERROR;
}
else
{
return (PtrS->Data[(PtrS->Top)--]);
}
}
int main()
{
Stack S = CreateStack(10);
int choice;
while(1)
{
printf("(1)进栈 (2)出栈 (3)读栈顶 (4)退出\n");
scanf("%d",&choice);
if(choice == 1)
{
ElementType X;
printf("输入进栈元素:");
scanf("%d",&X);
if(Push(S,X))
printf("\n元素进栈成功!\n");
}
else if(choice == 2)
{
ElementType X;
X = Pop(S);
if(X != ERROR)
printf("出栈元素为%d\n",X);
}
else
return 0;
}
}
(1)进栈 (2)出栈 (3)读栈顶 (4)退出
1
输入进栈元素:2
元素进栈成功!
(1)进栈 (2)出栈 (3)读栈顶 (4)退出
1
输入进栈元素:4
元素进栈成功!
(1)进栈 (2)出栈 (3)读栈顶 (4)退出
1
输入进栈元素:1
元素进栈成功!
(1)进栈 (2)出栈 (3)读栈顶 (4)退出
2
出栈元素为1
(1)进栈 (2)出栈 (3)读栈顶 (4)退出
2
出栈元素为4
(1)进栈 (2)出栈 (3)读栈顶 (4)退出
2
出栈元素为2
(1)进栈 (2)出栈 (3)读栈顶 (4)退出
2
栈已空!(1)进栈 (2)出栈 (3)读栈顶 (4)退出
4
Process returned 0 (0x0) execution time : 18.576 s
Press any key to continue.
实例PTA6-7 在一个数组中实现两个堆栈
本题要求在一个数组中实现两个堆栈。
函数接口定义:
Stack CreateStack( int MaxSize );
bool Push( Stack S, ElementType X, int Tag );
ElementType Pop( Stack S, int Tag );
其中Tag是堆栈编号,取1或2;MaxSize堆栈数组的规模;Stack结构定义如下:
typedef int Position;
struct SNode {
ElementType *Data;
Position Top1, Top2;
int MaxSize;
};
typedef struct SNode *Stack;
注意:如果堆栈已满,Push函数必须输出“Stack Full”并且返回false;如果某堆栈是空的,则Pop函数必须输出“Stack Tag Empty”(其中Tag是该堆栈的编号),并且返回ERROR。
裁判测试程序样例:
#include <stdio.h>
#include <stdlib.h>
#define ERROR 1e8
typedef int ElementType;
typedef enum { push, pop, end } Operation;
typedef enum { false, true } bool;
typedef int Position;
struct SNode {
ElementType *Data;
Position Top1, Top2;
int MaxSize;
};
typedef struct SNode *Stack;
Stack CreateStack( int MaxSize );
bool Push( Stack S, ElementType X, int Tag );
ElementType Pop( Stack S, int Tag );
Operation GetOp(); /* details omitted */
void PrintStack( Stack S, int Tag ); /* details omitted */
int main()
{
int N, Tag, X;
Stack S;
int done = 0;
scanf("%d", &N);
S = CreateStack(N);
while ( !done ) {
switch( GetOp() ) {
case push:
scanf("%d %d", &Tag, &X);
if (!Push(S, X, Tag)) printf("Stack %d is Full!\n", Tag);
break;
case pop:
scanf("%d", &Tag);
X = Pop(S, Tag);
if ( X==ERROR ) printf("Stack %d is Empty!\n", Tag);
break;
case end:
PrintStack(S, 1);
PrintStack(S, 2);
done = 1;
break;
}
}
return 0;
}
/* 你的代码将被嵌在这里 */
输入样例:
5
Push 1 1
Pop 2
Push 2 11
Push 1 2
Push 2 12
Pop 1
Push 2 13
Push 2 14
Push 1 3
Pop 2
End
输出样例:
Stack 2 Empty
Stack 2 is Empty!
Stack Full
Stack 1 is Full!
Pop from Stack 1: 1
Pop from Stack 2: 13 12 11
能AC的代码如下:
Stack CreateStack( int MaxSize )
{
Stack S = (Stack)malloc(sizeof(struct SNode));
S->Data = (ElementType*)malloc(sizeof(ElementType)*MaxSize);
S->Top1 = -1;
S->Top2 = MaxSize;
S->MaxSize = MaxSize;
return S;
}
bool Push( Stack S, ElementType X, int Tag )
{
if(S->Top1 + 1 == S->Top2)
{
printf("Stack Full\n");
return false;
}
if(Tag == 1)
{
S->Data[++(S->Top1)] = X;
return true;
}
else
{
S->Data[--(S->Top2)] = X;
return true;
}
}
ElementType Pop( Stack S, int Tag )
{
if(Tag == 1)
{
if(S->Top1 == -1)
{
printf("Stack %d Empty\n",Tag);
return ERROR;
}
else
return (S->Data[(S->Top1)--]);
}
else
{
if(S->Top2 == S->MaxSize)
{
printf("Stack %d Empty\n",Tag);
return ERROR;
}
else
return (S->Data[(S->Top2)++]);
}
}
栈的链式存储实现
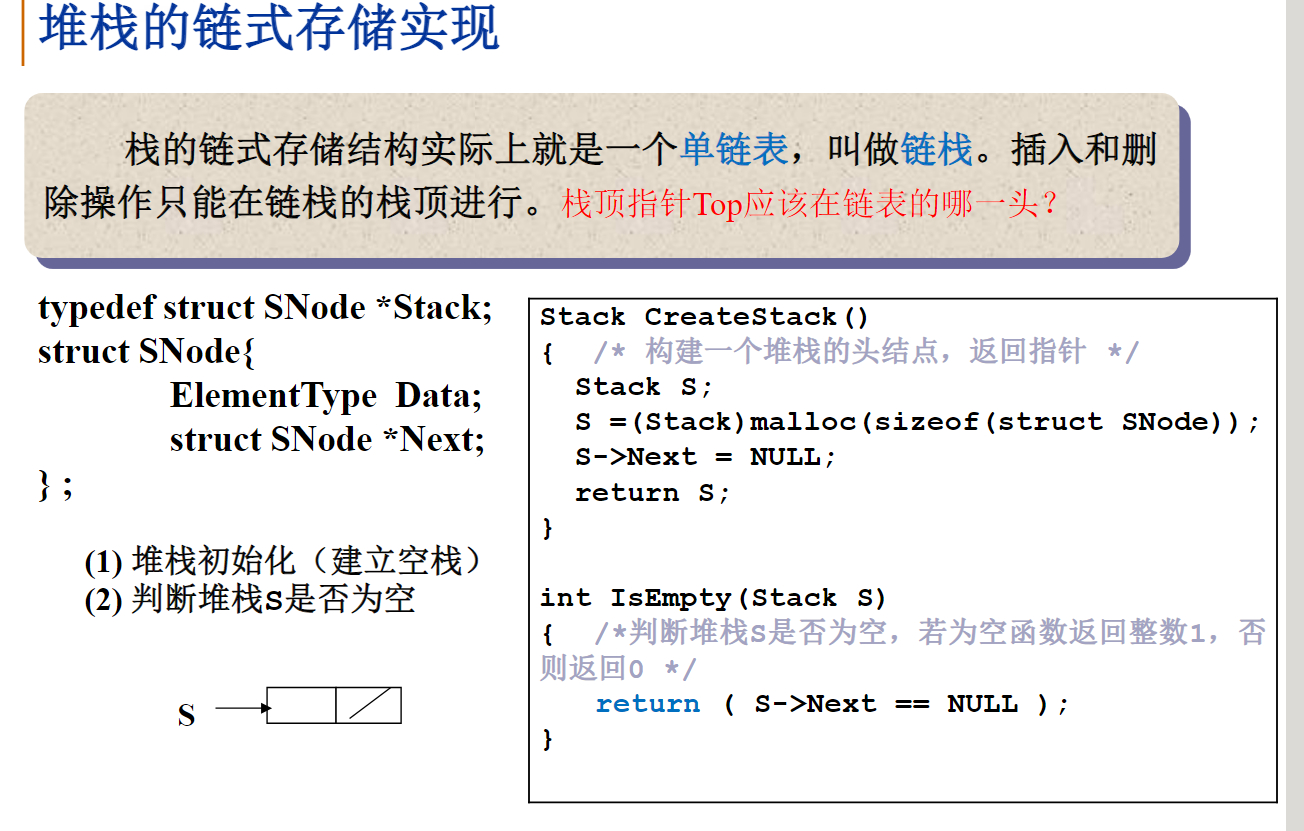
若用单向链表实现一个堆栈,只有链表的头可以作为top。
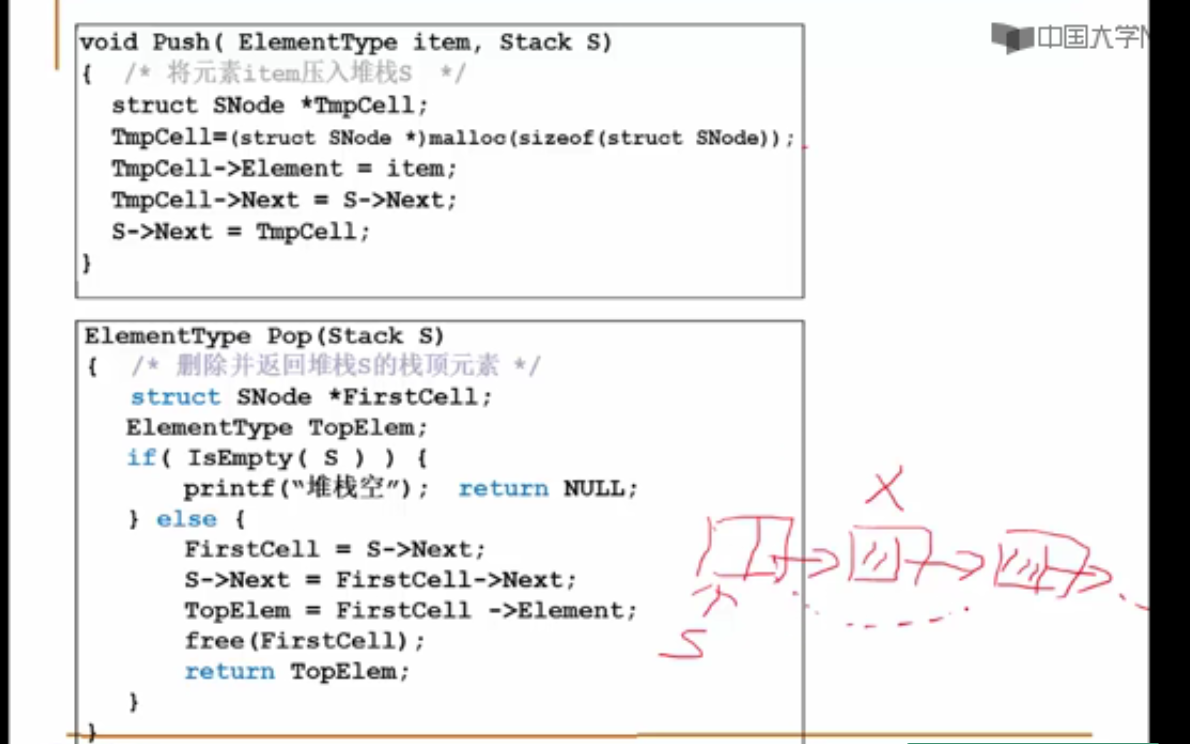
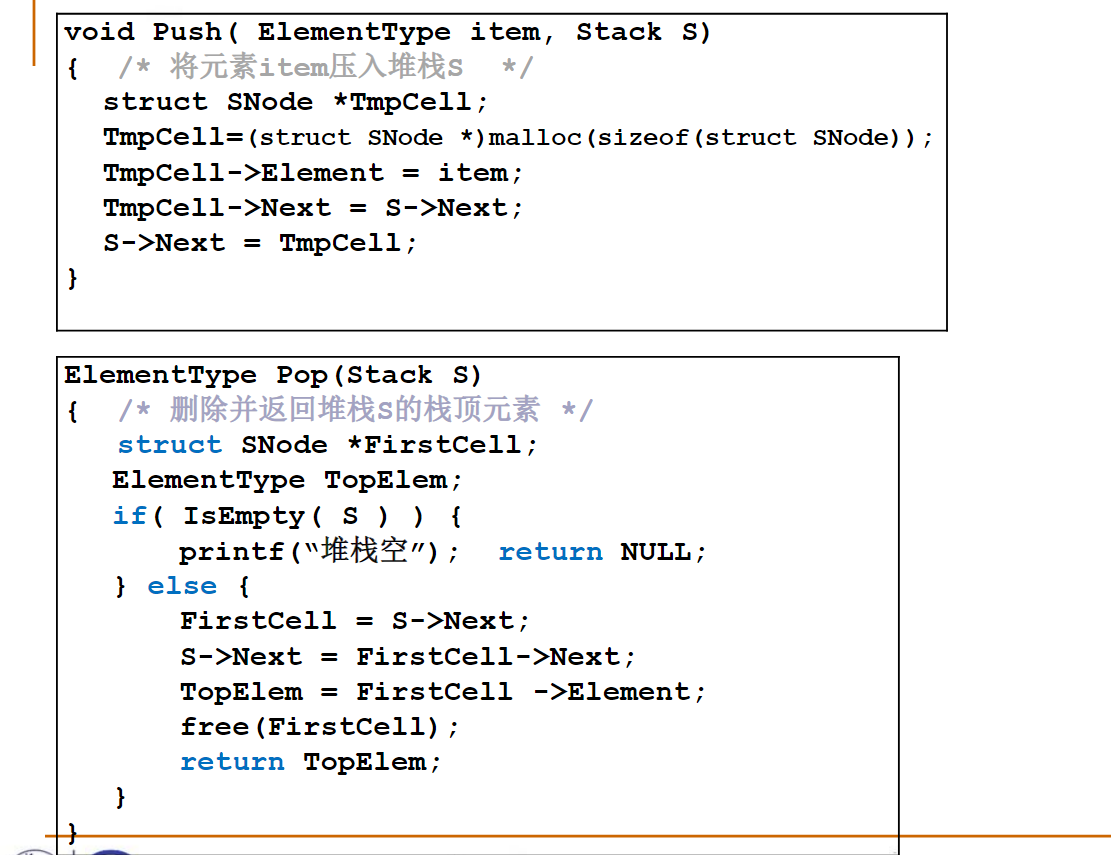
《数据结构》课程给出的代码如下:
typedef struct SNode *PtrToSNode;
struct SNode {
ElementType Data;
PtrToSNode Next;
};
typedef PtrToSNode Stack;
Stack CreateStack( )
{ /* 构建一个堆栈的头结点,返回该结点指针 */
Stack S;
S = (Stack)malloc(sizeof(struct SNode));
S->Next = NULL;
return S;
}
bool IsEmpty ( Stack S )
{ /* 判断堆栈S是否为空,若是返回true;否则返回false */
return ( S->Next == NULL );
}
bool Push( Stack S, ElementType X )
{ /* 将元素X压入堆栈S */
PtrToSNode TmpCell;
TmpCell = (PtrToSNode)malloc(sizeof(struct SNode));
TmpCell->Data = X;
TmpCell->Next = S->Next;
S->Next = TmpCell;
return true;
}
ElementType Pop( Stack S )
{ /* 删除并返回堆栈S的栈顶元素 */
PtrToSNode FirstCell;
ElementType TopElem;
if( IsEmpty(S) ) {
printf("堆栈空");
return ERROR;
}
else {
FirstCell = S->Next;
TopElem = FirstCell->Data;
S->Next = FirstCell->Next;
free(FirstCell);
return TopElem;
}
}
测试程序如下:
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#define ElementType int
#define ERROR -1
#define OK 0
typedef int Position;
typedef struct SNode *Stack;
struct SNode
{
ElementType Data;
Stack Next;
};
Stack CreateStack()
{
Stack S = (Stack)malloc(sizeof(struct SNode));
S->Next = NULL;
return S;
}
bool Push(Stack PtrS,ElementType X)
{
Stack TempCell = (Stack)malloc(sizeof(struct SNode));
TempCell->Data = X;
TempCell->Next = PtrS->Next;
PtrS->Next = TempCell;
return true;
}
bool IsEmpty(Stack S)
{
return (S->Next == NULL);
}
ElementType Pop(Stack PtrS)
{
Stack FirstCell;
ElementType TopElem;
if(IsEmpty(PtrS))
{
printf("栈已空!");
return ERROR;
}
else
{
FirstCell = PtrS->Next;
TopElem = FirstCell->Data;
PtrS->Next = FirstCell->Next;
free(FirstCell);
return TopElem;
}
}
int main()
{
Stack S = CreateStack();
int choice;
while(1)
{
printf("(1)进栈 (2)出栈 (3)读栈顶 (4)退出\n");
scanf("%d",&choice);
if(choice == 1)
{
ElementType X;
printf("输入进栈元素:");
scanf("%d",&X);
if(Push(S,X))
printf("\n元素进栈成功!\n");
}
else if(choice == 2)
{
ElementType X;
X = Pop(S);
if(X != ERROR)
printf("出栈元素为%d\n",X);
}
else
return 0;
}
}
(1)进栈 (2)出栈 (3)读栈顶 (4)退出
1
输入进栈元素:2
元素进栈成功!
(1)进栈 (2)出栈 (3)读栈顶 (4)退出
1
输入进栈元素:3
元素进栈成功!
(1)进栈 (2)出栈 (3)读栈顶 (4)退出
1
输入进栈元素:1
元素进栈成功!
(1)进栈 (2)出栈 (3)读栈顶 (4)退出
2
出栈元素为1
(1)进栈 (2)出栈 (3)读栈顶 (4)退出
2
出栈元素为3
(1)进栈 (2)出栈 (3)读栈顶 (4)退出
2
出栈元素为2
(1)进栈 (2)出栈 (3)读栈顶 (4)退出
2
栈已空!(1)进栈 (2)出栈 (3)读栈顶 (4)退出
4
Process returned 0 (0x0) execution time : 28.401 s
Press any key to continue.
栈应用:表达式求值
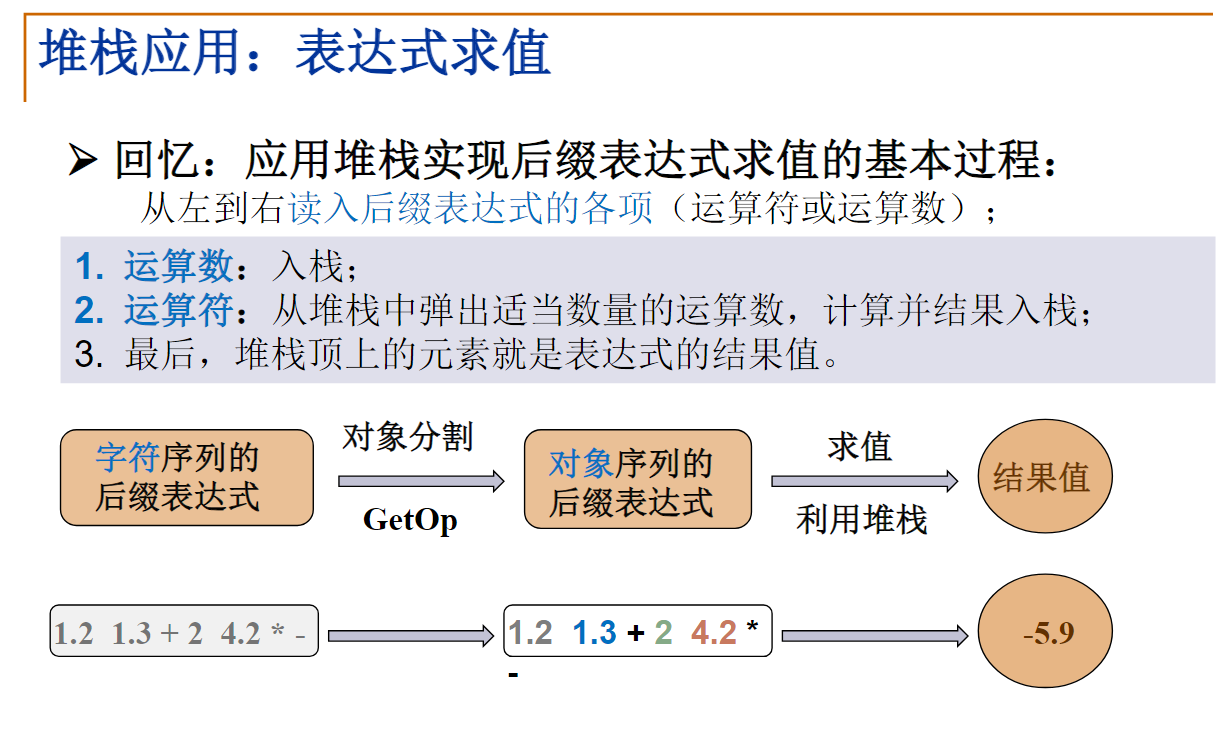

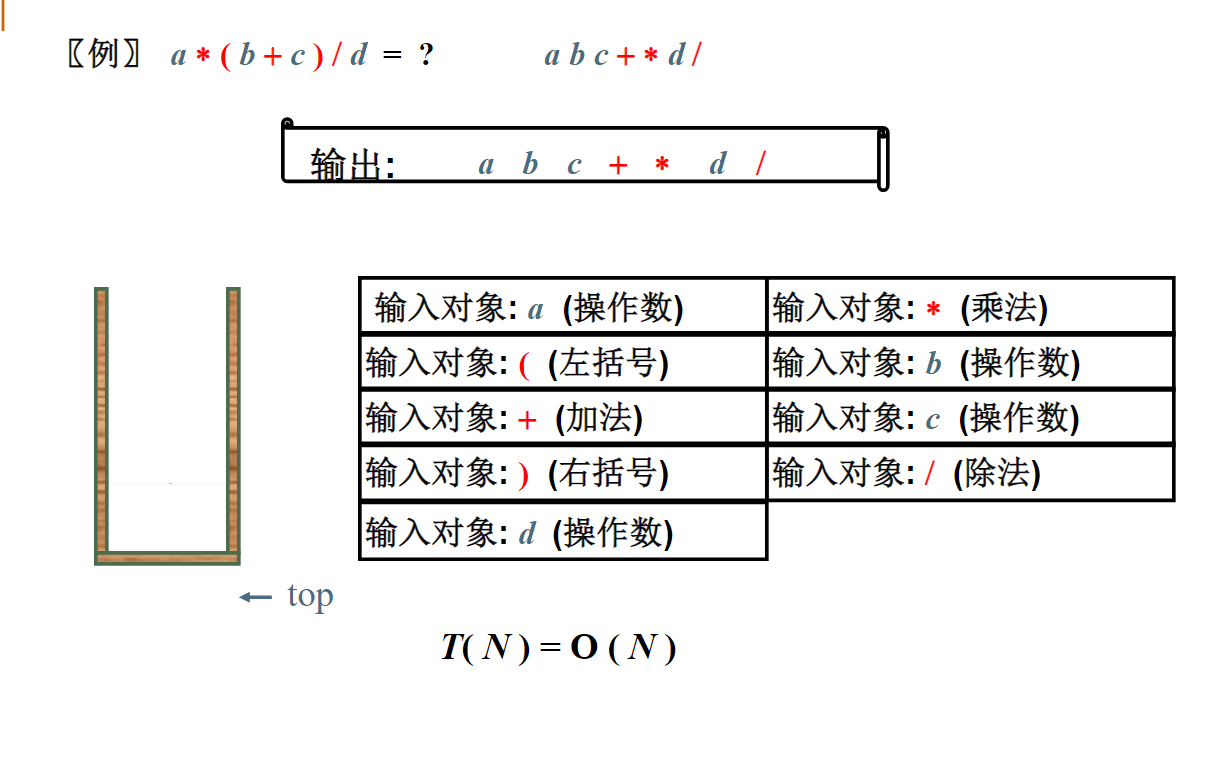
左括号一旦放到堆栈中优先级就变为最低。碰到右括号(右括号不入栈)就把栈顶元素抛出,直到抛出左括号为止。注:括号是不会出现在后缀表达式或前缀表达式中的
请试试应用堆栈将中缀表达式2*(6/3+4)-5转换为后缀表达式。在这个转换过程中,堆栈元素最多时元素个数是3。
借助堆栈将中缀表达式A-(B-C/D)*E转换为后缀表达式,则该堆栈的大小至少为:4
如果一堆栈的输入序列是aAbBc,输出为 abcBA,那么该堆栈所进行的操作序列是什么? 设P代表入栈,O代表出栈。 POPPOPPOOO
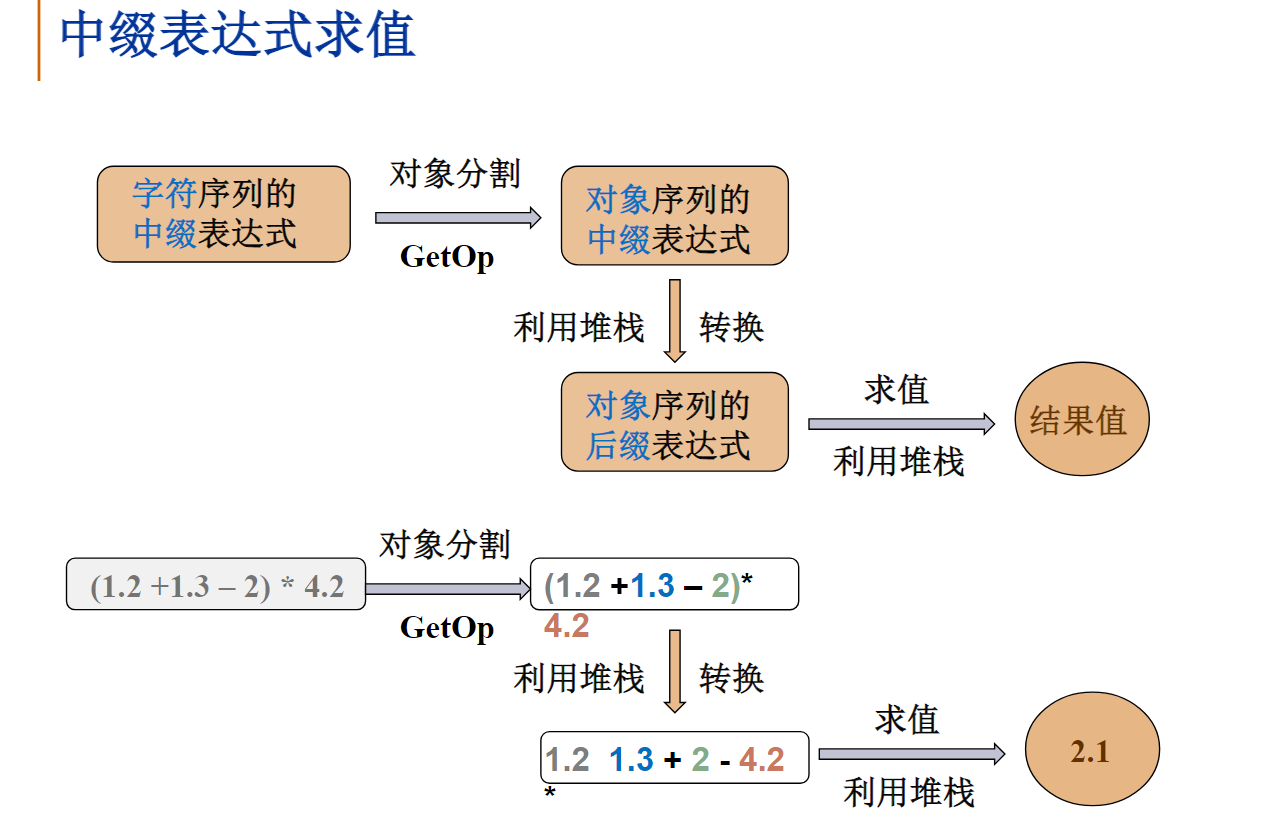

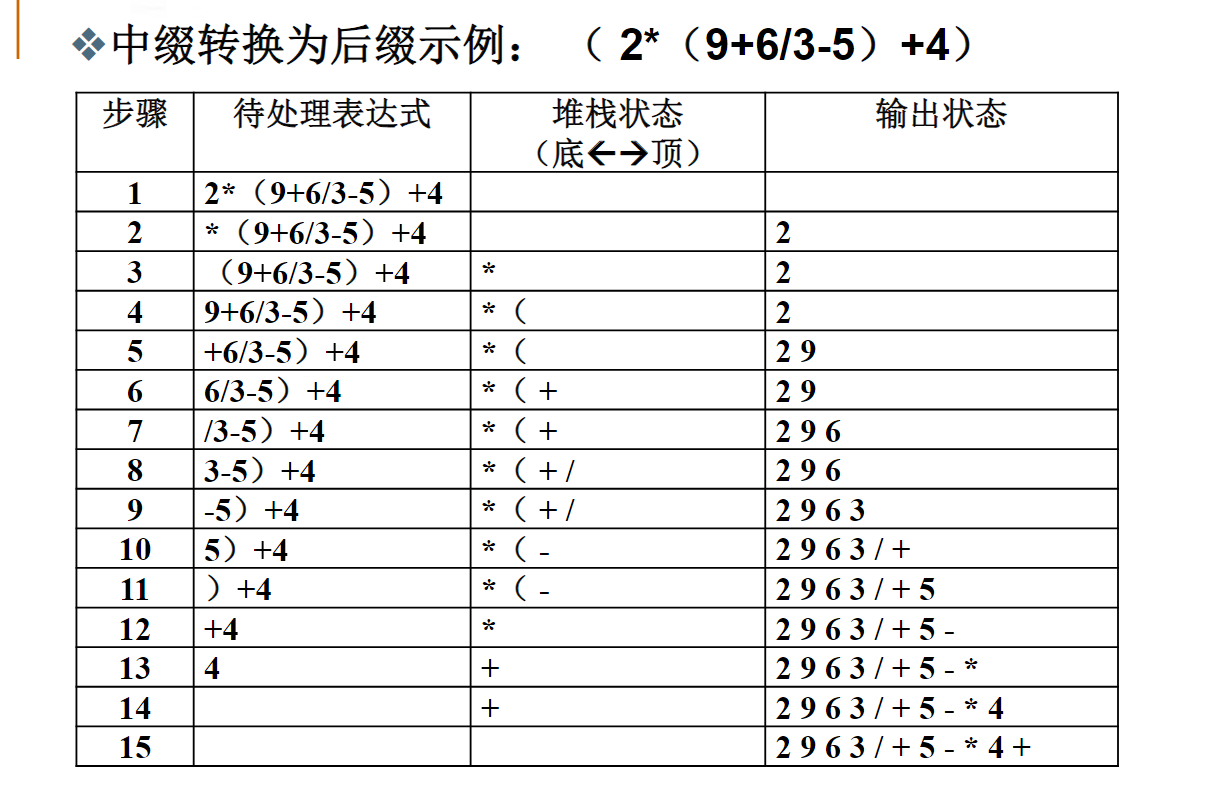

队列Queue
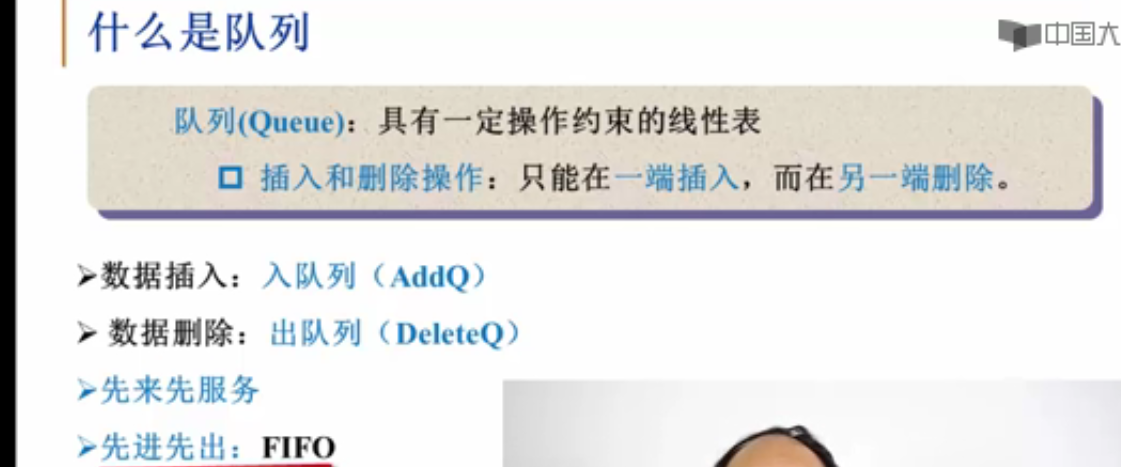

队列的顺序存储实现

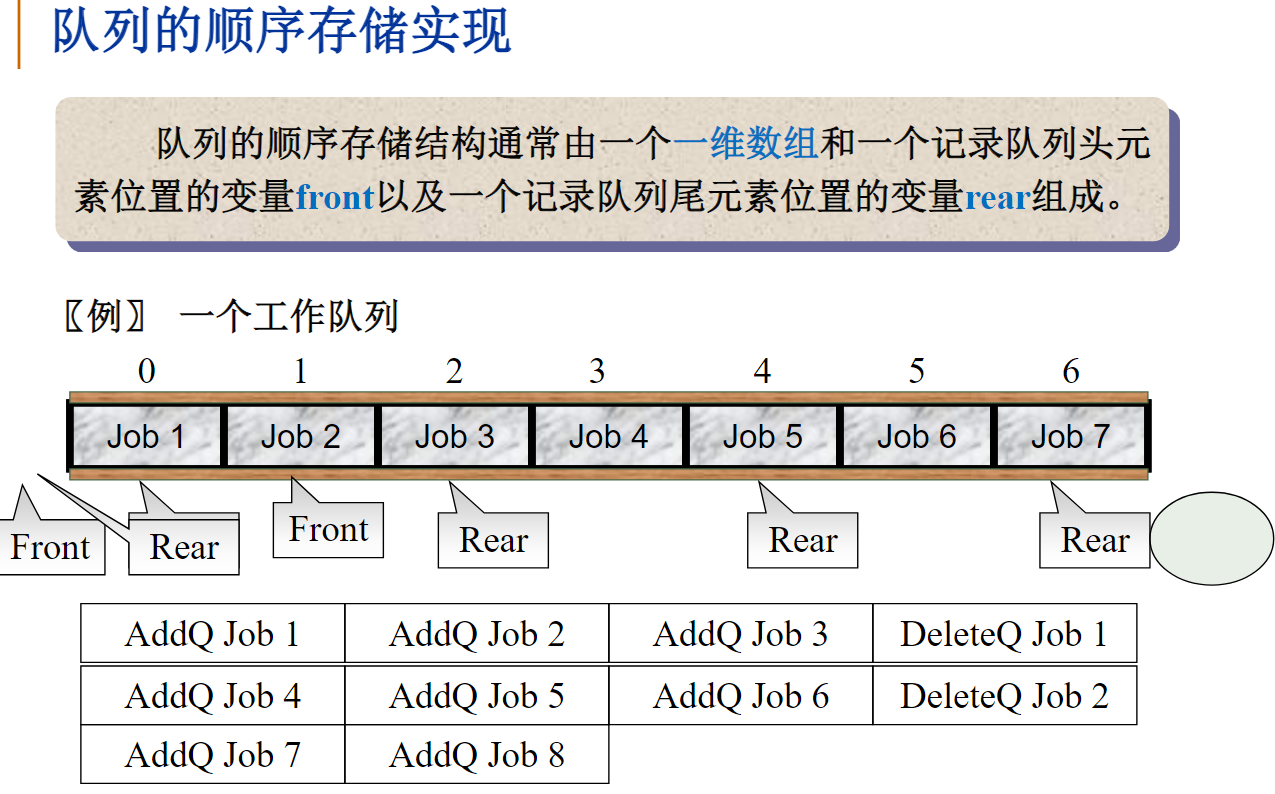
这里对rear和front位置无要求。
如果空队列开始时front和rear值都是-1,当插入4个元素并删除2个元素后,front和rear值分别是多少?1和3
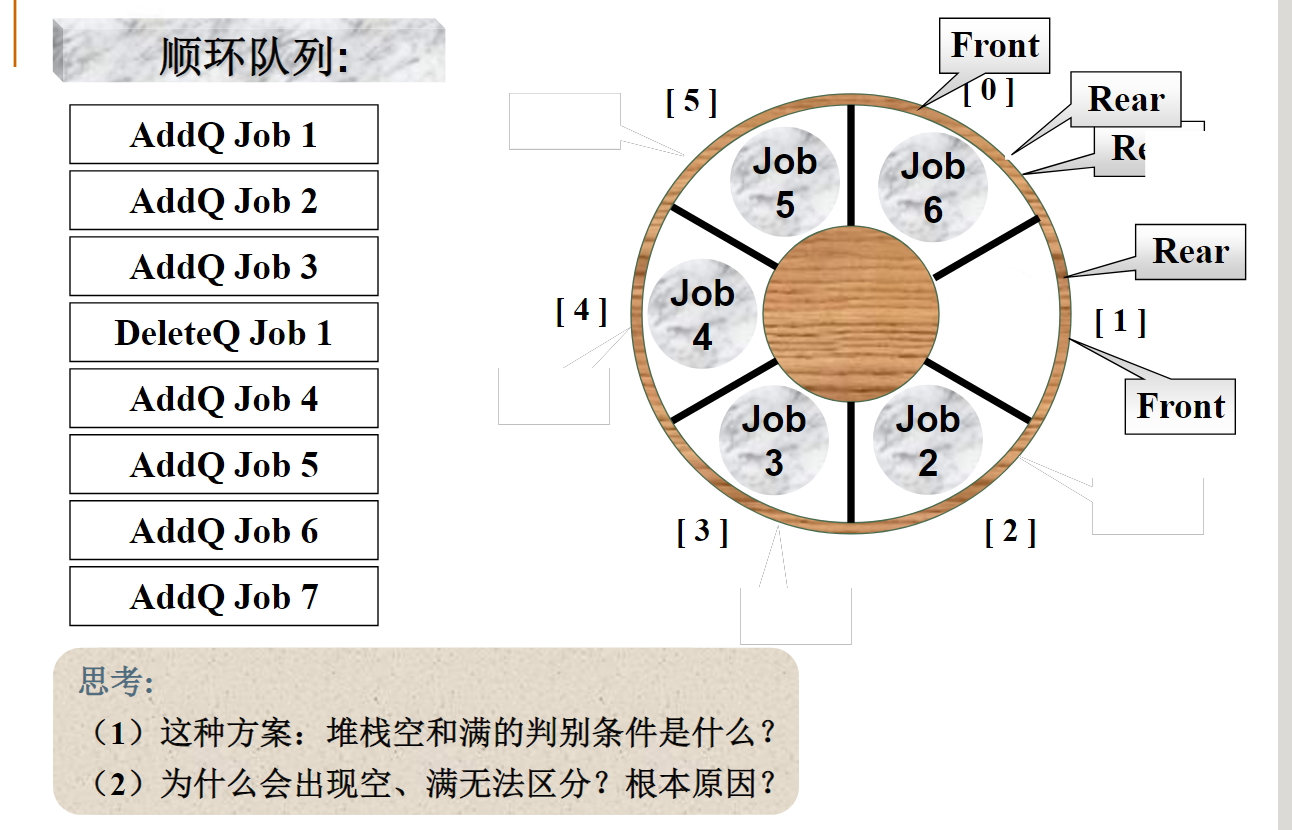
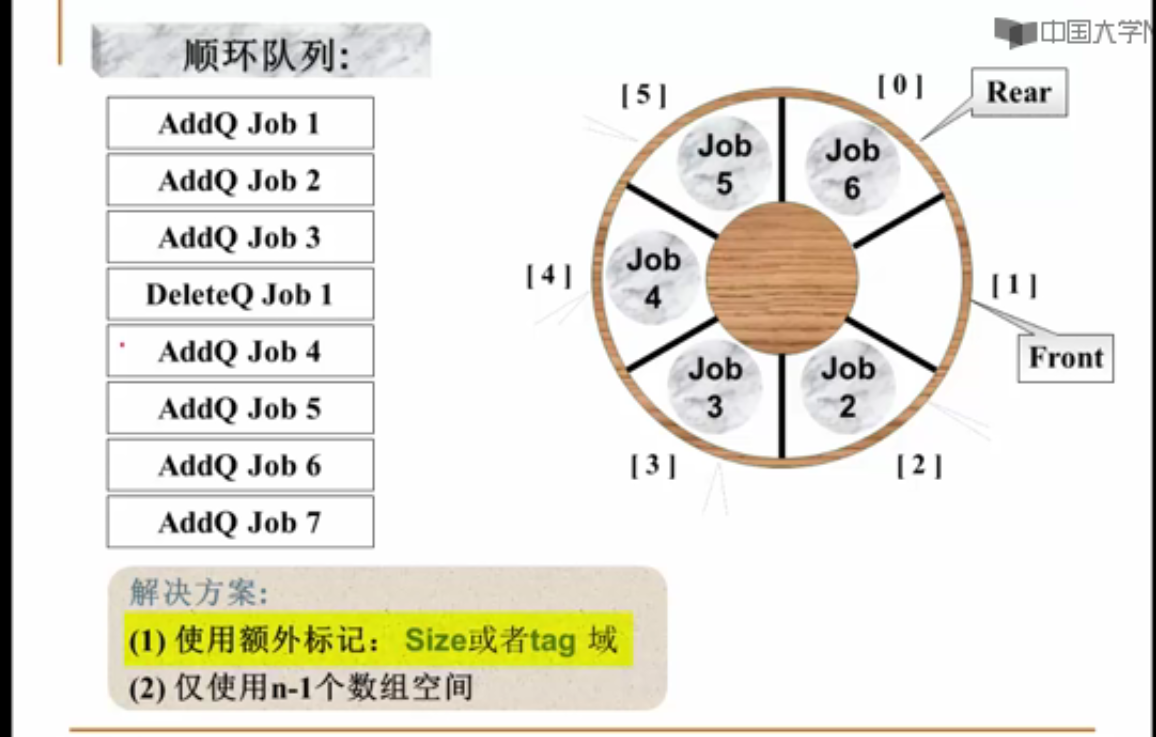
现采用大小为10的数组实现一个循环队列。设在某一时刻,队列为空且此时front和rear值均为5。经过若干操作后,front为8,rear为2,问:此时队列中有4个元素。
通用的队列长度计算公式:队列长度=(rear - front + MaxSize) % MaxSize
解释:front、rear方向一致,front指向实际存在的结点的前一个结点,rear指向实际存在的最后一个结点,此时队列中有9、0、1、2四个位置上的元素。
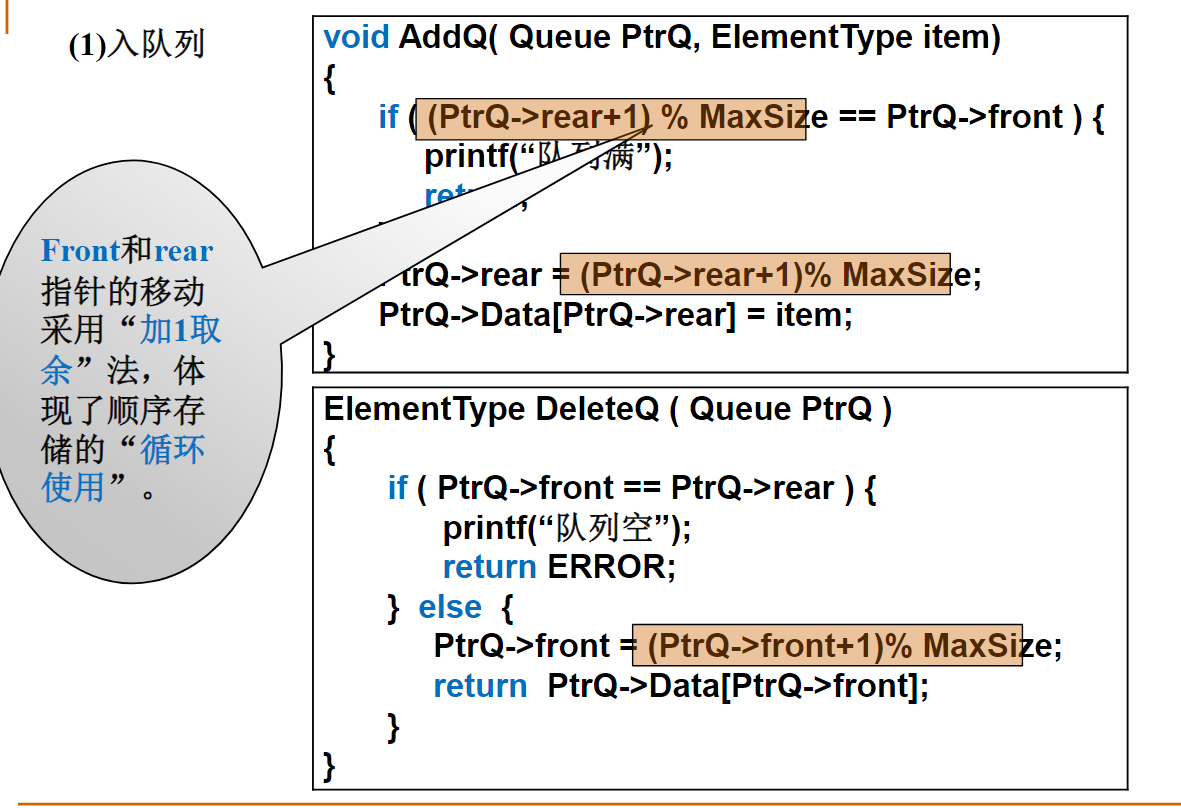
《数据结构》课程给出的队列顺序存储实现方式如下:
typedef int Position;
struct QNode {
ElementType *Data; /* 存储元素的数组 */
Position Front, Rear; /* 队列的头、尾指针 */
int MaxSize; /* 队列最大容量 */
};
typedef struct QNode *Queue;
Queue CreateQueue( int MaxSize )
{
Queue Q = (Queue)malloc(sizeof(struct QNode));
Q->Data = (ElementType *)malloc(MaxSize * sizeof(ElementType));
Q->Front = Q->Rear = 0;
Q->MaxSize = MaxSize;
return Q;
}
bool IsFull( Queue Q )
{
return ((Q->Rear+1)%Q->MaxSize == Q->Front);
}
bool AddQ( Queue Q, ElementType X )
{
if ( IsFull(Q) ) {
printf("队列满");
return false;
}
else {
Q->Rear = (Q->Rear+1)%Q->MaxSize;
Q->Data[Q->Rear] = X;
return true;
}
}
bool IsEmpty( Queue Q )
{
return (Q->Front == Q->Rear);
}
ElementType DeleteQ( Queue Q )
{
if ( IsEmpty(Q) ) {
printf("队列空");
return ERROR;
}
else {
Q->Front =(Q->Front+1)%Q->MaxSize;
return Q->Data[Q->Front];
}
}
测试程序如下:
#include <stdio.h>
#include <stdbool.h>
#define ERROR 0
typedef int ElementType;
typedef struct QNode *Queue;
struct QNode
{
ElementType *Data;
int MaxSize;
int front;
int rear;
};
Queue CreateQueue(int MaxSize)
{
Queue q = (Queue)malloc(sizeof(struct QNode));
q->Data = (ElementType*)malloc(sizeof(ElementType)*MaxSize);
q->front = 0;
q->rear = 0;
q->MaxSize = MaxSize;
return q;
}
bool IsFullQ(Queue q)
{
return (((q->rear+1)%q->MaxSize) == q->front);
}
bool AddQ(Queue q,ElementType item)
{
if(IsFullQ(q))
{
printf("队列已满\n");
return false;
}
else
{
q->rear = (q->rear+1)%(q->MaxSize);
q->Data[q->rear] = item;
return true;
}
}
bool IsEmptyQ(Queue q)
{
return (q->rear == q->front);
}
ElementType DeleteQ(Queue q)
{
if(IsEmptyQ(q))
{
printf("队列为空\n");
return ERROR;
}
else
{
q->front = (q->front+1)%(q->MaxSize);
return (q->Data[q->front]);
}
}
int main()
{
Queue q = CreateQueue(10);
int choice;
while(1)
{
printf("输入1添加1个元素,输入2删除1个元素,输入0结束循环\n");
scanf("%d",&choice);
if(choice == 1)
{
ElementType X;
scanf("%d",&X);
AddQ(q,X);
}
else if(choice == 2)
{
ElementType X = DeleteQ(q);
printf("%d\n",X);
}
else
return 0;
}
}
输入1添加1个元素,输入2删除1个元素,输入0结束循环
1
2
输入1添加1个元素,输入2删除1个元素,输入0结束循环
1
3
输入1添加1个元素,输入2删除1个元素,输入0结束循环
1
1
输入1添加1个元素,输入2删除1个元素,输入0结束循环
1
4
输入1添加1个元素,输入2删除1个元素,输入0结束循环
1
5
输入1添加1个元素,输入2删除1个元素,输入0结束循环
1
6
输入1添加1个元素,输入2删除1个元素,输入0结束循环
2
2
输入1添加1个元素,输入2删除1个元素,输入0结束循环
2
3
输入1添加1个元素,输入2删除1个元素,输入0结束循环
2
1
输入1添加1个元素,输入2删除1个元素,输入0结束循环
2
4
输入1添加1个元素,输入2删除1个元素,输入0结束循环
2
5
输入1添加1个元素,输入2删除1个元素,输入0结束循环
2
6
输入1添加1个元素,输入2删除1个元素,输入0结束循环
2
队列为空
0
输入1添加1个元素,输入2删除1个元素,输入0结束循环
0
Process returned 0 (0x0) execution time : 56.625 s
Press any key to continue.
队列的链式存储实现

队列的front只能设在链表头部。如果front放在链表尾部,删除当前结点后无法找到上一个结点。
在一个链表表示的队列中, f和r分别指向队列的头和尾。r->next=s; r=s;能正确地将s结点插入到队列中。

《数据结构》课程给出的队列链式存储实现方式如下:
typedef struct Node *PtrToNode;
struct Node { /* 队列中的结点 */
ElementType Data;
PtrToNode Next;
};
typedef PtrToNode Position;
struct QNode {
Position Front, Rear; /* 队列的头、尾指针 */
int MaxSize; /* 队列最大容量 */
};
typedef struct QNode *Queue;
bool IsEmpty( Queue Q )
{
return ( Q->Front == NULL);
}
ElementType DeleteQ( Queue Q )
{
Position FrontCell;
ElementType FrontElem;
if ( IsEmpty(Q) ) {
printf("队列空");
return ERROR;
}
else {
FrontCell = Q->Front;
if ( Q->Front == Q->Rear ) /* 若队列只有一个元素 */
Q->Front = Q->Rear = NULL; /* 删除后队列置为空 */
else
Q->Front = Q->Front->Next;
FrontElem = FrontCell->Data;
free( FrontCell ); /* 释放被删除结点空间 */
return FrontElem;
}
}
测试程序如下:
#include <stdio.h>
#include <stdbool.h>
#include <assert.h>
#define ERROR 0
typedef int ElementType;
typedef struct Node *PtrToNode;
struct Node
{
ElementType Data;
PtrToNode Next;
};
PtrToNode CreateNode(ElementType Data)
{
PtrToNode newNode = (PtrToNode)malloc(sizeof(struct Node));
assert(newNode);
newNode->Data = Data;
newNode->Next = NULL;
return newNode;
}
typedef PtrToNode Position;
typedef struct QNode *Queue;
struct QNode
{
PtrToNode Front,Rear;
int curSize;
};
Queue CreateQueue()
{
Queue q = (Queue)malloc(sizeof(struct QNode));
assert(q);
q->curSize = 0;
q->Front = q->Rear = NULL;
return q;
}
void AddQ(Queue q,ElementType item)
{
//PtrToNode s = (PtrToNode)malloc(sizeof(struct Node));
//s->Data = item;
//s->Next = NULL;
PtrToNode s = CreateNode(item);
if(q->curSize == 0)
q->Front = s;
else
q->Rear->Next = s;
q->Rear = s;
q->curSize++;
}
bool IsEmptyQ(Queue q)
{
return (q->Front == NULL);
}
ElementType DeleteQ(Queue q)
{
PtrToNode FrontCell;
ElementType FrontElem;
if(IsEmptyQ(q))
{
printf("队列空!\n");
return ERROR;
}
else
{
FrontCell = q->Front;
if(q->Front == q->Rear)
q->Front = q->Rear = NULL;
else
q->Front = q->Front->Next;
FrontElem = FrontCell->Data;
free(FrontCell);
q->curSize--;
return FrontElem;
}
}
int main()
{
Queue q = CreateQueue();
int choice;
while(1)
{
printf("输入1添加1个元素,输入2删除1个元素,输入0结束循环\n");
scanf("%d",&choice);
if(choice == 1)
{
ElementType X;
scanf("%d",&X);
AddQ(q,X);
}
else if(choice == 2)
{
ElementType X = DeleteQ(q);
printf("%d\n",X);
}
else
return 0;
}
}
输入1添加1个元素,输入2删除1个元素,输入0结束循环
1
2
输入1添加1个元素,输入2删除1个元素,输入0结束循环
1
3
输入1添加1个元素,输入2删除1个元素,输入0结束循环
1
4
输入1添加1个元素,输入2删除1个元素,输入0结束循环
1
5
输入1添加1个元素,输入2删除1个元素,输入0结束循环
2
2
输入1添加1个元素,输入2删除1个元素,输入0结束循环
2
3
输入1添加1个元素,输入2删除1个元素,输入0结束循环
2
4
输入1添加1个元素,输入2删除1个元素,输入0结束循环
2
5
输入1添加1个元素,输入2删除1个元素,输入0结束循环
2
队列空!
0
输入1添加1个元素,输入2删除1个元素,输入0结束循环
0
Process returned 0 (0x0) execution time : 22.052 s
Press any key to continue.
如何用两个堆栈模拟实现一个队列?
如何用两个堆栈模拟实现一个队列? 如果这两个堆栈的容量分别是m和n(m>n),你的方法能保证的队列容量是多少?
MOOC-PTA线性结构题目
- PTA 02-线性结构1 两个有序链表序列的合并
- PTA02-线性结构2 一元多项式的乘法与加法运算
- PTA 02-线性结构3 Reversing Linked List
- PTA 02-线性结构4 Pop Sequence
PTA 02-线性结构1 两个有序链表序列的合并
本题要求实现一个函数,将两个链表表示的递增整数序列合并为一个非递减的整数序列。
函数接口定义:
List Merge( List L1, List L2 );
其中List结构定义如下:
typedef struct Node *PtrToNode;
struct Node {
ElementType Data; /* 存储结点数据 */
PtrToNode Next; /* 指向下一个结点的指针 */
};
typedef PtrToNode List; /* 定义单链表类型 */
L1和L2是给定的带头结点的单链表,其结点存储的数据是递增有序的;函数Merge要将L1和L2合并为一个非递减的整数序列。应直接使用原序列中的结点,返回归并后的带头结点的链表头指针。
裁判测试程序样例:
#include <stdio.h>
#include <stdlib.h>
typedef int ElementType;
typedef struct Node *PtrToNode;
struct Node {
ElementType Data;
PtrToNode Next;
};
typedef PtrToNode List;
List Read(); /* 细节在此不表 */
void Print( List L ); /* 细节在此不表;空链表将输出NULL */
List Merge( List L1, List L2 );
int main()
{
List L1, L2, L;
L1 = Read();
L2 = Read();
L = Merge(L1, L2);
Print(L);
Print(L1);
Print(L2);
return 0;
}
/* 你的代码将被嵌在这里 */
输入样例:
3
1 3 5
5
2 4 6 8 10
输出样例:
1 2 3 4 5 6 8 10
NULL
NULL
能AC的代码如下:
List Merge( List L1, List L2 )
{
if(L1 == NULL || L2 == NULL)
return (L1 == NULL)?L2:L1;
List head = (List)malloc(sizeof(struct Node));
List cur1 = L1->Next;
List cur2 = L2->Next;
List pre = head;
while(cur1 != NULL && cur2 != NULL)
{
if(cur1->Data <= cur2->Data)
{
pre->Next = cur1;
cur1 = cur1->Next;
}
else
{
pre->Next = cur2;
cur2 = cur2->Next;
}
pre = pre->Next;
}
pre->Next = (cur1 != NULL)?cur1:cur2;
L1->Next = NULL;
L2->Next = NULL;
return head;
}
PTA02-线性结构2 一元多项式的乘法与加法运算
设计函数分别求两个一元多项式的乘积与和。
输入格式:
输入分2行,每行分别先给出多项式非零项的个数,再以指数递降方式输入一个多项式非零项系数和指数(绝对值均为不超过1000的整数)。数字间以空格分隔。
输出格式:
输出分2行,分别以指数递降方式输出乘积多项式以及和多项式非零项的系数和指数。数字间以空格分隔,但结尾不能有多余空格。零多项式应输出0 0。
输入样例:
4 3 4 -5 2 6 1 -2 0
3 5 20 -7 4 3 1
输出样例:
15 24 -25 22 30 21 -10 20 -21 8 35 6 -33 5 14 4 -15 3 18 2 -6 1
5 20 -4 4 -5 2 9 1 -2 0




如果当前p1指向项的(系数,指数)为(2,4),同时P2指向项为(2,6),那么循环中的switch是执行case -1。


#include <stdio.h>
#include <stdlib.h>
typedef struct PolyNode *Polynomial;
struct PolyNode
{
int coef;
int expon;
Polynomial link;
};
Polynomial ReadPoly()
{
Polynomial P,Rear,temp;
int n,e,c;
scanf("%d",&n);
P = (Polynomial)malloc(sizeof(struct PolyNode));
P->link = NULL;
Rear = P;
while(n--)
{
scanf("%d %d",&c,&e);
Attach(c,e,&Rear);
}
temp = P;
P = P->link;
free(temp);
return P;
}
void Attach(int c,int e,Polynomial *pRear)
{
Polynomial P = (Polynomial)malloc(sizeof(struct PolyNode));
P->coef = c;
P->expon = e;
P->link = NULL;
(*pRear)->link = P;
*pRear = P;
}
int Compare(int a,int b)
{
if(a>b)
return 1;
else if(a<b)
return -1;
else
return 0;
}
/*
Polynomial AddPoly(Polynomial P1,Polynomial P2)
{
Polynomial front,rear,temp;
int sum = 0;
rear = (Polynomial)malloc(sizeof(struct PolyNode));
front = rear;
while(P1&&P2)
{
switch(Compare(P1->expon,P2->expon))
{
case 1:
Attach(P1->coef,P1->expon,&rear);
P1 = P1->link;
break;
case -1:
Attach(P2->coef,P2->expon,&rear);
P2 = P2->link;
break;
case 0:
sum = P1->coef + P2->coef;
if(sum)
Attach(sum,P1->expon,&rear);
P1 = P1->link;
P2 = P2->link;
break;
}
for(;P1;P1 = P1->link)
Attach(P1->coef,P1->expon,&rear);
for(;P2;P2 = P2->link)
Attach(P2->coef,P2->expon,&rear);
rear->link = NULL;
temp = front;
front = front->link;
free(temp);
return front;
}
}
*/
Polynomial AddPoly(Polynomial P1,Polynomial P2)
{
Polynomial t1,t2,P,Rear,temp;
int sum;
t1 = P1;
t2 = P2;
P = (Polynomial)malloc(sizeof(struct PolyNode));
P->link = NULL;
Rear = P;
while(t1&&t2)
{
if(t1->expon == t2->expon)
{
sum = t1->coef + t2->coef;
if(sum)
Attach(sum,t1->expon,&Rear);
t1 = t1->link;
t2 = t2->link;
}
else if(t1->expon > t2->expon)
{
Attach(t1->coef,t1->expon,&Rear);
t1 = t1->link;
}
else
{
Attach(t2->coef,t2->expon,&Rear);
t2 = t2->link;
}
}
while(t1)
{
Attach(t1->coef,t1->expon,&Rear);
t1 = t1->link;
}
while(t2)
{
Attach(t2->coef,t2->expon,&Rear);
t2 = t2->link;
}
Rear->link = NULL;
temp = P;
P = P->link;
free(temp);
return P;
}
Polynomial MultPoly(Polynomial P1,Polynomial P2)
{
Polynomial t1,t2,temp,P,Rear;
int c,e;
if(!P1 || !P2)
return NULL;
t1 = P1;
t2 = P2;
P = (Polynomial)malloc(sizeof(struct PolyNode));
P->link = NULL;
Rear = P;
while(t2)
{
Attach(t1->coef * t2->coef,t1->expon + t2->expon,&Rear);
t2 = t2->link;
}
t1 = t1->link;
while(t1)
{
t2 = P2;
Rear = P;
while(t2)
{
e = t1->expon + t2->expon;
c = t1->coef * t2->coef;
while(Rear->link && Rear->link->expon > e)
Rear = Rear->link;
if(Rear->link && Rear->link->expon == e)
{
if(Rear->link->coef + c)
Rear->link->coef += c;
else
{
temp = Rear->link;
Rear->link = temp->link;
free(temp);
}
}
else
{
temp = (Polynomial)malloc(sizeof(struct PolyNode));
temp->coef = c;
temp->expon = e;
temp->link = Rear->link;
Rear->link = temp;
Rear = Rear->link;
}
t2 = t2->link;
}
t1 = t1->link;
}
t2 = P;
P = P->link;
free(t2);
return P;
}
void PrintPoly(Polynomial P)
{
int flag = 0;
if(!P)
{
printf("0 0\n");
return;
}
while(P)
{
if(!flag)
flag = 1;
else
printf(" ");
printf("%d %d",P->coef,P->expon);
P = P->link;
}
printf("\n");
}
int main()
{
Polynomial P1,P2,PP,PS;
P1 = ReadPoly();
P2 = ReadPoly();
PP = MultPoly(P1,P2);
PrintPoly(PP);
PS = AddPoly(P1,P2);
PrintPoly(PS);
return 0;
}
PTA 02-线性结构3 Reversing Linked List
Given a constant K and a singly linked list L, you are supposed to reverse the links of every K elements on L. For example, given L being 1→2→3→4→5→6, if K=3, then you must output 3→2→1→6→5→4; if K=4, you must output 4→3→2→1→5→6.
Input Specification:
Each input file contains one test case. For each case, the first line contains the address of the first node, a positive N (≤105) which is the total number of nodes, and a positive K (≤N) which is the length of the sublist to be reversed. The address of a node is a 5-digit nonnegative integer, and NULL is represented by -1.
Then N lines follow, each describes a node in the format:
Address Data Next
where Address is the position of the node, Data is an integer, and Next is the position of the next node.
Output Specification:
For each case, output the resulting ordered linked list. Each node occupies a line, and is printed in the same format as in the input.
Sample Input:
00100 6 4
00000 4 99999
00100 1 12309
68237 6 -1
33218 3 00000
99999 5 68237
12309 2 33218
Sample Output:
00000 4 33218
33218 3 12309
12309 2 00100
00100 1 99999
99999 5 68237
68237 6 -1
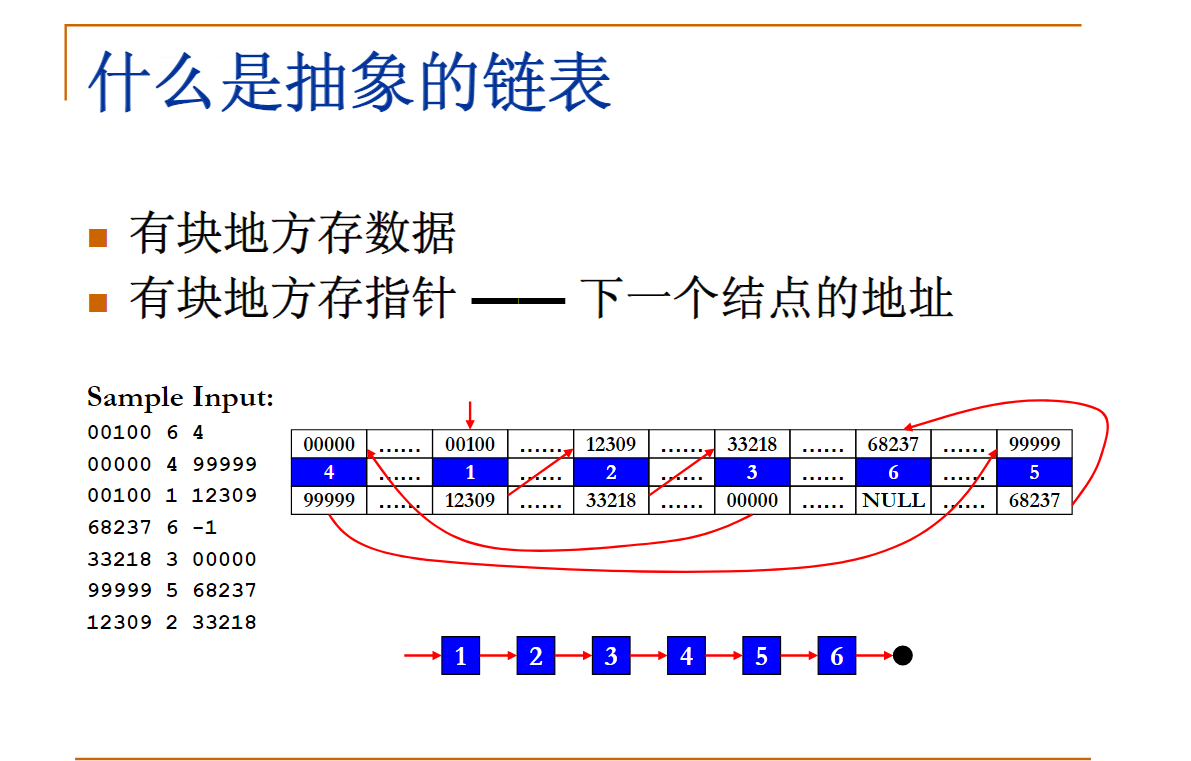
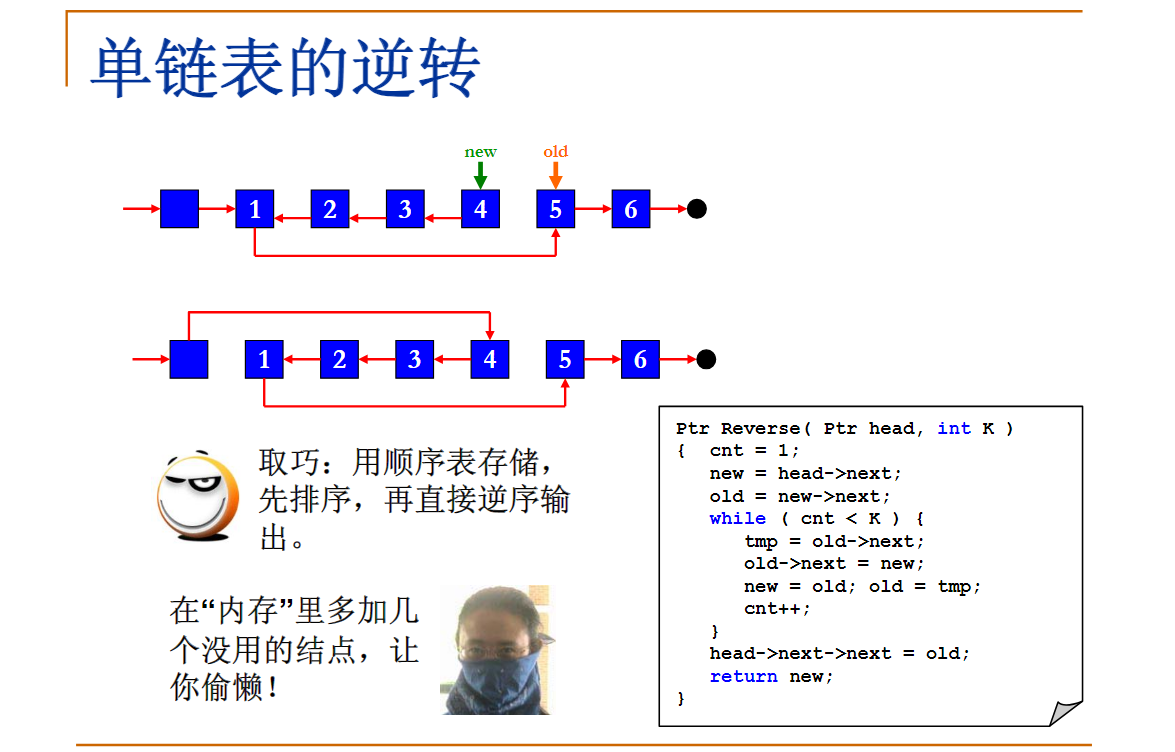

#include <stdio.h>
#include <stdlib.h>
typedef int Address;
typedef int Data;
typedef struct Node *Ptr;
#define MaxSize 100001
struct Node
{
Data data;
Address next;
}Nodes[MaxSize];
int List[MaxSize];
void Reverse(Address head, Address tail)
{
int tempHead = head;
int tempTail = tail;
int list;
while(tempTail > tempHead)
{
list = List[tempHead];
List[tempHead] = List[tempTail];
List[tempTail] = list;
tempHead++;
tempTail--;
}
}
int main()
{
int n;
Address root;
int K;
scanf("%d %d %d",&root,&n,&K);
Address address;
Data data;
Address next;
for(int i=0; i<n; i++)
{
scanf("%d %d %d", &address,&data,&next);
Nodes[address].data = data;
Nodes[address].next = next;
}
int maxn = 0;
int pMove = root;
while(pMove != -1)
{
List[maxn++] = pMove;
pMove = Nodes[pMove].next;
}
int i = 0;
while(i + K < maxn)
{
Reverse(i,i+K-1);
i = i + K;
}
for(i=0;i<maxn-1;i++)
printf("%05d %d %05d\n",List[i],Nodes[List[i]].data,List[i+1]);
printf("%05d %d -1\n",List[i],Nodes[List[i]].data);
return 0;
}
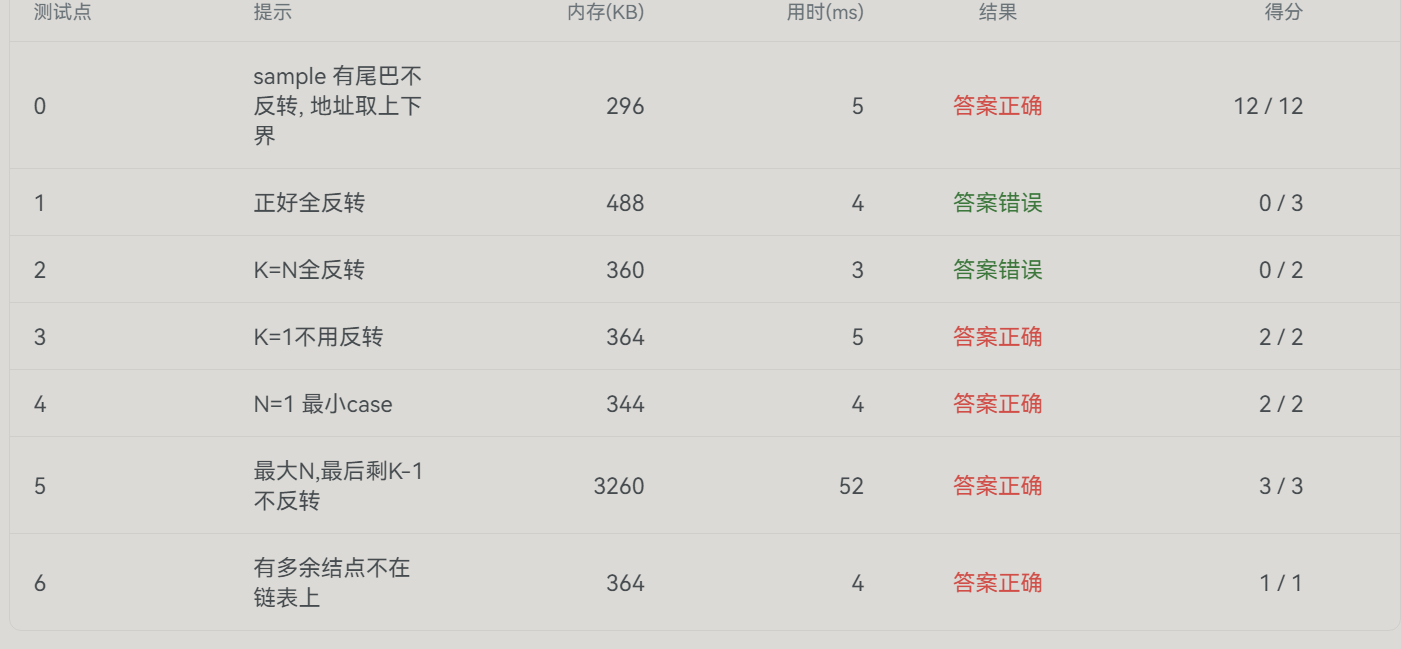
使用C++的reverse函数解法如下:
#include<iostream>
#include<stdio.h>
#include<algorithm> ///使用到reverse 翻转函数
using namespace std;
#define MAXSIZE 1000010 ///最大为五位数的地址
struct node ///使用顺序表存储data和下一地址next
{
int data;
int next;
}node[MAXSIZE];
int List[MAXSIZE]; ///存储可以连接上的顺序表
int main()
{
int First, n, k;
cin>>First>>n>>k; ///输入头地址 和 n,k;
int Address,Data,Next;
for(int i=0;i<n;i++)
{
cin>>Address>>Data>>Next;
node[Address].data=Data;
node[Address].next=Next;
}
int j=0; ///j用来存储能够首尾相连的节点数
int p=First; ///p指示当前结点
while(p!=-1)
{
List[j++]=p;
p=node[p].next;
}
int i=0;
while(i+k<=j) ///每k个节点做一次翻转
{
reverse(&List[i],&List[i+k]);
i=i+k;
}
for(i=0;i<j-1;i++)
printf("%05d %d %05d\n",List[i],node[List[i]].data,List[i+1]);
printf("%05d %d -1\n",List[i],node[List[i]].data);
return 0;
}
PTA 02-线性结构4 Pop Sequence
Given a stack which can keep M numbers at most. Push N numbers in the order of 1, 2, 3, ..., N and pop randomly. You are supposed to tell if a given sequence of numbers is a possible pop sequence of the stack. For example, if M is 5 and N is 7, we can obtain 1, 2, 3, 4, 5, 6, 7 from the stack, but not 3, 2, 1, 7, 5, 6, 4.
Input Specification:
Each input file contains one test case. For each case, the first line contains 3 numbers (all no more than 1000): M (the maximum capacity of the stack), N (the length of push sequence), and K (the number of pop sequences to be checked). Then K lines follow, each contains a pop sequence of N numbers. All the numbers in a line are separated by a space.
Output Specification:
For each pop sequence, print in one line "YES" if it is indeed a possible pop sequence of the stack, or "NO" if not.
Sample Input:
5 7 5 1 2 3 4 5 6 7 3 2 1 7 5 6 4 7 6 5 4 3 2 1 5 6 4 3 7 2 1 1 7 6 5 4 3 2
Sample Output:
YES
NO
NO
YES
NO
#include <stdio.h>
#include <stdlib.h>
#define Maxsize 1000//最大容量
typedef struct Node
{
int Top;//栈顶
int Data[Maxsize];//元素
int Capacity;//容量
}*Stack;
int Test(int Array[],int M,int N)
{
int count = 0;
Stack Pile = (Stack)malloc(sizeof(struct Node));//申请并初始化一个空栈
Pile->Capacity = M;
Pile->Top = -1;
for(int i = 1;i <= N;i++)
{
if(Pile->Capacity == Pile->Top+1)//栈满
return 0;
else
Pile->Data[++Pile->Top] = i;//入栈
while(Pile->Data[Pile->Top] == Array[count])
{//比较栈顶是否与某数相等
Pile->Top--;//出栈
count++;//数组往后移位
}
}
if(count == N)//全部找到并且输出时
return 1;
else
return 0;
}
int main()
{
int M,N,K;
scanf("%d %d %d",&M,&N,&K);
int Array[N];
for(int i=0; i<K; i++)
{
for(int j=0; j<N; j++)
{
scanf("%d",&Array[j]);
}
if(Test(Array,M,N))
printf("YES\n");
else
printf("NO\n");
}
return 0;
}
引子:二分查找



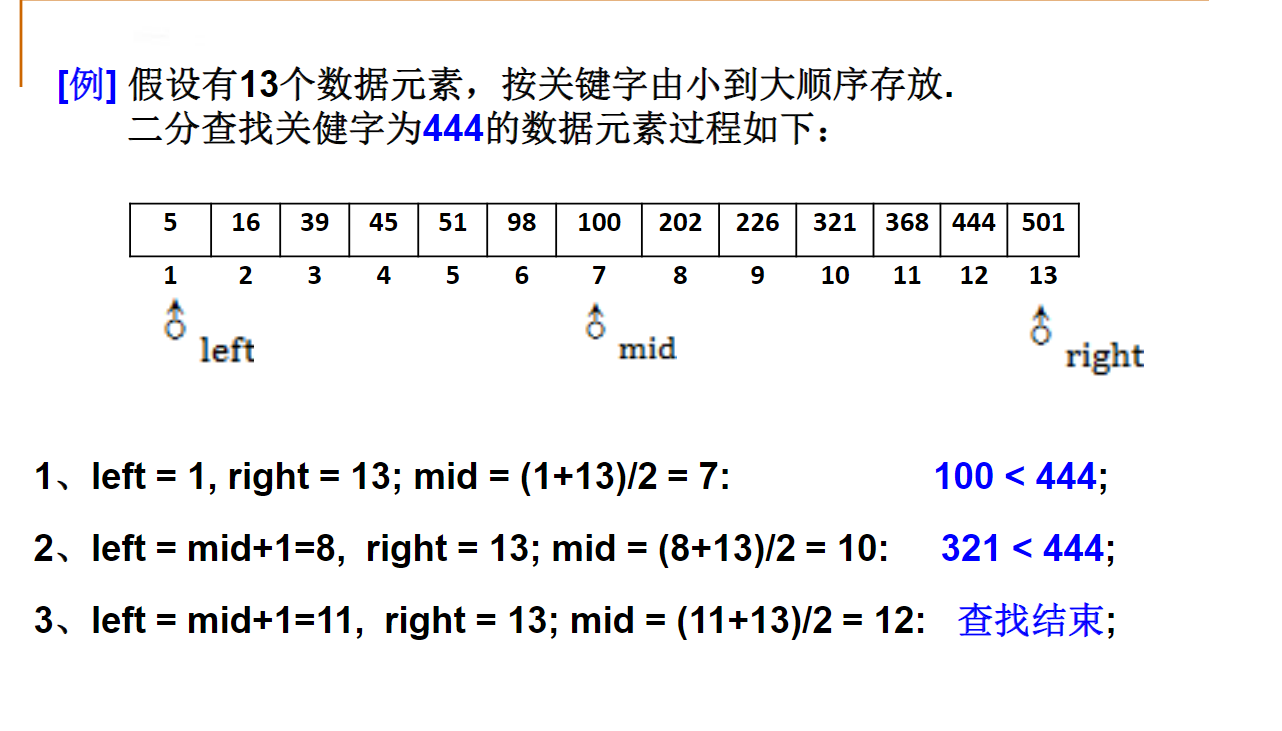
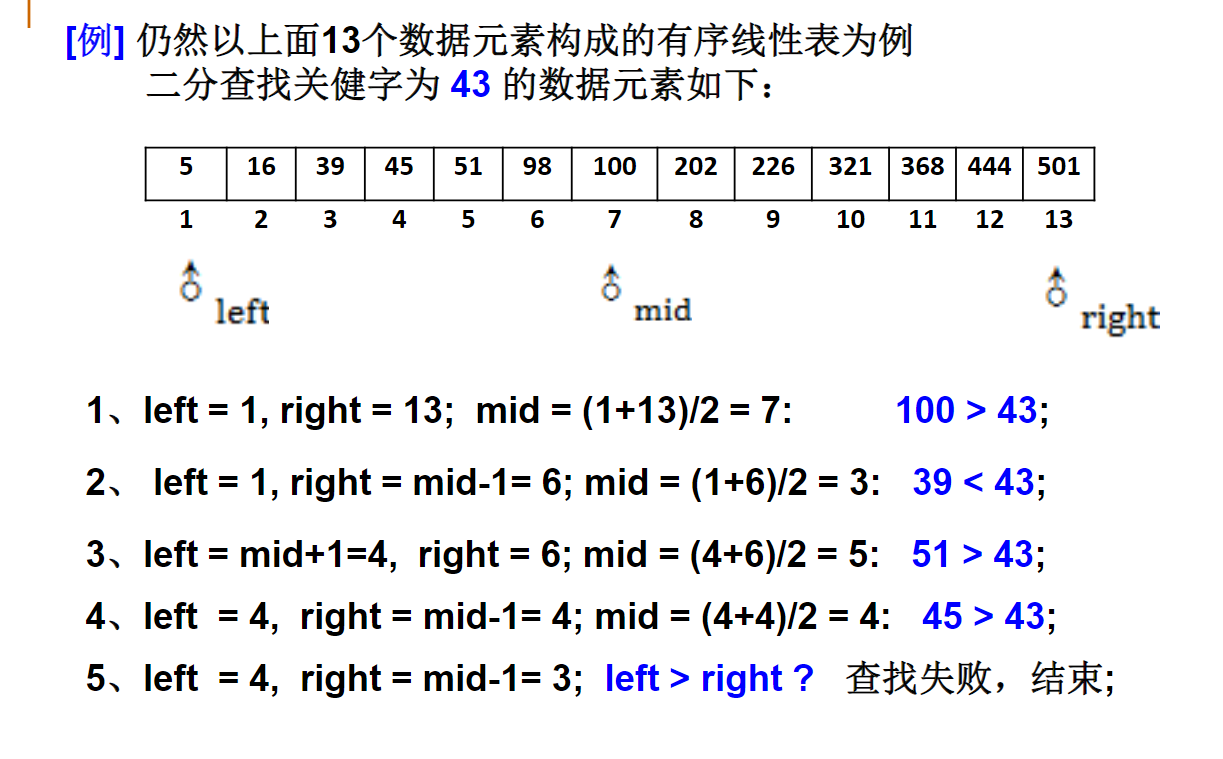

int BinarySearch(StaticTable *Tbl,ElementType K)
{
int left,right,mid,NotFound = -1;
left = 1;
right = Tbl->Length;
while(left <= right)
{
mid = (left + right) / 2;
if(K > Tbl->Element[mid])
left = mid + 1;
else if(K < Tbl->Element[mid])
right = mid - 1;
else
return mid;
}
return NotFound;
}
在分量1~11的数组中按从小到大顺序存放11个元素,如果用顺序查找和二分查找分别查找这11个元素,哪个位置的元素在这两种方法的查找中总次数最少?1
在分量1~11的数组中按从小到大顺序存放11个元素,如果进行二分查找,查找次数最少的元素位于什么位置?6
测试程序如下:
#include <stdio.h>
int OrderSearch(int arr[],int n,int x)
{
for(int i = 0 ; i < n; i++)
{
if(x == arr[i])
return i;
}
return -1;
}
int BinarySearch(int arr[],int n,int x)
{
int left = 0;
int right = n-1;
int mid;
while(left <= right)
{
mid = (left + right) / 2;
if(arr[mid] < x)
left = mid + 1;
else if(arr[mid] > x)
right = mid - 1;
else
return mid;
}
return -1;
}
int main()
{
int n = 10;
int arr[10] = {1,2,3,4,5,6,7,8,9,10};
int x = 3;
printf("%d\n",BinarySearch(arr,n,x));
printf("%d\n",OrderSearch(arr,n,x));
return 0;
}
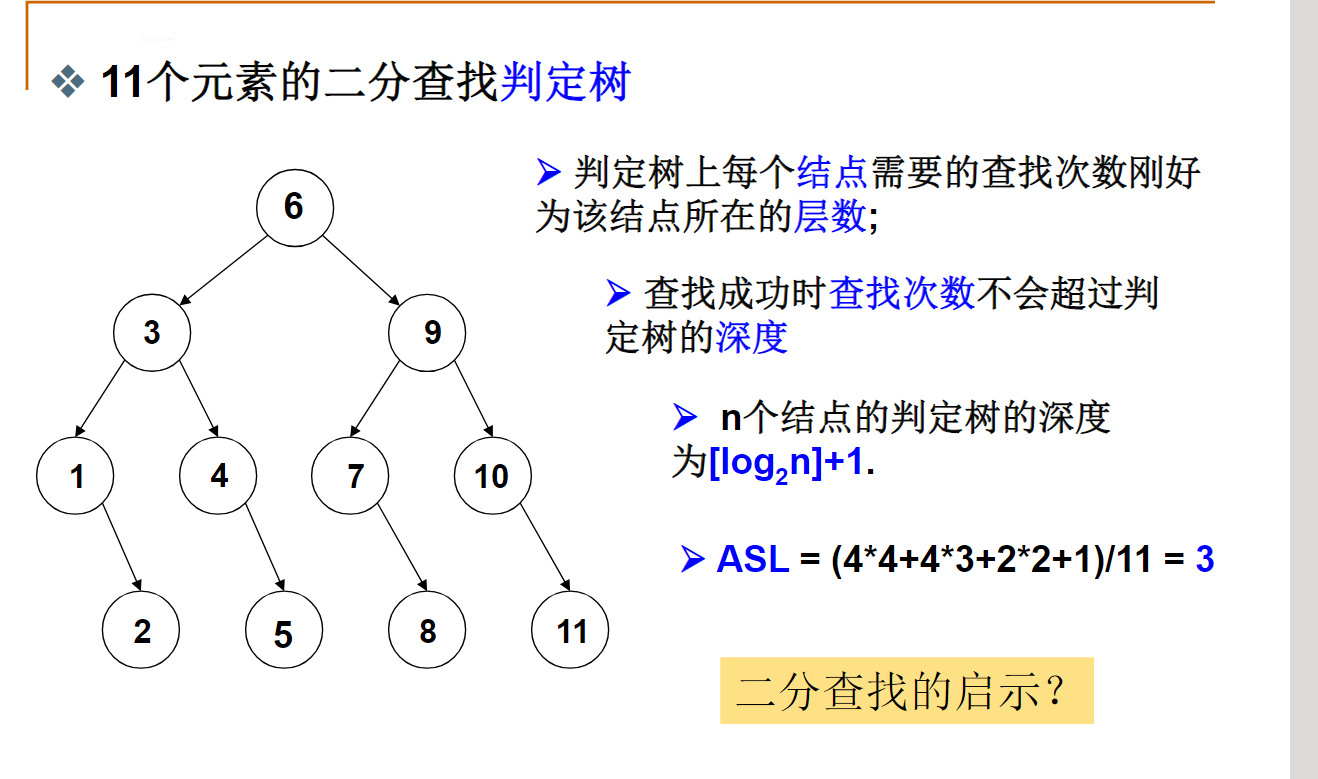
ASL:Average Search Length平均查找长度
树的定义
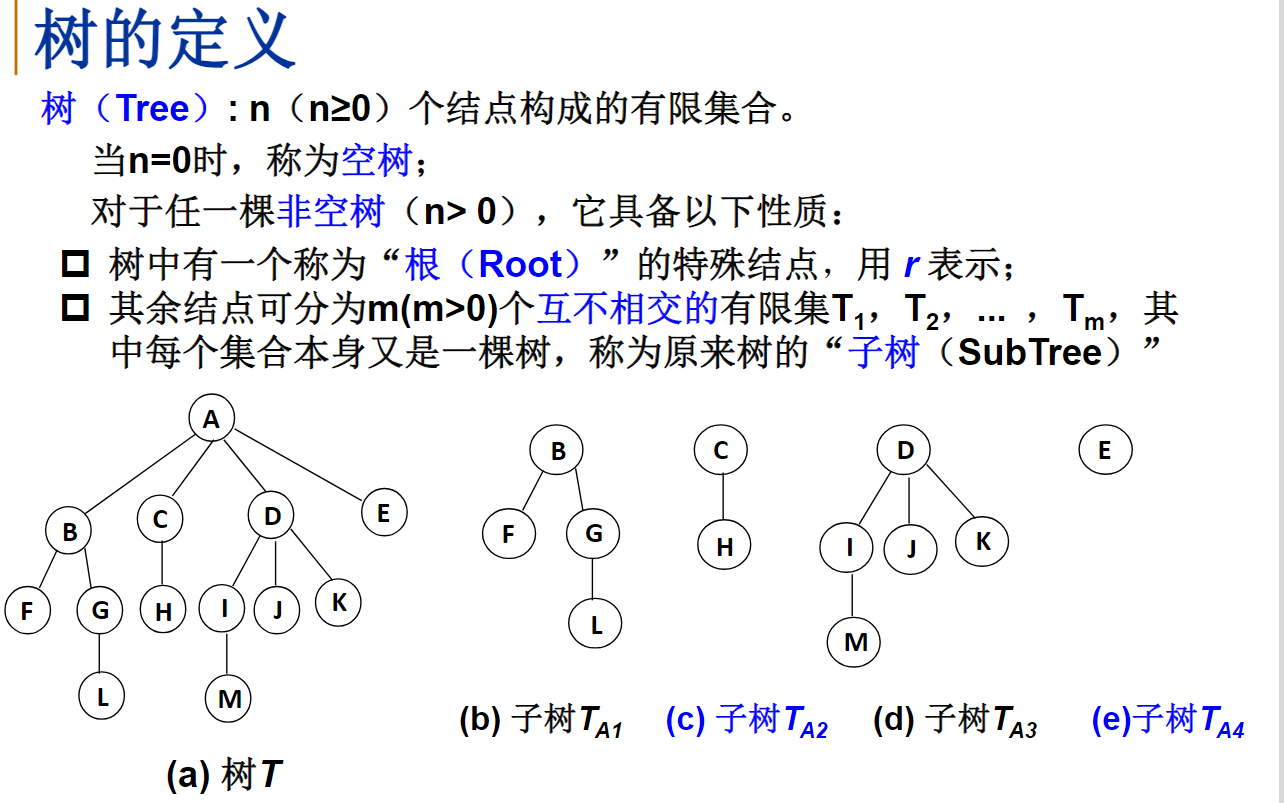
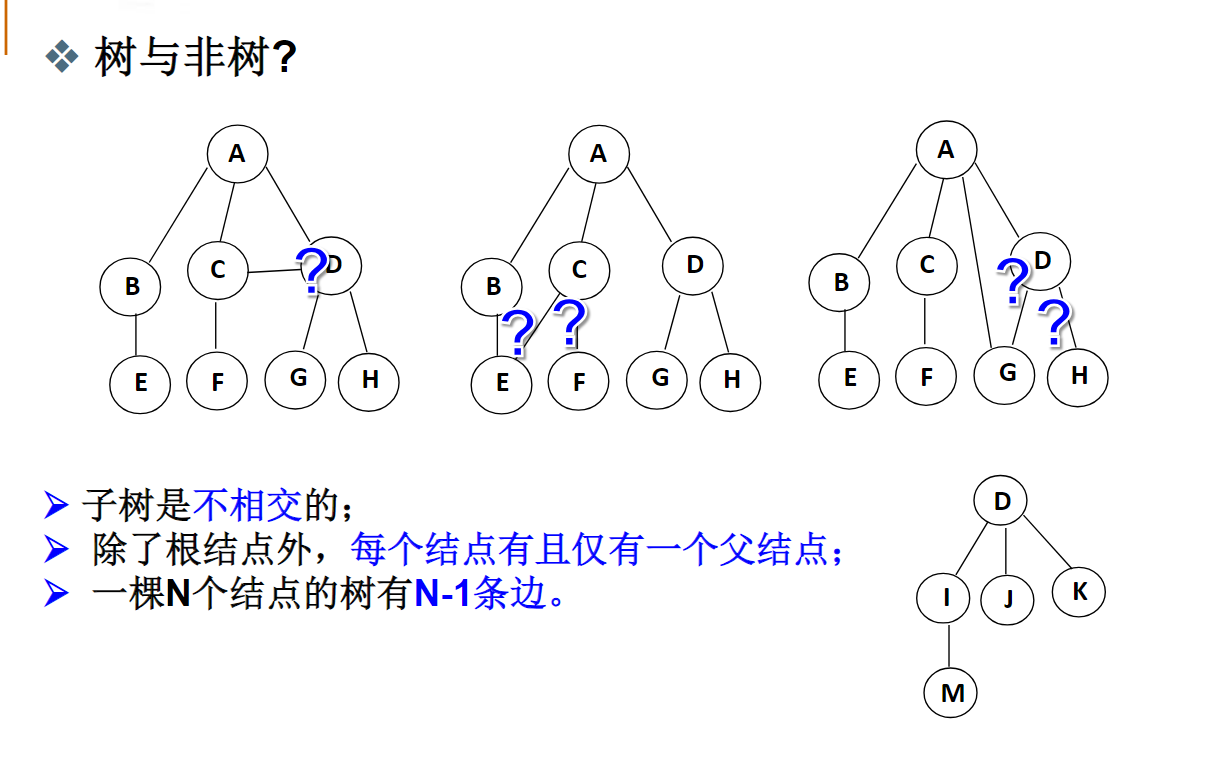
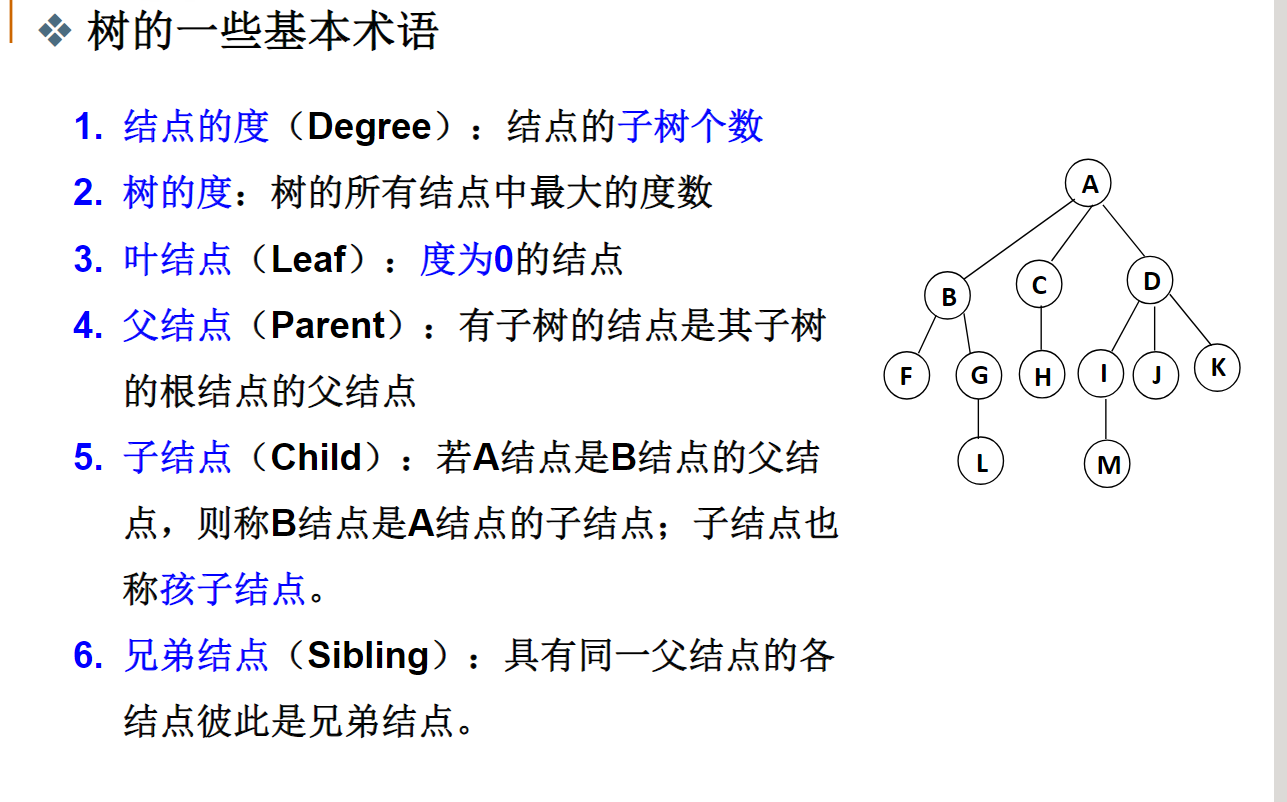

有一个m棵树的集合(也叫森林)共有k条边,问这m颗树共有多少个结点?k+m
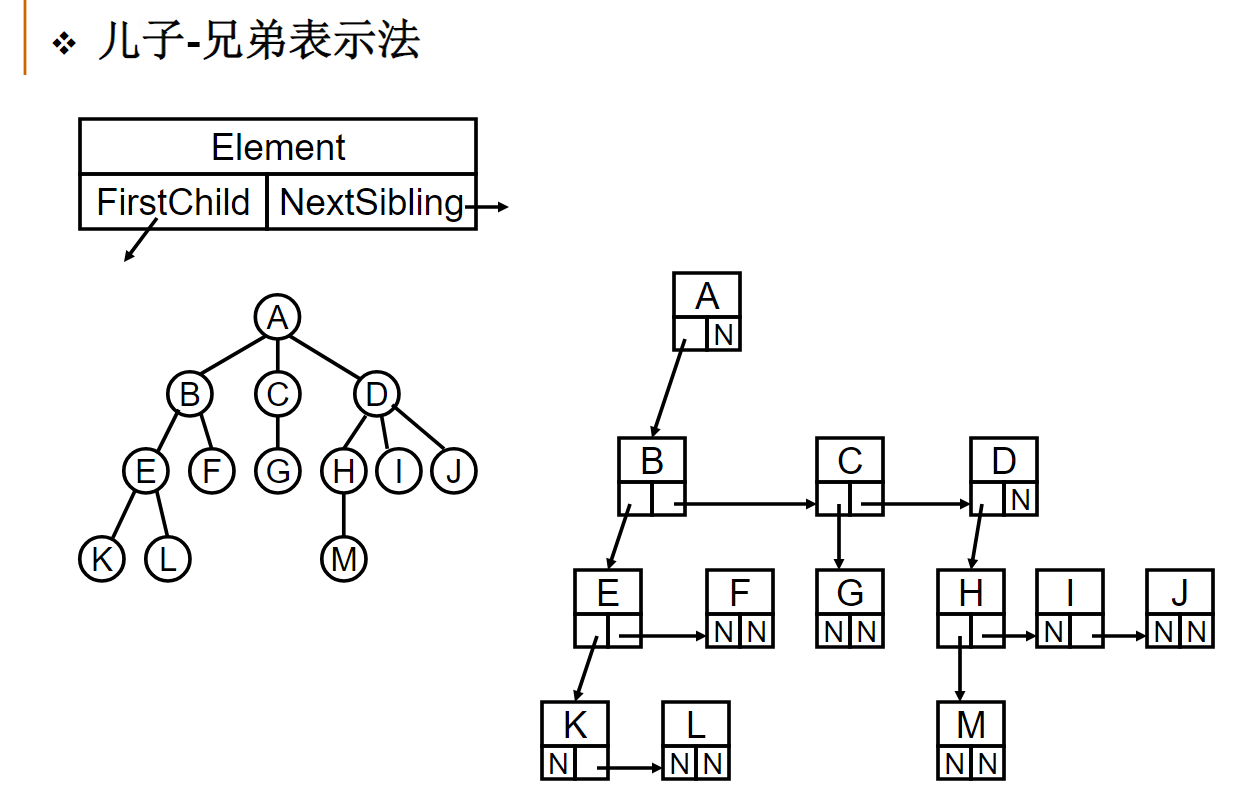
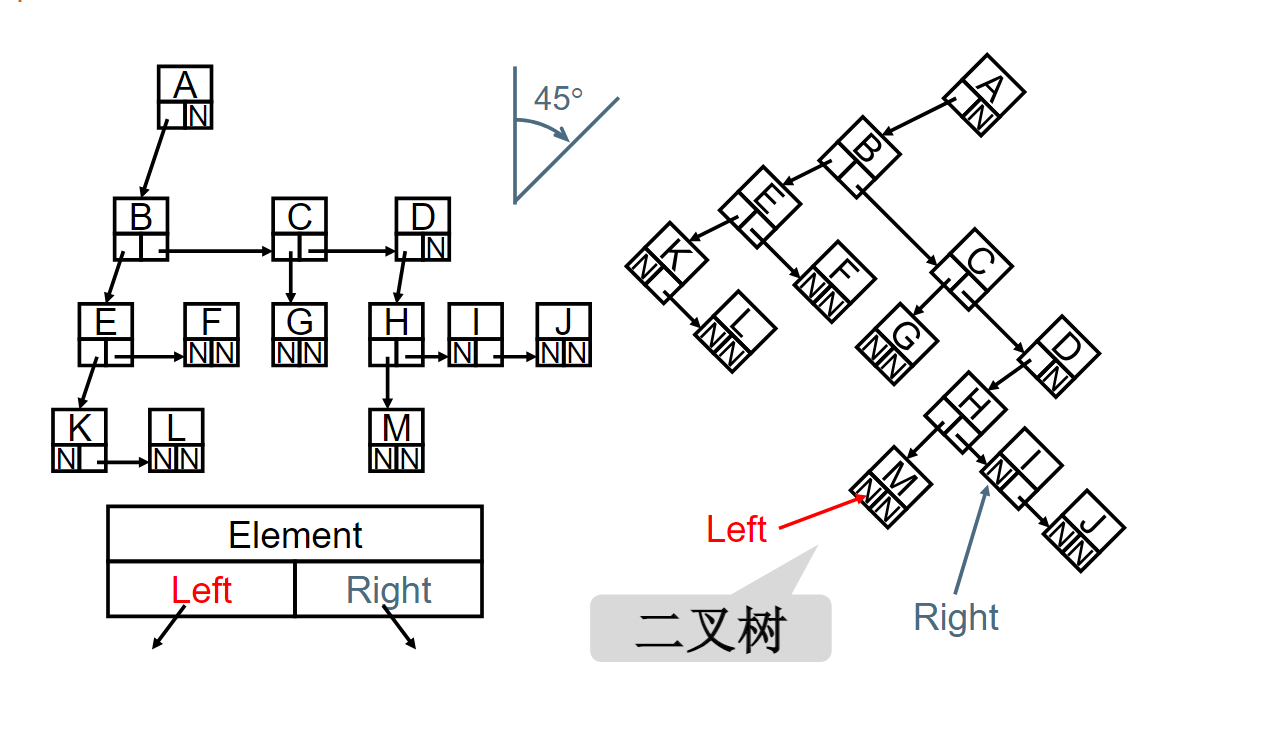
在用“儿子-兄弟”法表示的树中,如果从根结点开始访问其“次子”的“次子”,所经过的结点数与从根结点开始访问其“长子”的“长子”的“长子”的“长子”一样。(注意:比较的是结点数,而不是路径)
一棵度为 m的树有n个节点。若每个节点直接用m个链指向相应的儿子,则表示这个树所需要的总空间是n*(m+1) (假定每个链以及表示节点的数据域都是一个单位空间).。当采用儿子/兄弟(First Child/Next Sibling)表示法时,所需的总空间是:3n
树的集合称为森林。是否也可以使用“儿子-兄弟”表示法存储森林?如何实现?
是的,可以使用"儿子-兄弟"表示法(又称作"左孩子-右兄弟"表示法或"孩子兄弟链表")来存储森林,其中每个节点表示一棵树。这种表示法适用于多叉树和森林结构,它使用两个指针来表示树中的节点之间的关系:左孩子指针和右兄弟指针。左孩子指针指向当前节点的第一个子节点,而右兄弟指针指向当前节点的兄弟节点。
二叉树
二叉树的定义
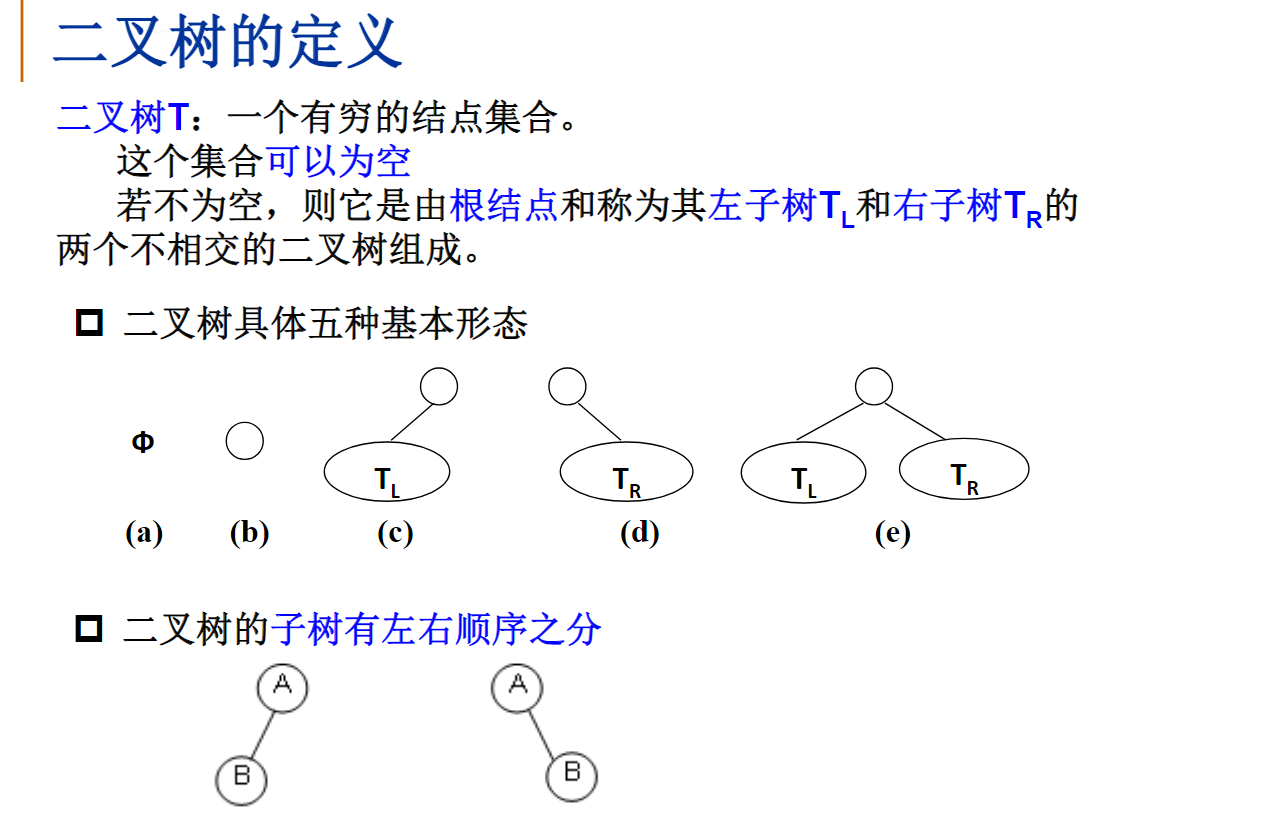
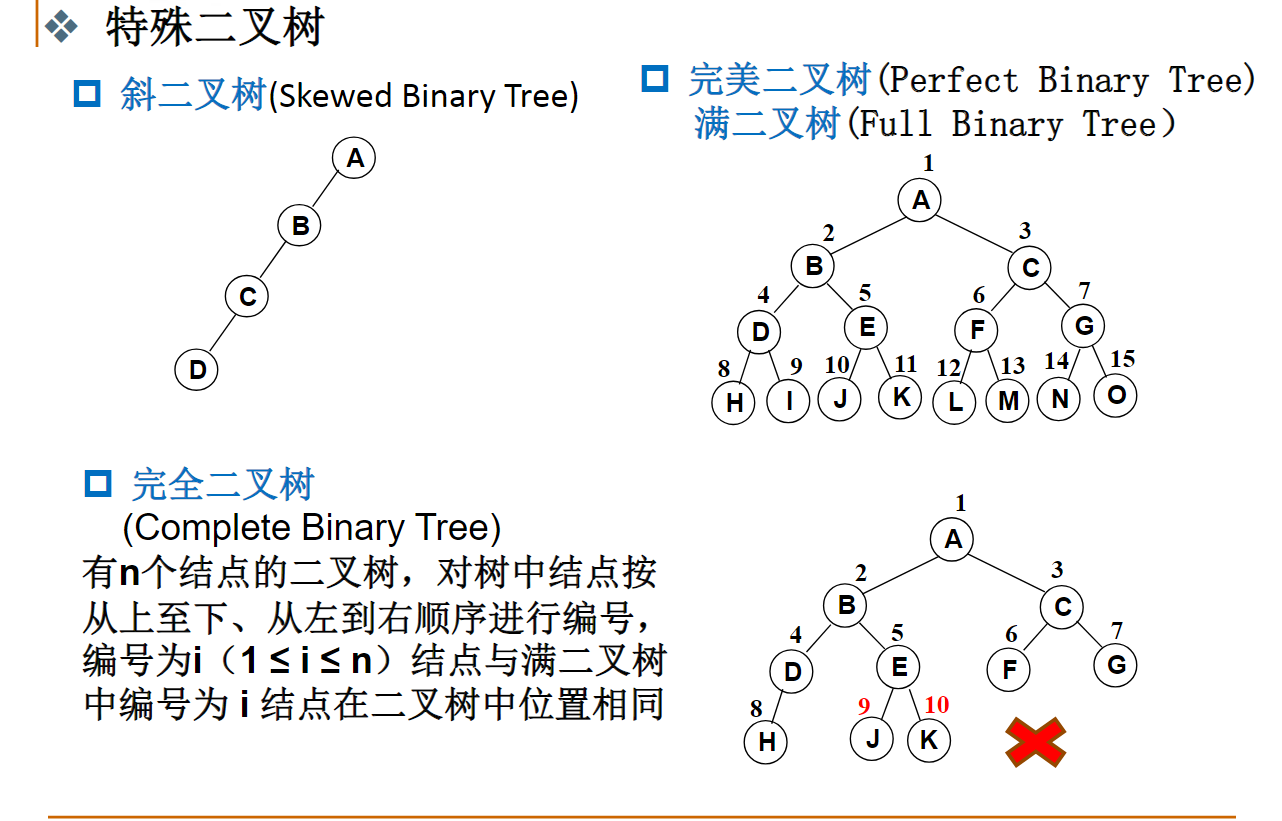


二叉树的存储结构
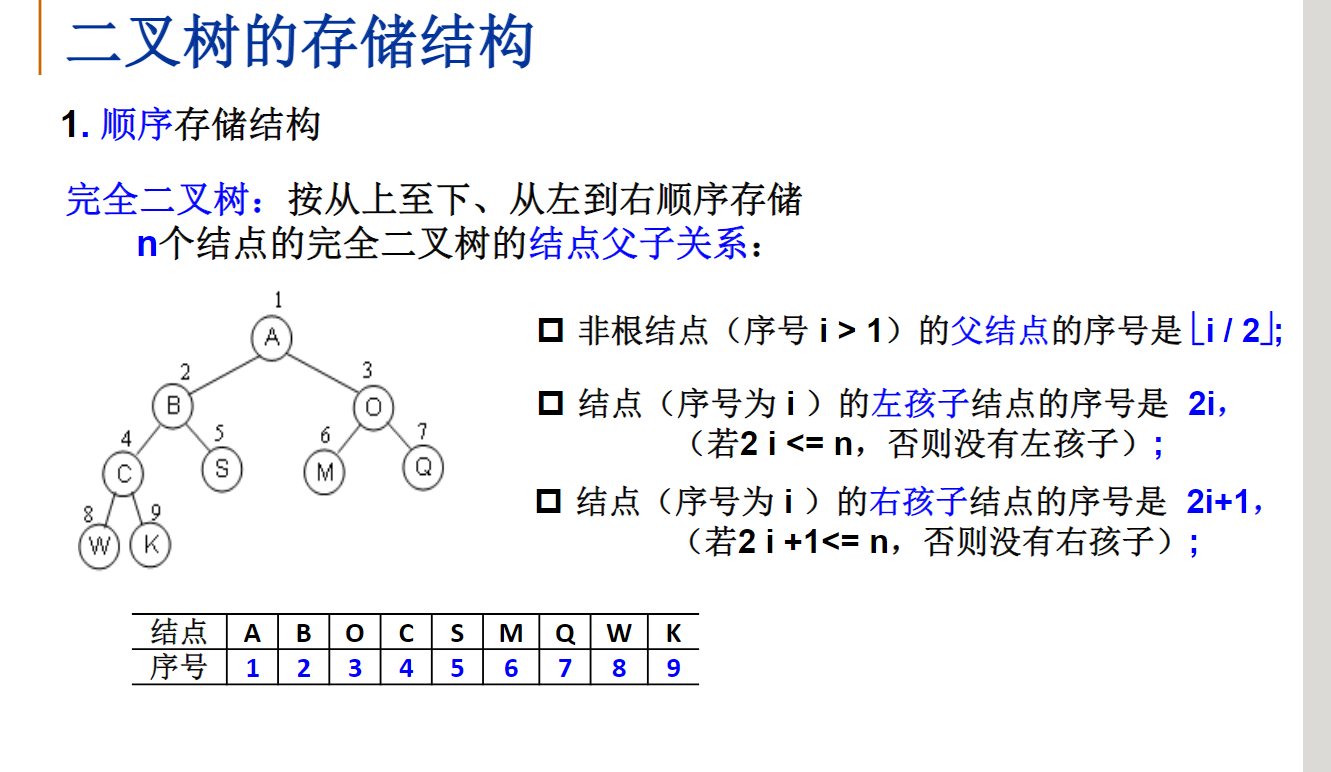
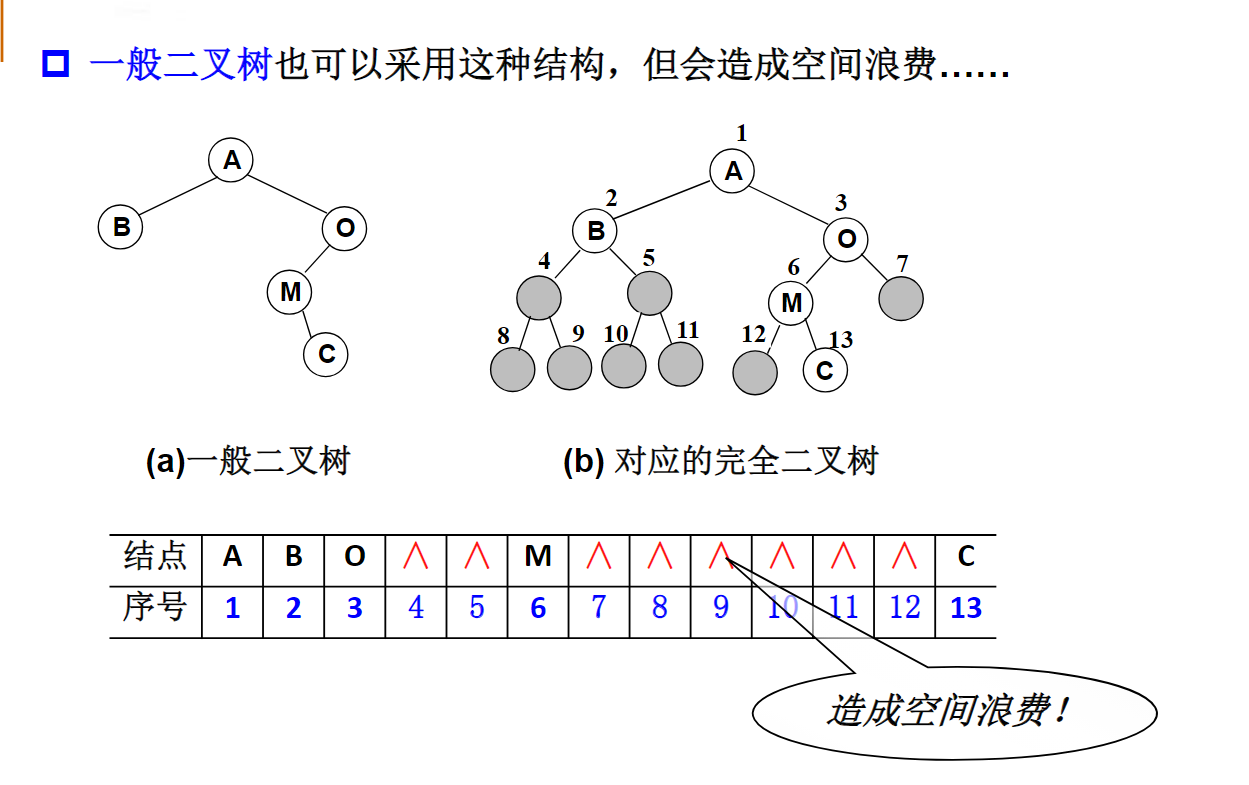
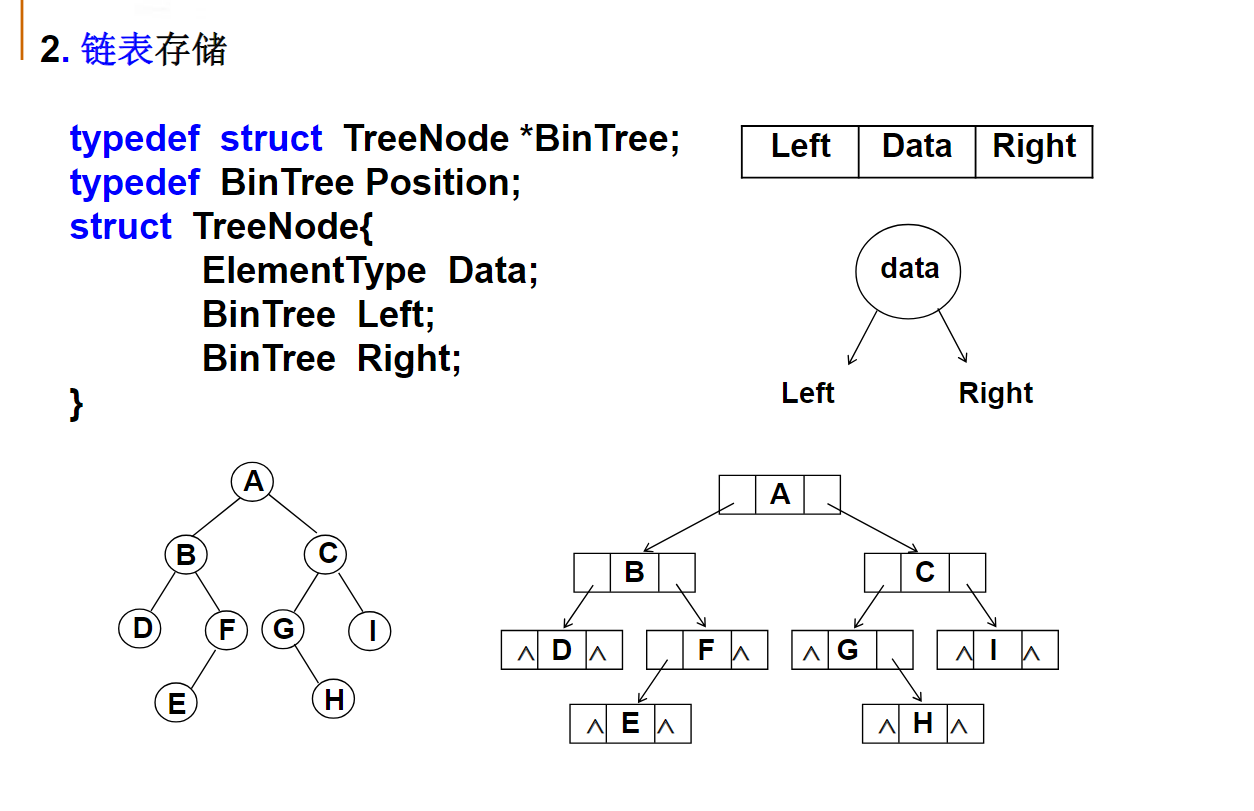
链表结构:
typedef struct TNode *Position;
typedef Position BinTree; /* 二叉树类型 */
struct TNode{ /* 树结点定义 */
ElementType Data; /* 结点数据 */
BinTree Left; /* 指向左子树 */
BinTree Right; /* 指向右子树 */
};
包含较多别名的写法如下:
typedef struct treenode
{
char data;
struct treenode* LChild;
struct treenode* RChild;
}NODE,*LPNODE,*LPTREE;
//struct treenode : NODE
//struct treenode* : LPNODE或LPTREE
NODE node1;
struct treenode* p = NULL;
LPNODE p1 = NULL;
二叉树的创建
非递归方式
实现代码如下:
#include <stdio.h>
#include <stdlib.h>
typedef struct TreeNode *LPNODE;
typedef LPNODE BinTree;
typedef char ElementType;
struct TreeNode
{
ElementType Data;
BinTree Left;
BinTree Right;
};
LPNODE CreateNode(ElementType Data)
{
LPNODE newNode = (LPNODE)malloc(sizeof(struct TreeNode));
newNode->Left = NULL;
newNode->Right = NULL;
newNode->Data = Data;
return newNode;
}
/* 非递归创建树 */
void InsertNode(BinTree parent, LPNODE Left, LPNODE Right)
{
parent->Left = Left;
parent->Right = Right;
}
void PreOrderTraversal(BinTree BT)
{
if(BT)
{
printf("%c ",BT->Data);
PreOrderTraversal(BT->Left);
PreOrderTraversal(BT->Right);
}
}
void InOrderTraversal(BinTree BT)
{
if(BT)
{
InOrderTraversal(BT->Left);
printf("%c ",BT->Data);
InOrderTraversal(BT->Right);
}
}
void PostOrderTraversal(BinTree BT)
{
if(BT)
{
PostOrderTraversal(BT->Left);
PostOrderTraversal(BT->Right);
printf("%c ",BT->Data);
}
}
int main()
{
LPNODE A = CreateNode('A');
LPNODE B = CreateNode('B');
LPNODE C = CreateNode('C');
LPNODE D = CreateNode('D');
LPNODE E = CreateNode('E');
LPNODE F = CreateNode('F');
InsertNode(A,B,C);
InsertNode(B,D,NULL);
InsertNode(C,E,NULL);
InsertNode(E,NULL,F);
PreOrderTraversal(A);
printf("\n");
InOrderTraversal(A);
printf("\n");
PostOrderTraversal(A);
printf("\n");
return 0;
}
A B D C E F
D B A E F C
D B F E C A
递归方式
实现代码如下:
#include <stdio.h>
#include <stdlib.h>
typedef char ElementType;
typedef struct TreeNode
{
ElementType Data;
struct TreeNode* Left;
struct TreeNode* Right;
}NODE,*LPNODE,*LPTREE;
/* 递归创建树 */
void createTree(LPTREE* root)
{
char userKey = '\0';
scanf_s("%c",&userKey,1);
if(userKey == '#')
{
*root = NULL;
}
else
{
*root = (LPTREE)malloc(sizeof(struct TreeNode));
(*root)->Data = userKey;
createTree(&(*root)->Left);
createTree(&(*root)->Right);
}
}
void PreOrderTraversal(LPTREE BT)
{
if(BT)
{
printf("%c ",BT->Data);
PreOrderTraversal(BT->Left);
PreOrderTraversal(BT->Right);
}
}
int main()
{
LPTREE root = NULL;
createTree(&root);
printf("PreOrderTraversal:\n");
PreOrderTraversal(root);
printf("\n");
return 0;
}
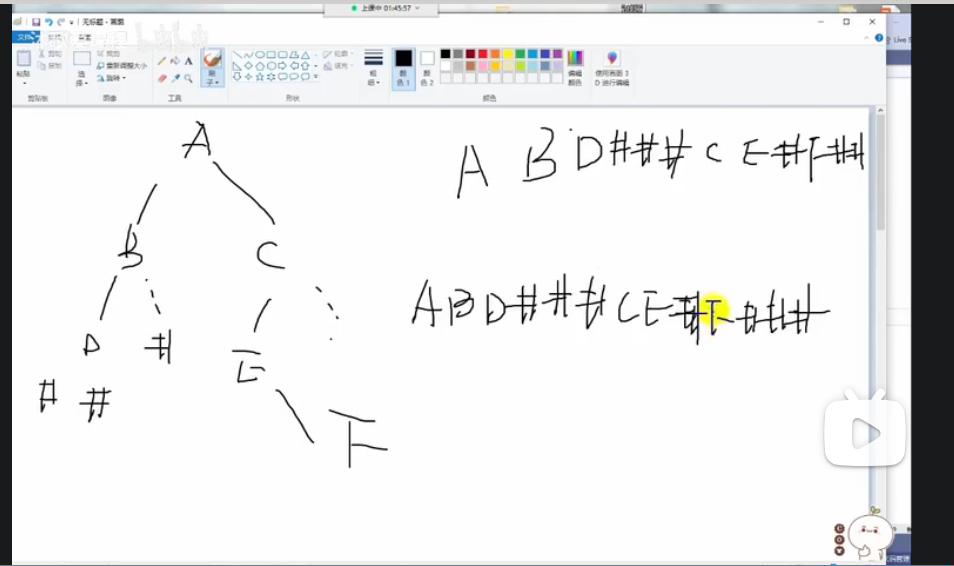
ABD###CE#F###
PreOrderTraversal:
A B D C E F
二叉树的遍历
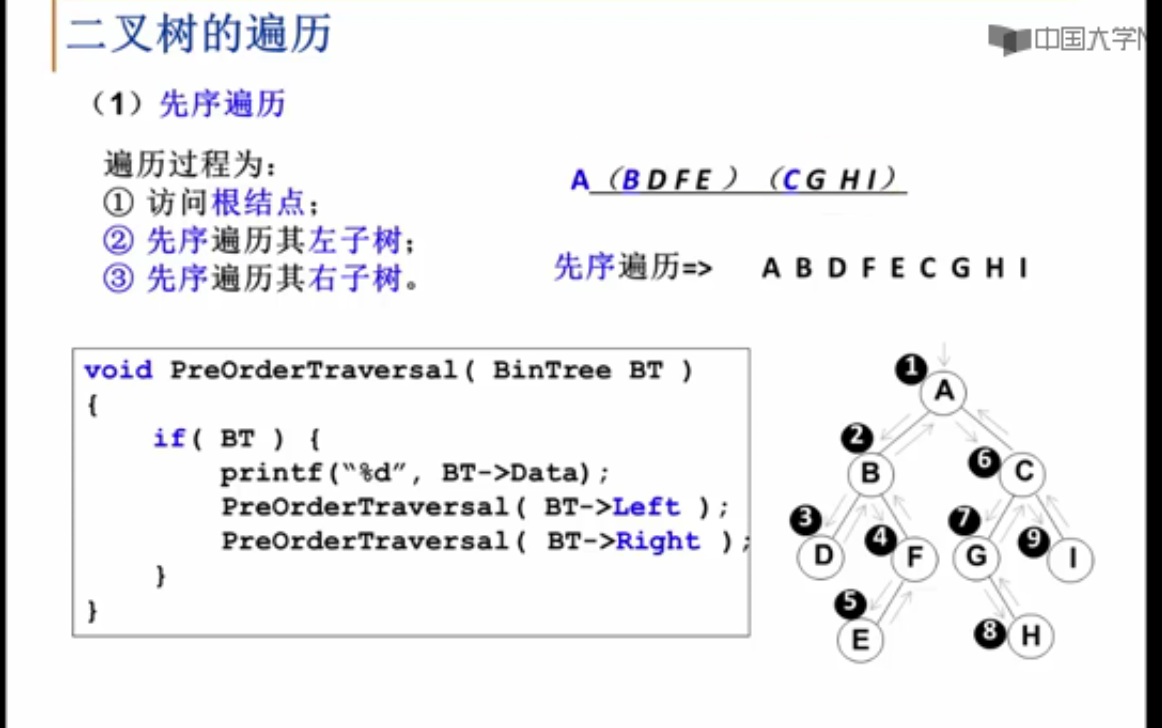
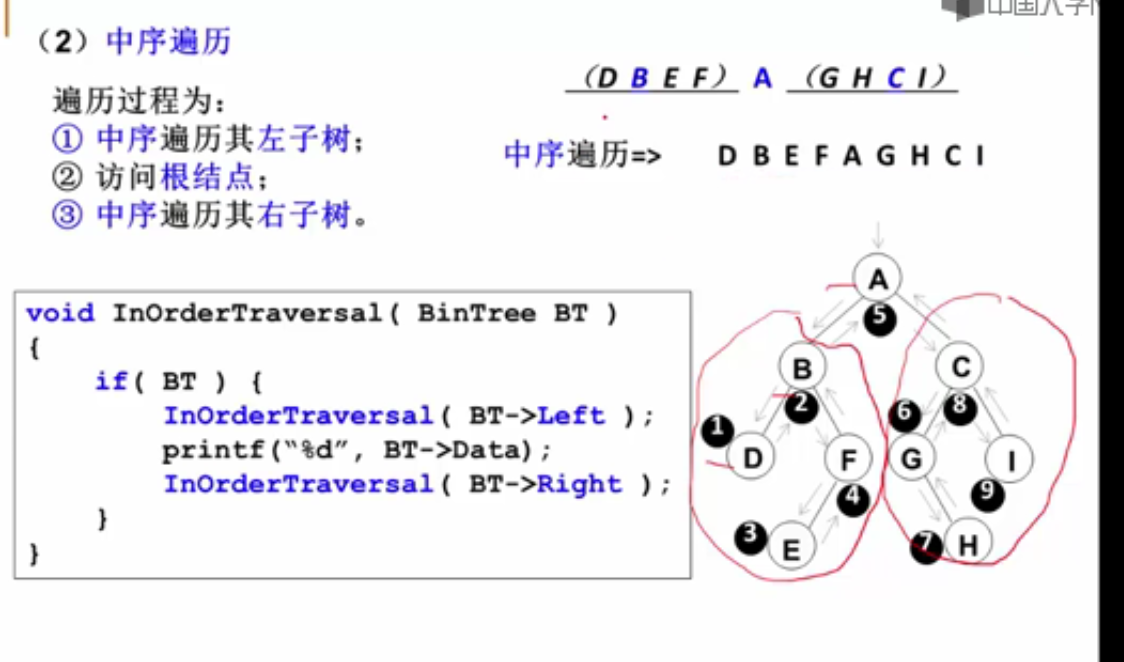
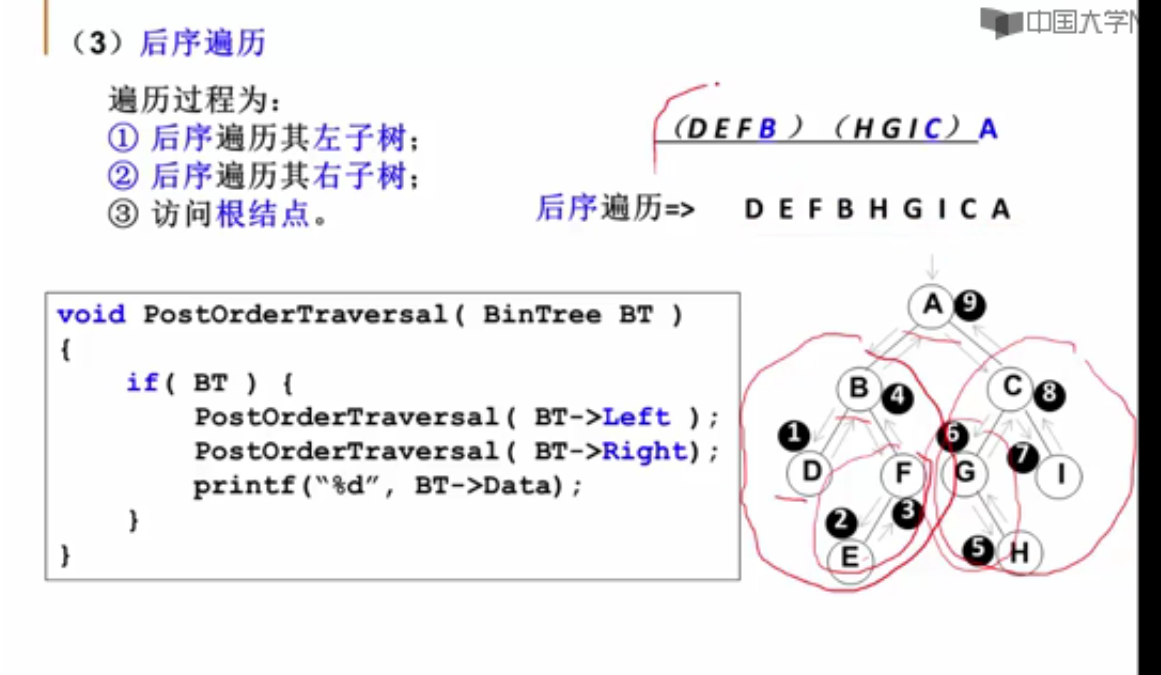
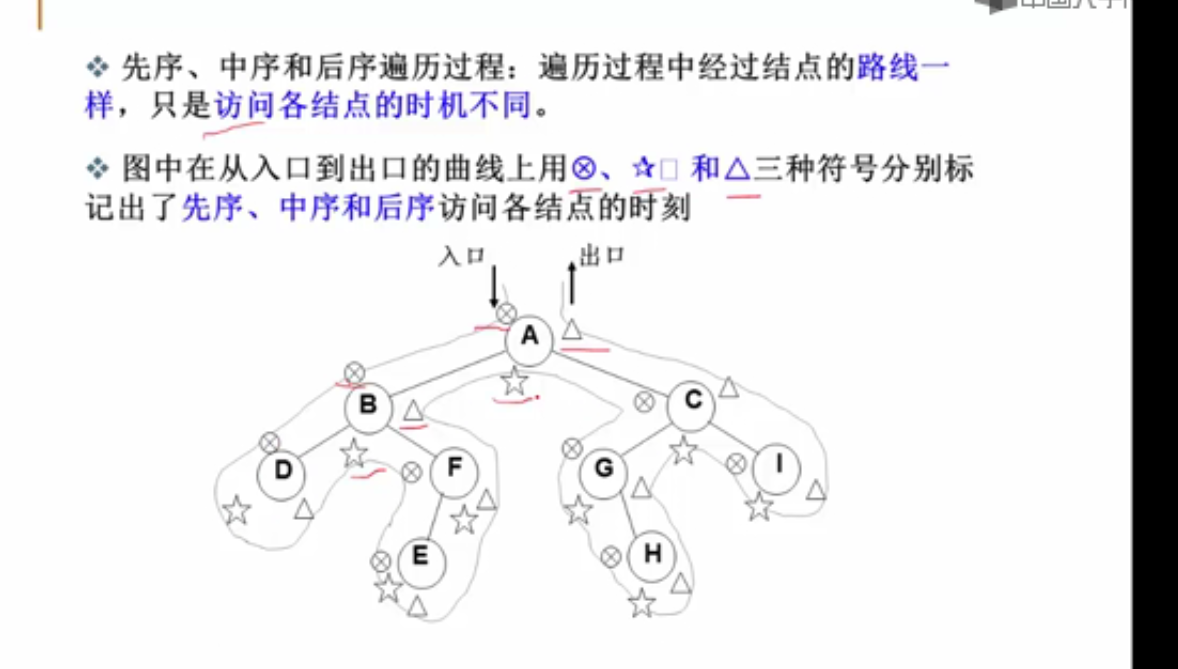
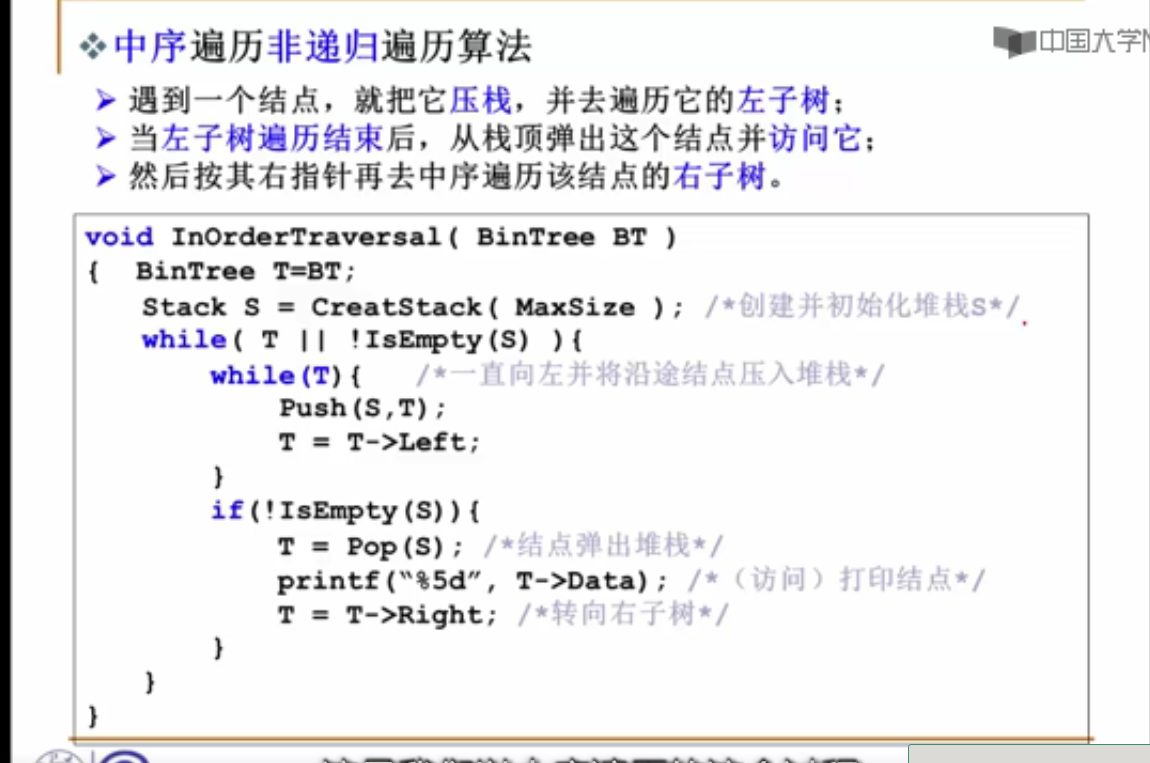

#include <stdio.h>
#include <stdlib.h>
typedef struct TreeNode *LPNODE;
typedef LPNODE BinTree;
typedef char ElementType;
struct TreeNode
{
ElementType Data;
BinTree Left;
BinTree Right;
};
LPNODE CreateNode(ElementType Data)
{
LPNODE newNode = (LPNODE)malloc(sizeof(struct TreeNode));
newNode->Left = NULL;
newNode->Right = NULL;
newNode->Data = Data;
return newNode;
}
void InsertNode(BinTree parent, LPNODE Left, LPNODE Right)
{
parent->Left = Left;
parent->Right = Right;
}
void PreOrderTraversal(BinTree BT)
{
if(BT)
{
printf("%c ",BT->Data);
PreOrderTraversal(BT->Left);
PreOrderTraversal(BT->Right);
}
}
void PreOrderTraversalByStack(BinTree BT)
{
if(BT == NULL)
return;
LPNODE pMove = BT;
LPNODE stack[100];
int stackTop = -1;
while(stackTop != -1 || pMove)
{
while(pMove)
{
printf("%c ",pMove->Data);
stack[++stackTop] = pMove;
pMove = pMove->Left;
}
if(stackTop != -1)
{
pMove = stack[stackTop--];
pMove = pMove->Right;
}
}
}
void InOrderTraversal(BinTree BT)
{
if(BT)
{
InOrderTraversal(BT->Left);
printf("%c ",BT->Data);
InOrderTraversal(BT->Right);
}
}
void InOrderTraversalByStack(BinTree BT)
{
if(BT == NULL)
return;
LPNODE pMove = BT;
LPNODE stack[100];
int stackTop = -1;
while(stackTop != -1 || pMove)
{
while(pMove)
{
stack[++stackTop] = pMove;
pMove = pMove->Left;
}
if(stackTop != -1)
{
pMove = stack[stackTop--];
printf("%c ",pMove->Data);
pMove = pMove->Right;
}
}
}
void PostOrderTraversal(BinTree BT)
{
if(BT)
{
PostOrderTraversal(BT->Left);
PostOrderTraversal(BT->Right);
printf("%c ",BT->Data);
}
}
void PostOrderTraversalByStack(BinTree BT)
{
if(BT == NULL)
return;
LPNODE pMove = BT;
LPNODE stack[100];
int stackTop = -1;
LPNODE placeVisited = NULL;
while(pMove)
{
stack[++stackTop] = pMove;
pMove = pMove->Left;
}
while(stackTop != -1)
{
pMove = stack[stackTop--];
if(pMove->Right == NULL || pMove->Right == placeVisited)
{
printf("%c ",pMove->Data);
placeVisited = pMove;
}
else
{
stack[++stackTop] = pMove;
pMove = pMove->Right;
while(pMove)
{
stack[++stackTop] = pMove;
pMove = pMove->Left;
}
}
}
}
void LevelTraversal(BinTree BT)
{
LPNODE pMove = BT;
LPNODE queue[100];
int front = 0;
int tail = 0;
queue[tail++] = pMove;
printf("%c ",pMove->Data);
while(front != tail)
{
pMove = queue[front++];
if(pMove->Left != NULL)
{
queue[tail++] = pMove->Left;
printf("%c ",pMove->Left->Data);
}
if(pMove->Right != NULL)
{
queue[tail++] = pMove->Right;
printf("%c ",pMove->Right->Data);
}
}
}
int main()
{
LPNODE A = CreateNode('A');
LPNODE B = CreateNode('B');
LPNODE C = CreateNode('C');
LPNODE D = CreateNode('D');
LPNODE E = CreateNode('E');
LPNODE F = CreateNode('F');
InsertNode(A,B,C);
InsertNode(B,D,NULL);
InsertNode(C,E,NULL);
InsertNode(E,NULL,F);
printf("PreOrderTraversal:\n");
PreOrderTraversal(A);
printf("\nPreOrderTraversalByStack:\n");
PreOrderTraversalByStack(A);
printf("\nInOrderTraversal:\n");
InOrderTraversal(A);
printf("\nInOrderTraversalByStack:\n");
InOrderTraversalByStack(A);
printf("\nPostOrderTraversal:\n");
PostOrderTraversal(A);
printf("\nPostOrderTraversalByStack:\n");
PostOrderTraversalByStack(A);
printf("\nLevelTraversal:\n");
LevelTraversal(A);
printf("\n");
return 0;
}
PreOrderTraversal:
A B D C E F
PreOrderTraversalByStack:
A B D C E F
InOrderTraversal:
D B A E F C
InOrderTraversalByStack:
D B A E F C
PostOrderTraversal:
D B F E C A
PostOrderTraversalByStack:
D B F E C A
LevelTraversal:
A B C D E F

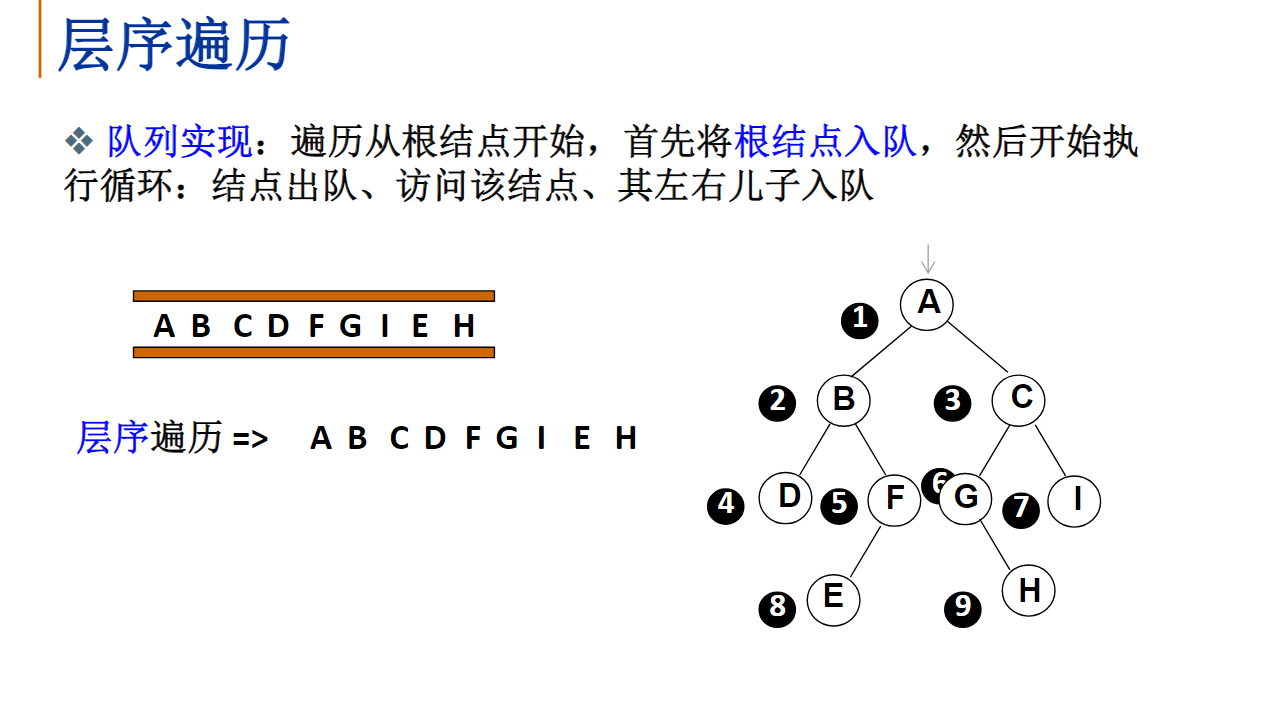


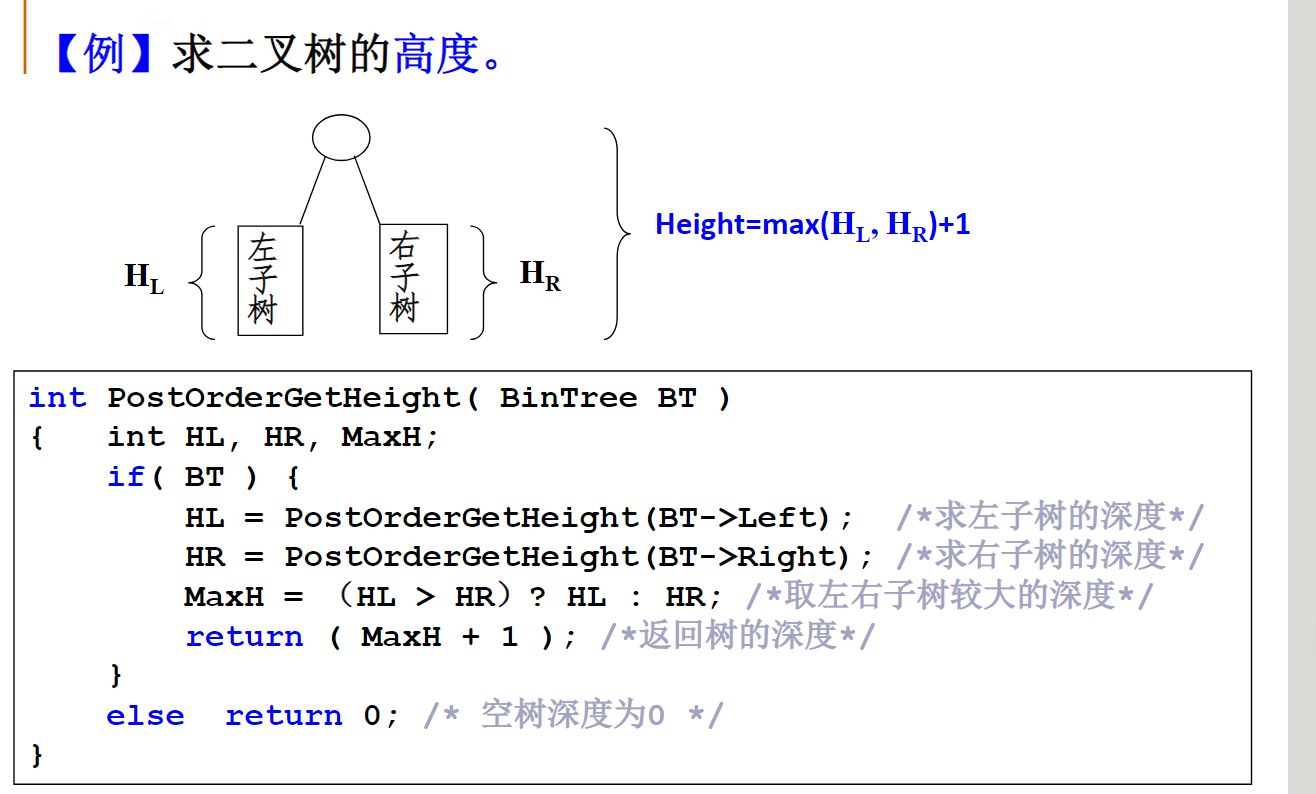
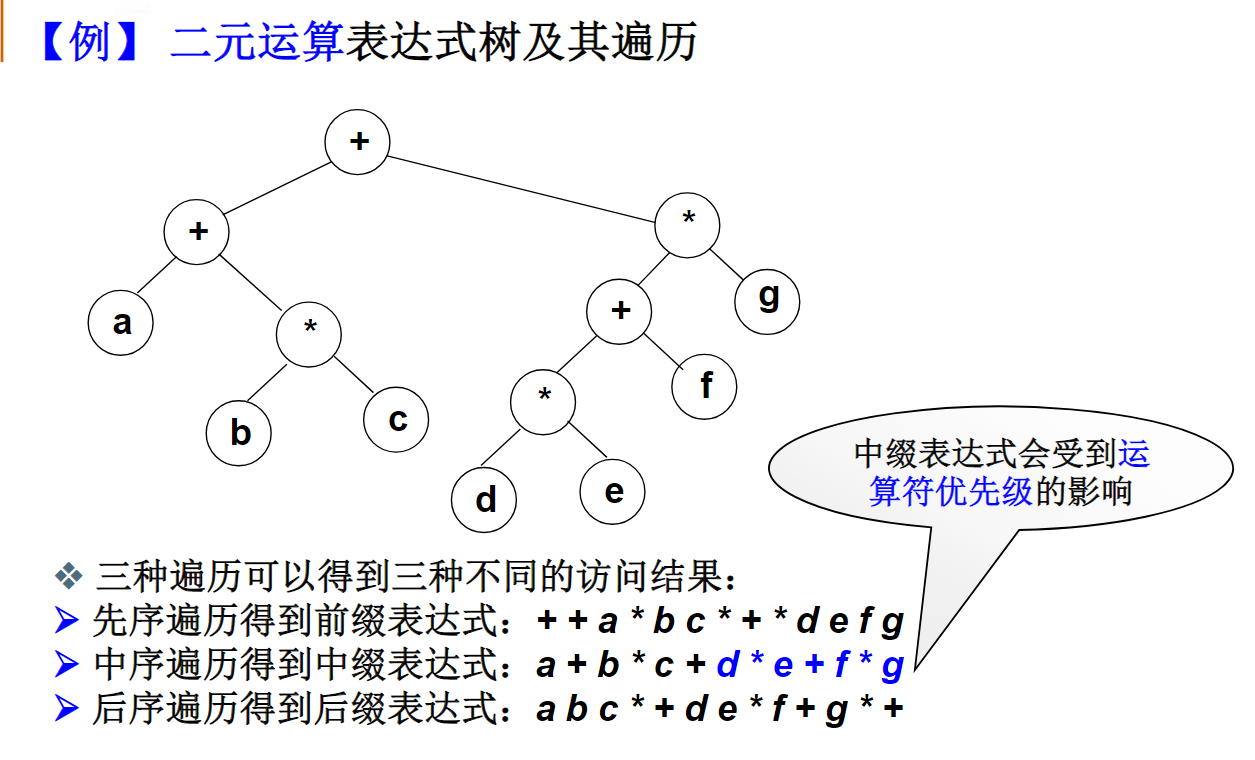
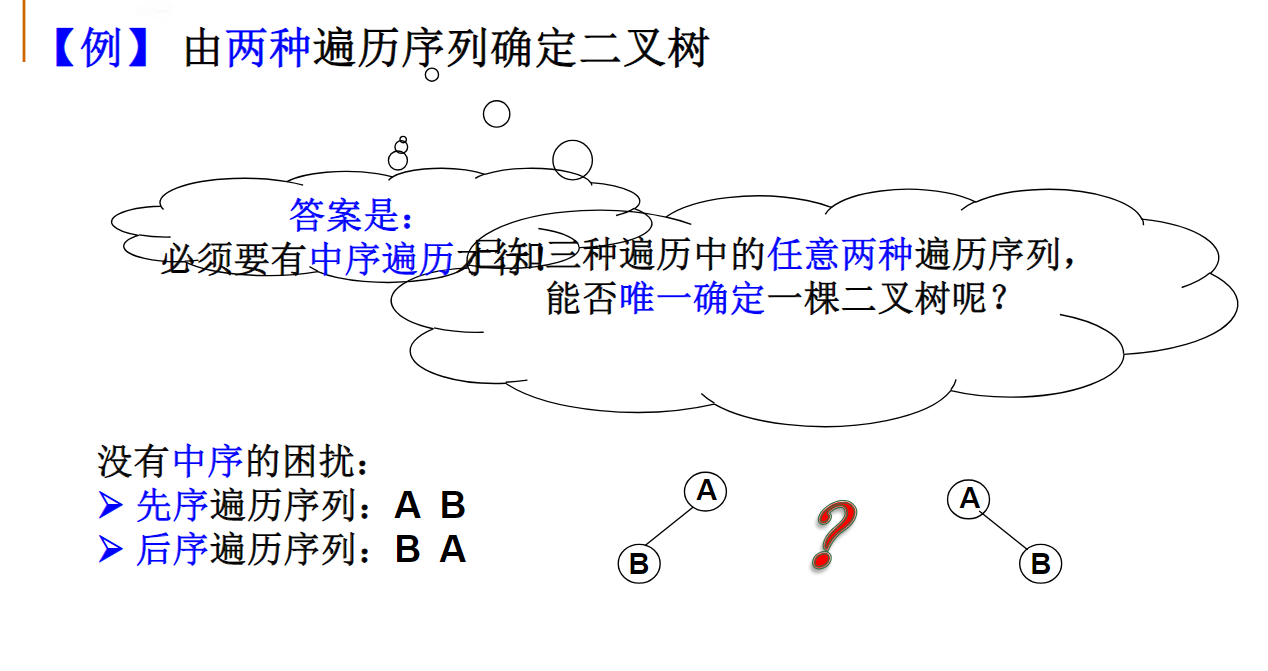
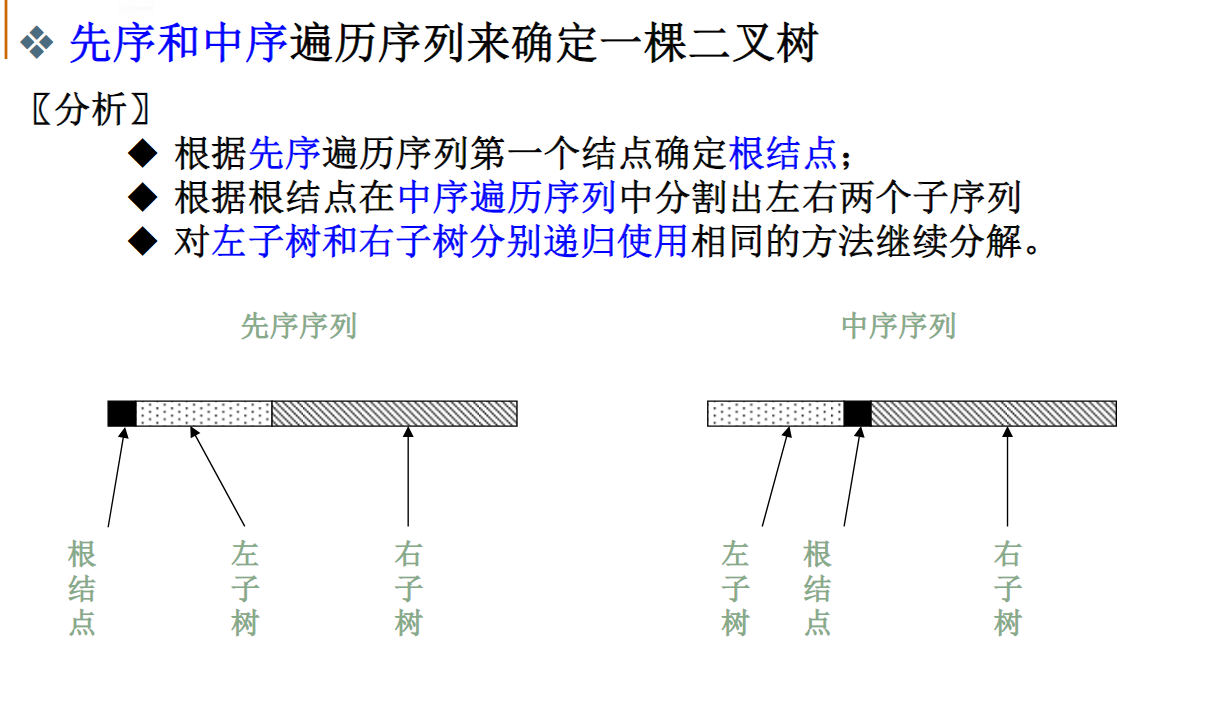
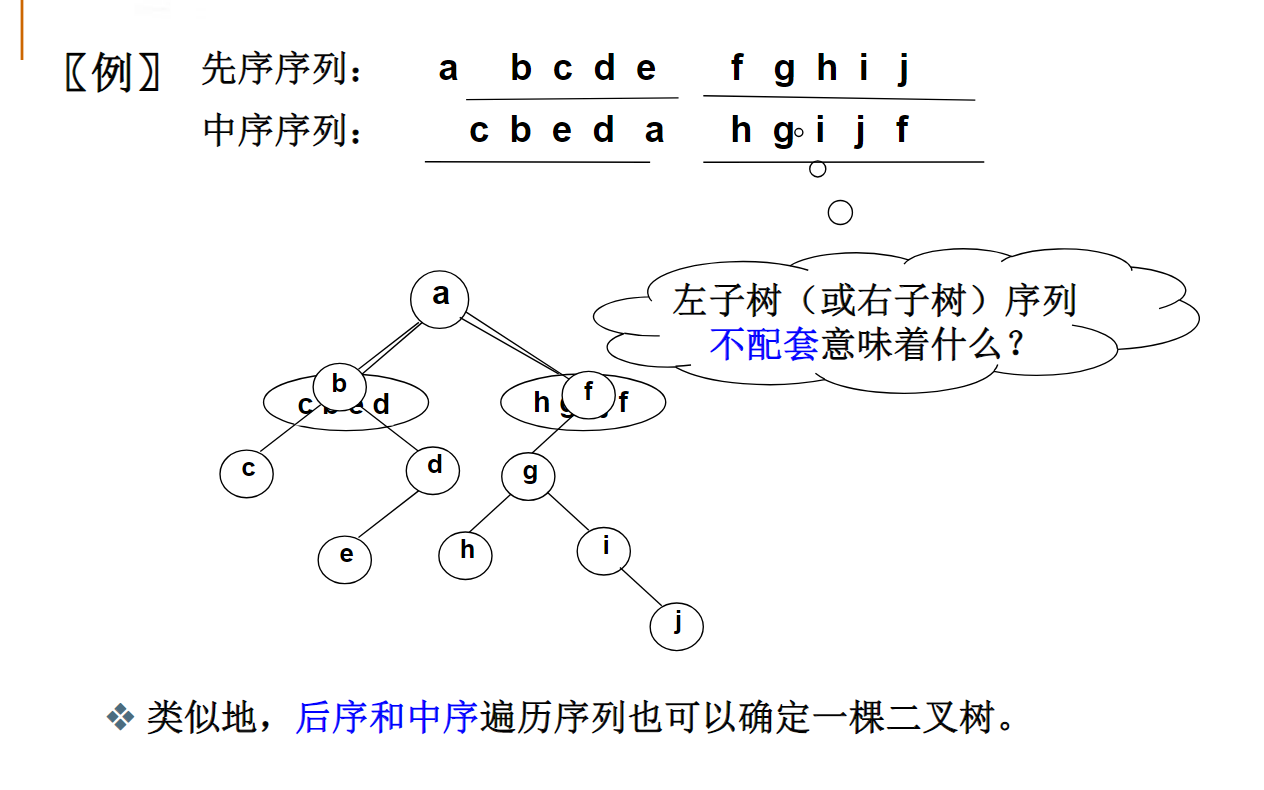
1.假定只有四个结点A、B、C、D的二叉树,其前序遍历序列为ABCD,则下面哪个序列是不可能的中序遍历序列?
A.ABCD
B.ACDB
C.DCBA
D.DABC
正确答案:D你选对了
2对于二叉树,如果其中序遍历结果与前序遍历结果一样,那么可以断定该二叉树________
A.是完全二叉树
B.所有结点都没有左儿子
C.所有结点都没有右儿子
D.这样的树不存在
正确答案:B你选对了
3已知一二叉树的后序和中序遍历的结果分别是FDEBGCA 和FDBEACG,那么该二叉树的前序遍历结果是什么?
A.ABDFECG
B.ABDEFCG
C.ABDFEGC
D.ABCDEFG
正确答案:A你选对了
二叉搜索树
查找分为静态查找和动态查找。静态查找可以使用二分查找方式。
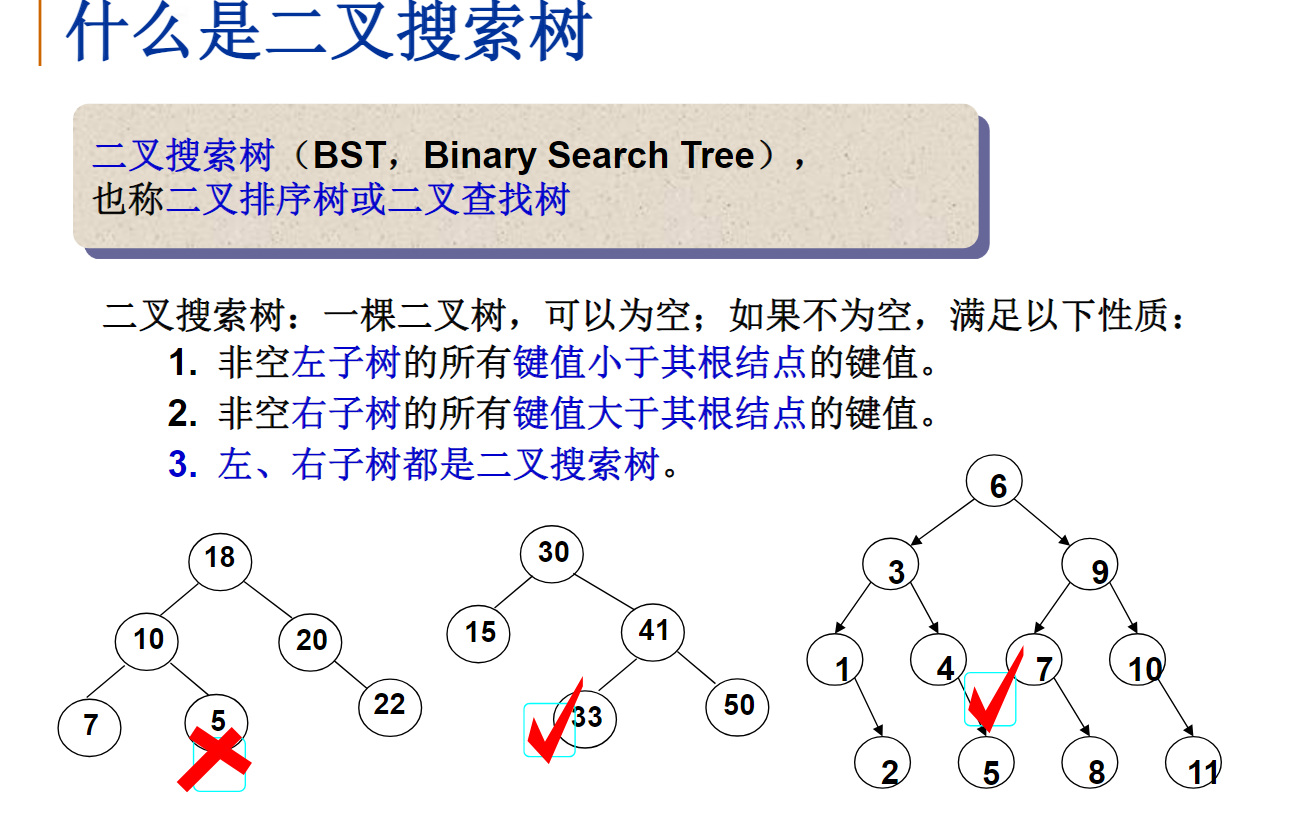




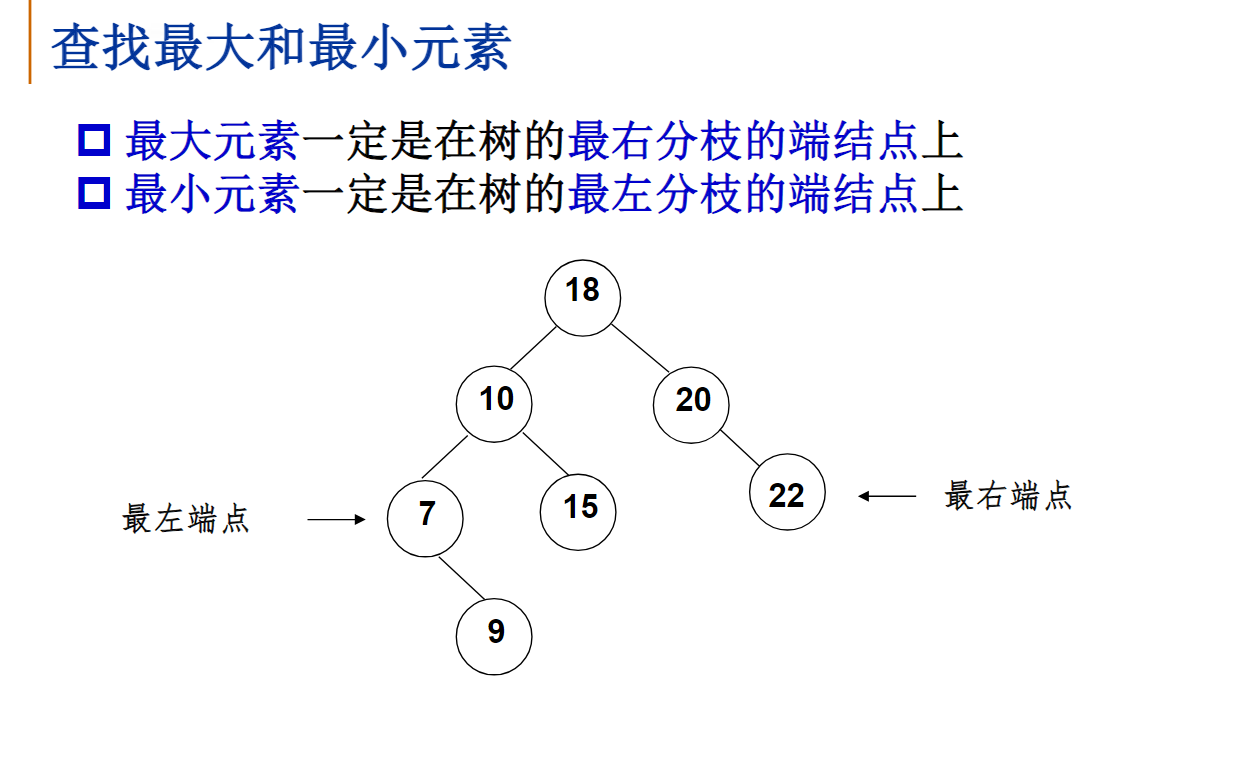

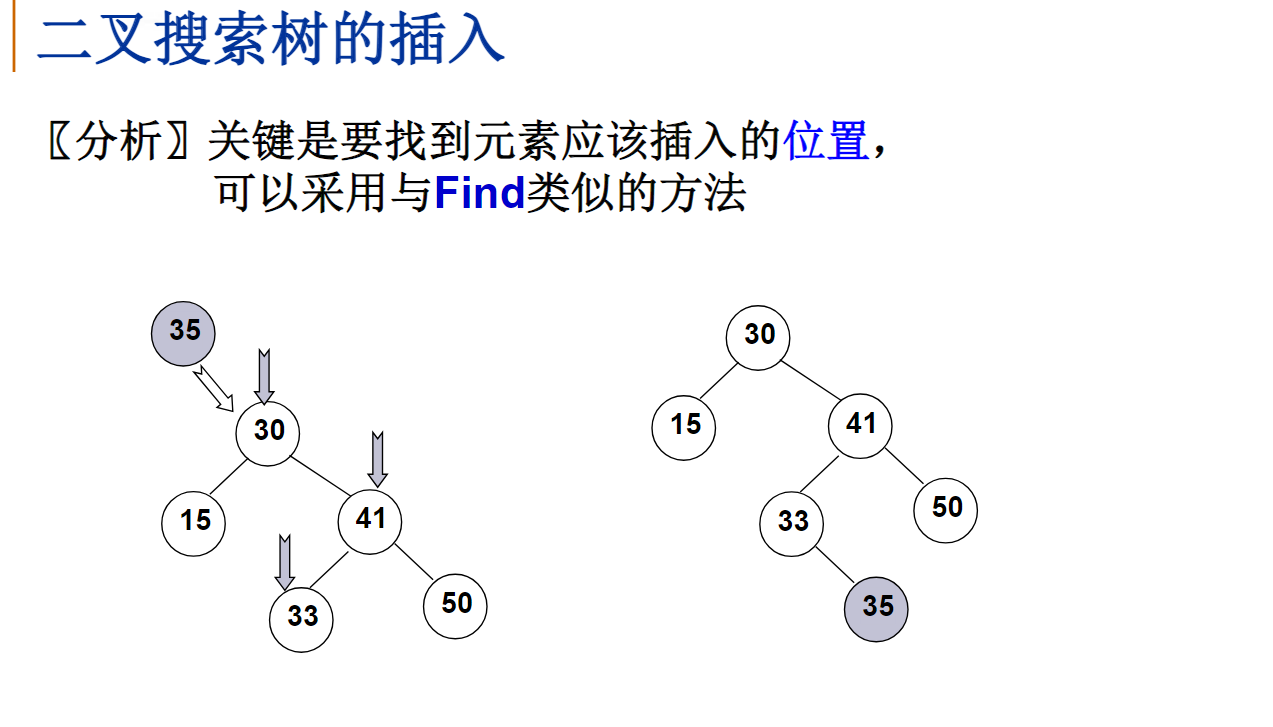

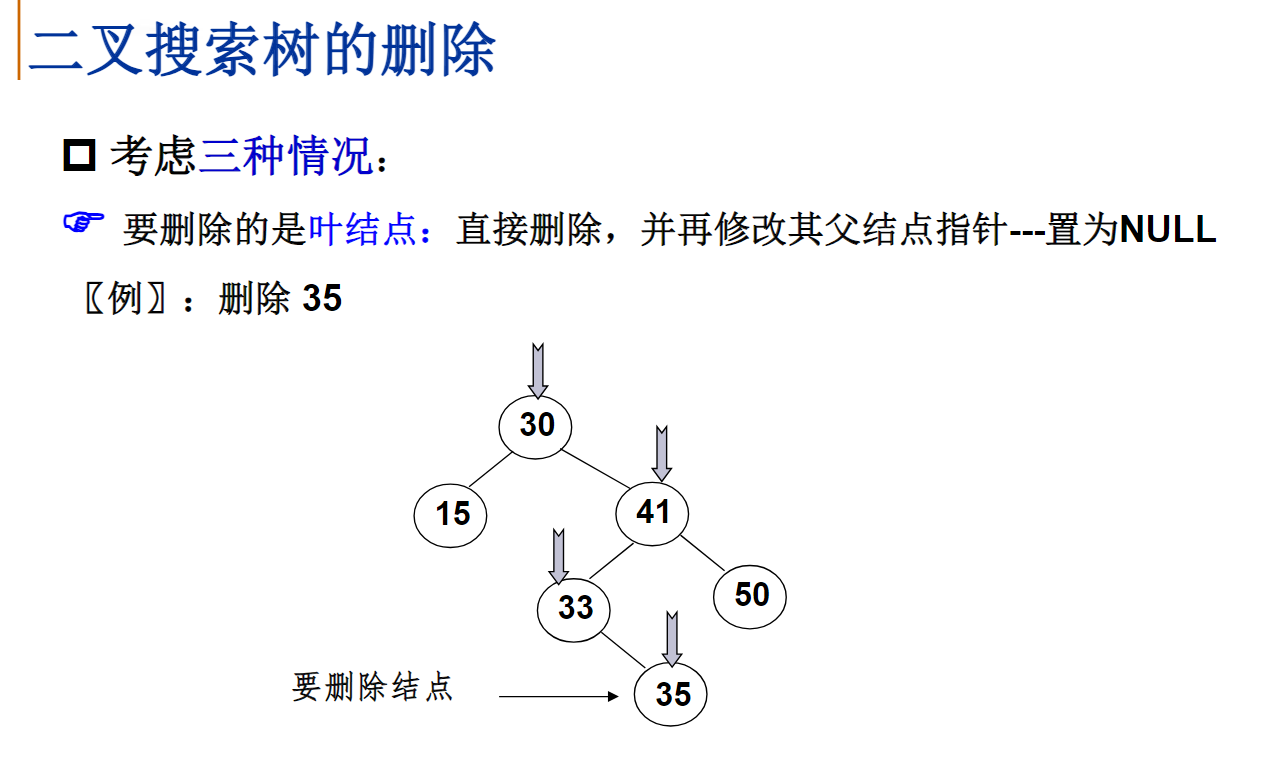
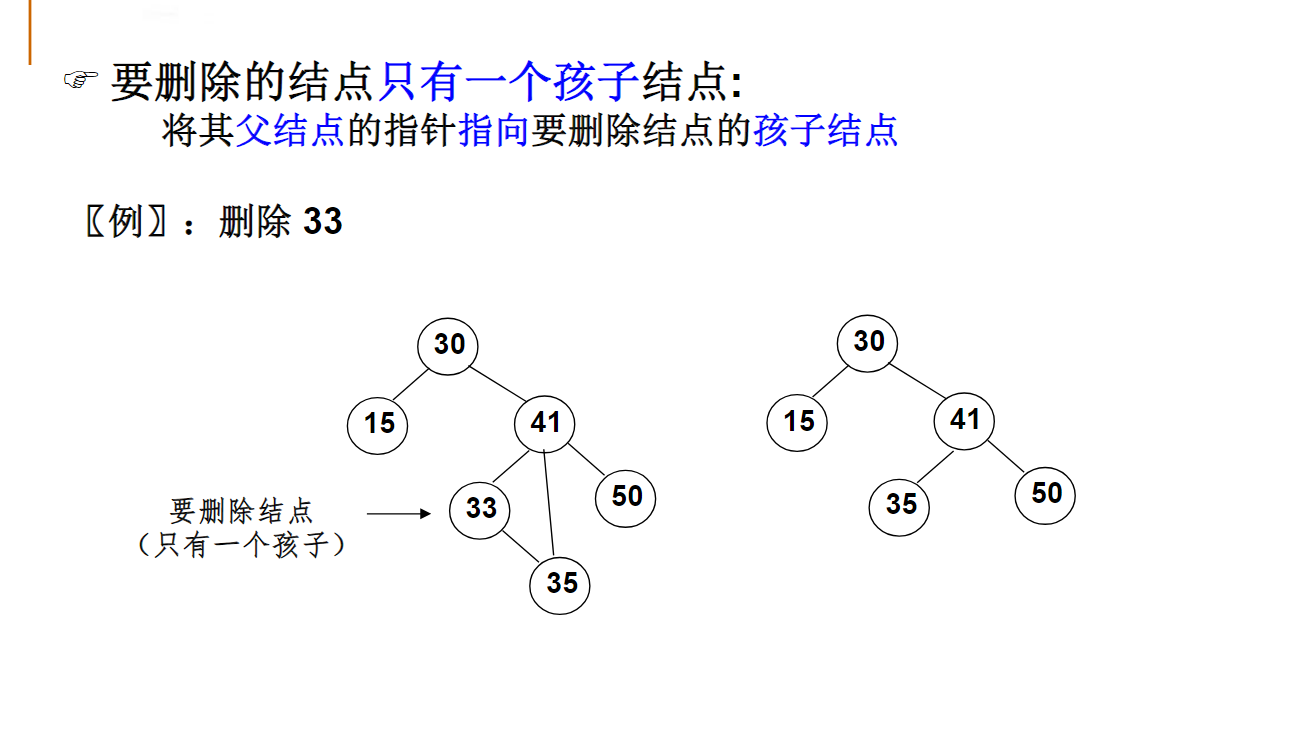
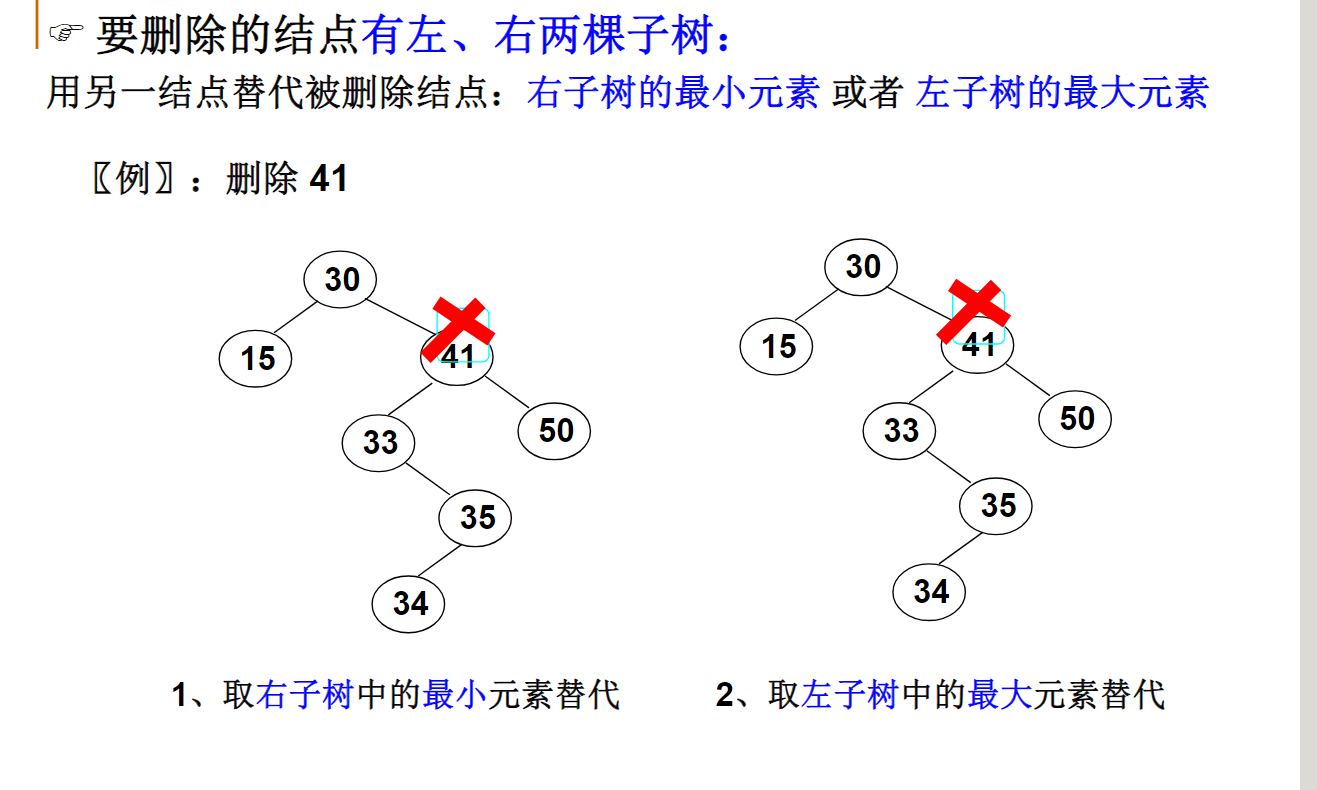
若一搜索树(查找树)是一个有n个结点的完全二叉树,则该树的最大值一定在叶结点上
错误
若一搜索树(查找树)是一个有n个结点的完全二叉树,则该树的最小值一定在叶结点上
正确

#include <stdio.h>
#include <stdlib.h>
typedef int ElementType;
typedef struct TreeNode *BinTree;
typedef BinTree Position;
typedef struct TreeNode
{
ElementType Data;
BinTree Left;
BinTree Right;
}*LPNODE;
BinTree Insert(ElementType X,BinTree BST)
{
if(!BST)
{
/*若原树为空,生成并返回一个结点的二叉搜索树*/
BST = (BinTree)malloc(sizeof(struct TreeNode));
BST->Data = X;
BST->Left = NULL;
BST->Right = NULL;
}
else /*开始找要插入元素的位置*/
{
if(BST->Data < X)
BST->Right = Insert(X,BST->Right);
else if(BST->Data > X)
BST->Left = Insert(X,BST->Left);
/*else X已经存在,什么都不做 */
}
return BST;
}
/*尾递归方式查找*/
ElementType Find(ElementType X,BinTree BST)
{
if(!BST)
return NULL;
if(BST->Data < X)
return Find(X,BST->Right);
else if(BST->Data > X)
return Find(X,BST->Left);
else /*X == BST->Data*/
return BST; /*查找成功,返回找到结点的地址*/
}
/*迭代、非递归方式*/
Position FindMax(BinTree BST)
{
if(BST)
while(BST->Right)
BST = BST->Right;
return BST;
}
Position FindMin(BinTree BST)
{
if(!BST)
return NULL;
else if(!BST->Left) /*有根结点,但没有左子树,直接返回根*/
return BST;
else
return FindMin(BST->Left);
}
BinTree Delete(ElementType X,BinTree BST)
{
Position Tmp;
if(!BST)
printf("找不到要删除的元素!\n");
else if(X < BST->Data)
BST->Left = Delete(X,BST->Left);
else if(X > BST->Data)
BST->Right = Delete(X,BST->Right);
else
{
if(BST->Left && BST->Right)
{
Tmp = FindMin(BST->Right);
BST->Data = Tmp->Data;
BST->Right = Delete(BST->Data,BST->Right);
}
else
{
Tmp = BST;
if(!BST->Left)
BST = BST->Right;
else if(!BST->Right)
BST = BST->Left;
free(Tmp);
}
}
return BST;
}
void PreOrderTraversalByStack(BinTree BST)
{
if(!BST)
return;
BinTree pMove = BST;
BinTree stack[100];
int stackTop = -1;
while(pMove || stackTop != -1 )
{
while(pMove)
{
printf("%d ",pMove->Data);
stack[++stackTop] = pMove;
pMove = pMove->Left;
}
if(stackTop != -1)
{
pMove = stack[stackTop--];
pMove = pMove->Right;
while(pMove)
{
printf("%d ",pMove->Data);
stack[++stackTop] = pMove;
pMove = pMove->Left;
}
}
}
}
void InOrderTraversalByStack(BinTree BST)
{
if(!BST)
return;
BinTree pMove = BST;
BinTree stack[100];
int stackTop = -1;
while(pMove || stackTop != -1 )
{
while(pMove)
{
stack[++stackTop] = pMove;
pMove = pMove->Left;
}
if(stackTop != -1)
{
pMove = stack[stackTop--];
printf("%d ",pMove->Data);
pMove = pMove->Right;
while(pMove)
{
stack[++stackTop] = pMove;
pMove = pMove->Left;
}
}
}
}
void LevelTraversal(BinTree BT)
{
LPNODE pMove = BT;
LPNODE queue[100];
int front = 0;
int tail = 0;
queue[tail++] = pMove;
printf("%d ",pMove->Data);
while(front != tail)
{
pMove = queue[front++];
if(pMove->Left != NULL)
{
queue[tail++] = pMove->Left;
printf("%d ",pMove->Left->Data);
}
if(pMove->Right != NULL)
{
queue[tail++] = pMove->Right;
printf("%d ",pMove->Right->Data);
}
}
}
int main()
{
BinTree BST = NULL;
BST = Insert(5,BST);
BST = Insert(3,BST);
BST = Insert(4,BST);
BST = Insert(9,BST);
BST = Insert(20,BST);
BST = Insert(30,BST);
BST = Insert(40,BST);
BST = Insert(43,BST);
BST = Insert(34,BST);
BST = Insert(6,BST);
BST = Insert(7,BST);
BST = Insert(8,BST);
LevelTraversal(BST);
printf("\n%d",FindMax(BST)->Data);
printf("\n%d",FindMin(BST)->Data);
BST = Delete(43,BST);
BST = Delete(3,BST);
printf("\n");
LevelTraversal(BST);
printf("\n%d",FindMax(BST)->Data);
printf("\n%d",FindMin(BST)->Data);
BinTree Tmp = Find(100,BST);
if(!Tmp)
printf("\nNULL\n");
else
printf("\n%d\n",Find(100,BST));
//printf("\n%d\n",Tmp->Data);
return 0;
}
5 3 9 4 6 20 7 30 8 40 34 43
43
3
5 4 9 6 20 7 30 8 40 34
40
4
NULL
平衡二叉树
定义
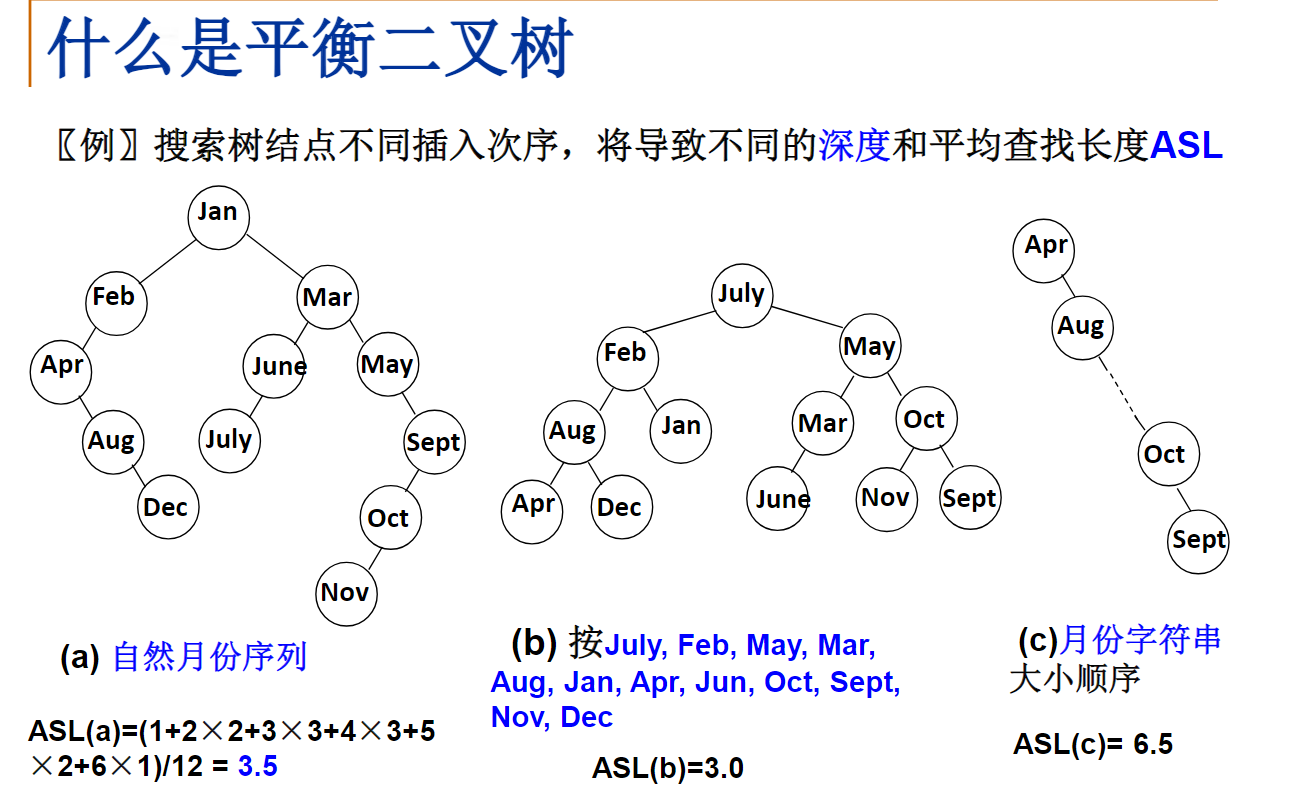
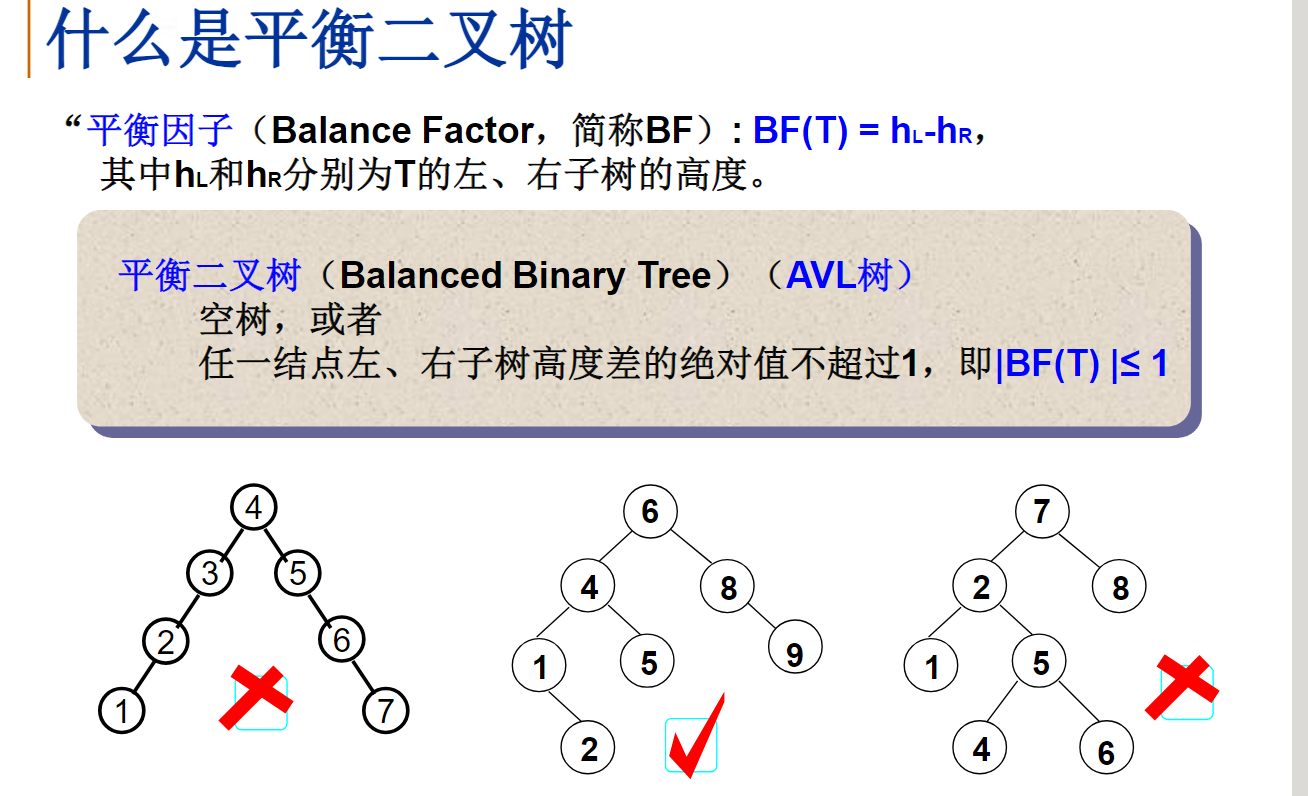


1将1、2、3、4、5、6顺序插入初始为空的AVL树中,当完成这6个元素的插入后,该AVL树共有多少层? 3
2若一AVL树的结点数是21,则该树的高度至多是多少?5
注:只有一个根节点的树高度为0
平衡二叉树的调整
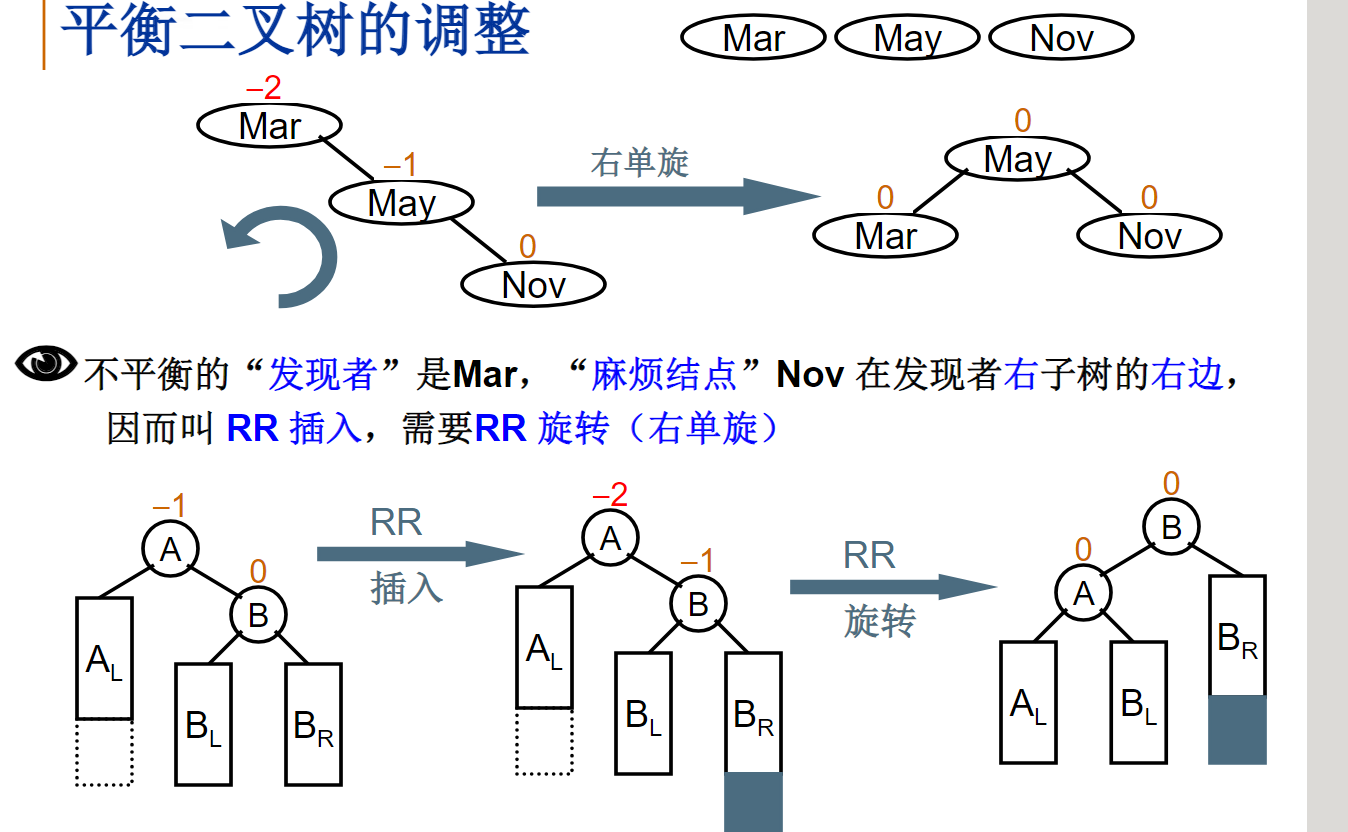
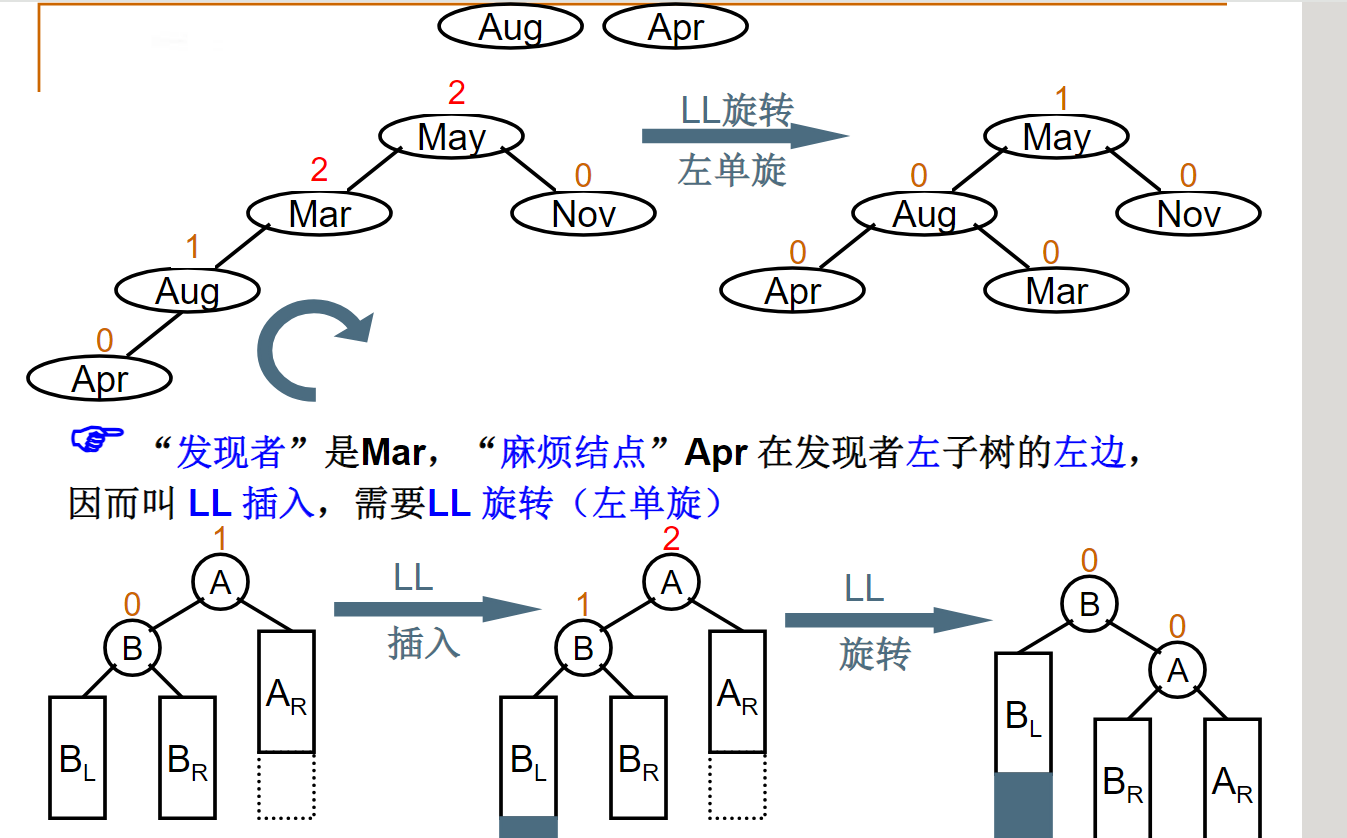
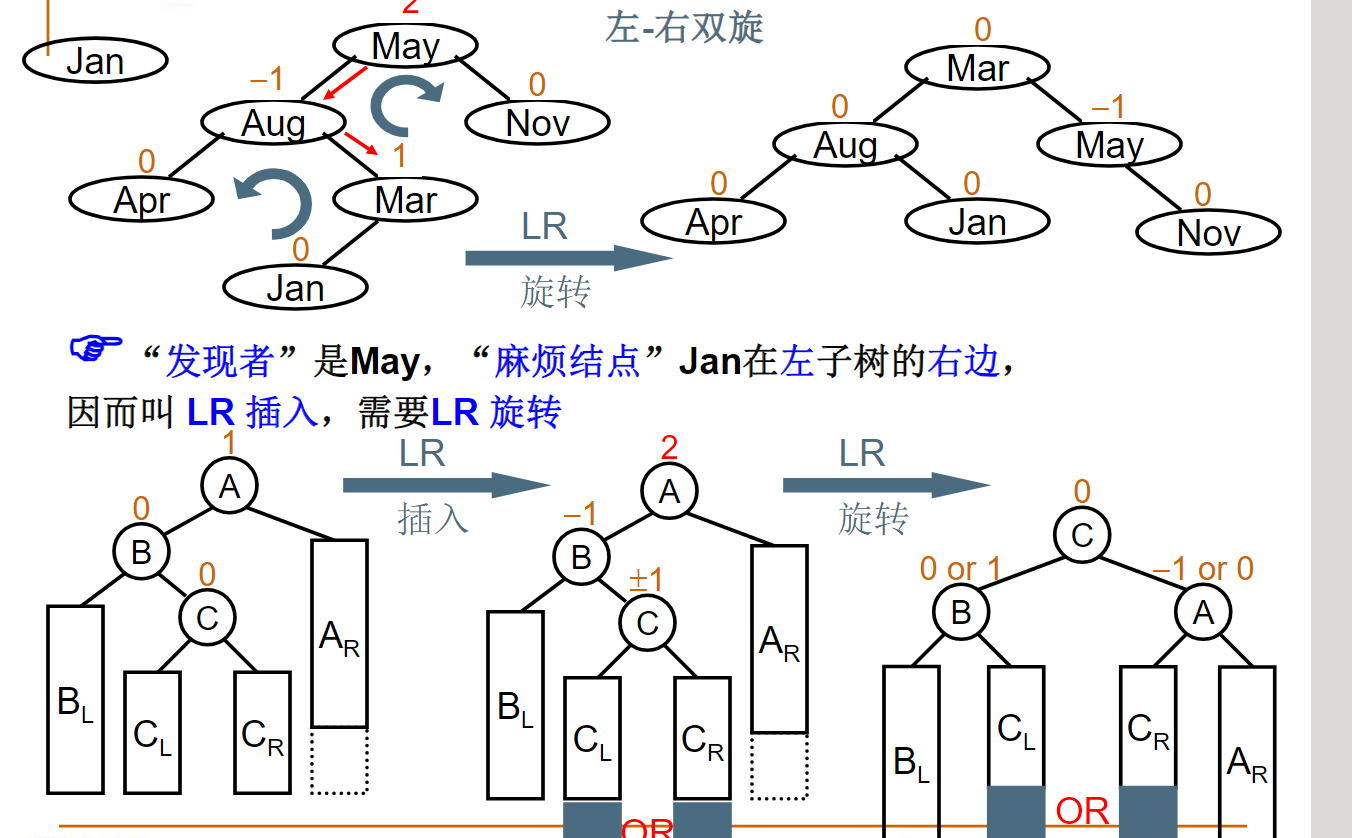
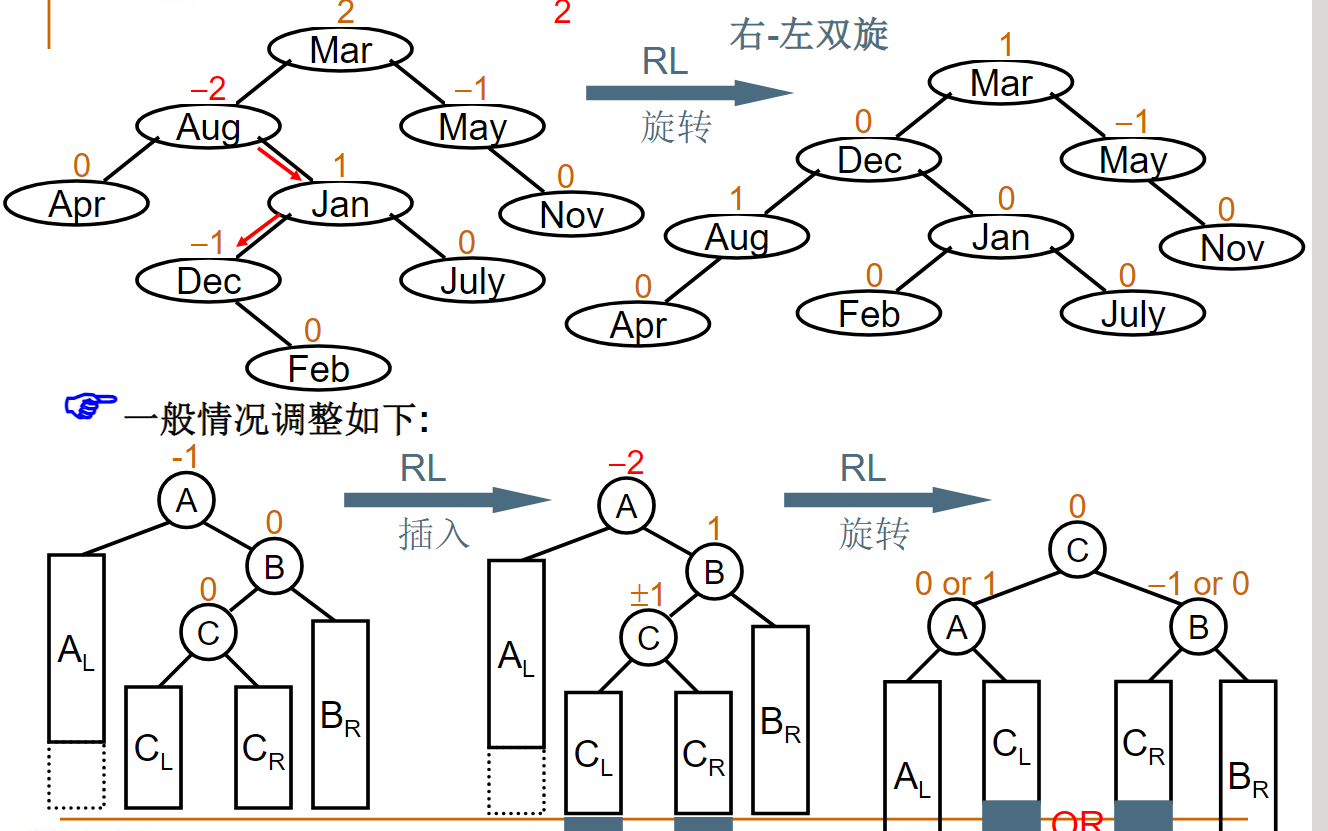
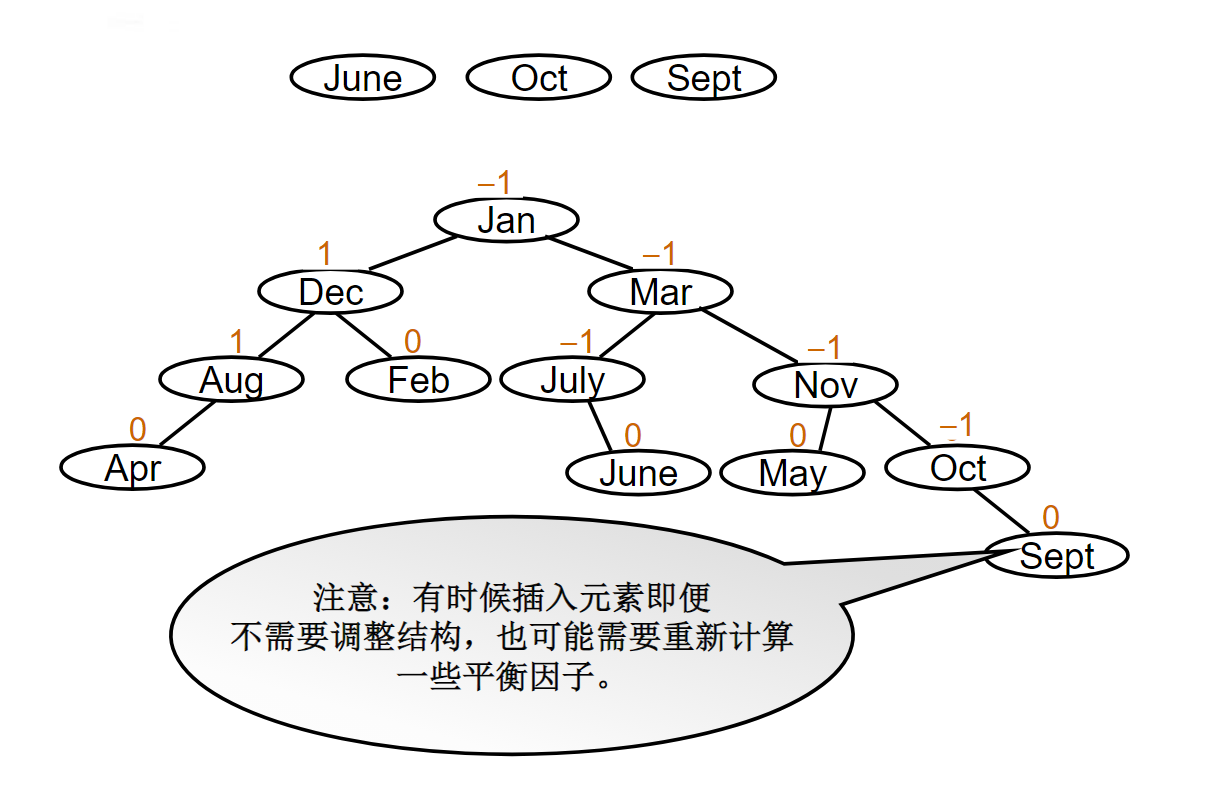
《数据结构》课程给出的代码如下:
typedef struct AVLNode *Position;
typedef Position AVLTree; /* AVL树类型 */
struct AVLNode{
ElementType Data; /* 结点数据 */
AVLTree Left; /* 指向左子树 */
AVLTree Right; /* 指向右子树 */
int Height; /* 树高 */
};
int Max ( int a, int b )
{
return a > b ? a : b;
}
AVLTree SingleLeftRotation ( AVLTree A )
{ /* 注意:A必须有一个左子结点B */
/* 将A与B做左单旋,更新A与B的高度,返回新的根结点B */
AVLTree B = A->Left;
A->Left = B->Right;
B->Right = A;
A->Height = Max( GetHeight(A->Left), GetHeight(A->Right) ) + 1;
B->Height = Max( GetHeight(B->Left), A->Height ) + 1;
return B;
}
AVLTree DoubleLeftRightRotation ( AVLTree A )
{ /* 注意:A必须有一个左子结点B,且B必须有一个右子结点C */
/* 将A、B与C做两次单旋,返回新的根结点C */
/* 将B与C做右单旋,C被返回 */
A->Left = SingleRightRotation(A->Left);
/* 将A与C做左单旋,C被返回 */
return SingleLeftRotation(A);
}
/*************************************/
/* 对称的右单旋与右-左双旋请自己实现 */
/*************************************/
AVLTree Insert( AVLTree T, ElementType X )
{ /* 将X插入AVL树T中,并且返回调整后的AVL树 */
if ( !T ) { /* 若插入空树,则新建包含一个结点的树 */
T = (AVLTree)malloc(sizeof(struct AVLNode));
T->Data = X;
T->Height = 0;
T->Left = T->Right = NULL;
} /* if (插入空树) 结束 */
else if ( X < T->Data ) {
/* 插入T的左子树 */
T->Left = Insert( T->Left, X);
/* 如果需要左旋 */
if ( GetHeight(T->Left)-GetHeight(T->Right) == 2 )
if ( X < T->Left->Data )
T = SingleLeftRotation(T); /* 左单旋 */
else
T = DoubleLeftRightRotation(T); /* 左-右双旋 */
} /* else if (插入左子树) 结束 */
else if ( X > T->Data ) {
/* 插入T的右子树 */
T->Right = Insert( T->Right, X );
/* 如果需要右旋 */
if ( GetHeight(T->Left)-GetHeight(T->Right) == -2 )
if ( X > T->Right->Data )
T = SingleRightRotation(T); /* 右单旋 */
else
T = DoubleRightLeftRotation(T); /* 右-左双旋 */
} /* else if (插入右子树) 结束 */
/* else X == T->Data,无须插入 */
/* 别忘了更新树高 */
T->Height = Max( GetHeight(T->Left), GetHeight(T->Right) ) + 1;
return T;
}
实例 PTA 04-树5 Root of AVL Tree
#include <stdio.h>
#include <stdlib.h>
typedef int ElementType;
typedef struct AVLNode *Position;
typedef Position AVLTree; /* AVL树类型 */
struct AVLNode{
ElementType Data; /* 结点数据 */
AVLTree Left; /* 指向左子树 */
AVLTree Right; /* 指向右子树 */
int Height; /* 树高 */
};
int Max ( int a, int b )
{
return a > b ? a : b;
}
int GetHeight(AVLTree T)
{
if (!T)
return -1;
else
return T->Height;
}
AVLTree SingleLeftRotation ( AVLTree A )
{ /* 注意:A必须有一个左子结点B */
/* 将A与B做左单旋,更新A与B的高度,返回新的根结点B */
AVLTree B = A->Left;
A->Left = B->Right;
B->Right = A;
A->Height = Max( GetHeight(A->Left), GetHeight(A->Right) ) + 1;
B->Height = Max( GetHeight(B->Left), A->Height ) + 1;
return B;
}
AVLTree SingleRightRotation(AVLTree A)//麻烦结点存在右子树的右边
{
AVLTree B=A->Right;
A->Right=B->Left;//右子树的左儿子赋给A的右子树
B->Left=A;//B变成A的父结点
A->Height=Max(GetHeight(A->Left),GetHeight(A->Right))+1;
B->Height=Max(A->Height,GetHeight(B->Right))+1;
return B;
}
AVLTree DoubleRightLeftRotation(AVLTree A)//麻烦结点存在右子树的左边
{
A->Right=SingleLeftRotation(A->Right);
return SingleRightRotation(A);
}
AVLTree DoubleLeftRightRotation ( AVLTree A )
{ /* 注意:A必须有一个左子结点B,且B必须有一个右子结点C */
/* 将A、B与C做两次单旋,返回新的根结点C */
/* 将B与C做右单旋,C被返回 */
A->Left = SingleRightRotation(A->Left);
/* 将A与C做左单旋,C被返回 */
return SingleLeftRotation(A);
}
AVLTree Insert( AVLTree T, ElementType X )
{ /* 将X插入AVL树T中,并且返回调整后的AVL树 */
if ( !T ) { /* 若插入空树,则新建包含一个结点的树 */
T = (AVLTree)malloc(sizeof(struct AVLNode));
T->Data = X;
T->Height = 0;
T->Left = T->Right = NULL;
} /* if (插入空树) 结束 */
else if ( X < T->Data ) {
/* 插入T的左子树 */
T->Left = Insert( T->Left, X);
/* 如果需要左旋 */
if ( GetHeight(T->Left)-GetHeight(T->Right) == 2 )
if ( X < T->Left->Data )
T = SingleLeftRotation(T); /* 左单旋 */
else
T = DoubleLeftRightRotation(T); /* 左-右双旋 */
} /* else if (插入左子树) 结束 */
else if ( X > T->Data ) {
/* 插入T的右子树 */
T->Right = Insert( T->Right, X );
/* 如果需要右旋 */
if ( GetHeight(T->Left)-GetHeight(T->Right) == -2 )
if ( X > T->Right->Data )
T = SingleRightRotation(T); /* 右单旋 */
else
T = DoubleRightLeftRotation(T); /* 右-左双旋 */
} /* else if (插入右子树) 结束 */
/* else X == T->Data,无须插入 */
/* 别忘了更新树高 */
T->Height = Max( GetHeight(T->Left), GetHeight(T->Right) ) + 1;
return T;
}
int main()
{
int n;
scanf("%d",&n);
ElementType X;
AVLTree T = NULL;
for(int i=0; i<n; i++)
{
scanf("%d", &X);
T = Insert(T,X);
}
if(T)
printf("%d",T->Data);
return 0;
}
堆
定义


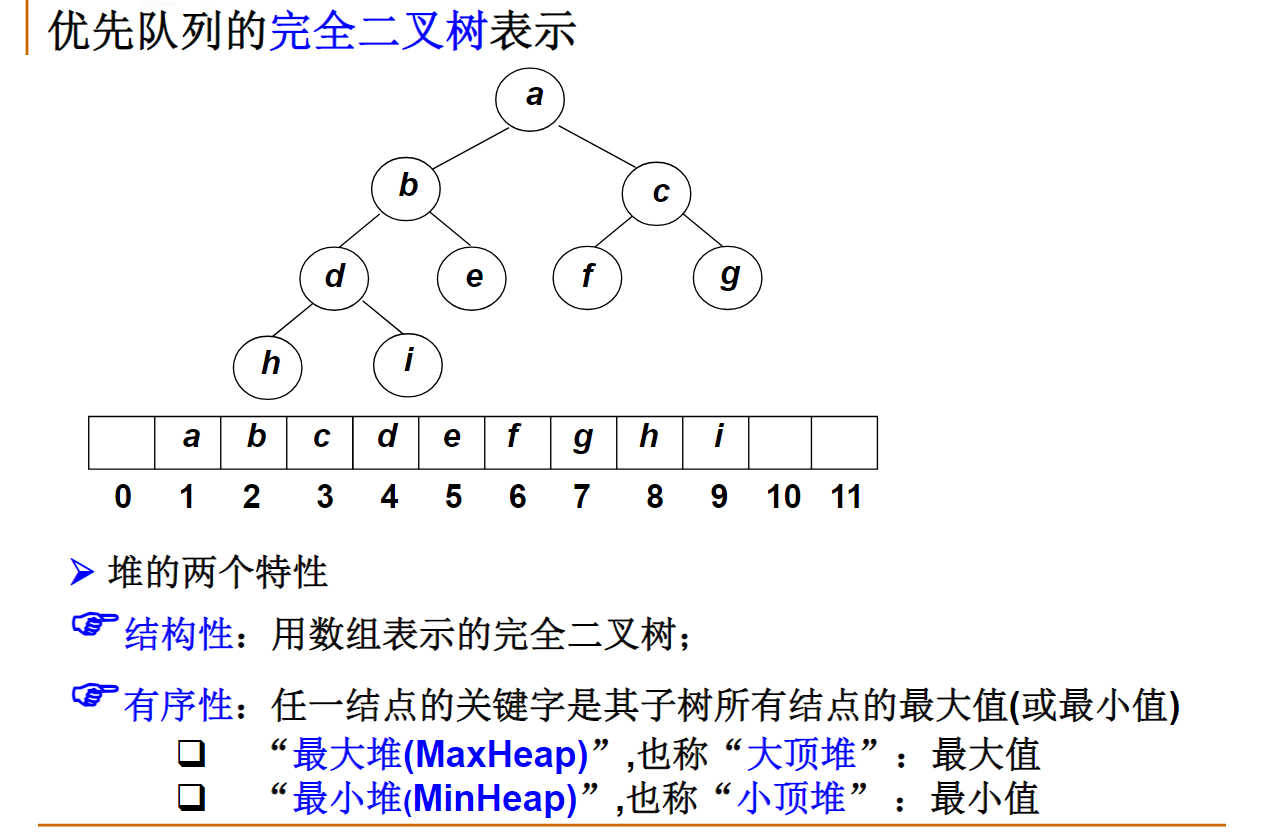
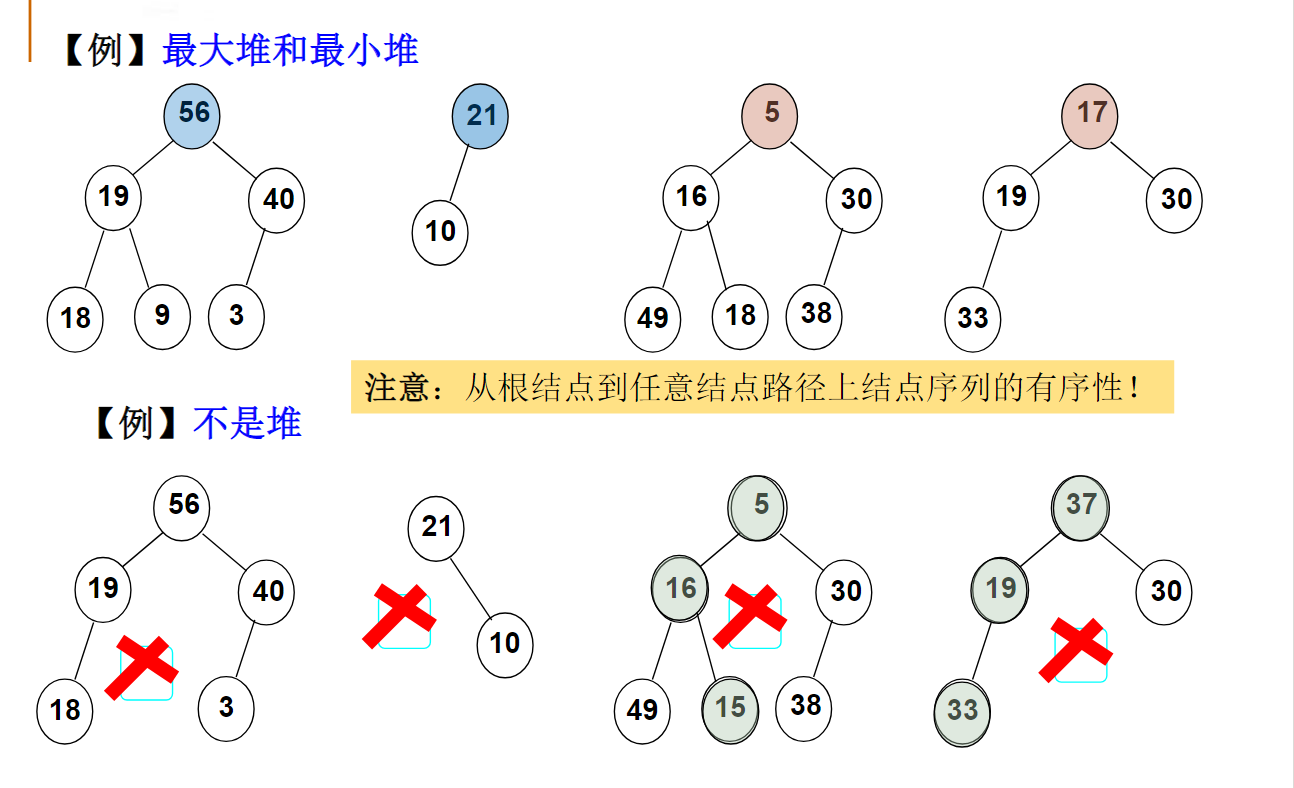

堆的定义与操作代码:
typedef struct HNode *Heap; /* 堆的类型定义 */
struct HNode {
ElementType *Data; /* 存储元素的数组 */
int Size; /* 堆中当前元素个数 */
int Capacity; /* 堆的最大容量 */
};
typedef Heap MaxHeap; /* 最大堆 */
typedef Heap MinHeap; /* 最小堆 */
#define MAXDATA 1000 /* 该值应根据具体情况定义为大于堆中所有可能元素的值 */
MaxHeap CreateHeap( int MaxSize )
{ /* 创建容量为MaxSize的空的最大堆 */
MaxHeap H = (MaxHeap)malloc(sizeof(struct HNode));
H->Data = (ElementType *)malloc((MaxSize+1)*sizeof(ElementType));
H->Size = 0;
H->Capacity = MaxSize;
H->Data[0] = MAXDATA; /* 定义"哨兵"为大于堆中所有可能元素的值*/
return H;
}
bool IsFull( MaxHeap H )
{
return (H->Size == H->Capacity);
}
bool Insert( MaxHeap H, ElementType X )
{ /* 将元素X插入最大堆H,其中H->Data[0]已经定义为哨兵 */
int i;
if ( IsFull(H) ) {
printf("最大堆已满");
return false;
}
i = ++H->Size; /* i指向插入后堆中的最后一个元素的位置 */
for ( ; H->Data[i/2] < X; i/=2 )
H->Data[i] = H->Data[i/2]; /* 上滤X */
H->Data[i] = X; /* 将X插入 */
return true;
}
#define ERROR -1 /* 错误标识应根据具体情况定义为堆中不可能出现的元素值 */
bool IsEmpty( MaxHeap H )
{
return (H->Size == 0);
}
ElementType DeleteMax( MaxHeap H )
{ /* 从最大堆H中取出键值为最大的元素,并删除一个结点 */
int Parent, Child;
ElementType MaxItem, X;
if ( IsEmpty(H) ) {
printf("最大堆已为空");
return ERROR;
}
MaxItem = H->Data[1]; /* 取出根结点存放的最大值 */
/* 用最大堆中最后一个元素从根结点开始向上过滤下层结点 */
X = H->Data[H->Size--]; /* 注意当前堆的规模要减小 */
for( Parent=1; Parent*2<=H->Size; Parent=Child ) {
Child = Parent * 2;
if( (Child!=H->Size) && (H->Data[Child]<H->Data[Child+1]) )
Child++; /* Child指向左右子结点的较大者 */
if( X >= H->Data[Child] ) break; /* 找到了合适位置 */
else /* 下滤X */
H->Data[Parent] = H->Data[Child];
}
H->Data[Parent] = X;
return MaxItem;
}
/*----------- 建造最大堆 -----------*/
void PercDown( MaxHeap H, int p )
{ /* 下滤:将H中以H->Data[p]为根的子堆调整为最大堆 */
int Parent, Child;
ElementType X;
X = H->Data[p]; /* 取出根结点存放的值 */
for( Parent=p; Parent*2<=H->Size; Parent=Child ) {
Child = Parent * 2;
if( (Child!=H->Size) && (H->Data[Child]<H->Data[Child+1]) )
Child++; /* Child指向左右子结点的较大者 */
if( X >= H->Data[Child] ) break; /* 找到了合适位置 */
else /* 下滤X */
H->Data[Parent] = H->Data[Child];
}
H->Data[Parent] = X;
}
void BuildHeap( MaxHeap H )
{ /* 调整H->Data[]中的元素,使满足最大堆的有序性 */
/* 这里假设所有H->Size个元素已经存在H->Data[]中 */
int i;
/* 从最后一个结点的父节点开始,到根结点1 */
for( i = H->Size/2; i>0; i-- )
PercDown( H, i );
}
最大堆

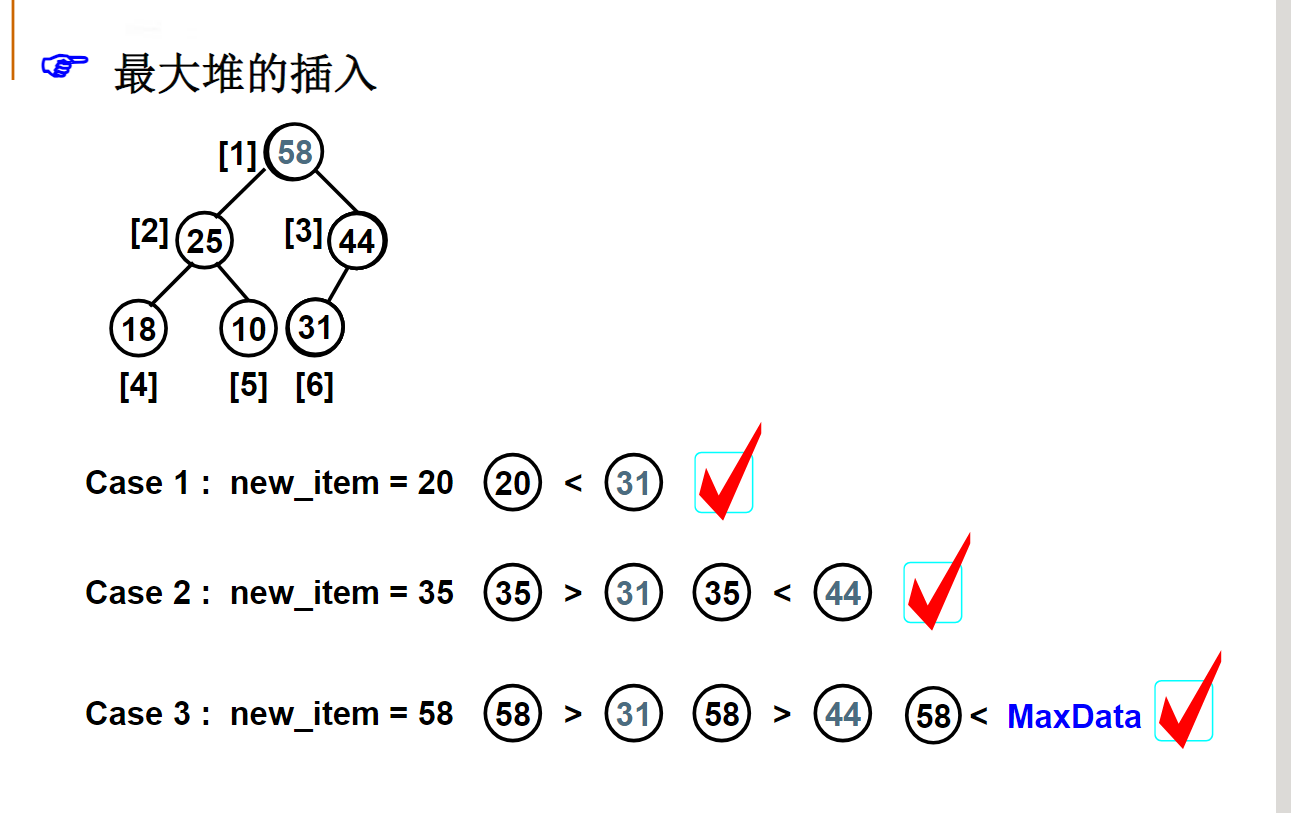


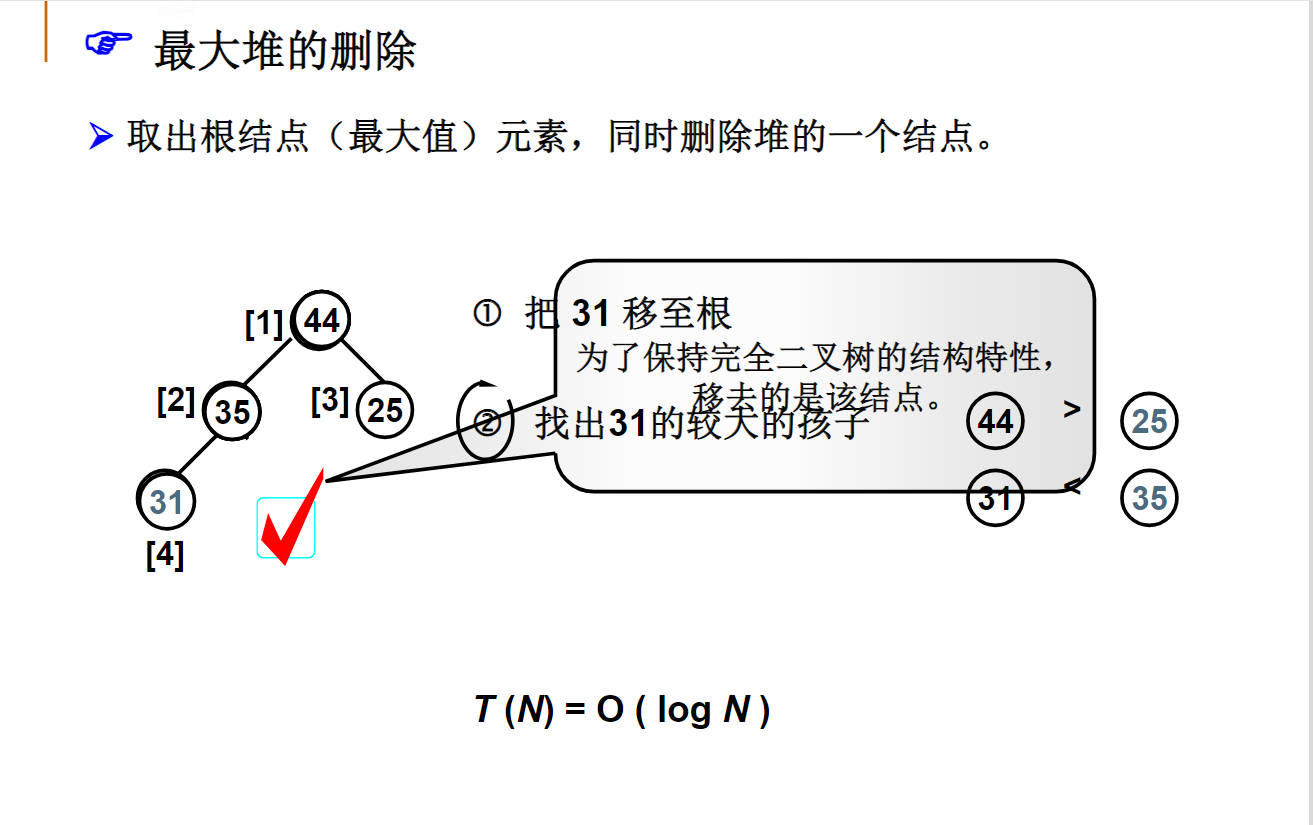


建堆时,最坏情况下需要挪动元素次数是等于树中各结点的高度和。问:对于元素个数为12的堆,其各结点的高度之和是多少?10

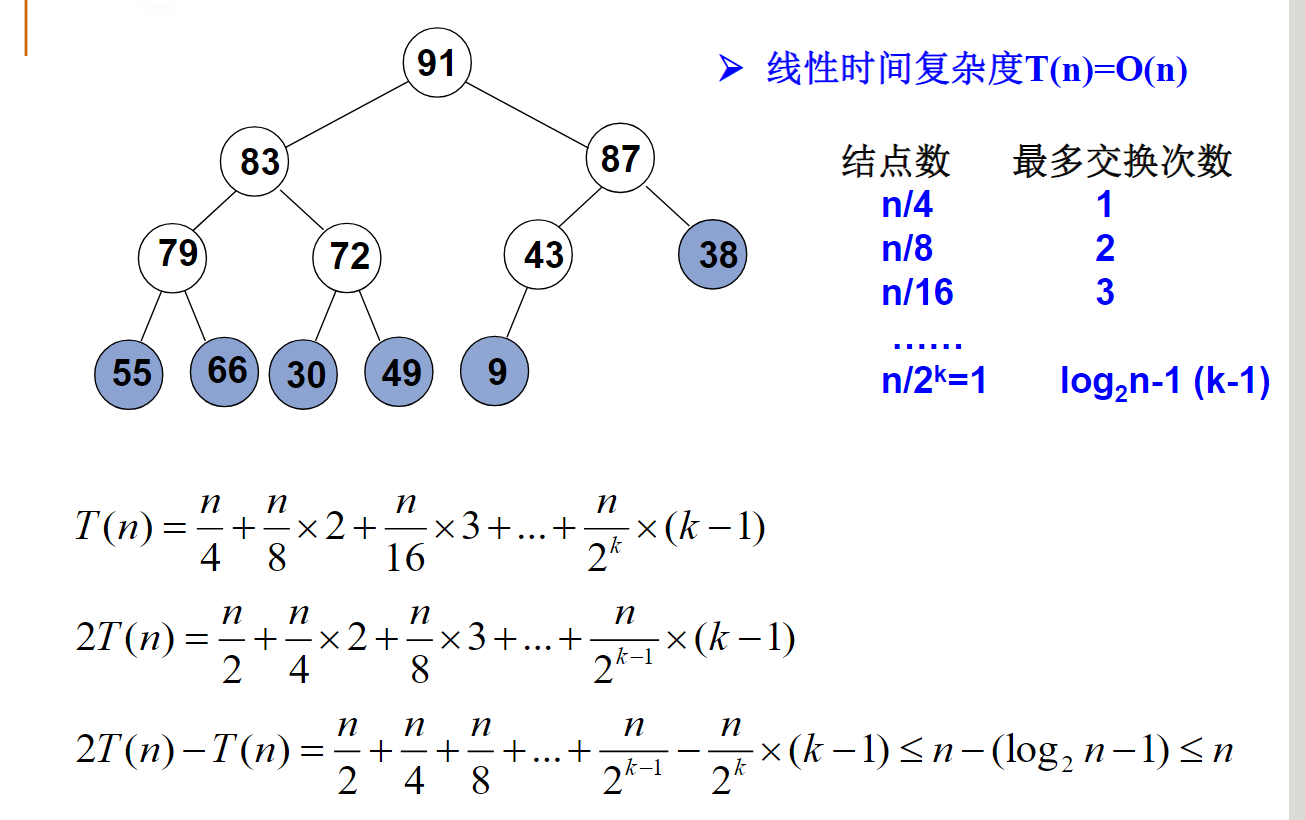
在最大堆 {97,76,65,50,49,13,27}中插入83后,该最大堆为: {97,83,65,76,49,13,27,50}
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
typedef int ElementType;
typedef struct HNode *Heap;
struct HNode
{
ElementType *Data; //存储元素的数组
int Size; //堆中当前元素个数
int Capacity; //堆的最大容量
};
typedef Heap MaxHeap;
typedef Heap MinHeap;
#define MAXDATA 1000 //该值应根据具体情况定义为大于堆中所有可能元素的值
MaxHeap CreateHeap(int MaxSize) //创建容量为MaxSize的空的最大堆
{
MaxHeap H = (Heap)malloc(sizeof(struct HNode));
H->Data = (ElementType *)malloc(sizeof(ElementType) * (MaxSize+1));
H->Capacity = MaxSize;
H->Size = 0;
H->Data[0] = MAXDATA; //定义"哨兵"为大于堆中所有可能元素的值
return H;
}
bool IsFull(MaxHeap H)
{
return (H->Size == H->Capacity);
}
bool Insert(MaxHeap H, ElementType X) //将元素X插入最大堆H,其中H->Data[0]已经定义为哨兵
{
if(IsFull(H))
{
printf("The heap is full!\n");
return false;
}
int i = ++H->Size; //i指向插入后堆中的最后一个元素的位置
for(;H->Data[i/2] < X;i/=2)
{
H->Data[i] = H->Data[i/2]; //上滤X
}
H->Data[i] = X;
return true;
}
bool IsEmpty(MaxHeap H)
{
return (H->Size == 0);
}
#define ERROR -1
ElementType Delete(MaxHeap H) //从最大堆H中取出键值为最大的元素,并删除一个结点
{
if(IsEmpty(H))
{
printf("The heap is empty!\n");
return ERROR;
}
ElementType MaxItem = H->Data[1]; //取出根结点存放的最大值
//用最大堆中最后一个元素从根结点开始向上过滤下层结点
ElementType X = H->Data[H->Size--]; //注意当前堆的规模要减小
int Parent, Child;
for(Parent=1; Parent*2<=H->Size; Parent=Child)
{
Child = Parent*2;
if((Child!=H->Size)&&(H->Data[Child]<H->Data[Child+1]))
Child++; //Child指向左右子结点的较大者
if(X > H->Data[Child]) //找到了合适位置
break;
else
H->Data[Parent] = H->Data[Child]; //下滤X
}
H->Data[Parent] = X;
return MaxItem;
}
int main()
{
int MaxSize = 100;
MaxHeap H = CreateHeap(MaxSize);
Insert(H,97);
Insert(H,76);
Insert(H,65);
Insert(H,50);
Insert(H,49);
Insert(H,13);
Insert(H,27);
Insert(H,83);
for(int i=1; i<=H->Size;i++)
printf("%d ",H->Data[i]);
printf("\n");
Delete(H);
for(int i=1; i<=H->Size;i++)
printf("%d ",H->Data[i]);
printf("\n");
Delete(H);
for(int i=1; i<=H->Size;i++)
printf("%d ",H->Data[i]);
return 0;
}
97 83 65 76 49 13 27 50
83 76 65 50 49 13 27
76 50 65 27 49 13
有个堆其元素在数组中的序列为:58,25,44,18,10,26,20,12。如果调用DeleteMax函数删除最大值元素,请猜猜看:程序中的for循环刚退出时变量parent的值是多少?6
最小堆
对由同样的n个整数构成的二叉搜索树(查找树)和最小堆,下面说法中D是 不正确 的:
A.二叉搜索树(查找树)高度大于等于最小堆高度
B.对该二叉搜索树(查找树)进行中序遍历可得到从小到大的序列
C.从最小堆根节点到其任何叶结点的路径上的结点值构成从小到大的序列
D.对该最小堆进行按层序(level order)遍历可得到从小到大的序列
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#define ERROR -1
typedef int ElementType;
typedef struct HNode *Heap;
typedef Heap MaxHeap;
typedef Heap MinHeap;
struct HNode
{
ElementType *Data;
int Size;
int Capacity;
};
MinHeap CreateHeap(int MaxSize)
{
MinHeap H = (MinHeap)malloc(sizeof(struct HNode));
H->Data = (ElementType*)malloc(sizeof(ElementType)*MaxSize);
H->Size = 0;
H->Capacity = MaxSize;
H->Data[0] = -100;
return H;
}
bool IsFull(MinHeap H)
{
return (H->Size == H->Capacity);
}
bool Insert(MinHeap H, ElementType X)
{
if(IsFull(H))
{
printf("The heap is full!\n");
return false;
}
int i = ++H->Size;
for(; H->Data[i/2] >= X; i /= 2)
{
H->Data[i] = H->Data[i/2];
}
H->Data[i] = X;
return true;
}
bool IsEmpty(MinHeap H)
{
return (H->Size == 0);
}
ElementType Delete(MinHeap H)
{
if(IsEmpty(H))
{
printf("The heap is empty!\n");
return ERROR;
}
int Parent, Child;
ElementType MinItem,X;
MinItem = H->Data[1];
X = H->Data[H->Size--];
for(Parent = 1; Parent * 2 <= H->Size; Parent = Child)
{
Child = Parent * 2;
if((Child!=H->Size)&&(H->Data[Child] > H->Data[Child + 1]))
Child++;
if(X < H->Data[Child])
break;
else
H->Data[Parent] = H->Data[Child];
}
H->Data[Parent] = X;
return MinItem;
}
int main()
{
int MaxSize = 100;
MinHeap H = CreateHeap(MaxSize);
Insert(H,97);
Insert(H,76);
Insert(H,65);
Insert(H,50);
Insert(H,49);
Insert(H,13);
Insert(H,27);
Insert(H,83);
for(int i=1; i<=H->Size;i++)
printf("%d ",H->Data[i]);
printf("\n");
Delete(H);
for(int i=1; i<=H->Size;i++)
printf("%d ",H->Data[i]);
printf("\n");
Delete(H);
for(int i=1; i<=H->Size;i++)
printf("%d ",H->Data[i]);
return 0;
}
13 50 27 83 65 76 49 97
27 50 49 83 65 76 97
49 50 76 83 65 97
实例 PTA 05-树7 堆中的路径
将一系列给定数字依次插入一个初始为空的小顶堆H[]。随后对任意给定的下标i,打印从H[i]到根结点的路径。
输入格式:
每组测试第1行包含2个正整数N和M(≤1000),分别是插入元素的个数、以及需要打印的路径条数。下一行给出区间[-10000, 10000]内的N个要被插入一个初始为空的小顶堆的整数。最后一行给出M个下标。
输出格式:
对输入中给出的每个下标i,在一行中输出从H[i]到根结点的路径上的数据。数字间以1个空格分隔,行末不得有多余空格。
输入样例:
5 3
46 23 26 24 10
5 4 3
输出样例:
24 23 10
46 23 10
26 10

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#define ERROR -1
typedef int ElementType;
typedef struct HNode *Heap;
typedef Heap MaxHeap;
typedef Heap MinHeap;
struct HNode
{
ElementType *Data;
int Size;
int Capacity;
};
MinHeap CreateHeap(int MaxSize)
{
MinHeap H = (MinHeap)malloc(sizeof(struct HNode));
H->Data = (ElementType*)malloc(sizeof(ElementType)*MaxSize);
H->Size = 0;
H->Capacity = MaxSize;
H->Data[0] = -10001;
return H;
}
bool IsFull(MinHeap H)
{
return (H->Size == H->Capacity);
}
bool Insert(MinHeap H, ElementType X)
{
if(IsFull(H))
{
printf("The heap is full!\n");
return false;
}
int i = ++H->Size;
for(; H->Data[i/2] >= X; i /= 2)
{
H->Data[i] = H->Data[i/2];
}
H->Data[i] = X;
return true;
}
bool IsEmpty(MinHeap H)
{
return (H->Size == 0);
}
ElementType Delete(MinHeap H)
{
if(IsEmpty(H))
{
printf("The heap is empty!\n");
return ERROR;
}
int Parent, Child;
ElementType MinItem,X;
MinItem = H->Data[1];
X = H->Data[H->Size--];
for(Parent = 1; Parent * 2 <= H->Size; Parent = Child)
{
Child = Parent * 2;
if((Child!=H->Size)&&(H->Data[Child] > H->Data[Child + 1]))
Child++;
if(X < H->Data[Child])
break;
else
H->Data[Parent] = H->Data[Child];
}
H->Data[Parent] = X;
return MinItem;
}
int main()
{
int MaxSize = 1001;
MinHeap H = CreateHeap(MaxSize);
int N,M;
scanf("%d %d",&N,&M);
for(int i=0; i<N; i++)
{
int num;
scanf("%d",&num);
Insert(H,num);
}
for(int i=0; i<M; i++)
{
int idx;
scanf("%d",&idx);
int Fisrt = 1;
for(int j=idx; j>=1; j/=2)
{
if(Fisrt)
{
printf("%d",H->Data[j]);
Fisrt = 0;
}
else
{
printf(" %d",H->Data[j]);
}
}
printf("\n");
}
return 0;
}
哈夫曼树
定义
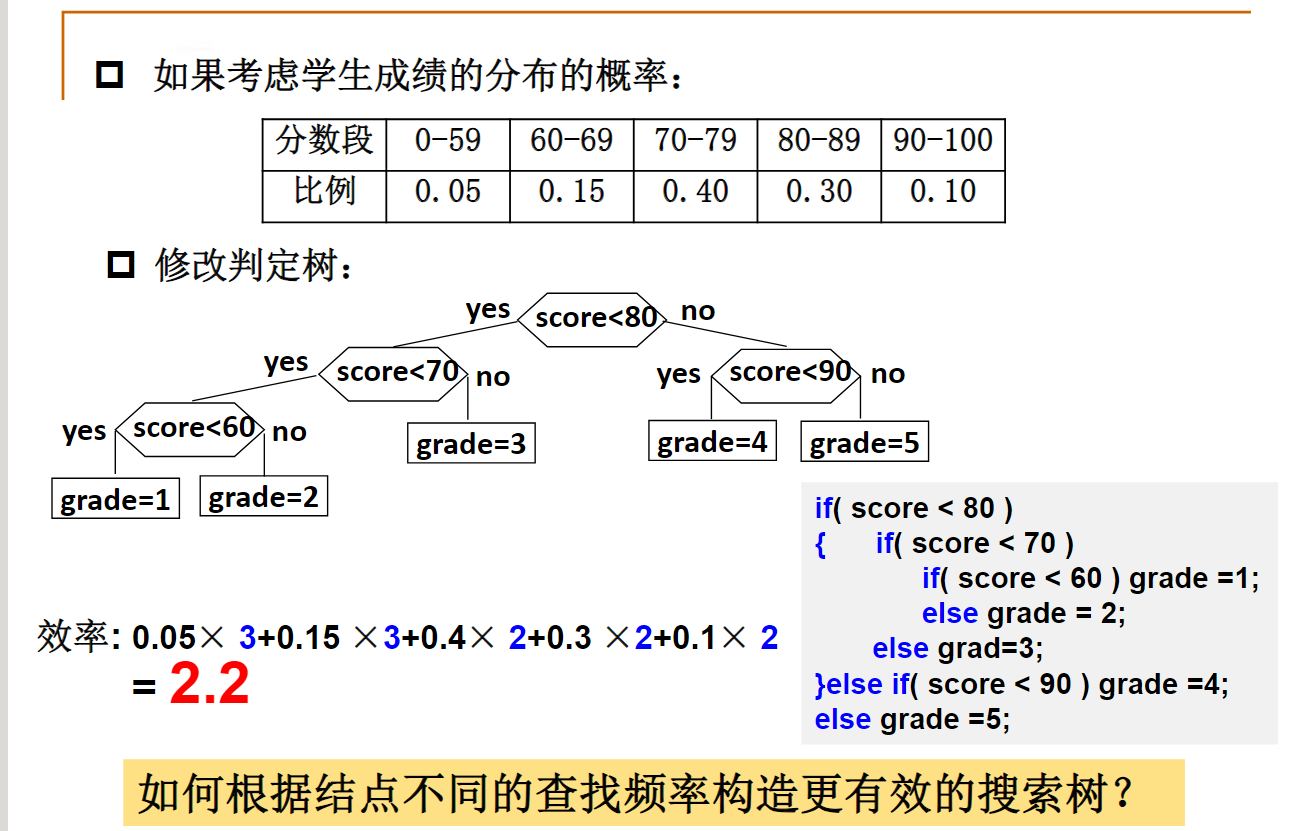
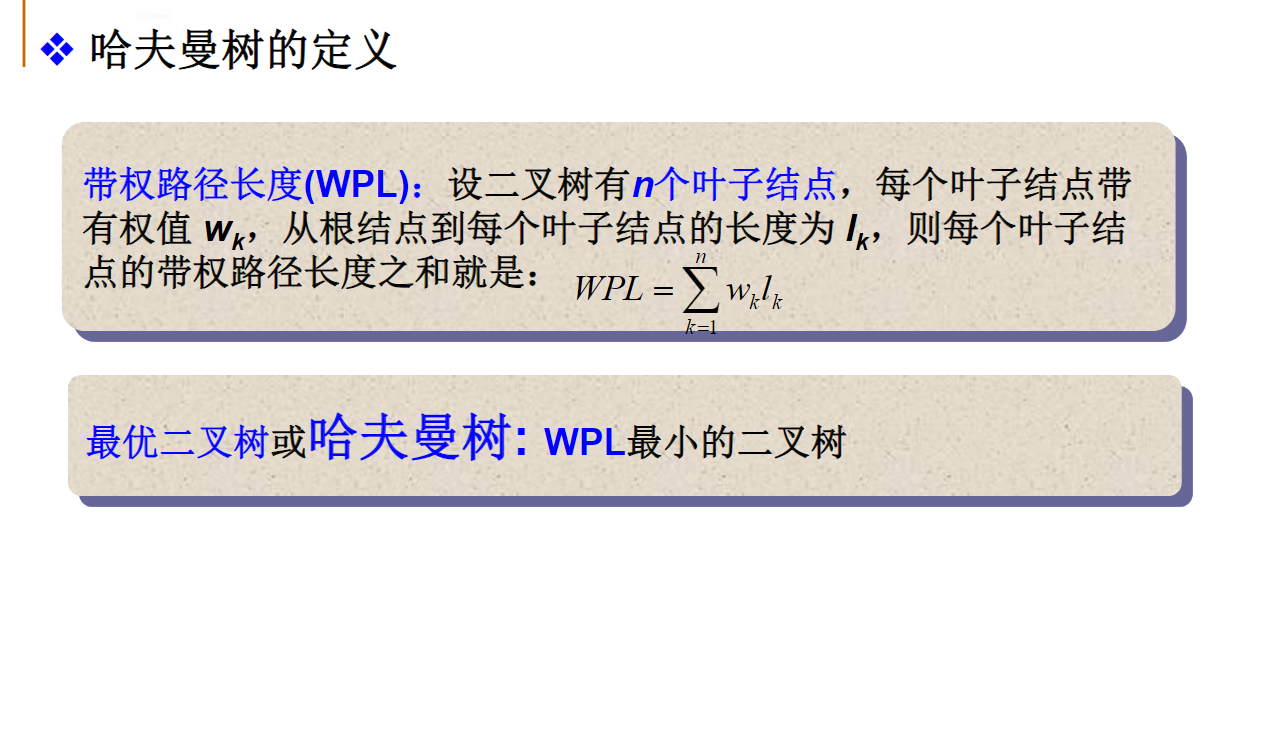
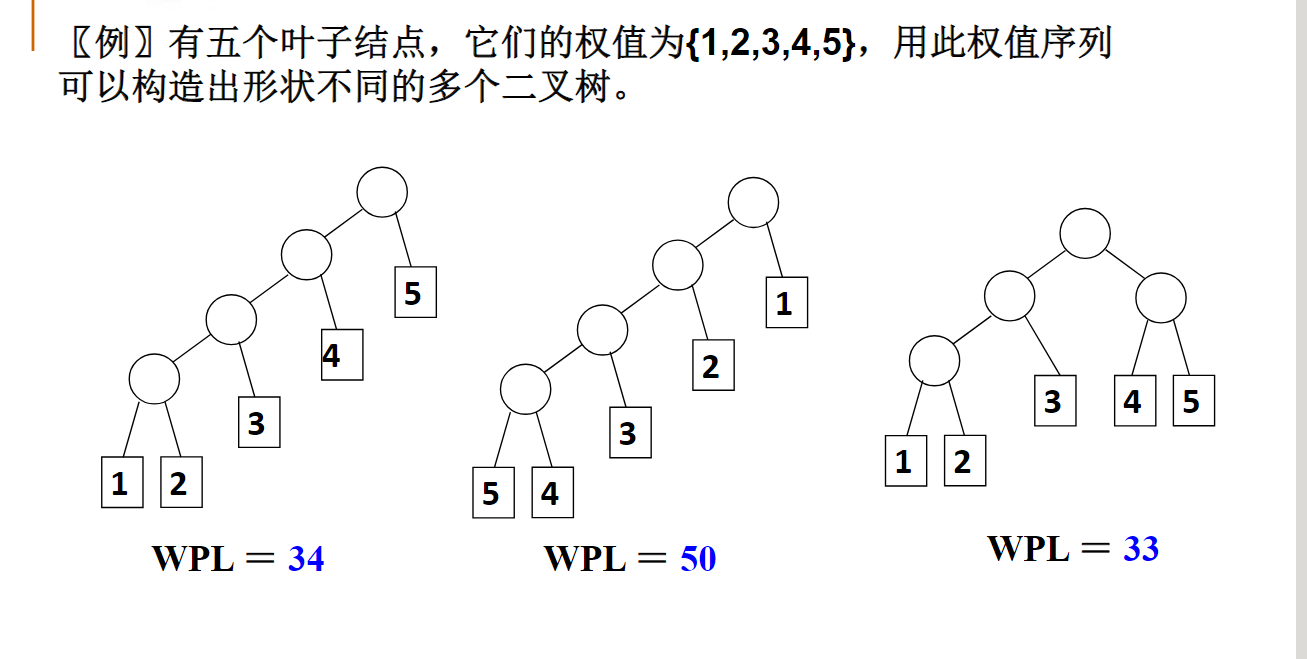
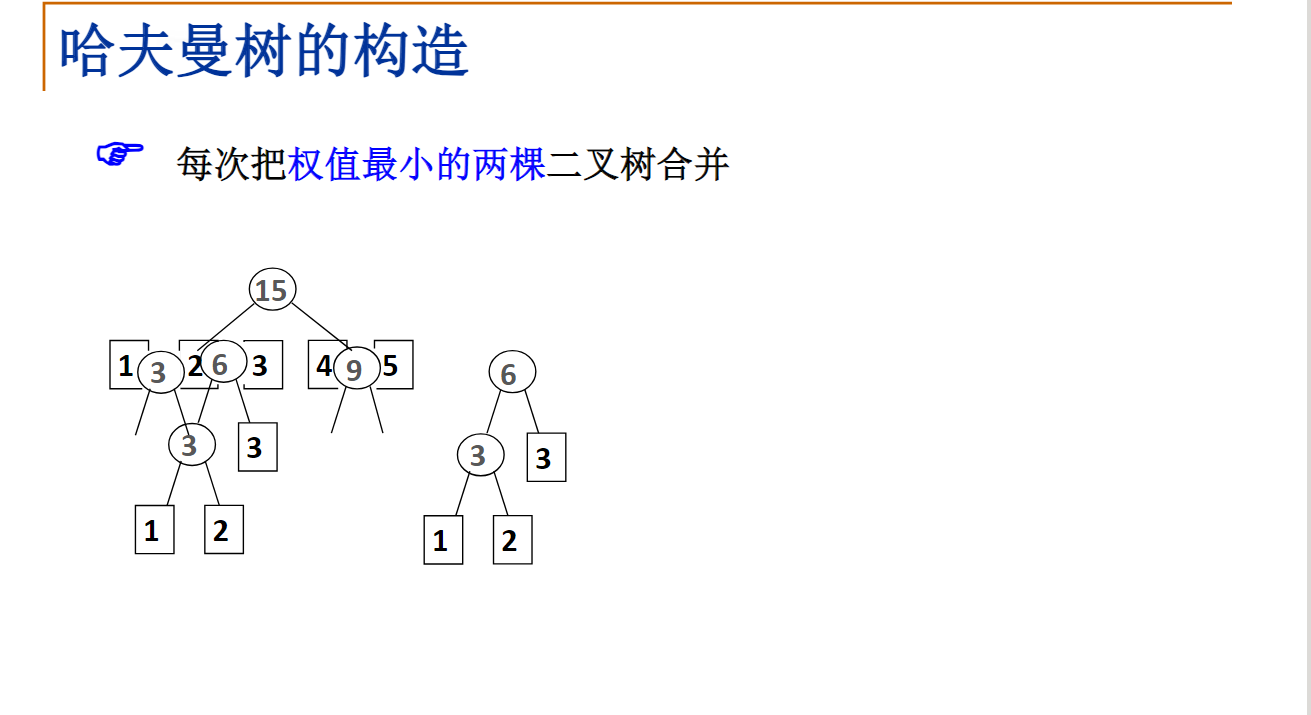

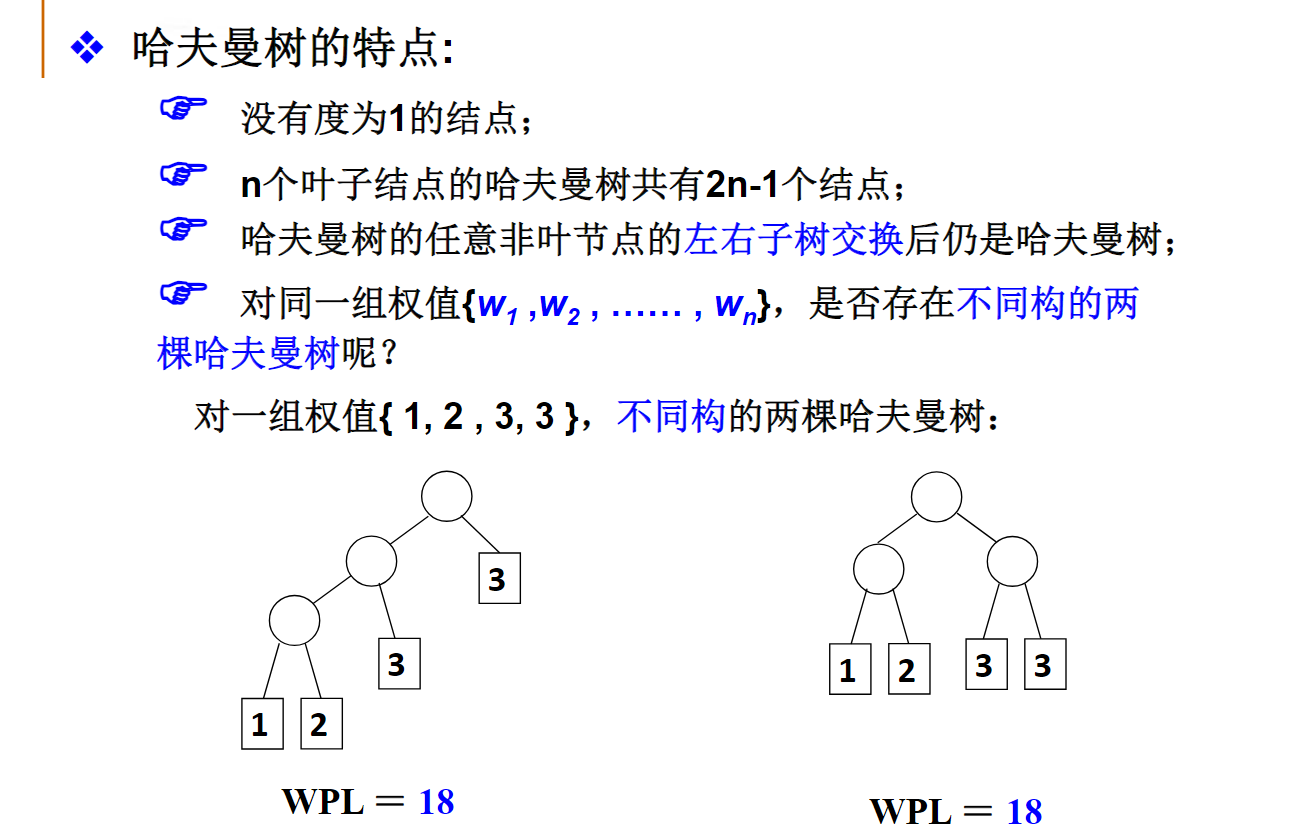
如果哈夫曼树有67个结点,则可知叶结点总数为:34
哈夫曼编码


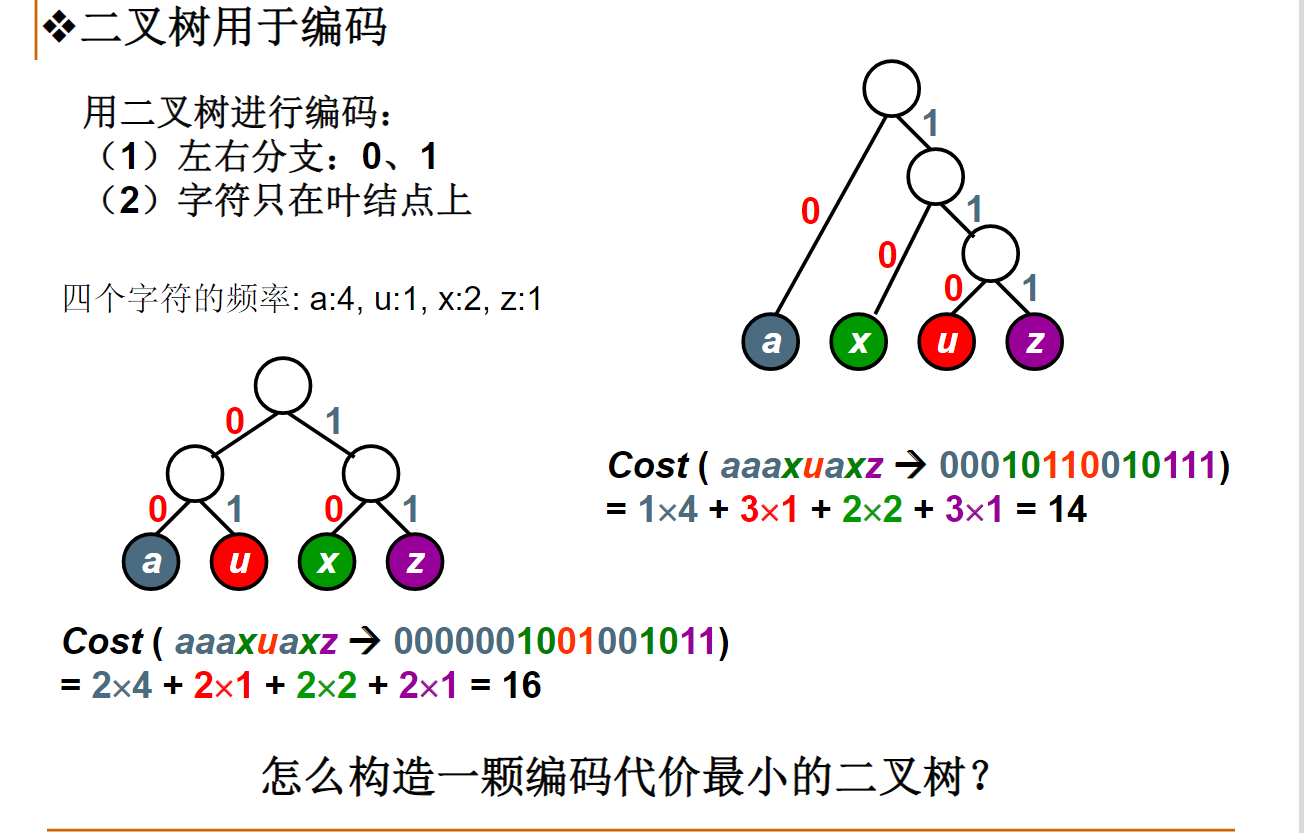
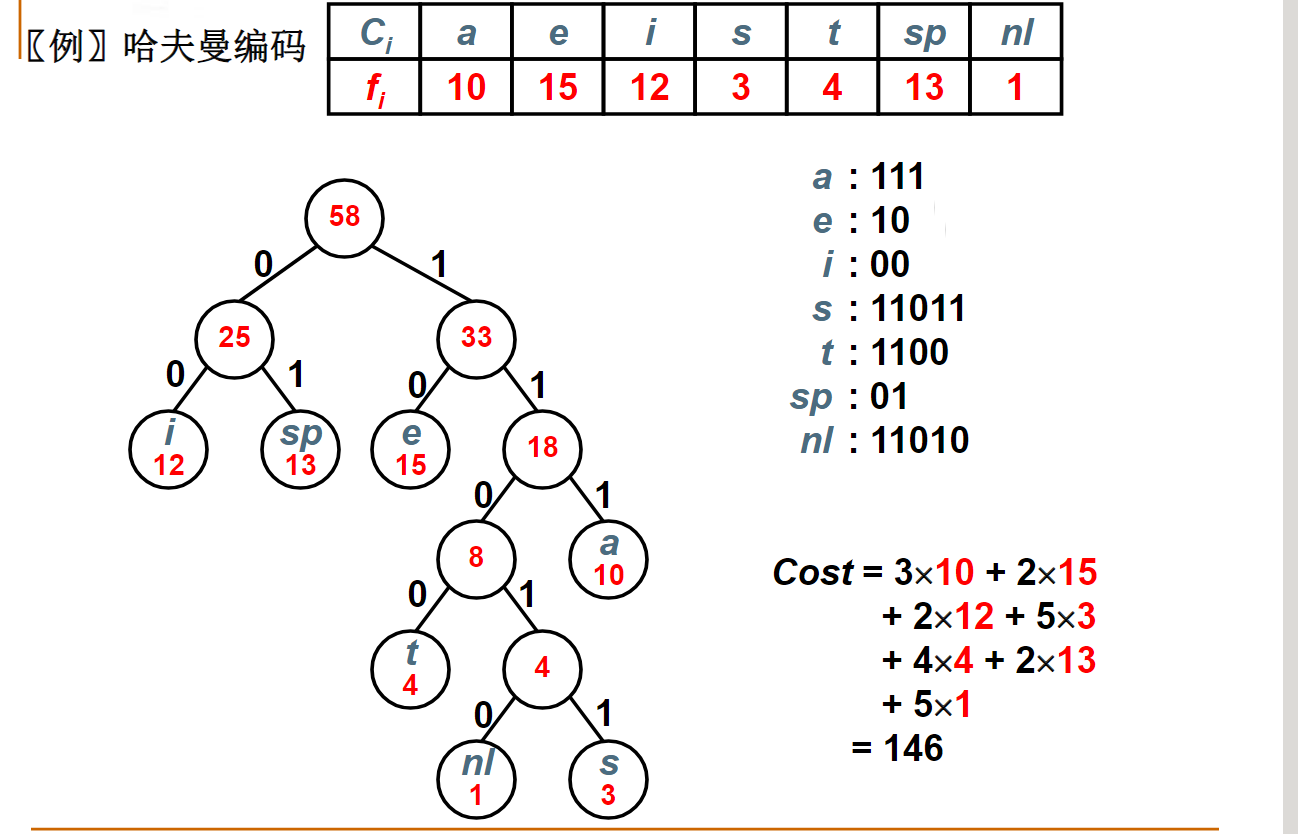
为五个使用频率不同的字符设计哈夫曼编码,下列方案中哪个不可能是哈夫曼编码?A
-
A.00,100,101,110,111
-
B.000,001,01,10,11
-
C.0000,0001,001,01,1
-
D.000,001,010,011,1
哈夫曼树的节点要么是叶子节点,要么是度为2的节点,不可能出现度为1的节点。
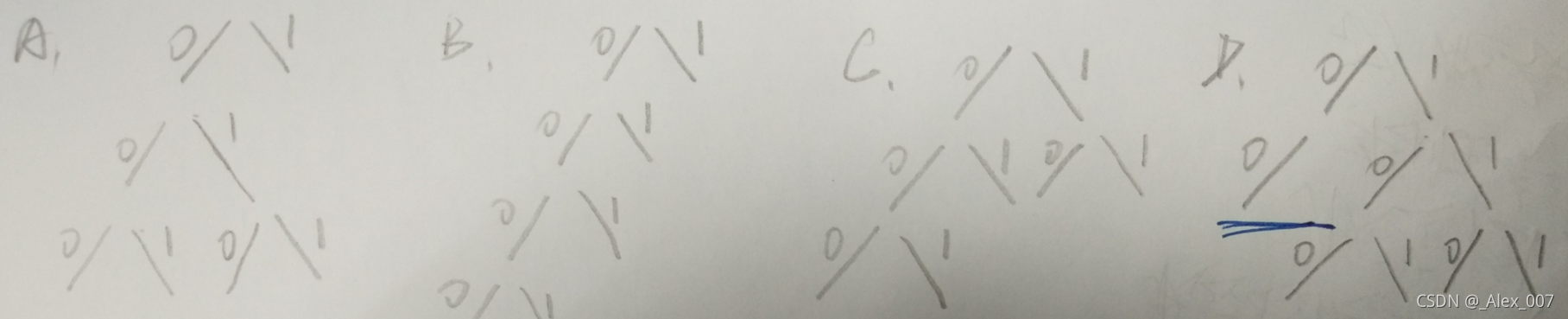
一段文本中包含对象{a,b,c,d,e},其出现次数相应为{3,2,4,2,1},则经过哈夫曼编码后,该文本所占总位数为:27
每次把权值最小的两棵二叉树合并
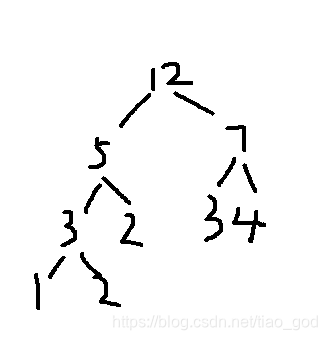
实例PTA 05-树9 Huffman Codes
In 1953, David A. Huffman published his paper "A Method for the Construction of Minimum-Redundancy Codes", and hence printed his name in the history of computer science. As a professor who gives the final exam problem on Huffman codes, I am encountering a big problem: the Huffman codes are NOT unique. For example, given a string "aaaxuaxz", we can observe that the frequencies of the characters 'a', 'x', 'u' and 'z' are 4, 2, 1 and 1, respectively. We may either encode the symbols as {'a'=0, 'x'=10, 'u'=110, 'z'=111}, or in another way as {'a'=1, 'x'=01, 'u'=001, 'z'=000}, both compress the string into 14 bits. Another set of code can be given as {'a'=0, 'x'=11, 'u'=100, 'z'=101}, but {'a'=0, 'x'=01, 'u'=011, 'z'=001} is NOT correct since "aaaxuaxz" and "aazuaxax" can both be decoded from the code 00001011001001. The students are submitting all kinds of codes, and I need a computer program to help me determine which ones are correct and which ones are not.
Input Specification:
Each input file contains one test case. For each case, the first line gives an integer N (2≤N≤63), then followed by a line that contains all the N distinct characters and their frequencies in the following format:
c[1] f[1] c[2] f[2] ... c[N] f[N]
where c[i] is a character chosen from {'0' - '9', 'a' - 'z', 'A' - 'Z', '_'}, and f[i] is the frequency of c[i] and is an integer no more than 1000. The next line gives a positive integer M (≤1000), then followed by M student submissions. Each student submission consists of N lines, each in the format:
c[i] code[i]
where c[i] is the i-th character and code[i] is an non-empty string of no more than 63 '0's and '1's.
Output Specification:
For each test case, print in each line either "Yes" if the student's submission is correct, or "No" if not.
Note: The optimal solution is not necessarily generated by Huffman algorithm. Any prefix code with code length being optimal is considered correct.
Sample Input:
7
A 1 B 1 C 1 D 3 E 3 F 6 G 6
4
A 00000
B 00001
C 0001
D 001
E 01
F 10
G 11
A 01010
B 01011
C 0100
D 011
E 10
F 11
G 00
A 000
B 001
C 010
D 011
E 100
F 101
G 110
A 00000
B 00001
C 0001
D 001
E 00
F 10
G 11
Sample Output:
Yes
Yes
No
No
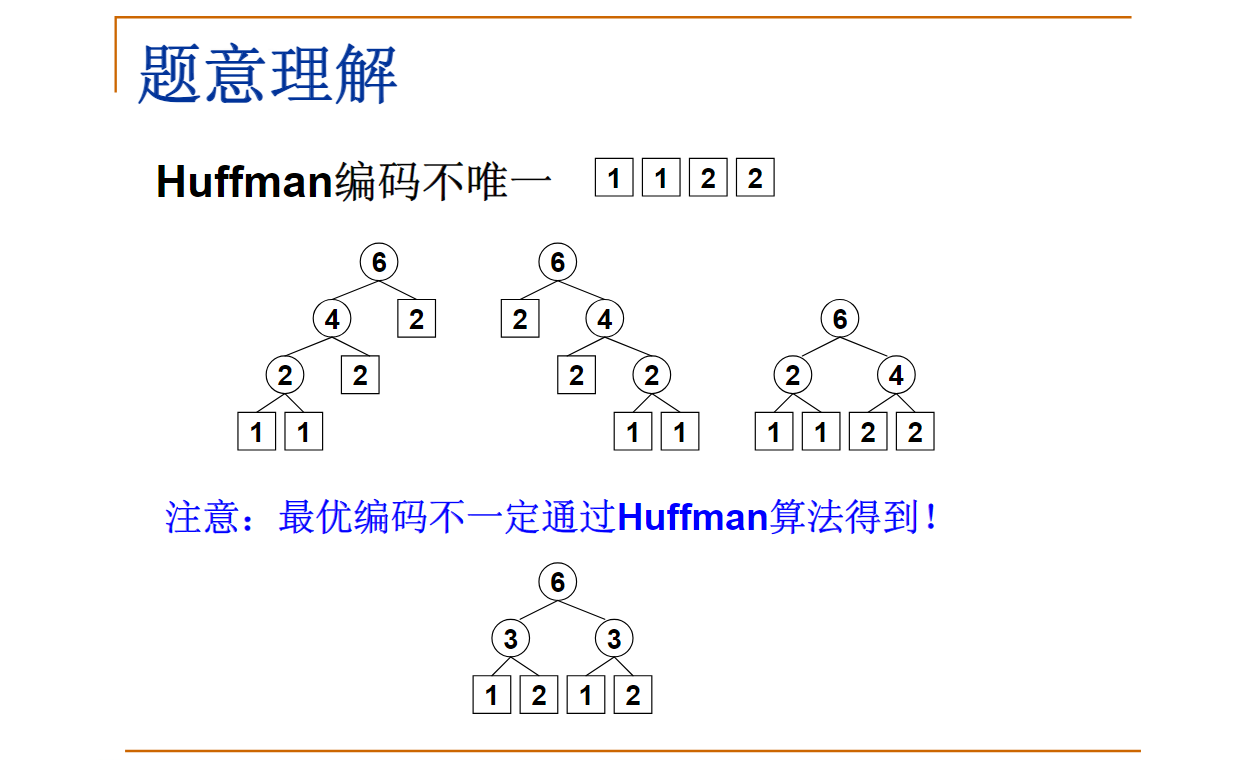

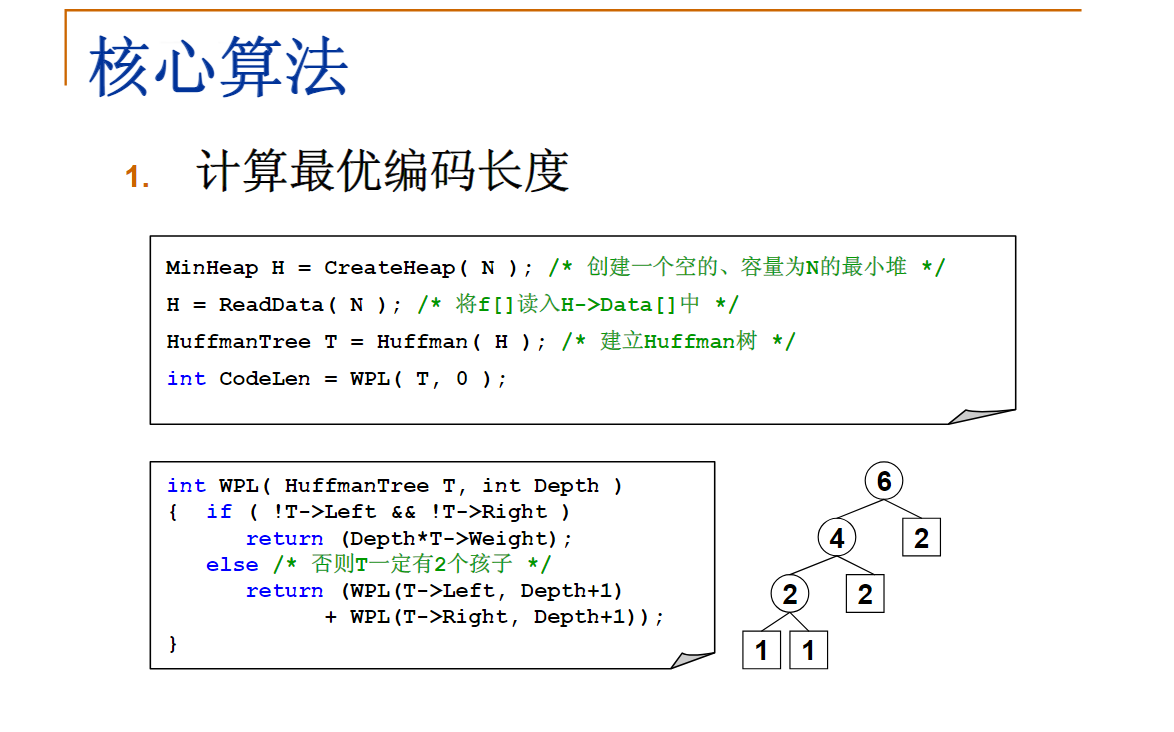
最优编码不一定通过Huffman算法得到。给定4个字符及其出现频率: A:1; B:1; C:2; D:2
下面哪一套不是用Huffman算法得到的正确的编码?
A.A:000; B:001; C:01; D:1
B.A:10; B:11; C:00; D:01
C.A:00; B:10; C:01; D:11
D.A:111; B:001; C:10; D:1
正确答案:C你选对了

这道题主要利用哈夫曼编码的两个性质:
- 哈夫曼编码可能不唯一,但是哈夫曼编码的长度是唯一的。字符串编码成01串后的长度实际上就是其以频率为权值所构成的任意一颗哈夫曼树的带权路径长度。
- 对于任何一个叶子结点,其编号一定不会成为其他任何一个结点编号的前缀—也就是说,题目中给出需要判断的的每个字符的编码,它不会是其他字符编码的前缀。
C++实现代码如下:
#include<bits/stdc++.h>
using namespace std;
int main(){
int s = 0, n, m, x, a[100];
char ch;
priority_queue<int,vector<int>,greater<int> > q; //优先队列
cin>>n;getchar();
for(int i = 0; i < n; i++) {
cin>>ch>>x;
a[i] = x;
q.push(x);
}
while(q.size() > 1) {
int x = q.top();
q.pop();
int y = q.top();
q.pop();
s = s + x + y;
q.push(x + y);
}
cin>>m;
while(m--) {
int s1 = 0;
string str[100];
for(int i = 0; i < n; i++) {
cin>>ch>>str[i];
s1 = s1 + str[i].size() * a[i];
}
if(s == s1) {
bool jdg = true;
for (int i = 0; i < n-1; i++) {
for (int j = i+1; j < n; j++) {
int flag = 0;
int size = str[i].size() > str[j].size() ? str[j].size() : str[i].size();
for(int k = 0; k < size; k++)
if(str[i][k] != str[j][k])
flag = 1;
if (!flag)
jdg = false;
}
}
if(jdg)
cout<<"Yes\n";
else
cout<<"No\n";
}
else
cout<<"No\n";
}
return 0;
}
并查集
集合表示
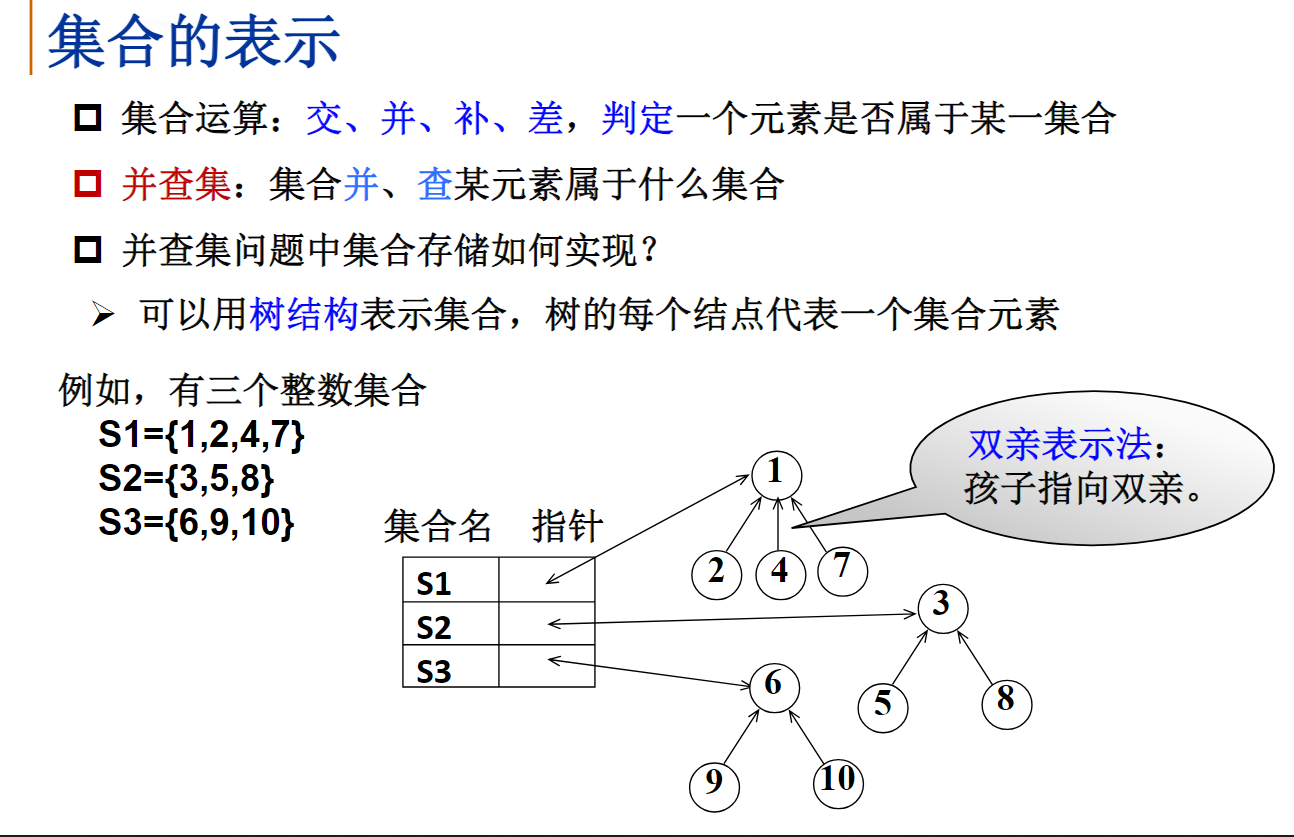
如果有10台电脑{1,2,3,4,...,9,10},已知下列电脑之间实现了连接:1和2,2和4,3和5,4和7,5和8,6和9,6和10问:2和7,5和9之间是否可以连通?2和7是连通的,5和9不连通
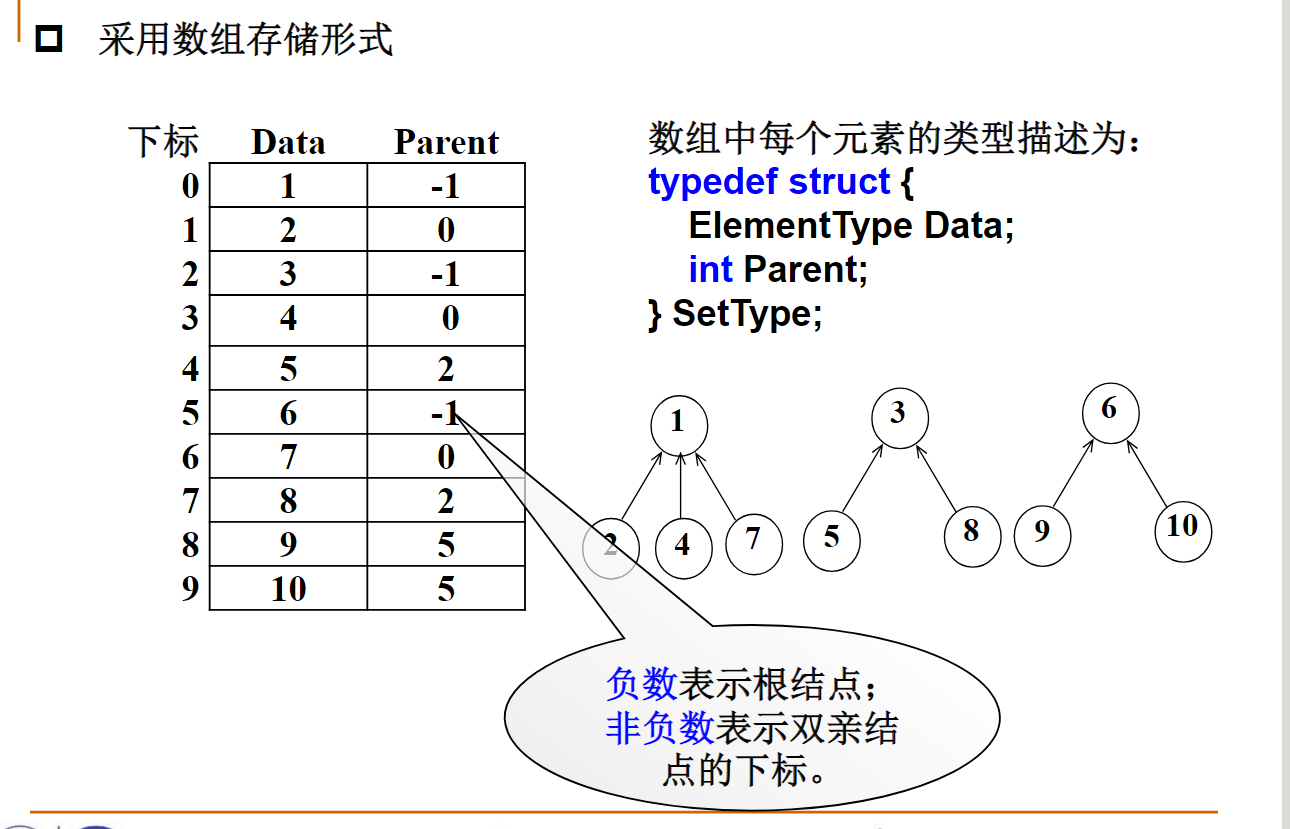
集合运算


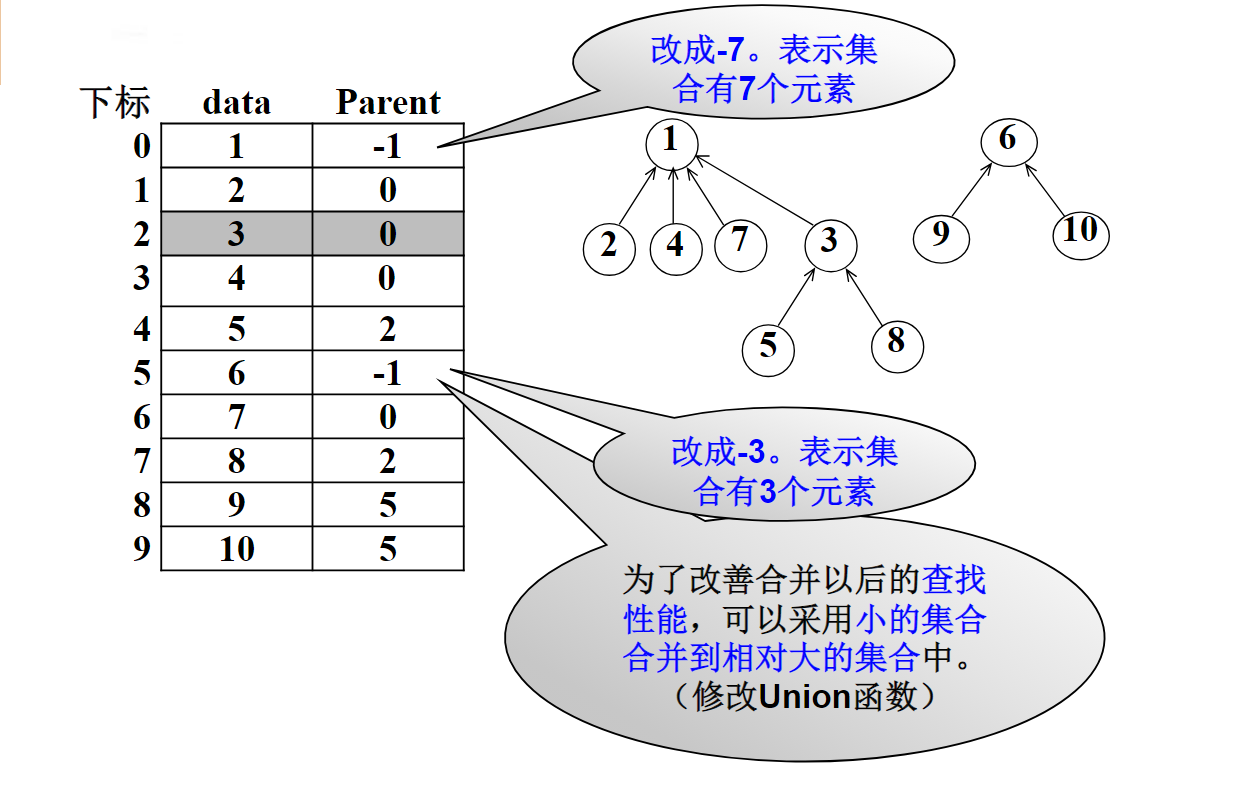
已知a、b两个元素均是所在集合的根结点,且分别位于数组分量3和2位置上,其parent值分别为-3,-2。问:将这两个集合按集合大小合并后,a和b的parent值分别是多少?-5,3
集合的定义与并查操作(已加入按秩归并方法):
#define MAXN 1000 /* 集合最大元素个数 */
typedef int ElementType; /* 默认元素可以用非负整数表示 */
typedef int SetName; /* 默认用根结点的下标作为集合名称 */
typedef ElementType SetType[MAXN]; /* 假设集合元素下标从0开始 */
void Union( SetType S, SetName Root1, SetName Root2 )
{ /* 这里默认Root1和Root2是不同集合的根结点 */
/* 保证小集合并入大集合 */
if ( S[Root2] < S[Root1] ) { /* 如果集合2比较大 */
S[Root2] += S[Root1]; /* 集合1并入集合2 */
S[Root1] = Root2;
}
else { /* 如果集合1比较大 */
S[Root1] += S[Root2]; /* 集合2并入集合1 */
S[Root2] = Root1;
}
}
SetName Find( SetType S, ElementType X )
{ /* 默认集合元素全部初始化为-1 */
if ( S[X] < 0 ) /* 找到集合的根 */
return X;
else
return S[X] = Find( S, S[X] ); /* 路径压缩 */
}
并查集实例PTA 05-树8 File Transfer
We have a network of computers and a list of bi-directional connections. Each of these connections allows a file transfer from one computer to another. Is it possible to send a file from any computer on the network to any other?
Input Specification:
Each input file contains one test case. For each test case, the first line contains N (2≤N≤104), the total number of computers in a network. Each computer in the network is then represented by a positive integer between 1 and N. Then in the following lines, the input is given in the format:
I c1 c2
where I stands for inputting a connection between c1 and c2; or
C c1 c2
where C stands for checking if it is possible to transfer files between c1 and c2; or
S
where S stands for stopping this case.
Output Specification:
For each C case, print in one line the word "yes" or "no" if it is possible or impossible to transfer files between c1 and c2, respectively. At the end of each case, print in one line "The network is connected." if there is a path between any pair of computers; or "There are k components." where k is the number of connected components in this network.
Sample Input 1:
5
C 3 2
I 3 2
C 1 5
I 4 5
I 2 4
C 3 5
S
Sample Output 1:
no
no
yes
There are 2 components.
Sample Input 2:
5
C 3 2
I 3 2
C 1 5
I 4 5
I 2 4
C 3 5
I 1 3
C 1 5
S
Sample Output 2:
no
no
yes
yes
The network is connected.

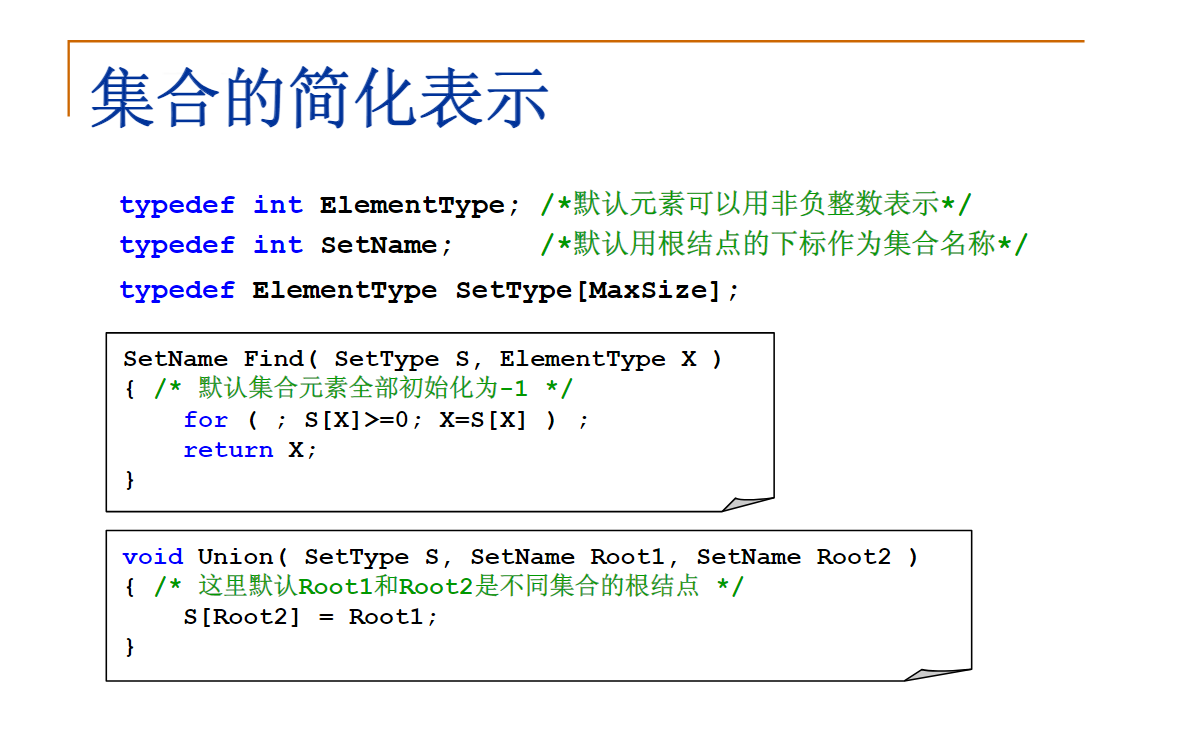
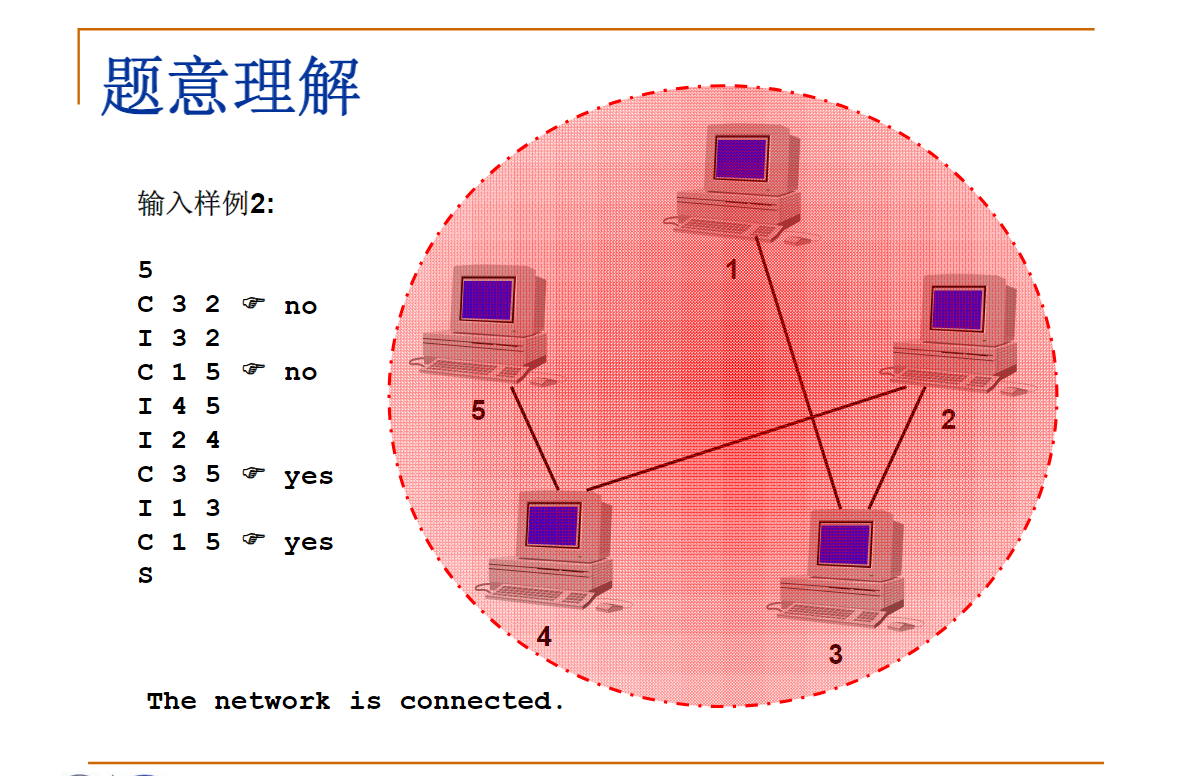


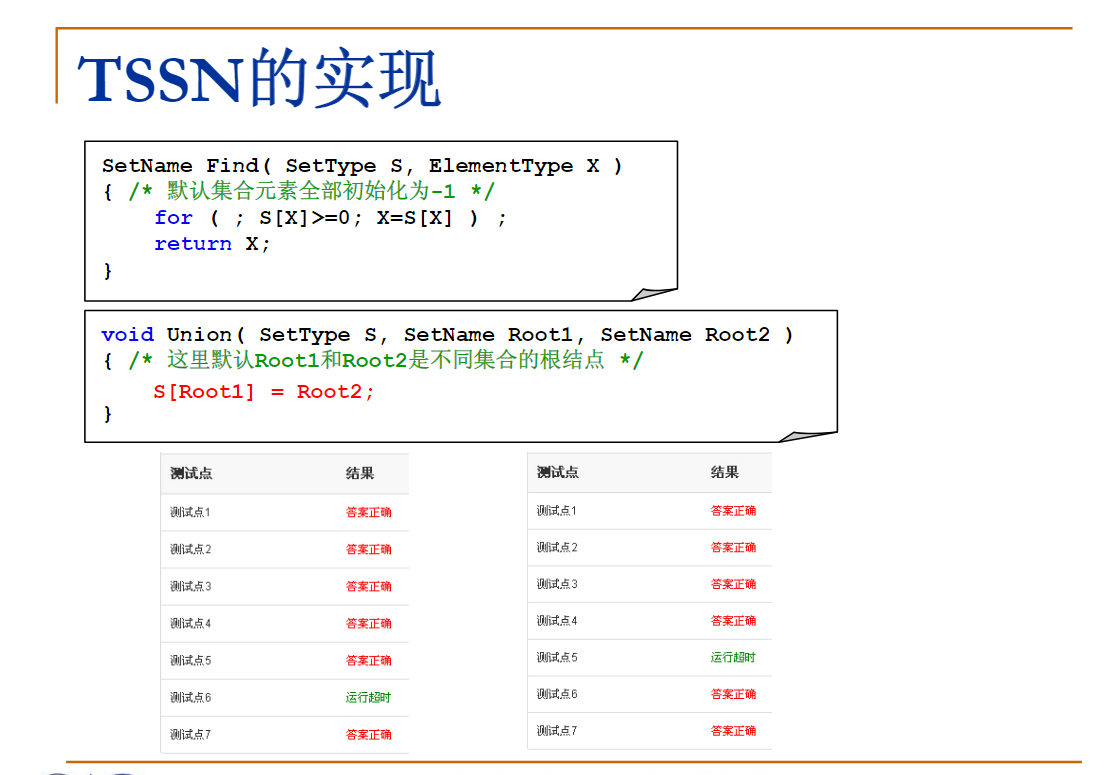
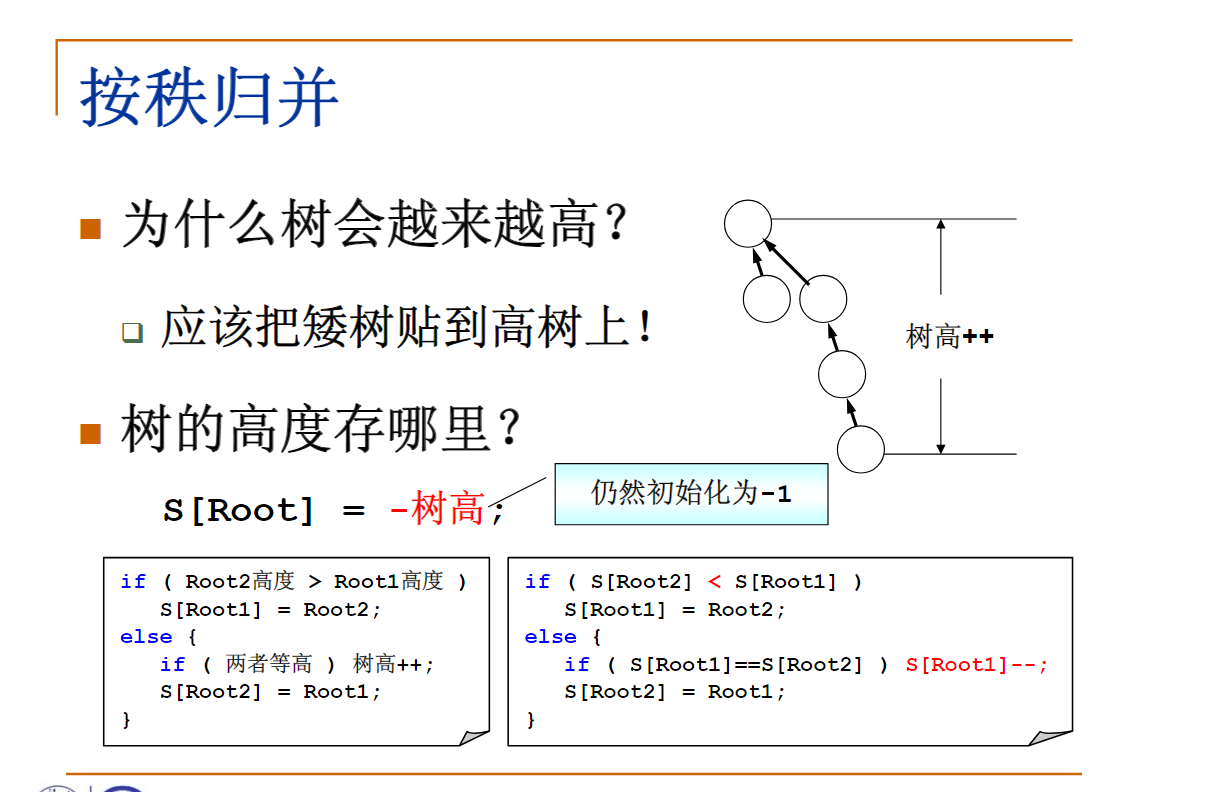

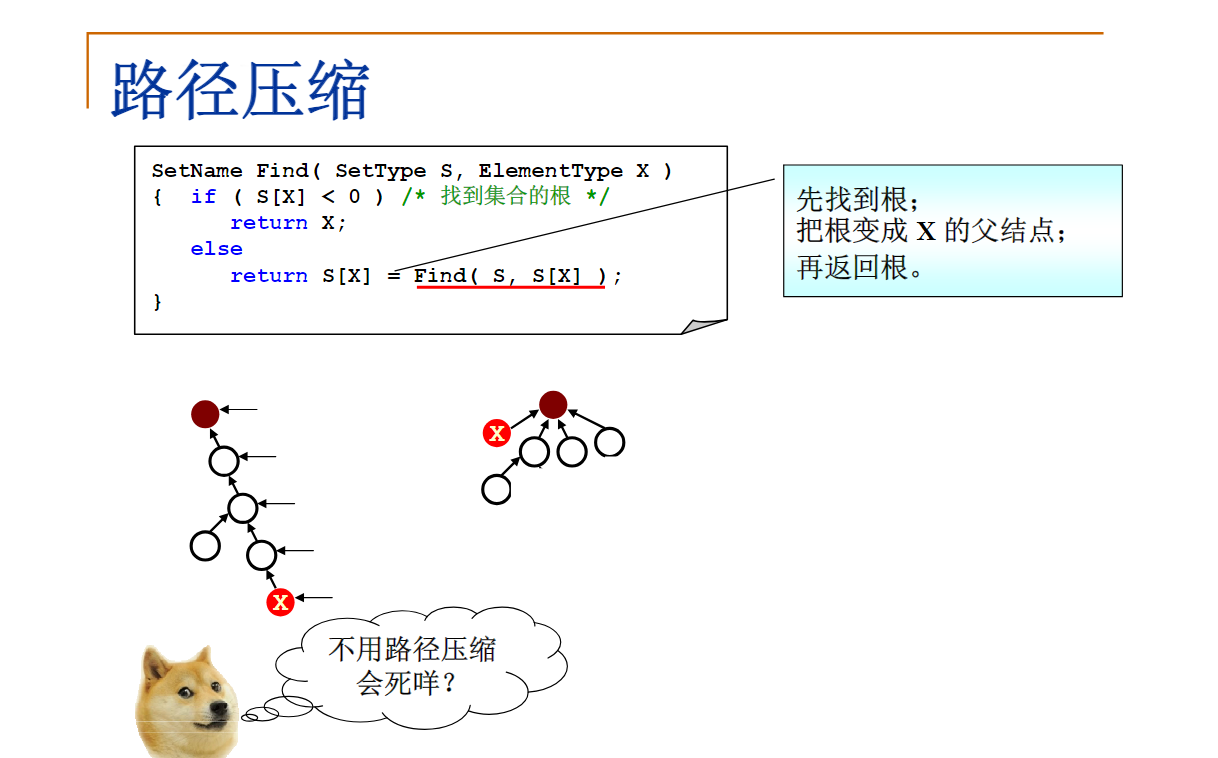
这里代码是伪递归形式的,会被编译器优化成循环形式。

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAXN 10001 /* 集合最大元素个数 */
typedef int ElementType; /* 默认元素可以用非负整数表示 */
typedef int SetName; /* 默认用根结点的下标作为集合名称 */
typedef ElementType SetType[MAXN]; /* 假设集合元素下标从0开始 */
void Union( SetType S, SetName Root1, SetName Root2 )
{ /* 这里默认Root1和Root2是不同集合的根结点 */
/* 保证小集合并入大集合 */
if ( S[Root2] < S[Root1] ) { /* 如果集合2比较大 */
S[Root2] += S[Root1]; /* 集合1并入集合2 */
S[Root1] = Root2;
}
else { /* 如果集合1比较大 */
S[Root1] += S[Root2]; /* 集合2并入集合1 */
S[Root2] = Root1;
}
}
SetName Find( SetType S, ElementType X )
{ /* 默认集合元素全部初始化为-1 */
if ( S[X] < 0 ) /* 找到集合的根 */
return X;
else
return S[X] = Find( S, S[X] ); /* 路径压缩 */
}
void Initialization(SetType S, int N)
{
for(int i=0; i<N; i++)
S[i] = -1;
}
void Input_connection(SetType S)
{
ElementType u,v;
SetName Root1, Root2;
scanf("%d %d\n",&u,&v);
Root1 = Find(S, u-1);
Root2 = Find(S, v-1);
if(Root1 != Root2)
Union(S, Root1, Root2);
}
void Check_connection(SetType S)
{
ElementType u,v;
SetName Root1,Root2;
scanf("%d %d\n",&u,&v);
Root1 = Find(S, u-1);
Root2 = Find(S, v-1);
if(Root1 == Root2)
printf("yes\n");
else
printf("no\n");
}
void Check_network(SetType S, int n)
{
int i,counter = 0;
for(i=0; i<n; i++)
{
if(S[i] < 0)
counter++;
}
if(counter == 1)
printf("The network is connected.\n");
else
printf("There are %d components.\n",counter);
}
int main()
{
int N;
scanf("%d",&N);
SetType S;
char in;
Initialization(S, N);
do
{
scanf("%c",&in);
switch(in)
{
case 'I':
Input_connection(S);
break;
case 'C':
Check_connection(S);
break;
case 'S':
Check_network(S, N);
break;
}
}while(in != 'S');
return 0;
}
MOOC-PTA树题目
- PTA 03-树1 树的同构
- PTA 03-树2 List Leaves
- PTA 03-树3 Tree Traversals Again
- PTA 04-树4 是否同一棵二叉搜索树
- PTA 04-树5 Root of AVL Tree
- PTA 04-树6 Complete Binary Search Tree
- PTA 04-树7 二叉搜索树的操作集
- PTA 05-树7 堆中的路径
- PTA 05-树8 File Transfer
- PTA 05-树9 Huffman Codes
PTA 03-树1 树的同构
给定两棵树T1和T2。如果T1可以通过若干次左右孩子互换就变成T2,则我们称两棵树是“同构”的。例如图1给出的两棵树就是同构的,因为我们把其中一棵树的结点A、B、G的左右孩子互换后,就得到另外一棵树。而图2就不是同构的。
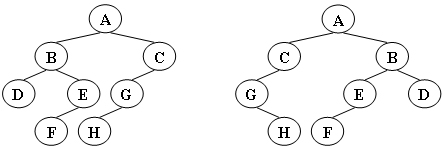 |
|---|
| 图1 |
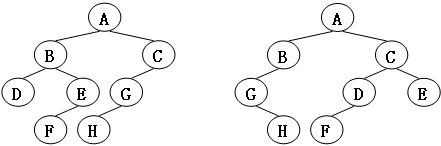 |
| 图2 |
现给定两棵树,请你判断它们是否是同构的。
输入格式:
输入给出2棵二叉树树的信息。对于每棵树,首先在一行中给出一个非负整数N (≤10),即该树的结点数(此时假设结点从0到N−1编号);随后N行,第i行对应编号第i个结点,给出该结点中存储的1个英文大写字母、其左孩子结点的编号、右孩子结点的编号。如果孩子结点为空,则在相应位置上给出“-”。给出的数据间用一个空格分隔。注意:题目保证每个结点中存储的字母是不同的。
输出格式:
如果两棵树是同构的,输出“Yes”,否则输出“No”。
输入样例1(对应图1):
8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -
输出样例1:
Yes
输入样例2(对应图2):
8
B 5 7
F - -
A 0 3
C 6 -
H - -
D - -
G 4 -
E 1 -
8
D 6 -
B 5 -
E - -
H - -
C 0 2
G - 3
F - -
A 1 4
输出样例2:
No
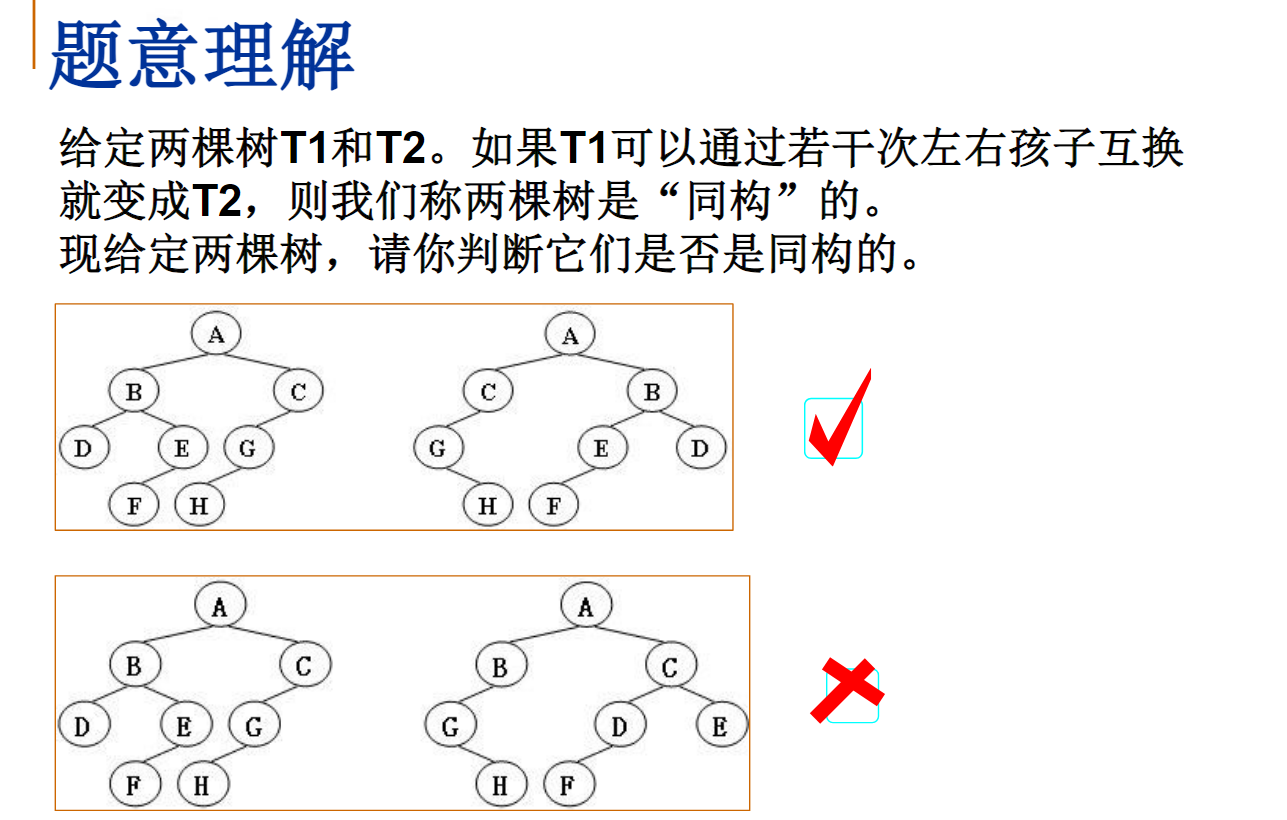
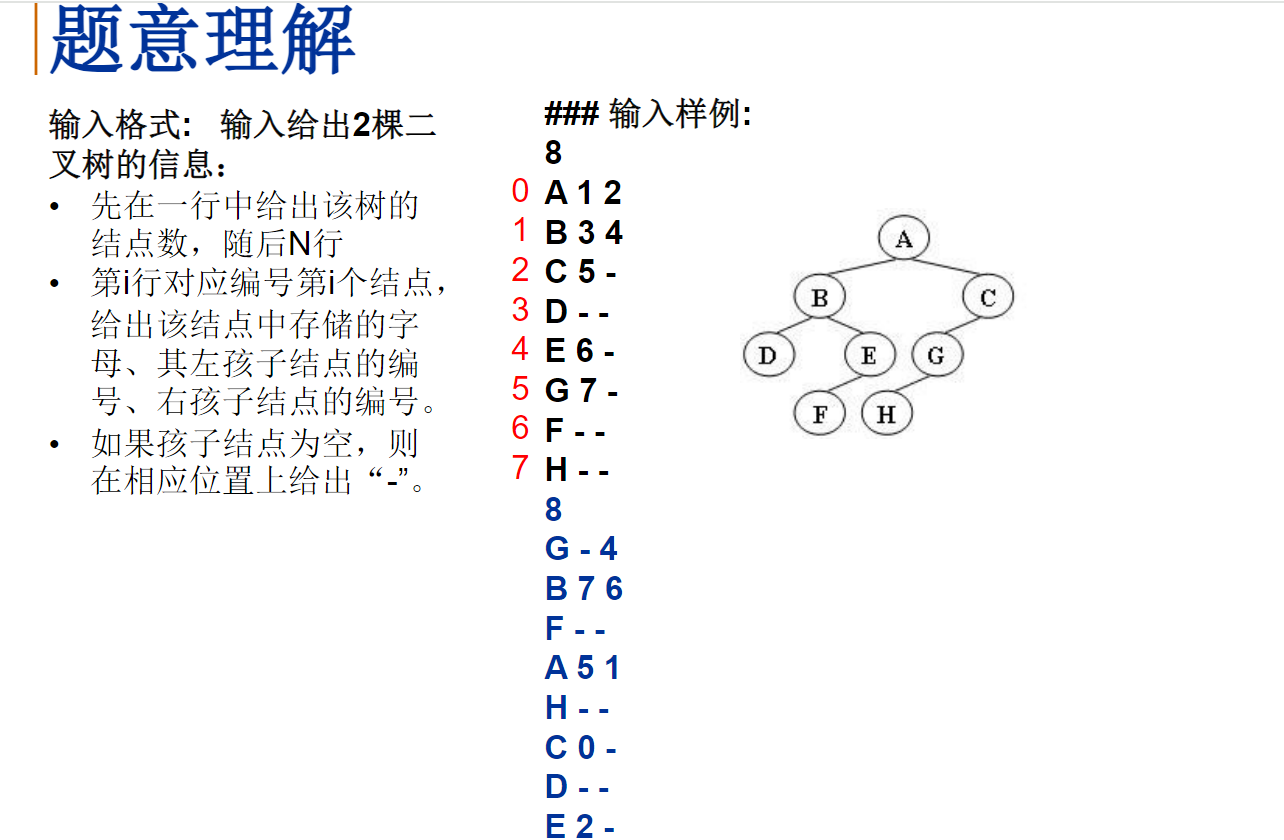
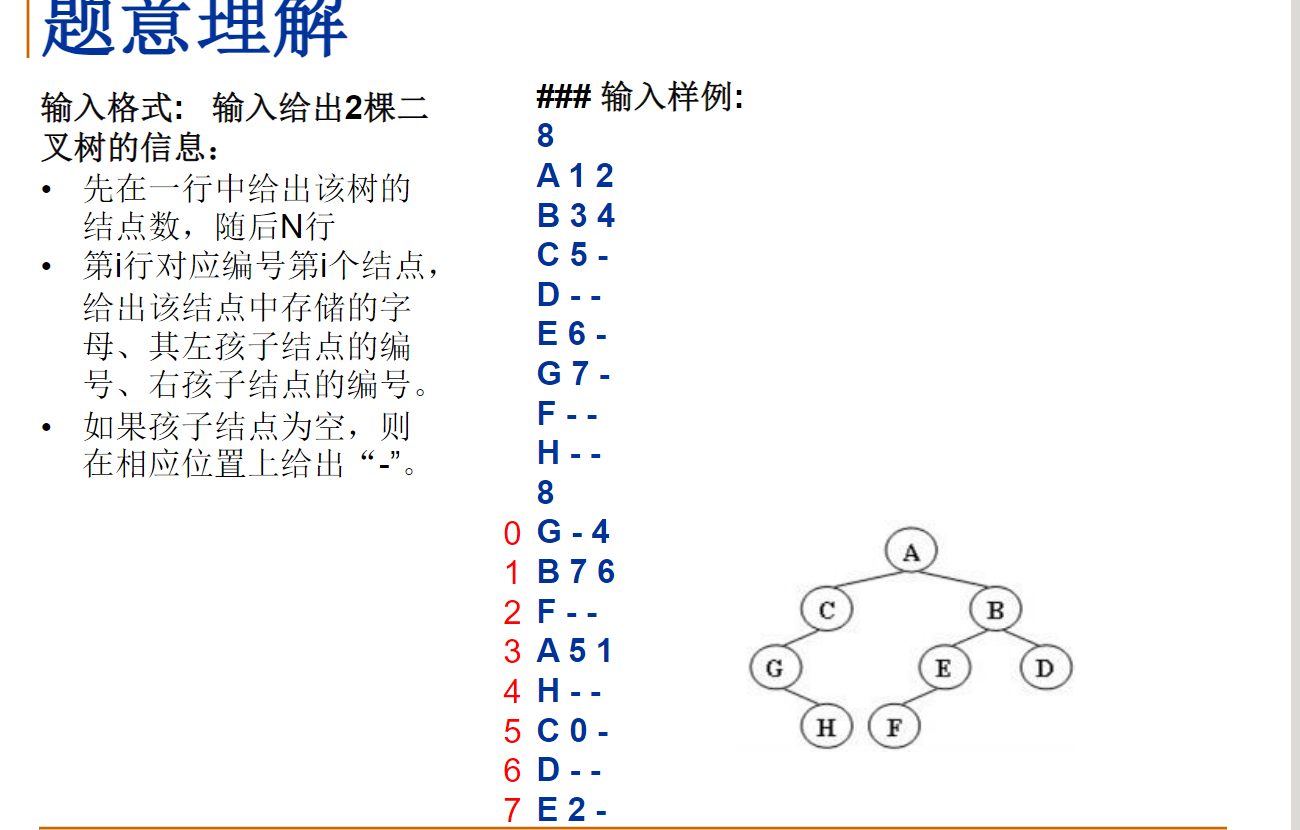
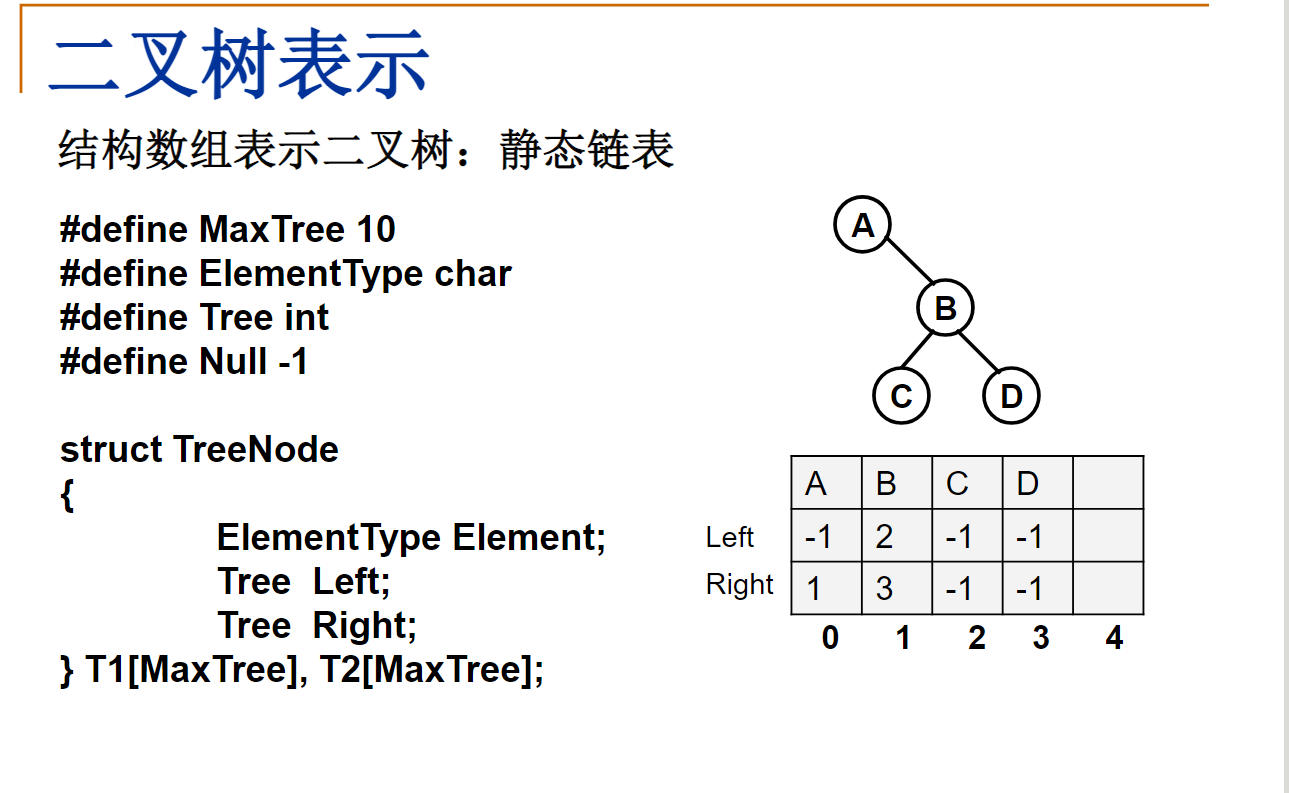






#include <stdio.h>
#include <stdlib.h>
#define MaxSize 10
#define Null -1
#define ElementType char
#define Tree int
struct TreeNode
{
ElementType Element;
Tree Left;
Tree Right;
}T1[MaxSize],T2[MaxSize];
Tree BuildTree(struct TreeNode T[])
{
int N;
int Root = 0;
scanf("%d",&N);
getchar();
if(N)
{
int check[MaxSize];
char cl,cr;
for(int i = 0;i < N;i++)
check[i] = 0;
for(int i = 0;i < N;i++)
{
scanf("%c %c %c\n",&T[i].Element,&cl,&cr);
if(cl != '-')
{
T[i].Left = cl - '0';
check[T[i].Left] = 1;
}
else
T[i].Left = Null;
if(cr != '-')
{
T[i].Right = cr - '0';
check[T[i].Right] = 1;
}
else
T[i].Right = Null;
//getchar();
}
for(int i = 0;i < N;i++)
if(!check[i])
{
Root = i;
break;
}
}
else
return Null;
return Root;
}
int Isomorphic(Tree R1,Tree R2)
{
if(R1 == Null && R2 == Null)
return 1;
if((R1 != Null && R2 == Null)||(R1 == Null && R2 != Null))
return 0;
if(T1[R1].Element != T2[R2].Element)
return 0;
if((T1[R1].Left == Null)&&T2[R2].Left == Null)
Isomorphic(T1[R1].Right,T2[R2].Right);
if((T1[R1].Left != Null)&&T2[R2].Left != Null && (T1[T1[R1].Left].Element) == (T2[T2[R2].Left].Element))
return Isomorphic(T1[R1].Right,T2[R2].Right) && Isomorphic(T1[R1].Left,T2[R2].Left);
else
Isomorphic(T1[R1].Left,T2[R2].Right) && Isomorphic(T1[R1].Right,T2[R2].Left);
}
int main()
{
Tree R1,R2;
R1 = BuildTree(T1);
R2 = BuildTree(T2);
if(Isomorphic(R1,R2))
printf("Yes\n");
else
printf("No\n");
return 0;
}
PTA 03-树2 List Leaves
Given a tree, you are supposed to list all the leaves in the order of top down, and left to right.
Input Specification:
Each input file contains one test case. For each case, the first line gives a positive integer N (≤10) which is the total number of nodes in the tree -- and hence the nodes are numbered from 0 to N−1. Then N lines follow, each corresponds to a node, and gives the indices of the left and right children of the node. If the child does not exist, a "-" will be put at the position. Any pair of children are separated by a space.
Output Specification:
For each test case, print in one line all the leaves' indices in the order of top down, and left to right. There must be exactly one space between any adjacent numbers, and no extra space at the end of the line.
Sample Input:
8
1 -
- -
0 -
2 7
- -
- -
5 -
4 6
Sample Output:
4 1 5
#include <stdio.h>
#include <stdlib.h>
#define MAXTREE 10
typedef int Tree;
#define Null -1
struct TreeNode
{
Tree id;
Tree left;
Tree right;
}T[MAXTREE];
Tree BuildTree(struct TreeNode T[])
{
for(int i=0; i<MAXTREE; i++)
T[i].left = T[i].right = 0;
int N;
scanf("%d",&N);
getchar();
int check[MAXTREE];
for(int i=0; i<N; i++)
check[i] = 0;
char cl,cr;
for(int i=0; i<N; i++)
{
T[i].id = i;
scanf("%c %c\n",&cl,&cr);
if(cl != '-')
{
T[i].left = cl - '0';
check[T[i].left] = 1;
}
else
T[i].left = Null;
if(cr != '-')
{
T[i].right = cr - '0';
check[T[i].right] = 1;
}
else
T[i].right = Null;
}
Tree root;
for(int i=0; i<N; i++)
{
if(check[i] == 0)
{
root = i;
break;
}
}
return root;
}
void Traversal(struct TreeNode T[], Tree root)
{
Tree pMove = root;
Tree queue[MAXTREE];
int front = 0;
int rear = 0;
queue[rear++] = pMove;
int IsFirst = 1;
while(front != rear)
{
pMove = queue[front++];
if(T[pMove].left == Null && T[pMove].right == Null)
{
if(IsFirst)
{
printf("%d",T[pMove].id);
IsFirst = 0;
}
else
printf(" %d",T[pMove].id);
}
if(T[pMove].left != Null)
{
queue[rear++] = T[pMove].left;
}
if(T[pMove].right != Null)
{
queue[rear++] = T[pMove].right;
}
}
}
int main()
{
struct TreeNode T[MAXTREE];
Tree root = BuildTree(T);
Traversal(T, root);
return 0;
}
核心要点:
- 静态链表存储
- 读入数据创建相应的树,并找到相应的根节点
- 改造层次遍历
PTA 03-树3 Tree Traversals Again
An inorder binary tree traversal can be implemented in a non-recursive way with a stack. For example, suppose that when a 6-node binary tree (with the keys numbered from 1 to 6) is traversed, the stack operations are: push(1); push(2); push(3); pop(); pop(); push(4); pop(); pop(); push(5); push(6); pop(); pop(). Then a unique binary tree (shown in Figure 1) can be generated from this sequence of operations. Your task is to give the postorder traversal sequence of this tree.
Input Specification:
Each input file contains one test case. For each case, the first line contains a positive integer N (≤30) which is the total number of nodes in a tree (and hence the nodes are numbered from 1 to N). Then 2N lines follow, each describes a stack operation in the format: "Push X" where X is the index of the node being pushed onto the stack; or "Pop" meaning to pop one node from the stack.
Output Specification:
For each test case, print the postorder traversal sequence of the corresponding tree in one line. A solution is guaranteed to exist. All the numbers must be separated by exactly one space, and there must be no extra space at the end of the line.
Sample Input:
6
Push 1
Push 2
Push 3
Pop
Pop
Push 4
Pop
Pop
Push 5
Push 6
Pop
Pop
Sample Output:
3 4 2 6 5 1
在这一道题里面,把树的三种遍历——前序遍历、中序遍历和后序遍历全部都包括了,而且最重要的是,你根本就不需要建一棵树。
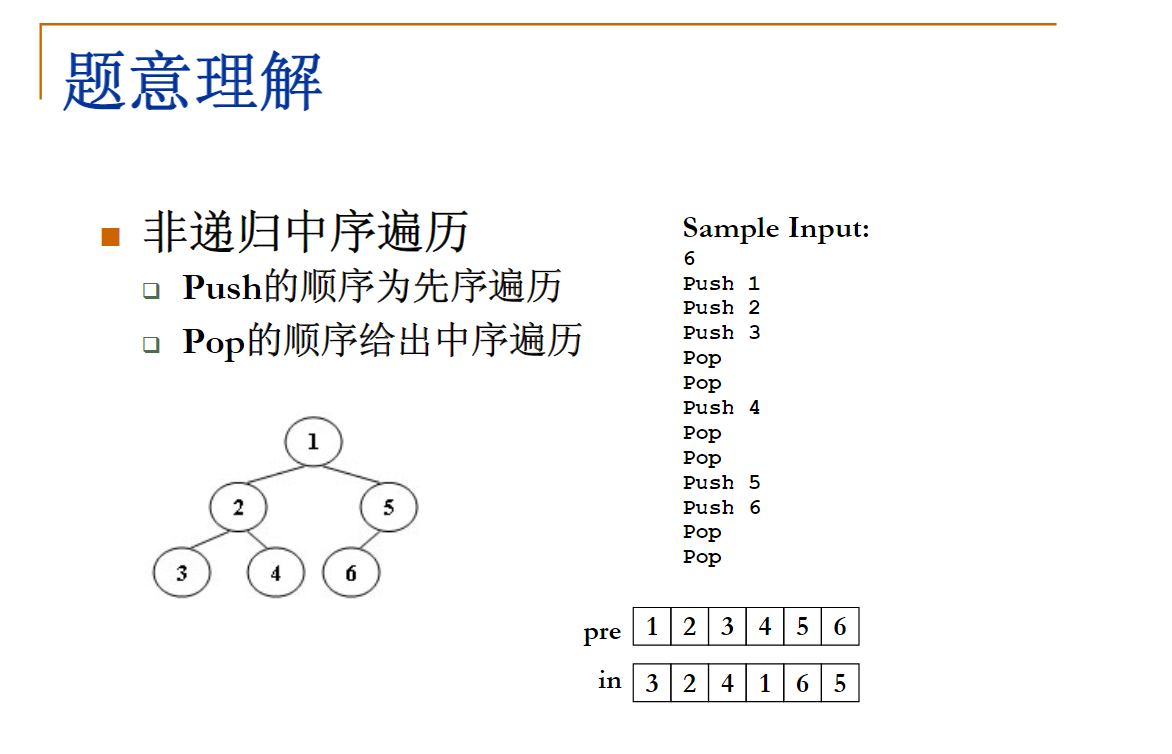
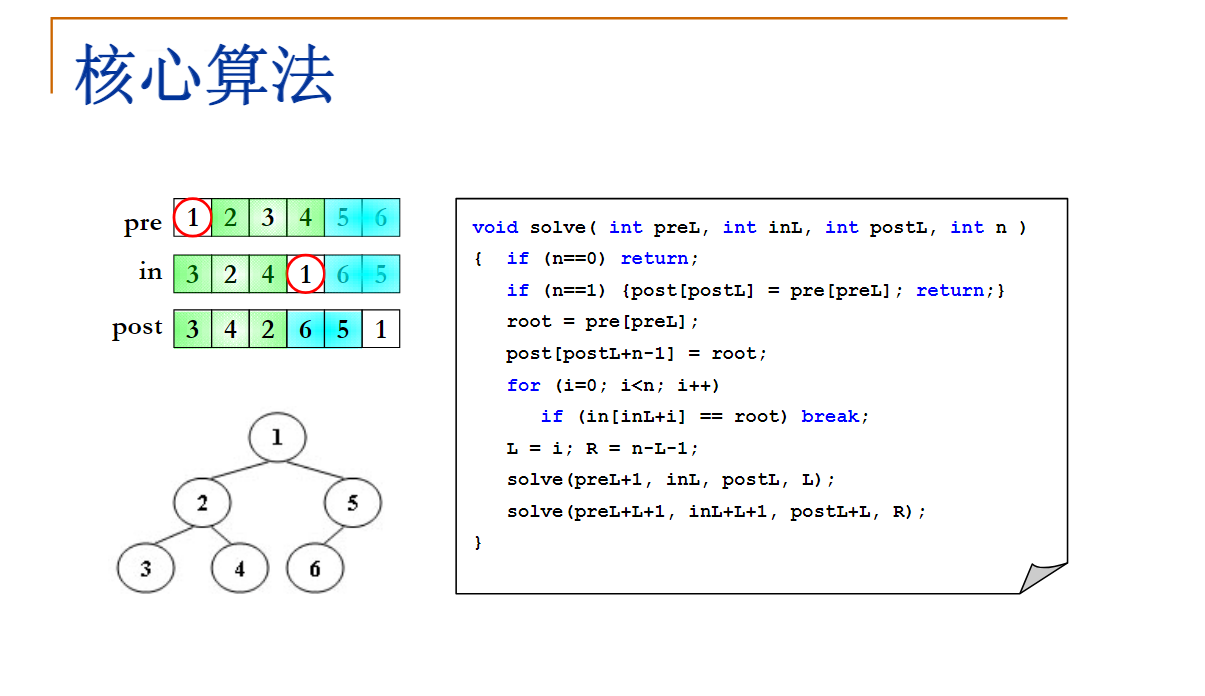
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define MAXSIZE 30
int pre[MAXSIZE];
int in[MAXSIZE];
int post[MAXSIZE];
void Solve(int preIndex, int inIndex, int postIndex, int N)
{
if(N == 0)
return;
if(N == 1)
{
post[postIndex] = pre[preIndex];
return;
}
int root = pre[preIndex];
post[postIndex+N-1] = root;
int L,R,i;
for(i=0; i<N; i++)
{
if(in[inIndex+i] == root)
break;
}
L = i;
R = N - L -1;
Solve(preIndex+1, inIndex, postIndex, L);
Solve(preIndex+1+L, inIndex+L+1, postIndex+L, R);
}
int main()
{
int N;
scanf("%d", &N);
for(int i=0; i<N; i++)
{
pre[i] = 0;
in[i] = 0;
post[i] = 0;
}
int preIndex = 0, inIndex = 0, postIndex = 0;
int stack[6];
int count = 0;
for(int i=0; i<N*2; i++)
{
char str[5];
scanf("%s",str);
if(strcmp(str,"Push") == 0)
{
int num;
scanf("%d\n",&num);
count++;
stack[count] = num;
pre[preIndex] = num;
preIndex++;
}
else if(strcmp(str,"Pop") == 0)
{
in[inIndex] = stack[count];
count--;
inIndex++;
}
}
Solve(0, 0, 0, N);
int First = 1;
for(int i=0; i<N; i++)
{
if(First)
{
printf("%d", post[i]);
First = 0;
}
else
printf(" %d", post[i]);
}
return 0;
}
核心要点:
- 读入字符串并比较
- 使用栈获得中序遍历相应数组
- 分治算法
- 递归结束条件要有n=0
PTA 04-树4 是否同一棵二叉搜索树
给定一个插入序列就可以唯一确定一棵二叉搜索树。然而,一棵给定的二叉搜索树却可以由多种不同的插入序列得到。例如分别按照序列{2, 1, 3}和{2, 3, 1}插入初始为空的二叉搜索树,都得到一样的结果。于是对于输入的各种插入序列,你需要判断它们是否能生成一样的二叉搜索树。
输入格式:
输入包含若干组测试数据。每组数据的第1行给出两个正整数N (≤10)和L,分别是每个序列插入元素的个数和需要检查的序列个数。第2行给出N个以空格分隔的正整数,作为初始插入序列。随后L行,每行给出N个插入的元素,属于L个需要检查的序列。
简单起见,我们保证每个插入序列都是1到N的一个排列。当读到N为0时,标志输入结束,这组数据不要处理。
输出格式:
对每一组需要检查的序列,如果其生成的二叉搜索树跟对应的初始序列生成的一样,输出“Yes”,否则输出“No”。
输入样例:
4 2
3 1 4 2
3 4 1 2
3 2 4 1
2 1
2 1
1 2
0
输出样例:
Yes
No
No
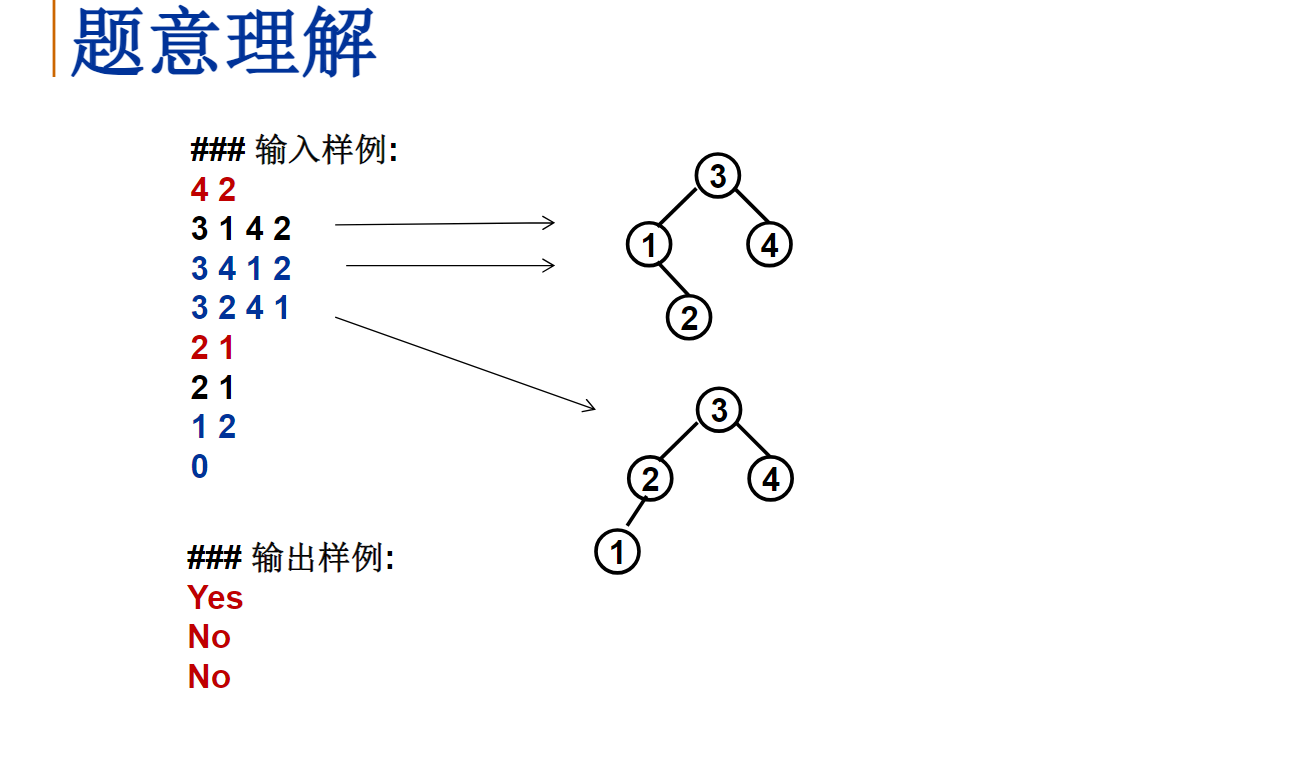
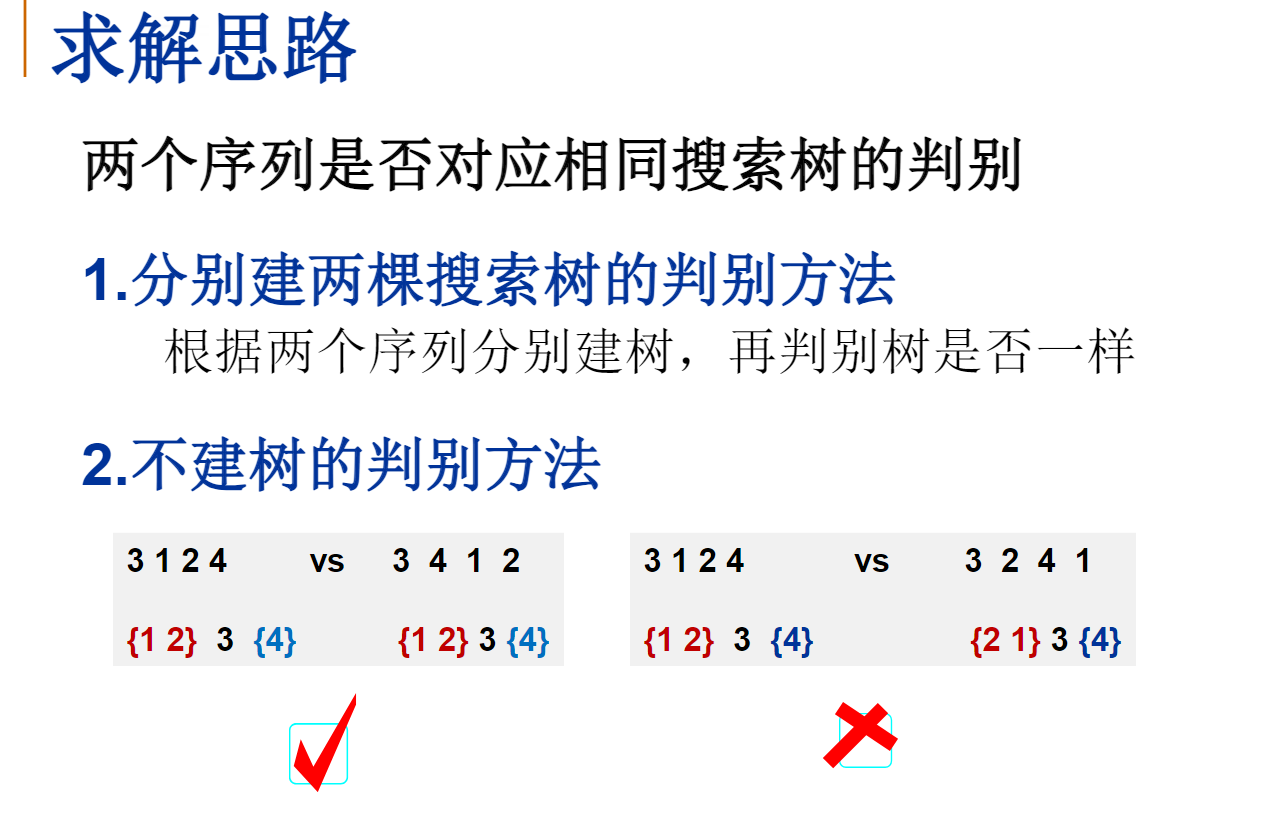


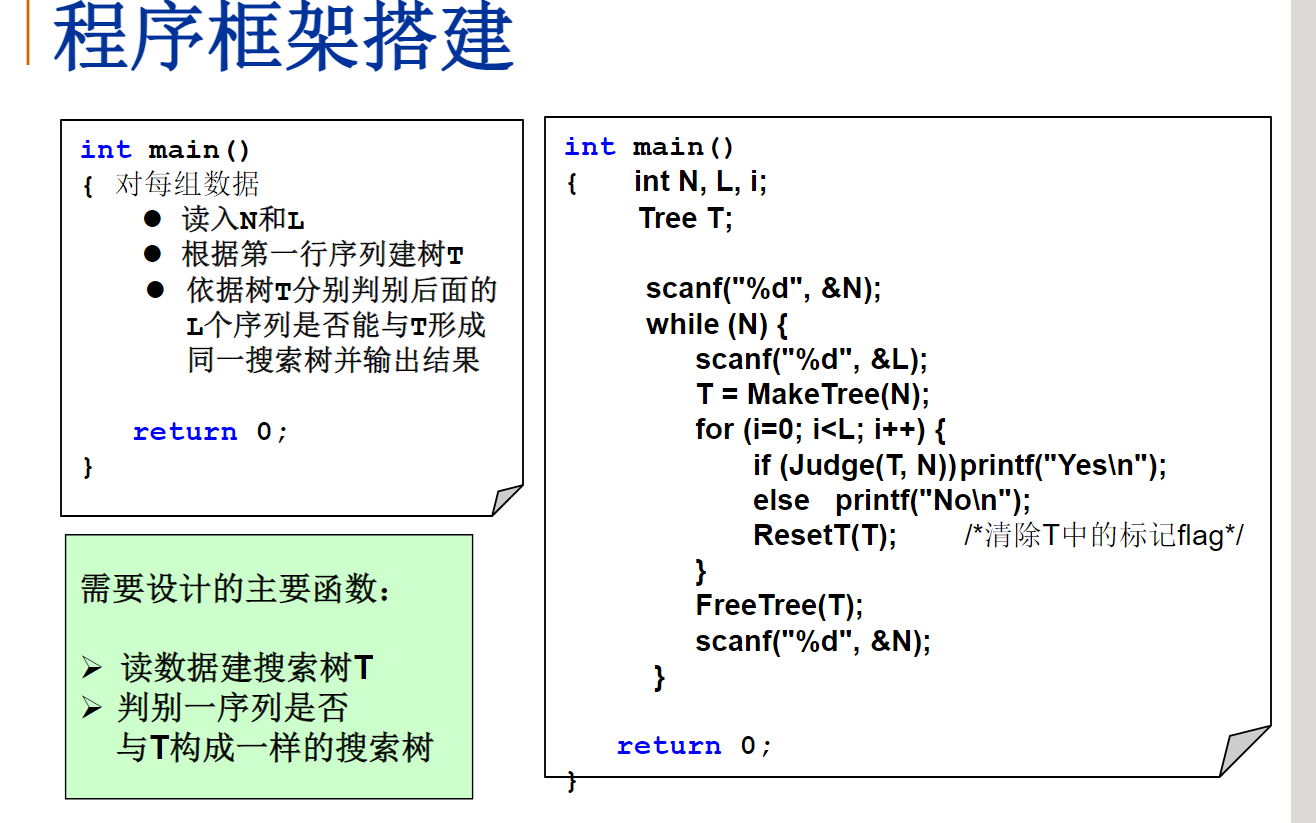

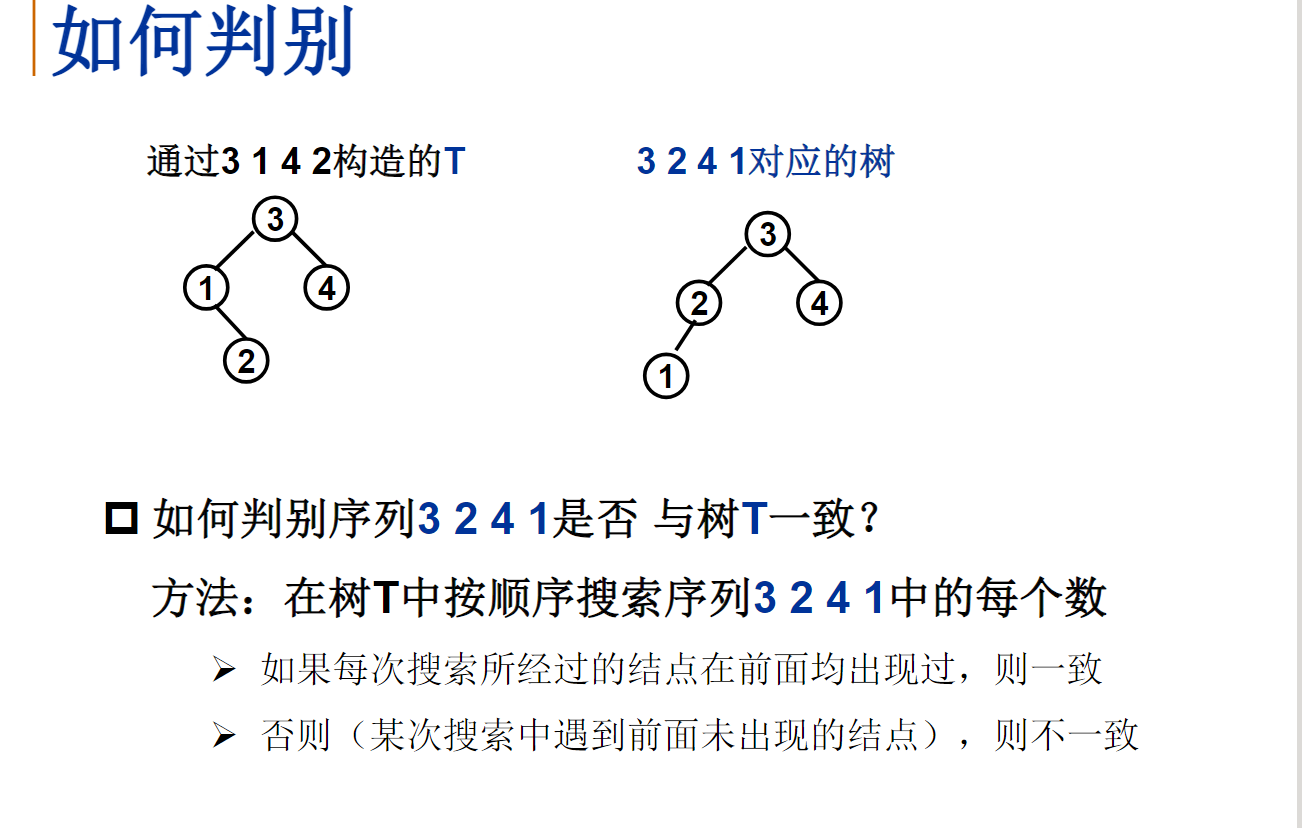




#include <stdio.h>
#include <stdlib.h>
typedef int ElementType;
typedef struct TreeNode *Tree;
struct TreeNode
{
ElementType Data;
Tree Left;
Tree Right;
int flag;
};
Tree NewNode(ElementType v)
{
Tree T = (Tree)malloc(sizeof(struct TreeNode));
T->Data = v;
T->Left = NULL;
T->Right = NULL;
T->flag = 0;
return T;
}
Tree Insert(Tree T,ElementType v)
{
if(!T)
T = NewNode(v);
else
{
if(T->Data < v)
T->Right = Insert(T->Right,v);
else
T->Left = Insert(T->Left,v);
}
return T;
}
Tree MakeTree(int N)
{
Tree T;
int i,v;
scanf("%d",&v);
T = NewNode(v);
for(i = 1;i < N;i++)
{
scanf("%d",&v);
T = Insert(T,v);
}
return T;
}
void ResetT(Tree T)
{
if(T->Left)
ResetT(T->Left);
if(T->Right)
ResetT(T->Right);
T->flag = 0;
}
void FreeTree(Tree T)
{
if(T->Left)
FreeTree(T->Left);
if(T->Right)
FreeTree(T->Right);
free(T);
}
int check(Tree T, ElementType v)
{
if(T->flag)
{
if(v > T->Data)
return check(T->Right, v);
else if(v < T->Data)
return check(T->Left,v);
else
return 0;
}
else
{
if(v == T->Data)
{
T->flag = 1;
return 1;
}
else
return 0;
}
}
int Judge(Tree T, int N)
{
int i, V, flag = 0;
scanf("%d",&V);
if(T->Data != V)
flag = 1;
else
T->flag = 1;
for(i = 1;i < N;i++)
{
scanf("%d",&V);
if((!flag)&&(!check(T,V)))
flag = 1;
}
if(flag)
return 0;
else
return 1;
}
int main()
{
int N,L,i;
Tree T;
scanf("%d",&N);
while(N != 0)
{
scanf("%d",&L);
T = MakeTree(N);
for(i = 0;i < L;i++)
{
if(Judge(T,N))
printf("Yes\n");
else
printf("No\n");
ResetT(T);
}
FreeTree(T);
scanf("%d",&N);
}
return 0;
}
PTA 04-树5 Root of AVL Tree
An AVL tree is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Figures 1-4 illustrate the rotation rules.
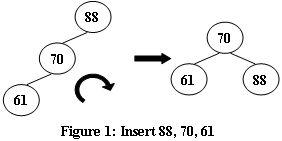
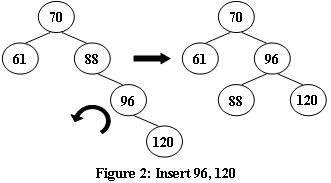
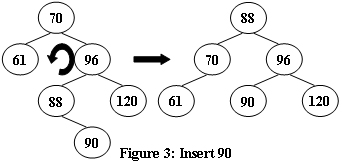
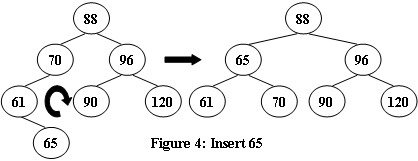
Now given a sequence of insertions, you are supposed to tell the root of the resulting AVL tree.
Input Specification:
Each input file contains one test case. For each case, the first line contains a positive integer N (≤20) which is the total number of keys to be inserted. Then N distinct integer keys are given in the next line. All the numbers in a line are separated by a space.
Output Specification:
For each test case, print the root of the resulting AVL tree in one line.
Sample Input 1:
5
88 70 61 96 120
Sample Output 1:
70
Sample Input 2:
7
88 70 61 96 120 90 65
Sample Output 2:
88
#include <stdio.h>
#include <stdlib.h>
typedef int ElementType;
typedef struct AVLNode *Position;
typedef Position AVLTree; /* AVL树类型 */
struct AVLNode{
ElementType Data; /* 结点数据 */
AVLTree Left; /* 指向左子树 */
AVLTree Right; /* 指向右子树 */
int Height; /* 树高 */
};
int Max ( int a, int b )
{
return a > b ? a : b;
}
int GetHeight(AVLTree T)
{
if (!T)
return -1;
else
return T->Height;
}
AVLTree SingleLeftRotation ( AVLTree A )
{ /* 注意:A必须有一个左子结点B */
/* 将A与B做左单旋,更新A与B的高度,返回新的根结点B */
AVLTree B = A->Left;
A->Left = B->Right;
B->Right = A;
A->Height = Max( GetHeight(A->Left), GetHeight(A->Right) ) + 1;
B->Height = Max( GetHeight(B->Left), A->Height ) + 1;
return B;
}
AVLTree SingleRightRotation(AVLTree A)//麻烦结点存在右子树的右边
{
AVLTree B=A->Right;
A->Right=B->Left;//右子树的左儿子赋给A的右子树
B->Left=A;//B变成A的父结点
A->Height=Max(GetHeight(A->Left),GetHeight(A->Right))+1;
B->Height=Max(A->Height,GetHeight(B->Right))+1;
return B;
}
AVLTree DoubleRightLeftRotation(AVLTree A)//麻烦结点存在右子树的左边
{
A->Right=SingleLeftRotation(A->Right);
return SingleRightRotation(A);
}
AVLTree DoubleLeftRightRotation ( AVLTree A )
{ /* 注意:A必须有一个左子结点B,且B必须有一个右子结点C */
/* 将A、B与C做两次单旋,返回新的根结点C */
/* 将B与C做右单旋,C被返回 */
A->Left = SingleRightRotation(A->Left);
/* 将A与C做左单旋,C被返回 */
return SingleLeftRotation(A);
}
AVLTree Insert( AVLTree T, ElementType X )
{ /* 将X插入AVL树T中,并且返回调整后的AVL树 */
if ( !T ) { /* 若插入空树,则新建包含一个结点的树 */
T = (AVLTree)malloc(sizeof(struct AVLNode));
T->Data = X;
T->Height = 0;
T->Left = T->Right = NULL;
} /* if (插入空树) 结束 */
else if ( X < T->Data ) {
/* 插入T的左子树 */
T->Left = Insert( T->Left, X);
/* 如果需要左旋 */
if ( GetHeight(T->Left)-GetHeight(T->Right) == 2 )
if ( X < T->Left->Data )
T = SingleLeftRotation(T); /* 左单旋 */
else
T = DoubleLeftRightRotation(T); /* 左-右双旋 */
} /* else if (插入左子树) 结束 */
else if ( X > T->Data ) {
/* 插入T的右子树 */
T->Right = Insert( T->Right, X );
/* 如果需要右旋 */
if ( GetHeight(T->Left)-GetHeight(T->Right) == -2 )
if ( X > T->Right->Data )
T = SingleRightRotation(T); /* 右单旋 */
else
T = DoubleRightLeftRotation(T); /* 右-左双旋 */
} /* else if (插入右子树) 结束 */
/* else X == T->Data,无须插入 */
/* 别忘了更新树高 */
T->Height = Max( GetHeight(T->Left), GetHeight(T->Right) ) + 1;
return T;
}
int main()
{
int n;
scanf("%d",&n);
ElementType X;
AVLTree T = NULL;
for(int i=0; i<n; i++)
{
scanf("%d", &X);
T = Insert(T,X);
}
if(T)
printf("%d",T->Data);
return 0;
}
PTA 04-树6 Complete Binary Search Tree
A Binary Search Tree (BST) is recursively defined as a binary tree which has the following properties:
- The left subtree of a node contains only nodes with keys less than the node's key.
- The right subtree of a node contains only nodes with keys greater than or equal to the node's key.
- Both the left and right subtrees must also be binary search trees.
A Complete Binary Tree (CBT) is a tree that is completely filled, with the possible exception of the bottom level, which is filled from left to right.
Now given a sequence of distinct non-negative integer keys, a unique BST can be constructed if it is required that the tree must also be a CBT. You are supposed to output the level order traversal sequence of this BST.
Input Specification:
Each input file contains one test case. For each case, the first line contains a positive integer N (≤1000). Then N distinct non-negative integer keys are given in the next line. All the numbers in a line are separated by a space and are no greater than 2000.
Output Specification:
For each test case, print in one line the level order traversal sequence of the corresponding complete binary search tree. All the numbers in a line must be separated by a space, and there must be no extra space at the end of the line.
Sample Input:
10
1 2 3 4 5 6 7 8 9 0
Sample Output:
6 3 8 1 5 7 9 0 2 4
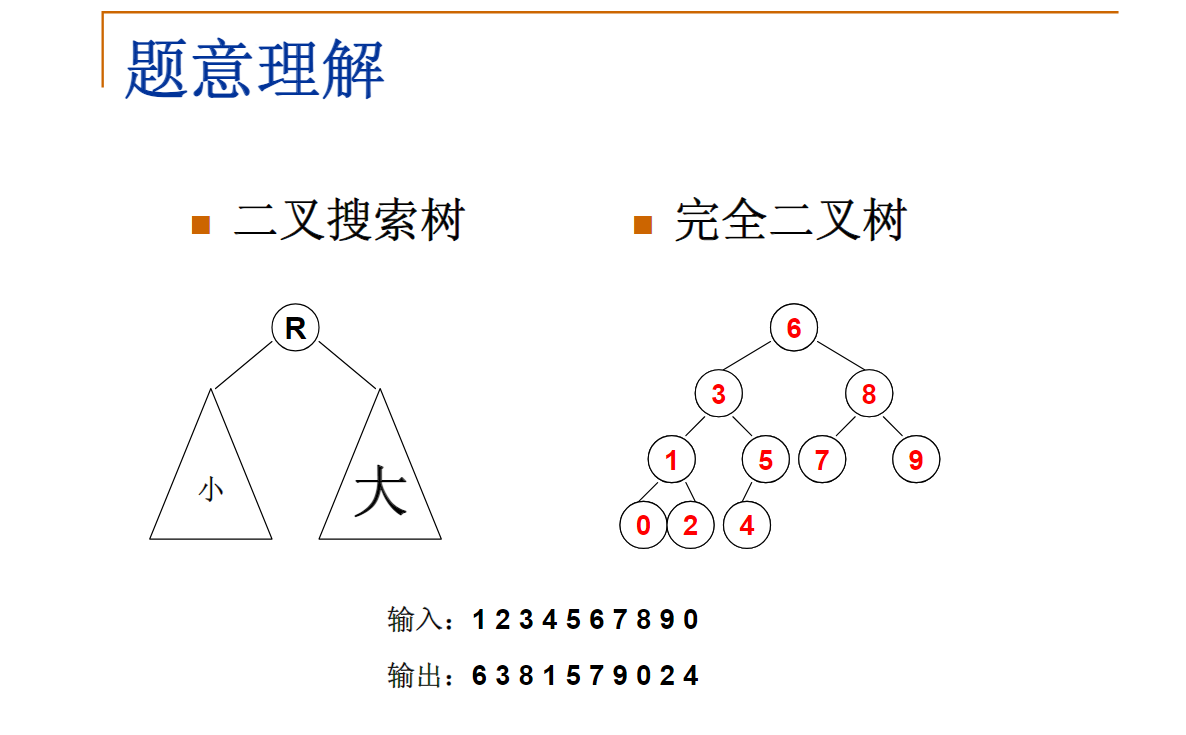

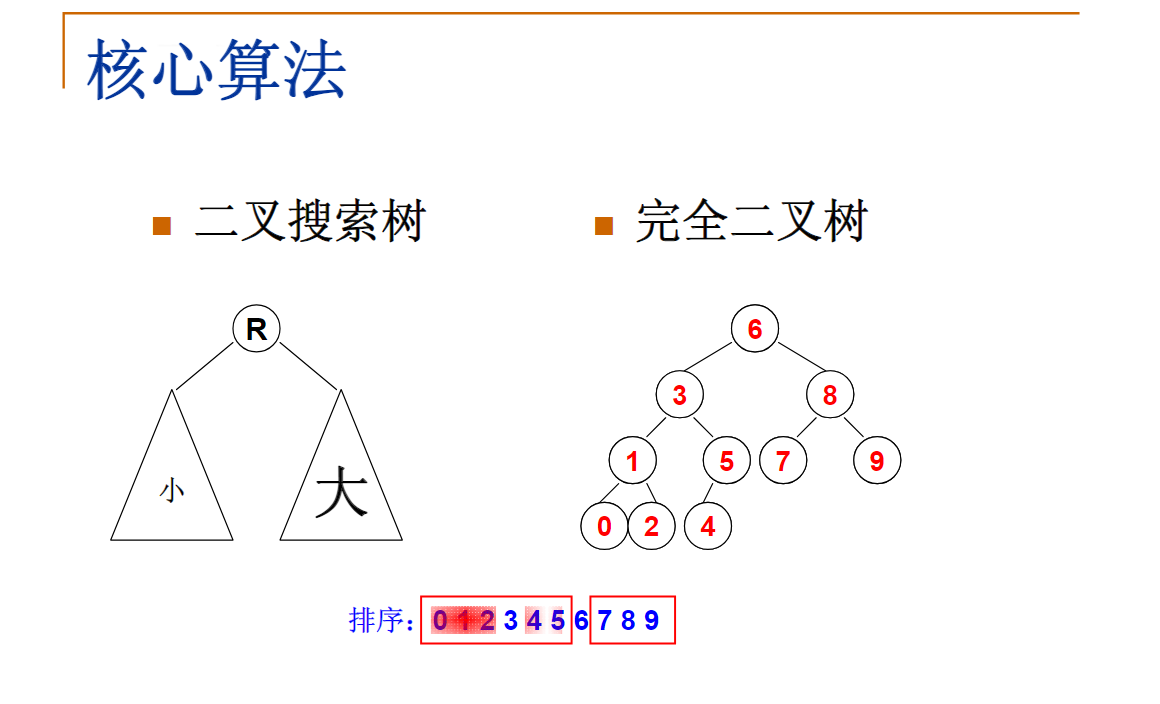

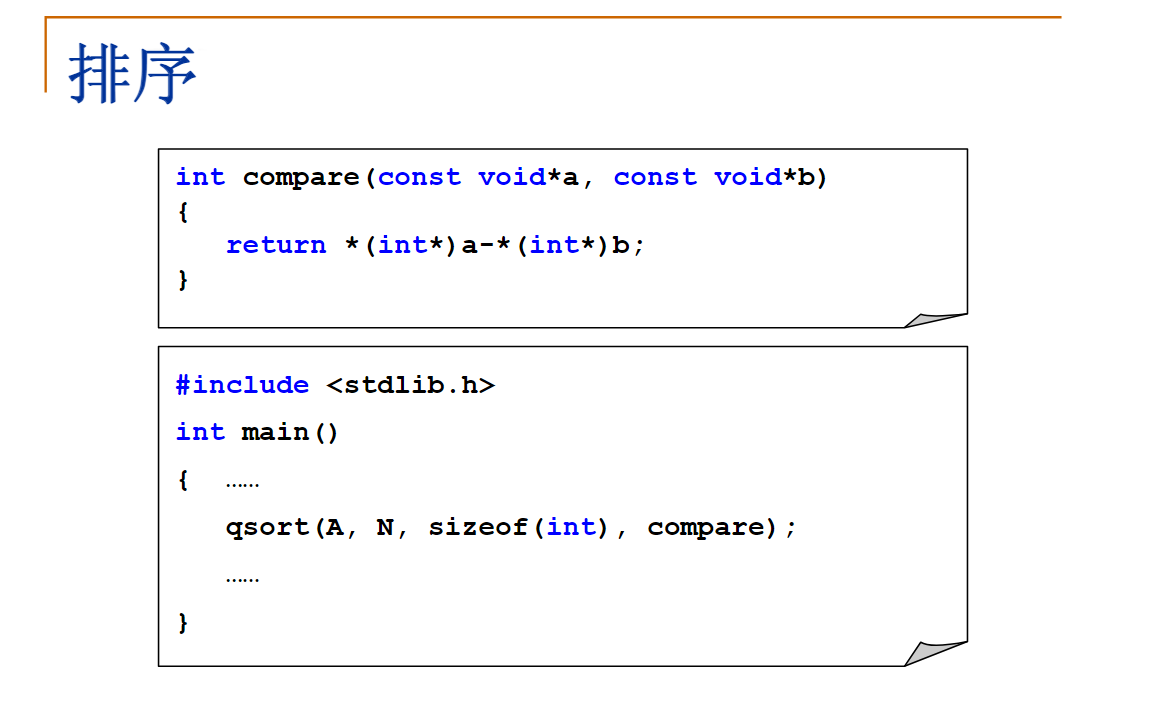
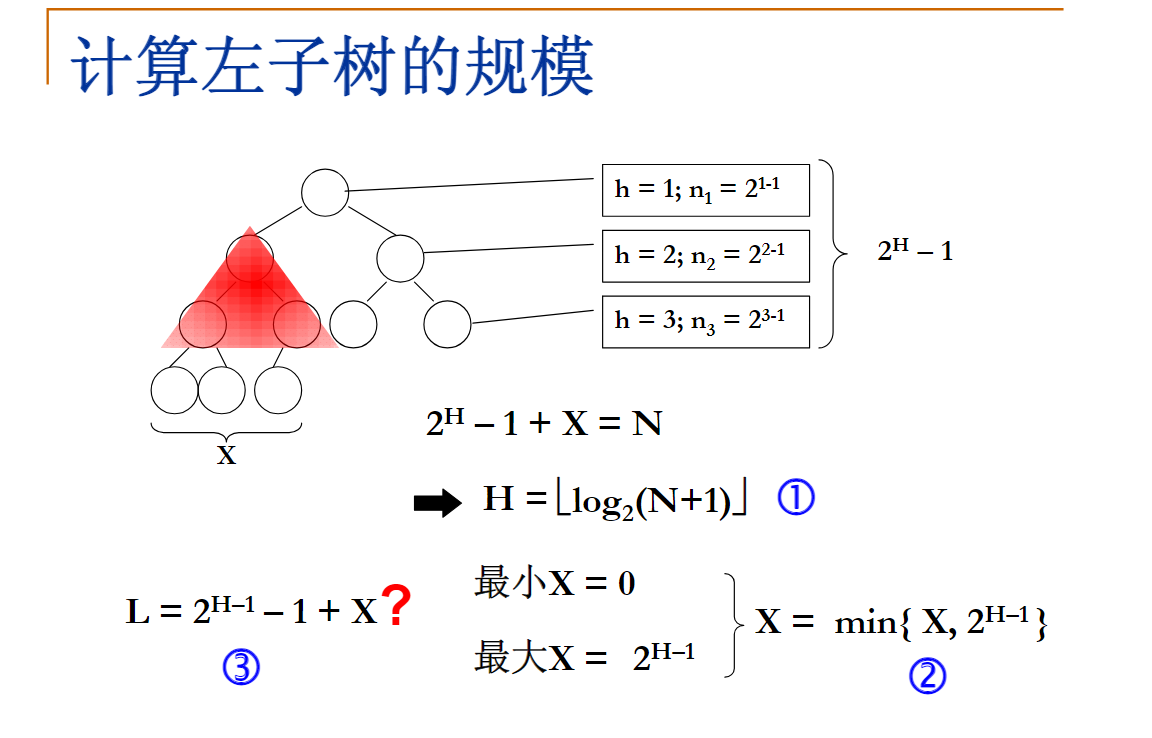
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
int Nodes[1005] = {0};
int T[1005] = {0};
int compare(const void * a, const void * b)
{
return *(int *)a - *(int *)b;
}
int GetLeftLength(int N)
{
int L;
int H = (int)(log(N+1)/log(2));
int X = (N+1-pow(2,H));
X = X<pow(2,H-1)?X:pow(2,H-1);
L = pow(2,H-1) - 1 + X;
return L;
}
void solve(int ALeft, int ARight, int TRoot)
{
int n = ARight - ALeft + 1;
if(n==0)
return;
int L = GetLeftLength(n);
T[TRoot] = Nodes[ALeft+L];
int LeftRoot = TRoot * 2 + 1;
int RightRoot = TRoot * 2 + 2;
solve(ALeft, ALeft+L-1, LeftRoot);
solve(ALeft+L+1, ARight,RightRoot);
}
int main()
{
int n;
scanf("%d",&n);
for(int i=0; i<n; i++)
{
scanf("%d", &Nodes[i]);
}
qsort(Nodes,n,sizeof(int),compare);
solve(0, n-1, 0);
int First = 1;
for(int i=0; i<n; i++)
{
if(First)
{
printf("%d", T[i]);
First = 0;
}
else
{
printf(" %d",T[i]);
}
}
return 0;
}
柳婼cpp题解:
题目大意:给一串构成树的序列,已知该树是完全二叉搜索树,求它的层序遍历的序列 分析:总得概括来说,已知中序,从根节点开始中序遍历,按中序数组给出的顺序依次将值填入level数组对应的下标中,输出level数组可得层序遍历。 1. 因为二叉搜索树的中序满足:是一组序列的从小到大排列,所以只需将所给序列排序即可得到中序数组in 2. 假设把树按从左到右、从上到下的顺序依次编号,根节点为0,则从根结点root = 0开始中序遍历,root结点的左孩子下标是root_2+1,右孩子下标是root_2+2 3. 因为是中序遍历,所以遍历结果与中序数组in中的值从0开始依次递增的结果相同,即in[t++](t从0开始),将in[t++]赋值给level[root]数组 4. 因为树是按从左到右、从上到下的顺序依次编号的,所以level数组从0到n-1的值即所求的层序遍历的值,输出level数组即可~
#include <iostream>
#include <algorithm>
using namespace std;
int in[1010], level[1010], n, t = 0;
void inOrder(int root) {
if (root >= n) return ;
inOrder(root * 2 + 1);
level[root] = in[t++];
inOrder(root * 2 + 2);
}
int main() {
scanf("%d", &n);
for (int i = 0; i < n; i++)
scanf("%d", &in[i]);
sort(in, in + n);
inOrder(0);
printf("%d", level[0]);
for (int i = 1; i < n; i++)
printf(" %d", level[i]);
return 0;
}
PTA 04-树7 二叉搜索树的操作集
本题要求实现给定二叉搜索树的5种常用操作。
函数接口定义:
BinTree Insert( BinTree BST, ElementType X );
BinTree Delete( BinTree BST, ElementType X );
Position Find( BinTree BST, ElementType X );
Position FindMin( BinTree BST );
Position FindMax( BinTree BST );
其中BinTree结构定义如下:
typedef struct TNode *Position;
typedef Position BinTree;
struct TNode{
ElementType Data;
BinTree Left;
BinTree Right;
};
- 函数
Insert将X插入二叉搜索树BST并返回结果树的根结点指针; - 函数
Delete将X从二叉搜索树BST中删除,并返回结果树的根结点指针;如果X不在树中,则打印一行Not Found并返回原树的根结点指针; - 函数
Find在二叉搜索树BST中找到X,返回该结点的指针;如果找不到则返回空指针; - 函数
FindMin返回二叉搜索树BST中最小元结点的指针; - 函数
FindMax返回二叉搜索树BST中最大元结点的指针。
裁判测试程序样例:
#include <stdio.h>
#include <stdlib.h>
typedef int ElementType;
typedef struct TNode *Position;
typedef Position BinTree;
struct TNode{
ElementType Data;
BinTree Left;
BinTree Right;
};
void PreorderTraversal( BinTree BT ); /* 先序遍历,由裁判实现,细节不表 */
void InorderTraversal( BinTree BT ); /* 中序遍历,由裁判实现,细节不表 */
BinTree Insert( BinTree BST, ElementType X );
BinTree Delete( BinTree BST, ElementType X );
Position Find( BinTree BST, ElementType X );
Position FindMin( BinTree BST );
Position FindMax( BinTree BST );
int main()
{
BinTree BST, MinP, MaxP, Tmp;
ElementType X;
int N, i;
BST = NULL;
scanf("%d", &N);
for ( i=0; i<N; i++ ) {
scanf("%d", &X);
BST = Insert(BST, X);
}
printf("Preorder:"); PreorderTraversal(BST); printf("\n");
MinP = FindMin(BST);
MaxP = FindMax(BST);
scanf("%d", &N);
for( i=0; i<N; i++ ) {
scanf("%d", &X);
Tmp = Find(BST, X);
if (Tmp == NULL) printf("%d is not found\n", X);
else {
printf("%d is found\n", Tmp->Data);
if (Tmp==MinP) printf("%d is the smallest key\n", Tmp->Data);
if (Tmp==MaxP) printf("%d is the largest key\n", Tmp->Data);
}
}
scanf("%d", &N);
for( i=0; i<N; i++ ) {
scanf("%d", &X);
BST = Delete(BST, X);
}
printf("Inorder:"); InorderTraversal(BST); printf("\n");
return 0;
}
/* 你的代码将被嵌在这里 */
输入样例:
10
5 8 6 2 4 1 0 10 9 7
5
6 3 10 0 5
5
5 7 0 10 3
输出样例:
Preorder: 5 2 1 0 4 8 6 7 10 9
6 is found
3 is not found
10 is found
10 is the largest key
0 is found
0 is the smallest key
5 is found
Not Found
Inorder: 1 2 4 6 8 9
BinTree Insert(BinTree BST, ElementType X)
{
if(!BST)
{
/*若原树为空,生成并返回一个结点的二叉搜索树*/
BST = (BinTree)malloc(sizeof(struct TNode));
BST->Data = X;
BST->Left = NULL;
BST->Right = NULL;
}
else /*开始找要插入元素的位置*/
{
if(BST->Data < X)
BST->Right = Insert(BST->Right, X);
else if(BST->Data > X)
BST->Left = Insert(BST->Left, X);
/*else X已经存在,什么都不做 */
}
return BST;
}
BinTree Delete(BinTree BST, ElementType X)
{
Position Tmp;
if(!BST)
printf("Not Found\n");
else if(X < BST->Data)
BST->Left = Delete(BST->Left,X);
else if(X > BST->Data)
BST->Right = Delete(BST->Right,X);
else
{
if(BST->Left && BST->Right)
{
Tmp = FindMin(BST->Right);
BST->Data = Tmp->Data;
BST->Right = Delete(BST->Right,BST->Data);
}
else
{
Tmp = BST;
if(!BST->Left)
BST = BST->Right;
else if(!BST->Right)
BST = BST->Left;
free(Tmp);
}
}
return BST;
}
Position Find(BinTree BST,ElementType X)
{
if(!BST)
return NULL;
else
{
if(BST->Data == X)
return BST; /*查找成功,返回找到结点的地址*/
else if(BST->Data > X)
return Find(BST->Left, X);
else
return Find(BST->Right, X);
}
return NULL;
}
/*迭代、非递归方式*/
Position FindMax(BinTree BST)
{
if(BST)
while(BST->Right)
BST = BST->Right;
return BST;
}
Position FindMin(BinTree BST)
{
if(!BST)
return NULL;
else if(!BST->Left) /*有根结点,但没有左子树,直接返回根*/
return BST;
else
return FindMin(BST->Left);
}
PTA 05-树7 堆中的路径
将一系列给定数字依次插入一个初始为空的小顶堆H[]。随后对任意给定的下标i,打印从H[i]到根结点的路径。
输入格式:
每组测试第1行包含2个正整数N和M(≤1000),分别是插入元素的个数、以及需要打印的路径条数。下一行给出区间[-10000, 10000]内的N个要被插入一个初始为空的小顶堆的整数。最后一行给出M个下标。
输出格式:
对输入中给出的每个下标i,在一行中输出从H[i]到根结点的路径上的数据。数字间以1个空格分隔,行末不得有多余空格。
输入样例:
5 3
46 23 26 24 10
5 4 3
输出样例:
24 23 10
46 23 10
26 10
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#define ERROR -1
typedef int ElementType;
typedef struct HNode *Heap;
typedef Heap MaxHeap;
typedef Heap MinHeap;
struct HNode
{
ElementType *Data;
int Size;
int Capacity;
};
MinHeap CreateHeap(int MaxSize)
{
MinHeap H = (MinHeap)malloc(sizeof(struct HNode));
H->Data = (ElementType*)malloc(sizeof(ElementType)*MaxSize);
H->Size = 0;
H->Capacity = MaxSize;
H->Data[0] = -10001;
return H;
}
bool IsFull(MinHeap H)
{
return (H->Size == H->Capacity);
}
bool Insert(MinHeap H, ElementType X)
{
if(IsFull(H))
{
printf("The heap is full!\n");
return false;
}
int i = ++H->Size;
for(; H->Data[i/2] >= X; i /= 2)
{
H->Data[i] = H->Data[i/2];
}
H->Data[i] = X;
return true;
}
bool IsEmpty(MinHeap H)
{
return (H->Size == 0);
}
ElementType Delete(MinHeap H)
{
if(IsEmpty(H))
{
printf("The heap is empty!\n");
return ERROR;
}
int Parent, Child;
ElementType MinItem,X;
MinItem = H->Data[1];
X = H->Data[H->Size--];
for(Parent = 1; Parent * 2 <= H->Size; Parent = Child)
{
Child = Parent * 2;
if((Child!=H->Size)&&(H->Data[Child] > H->Data[Child + 1]))
Child++;
if(X < H->Data[Child])
break;
else
H->Data[Parent] = H->Data[Child];
}
H->Data[Parent] = X;
return MinItem;
}
int main()
{
int MaxSize = 1001;
MinHeap H = CreateHeap(MaxSize);
int N,M;
scanf("%d %d",&N,&M);
for(int i=0; i<N; i++)
{
int num;
scanf("%d",&num);
Insert(H,num);
}
for(int i=0; i<M; i++)
{
int idx;
scanf("%d",&idx);
int Fisrt = 1;
for(int j=idx; j>=1; j/=2)
{
if(Fisrt)
{
printf("%d",H->Data[j]);
Fisrt = 0;
}
else
{
printf(" %d",H->Data[j]);
}
}
printf("\n");
}
return 0;
}
PTA 05-树8 File Transfer
We have a network of computers and a list of bi-directional connections. Each of these connections allows a file transfer from one computer to another. Is it possible to send a file from any computer on the network to any other?
Input Specification:
Each input file contains one test case. For each test case, the first line contains N (2≤N≤104), the total number of computers in a network. Each computer in the network is then represented by a positive integer between 1 and N. Then in the following lines, the input is given in the format:
I c1 c2
where I stands for inputting a connection between c1 and c2; or
C c1 c2
where C stands for checking if it is possible to transfer files between c1 and c2; or
S
where S stands for stopping this case.
Output Specification:
For each C case, print in one line the word "yes" or "no" if it is possible or impossible to transfer files between c1 and c2, respectively. At the end of each case, print in one line "The network is connected." if there is a path between any pair of computers; or "There are k components." where k is the number of connected components in this network.
Sample Input 1:
5
C 3 2
I 3 2
C 1 5
I 4 5
I 2 4
C 3 5
S
Sample Output 1:
no
no
yes
There are 2 components.
Sample Input 2:
5
C 3 2
I 3 2
C 1 5
I 4 5
I 2 4
C 3 5
I 1 3
C 1 5
S
Sample Output 2:
no
no
yes
yes
The network is connected.









这里代码是伪递归形式的,会被编译器优化成循环形式。

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAXN 10001 /* 集合最大元素个数 */
typedef int ElementType; /* 默认元素可以用非负整数表示 */
typedef int SetName; /* 默认用根结点的下标作为集合名称 */
typedef ElementType SetType[MAXN]; /* 假设集合元素下标从0开始 */
void Union( SetType S, SetName Root1, SetName Root2 )
{ /* 这里默认Root1和Root2是不同集合的根结点 */
/* 保证小集合并入大集合 */
if ( S[Root2] < S[Root1] ) { /* 如果集合2比较大 */
S[Root2] += S[Root1]; /* 集合1并入集合2 */
S[Root1] = Root2;
}
else { /* 如果集合1比较大 */
S[Root1] += S[Root2]; /* 集合2并入集合1 */
S[Root2] = Root1;
}
}
SetName Find( SetType S, ElementType X )
{ /* 默认集合元素全部初始化为-1 */
if ( S[X] < 0 ) /* 找到集合的根 */
return X;
else
return S[X] = Find( S, S[X] ); /* 路径压缩 */
}
void Initialization(SetType S, int N)
{
for(int i=0; i<N; i++)
S[i] = -1;
}
void Input_connection(SetType S)
{
ElementType u,v;
SetName Root1, Root2;
scanf("%d %d\n",&u,&v);
Root1 = Find(S, u-1);
Root2 = Find(S, v-1);
if(Root1 != Root2)
Union(S, Root1, Root2);
}
void Check_connection(SetType S)
{
ElementType u,v;
SetName Root1,Root2;
scanf("%d %d\n",&u,&v);
Root1 = Find(S, u-1);
Root2 = Find(S, v-1);
if(Root1 == Root2)
printf("yes\n");
else
printf("no\n");
}
void Check_network(SetType S, int n)
{
int i,counter = 0;
for(i=0; i<n; i++)
{
if(S[i] < 0)
counter++;
}
if(counter == 1)
printf("The network is connected.\n");
else
printf("There are %d components.\n",counter);
}
int main()
{
int N;
scanf("%d",&N);
SetType S;
char in;
Initialization(S, N);
do
{
scanf("%c",&in);
switch(in)
{
case 'I':
Input_connection(S);
break;
case 'C':
Check_connection(S);
break;
case 'S':
Check_network(S, N);
break;
}
}while(in != 'S');
return 0;
}
PTA 05-树9 Huffman Codes
In 1953, David A. Huffman published his paper "A Method for the Construction of Minimum-Redundancy Codes", and hence printed his name in the history of computer science. As a professor who gives the final exam problem on Huffman codes, I am encountering a big problem: the Huffman codes are NOT unique. For example, given a string "aaaxuaxz", we can observe that the frequencies of the characters 'a', 'x', 'u' and 'z' are 4, 2, 1 and 1, respectively. We may either encode the symbols as {'a'=0, 'x'=10, 'u'=110, 'z'=111}, or in another way as {'a'=1, 'x'=01, 'u'=001, 'z'=000}, both compress the string into 14 bits. Another set of code can be given as {'a'=0, 'x'=11, 'u'=100, 'z'=101}, but {'a'=0, 'x'=01, 'u'=011, 'z'=001} is NOT correct since "aaaxuaxz" and "aazuaxax" can both be decoded from the code 00001011001001. The students are submitting all kinds of codes, and I need a computer program to help me determine which ones are correct and which ones are not.
Input Specification:
Each input file contains one test case. For each case, the first line gives an integer N (2≤N≤63), then followed by a line that contains all the N distinct characters and their frequencies in the following format:
c[1] f[1] c[2] f[2] ... c[N] f[N]
where c[i] is a character chosen from {'0' - '9', 'a' - 'z', 'A' - 'Z', '_'}, and f[i] is the frequency of c[i] and is an integer no more than 1000. The next line gives a positive integer M (≤1000), then followed by M student submissions. Each student submission consists of N lines, each in the format:
c[i] code[i]
where c[i] is the i-th character and code[i] is an non-empty string of no more than 63 '0's and '1's.
Output Specification:
For each test case, print in each line either "Yes" if the student's submission is correct, or "No" if not.
Note: The optimal solution is not necessarily generated by Huffman algorithm. Any prefix code with code length being optimal is considered correct.
Sample Input:
7
A 1 B 1 C 1 D 3 E 3 F 6 G 6
4
A 00000
B 00001
C 0001
D 001
E 01
F 10
G 11
A 01010
B 01011
C 0100
D 011
E 10
F 11
G 00
A 000
B 001
C 010
D 011
E 100
F 101
G 110
A 00000
B 00001
C 0001
D 001
E 00
F 10
G 11
Sample Output:
Yes
Yes
No
No



最优编码不一定通过Huffman算法得到。给定4个字符及其出现频率: A:1; B:1; C:2; D:2
下面哪一套不是用Huffman算法得到的正确的编码?
A.A:000; B:001; C:01; D:1
B.A:10; B:11; C:00; D:01
C.A:00; B:10; C:01; D:11
D.A:111; B:001; C:10; D:1
正确答案:C你选对了

这道题主要利用哈夫曼编码的两个性质:
- 哈夫曼编码可能不唯一,但是哈夫曼编码的长度是唯一的。字符串编码成01串后的长度实际上就是其以频率为权值所构成的任意一颗哈夫曼树的带权路径长度。
- 对于任何一个叶子结点,其编号一定不会成为其他任何一个结点编号的前缀—也就是说,题目中给出需要判断的的每个字符的编码,它不会是其他字符编码的前缀。
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#define ERROR -1
typedef HuffmanTree ElementType;
typedef struct HNode *Heap;
typedef Heap MinHeap;
typedef struct TreeNode* HuffmanTree;
struct TreeNode
{ //A 1 B 1 C 1 D 3 E 3 F 6 G 6
int Weight;//为什么不记录A B C 只记录频率1 1 1? 因为根据哈夫曼树的特点,待计算WPL的结点都位于叶结点(知道出现频率就可以了)
HuffmanTree Left;
HuffmanTree Right;
};
struct HNode
{
ElementType *Data;
int Size;
int Capacity;
};
MinHeap CreateHeap(int MaxSize)
{
MinHeap H = (MinHeap)malloc(sizeof(struct HNode));
H->Data = (ElementType*)malloc(sizeof(ElementType)*MaxSize);
H->Size = 0;
H->Capacity = MaxSize;
H->Data[0] = -10001;
return H;
}
bool IsFull(MinHeap H)
{
return (H->Size == H->Capacity);
}
bool Insert(MinHeap H, ElementType X)
{
if(IsFull(H))
{
printf("The heap is full!\n");
return false;
}
int i = ++H->Size;
for(; H->Data[i/2] >= X; i /= 2)
{
H->Data[i] = H->Data[i/2];
}
H->Data[i] = X;
return true;
}
bool IsEmpty(MinHeap H)
{
return (H->Size == 0);
}
ElementType Delete(MinHeap H)
{
if(IsEmpty(H))
{
printf("The heap is empty!\n");
return ERROR;
}
int Parent, Child;
ElementType MinItem,X;
MinItem = H->Data[1];
X = H->Data[H->Size--];
for(Parent = 1; Parent * 2 <= H->Size; Parent = Child)
{
Child = Parent * 2;
if((Child!=H->Size)&&(H->Data[Child] > H->Data[Child + 1]))
Child++;
if(X < H->Data[Child])
break;
else
H->Data[Parent] = H->Data[Child];
}
H->Data[Parent] = X;
return MinItem;
}
MinHeap ReadData(int N)
{
MinHeap H = CreateHeap(N);
char Symbol;
int Weight;
for(int i=0; i<N; i++)
{
scanf("%c %d",&Symbol,&Weight);
HuffmanTree HTree = (HuffmanTree)malloc(sizeof(struct TreeNode));
HTree->Weight = Weight;
HTree->Left = NULL;
HTree->Right = NULL;
}
}
int WPL(HuffmanTree T, int Depth)
{
if (!T->Left && !T->Right) //叶结点就是待计算的结点
return T->Weight * Depth;
else
return WPL(T->Left, Depth + 1) + WPL(T->Right, Depth + 1);
}
int main()
{
int N;
scanf("%d",&N);
MinHeap H = CreateHeap(N);
H = ReadData(N);
HuffmanTree T = Huffman(H);
int CodeLen = WPL(T, 0);
int N,M;
scanf("%d %d",&N,&M);
for(int i=0; i<N; i++)
{
int num;
scanf("%d",&num);
Insert(H,num);
}
for(int i=0; i<M; i++)
{
int idx;
scanf("%d",&idx);
int Fisrt = 1;
for(int j=idx; j>=1; j/=2)
{
if(Fisrt)
{
printf("%d",H->Data[j]);
Fisrt = 0;
}
else
{
printf(" %d",H->Data[j]);
}
}
printf("\n");
}
return 0;
}
未完待续
C++实现代码如下:
#include<bits/stdc++.h>
using namespace std;
int main(){
int s = 0, n, m, x, a[100];
char ch;
priority_queue<int,vector<int>,greater<int> > q; //优先队列
cin>>n;getchar();
for(int i = 0; i < n; i++) {
cin>>ch>>x;
a[i] = x;
q.push(x);
}
while(q.size() > 1) {
int x = q.top();
q.pop();
int y = q.top();
q.pop();
s = s + x + y;
q.push(x + y);
}
cin>>m;
while(m--) {
int s1 = 0;
string str[100];
for(int i = 0; i < n; i++) {
cin>>ch>>str[i];
s1 = s1 + str[i].size() * a[i];
}
if(s == s1) {
bool jdg = true;
for (int i = 0; i < n-1; i++) {
for (int j = i+1; j < n; j++) {
int flag = 0;
int size = str[i].size() > str[j].size() ? str[j].size() : str[i].size();
for(int k = 0; k < size; k++)
if(str[i][k] != str[j][k])
flag = 1;
if (!flag)
jdg = false;
}
}
if(jdg)
cout<<"Yes\n";
else
cout<<"No\n";
}
else
cout<<"No\n";
}
return 0;
}
图

多对多的数据结构

图的存储
邻接矩阵
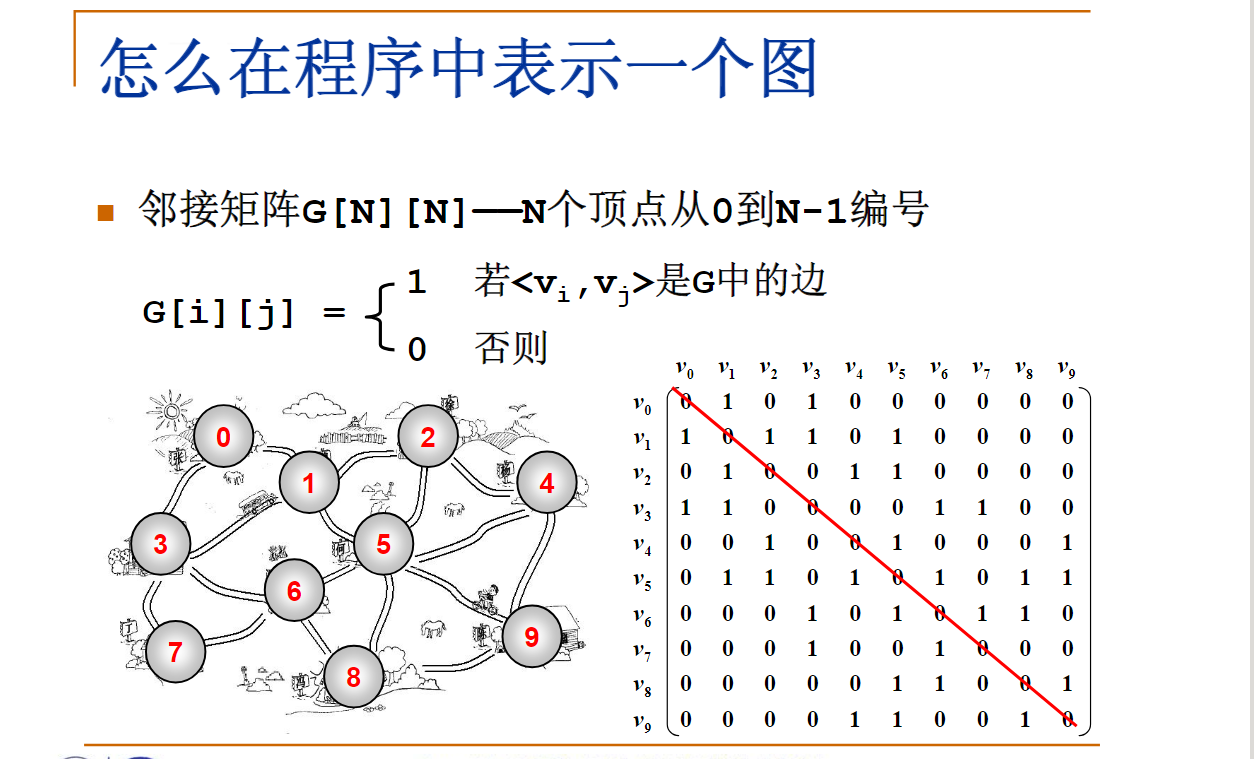
对于有N个顶点的无向图,怎样存储可以省一半空间?
正确答案:用一个长度为N(N+1)/2的1维数组
用一维数组G[ ]存储有4个顶点的无向图如下:G[ ] = { 0, 1, 0, 1, 1, 0, 0, 0, 1, 0 }
则顶点2和顶点0之间是有边的。 ✔
有N个顶点的无向完全图有多少条边?N(N-1)/2



完整版本代码
#include <stdio.h>
#include <stdlib.h>
/* 图的邻接矩阵表示法 */
#define MaxVertexNum 100 /* 最大顶点数设为100 */
#define INFINITY 65535 /* ∞设为双字节无符号整数的最大值65535*/
typedef int Vertex; /* 用顶点下标表示顶点,为整型 */
typedef int WeightType; /* 边的权值设为整型 */
typedef char DataType; /* 顶点存储的数据类型设为字符型 */
/* 边的定义 */
typedef struct ENode *PtrToENode;
struct ENode{
Vertex V1, V2; /* 有向边<V1, V2> */
WeightType Weight; /* 权重 */
};
typedef PtrToENode Edge;
/* 图结点的定义 */
typedef struct GNode *PtrToGNode;
struct GNode{
int Nv; /* 顶点数 */
int Ne; /* 边数 */
WeightType G[MaxVertexNum][MaxVertexNum]; /* 邻接矩阵 */
DataType Data[MaxVertexNum]; /* 存顶点的数据 */
/* 注意:很多情况下,顶点无数据,此时Data[]可以不用出现 */
};
typedef PtrToGNode MGraph; /* 以邻接矩阵存储的图类型 */
MGraph CreateGraph( int VertexNum )
{ /* 初始化一个有VertexNum个顶点但没有边的图 */
Vertex V, W;
MGraph Graph;
Graph = (MGraph)malloc(sizeof(struct GNode)); /* 建立图 */
Graph->Nv = VertexNum;
Graph->Ne = 0;
/* 初始化邻接矩阵 */
/* 注意:这里默认顶点编号从0开始,到(Graph->Nv - 1) */
for (V=0; V<Graph->Nv; V++)
for (W=0; W<Graph->Nv; W++)
Graph->G[V][W] = INFINITY;
return Graph;
}
void InsertEdge( MGraph Graph, Edge E )
{
/* 插入边 <V1, V2> */
Graph->G[E->V1][E->V2] = E->Weight;
/* 若是无向图,还要插入边<V2, V1> */
Graph->G[E->V2][E->V1] = E->Weight;
}
MGraph BuildGraph()
{
MGraph Graph;
Edge E;
Vertex V;
int Nv, i;
scanf("%d", &Nv); /* 读入顶点个数 */
Graph = CreateGraph(Nv); /* 初始化有Nv个顶点但没有边的图 */
scanf("%d", &(Graph->Ne)); /* 读入边数 */
if ( Graph->Ne != 0 ) { /* 如果有边 */
E = (Edge)malloc(sizeof(struct ENode)); /* 建立边结点 */
/* 读入边,格式为"起点 终点 权重",插入邻接矩阵 */
for (i=0; i<Graph->Ne; i++) {
scanf("%d %d %d", &E->V1, &E->V2, &E->Weight);
/* 注意:如果权重不是整型,Weight的读入格式要改 */
InsertEdge( Graph, E );
}
}
/* 如果顶点有数据的话,读入数据 */
for (V=0; V<Graph->Nv; V++)
scanf(" %c", &(Graph->Data[V]));
return Graph;
}
简化版本代码
#include <stdio.h>
#include <stdlib.h>
#define MAXN 100
int G[MAXN][MAXN];
int visited[MAXN];
int Ne,Nv;
void InitVisited()
{
for(int i=0; i<MAXN; i++)
visited[i] = 0;
}
void BuildGraph()
{
for(int i=0; i<MAXN; i++)
{
for(int j=0; j<MAXN; j++)
{
G[i][j] = 0;
}
}
scanf("%d %d",&Nv, &Ne);
if(Ne)
{
for(int i=0; i<Ne; i++)
{
int v1,v2,weight;
scanf("%d %d %d",&v1,&v2,&weight);
G[v1][v2] = weight;
G[v2][v1] = weight;
}
}
}
void dfs(int v)
{
visited[v] = 1;
printf("%d ",v);
for(int i=0; i<Nv; i++)
{
if(visited[i]==0 &&G[v][i]!=0)
{
dfs(i);
}
}
}
int main()
{
BuildGraph();
InitVisited();
dfs(0);
return 0;
}
输入数据:
6 7
0 1 1
0 2 1
0 4 1
1 4 1
2 5 1
3 4 1
3 5 1
输出结果:
0 1 4 3 5 2
邻接表
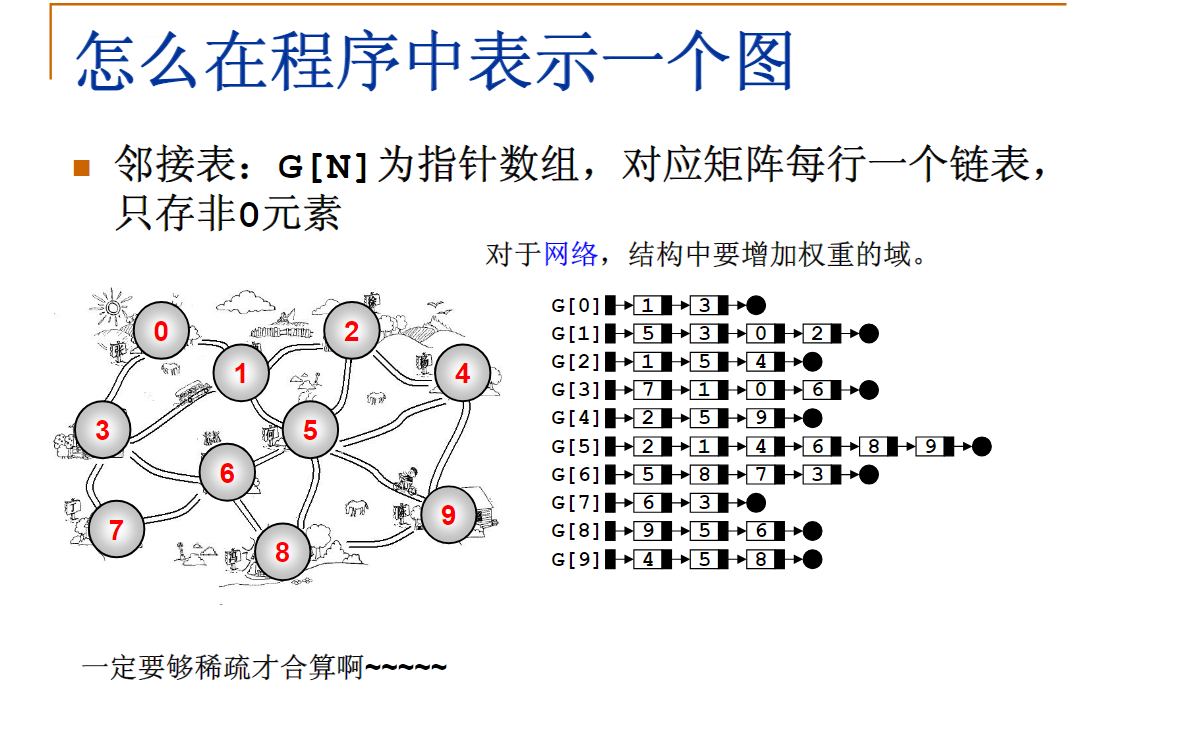

用邻接表表示有N个顶点、E条边的图,则遍历图中所有边的时间复杂度为:O(N+E)
需要N个头指针 + 2E个结点(每个结点至少2个域),则E小于多少是省空间的?
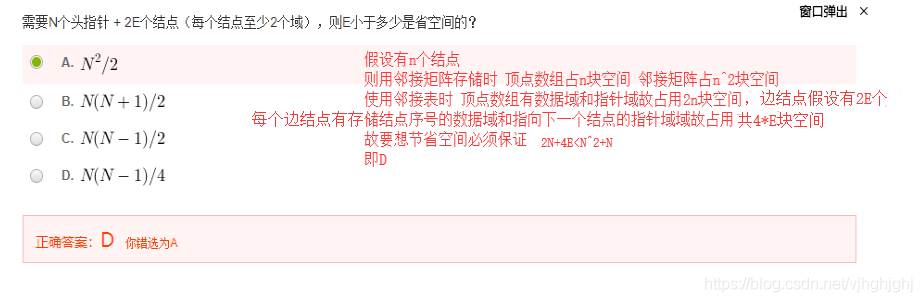
《数据结构》课程给出的图的邻接表表示法如下:
完整版本代码
/* 图的邻接表表示法 */
#define MaxVertexNum 100 /* 最大顶点数设为100 */
typedef int Vertex; /* 用顶点下标表示顶点,为整型 */
typedef int WeightType; /* 边的权值设为整型 */
typedef char DataType; /* 顶点存储的数据类型设为字符型 */
/* 边的定义 */
typedef struct ENode *PtrToENode;
struct ENode{
Vertex V1, V2; /* 有向边<V1, V2> */
WeightType Weight; /* 权重 */
};
typedef PtrToENode Edge;
/* 邻接点的定义 */
typedef struct AdjVNode *PtrToAdjVNode;
struct AdjVNode{
Vertex AdjV; /* 邻接点下标 */
WeightType Weight; /* 边权重 */
PtrToAdjVNode Next; /* 指向下一个邻接点的指针 */
};
/* 顶点表头结点的定义 */
typedef struct Vnode{
PtrToAdjVNode FirstEdge;/* 边表头指针 */
DataType Data; /* 存顶点的数据 */
/* 注意:很多情况下,顶点无数据,此时Data可以不用出现 */
} AdjList[MaxVertexNum]; /* AdjList是邻接表类型 */
/* 图结点的定义 */
typedef struct GNode *PtrToGNode;
struct GNode{
int Nv; /* 顶点数 */
int Ne; /* 边数 */
AdjList G; /* 邻接表 */
};
typedef PtrToGNode LGraph; /* 以邻接表方式存储的图类型 */
LGraph CreateGraph( int VertexNum )
{ /* 初始化一个有VertexNum个顶点但没有边的图 */
Vertex V;
LGraph Graph;
Graph = (LGraph)malloc( sizeof(struct GNode) ); /* 建立图 */
Graph->Nv = VertexNum;
Graph->Ne = 0;
/* 初始化邻接表头指针 */
/* 注意:这里默认顶点编号从0开始,到(Graph->Nv - 1) */
for (V=0; V<Graph->Nv; V++)
Graph->G[V].FirstEdge = NULL;
return Graph;
}
void InsertEdge( LGraph Graph, Edge E )
{
PtrToAdjVNode NewNode;
/* 插入边 <V1, V2> */
/* 为V2建立新的邻接点 */
NewNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
NewNode->AdjV = E->V2;
NewNode->Weight = E->Weight;
/* 将V2插入V1的表头 */
NewNode->Next = Graph->G[E->V1].FirstEdge;
Graph->G[E->V1].FirstEdge = NewNode;
/* 若是无向图,还要插入边 <V2, V1> */
/* 为V1建立新的邻接点 */
NewNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
NewNode->AdjV = E->V1;
NewNode->Weight = E->Weight;
/* 将V1插入V2的表头 */
NewNode->Next = Graph->G[E->V2].FirstEdge;
Graph->G[E->V2].FirstEdge = NewNode;
}
LGraph BuildGraph()
{
LGraph Graph;
Edge E;
Vertex V;
int Nv, i;
scanf("%d", &Nv); /* 读入顶点个数 */
Graph = CreateGraph(Nv); /* 初始化有Nv个顶点但没有边的图 */
scanf("%d", &(Graph->Ne)); /* 读入边数 */
if ( Graph->Ne != 0 ) { /* 如果有边 */
E = (Edge)malloc( sizeof(struct ENode) ); /* 建立边结点 */
/* 读入边,格式为"起点 终点 权重",插入邻接矩阵 */
for (i=0; i<Graph->Ne; i++) {
scanf("%d %d %d", &E->V1, &E->V2, &E->Weight);
/* 注意:如果权重不是整型,Weight的读入格式要改 */
InsertEdge( Graph, E );
}
}
/* 如果顶点有数据的话,读入数据 */
for (V=0; V<Graph->Nv; V++)
scanf(" %c", &(Graph->G[V].Data));
return Graph;
}
邻接表存储、DFS遍历实例
#include <stdio.h>
#include <stdlib.h>
#define MaxVertexNum 100 /* 最大顶点数设为100 */
typedef int Vertex; /* 用顶点下标表示顶点,为整型 */
typedef int WeightType; /* 边的权值设为整型 */
typedef char DataType; /* 顶点存储的数据类型设为字符型 */
int Visited[MaxVertexNum];
void InitVisited()
{
for(int i=0; i<MaxVertexNum; i++)
Visited[i] = 0;
}
/* 边的定义 */
typedef struct ENode *PtrToENode;
struct ENode{
Vertex V1, V2; /* 有向边<V1, V2> */
WeightType Weight; /* 权重 */
};
typedef PtrToENode Edge;
typedef struct AdjVNode *PtrToAdjVNode;
struct AdjVNode
{
Vertex AdjV;
WeightType Weight;
PtrToAdjVNode Next;
};
typedef struct VNode
{
PtrToAdjVNode FirstEdge;
}AdjList[MaxVertexNum];
typedef struct GNode *PtrToGNode;
struct GNode
{
int Ne;
int Nv;
AdjList G;
};
typedef PtrToGNode LGraph;
LGraph CreateGraph(int VertexNum)
{
LGraph Graph = (LGraph)malloc(sizeof(struct GNode));
Graph->Nv = VertexNum;
Graph->Ne = 0;
for(int i=0; i<Graph->Nv; i++)
{
Graph->G[i].FirstEdge = NULL;
}
return Graph;
}
void InsertEdge(LGraph Graph, Edge E)
{
PtrToAdjVNode newNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
newNode->AdjV = E->V2;
newNode->Weight = E->Weight;
newNode->Next = Graph->G[E->V1].FirstEdge;
Graph->G[E->V1].FirstEdge = newNode;
newNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
newNode->AdjV = E->V1;
newNode->Weight = E->Weight;
newNode->Next = Graph->G[E->V2].FirstEdge;
Graph->G[E->V2].FirstEdge = newNode;
}
LGraph BuildGraph()
{
LGraph Graph = (LGraph)malloc(sizeof(struct GNode));
Edge E;
int Nv;
scanf("%d", &Nv);
Graph = CreateGraph(Nv);
scanf("%d", &(Graph->Ne));
if(Graph->Ne != 0)
{
for(int i=0; i<Graph->Ne; i++)
{
E = (Edge)malloc(sizeof(struct ENode));
scanf("%d %d %d",&E->V1,&E->V2,&E->Weight);
InsertEdge(Graph, E);
}
}
return Graph;
}
/* 邻接表存储的图 - DFS */
void Visit( Vertex V )
{
printf("正在访问顶点%d\n", V);
}
/* Visited[]为全局变量,已经初始化为false */
void DFS( LGraph Graph, Vertex V, void (*Visit)(Vertex) )
{ /* 以V为出发点对邻接表存储的图Graph进行DFS搜索 */
PtrToAdjVNode W;
Visit( V ); /* 访问第V个顶点 */
Visited[V] = 1; /* 标记V已访问 */
for( W=Graph->G[V].FirstEdge; W; W=W->Next ) /* 对V的每个邻接点W->AdjV */
if ( !Visited[W->AdjV] ) /* 若W->AdjV未被访问 */
DFS( Graph, W->AdjV, Visit ); /* 则递归访问之 */
}
void PrintList(LGraph Graph)
{
for(int i=0; i<Graph->Nv; i++)
{
PtrToAdjVNode W = Graph->G[i].FirstEdge;
printf("G[%d]:", i);
int IsFirst = 1;
while(W)
{
if(IsFirst)
{
printf("%d", W->AdjV);
IsFirst = 0;
}
else
printf("->%d", W->AdjV);
W = W->Next;
}
printf("\n");
}
}
int main()
{
LGraph Graph = BuildGraph();
InitVisited();
DFS(Graph, 0, Visit);
PrintList(Graph);
return 0;
}
输入数据:
6
7
0 1 1
0 2 1
0 4 1
1 4 1
2 5 1
3 4 1
3 5 1
输出结果:
正在访问顶点0
正在访问顶点4
正在访问顶点3
正在访问顶点5
正在访问顶点2
正在访问顶点1
G[0]:4->2->1
G[1]:4->0
G[2]:5->0
G[3]:5->4
G[4]:3->1->0
G[5]:3->2
十字链表
邻接多重表
图的遍历
深度优先搜索DFS

邻接矩阵存储
#include <stdio.h>
#include <stdlib.h>
#define MAXN 100
int G[MAXN][MAXN], Nv, Ne;
void BuildGraph()
{
int i,j,v1,v2,w;
scanf("%d",&Nv);
for(i=0; i<Nv; i++)
{
for(j=0; j<Nv; j++)
{
G[i][j] = 0;
}
}
scanf("%d",&Ne);
for(i=0; i<Ne; i++)
{
scanf("%d %d %d",&v1,&v2,&w);
G[v1][v2] = w;
G[v2][v1] = w;
}
}
void printGraph()
{
for(int i=0;i < Nv; i++)
{
for(int j=0; j<Nv; j++)
{
printf("%d ", G[i][j]);
}
printf("\n");
}
}
typedef int Vertex;
#define TRUE 1
#define FALSE 0
typedef int Boolean;
Boolean visited[MAXN];
Boolean IsFirst = TRUE;
void dfs(Vertex V)
{
visited[V] = TRUE;
if(IsFirst)
{
printf("%c",(char)(97 + V));
IsFirst = FALSE;
}
else
printf("->%c",(char)(97 + V));
for(int j=0; j<Nv; j++)
{
if(G[V][j]==1 && visited[j] == FALSE)
dfs(j);
}
}
int main()
{
BuildGraph();
printGraph();
bfs(0);
return 0;
}
6
7
0 1 1
0 2 1
0 4 1
1 4 1
2 5 1
3 4 1
3 5 1
0 1 1 0 1 0
1 0 0 0 1 0
1 0 0 0 0 1
0 0 0 0 1 1
1 1 0 1 0 0
0 0 1 1 0 0
a->b->e->d->f->c
邻接表存储
/* 邻接表存储的图 - DFS */
void Visit( Vertex V )
{
printf("正在访问顶点%d\n", V);
}
/* Visited[]为全局变量,已经初始化为false */
void DFS( LGraph Graph, Vertex V, void (*Visit)(Vertex) )
{ /* 以V为出发点对邻接表存储的图Graph进行DFS搜索 */
PtrToAdjVNode W;
Visit( V ); /* 访问第V个顶点 */
Visited[V] = true; /* 标记V已访问 */
for( W=Graph->G[V].FirstEdge; W; W=W->Next ) /* 对V的每个邻接点W->AdjV */
if ( !Visited[W->AdjV] ) /* 若W->AdjV未被访问 */
DFS( Graph, W->AdjV, Visit ); /* 则递归访问之 */
}
广度优先搜索BFS
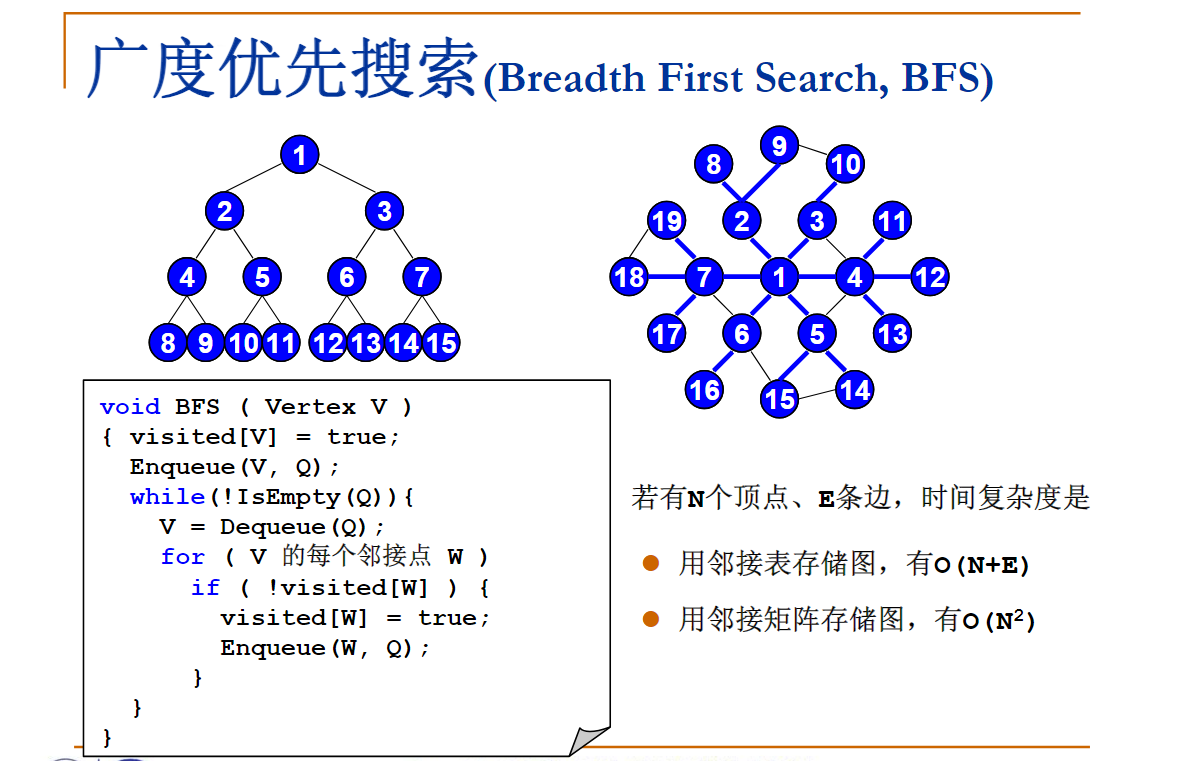
邻接矩阵存储
/* 邻接矩阵存储的图 - BFS */
/* IsEdge(Graph, V, W)检查<V, W>是否图Graph中的一条边,即W是否V的邻接点。 */
/* 此函数根据图的不同类型要做不同的实现,关键取决于对不存在的边的表示方法。*/
/* 例如对有权图, 如果不存在的边被初始化为INFINITY, 则函数实现如下: */
bool IsEdge( MGraph Graph, Vertex V, Vertex W )
{
return Graph->G[V][W]<INFINITY ? true : false;
}
/* Visited[]为全局变量,已经初始化为false */
void BFS ( MGraph Graph, Vertex S, void (*Visit)(Vertex) )
{ /* 以S为出发点对邻接矩阵存储的图Graph进行BFS搜索 */
Queue Q;
Vertex V, W;
Q = CreateQueue( MaxSize ); /* 创建空队列, MaxSize为外部定义的常数 */
/* 访问顶点S:此处可根据具体访问需要改写 */
Visit( S );
Visited[S] = true; /* 标记S已访问 */
AddQ(Q, S); /* S入队列 */
while ( !IsEmpty(Q) ) {
V = DeleteQ(Q); /* 弹出V */
for( W=0; W<Graph->Nv; W++ ) /* 对图中的每个顶点W */
/* 若W是V的邻接点并且未访问过 */
if ( !Visited[W] && IsEdge(Graph, V, W) ) {
/* 访问顶点W */
Visit( W );
Visited[W] = true; /* 标记W已访问 */
AddQ(Q, W); /* W入队列 */
}
} /* while结束*/
}
邻接矩阵存储、BFS实例
#include <stdio.h>
#include <stdlib.h>
#define MAXN 100
int G[MAXN][MAXN], Nv, Ne;
void BuildGraph()
{
int i,j,v1,v2,w;
scanf("%d",&Nv);
for(i=0; i<Nv; i++)
{
for(j=0; j<Nv; j++)
{
G[i][j] = 0;
}
}
scanf("%d",&Ne);
for(i=0; i<Ne; i++)
{
scanf("%d %d %d",&v1,&v2,&w);
G[v1][v2] = w;
G[v2][v1] = w;
}
}
void printGraph()
{
for(int i=0;i < Nv; i++)
{
for(int j=0; j<Nv; j++)
{
printf("%d ", G[i][j]);
}
printf("\n");
}
}
typedef int Vertex;
#define TRUE 1
#define FALSE 0
typedef int Boolean;
Boolean visited[MAXN];
Boolean IsFirst = TRUE;
void bfs(Vertex V)
{
int queue[100];
int front = 0;
int tail = 0;
visited[V] = TRUE;
queue[tail++] = V;
int temp;
while(front != tail)
{
temp = queue[front++];
if(IsFirst)
{
printf("%c",(char)(97 + temp));
IsFirst = FALSE;
}
else
printf("->%c",(char)(97 + temp));
for(int i=0;i <Nv; i++)
{
if(G[temp][i] == 1 && visited[i] == FALSE)
{
visited[i] = TRUE;
queue[tail++] = i;
}
}
}
}
int main()
{
BuildGraph();
printGraph();
bfs(0);
return 0;
}
0 1 1 0 1 0
1 0 0 0 1 0
1 0 0 0 0 1
0 0 0 0 1 1
1 1 0 1 0 0
0 0 1 1 0 0
a->b->c->e->f->d
连通图

具有N个顶点的无向图至多有多少个连通分量?N
如果从无向图的任一顶点出发进行一次深度优先搜索可访问所有顶点,则该图一定是连通图
具有N个顶点的无向图至少有多少个连通分量?1
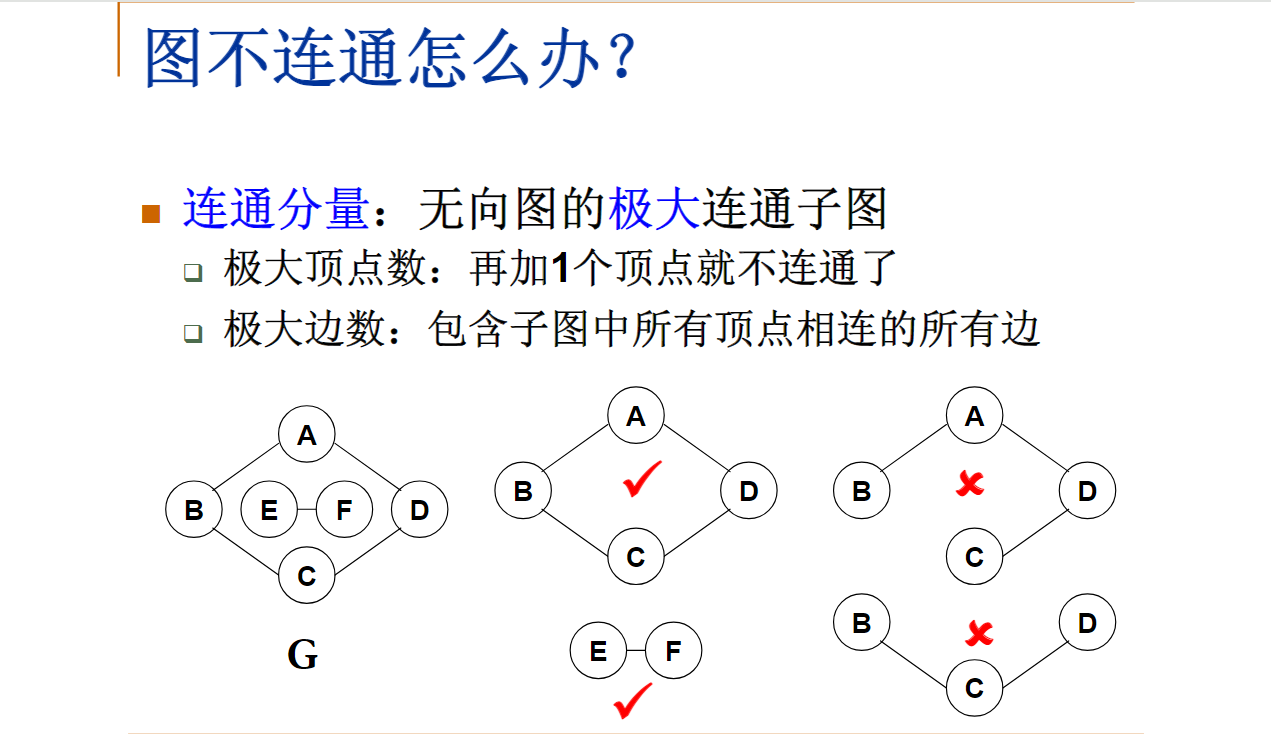
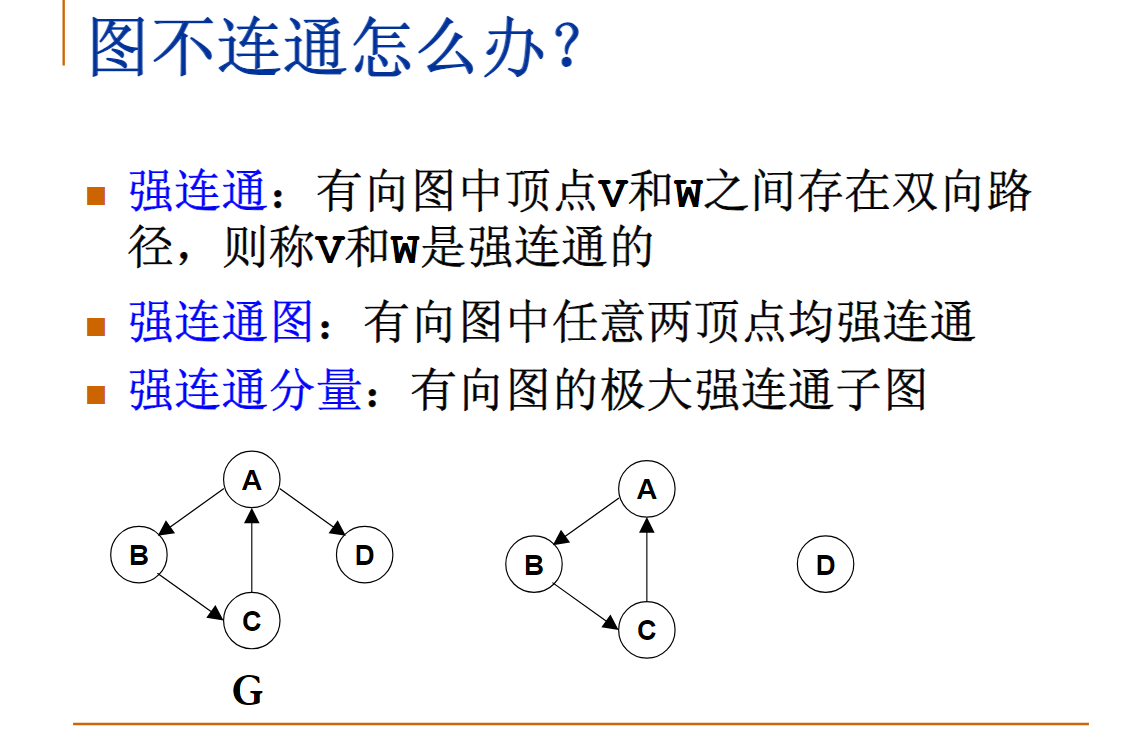
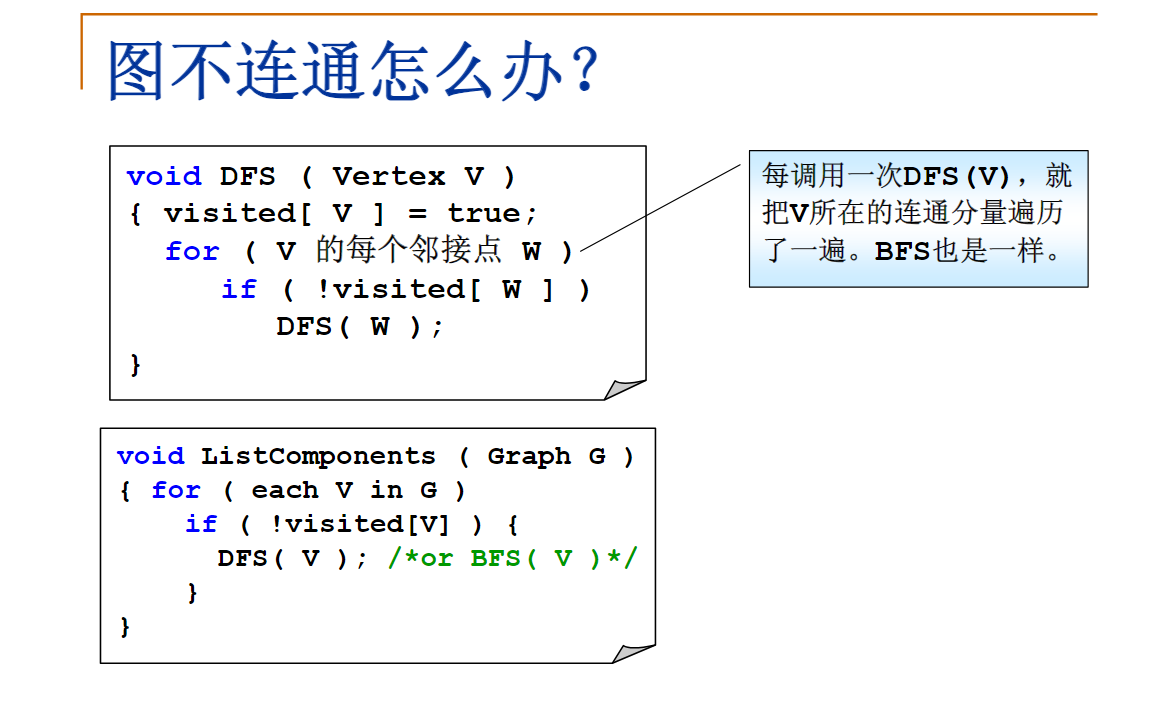
最短路径算法


单源无权图最短路算法
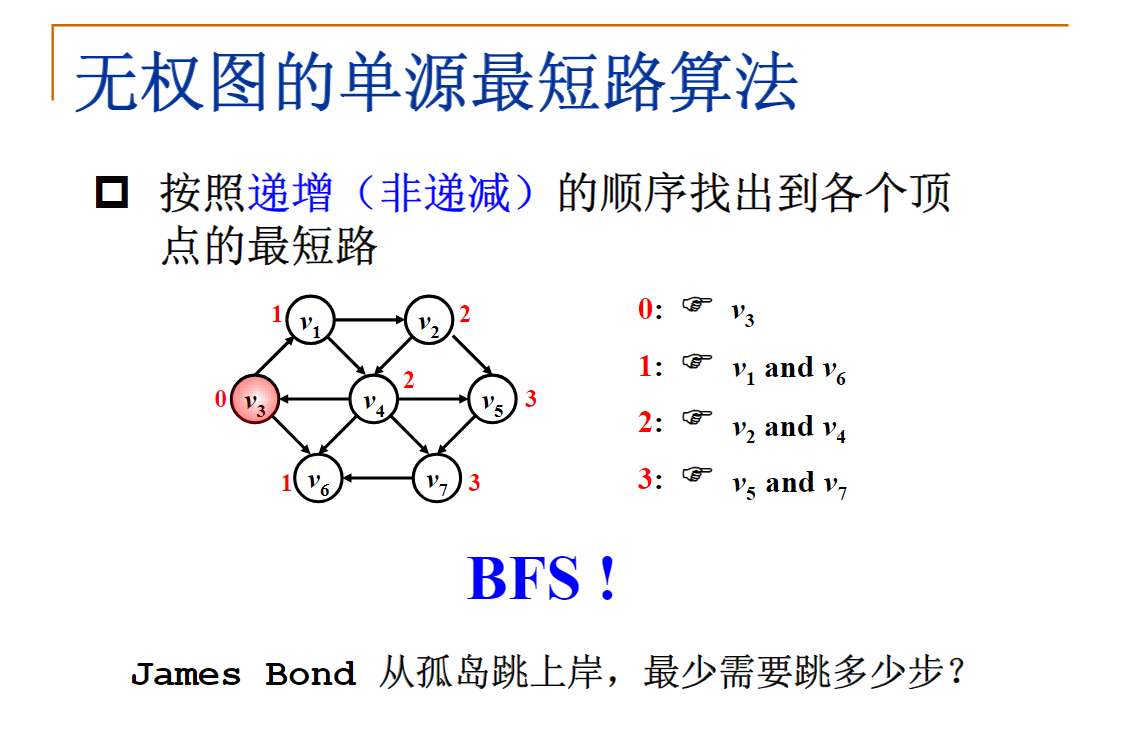

dist[W] = V 到 W 的最短距离;那么dist[W]应该被初始化为多少呢?D
- A.正无穷
- B.负无穷
- C.-1
- D.这三种都可以
随便一个不可能的数字即可表示没被访问,注意这里是无权图。
如果有|V|个顶点和|E|条边的图用邻接表存储,则算法的时间复杂度是多少?
void Unweighted ( Vertex S )
{
Enqueue(S, Q);
while(!IsEmpty(Q)){
V = Dequeue(Q);
for ( V 的每个邻接点 W )
if ( dist[W] == -1 ) {
dist[W] = dist[V]+1;
path[W] = V;
Enqueue(W, Q);
}
}
}
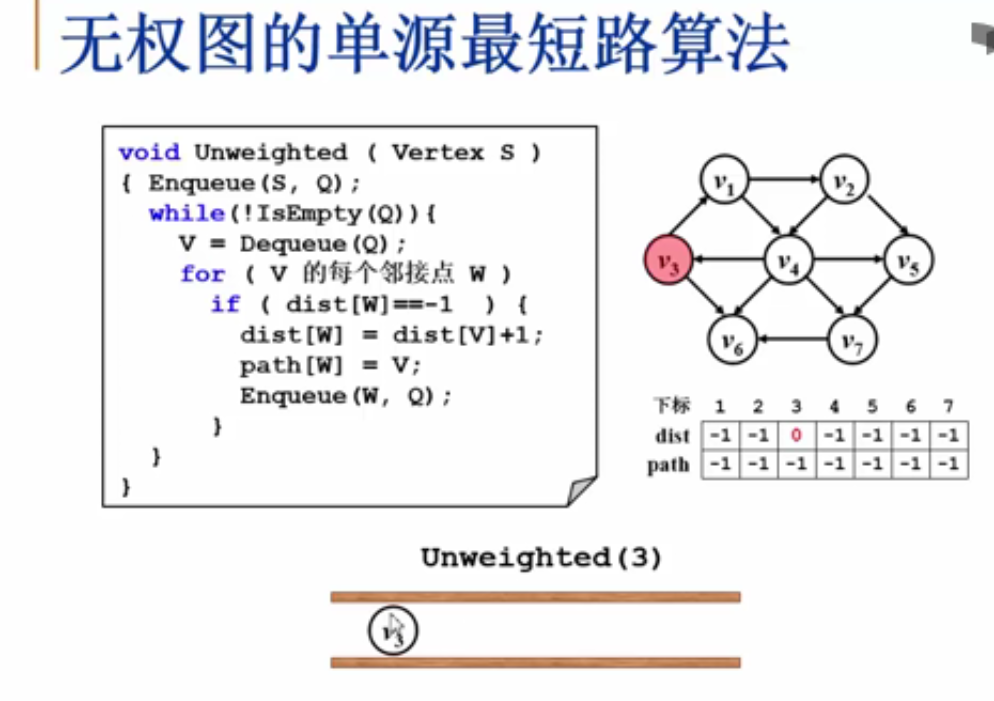
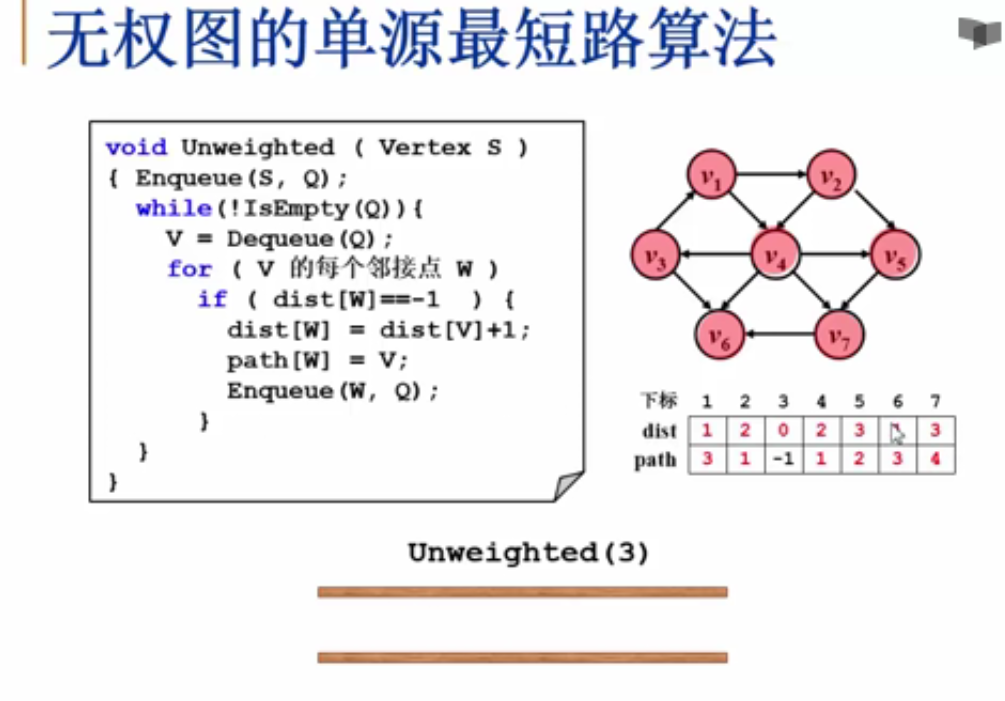
邻接表存储 - 无权图的单源最短路算法
/* 邻接表存储 - 无权图的单源最短路算法 */
/* dist[]和path[]全部初始化为-1 */
void Unweighted ( LGraph Graph, int dist[], int path[], Vertex S )
{
Queue Q;
Vertex V;
PtrToAdjVNode W;
Q = CreateQueue( Graph->Nv ); /* 创建空队列, MaxSize为外部定义的常数 */
dist[S] = 0; /* 初始化源点 */
AddQ (Q, S);
while( !IsEmpty(Q) ){
V = DeleteQ(Q);
for ( W=Graph->G[V].FirstEdge; W; W=W->Next ) /* 对V的每个邻接点W->AdjV */
if ( dist[W->AdjV]==-1 ) { /* 若W->AdjV未被访问过 */
dist[W->AdjV] = dist[V]+1; /* W->AdjV到S的距离更新 */
path[W->AdjV] = V; /* 将V记录在S到W->AdjV的路径上 */
AddQ(Q, W->AdjV);
}
} /* while结束*/
}
单源有权图最短路径算法——Dijkstra算法
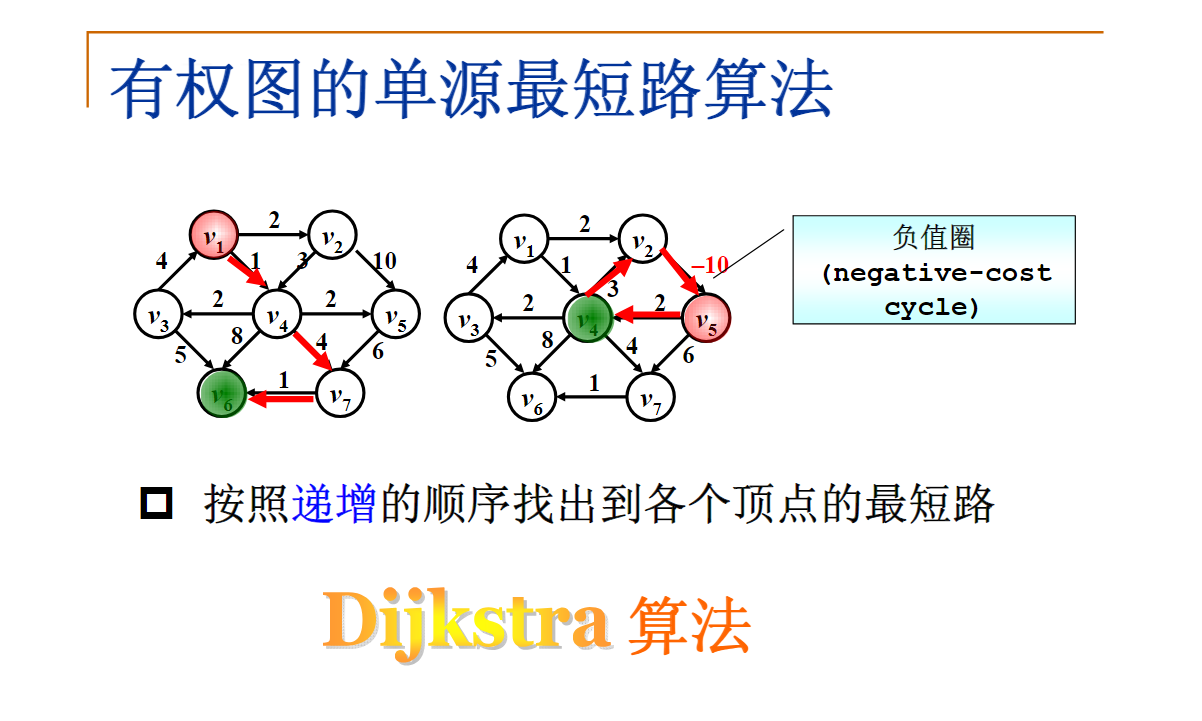

如果收录v使得s到w的路径变短,则:s到w的路径一定经过v,并且v到w有一条边

Dijkstra算法中的dist应该如何初始化?如果s到w有直接的边,则dist[w]=<s,w>的权重;否则dist[w]定义为A
- A.正无穷
- B.负无穷
- C. -1
- D.这三种都可以
注:这里是根据不等式结果更新dist数组的,不能随便初始化
void Dijkstra( Vertex s )
{ while (1) {
V = 未收录顶点中dist最小者;
if ( 这样的V不存在 )
break;
collected[V] = true;
for ( V 的每个邻接点 W )
if ( collected[W] == false )
if ( dist[V]+E<V,W> < dist[W] ) {
dist[W] = dist[V] + E<V,W> ;
path[W] = V;
}
}
}
算法的时间复杂度是多少?
不好计算,取决于如何从未收录顶点中选出dist最小者

邻接矩阵存储 - 有权图的单源最短路算法
/* 邻接矩阵存储 - 有权图的单源最短路算法 */
Vertex FindMinDist( MGraph Graph, int dist[], int collected[] )
{ /* 返回未被收录顶点中dist最小者 */
Vertex MinV, V;
int MinDist = INFINITY;
for (V=0; V<Graph->Nv; V++) {
if ( collected[V]==false && dist[V]<MinDist) {
/* 若V未被收录,且dist[V]更小 */
MinDist = dist[V]; /* 更新最小距离 */
MinV = V; /* 更新对应顶点 */
}
}
if (MinDist < INFINITY) /* 若找到最小dist */
return MinV; /* 返回对应的顶点下标 */
else return ERROR; /* 若这样的顶点不存在,返回错误标记 */
}
bool Dijkstra( MGraph Graph, int dist[], int path[], Vertex S )
{
int collected[MaxVertexNum];
Vertex V, W;
/* 初始化:此处默认邻接矩阵中不存在的边用INFINITY表示 */
for ( V=0; V<Graph->Nv; V++ ) {
dist[V] = Graph->G[S][V];
if ( dist[V]<INFINITY )
path[V] = S;
else
path[V] = -1;
collected[V] = false;
}
/* 先将起点收入集合 */
dist[S] = 0;
collected[S] = true;
while (1) {
/* V = 未被收录顶点中dist最小者 */
V = FindMinDist( Graph, dist, collected );
if ( V==ERROR ) /* 若这样的V不存在 */
break; /* 算法结束 */
collected[V] = true; /* 收录V */
for( W=0; W<Graph->Nv; W++ ) /* 对图中的每个顶点W */
/* 若W是V的邻接点并且未被收录 */
if ( collected[W]==false && Graph->G[V][W]<INFINITY ) {
if ( Graph->G[V][W]<0 ) /* 若有负边 */
return false; /* 不能正确解决,返回错误标记 */
/* 若收录V使得dist[W]变小 */
if ( dist[V]+Graph->G[V][W] < dist[W] ) {
dist[W] = dist[V]+Graph->G[V][W]; /* 更新dist[W] */
path[W] = V; /* 更新S到W的路径 */
}
}
} /* while结束*/
return true; /* 算法执行完毕,返回正确标记 */
}
邻接矩阵存储 - 有权图的单源最短路算法实例
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#define MaxVertexNum 100
#define INFINITY 65535
int visited[MaxVertexNum];
int dist[MaxVertexNum];
int path[MaxVertexNum];
typedef int Vertex;
typedef int WeightType;
typedef struct ENode *PtrToENode;
struct ENode
{
Vertex V1;
Vertex V2;
WeightType Weight;
};
typedef PtrToENode Edge;
typedef struct GNode *PtrToGNode;
struct GNode
{
int Nv;
int Ne;
WeightType G[MaxVertexNum][MaxVertexNum];
};
typedef PtrToGNode MGraph;
MGraph CreateGraph(int VertexNum)
{
MGraph Graph = (MGraph)malloc(sizeof(struct GNode));
Graph->Nv = VertexNum;
Graph->Ne = 0;
Vertex V1,V2;
for(Vertex V1=0; V1<Graph->Nv; V1++)
for(Vertex V2=0; V2<Graph->Nv; V2++)
Graph->G[V1][V2] = 0;
return Graph;
}
void InsertEdge(MGraph Graph, Edge E)
{
Graph->G[E->V1][E->V2] = E->Weight;
}
MGraph BuildGraph()
{
int Nv;
Edge E;
scanf("%d", &Nv);
MGraph Graph = CreateGraph(Nv);
scanf("%d", &(Graph->Ne));
if((Graph->Ne) != 0)
{
E = (Edge)malloc(sizeof(struct ENode));
for(int i=0; i<Graph->Ne; i++)
{
scanf("%d %d %d",&E->V1,&E->V2,&E->Weight);
InsertEdge(Graph, E);
}
}
return Graph;
}
void ResetVisited()
{
for(int i=0; i<MaxVertexNum; i++)
visited[i] = 0;
}
void Dijkstra(MGraph Graph, Vertex V)
{
ResetVisited();
for(int i=0; i<Graph->Nv; i++)
{
if(Graph->G[V][i]>0 && V!=i)
{
dist[i] = Graph->G[V][i];
path[i] = V;
}
else
{
dist[i] = INFINITY;
path[i] = -1;
}
}
dist[V] = 0;
path[V] = V;
visited[V] = 1;
for(int i=1; i<Graph->Nv; i++)
{
int minDist = INT_MAX;
int index;
for(int j=0; j<Graph->Nv; j++)
{
if(visited[j]==0 && dist[j]<minDist)
{
minDist = dist[j];
index = j;
}
}
visited[index] = 1;
for(int k=0; k<Graph->Nv; k++)
{
if(visited[k]==0 && Graph->G[index][k]>0 && minDist+Graph->G[index][k]<dist[k])
{
dist[k] = minDist+Graph->G[index][k];
path[k] = index;
}
}
}
}
void PrintPath(int path[], int distance)
{
int temp = distance;
int count = 1;
int collected[MaxVertexNum] = {0};
while(path[temp]!=0)
{
collected[count] = path[temp];
count++;
temp = path[temp];
}
collected[count] = path[temp];
while(count!=0)
{
printf("v%d->", collected[count]);
count--;
}
printf("v%d",distance);
}
int main()
{
MGraph Graph = BuildGraph();
Dijkstra(Graph, 0);
int distance = 5;
PrintPath(path, distance);
printf("\ncost distance :%d",dist[distance]);
return 0;
}
输入数据:
7 12
2 0 4
2 5 5
0 1 2
0 3 1
1 4 10
1 3 3
3 2 2
3 5 8
3 6 4
3 4 2
4 6 6
6 5 1
输出结果:
v0->v3->v6->v5
cost distance :6
多源最短路算法——Floyd算法


D矩阵应该初始化为什么?
- A.带权的邻接矩阵,对角元是0
- B.带权的邻接矩阵,对角元是无穷大
- C.全是0的矩阵
- D.全是无穷大的矩阵
正确答案:A你选对了
如果i和j之间没有直接的边,D[i][j]应该定义为什么?
- A.正无穷
- B.0
- C.负无穷
- D.这三种都可以
正确答案:A你选对了

邻接矩阵存储 - 多源最短路算法
/* 邻接矩阵存储 - 多源最短路算法 */
bool Floyd( MGraph Graph, WeightType D[][MaxVertexNum], Vertex path[][MaxVertexNum] )
{
Vertex i, j, k;
/* 初始化 */
for ( i=0; i<Graph->Nv; i++ )
for( j=0; j<Graph->Nv; j++ ) {
D[i][j] = Graph->G[i][j];
path[i][j] = -1;
}
for( k=0; k<Graph->Nv; k++ )
for( i=0; i<Graph->Nv; i++ )
for( j=0; j<Graph->Nv; j++ )
if( D[i][k] + D[k][j] < D[i][j] ) {
D[i][j] = D[i][k] + D[k][j];
if ( i==j && D[i][j]<0 ) /* 若发现负值圈 */
return false; /* 不能正确解决,返回错误标记 */
path[i][j] = k;
}
return true; /* 算法执行完毕,返回正确标记 */
}
分支限界法
https://blog.csdn.net/lcw_2015/article/details/52892501
Bellman-Ford算法
最小生成树算法
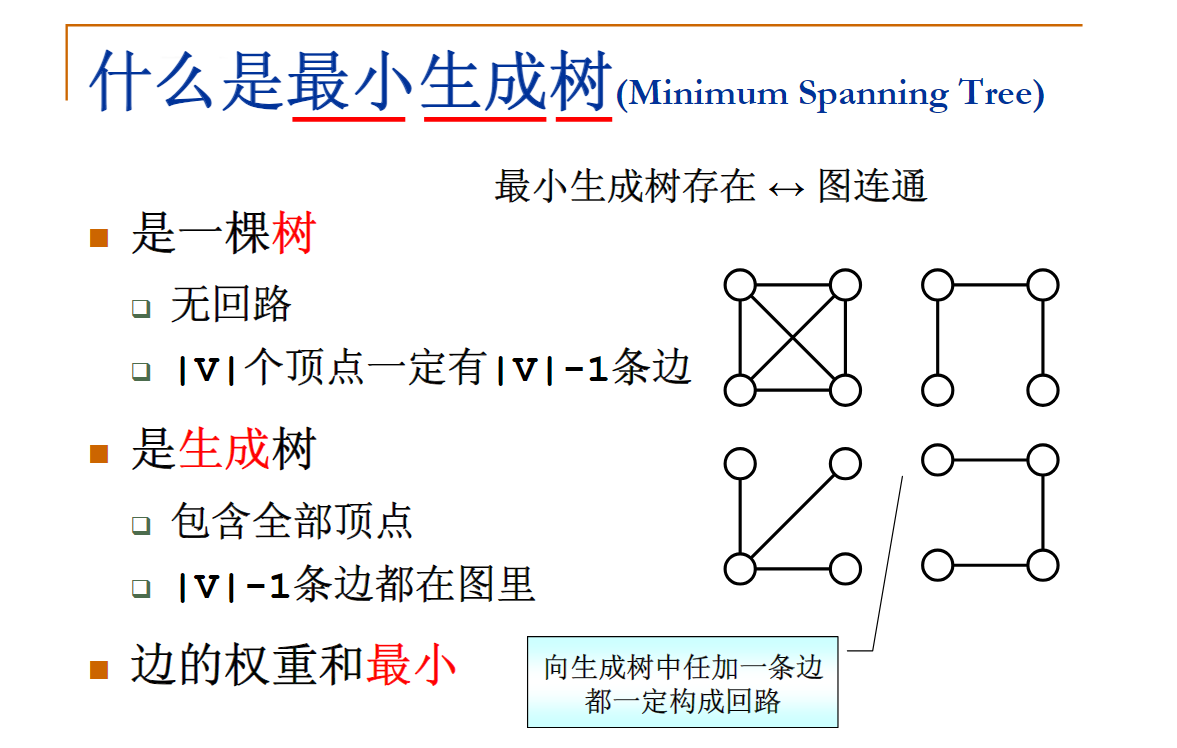

连通图的最小生成树不一定是唯一的
Prim算法
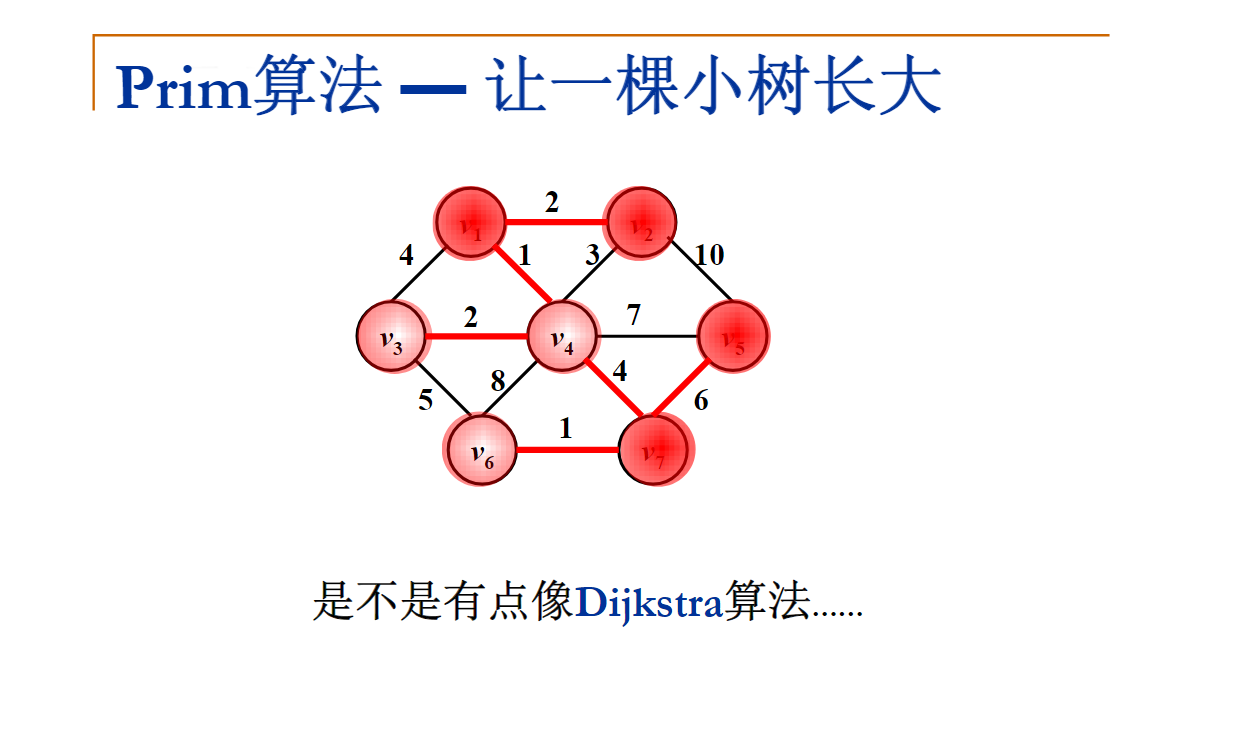

Prim算法中的dist[V]应该初始化为E(s,V) 或 正无穷
邻接矩阵存储 - Prim最小生成树算法
/* 邻接矩阵存储 - Prim最小生成树算法 */
Vertex FindMinDist( MGraph Graph, WeightType dist[] )
{ /* 返回未被收录顶点中dist最小者 */
Vertex MinV, V;
WeightType MinDist = INFINITY;
for (V=0; V<Graph->Nv; V++) {
if ( dist[V]!=0 && dist[V]<MinDist) {
/* 若V未被收录,且dist[V]更小 */
MinDist = dist[V]; /* 更新最小距离 */
MinV = V; /* 更新对应顶点 */
}
}
if (MinDist < INFINITY) /* 若找到最小dist */
return MinV; /* 返回对应的顶点下标 */
else return ERROR; /* 若这样的顶点不存在,返回-1作为标记 */
}
int Prim( MGraph Graph, LGraph MST )
{ /* 将最小生成树保存为邻接表存储的图MST,返回最小权重和 */
WeightType dist[MaxVertexNum], TotalWeight;
Vertex parent[MaxVertexNum], V, W;
int VCount;
Edge E;
/* 初始化。默认初始点下标是0 */
for (V=0; V<Graph->Nv; V++) {
/* 这里假设若V到W没有直接的边,则Graph->G[V][W]定义为INFINITY */
dist[V] = Graph->G[0][V];
parent[V] = 0; /* 暂且定义所有顶点的父结点都是初始点0 */
}
TotalWeight = 0; /* 初始化权重和 */
VCount = 0; /* 初始化收录的顶点数 */
/* 创建包含所有顶点但没有边的图。注意用邻接表版本 */
MST = CreateGraph(Graph->Nv);
E = (Edge)malloc( sizeof(struct ENode) ); /* 建立空的边结点 */
/* 将初始点0收录进MST */
dist[0] = 0;
VCount ++;
parent[0] = -1; /* 当前树根是0 */
while (1) {
V = FindMinDist( Graph, dist );
/* V = 未被收录顶点中dist最小者 */
if ( V==ERROR ) /* 若这样的V不存在 */
break; /* 算法结束 */
/* 将V及相应的边<parent[V], V>收录进MST */
E->V1 = parent[V];
E->V2 = V;
E->Weight = dist[V];
InsertEdge( MST, E );
TotalWeight += dist[V];
dist[V] = 0;
VCount++;
for( W=0; W<Graph->Nv; W++ ) /* 对图中的每个顶点W */
if ( dist[W]!=0 && Graph->G[V][W]<INFINITY ) {
/* 若W是V的邻接点并且未被收录 */
if ( Graph->G[V][W] < dist[W] ) {
/* 若收录V使得dist[W]变小 */
dist[W] = Graph->G[V][W]; /* 更新dist[W] */
parent[W] = V; /* 更新树 */
}
}
} /* while结束*/
if ( VCount < Graph->Nv ) /* MST中收的顶点不到|V|个 */
TotalWeight = ERROR;
return TotalWeight; /* 算法执行完毕,返回最小权重和或错误标记 */
}
Kruskal算法
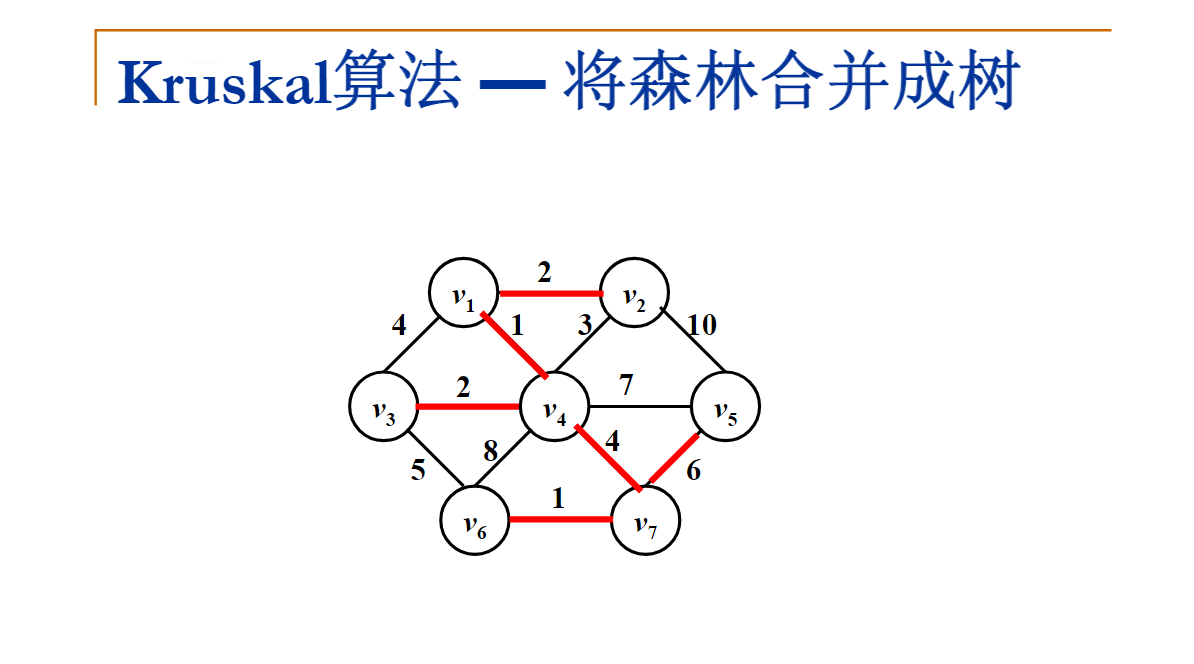

邻接表存储 - Kruskal最小生成树算法
/* 邻接表存储 - Kruskal最小生成树算法 */
/*-------------------- 顶点并查集定义 --------------------*/
typedef Vertex ElementType; /* 默认元素可以用非负整数表示 */
typedef Vertex SetName; /* 默认用根结点的下标作为集合名称 */
typedef ElementType SetType[MaxVertexNum]; /* 假设集合元素下标从0开始 */
void InitializeVSet( SetType S, int N )
{ /* 初始化并查集 */
ElementType X;
for ( X=0; X<N; X++ ) S[X] = -1;
}
void Union( SetType S, SetName Root1, SetName Root2 )
{ /* 这里默认Root1和Root2是不同集合的根结点 */
/* 保证小集合并入大集合 */
if ( S[Root2] < S[Root1] ) { /* 如果集合2比较大 */
S[Root2] += S[Root1]; /* 集合1并入集合2 */
S[Root1] = Root2;
}
else { /* 如果集合1比较大 */
S[Root1] += S[Root2]; /* 集合2并入集合1 */
S[Root2] = Root1;
}
}
SetName Find( SetType S, ElementType X )
{ /* 默认集合元素全部初始化为-1 */
if ( S[X] < 0 ) /* 找到集合的根 */
return X;
else
return S[X] = Find( S, S[X] ); /* 路径压缩 */
}
bool CheckCycle( SetType VSet, Vertex V1, Vertex V2 )
{ /* 检查连接V1和V2的边是否在现有的最小生成树子集中构成回路 */
Vertex Root1, Root2;
Root1 = Find( VSet, V1 ); /* 得到V1所属的连通集名称 */
Root2 = Find( VSet, V2 ); /* 得到V2所属的连通集名称 */
if( Root1==Root2 ) /* 若V1和V2已经连通,则该边不能要 */
return false;
else { /* 否则该边可以被收集,同时将V1和V2并入同一连通集 */
Union( VSet, Root1, Root2 );
return true;
}
}
/*-------------------- 并查集定义结束 --------------------*/
/*-------------------- 边的最小堆定义 --------------------*/
void PercDown( Edge ESet, int p, int N )
{ /* 改编代码4.24的PercDown( MaxHeap H, int p ) */
/* 将N个元素的边数组中以ESet[p]为根的子堆调整为关于Weight的最小堆 */
int Parent, Child;
struct ENode X;
X = ESet[p]; /* 取出根结点存放的值 */
for( Parent=p; (Parent*2+1)<N; Parent=Child ) {
Child = Parent * 2 + 1;
if( (Child!=N-1) && (ESet[Child].Weight>ESet[Child+1].Weight) )
Child++; /* Child指向左右子结点的较小者 */
if( X.Weight <= ESet[Child].Weight ) break; /* 找到了合适位置 */
else /* 下滤X */
ESet[Parent] = ESet[Child];
}
ESet[Parent] = X;
}
void InitializeESet( LGraph Graph, Edge ESet )
{ /* 将图的边存入数组ESet,并且初始化为最小堆 */
Vertex V;
PtrToAdjVNode W;
int ECount;
/* 将图的边存入数组ESet */
ECount = 0;
for ( V=0; V<Graph->Nv; V++ )
for ( W=Graph->G[V].FirstEdge; W; W=W->Next )
if ( V < W->AdjV ) { /* 避免重复录入无向图的边,只收V1<V2的边 */
ESet[ECount].V1 = V;
ESet[ECount].V2 = W->AdjV;
ESet[ECount++].Weight = W->Weight;
}
/* 初始化为最小堆 */
for ( ECount=Graph->Ne/2; ECount>=0; ECount-- )
PercDown( ESet, ECount, Graph->Ne );
}
int GetEdge( Edge ESet, int CurrentSize )
{ /* 给定当前堆的大小CurrentSize,将当前最小边位置弹出并调整堆 */
/* 将最小边与当前堆的最后一个位置的边交换 */
Swap( &ESet[0], &ESet[CurrentSize-1]);
/* 将剩下的边继续调整成最小堆 */
PercDown( ESet, 0, CurrentSize-1 );
return CurrentSize-1; /* 返回最小边所在位置 */
}
/*-------------------- 最小堆定义结束 --------------------*/
int Kruskal( LGraph Graph, LGraph MST )
{ /* 将最小生成树保存为邻接表存储的图MST,返回最小权重和 */
WeightType TotalWeight;
int ECount, NextEdge;
SetType VSet; /* 顶点数组 */
Edge ESet; /* 边数组 */
InitializeVSet( VSet, Graph->Nv ); /* 初始化顶点并查集 */
ESet = (Edge)malloc( sizeof(struct ENode)*Graph->Ne );
InitializeESet( Graph, ESet ); /* 初始化边的最小堆 */
/* 创建包含所有顶点但没有边的图。注意用邻接表版本 */
MST = CreateGraph(Graph->Nv);
TotalWeight = 0; /* 初始化权重和 */
ECount = 0; /* 初始化收录的边数 */
NextEdge = Graph->Ne; /* 原始边集的规模 */
while ( ECount < Graph->Nv-1 ) { /* 当收集的边不足以构成树时 */
NextEdge = GetEdge( ESet, NextEdge ); /* 从边集中得到最小边的位置 */
if (NextEdge < 0) /* 边集已空 */
break;
/* 如果该边的加入不构成回路,即两端结点不属于同一连通集 */
if ( CheckCycle( VSet, ESet[NextEdge].V1, ESet[NextEdge].V2 )==true ) {
/* 将该边插入MST */
InsertEdge( MST, ESet+NextEdge );
TotalWeight += ESet[NextEdge].Weight; /* 累计权重 */
ECount++; /* 生成树中边数加1 */
}
}
if ( ECount < Graph->Nv-1 )
TotalWeight = -1; /* 设置错误标记,表示生成树不存在 */
return TotalWeight;
}
拓扑排序和关键路径
AOV网络和拓扑排序
定义
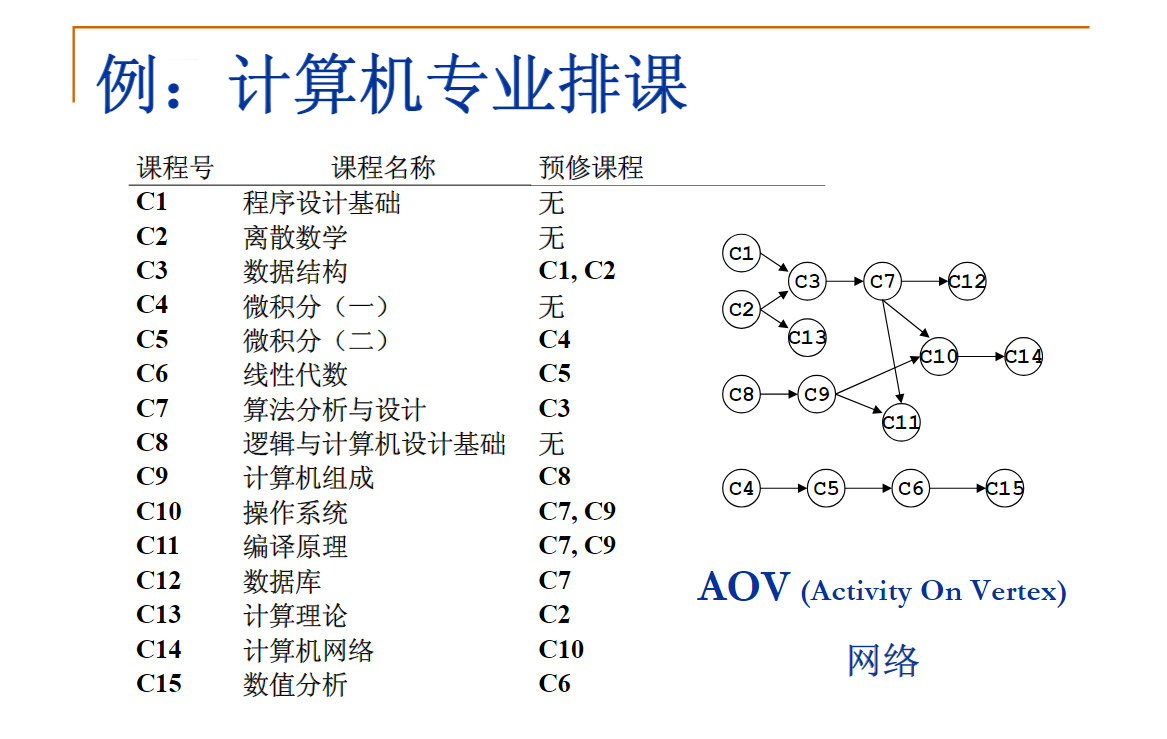

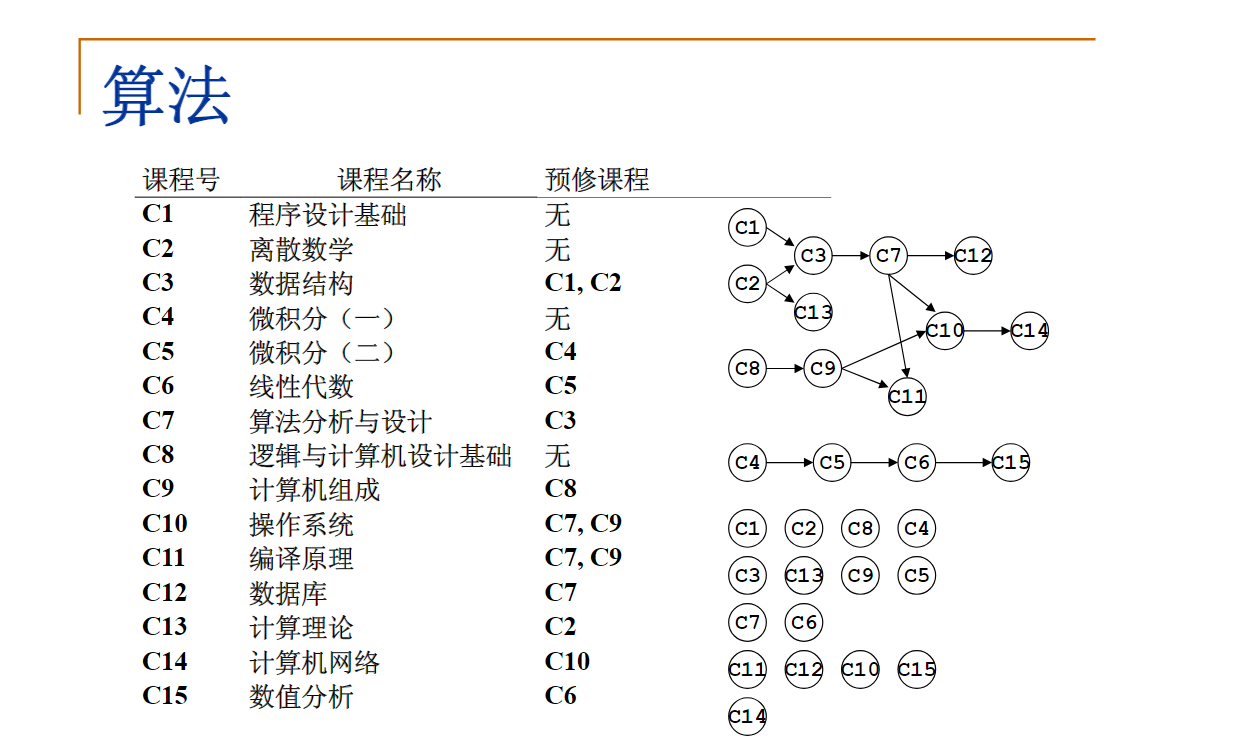


在TopSort函数中,如果外循环还没结束,就已经找不到“未输出的入度为0的顶点”,则说明图中必定存在回路。
容器的影响
分别用队列和堆栈作为容器,对计算机专业课程进行拓扑排序,得到的序列有什么区别?用哪种容器排课更合理?
队列拓扑排序得到的结果是从上到下的顺序,类似于一层一层地拓扑排序。 堆栈拓扑排序得到的结果是从下到上的顺序,类似于逆序的拓扑排序。 选择合理的容器: 如果你希望按照正常的学习顺序,从基础课程开始,逐渐深入,那么队列拓扑排序更合理。 如果你更关注最终课程的先修条件,或者希望从高级课程逆向推导,那么堆栈拓扑排序更合理。
分别用队列和堆栈作为容器,对计算机专业课程进行拓扑排序,得到的序列有什么区别?用哪种容器排课更合理?
在进行拓扑排序时,可以使用队列或堆栈作为辅助容器。这两种方法都能够正确地产生拓扑排序,但得到的序列可能会不同,这取决于容器的数据结构特性。
使用队列进行拓扑排序
当使用队列进行拓扑排序时,通常是实现了所谓的Kahn算法。这种方法是基于入度(指向某个顶点的边的数量)的概念:
首先将所有入度为0的顶点加入队列。
然后依次从队列中取出一个顶点,将其添加到排序结果中,并移除所有从该顶点出发的边,更新相关顶点的入度。
如果某个顶点的入度变为0,则将其加入队列。
重复步骤2和3,直到队列为空。
使用队列的拓扑排序通常产生多种合法的排序结果,对于同一张图,不同的顶点加入队列的顺序可能会产生不同的拓扑排序序列。
使用堆栈进行拓扑排序
使用堆栈进行拓扑排序通常是基于深度优先搜索(DFS):
对每个尚未访问的顶点,执行DFS。
在DFS的过程中,当从某个顶点出发的所有边都被探索过后,将该顶点压入堆栈。
DFS完成后,依次从堆栈中弹出顶点,这个顺序就是拓扑排序的结果。
这种方法也可能产生多种拓扑排序,具体结果取决于DFS的顺序。
哪种方法更合理?
在排课程时,选择哪种方法取决于具体的需求:
如果你想要的是一种可能的顺序,并且希望尽快开始没有先决条件的课程(即入度为0的课程),那么使用基于队列的Kahn算法更合适。
如果你对课程之间的依赖关系有更深入的探究,或者对课程的探索顺序有特定需求,使用基于DFS的堆栈方法可能更合适。
在大多数情况下,使用队列的方法更直观,因为它直接处理了课程之间的依赖关系。然而,最终的选择应该基于具体场景和需求。
邻接表存储——拓扑排序算法
/* 邻接表存储 - 拓扑排序算法 */
bool TopSort( LGraph Graph, Vertex TopOrder[] )
{ /* 对Graph进行拓扑排序, TopOrder[]顺序存储排序后的顶点下标 */
int Indegree[MaxVertexNum], cnt;
Vertex V;
PtrToAdjVNode W;
Queue Q = CreateQueue( Graph->Nv );
/* 初始化Indegree[] */
for (V=0; V<Graph->Nv; V++)
Indegree[V] = 0;
/* 遍历图,得到Indegree[] */
for (V=0; V<Graph->Nv; V++)
for (W=Graph->G[V].FirstEdge; W; W=W->Next)
Indegree[W->AdjV]++; /* 对有向边<V, W->AdjV>累计终点的入度 */
/* 将所有入度为0的顶点入列 */
for (V=0; V<Graph->Nv; V++)
if ( Indegree[V]==0 )
AddQ(Q, V);
/* 下面进入拓扑排序 */
cnt = 0;
while( !IsEmpty(Q) ){
V = DeleteQ(Q); /* 弹出一个入度为0的顶点 */
TopOrder[cnt++] = V; /* 将之存为结果序列的下一个元素 */
/* 对V的每个邻接点W->AdjV */
for ( W=Graph->G[V].FirstEdge; W; W=W->Next )
if ( --Indegree[W->AdjV] == 0 )/* 若删除V使得W->AdjV入度为0 */
AddQ(Q, W->AdjV); /* 则该顶点入列 */
} /* while结束*/
if ( cnt != Graph->Nv )
return false; /* 说明图中有回路, 返回不成功标志 */
else
return true;
}
邻接表存储——拓扑排序算法实例
#include <stdio.h>
#include <stdlib.h>
#define MaxVertexNum 100
typedef int WeightType;
typedef int Vertex;
typedef struct ENode *PtrToENode;
struct ENode
{
Vertex V1;
Vertex V2;
WeightType Weight;
};
typedef PtrToENode Edge;
typedef struct AdjVNode *PtrToAdjVNode;
struct AdjVNode
{
PtrToAdjVNode Next;
Vertex AdjV;
WeightType Weight;
};
typedef struct VNode
{
PtrToAdjVNode FirstEdge;
}AdjList[MaxVertexNum];
typedef struct GNode *PtrToGNode;
struct GNode
{
int Ne;
int Nv;
AdjList G;
};
typedef PtrToGNode LGraph;
void InsertEdge(LGraph Graph, Edge E)
{
PtrToAdjVNode newNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
newNode->AdjV = E->V2;
newNode->Weight = E->Weight;
newNode->Next = Graph->G[E->V1].FirstEdge;
Graph->G[E->V1].FirstEdge = newNode;
//newNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
//newNode->AdjV = E->V1;
//newNode->Weight = E->Weight;
//newNode->Next = Graph->G[E->V2].FirstEdge;
//Graph->G[E->V2].FirstEdge = newNode;
}
LGraph CreateGraph(int VertexNum)
{
LGraph Graph = (LGraph)malloc(sizeof(struct GNode));
Graph->Nv = VertexNum;
Graph->Ne = 0;
for(int i=0; i<Graph->Nv; i++)
Graph->G[i].FirstEdge = NULL;
return Graph;
}
LGraph BuildGraph()
{
int N;
Edge E;
scanf("%d",&N);
LGraph Graph = CreateGraph(N);
scanf("%d",&Graph->Ne);
if(Graph->Ne != 0)
{
for(int i=0; i<Graph->Ne; i++)
{
E = (Edge)malloc(sizeof(struct ENode));
scanf("%d %d %d",&E->V1,&E->V2,&E->Weight);
InsertEdge(Graph, E);
}
}
return Graph;
}
void TopSort(LGraph Graph, int TopOrder[])
{
int Indegree[MaxVertexNum], count;
Vertex V;
PtrToAdjVNode W;
//Queue Q = CreateQueue( Graph->Nv );
Vertex queue[Graph->Nv];
int front = 0;
int rear = 0;
for (V=0; V<Graph->Nv; V++)
Indegree[V] = 0;
for(V=0; V<Graph->Nv; V++)
{
for(W=Graph->G[V].FirstEdge; W; W=W->Next)
{
Indegree[W->AdjV]++;
}
}
for(V=0; V<Graph->Nv; V++)
{
if(Indegree[V] == 0)
{
queue[rear++] = V;
}
}
//下面进入拓扑排序
count = 0;
while(front != rear)
{
V = queue[front++];
TopOrder[count++] = V;
for(W=Graph->G[V].FirstEdge; W; W=W->Next)
{
if(--Indegree[W->AdjV] == 0)
{
queue[rear++] = W->AdjV;
}
}
}
if(count != Graph->Nv)
{
printf("图中存在循环路径!\n");
}
else
{
for(int i=0; i<count; i++)
printf("%d ",TopOrder[i]);
}
}
int main()
{
LGraph Graph = BuildGraph();
Vertex TopOrder[MaxVertexNum];
TopSort(Graph, TopOrder);
return 0;
}
输入数据:
6
7
0 2 1
1 2 1
1 0 1
2 5 1
2 3 1
3 5 1
4 5 1
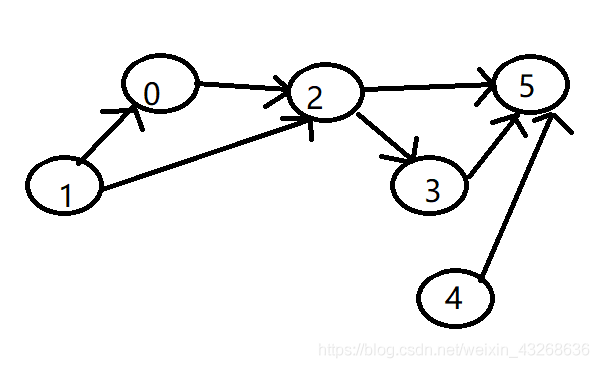
输出结果:
1 4 0 2 3 5
说明一下,拓扑排序可能有多种结果。
另一种结果可以是4 1 0 2 3 5。
#include <stdio.h>
#include <stdlib.h>
#define MaxVertexNum 100
typedef int WeightType;
typedef int Vertex;
typedef struct ENode *PtrToENode;
struct ENode
{
Vertex V1;
Vertex V2;
WeightType Weight;
};
typedef PtrToENode Edge;
typedef struct AdjVNode *PtrToAdjVNode;
struct AdjVNode
{
PtrToAdjVNode Next;
Vertex AdjV;
WeightType Weight;
};
typedef struct VNode
{
PtrToAdjVNode FirstEdge;
}AdjList[MaxVertexNum];
typedef struct GNode *PtrToGNode;
struct GNode
{
int Ne;
int Nv;
AdjList G;
};
typedef PtrToGNode LGraph;
void InsertEdge(LGraph Graph, Edge E)
{
PtrToAdjVNode newNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
newNode->AdjV = E->V2;
newNode->Weight = E->Weight;
newNode->Next = Graph->G[E->V1].FirstEdge;
Graph->G[E->V1].FirstEdge = newNode;
//newNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
//newNode->AdjV = E->V1;
//newNode->Weight = E->Weight;
//newNode->Next = Graph->G[E->V2].FirstEdge;
//Graph->G[E->V2].FirstEdge = newNode;
}
LGraph CreateGraph(int VertexNum)
{
LGraph Graph = (LGraph)malloc(sizeof(struct GNode));
Graph->Nv = VertexNum;
Graph->Ne = 0;
for(int i=0; i<Graph->Nv; i++)
Graph->G[i].FirstEdge = NULL;
return Graph;
}
LGraph BuildGraph()
{
int N;
Edge E;
scanf("%d",&N);
LGraph Graph = CreateGraph(N);
scanf("%d",&Graph->Ne);
if(Graph->Ne != 0)
{
for(int i=0; i<Graph->Ne; i++)
{
E = (Edge)malloc(sizeof(struct ENode));
scanf("%d %d %d",&E->V1,&E->V2,&E->Weight);
InsertEdge(Graph, E);
}
}
return Graph;
}
void PrintList(LGraph Graph)
{
for(int i=0; i<Graph->Nv; i++)
{
PtrToAdjVNode W = Graph->G[i].FirstEdge;
printf("G[%d]:", i);
int IsFirst = 1;
while(W)
{
if(IsFirst)
{
printf("%d", W->AdjV);
IsFirst = 0;
}
else
printf("->%d", W->AdjV);
W = W->Next;
}
printf("\n");
}
}
void TopSort(LGraph Graph, int TopOrder[])
{
int Indegree[MaxVertexNum], count;
Vertex V;
PtrToAdjVNode W;
//Queue Q = CreateQueue( Graph->Nv );
Vertex queue[Graph->Nv];
int front = 0;
int rear = 0;
for (V=0; V<Graph->Nv; V++)
Indegree[V] = 0;
for(V=0; V<Graph->Nv; V++)
{
for(W=Graph->G[V].FirstEdge; W; W=W->Next)
{
Indegree[W->AdjV]++;
}
}
for(V=0; V<Graph->Nv; V++)
{
if(Indegree[V] == 0)
{
queue[rear++] = V;
}
}
//下面进入拓扑排序
count = 0;
while(front != rear)
{
V = queue[front++];
TopOrder[count++] = V;
for(W=Graph->G[V].FirstEdge; W; W=W->Next)
{
if(--Indegree[W->AdjV] == 0)
{
queue[rear++] = W->AdjV;
}
}
}
if(count != Graph->Nv)
{
printf("图中存在循环路径!\n");
}
else
{
for(int i=0; i<count; i++)
printf("%d ",TopOrder[i]);
}
}
int main()
{
LGraph Graph = BuildGraph();
PrintList(Graph);
Vertex TopOrder[MaxVertexNum];
TopSort(Graph, TopOrder);
return 0;
}
输入数据:
6
7
0 2 1
1 0 1
2 1 1
2 5 1
2 3 1
3 5 1
4 5 1
输出结果:
G[0]:2
G[1]:0
G[2]:3->5->1
G[3]:5
G[4]:5
G[5]:
图中存在循环路径!
AOE网络和关键路径
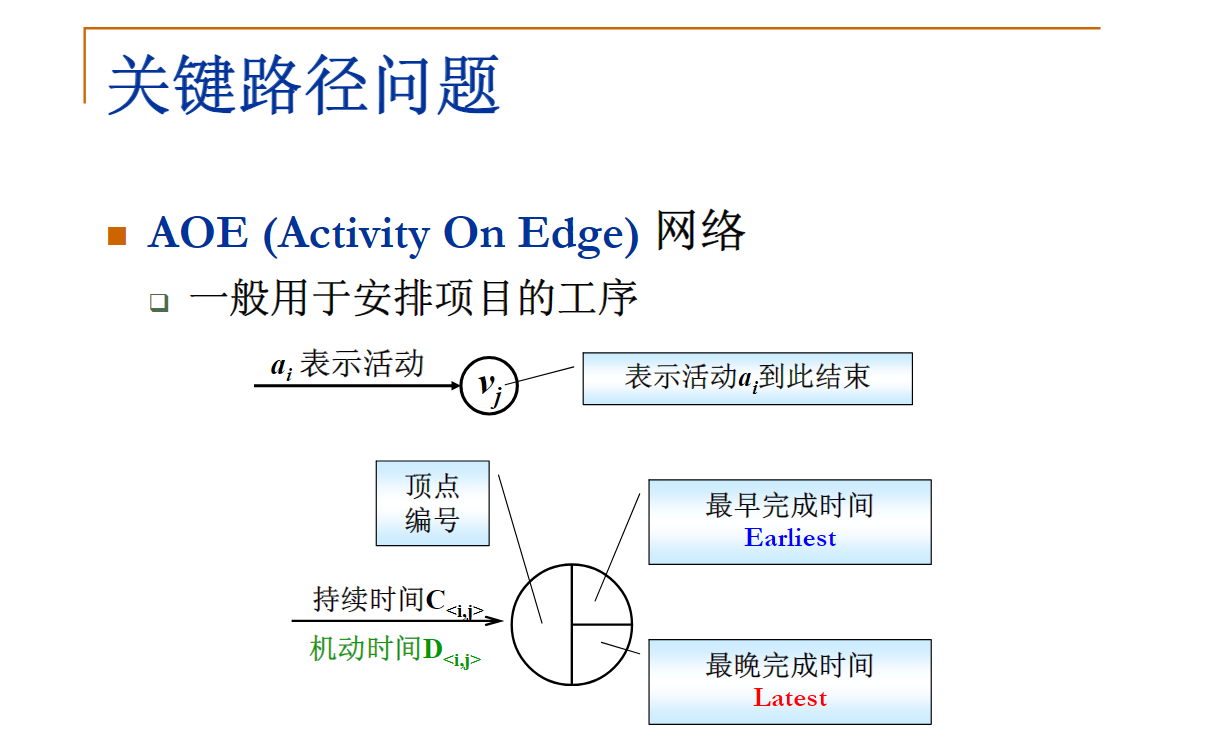
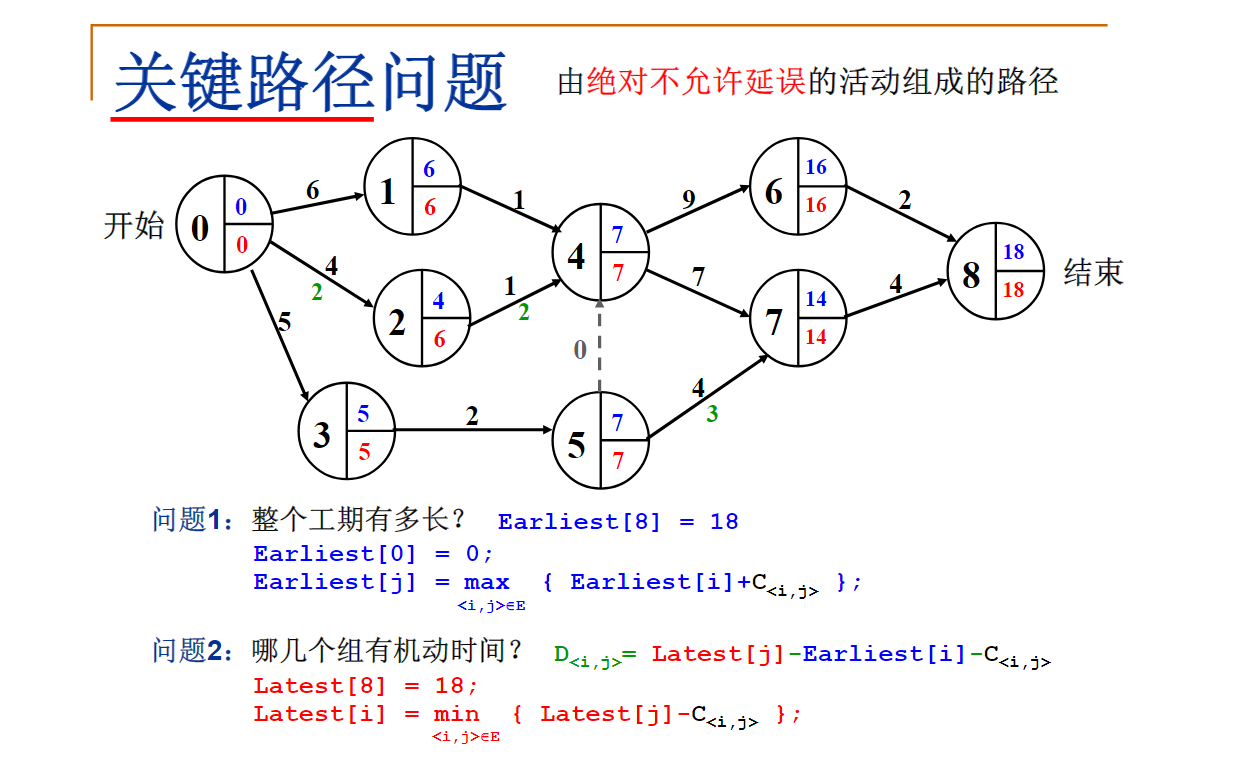
下图给定了一个项目的AOE。整个项目最早完工需要的时间是

- A.17
- B.19
- C.20
- D.23
正确答案:D你选对了
2在上图中,如果<0,2>组能加快进度,整个项目就能提前完工。
✔
正确答案:A你选对了
MOOC-PTA图题目
- PTA 06-图1 列出连通集
- PTA 06-图2 Saving James Bond - Easy Version
- PTA 06-图3 六度空间
- PTA 07-图4 哈利·波特的考试
- PTA 07-图5 Saving James Bond - Hard Version
- PTA 07-图6 旅游规划
- PTA 08-图7 公路村村通
- PTA 08-图8 How Long Does It Take
- PTA 08-图9 关键活动
PTA 06-图1 列出连通集
给定一个有N个顶点和E条边的无向图,请用DFS和BFS分别列出其所有的连通集。假设顶点从0到N−1编号。进行搜索时,假设我们总是从编号最小的顶点出发,按编号递增的顺序访问邻接点。
输入格式:
输入第1行给出2个整数N(0<N≤10)和E,分别是图的顶点数和边数。随后E行,每行给出一条边的两个端点。每行中的数字之间用1空格分隔。
输出格式:
按照"{ v1 v2 ... vk }"的格式,每行输出一个连通集。先输出DFS的结果,再输出BFS的结果。
输入样例:
8 6
0 7
0 1
2 0
4 1
2 4
3 5
输出样例:
{ 0 1 4 2 7 }
{ 3 5 }
{ 6 }
{ 0 1 2 7 4 }
{ 3 5 }
{ 6 }
#include <stdio.h>
#include <stdlib.h>
#define MAXN 100
int G[MAXN][MAXN], Nv, Ne;
void BuildGraph()
{
int i,j,v1,v2,w;
scanf("%d",&Nv);
for(i=0; i<Nv; i++)
{
for(j=0; j<Nv; j++)
{
G[i][j] = 0;
}
}
scanf("%d",&Ne);
for(i=0; i<Ne; i++)
{
scanf("%d %d",&v1,&v2);
G[v1][v2] = 1;
G[v2][v1] = 1;
}
}
void printGraph()
{
for(int i=0;i < Nv; i++)
{
for(int j=0; j<Nv; j++)
{
printf("%d ", G[i][j]);
}
printf("\n");
}
}
typedef int Vertex;
#define TRUE 1
#define FALSE 0
typedef int Boolean;
Boolean visited[MAXN];
Boolean IsFirst = TRUE;
void dfs(Vertex V)
{
visited[V] = TRUE;
if(IsFirst)
{
printf("%d",V);
IsFirst = FALSE;
}
else
printf(" %d",V);
for(int j=0; j<Nv; j++)
{
if(G[V][j]==1 && visited[j] == FALSE)
dfs(j);
}
}
void bfs(Vertex V)
{
int queue[100];
int front = 0;
int tail = 0;
visited[V] = TRUE;
queue[tail++] = V;
int temp;
while(front != tail)
{
temp = queue[front++];
if(IsFirst)
{
printf("%d", temp);
IsFirst = FALSE;
}
else
printf(" %d",temp);
for(int i=0;i <Nv; i++)
{
if(G[temp][i] == 1 && visited[i] == FALSE)
{
visited[i] = TRUE;
queue[tail++] = i;
}
}
}
}
int main()
{
BuildGraph();
//printGraph();
for(int i=0; i<Nv;i++)
{
if(visited[i] == FALSE)
{
printf("{ ");
dfs(i);
printf(" }\n");
}
IsFirst = TRUE;
}
for(int i=0; i<Nv; i++)
visited[i] = FALSE;
for(int i=0; i<Nv;i++)
{
if(visited[i] == FALSE)
{
printf("{ ");
bfs(i);
printf(" }\n");
}
IsFirst = TRUE;
}
return 0;
}
PTA 06-图2 Saving James Bond - Easy Version
This time let us consider the situation in the movie "Live and Let Die" in which James Bond, the world's most famous spy, was captured by a group of drug dealers. He was sent to a small piece of land at the center of a lake filled with crocodiles. There he performed the most daring action to escape -- he jumped onto the head of the nearest crocodile! Before the animal realized what was happening, James jumped again onto the next big head... Finally he reached the bank before the last crocodile could bite him (actually the stunt man was caught by the big mouth and barely escaped with his extra thick boot).
Assume that the lake is a 100 by 100 square one. Assume that the center of the lake is at (0,0) and the northeast corner at (50,50). The central island is a disk centered at (0,0) with the diameter of 15. A number of crocodiles are in the lake at various positions. Given the coordinates of each crocodile and the distance that James could jump, you must tell him whether or not he can escape.
Input Specification:
Each input file contains one test case. Each case starts with a line containing two positive integers N (≤100), the number of crocodiles, and D, the maximum distance that James could jump. Then N lines follow, each containing the (x,y) location of a crocodile. Note that no two crocodiles are staying at the same position.
Output Specification:
For each test case, print in a line "Yes" if James can escape, or "No" if not.
Sample Input 1:
14 20
25 -15
-25 28
8 49
29 15
-35 -2
5 28
27 -29
-8 -28
-20 -35
-25 -20
-13 29
-30 15
-35 40
12 12
Sample Output 1:
Yes
Sample Input 2:
4 13
-12 12
12 12
-12 -12
12 -12
Sample Output 2:
No


#include <stdio.h>
#include <stdlib.h>
#define MAXN 100
#define TRUE 1
#define FALSE 0
typedef int Boolean;
Boolean visited[MAXN];
struct coordinate
{
int x;
int y;
}Points[MAXN];
int D = 0;
/*初始化标记矩阵*/
void ResetVisit()
{
for(int i=0;i<MAXN;i++)
visited[i]=0;
}
Boolean FirstJump(int i)
{
int x = Points[i].x;
int y = Points[i].y;
if((7.5+D)*(7.5+D) >= (x*x + y*y))
{
return TRUE;
}
else
{
return FALSE;
}
}
Boolean Jump(int i, int j)
{
int x1 = Points[i].x;
int y1 = Points[i].y;
int x2 = Points[j].x;
int y2 = Points[j].y;
if(D*D >= ((x1-x2)*(x1-x2) + (y1-y2)*(y1-y2)))
{
return TRUE;
}
else
{
return FALSE;
}
}
Boolean IsSafe(int i)
{
int x = Points[i].x;
int y = Points[i].y;
if(x<0)
x = -x;
if(y<0)
y = -y;
if(50-x<=D || 50-y<=D)
return TRUE;
else
return FALSE;
}
Boolean dfs(int i)
{
visited[i] = TRUE;
int answer;
if(IsSafe(i))
answer = TRUE;
else
{
for(int j=0; j<MAXN; j++)
{
//如果j节点未被访问,且能从j结点跳至j结点
if(Jump(i,j) && visited[j]!=TRUE)
{
answer = dfs(j);
if(answer == TRUE)
break;
}
}
}
return answer;
}
void Save007()
{
int answer;
ResetVisit();
for(int i=0; i<MAXN; i++)
{
if(FirstJump(i) && visited[i]!=TRUE)
{
answer = dfs(i);
if(answer==TRUE)
break;
}
}
if(answer==TRUE)
printf("Yes\n");
else
printf("No\n");
}
int main()
{
int N;
scanf("%d %d",&N,&D);
for(int i=0; i<N; i++)
{
scanf("%d %d",&(Points[i].x),&(Points[i].y));
}
Save007();
return 0;
}
PTA 06-图3 六度空间
“六度空间”理论又称作“六度分隔(Six Degrees of Separation)”理论。这个理论可以通俗地阐述为:“你和任何一个陌生人之间所间隔的人不会超过六个,也就是说,最多通过五个人你就能够认识任何一个陌生人。”如图1所示。
图1 六度空间示意图
“六度空间”理论虽然得到广泛的认同,并且正在得到越来越多的应用。但是数十年来,试图验证这个理论始终是许多社会学家努力追求的目标。然而由于历史的原因,这样的研究具有太大的局限性和困难。随着当代人的联络主要依赖于电话、短信、微信以及因特网上即时通信等工具,能够体现社交网络关系的一手数据已经逐渐使得“六度空间”理论的验证成为可能。
假如给你一个社交网络图,请你对每个节点计算符合“六度空间”理论的结点占结点总数的百分比。
输入格式:
输入第1行给出两个正整数,分别表示社交网络图的结点数N(1<N≤10^3,表示人数)、边数M(≤33×N,表示社交关系数)。随后的M行对应M条边,每行给出一对正整数,分别是该条边直接连通的两个结点的编号(节点从1到N编号)。
输出格式:
对每个结点输出与该结点距离不超过6的结点数占结点总数的百分比,精确到小数点后2位。每个结节点输出一行,格式为“结点编号:(空格)百分比%”。
输入样例:
10 9
1 2
2 3
3 4
4 5
5 6
6 7
7 8
8 9
9 10
输出样例:
1: 70.00%
2: 80.00%
3: 90.00%
4: 100.00%
5: 100.00%
6: 100.00%
7: 100.00%
8: 90.00%
9: 80.00%
10: 70.00%

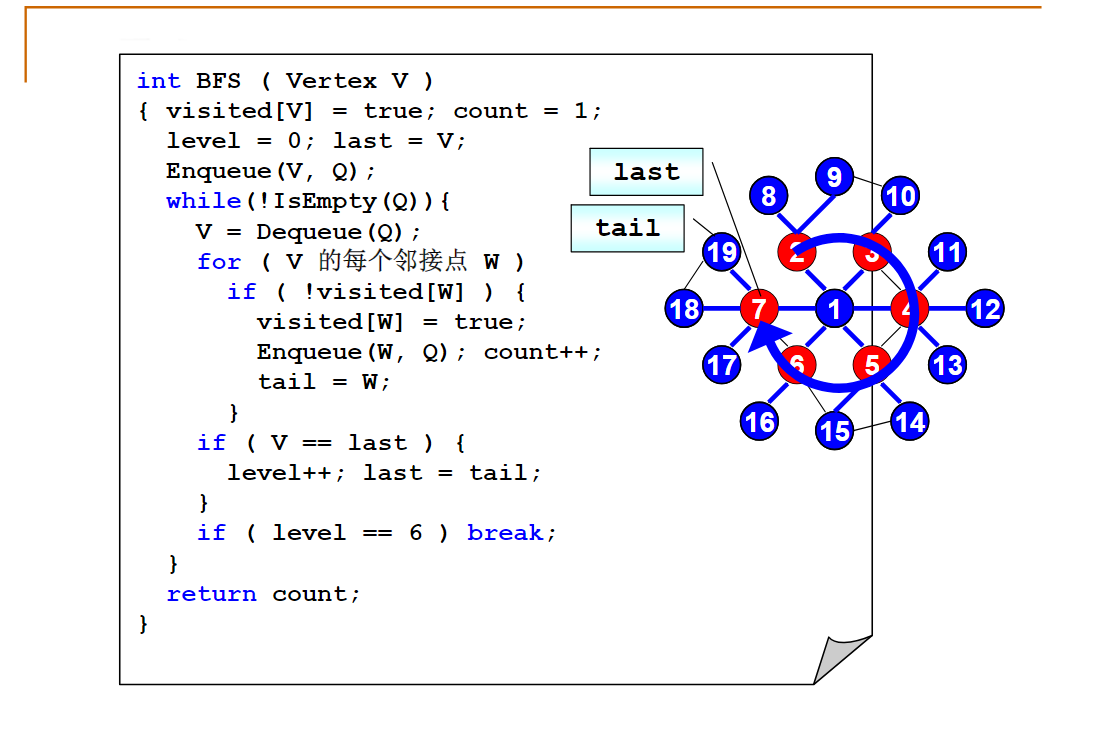
注意:
- 不要忘记初始化,每个顶点统计完毕后都需要进行 /(ㄒoㄒ)/~~
- 统计结果的变量count需要设定初始值为1,因为该节点也满足统计要求
#include <stdio.h>
#include <stdlib.h>
#define TRUE 1
#define FALSE 0
int G[1001][1001];
int visited[1001];
int N = 0;
int last = 0;
int tail = 0;
void ResetVisited()
{
for(int i=0; i<1001; i++)
visited[i] = 0;
}
int bfs(int v)
{
visited[v] = TRUE;
int count = 1;
int level = 0;
last = v;
tail = 0;
int queue[1001];
int front = 0;
int rear = 0;
queue[rear++] = v;
while(rear != front)
{
int temp = queue[front++];
for(int i=1; i<=N; i++)
{
if(visited[i]==FALSE && G[temp][i]==1)
{
visited[i] = TRUE;
queue[rear++] = i;
tail = i;
count++;
}
}
if(temp == last)
{
level++;
last = tail;
}
if(level == 6)
break;
}
return count;
}
int main()
{
int M,v1,v2;
scanf("%d %d",&N,&M);
for(int i=0; i<N; i++)
{
for(int j=0; j<N; j++)
G[i][j] = 0;
}
for(int i=0; i<M; i++)
{
scanf("%d %d",&v1, &v2);
G[v1][v2] = 1;
G[v2][v1] = 1;
}
for(int i=1; i<=N; i++)
{
ResetVisited();
int count = bfs(i);
printf("%d: %.2f%%\n",i, count*1.0*100/N);
}
}
PTA 07-图4 哈利·波特的考试
哈利·波特要考试了,他需要你的帮助。这门课学的是用魔咒将一种动物变成另一种动物的本事。例如将猫变成老鼠的魔咒是haha,将老鼠变成鱼的魔咒是hehe等等。反方向变化的魔咒就是简单地将原来的魔咒倒过来念,例如ahah可以将老鼠变成猫。另外,如果想把猫变成鱼,可以通过念一个直接魔咒lalala,也可以将猫变老鼠、老鼠变鱼的魔咒连起来念:hahahehe。
现在哈利·波特的手里有一本教材,里面列出了所有的变形魔咒和能变的动物。老师允许他自己带一只动物去考场,要考察他把这只动物变成任意一只指定动物的本事。于是他来问你:带什么动物去可以让最难变的那种动物(即该动物变为哈利·波特自己带去的动物所需要的魔咒最长)需要的魔咒最短?例如:如果只有猫、鼠、鱼,则显然哈利·波特应该带鼠去,因为鼠变成另外两种动物都只需要念4个字符;而如果带猫去,则至少需要念6个字符才能把猫变成鱼;同理,带鱼去也不是最好的选择。
输入格式:
输入说明:输入第1行给出两个正整数N (≤100)和M,其中N是考试涉及的动物总数,M是用于直接变形的魔咒条数。为简单起见,我们将动物按1~N编号。随后M行,每行给出了3个正整数,分别是两种动物的编号、以及它们之间变形需要的魔咒的长度(≤100),数字之间用空格分隔。
输出格式:
输出哈利·波特应该带去考场的动物的编号、以及最长的变形魔咒的长度,中间以空格分隔。如果只带1只动物是不可能完成所有变形要求的,则输出0。如果有若干只动物都可以备选,则输出编号最小的那只。
输入样例:
6 11
3 4 70
1 2 1
5 4 50
2 6 50
5 6 60
1 3 70
4 6 60
3 6 80
5 1 100
2 4 60
5 2 80
输出样例:
4 70
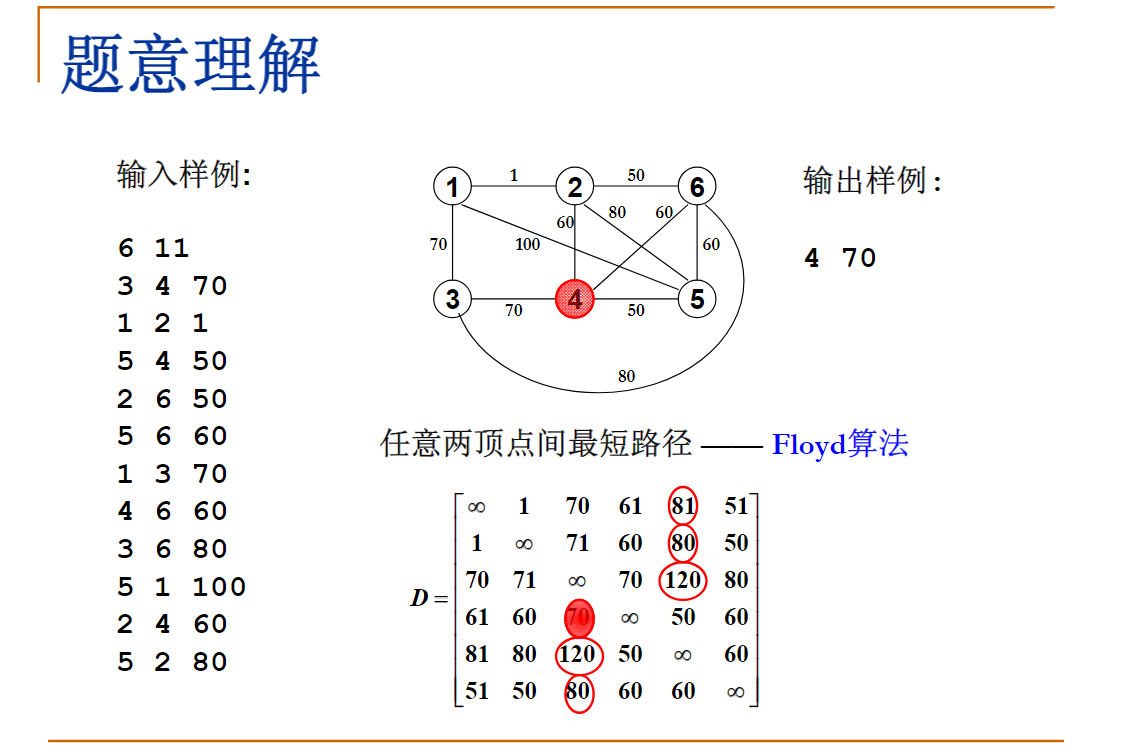
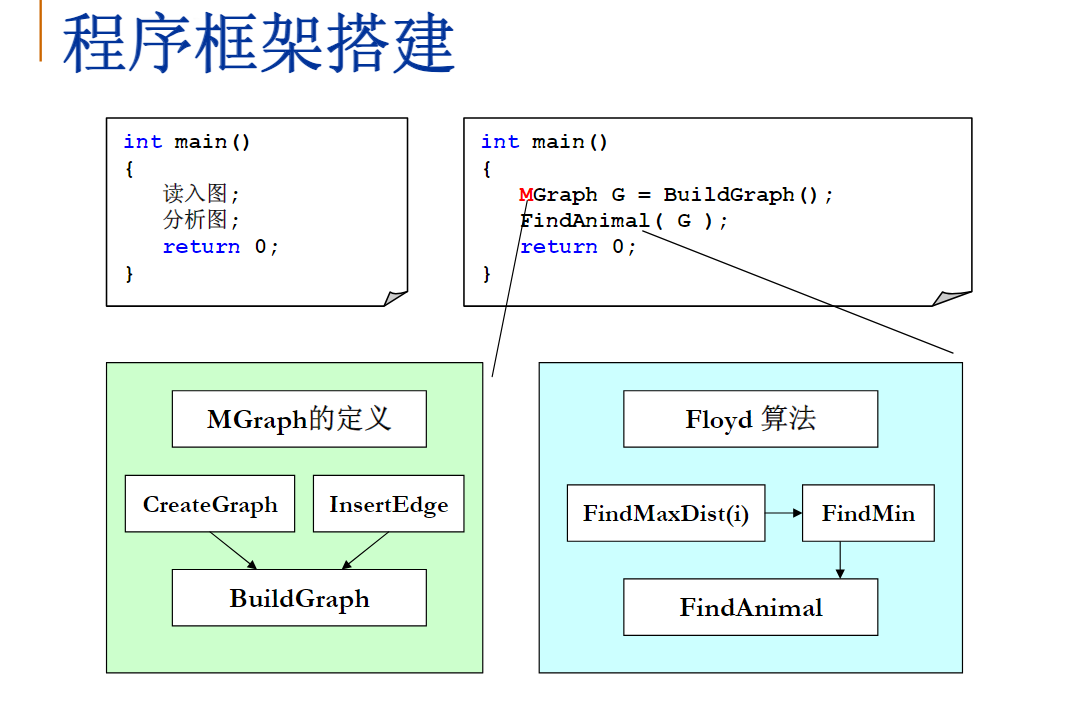
#include <stdio.h>
#include <stdlib.h>
#define MaxVertexNum 100
#define INFINITY 65535
typedef int Vertex;
typedef int WeightType;
typedef struct ENode *PtrToENode;
struct ENode
{
Vertex V1;
Vertex V2;
WeightType Weight;
};
typedef PtrToENode Edge;
typedef struct GNode *PtrToGNode;
struct GNode
{
int Nv;
int Ne;
WeightType G[MaxVertexNum][MaxVertexNum];
};
typedef PtrToGNode MGraph;
MGraph CreateGraph(int VertexNum)
{
MGraph Graph = (MGraph)malloc(sizeof(struct GNode));
Graph->Nv = VertexNum;
Graph->Ne = 0;
Vertex V1,V2;
for(Vertex V1=0; V1<Graph->Nv; V1++)
for(Vertex V2=0; V2<Graph->Nv; V2++)
Graph->G[V1][V2] = INFINITY;
return Graph;
}
void InsertEdge(MGraph Graph, Edge E)
{
Graph->G[E->V1][E->V2] = E->Weight;
Graph->G[E->V2][E->V1] = E->Weight;
}
MGraph BuildGraph()
{
int Nv;
Edge E;
scanf("%d", &Nv);
MGraph Graph = CreateGraph(Nv);
scanf("%d", &(Graph->Ne));
if((Graph->Ne) != 0)
{
E = (Edge)malloc(sizeof(struct ENode));
for(int i=0; i<Graph->Ne; i++)
{
scanf("%d %d %d",&E->V1,&E->V2,&E->Weight);
E->V1--;
E->V2--;
InsertEdge(Graph, E);
}
}
return Graph;
}
void Floyd(MGraph Graph, WeightType D[][MaxVertexNum])
{
Vertex i,j,k;
//初始化
for(i=0; i<Graph->Nv; i++)
for(j=0; j<Graph->Nv; j++)
D[i][j] = Graph->G[i][j];
for(k = 0; k < Graph->Nv; ++k){
for(i = 0; i < Graph->Nv; ++i){
for(j = 0; j < Graph->Nv; ++j){
if(D[i][k] + D[k][j] < D[i][j]){
D[i][j] = D[i][k] + D[k][j];
}
}
}
}
}
WeightType FindMaxDist(WeightType D[MaxVertexNum][MaxVertexNum], Vertex i, int N)
{
WeightType MaxDist = 0;
for(Vertex j=0; j<N; j++)
{
if(i!=j && D[i][j]>MaxDist)
MaxDist = D[i][j];
}
return MaxDist;
}
void FindAnimal(MGraph Graph)
{
WeightType D[MaxVertexNum][MaxVertexNum], MaxDist, MinDist;
Vertex Animal, i;
Floyd(Graph, D);
MinDist = INFINITY;
for(i=0; i<Graph->Nv; i++)
{
MaxDist = FindMaxDist(D, i, Graph->Nv);
if(MaxDist == INFINITY)
{
printf("0\n");
return;
}
if(MaxDist < MinDist)
{
MinDist = MaxDist;
Animal = i + 1;
}
}
printf("%d %d\n", Animal, MinDist);
}
int main()
{
MGraph Graph = BuildGraph();
FindAnimal(Graph);
return 0;
}
注意:Floyd算法中的三重循环顺序不能更改,写成下面这样就无法通过部分测试用例。
for(i=0; i<Graph->Nv; i++)
{
for(j=0; j<Graph->Nv; j++)
{
for(k=0; k<Graph->Nv; k++)
{
if(D[i][k] + D[k][j] < D[i][j])
{
D[i][j] = D[i][k] + D[k][j];
}
}
}
PTA 07-图5 Saving James Bond - Hard Version
This time let us consider the situation in the movie "Live and Let Die" in which James Bond, the world's most famous spy, was captured by a group of drug dealers. He was sent to a small piece of land at the center of a lake filled with crocodiles. There he performed the most daring action to escape -- he jumped onto the head of the nearest crocodile! Before the animal realized what was happening, James jumped again onto the next big head... Finally he reached the bank before the last crocodile could bite him (actually the stunt man was caught by the big mouth and barely escaped with his extra thick boot).
Assume that the lake is a 100 by 100 square one. Assume that the center of the lake is at (0,0) and the northeast corner at (50,50). The central island is a disk centered at (0,0) with the diameter of 15. A number of crocodiles are in the lake at various positions. Given the coordinates of each crocodile and the distance that James could jump, you must tell him a shortest path to reach one of the banks. The length of a path is the number of jumps that James has to make.
Input Specification:
Each input file contains one test case. Each case starts with a line containing two positive integers N (≤100), the number of crocodiles, and D, the maximum distance that James could jump. Then N lines follow, each containing the (x,y) location of a crocodile. Note that no two crocodiles are staying at the same position.
Output Specification:
For each test case, if James can escape, output in one line the minimum number of jumps he must make. Then starting from the next line, output the position (x,y) of each crocodile on the path, each pair in one line, from the island to the bank. If it is impossible for James to escape that way, simply give him 0 as the number of jumps. If there are many shortest paths, just output the one with the minimum first jump, which is guaranteed to be unique.
Sample Input 1:
17 15
10 -21
10 21
-40 10
30 -50
20 40
35 10
0 -10
-25 22
40 -40
-30 30
-10 22
0 11
25 21
25 10
10 10
10 35
-30 10
Sample Output 1:
4
0 11
10 21
10 35
Sample Input 2:
4 13
-12 12
12 12
-12 -12
12 -12
Sample Output 2:
0
思路:
单源无权图最短路径问题
我们可以看到 If there are many shortest paths, just output the one with the minimum first jump, which is guaranteed to be unique.(当有多条最短路时,输出第一跳最小的最短路) 首先需要对图中的相关顶点(鳄鱼坐标),按第一跳的距离从小到大排序。
从岛中心开始进行BFS,按第一跳从小到大的顺序收入顶点,在遍历顶点的过程中,实时记录各顶点到源点的距离(dist数组) 以及当前顶点的前一跳顶点(path数组),这样才能满足题目的输出要求。
PTA 07-图6 旅游规划
有了一张自驾旅游路线图,你会知道城市间的高速公路长度、以及该公路要收取的过路费。现在需要你写一个程序,帮助前来咨询的游客找一条出发地和目的地之间的最短路径。如果有若干条路径都是最短的,那么需要输出最便宜的一条路径。
输入格式:
输入说明:输入数据的第1行给出4个正整数N、M、S、D,其中N(2≤N≤500)是城市的个数,顺便假设城市的编号为0~(N−1);M是高速公路的条数;S是出发地的城市编号;D是目的地的城市编号。随后的M行中,每行给出一条高速公路的信息,分别是:城市1、城市2、高速公路长度、收费额,中间用空格分开,数字均为整数且不超过500。输入保证解的存在。
输出格式:
在一行里输出路径的长度和收费总额,数字间以空格分隔,输出结尾不能有多余空格。
输入样例:
4 5 0 3
0 1 1 20
1 3 2 30
0 3 4 10
0 2 2 20
2 3 1 20
输出样例:
3 40
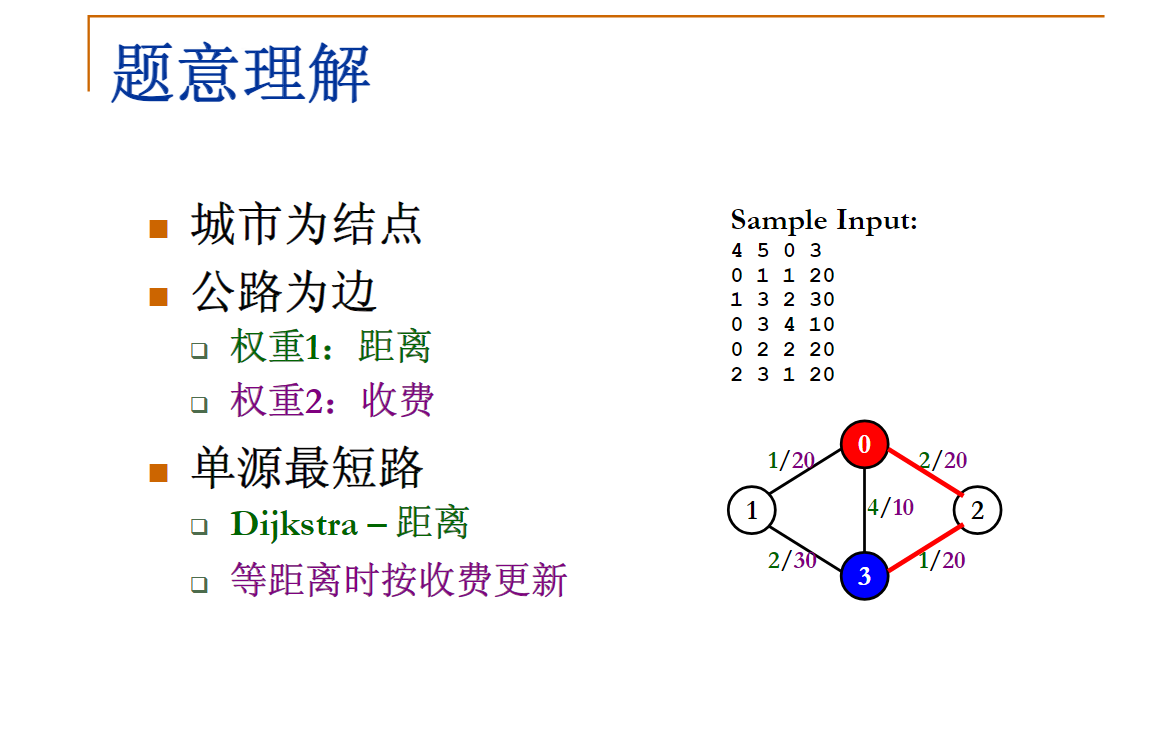


#include <iostream>
#include <vector>
using namespace std;
class vertexNode{
public:
int s;//源城市
int d;//目的城市
int weight;//路程长 权值
int charge;//收费
vertexNode()=default;
vertexNode(int s_,int d_,int w_,int c_):s{s_},d{d_},weight{w_},charge{c_}{};
};
class AdjacencyLinkGraphic{
public:
vector<vector<vertexNode*>> vertexs;//二维数组, 存的值是结点 包含该点的路径和收费 vertexs[i][j] i是起点 j是终点
int cityNum{0};
int highwayNum{0};
int s;//出发城市
int d;//目的城市
AdjacencyLinkGraphic()=default;
AdjacencyLinkGraphic(int n_,int m_,int s_,int d_):cityNum{n_},highwayNum{m_},s{s_},d{d_}{};
void build(){
vertexs=vector<vector<vertexNode*>>(cityNum,vector<vertexNode*>(cityNum,nullptr));
int s,d,w,c;
for(int i=0;i<highwayNum;i++){
scanf("%d %d %d %d",&s,&d,&w,&c);
vertexs[s][d]=new vertexNode{s,d,w,c};
vertexs[d][s]=new vertexNode{d,s,w,c};
}
}
void dijkstra(){
vector<int> visited(cityNum);
visited[s]=1;
int u;//起点 的 未访问的 最小权值的 邻接点
// 先将s的访问位置为1,
// 1.找到u 然后将u的访问位置为1
// 2.先由起点的最小权值邻接点 u 开始, 寻找起点s 经由 u 到u的邻接点 j 的总权值是否小于 s到j的权值
// 3.如果经由 s 经由 u 到 j 的的路径权值小于s到j的权值 ,就更新s到j的权值为 (s到u的权值)+(u到j的权值)
// 循环直到s的邻接点全部遍历完毕,这时就得到了s到任意连通点的最小路径长 和 对应的收费
//直接输出 vertexs[s][d]的路径长 和 收费
for(int i=0;i<cityNum;i++){
int min=999999;
for(int j=0;j<cityNum;j++){
if( vertexs[s][j] && !visited[j] && vertexs[s][j]->weight < min){
min= vertexs[s][j]->weight;
u = j;
}
}
visited[u]=1;
for(int j=0; j<cityNum; j++){
if( vertexs[u][j] && vertexs[u][j]->weight <= 99999 ){
if( vertexs[u][j] && vertexs[s][u] && vertexs[s][j] ){//确认为连通点
if(vertexs[s][j]->weight == vertexs[s][u]->weight + vertexs[u][j]->weight){
if(vertexs[s][j]->charge > vertexs[s][u]->charge + vertexs[u][j]->charge)
vertexs[s][j]->charge=vertexs[s][u]->charge+vertexs[u][j]->charge;
}else if(vertexs[s][j]->weight > vertexs[s][u]->weight + vertexs[u][j]->weight){
//更新由s到j的最小权值和对应的路费
vertexs[s][j]->weight = vertexs[s][u]->weight + vertexs[u][j]->weight;
vertexs[s][j]->charge = vertexs[s][u]->charge + vertexs[u][j]->charge;
}
}
}
}
}
cout << vertexs[s][d]->weight <<" "<< vertexs[s][d]->charge<<endl;
}
};
int main(){
int n,m,s,d;
cin >> n >> m >> s >> d ;
AdjacencyLinkGraphic ALG{n,m,s,d};
ALG.build();
ALG.dijkstra();
return 0;
}
注:下面是我自己写的,只通过了第一个测试样例,过几天考完试接着搞!!
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#define MaxVertexNum 10000
#define INFINITY 65535
#define INT_MAX 65535
int visited[MaxVertexNum];
int dist[MaxVertexNum];
int path[MaxVertexNum];
int cost[MaxVertexNum];
typedef int Vertex;
typedef int WeightType;
typedef struct ENode *PtrToENode;
struct ENode
{
Vertex V1;
Vertex V2;
WeightType Weight;
WeightType Charge;
};
typedef PtrToENode Edge;
typedef struct GNode *PtrToGNode;
struct GNode
{
int Nv;
int Ne;
WeightType G[MaxVertexNum][MaxVertexNum];
WeightType Cost[MaxVertexNum][MaxVertexNum];
};
typedef PtrToGNode MGraph;
MGraph CreateGraph(int VertexNum)
{
MGraph Graph = (MGraph)malloc(sizeof(struct GNode));
Graph->Nv = VertexNum;
Graph->Ne = 0;
for(Vertex V1=0; V1<Graph->Nv; V1++)
for(Vertex V2=0; V2<Graph->Nv; V2++)
{
Graph->G[V1][V2] = 0;
Graph->Cost[V1][V2] = 0;
}
return Graph;
}
void InsertEdge(MGraph Graph, Edge E)
{
Graph->G[E->V1][E->V2] = E->Weight;
Graph->Cost[E->V1][E->V2] = E->Charge;
}
void ResetVisited()
{
for(int i=0; i<MaxVertexNum; i++)
visited[i] = 0;
}
void Dijkstra(MGraph Graph, Vertex V, Vertex dest)
{
ResetVisited();
for(int i=0; i<Graph->Nv; i++)
{
if(Graph->G[V][i]>0 && V!=i)
{
dist[i] = Graph->G[V][i];
path[i] = V;
cost[i] = Graph->Cost[V][i];
}
else
{
dist[i] = INFINITY;
path[i] = -1;
cost[i] = 0;
}
}
dist[V] = 0;
path[V] = V;
cost[V] = 0;
visited[V] = 1;
for(int i=1; i<Graph->Nv; i++)
{
int minDist = INT_MAX;
int index;
for(int j=0; j<Graph->Nv; j++)
{
if(visited[j]==0 && dist[j]<minDist)
{
minDist = dist[j];
index = j;
}
}
visited[index] = 1;
for(int k=0; k<Graph->Nv; k++)
{
if(visited[k]==0)
{
if(Graph->G[index][k]>0 && minDist+Graph->G[index][k]<dist[k])
{
dist[k] = minDist+Graph->G[index][k];
path[k] = index;
cost[k] = cost[index] + Graph->Cost[index][k];
}
else if(Graph->G[index][k]>0 && minDist+Graph->G[index][k]==dist[k] && cost[V] + Graph->Cost[index][k]<cost[k])
{
cost[k] = cost[index] + Graph->Cost[index][k];
}
}
}
}
printf("%d %d\n",dist[dest],cost[dest]);
}
int main()
{
int Nv;
Edge E;
scanf("%d", &Nv);
MGraph Graph = CreateGraph(Nv);
scanf("%d", &(Graph->Ne));
int src, dest;
scanf("%d %d",&src,&dest);
int fee;
if((Graph->Ne) != 0)
{
E = (Edge)malloc(sizeof(struct ENode));
for(int i=0; i<Graph->Ne; i++)
{
scanf("%d %d %d %d",&E->V1,&E->V2,&E->Weight,&E->Charge);
InsertEdge(Graph, E);
}
}
Dijkstra(Graph, src, dest);
return 0;
}
PTA 08-图7 公路村村通
现有村落间道路的统计数据表中,列出了有可能建设成标准公路的若干条道路的成本,求使每个村落都有公路连通所需要的最低成本。
输入格式:
输入数据包括城镇数目正整数N(≤1000)和候选道路数目M(≤3N);随后的M行对应M条道路,每行给出3个正整数,分别是该条道路直接连通的两个城镇的编号以及该道路改建的预算成本。为简单起见,城镇从1到N编号。
输出格式:
输出村村通需要的最低成本。如果输入数据不足以保证畅通,则输出−1,表示需要建设更多公路。
输入样例:
6 15
1 2 5
1 3 3
1 4 7
1 5 4
1 6 2
2 3 4
2 4 6
2 5 2
2 6 6
3 4 6
3 5 1
3 6 1
4 5 10
4 6 8
5 6 3
输出样例:
12
PTA 08-图8 How Long Does It Take
Given the relations of all the activities of a project, you are supposed to find the earliest completion time of the project.
Input Specification:
Each input file contains one test case. Each case starts with a line containing two positive integers N (≤100), the number of activity check points (hence it is assumed that the check points are numbered from 0 to N−1), and M, the number of activities. Then M lines follow, each gives the description of an activity. For the i-th activity, three non-negative numbers are given: S[i], E[i], and L[i], where S[i] is the index of the starting check point, E[i] of the ending check point, and L[i] the lasting time of the activity. The numbers in a line are separated by a space.
Output Specification:
For each test case, if the scheduling is possible, print in a line its earliest completion time; or simply output "Impossible".
Sample Input 1:
9 12
0 1 6
0 2 4
0 3 5
1 4 1
2 4 1
3 5 2
5 4 0
4 6 9
4 7 7
5 7 4
6 8 2
7 8 4
Sample Output 1:
18
Sample Input 2:
4 5
0 1 1
0 2 2
2 1 3
1 3 4
3 2 5
Sample Output 2:
Impossible
PTA 08-图9 关键活动
假定一个工程项目由一组子任务构成,子任务之间有的可以并行执行,有的必须在完成了其它一些子任务后才能执行。“任务调度”包括一组子任务、以及每个子任务可以执行所依赖的子任务集。
比如完成一个专业的所有课程学习和毕业设计可以看成一个本科生要完成的一项工程,各门课程可以看成是子任务。有些课程可以同时开设,比如英语和C程序设计,它们没有必须先修哪门的约束;有些课程则不可以同时开设,因为它们有先后的依赖关系,比如C程序设计和数据结构两门课,必须先学习前者。
但是需要注意的是,对一组子任务,并不是任意的任务调度都是一个可行的方案。比如方案中存在“子任务A依赖于子任务B,子任务B依赖于子任务C,子任务C又依赖于子任务A”,那么这三个任务哪个都不能先执行,这就是一个不可行的方案。
任务调度问题中,如果还给出了完成每个子任务需要的时间,则我们可以算出完成整个工程需要的最短时间。在这些子任务中,有些任务即使推迟几天完成,也不会影响全局的工期;但是有些任务必须准时完成,否则整个项目的工期就要因此延误,这种任务就叫“关键活动”。
请编写程序判定一个给定的工程项目的任务调度是否可行;如果该调度方案可行,则计算完成整个工程项目需要的最短时间,并输出所有的关键活动。
输入格式:
输入第1行给出两个正整数N(≤100)和M,其中N是任务交接点(即衔接相互依赖的两个子任务的节点,例如:若任务2要在任务1完成后才开始,则两任务之间必有一个交接点)的数量。交接点按1N编号,M是子任务的数量,依次编号为1M。随后M行,每行给出了3个正整数,分别是该任务开始和完成涉及的交接点编号以及该任务所需的时间,整数间用空格分隔。
输出格式:
如果任务调度不可行,则输出0;否则第1行输出完成整个工程项目需要的时间,第2行开始输出所有关键活动,每个关键活动占一行,按格式“V->W”输出,其中V和W为该任务开始和完成涉及的交接点编号。关键活动输出的顺序规则是:任务开始的交接点编号小者优先,起点编号相同时,与输入时任务的顺序相反。
输入样例:
7 8
1 2 4
1 3 3
2 4 5
3 4 3
4 5 1
4 6 6
5 7 5
6 7 2
输出样例:
17
1->2
2->4
4->6
6->7
排序算法



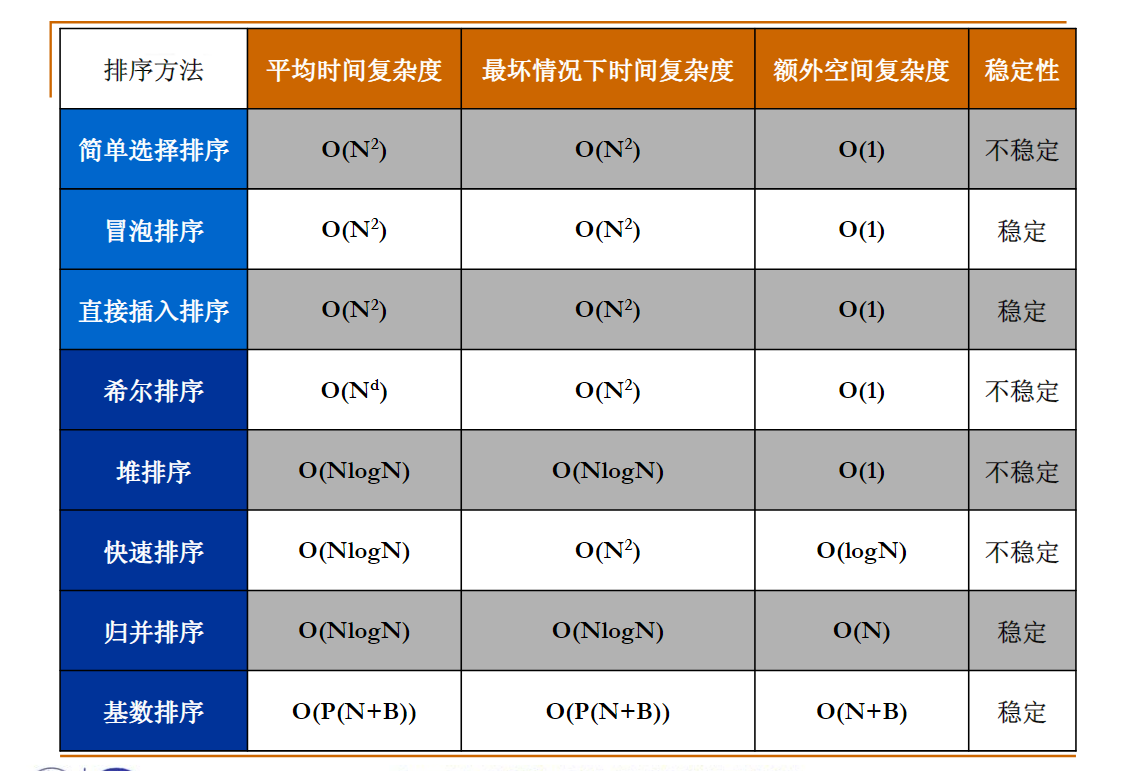
1请选择下面四种排序算法中最快又是稳定的排序算法:
- A. 希尔排序
- B. 堆排序
- C.归并排序
- D.快速排序
正确答案:C你选对了
2下列排序算法中,哪种算法可能出现:在最后一趟开始之前,所有的元素都不在其最终的位置上
- A.堆排序
- B.插入排序
- C.冒泡排序
- D.快速排序
正确答案:B你选对了
3当待排序列已经基本有序时,下面哪个排序算法效率最差
- A. 快速排序
- B.直接插入
- C.选择排序
- D.堆排序
正确答案:C你错选为B
4数据序列(3,2,4,9,8,11,6,20)只能是下列哪种排序算法的两趟排序结果
- A.冒泡排序
- B.插入排序
- C.选择排序
- D.快速排序
正确答案:D你选对了
冒泡排序
交换相邻元素

优点:稳定、能处理链表排序
对于7个数进行冒泡排序,最坏情况下需要进行的比较次数为21
1. 基本思想
冒泡排序是一种交换排序,核心是冒泡,把数组中最小的那个往上冒,冒的过程就是和他相邻的元素交换。
重复走访要排序的数列,通过两两比较相邻记录的排序码。排序过程中每次从后往前冒一个最小值,且每次能确定一个数在序列中的最终位置。若发生逆序,则交换;有俩种方式进行冒泡,一种是先把小的冒泡到前边去,另一种是把大的元素冒泡到后边。
趣味解释:
有一群泡泡,其中一个泡泡跑到一个泡小妹说,小妹小妹你过来咱俩比比谁大,小妹说哇你好大,于是他跑到了泡小妹前面,又跟前面的一个泡大哥说,大哥,咱俩比比谁大呗。泡大哥看了他一眼他就老实了。这就是内层的for,那个泡泡跟每个人都比一次。
话说那个泡泡刚老实下来,另一个泡泡又开始跟别人比谁大了,这就是外层的for,每个泡泡都会做一次跟其他泡泡比个没完的事。
2. 实现逻辑
- 比较相邻的元素。如果第一个比第二个大,就交换他们两个。
- 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。在这一点,最后的元素应该会是最大的数。
- 针对所有的元素重复以上的步骤,除了最后一个。
- 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
通过两层循环控制:
- 第一个循环(外循环),负责把需要冒泡的那个数字排除在外;
- 第二个循环(内循环),负责两两比较交换。
3. 动图演示bubble_sort
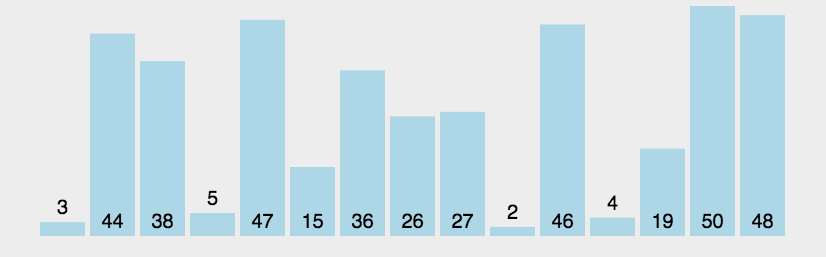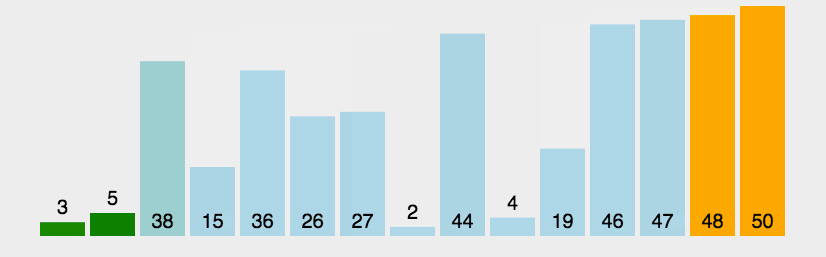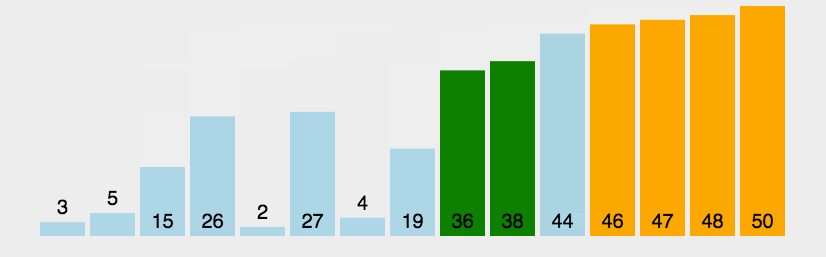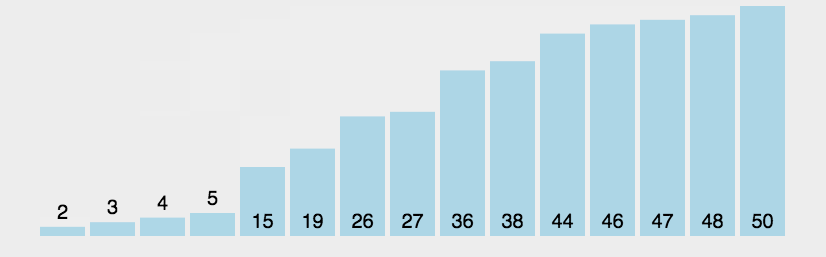
冒泡排序
4. 性能分析
- 平均时间复杂度:O(N^2)
- 最佳时间复杂度:O(N)
- 最差时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 排序方式:In-place
- 稳定性:稳定
解析说明:
冒泡排序涉及相邻两两数据的比较,故需要嵌套两层 for 循环来控制;
外层循环 n 次,内层最多时循环 n – 1次、最少循环 0 次,平均循环(n-1)/2;
所以循环体内总的比较交换次数为:n*(n-1) / 2 = (n^2-n)/2 ;
按照计算时间复杂度的规则,去掉常数、去掉最高项系数,其复杂度为O(N^2) ;
最优的空间复杂度为开始元素已排序,则空间复杂度为 0;
最差的空间复杂度为开始元素为逆排序,则空间复杂度为 O(N);
平均的空间复杂度为O(1) 。
5.完整代码
#include <stdio.h>
typedef int ElementType;
void Bubble_Sort(ElementType A[], int N)
{
for(int P=N-1; P>=0; P--)
{
int flag = 0;
for(int i=0; i<P; i++)
{
if(A[i]>A[i+1])
{
int temp;
temp = A[i];
A[i] = A[i+1];
A[i+1] = temp;
}
flag = 1;
}
if(flag == 0)
break;
}
}
int main()
{
int N;
scanf("%d", &N);
ElementType A[N];
for(int i=0; i<N; i++)
{
scanf("%d", &A[i]);
}
Bubble_Sort(A, N);
int First = 1;
for(int i=0; i<N; i++)
{
if(First)
{
printf("%d",A[i]);
First = 0;
}
else
{
printf(" %d", A[i]);
}
}
printf("\n");
return 0;
}
插入排序
交换相邻元素

给定初始序列{34, 8, 64, 51, 32, 21},冒泡排序和插入排序分别需要多少次元素交换才能完成? 冒泡9次,插入9次
序列{34, 8, 64, 51, 32, 21}中有多少逆序对? 9
对一组包含10个元素的非递减有序序列,采用插入排序排成非递增序列,其可能的比较次数和移动次数分别是 45, 44
1.基本思想
插入排序的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在实现上,通常采用in-place排序(即只需用到O(1)的额外空间的排序),因而在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位,为最新元素提供插入空间。
趣味解释:
插入排序操作类似于摸牌并将其从大到小排列。每次摸到一张牌后,根据其点数插入到确切位置。
如上图:表示的是摸到草花7后进行插入的过程。忽略最右边的草花10,相当于一开始7在最右边,然后逐个与左边的排相比较(当然左边的牌早已排好顺序),将其放置在合适的位置。当摸到草花10后重复上述过程即可。
而实际中,如何将插入牌的这个过程应用到实际排序操作中呢?具体我们以一组数字来说操作说明:
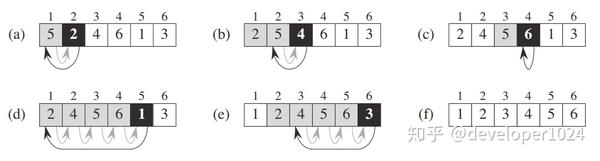
例如我们有一组数字:{5,2,4,6,1,3},我们要将这组数字从小到大进行排列。 我们从第二个数字开始,将其认为是新增加的数字,这样第二个数字只需与其左边的第一个数字比较后排好序;在第三个数字,认为前两个已经排好序的数字为手里整理好的牌,那么只需将第三个数字与前两个数字比较即可;以此类推,直到最后一个数字与前面的所有数字比较结束,插入排序完成。
2. 实现逻辑
① 从第一个元素开始,该元素可以认为已经被排序
② 取出下一个元素,在已经排序的元素序列中从后向前扫描
③如果该元素(已排序)大于新元素,将该元素移到下一位置
④ 重复步骤③,直到找到已排序的元素小于或者等于新元素的位置
⑤将新元素插入到该位置后
⑥ 重复步骤②~⑤
3. 动图演示
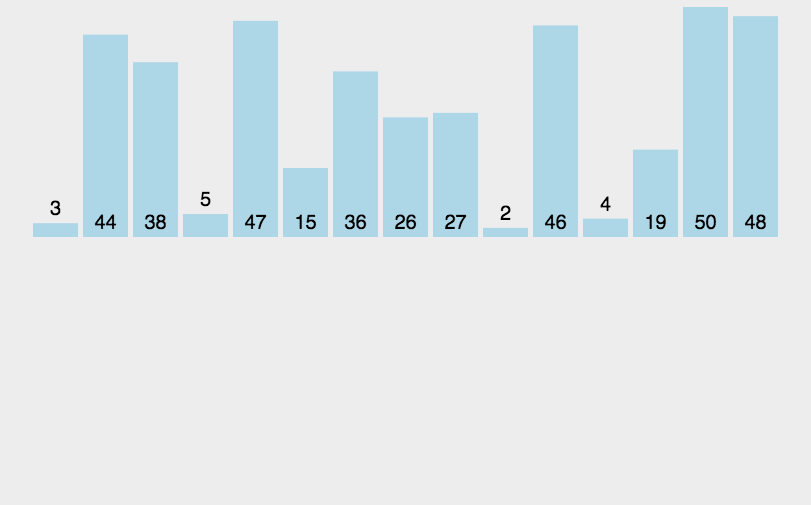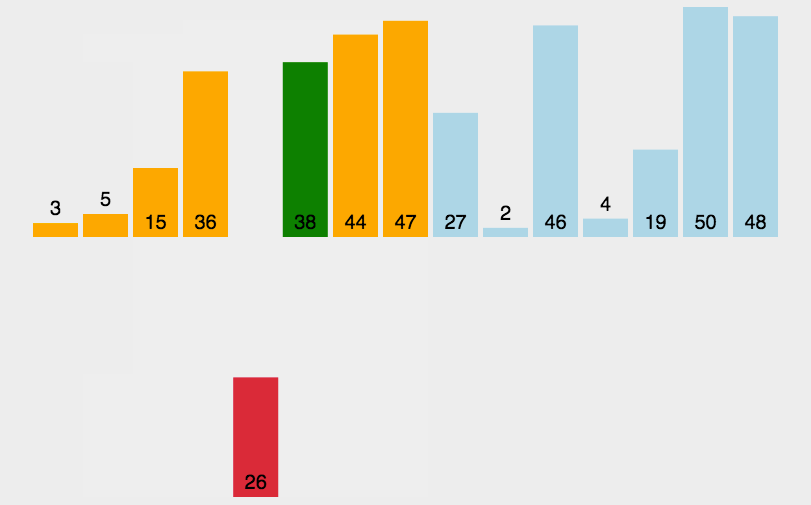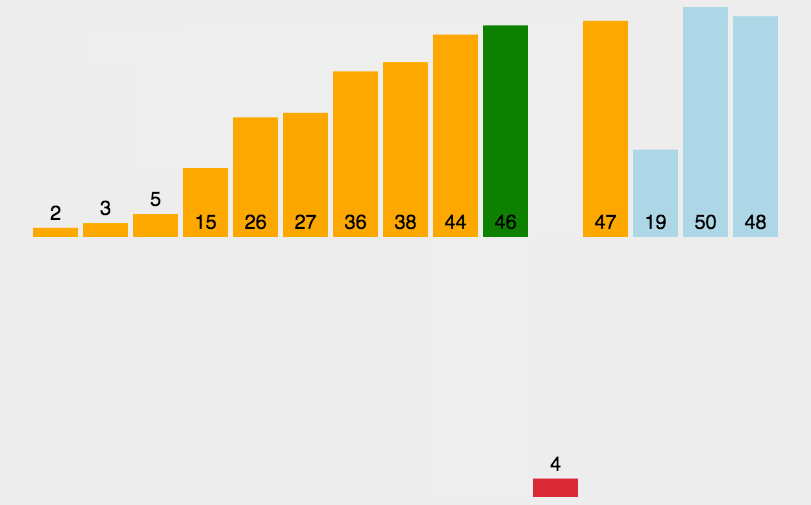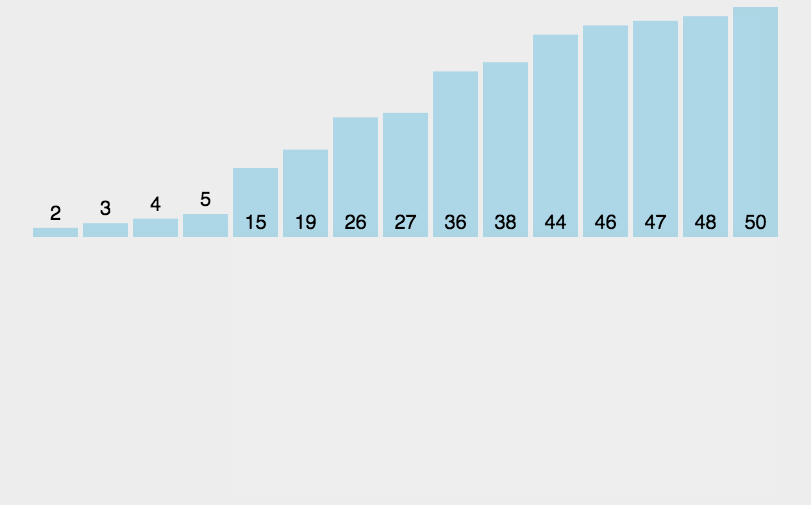
插入排序
4. 性能分析
平均时间复杂度:O(N^2)
最差时间复杂度:O(N^2)
空间复杂度:O(1)
排序方式:In-place
稳定性:稳定
如果插入排序的目标是把n个元素的序列升序排列,那么采用插入排序存在最好情况和最坏情况:
(1) 最好情况:序列已经是升序排列,在这种情况下,需要进行的比较操作需(n-1)次即可。
(2) 最坏情况:序列是降序排列,那么此时需要进行的比较共有n(n-1)/2次。
插入排序的赋值操作是比较操作的次数减去(n-1)次。平均来说插入排序算法复杂度为O(N^2)。
最优的空间复杂度为开始元素已排序,则空间复杂度为 0;
最差的空间复杂度为开始元素为逆排序,则空间复杂度最坏时为 O(N);
平均的空间复杂度为O(1)
5.完整代码
#include <stdio.h>
typedef int ElementType;
void Insertion_Sort( ElementType A[], int N )
{ /* 插入排序 */
int P, i;
ElementType Tmp;
for ( P=1; P<N; P++ ) {
Tmp = A[P]; /* 取出未排序序列中的第一个元素*/
for ( i=P; i>0 && A[i-1]>Tmp; i-- )
A[i] = A[i-1]; /*依次与已排序序列中元素比较并右移*/
A[i] = Tmp; /* 放进合适的位置 */
}
}
int main()
{
int N;
scanf("%d", &N);
ElementType A[N];
for(int i=0; i<N; i++)
{
scanf("%d", &A[i]);
}
Insertion_Sort(A, N);
int First = 1;
for(int i=0; i<N; i++)
{
if(First)
{
printf("%d",A[i]);
First = 0;
}
else
{
printf(" %d", A[i]);
}
}
printf("\n");
return 0;
}
希尔排序
希尔排序是不稳定的。
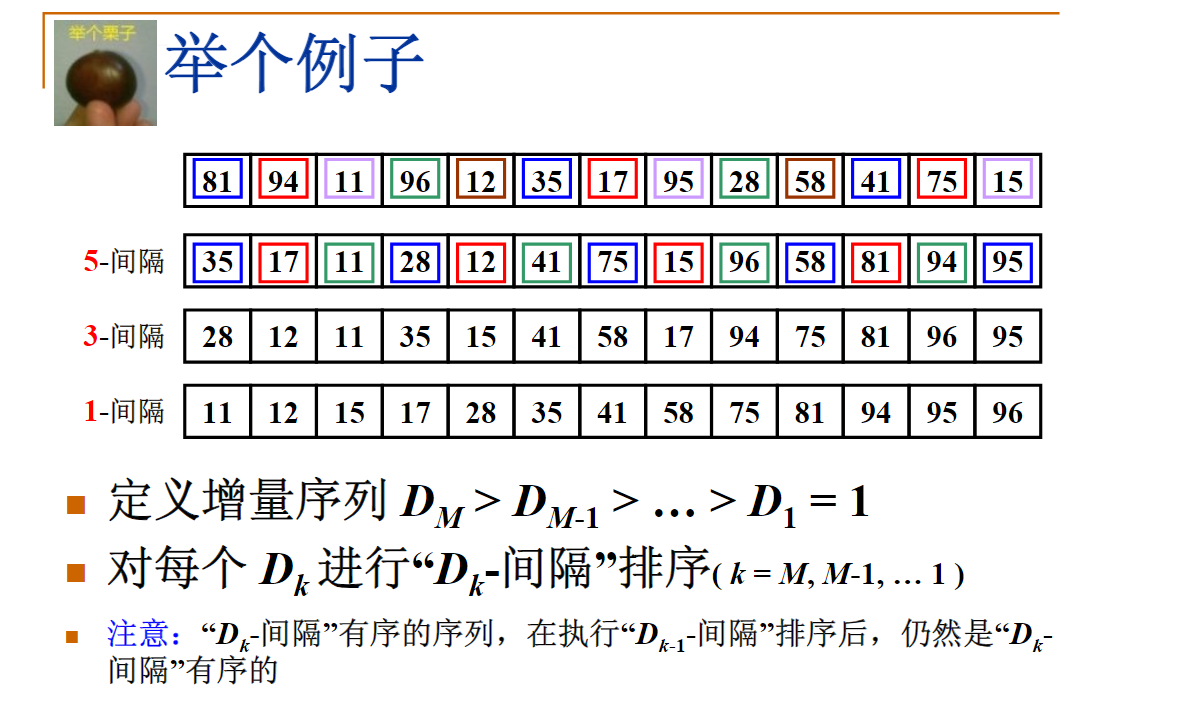

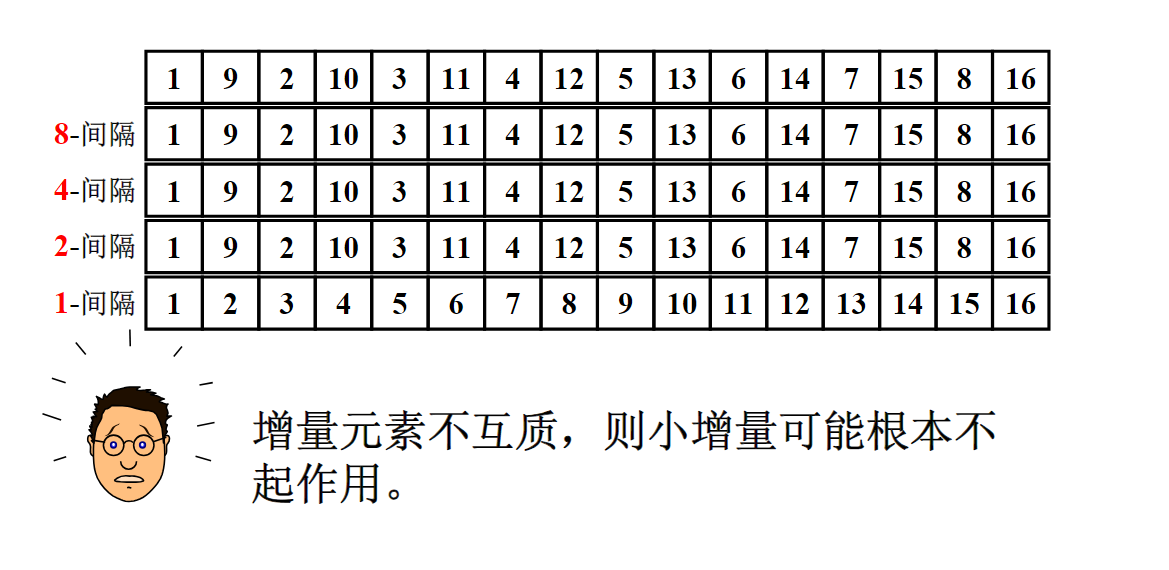
希尔排序的实质就是分组插入排序,该方法又称递减增量排序算法,因DL.Shell于1959年提出而得名。希尔排序是非稳定的排序算法。
希尔排序是基于插入排序的以下两点性质而提出改进方法的:
插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率但插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位
1. 基本思想
先将整个待排元素序列分割成若干个子序列(由相隔某个“增量”的元素组成的)分别进行直接插入排序,然后依次缩减增量再进行排序,待整个序列中的元素基本有序(增量足够小)时,再对全体元素进行一次直接插入排序。
因为直接插入排序在元素基本有序的情况下(接近最好情况),效率是很高的,因此希尔排序在时间效率上比前两种方法有较大提高。
2. 实现逻辑
① 先取一个小于n的整数d1作为第一个增量,把文件的全部记录分成d1个组。
② 所有距离为d1的倍数的记录放在同一个组中,在各组内进行直接插入排序。
③ 取第二个增量d2小于d1重复上述的分组和排序,直至所取的增量dt=1(dt小于dt-l小于…小于d2小于d1),即所有记录放在同一组中进行直接插入排序为止。
3. 动图演示
希尔排序
以一组数字来说操作说明:
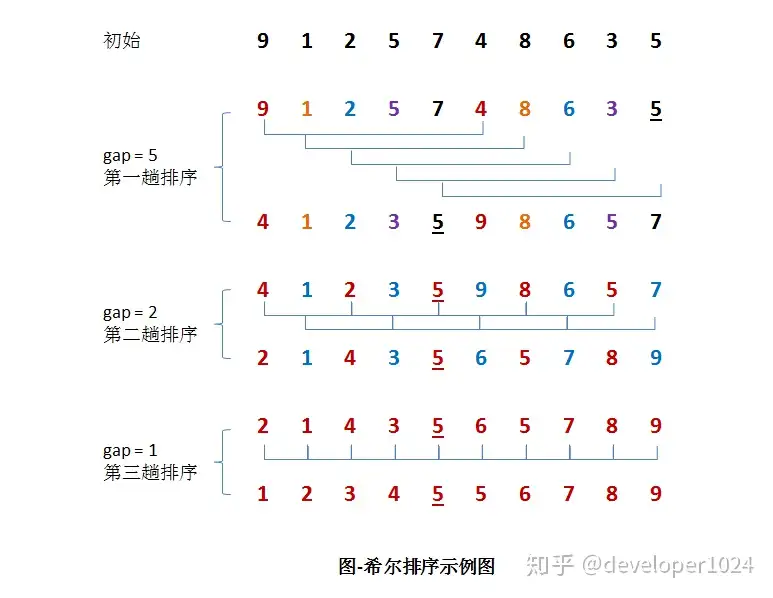
假设有一组{9, 1, 2, 5, 7, 4, 8, 6, 3, 5}无需序列。
第一趟排序: 设 gap1 = N / 2 = 5,即相隔距离为 5 的元素组成一组,可以分为 5 组。接下来,按照直接插入排序的方法对每个组进行排序。
第二趟排序:
将上次的 gap 缩小一半,即 gap2 = gap1 / 2 = 2 (取整数)。这样每相隔距离为 2 的元素组成一组,可以分为2组。按照直接插入排序的方法对每个组进行排序。
第三趟排序:
再次把 gap 缩小一半,即gap3 = gap2 / 2 = 1。 这样相隔距离为1的元素组成一组,即只有一组。按照直接插入排序的方法对每个组进行排序。此时,排序已经结束。
注:需要注意一下的是,图中有两个相等数值的元素5和5。我们可以清楚的看到,在排序过程中,两个元素位置交换了。
4. 性能分析
平均时间复杂度:O(Nlog2N)
最佳时间复杂度:
最差时间复杂度:O(N^2)
空间复杂度:O(1)
稳定性:不稳定
复杂性:较复杂
希尔排序的效率取决于增量值gap的选取,时间复杂度并不是一个定值。
开始时,gap取值较大,子序列中的元素较少,排序速度快,克服了直接插入排序的缺点;其次,gap值逐渐变小后,虽然子序列的元素逐渐变多,但大多元素已基本有序,所以继承了直接插入排序的优点,能以近线性的速度排好序。
最优的空间复杂度为开始元素已排序,则空间复杂度为 0;最差的空间复杂度为开始元素为逆排序,则空间复杂度为 O(N);平均的空间复杂度为O(1)希尔排序并不只是相邻元素的比较,有许多跳跃式的比较,难免会出现相同元素之间的相对位置发生变化。比如上面的例子中希尔排序中相等数据5就交换了位置,所以希尔排序是不稳定的算法。
5. 完整代码

原始希尔排序
void Shell_Sort(ElementType A[], int N)
{
for(int D=N/2; D>0; D=D/2)
{
for(int P=D; P<N; P++)
{
ElementType temp = A[P];
int i;
for(i=P; i>=D && A[i-D]>temp; i-=D)
{
A[i] = A[i-D];
}
A[i] = temp;
}
}
}
希尔排序 - 用Sedgewick增量序列
#include <stdio.h>
typedef int ElementType;
void Shell_Sort( ElementType A[], int N )
{ /* 希尔排序 - 用Sedgewick增量序列 */
int Si, D, P, i;
ElementType Tmp;
/* 这里只列出一小部分增量 */
int Sedgewick[] = {929, 505, 209, 109, 41, 19, 5, 1, 0};
for ( Si=0; Sedgewick[Si]>=N; Si++ )
; /* 初始的增量Sedgewick[Si]不能超过待排序列长度 */
for ( D=Sedgewick[Si]; D>0; D=Sedgewick[++Si] )
for ( P=D; P<N; P++ ) { /* 插入排序*/
Tmp = A[P];
for ( i=P; i>=D && A[i-D]>Tmp; i-=D )
A[i] = A[i-D];
A[i] = Tmp;
}
}
int main()
{
int N;
scanf("%d", &N);
ElementType A[N];
for(int i=0; i<N; i++)
{
scanf("%d", &A[i]);
}
Shell_Sort(A, N);
int First = 1;
for(int i=0; i<N; i++)
{
if(First)
{
printf("%d",A[i]);
First = 0;
}
else
{
printf(" %d", A[i]);
}
}
printf("\n");
return 0;
}
选择排序
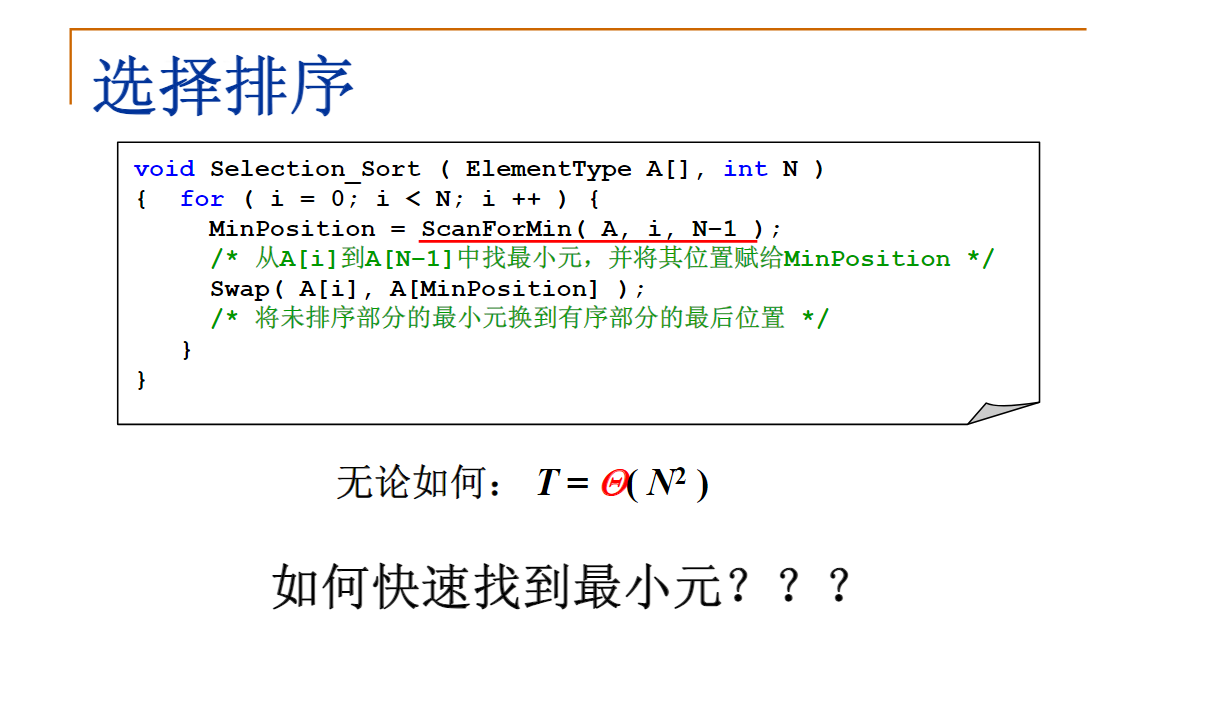
选择排序(Selection sort) 是一种简单直观的排序算法。
1.基本思想
首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
选择排序的思想其实和冒泡排序有点类似,都是在一次排序后把最小的元素放到最前面,或者将最大值放在最后面。但是过程不同,冒泡排序是通过相邻的比较和交换。而选择排序是通过对整体的选择,每一趟从前往后查找出无序区最小值,将最小值交换至无序区最前面的位置。
2.实现逻辑
① 第一轮从下标为 1 到下标为 n-1 的元素中选取最小值,若小于第一个数,则交换
② 第二轮从下标为 2 到下标为 n-1 的元素中选取最小值,若小于第二个数,则交换
③ 依次类推下去……
3.动图演示
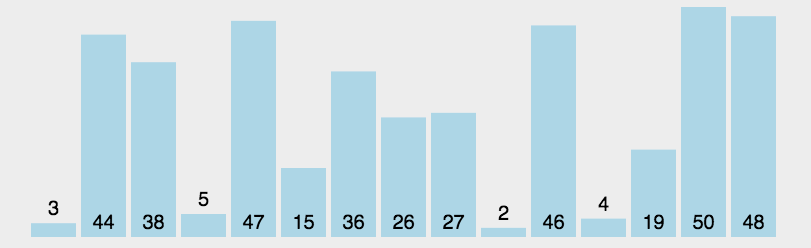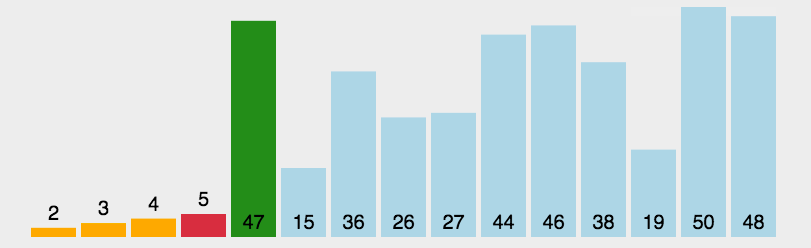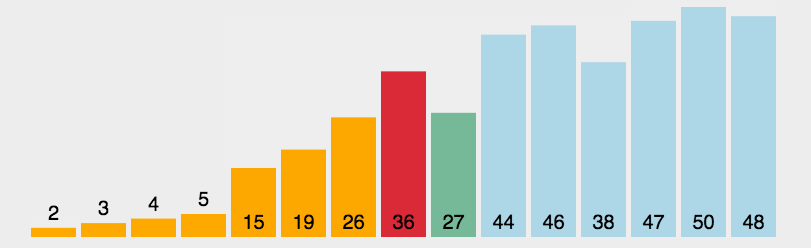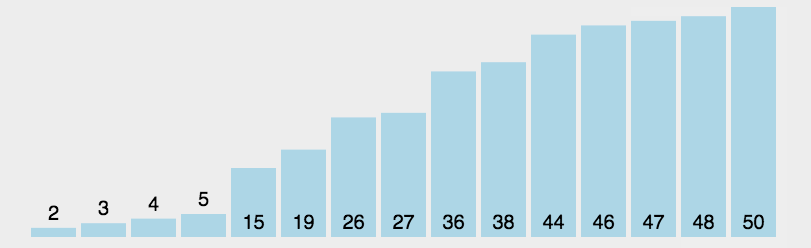
选择排序
注:红色表示当前最小值,黄色表示已排序序列,绿色表示当前位置。
具体的我们以一组无序数列{20,40,30,10,60,50}为例分解说明,如下图所示:

4. 复杂度分析
平均时间复杂度:O(N^2)
最佳时间复杂度:O(N^2)
最差时间复杂度:O(N^2)
空间复杂度:O(1)
排序方式:In-place
稳定性:不稳定
选择排序的交换操作介于和(n-1)次之间。选择排序的比较操作为n(n-1)/2次之间。选择排序的赋值操作介于0和3(n-1)次之间。
比较次数O(n^2),比较次数与关键字的初始状态无关,总的比较次数N = (n-1) + (n-2) +…+ 1 = n x (n-1)/2。交换次数O(n),最好情况是,已经有序,交换0次;最坏情况是,逆序,交换n-1次。
5.完整代码
#include <stdio.h>
typedef int ElementType;
void Selection_Sort( ElementType A[], int N )
{
ElementType min, temp;
for(int i=0; i<N-1; i++)
{
min = i;
for(int j=i+1; j<N; j++)
{
if(A[j] < A[min])
min = j;
}
temp = A[i];
A[i] = A[min];
A[min] = temp;
}
}
int main()
{
int N;
scanf("%d", &N);
ElementType A[N];
for(int i=0; i<N; i++)
{
scanf("%d", &A[i]);
}
Selection_Sort(A, N);
int First = 1;
for(int i=0; i<N; i++)
{
if(First)
{
printf("%d",A[i]);
First = 0;
}
else
{
printf(" %d", A[i]);
}
}
printf("\n");
return 0;
}
堆排序
堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。

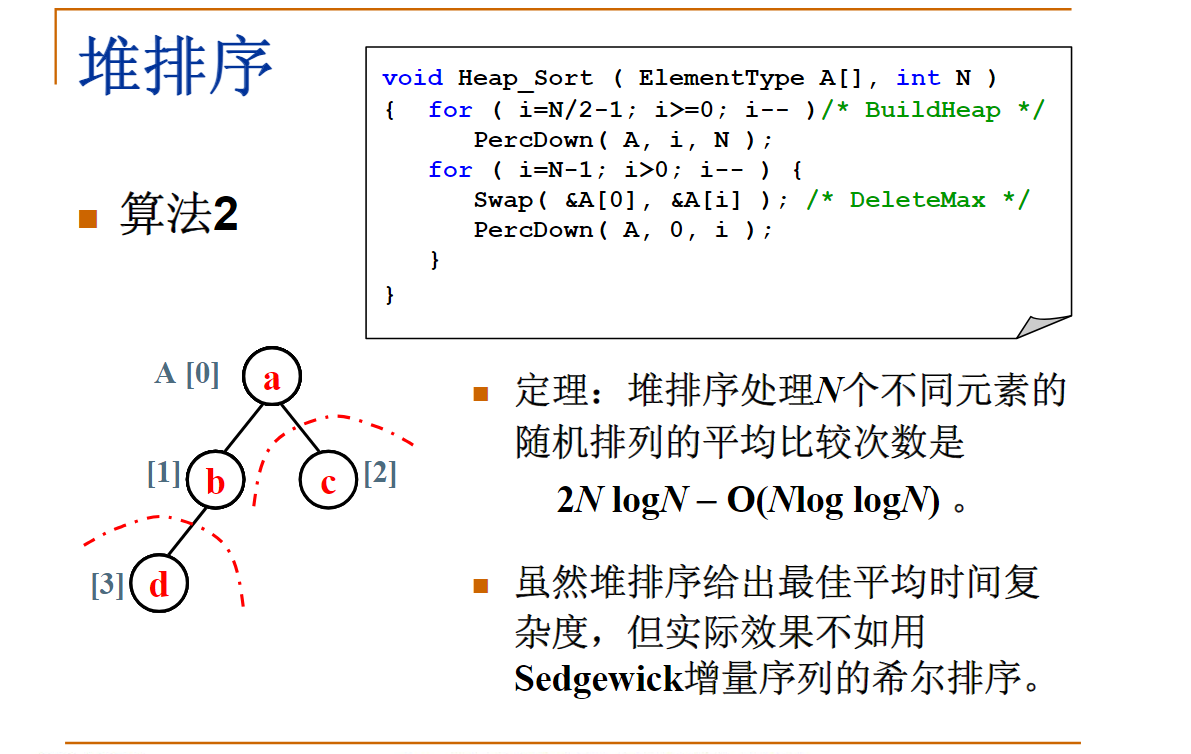
在堆排序中,元素下标从0开始。则对于下标为i的元素,其左、右孩子的下标分别为: 2i+1, 2i+2
有一组记录(46,77,55,38,41,85),用堆排序建立的初始堆为85,77,55,38,41,46
注:先建立一个堆再调整
堆排序最适合解决什么样的问题?
对时间复杂度要求较高的场景: 堆排序的时间复杂度为 O(n log n),其中 n 是要排序的元素数量。这使得堆排序在大规模数据集上的性能表现较好,适合对时间效率要求较高的情况。
对内存空间要求较高的场景: 堆排序是一种原地排序算法,不需要额外的辅助空间,只需要一个数组来存储待排序的元素。这对于内存空间有限的情况下非常有优势。
不要求稳定排序的场景: 堆排序是一种不稳定的排序算法,即在排序过程中相同元素的相对顺序可能会发生变化。如果对稳定性有要求的话,可能会选择其他稳定的排序算法,如归并排序。
动态数据流的场景: 堆排序适用于动态数据流,即不断有新的数据加入并需要保持排序状态的情况。由于堆结构的特性,可以较容易地实现在动态数据中插入元素和删除最大/最小元素的操作。
选择最大/最小的 k 个元素: 由于堆排序的特性,可以方便地找到最大(大顶堆)或最小(小顶堆)的 k 个元素,这在一些特定场景中是很有用的,比如求 Top K 问题。
1. 基本思想
利用大顶堆(小顶堆)堆顶记录的是最大关键字(最小关键字)这一特性,使得每次从无序中选择最大记录(最小记录)变得简单。
① 将待排序的序列构造成一个最大堆,此时序列的最大值为根节点
② 依次将根节点与待排序序列的最后一个元素交换
③ 再维护从根节点到该元素的前一个节点为最大堆,如此往复,最终得到一个递增序列
2. 实现逻辑
① 先将初始的
R[0…n-1]建立成最大堆,此时是无序堆,而堆顶是最大元素。
② 再将堆顶R[0]和无序区的最后一个记录R[n-1]交换,由此得到新的无序区R[0…n-2]和有序区R[n-1],且满足R[0…n-2].keys ≤ R[n-1].key③ 由于交换后新的根R[1]可能违反堆性质,故应将当前无序区R[1..n-1]调整为堆。然后再次将R[1..n-1]中关键字最大的记录R[1]和该区间的最后一个记录R[n-1]交换,由此得到新的无序区R[1..n-2]和有序区R[n-1..n],且仍满足关系R[1..n-2].keys≤R[n-1..n].keys,同样要将R[1..n-2]调整为堆。
④ 直到无序区只有一个元素为止。
3. 动图演示
堆排序算法的演示。首先,将元素进行重排,以匹配堆的条件。图中排序过程之前简单的绘出了堆树的结构。
分步解析说明:
实现堆排序需要解决两个问题:
1、如何由一个无序序列建成一个堆?
2、如何在输出堆顶元素之后,调整剩余元素成为一个新的堆?
假设给定一个组无序数列{100,5,3,11,6,8,7},带着问题,我们对其进行堆排序操作进行分步操作说明。

3.1 创建最大堆
①首先我们将数组我们将数组从上至下按顺序排列,转换成二叉树:一个无序堆。每一个三角关系都是一个堆,上面是父节点,下面两个分叉是子节点,两个子节点俗称左孩子、右孩子;
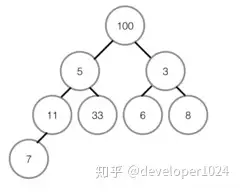
②转换成无序堆之后,我们要努力让这个无序堆变成最大堆(或是最小堆),即每个堆里都实现父节点的值都大于任何一个子节点的值。

③从最后一个堆开始,即左下角那个没有右孩子的那个堆开始;首先对比左右孩子,由于这个堆没有右孩子,所以只能用左孩子,左孩子的值比父节点的值小所以不需要交换。如果发生交换,要检测子节点是否为其他堆的父节点,如果是,递归进行同样的操作。
④第二次对比红色三角形内的堆,取较大的子节点,右孩子8胜出,和父节点比较,右孩子8大于父节点3,升级做父节点,与3交换位置,3的位置没有子节点,这个堆建成最大堆。
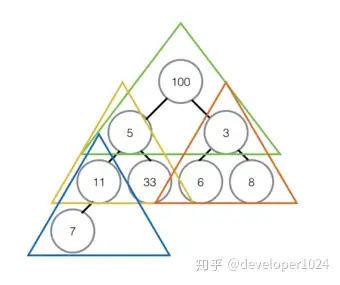
⑤对黄色三角形内堆进行排序,过程和上面一样,最终是右孩子33升为父节点,被交换的右孩子下面也没有子节点,所以直接结束对比。
⑥最顶部绿色的堆,堆顶100比左右孩子都大,所以不用交换,至此最大堆创建完成。
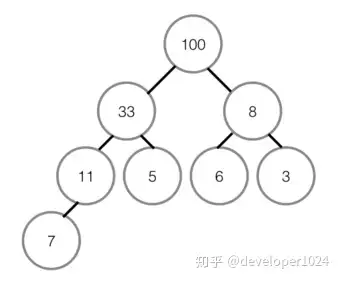
3.2 堆排序(最大堆调整)
①首先将堆顶元素100交换至最底部7的位置,7升至堆顶,100所在的底部位置即为有序区,有序区不参与之后的任何对比。
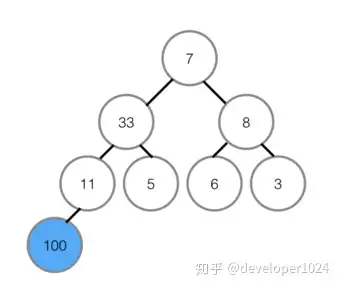
②在7升至顶部之后,对顶部重新做最大堆调整,左孩子33代替7的位置。
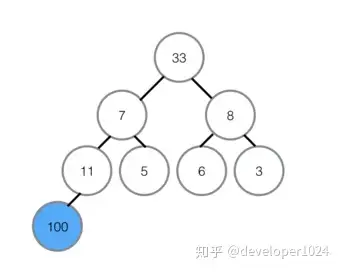
③在7被交换下来后,下面还有子节点,所以需要继续与子节点对比,左孩子11比7大,所以11与7交换位置,交换位置后7下面为有序区,不参与对比,所以本轮结束,无序区再次形成一个最大堆。
④将最大堆堆顶33交换至堆末尾,扩大有序区;
⑤不断建立最大堆,并且扩大有序区,最终全部有序。
4. 复杂度分析
- 平均时间复杂度:O(nlogn)
- 最佳时间复杂度:O(nlogn)
- 最差时间复杂度:O(nlogn)
- 稳定性:不稳定
堆排序其实也是一种选择排序,是一种树形选择排序。只不过直接选择排序中,为了从R[1…n]中选择最大记录,需比较n-1次,然后从R[1…n-2]中选择最大记录需比较n-2次。事实上这n-2次比较中有很多已经在前面的n-1次比较中已经做过,而树形选择排序恰好利用树形的特点保存了部分前面的比较结果,因此可以减少比较次数。对于n个关键字序列,最坏情况下每个节点需比较log2(n)次,因此其最坏情况下时间复杂度为nlogn。堆排序为不稳定排序,不适合记录较少的排序。
5.完整代码
#include <stdio.h>
typedef int ElementType;
void Swap( ElementType *a, ElementType *b )
{
ElementType t = *a; *a = *b; *b = t;
}
void PercDown( ElementType A[], int p, int N )
{ /* 改编代码4.24的PercDown( MaxHeap H, int p ) */
/* 将N个元素的数组中以A[p]为根的子堆调整为最大堆 */
int Parent, Child;
ElementType X;
X = A[p]; /* 取出根结点存放的值 */
for( Parent=p; (Parent*2+1)<N; Parent=Child ) {
Child = Parent * 2 + 1;
if( (Child!=N-1) && (A[Child]<A[Child+1]) )
Child++; /* Child指向左右子结点的较大者 */
if( X >= A[Child] ) break; /* 找到了合适位置 */
else /* 下滤X */
A[Parent] = A[Child];
}
A[Parent] = X;
}
void HeapSort( ElementType A[], int N )
{ /* 堆排序 */
int i;
for ( i=N/2-1; i>=0; i-- )/* 建立最大堆 */
PercDown( A, i, N );
for ( i=N-1; i>0; i-- ) {
/* 删除最大堆顶 */
Swap( &A[0], &A[i] ); /* 见代码7.1 */
PercDown( A, 0, i );
}
}
int main()
{
int N;
scanf("%d", &N);
ElementType A[N];
for(int i=0; i<N; i++)
{
scanf("%d", &A[i]);
}
Heap_Sort(A, N);
int First = 1;
for(int i=0; i<N; i++)
{
if(First)
{
printf("%d",A[i]);
First = 0;
}
else
{
printf(" %d", A[i]);
}
}
printf("\n");
return 0;
}
归并排序
内部排序(数据一次性全部读入内存然后排序)通常不使用归并排序
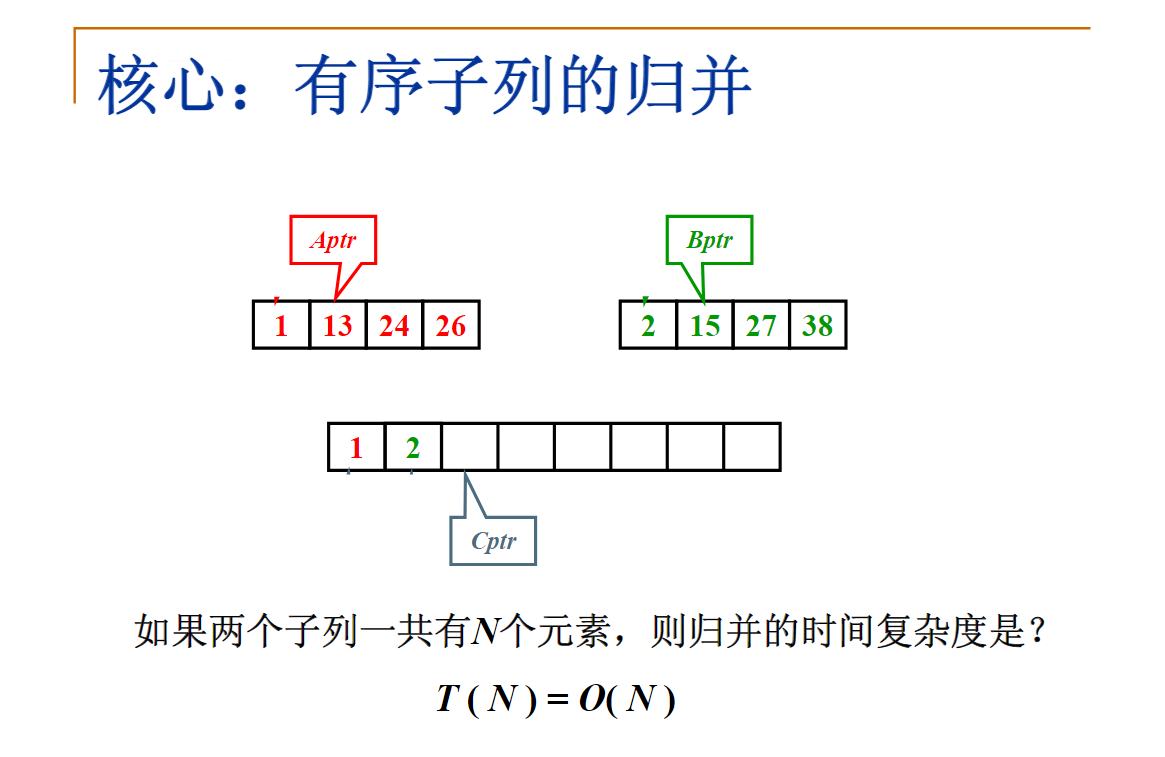

归并排序,是创建在归并操作上的一种有效的排序算法。算法是采用分治法(Divide and Conquer)的一个非常典型的应用,且各层分治递归可以同时进行。归并排序思路简单,速度仅次于快速排序,为稳定排序算法,一般用于对总体无序,但是各子项相对有序的数列。
1. 基本思想
归并排序是用分治思想,分治模式在每一层递归上有三个步骤:
- 分解(Divide):将n个元素分成个含n/2个元素的子序列。
- 解决(Conquer):用合并排序法对两个子序列递归的排序。
- 合并(Combine):合并两个已排序的子序列已得到排序结果。
2. 实现逻辑
2.1 迭代法
① 申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列
② 设定两个指针,最初位置分别为两个已经排序序列的起始位置
③ 比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置
④ 重复步骤③直到某一指针到达序列尾
⑤ 将另一序列剩下的所有元素直接复制到合并序列尾
2.2 递归法
① 将序列每相邻两个数字进行归并操作,形成floor(n/2)个序列,排序后每个序列包含两个元素
② 将上述序列再次归并,形成floor(n/4)个序列,每个序列包含四个元素
③ 重复步骤②,直到所有元素排序完毕
3. 动图演示

归并排序演示
具体的我们以一组无序数列{14,12,15,13,11,16}为例分解说明,如下图所示:
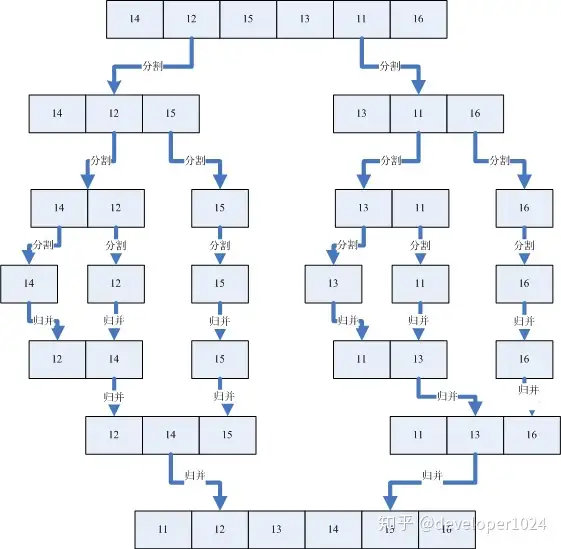
上图中首先把一个未排序的序列从中间分割成2部分,再把2部分分成4部分,依次分割下去,直到分割成一个一个的数据,再把这些数据两两归并到一起,使之有序,不停的归并,最后成为一个排好序的序列。
4. 复杂度分析
平均时间复杂度:O(nlogn)
最佳时间复杂度:O(n)
最差时间复杂度:O(nlogn)
空间复杂度:O(n)
排序方式:In-place
稳定性:稳定
不管元素在什么情况下都要做这些步骤,所以花销的时间是不变的,所以该算法的最优时间复杂度和最差时间复杂度及平均时间复杂度都是一样的为:O( nlogn )
归并的空间复杂度就是那个临时的数组和递归时压入栈的数据占用的空间:n + logn;所以空间复杂度为: O(n)。
归并排序算法中,归并最后到底都是相邻元素之间的比较交换,并不会发生相同元素的相对位置发生变化,故是稳定性算法。
递归实现(分而治之)

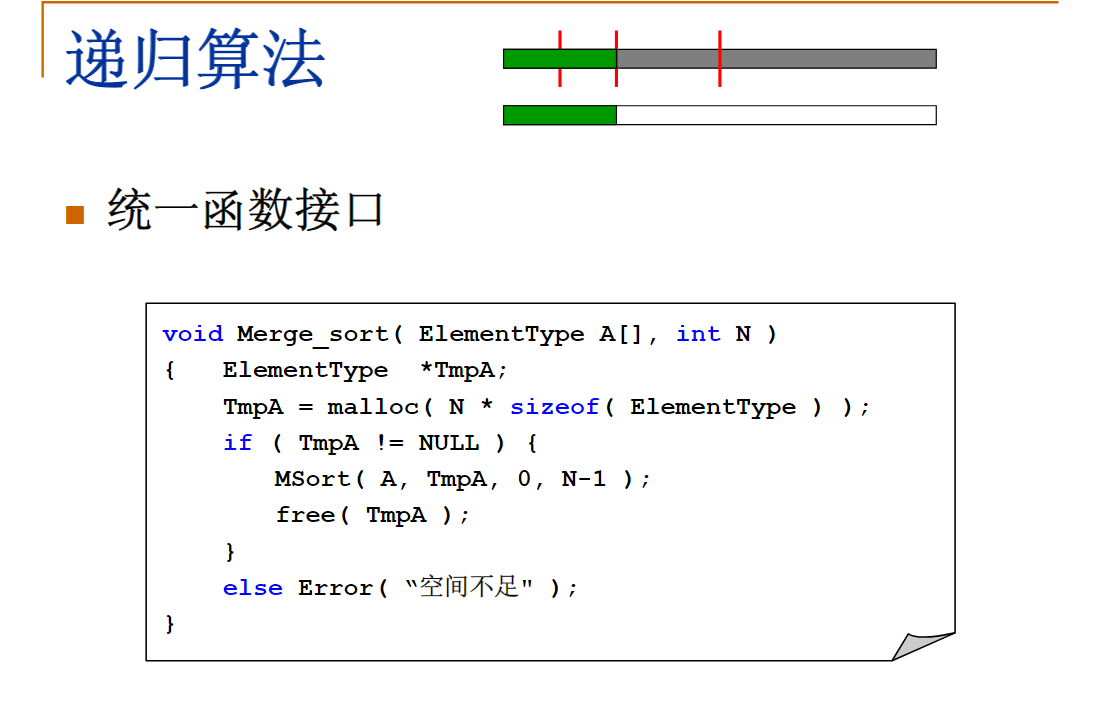

/* 归并排序 - 递归实现 */
/* L = 左边起始位置, R = 右边起始位置, RightEnd = 右边终点位置*/
void Merge( ElementType A[], ElementType TmpA[], int L, int R, int RightEnd )
{ /* 将有序的A[L]~A[R-1]和A[R]~A[RightEnd]归并成一个有序序列 */
int LeftEnd, NumElements, Tmp;
int i;
LeftEnd = R - 1; /* 左边终点位置 */
Tmp = L; /* 有序序列的起始位置 */
NumElements = RightEnd - L + 1;
while( L <= LeftEnd && R <= RightEnd ) {
if ( A[L] <= A[R] )
TmpA[Tmp++] = A[L++]; /* 将左边元素复制到TmpA */
else
TmpA[Tmp++] = A[R++]; /* 将右边元素复制到TmpA */
}
while( L <= LeftEnd )
TmpA[Tmp++] = A[L++]; /* 直接复制左边剩下的 */
while( R <= RightEnd )
TmpA[Tmp++] = A[R++]; /* 直接复制右边剩下的 */
for( i = 0; i < NumElements; i++, RightEnd -- )
A[RightEnd] = TmpA[RightEnd]; /* 将有序的TmpA[]复制回A[] */
}
void Msort( ElementType A[], ElementType TmpA[], int L, int RightEnd )
{ /* 核心递归排序函数 */
int Center;
if ( L < RightEnd ) {
Center = (L+RightEnd) / 2;
Msort( A, TmpA, L, Center ); /* 递归解决左边 */
Msort( A, TmpA, Center+1, RightEnd ); /* 递归解决右边 */
Merge( A, TmpA, L, Center+1, RightEnd ); /* 合并两段有序序列 */
}
}
void MergeSort( ElementType A[], int N )
{ /* 归并排序 */
ElementType *TmpA;
TmpA = (ElementType *)malloc(N*sizeof(ElementType));
if ( TmpA != NULL ) {
Msort( A, TmpA, 0, N-1 );
free( TmpA );
}
else printf( "空间不足" );
}
非递归实现
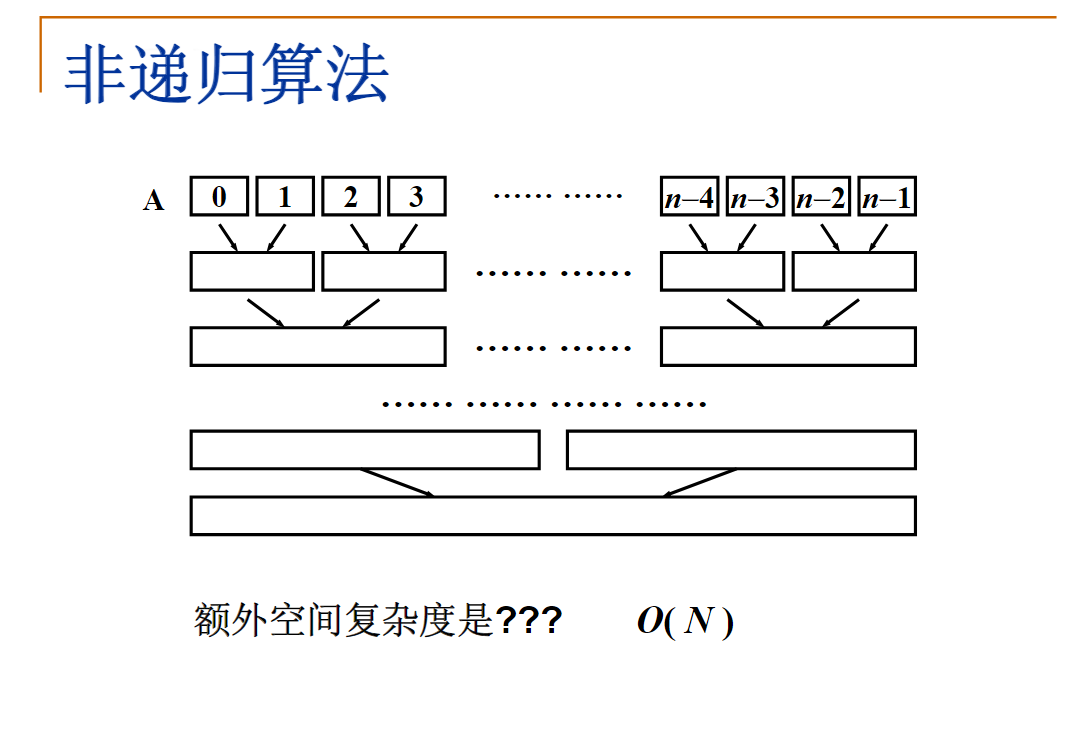


/* 归并排序 - 循环实现 */
/* L = 左边起始位置, R = 右边起始位置, RightEnd = 右边终点位置*/
void Merge( ElementType A[], ElementType TmpA[], int L, int R, int RightEnd )
{ /* 将有序的A[L]~A[R-1]和A[R]~A[RightEnd]归并成一个有序序列 */
int LeftEnd, NumElements, Tmp;
int i;
LeftEnd = R - 1; /* 左边终点位置 */
Tmp = L; /* 有序序列的起始位置 */
NumElements = RightEnd - L + 1;
while( L <= LeftEnd && R <= RightEnd ) {
if ( A[L] <= A[R] )
TmpA[Tmp++] = A[L++]; /* 将左边元素复制到TmpA */
else
TmpA[Tmp++] = A[R++]; /* 将右边元素复制到TmpA */
}
while( L <= LeftEnd )
TmpA[Tmp++] = A[L++]; /* 直接复制左边剩下的 */
while( R <= RightEnd )
TmpA[Tmp++] = A[R++]; /* 直接复制右边剩下的 */
for( i = 0; i < NumElements; i++, RightEnd -- )
A[RightEnd] = TmpA[RightEnd]; /* 将有序的TmpA[]复制回A[] */
}
/* length = 当前有序子列的长度*/
void Merge_pass( ElementType A[], ElementType TmpA[], int N, int length )
{ /* 两两归并相邻有序子列 */
int i, j;
for ( i=0; i <= N-2*length; i += 2*length )
Merge( A, TmpA, i, i+length, i+2*length-1 );
if ( i+length < N ) /* 归并最后2个子列*/
Merge( A, TmpA, i, i+length, N-1);
else /* 最后只剩1个子列*/
for ( j = i; j < N; j++ ) TmpA[j] = A[j];
}
void Merge_Sort( ElementType A[], int N )
{
int length;
ElementType *TmpA;
length = 1; /* 初始化子序列长度*/
TmpA = malloc( N * sizeof( ElementType ) );
if ( TmpA != NULL ) {
while( length < N ) {
Merge_pass( A, TmpA, N, length );
length *= 2;
Merge_pass( TmpA, A, N, length );
length *= 2;
}
free( TmpA );
}
else printf( "空间不足" );
}
快速排序
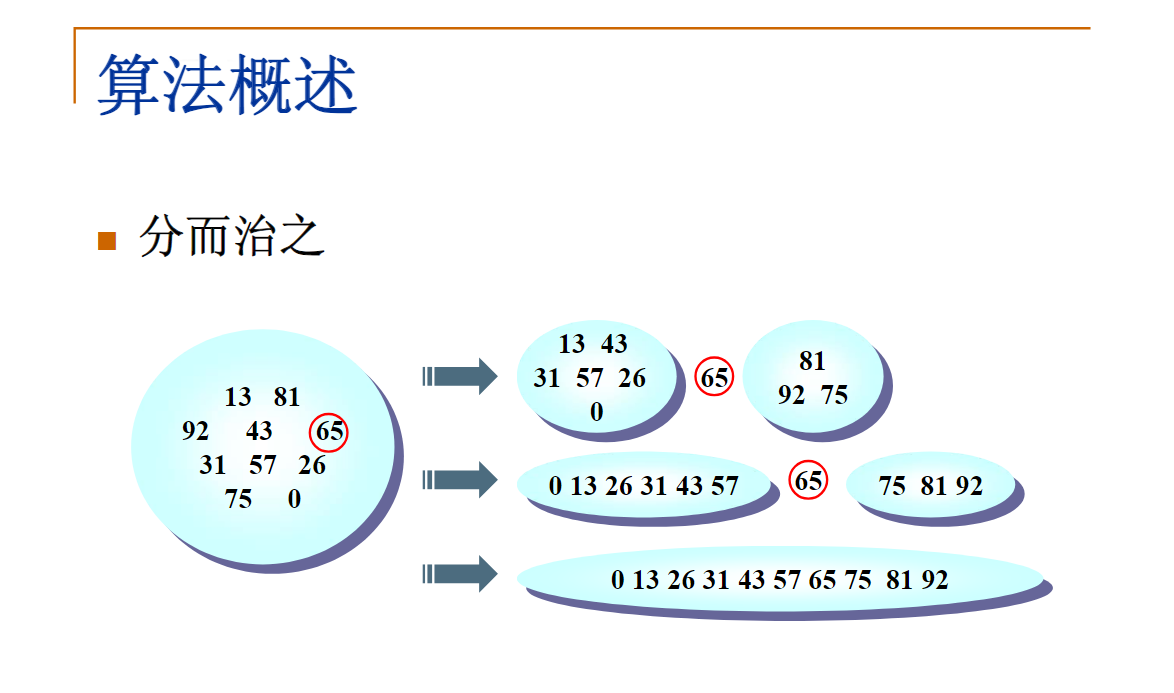

什么是快速排序算法的最好情况?每次正好中分
快速排序,又称划分交换排序(partition-exchange sort)
主要步骤:选主元、划分子集、分别处理


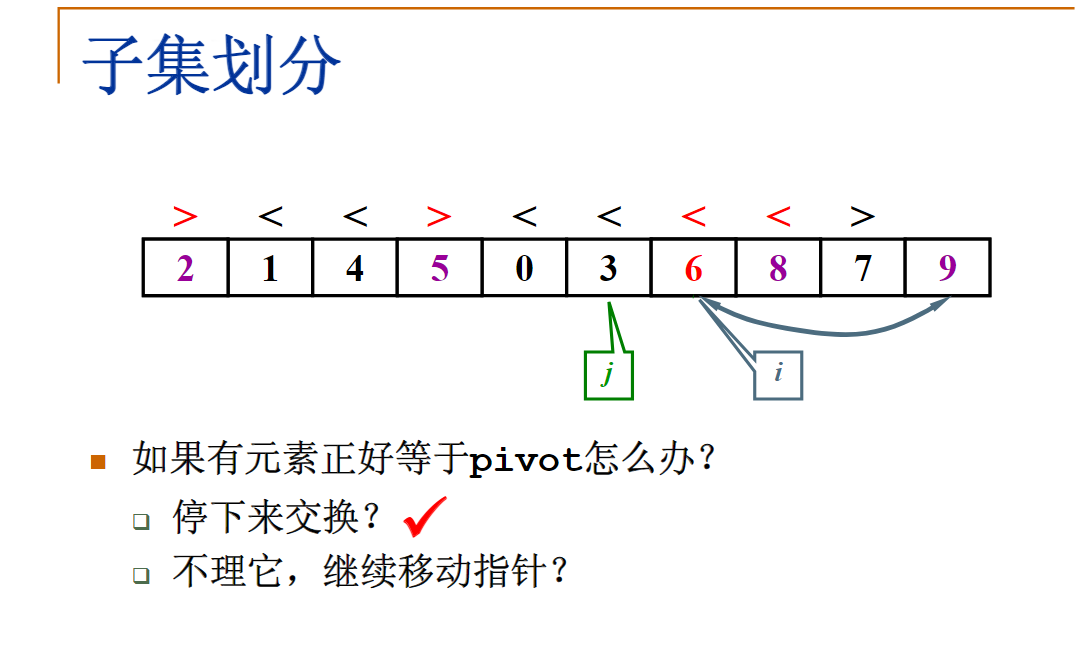

1.基本思想
通过一趟排序将待排记录分隔成独立的两部分,其中一部分记录的关键字均比另一部分的关键字小,则可分别对这两部分记录继续进行排序,以达到整个序列有序。
2. 实现逻辑
快速排序使用分治法(Divide and conquer)策略来把一个序列(list)分为两个子序列(sub-lists)。
① 从数列中挑出一个元素,称为 “基准”(pivot),
② 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作。
③ 递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
递归到最底部时,数列的大小是零或一,也就是已经排序好了。这个算法一定会结束,因为在每次的迭代(iteration)中,它至少会把一个元素摆到它最后的位置去。
3. 动图演示

快速排序
4. 复杂度
平均时间复杂度:O(NlogN)
最佳时间复杂度:O(NlogN)
最差时间复杂度:O(N^2)
空间复杂度:根据实现方式的不同而不同
5. 代码实现

/* 快速排序 */
ElementType Median3( ElementType A[], int Left, int Right )
{
int Center = (Left+Right) / 2;
if ( A[Left] > A[Center] )
Swap( &A[Left], &A[Center] );
if ( A[Left] > A[Right] )
Swap( &A[Left], &A[Right] );
if ( A[Center] > A[Right] )
Swap( &A[Center], &A[Right] );
/* 此时A[Left] <= A[Center] <= A[Right] */
Swap( &A[Center], &A[Right-1] ); /* 将基准Pivot藏到右边*/
/* 只需要考虑A[Left+1] … A[Right-2] */
return A[Right-1]; /* 返回基准Pivot */
}
void Qsort( ElementType A[], int Left, int Right )
{ /* 核心递归函数 */
int Pivot, Cutoff, Low, High;
if ( Cutoff <= Right-Left ) { /* 如果序列元素充分多,进入快排 */
Pivot = Median3( A, Left, Right ); /* 选基准 */
Low = Left; High = Right-1;
while (1) { /*将序列中比基准小的移到基准左边,大的移到右边*/
while ( A[++Low] < Pivot ) ;
while ( A[--High] > Pivot ) ;
if ( Low < High ) Swap( &A[Low], &A[High] );
else break;
}
Swap( &A[Low], &A[Right-1] ); /* 将基准换到正确的位置 */
Qsort( A, Left, Low-1 ); /* 递归解决左边 */
Qsort( A, Low+1, Right ); /* 递归解决右边 */
}
else InsertionSort( A+Left, Right-Left+1 ); /* 元素太少,用简单排序 */
}
void QuickSort( ElementType A[], int N )
{ /* 统一接口 */
Qsort( A, 0, N-1 );
}
6快速排序-直接调用库函数
/* 快速排序 - 直接调用库函数 */
#include <stdlib.h>
/*---------------简单整数排序--------------------*/
int compare(const void *a, const void *b)
{ /* 比较两整数。非降序排列 */
return (*(int*)a - *(int*)b);
}
/* 调用接口 */
qsort(A, N, sizeof(int), compare);
/*---------------简单整数排序--------------------*/
/*--------------- 一般情况下,对结构体Node中的某键值key排序 ---------------*/
struct Node {
int key1, key2;
} A[MAXN];
int compare2keys(const void *a, const void *b)
{ /* 比较两种键值:按key1非升序排列;如果key1相等,则按key2非降序排列 */
int k;
if ( ((const struct Node*)a)->key1 < ((const struct Node*)b)->key1 )
k = 1;
else if ( ((const struct Node*)a)->key1 > ((const struct Node*)b)->key1 )
k = -1;
else { /* 如果key1相等 */
if ( ((const struct Node*)a)->key2 < ((const struct Node*)b)->key2 )
k = -1;
else
k = 1;
}
return k;
}
/* 调用接口 */
qsort(A, N, sizeof(struct Node), compare2keys);
/*--------------- 一般情况下,对结构体Node中的某键值key排序 ---------------*/
表排序
当待排序的元素是结构体等复杂元素时,可以使用表排序
间接排序:不移动元素本身,只移动指针
原因:移动元素本身耗时较长
例如下面按照关键字排序:
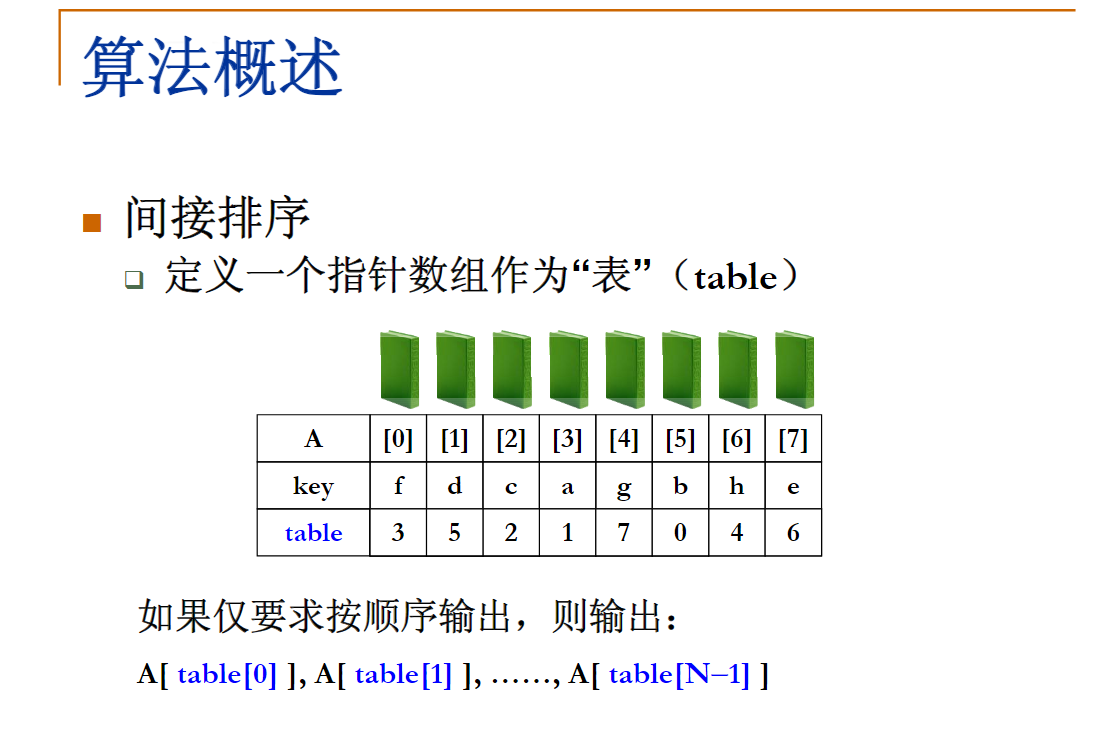
key行中元素不变,用插入排序改变table行中的元素
table等于3说明这里放的是A[3]
1给定A[]={46, 23, 8, 99, 31, 12, 85},调用非递归的归并排序加表排序执行第1趟后,表元素的结果是:
- A.0, 1, 2, 3, 4, 5, 6
- B.1, 0, 3, 2, 6, 5, 4
- C.1, 0, 2, 3, 5, 4, 6
- D.0, 2, 1, 4, 3, 5, 6
正确答案:C你选对了
非递归的归并排序第一趟:两两比较
2给定A[]={23, 46, 8, 99, 31, 12, 85},调用表排序后,表元素的结果是:
- A.1, 2, 3, 4, 5, 6, 7
- B.2, 0, 3, 5, 1, 4, 6
- C.3, 6, 1, 5, 2, 7, 4
- D.2, 5, 0, 4, 1, 6, 3
正确答案:D你选对了
物理排序
在表排序的基础上移动元素本身

三种颜色对应三个环
如何判断一个环的结束?
正确答案:每访问一个空位i后,就令table[i]=i。当发现table[i]==i时,环就结束了。
注:有个临时变量Temp

物理排序过程的最坏情况是:有N/2个环,每个环包含2个元素
计数排序
**计数排序(Counting sort)**是一种稳定的线性时间排序算法。
1. 基本思想
计数排序使用一个额外的数组C,其中第i个元素是待排序数组A中值等于i的元素的个数。
计数排序的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。
用来计数的数组C的长度取决于待排序数组中数据的范围(等于待排序数组的最大值与最小值的差加上1),然后进行分配、收集处理:
① 分配。扫描一遍原始数组,以当前值-minValue作为下标,将该下标的计数器增1。
② 收集。扫描一遍计数器数组,按顺序把值收集起来。
2. 实现逻辑
① 找出待排序的数组中最大和最小的元素
② 统计数组中每个值为i的元素出现的次数,存入数组C的第i项
③ 对所有的计数累加(从C中的第一个元素开始,每一项和前一项相加)
④ 反向填充目标数组:将每个元素i放在新数组的第C(i)项,每放一个元素就将C(i)减去1
3. 动图演示
计数排序演示
举个例子,假设有无序数列nums=[2, 1, 3, 1, 5], 首先扫描一遍获取最小值和最大值,maxValue=5, minValue=1,于是开一个长度为5的计数器数组counter
(1) 分配
统计每个元素出现的频率,得到counter=[2, 1, 1, 0, 1],例如counter[0]表示值0+minValue=1出现了2次。
(2) 收集
counter[0]=2表示1出现了两次,那就向原始数组写入两个1,counter[1]=1表示2出现了1次,那就向原始数组写入一个2,依次类推,最终原始数组变为[1,1,2,3,5],排好序了。
4. 复杂度分析
平均时间复杂度:O(n + k)
最佳时间复杂度:O(n + k)
最差时间复杂度:O(n + k)
空间复杂度:O(n + k)
当输入的元素是n 个0到k之间的整数时,它的运行时间是 O(n + k)。。在实际工作中,当k=O(n)时,我们一般会采用计数排序,这时的运行时间为O(n)。
计数排序需要两个额外的数组用来对元素进行计数和保存排序的输出结果,所以空间复杂度为O(k+n)。
计数排序的一个重要性质是它是稳定的:具有相同值的元素在输出数组中的相对次序与它们在输入数组中的相对次序是相同的。也就是说,对两个相同的数来说,在输入数组中先出现的数,在输出数组中也位于前面。
计数排序的稳定性很重要的一个原因是:计数排序经常会被用于基数排序算法的一个子过程。我们将在后面文章中介绍,为了使基数排序能够正确运行,计数排序必须是稳定的。
5. 代码实现
// 计数排序(C)
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
void print_arr(int *arr, int n) {
int i;
printf("%d", arr[0]);
for (i = 1; i < n; i++)
printf(" %d", arr[i]);
printf("\n");
}
void counting_sort(int *ini_arr, int *sorted_arr, int n) {
int *count_arr = (int *) malloc(sizeof(int) * 100);
int i, j, k;
for (k = 0; k < 100; k++)
count_arr[k] = 0;
for (i = 0; i < n; i++)
count_arr[ini_arr[i]]++;
for (k = 1; k < 100; k++)
count_arr[k] += count_arr[k - 1];
for (j = n; j > 0; j--)
sorted_arr[--count_arr[ini_arr[j - 1]]] = ini_arr[j - 1];
free(count_arr);
}
int main(int argc, char **argv) {
int n = 10;
int i;
int *arr = (int *) malloc(sizeof(int) * n);
int *sorted_arr = (int *) malloc(sizeof(int) * n);
srand(time(0));
for (i = 0; i < n; i++)
arr[i] = rand() % 100;
printf("ini_array: ");
print_arr(arr, n);
counting_sort(arr, sorted_arr, n);
printf("sorted_array: ");
print_arr(sorted_arr, n);
free(arr);
free(sorted_arr);
return 0;
}
计数算法只能使用在已知序列中的元素在0-k之间,且要求排序的复杂度在线性效率上。 Â 计数排序和基数排序很类似,都是非比较型排序算法。但是,它们的核心思想是不同的,基数排序主要是按照进制位对整数进行依次排序,而计数排序主要侧重于对有限范围内对象的统计。基数排序可以采用计数排序来实现。
桶排序

桶排序(Bucket sort)或所谓的箱排序,是一个排序算法,工作的原理是将数组分到有限数量的桶里。每个桶再个别排序(有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排序),最后依次把各个桶中的记录列出来记得到有序序列。桶排序是鸽巢排序的一种归纳结果。当要被排序的数组内的数值是均匀分配的时候,桶排序使用线性时间(Θ(n))。但桶排序并不是比较排序,他不受到O(n log n)下限的影响。
1. 基本思想
桶排序的思想近乎彻底的分治思想。
桶排序假设待排序的一组数均匀独立的分布在一个范围中,并将这一范围划分成几个子范围(桶)。
然后基于某种映射函数f ,将待排序列的关键字 k 映射到第i个桶中 (即桶数组B 的下标i) ,那么该关键字k 就作为 B[i]中的元素 (每个桶B[i]都是一组大小为N/M 的序列 )。
接着将各个桶中的数据有序的合并起来 : 对每个桶B[i] 中的所有元素进行比较排序 (可以使用快排)。然后依次枚举输出 B[0]….B[M] 中的全部内容即是一个有序序列。
补充: 映射函数一般是
f = array[i] / k; k^2 = n; n是所有元素个数
为了使桶排序更加高效,我们需要做到这两点:
1、在额外空间充足的情况下,尽量增大桶的数量;
2、使用的映射函数能够将输入的 N 个数据均匀的分配到 K 个桶中;
同时,对于桶中元素的排序,选择何种比较排序算法对于性能的影响至关重要。
2. 实现逻辑
- 设置一个定量的数组当作空桶子。
- 寻访序列,并且把项目一个一个放到对应的桶子去。
- 对每个不是空的桶子进行排序。
- 从不是空的桶子里把项目再放回原来的序列中。
3. 动图演示
桶排序演示
分步骤图示说明:设有数组 array = [63, 157, 189, 51, 101, 47, 141, 121, 157, 156, 194, 117, 98, 139, 67, 133, 181, 13, 28, 109],对其进行桶排序:
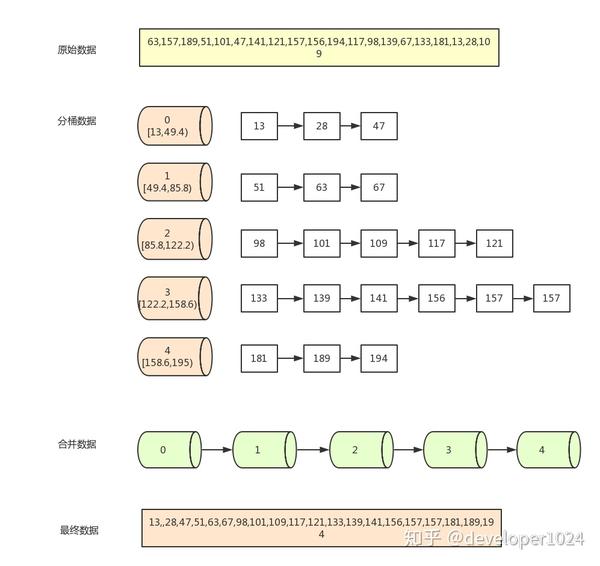
4. 复杂度分析
平均时间复杂度:O(n + k)
最佳时间复杂度:O(n + k)
最差时间复杂度:O(n ^ 2)
空间复杂度:O(n * k)
稳定性:稳定
桶排序最好情况下使用线性时间O(n),桶排序的时间复杂度,取决与对各个桶之间数据进行排序的时间复杂度,因为其它部分的时间复杂度都为O(n)。很显然,桶划分的越小,各个桶之间的数据越少,排序所用的时间也会越少。但相应的空间消耗就会增大。
5. 代码实现
假设数据分布在[0,100)之间,每个桶内部用链表表示,在数据入桶的同时插入排序。然后把各个桶中的数据合并。
#include<iterator>
#include<iostream>
#include<vector>
using namespace std;
const int BUCKET_NUM = 10;
struct ListNode{
explicit ListNode(int i=0):mData(i),mNext(NULL){}
ListNode* mNext;
int mData;
};
ListNode* insert(ListNode* head,int val){
ListNode dummyNode;
ListNode *newNode = new ListNode(val);
ListNode *pre,*curr;
dummyNode.mNext = head;
pre = &dummyNode;
curr = head;
while(NULL!=curr && curr->mData<=val){
pre = curr;
curr = curr->mNext;
}
newNode->mNext = curr;
pre->mNext = newNode;
return dummyNode.mNext;
}
ListNode* Merge(ListNode *head1,ListNode *head2){
ListNode dummyNode;
ListNode *dummy = &dummyNode;
while(NULL!=head1 && NULL!=head2){
if(head1->mData <= head2->mData){
dummy->mNext = head1;
head1 = head1->mNext;
}else{
dummy->mNext = head2;
head2 = head2->mNext;
}
dummy = dummy->mNext;
}
if(NULL!=head1) dummy->mNext = head1;
if(NULL!=head2) dummy->mNext = head2;
return dummyNode.mNext;
}
void BucketSort(int n,int arr[]){
vector<ListNode*> buckets(BUCKET_NUM,(ListNode*)(0));
for(int i=0;i<n;++i){
int index = arr[i]/BUCKET_NUM;
ListNode *head = buckets.at(index);
buckets.at(index) = insert(head,arr[i]);
}
ListNode *head = buckets.at(0);
for(int i=1;i<BUCKET_NUM;++i){
head = Merge(head,buckets.at(i));
}
for(int i=0;i<n;++i){
arr[i] = head->mData;
head = head->mNext;
}
}
桶排序是计数排序的变种,它利用了函数的映射关系,高效与否的关键就在于这个映射函数的确定。把计数排序中相邻的m个”小桶”放到一个”大桶”中,在分完桶后,对每个桶进行排序(一般用快排),然后合并成最后的结果。
算法思想和散列中的开散列法差不多,当冲突时放入同一个桶中;可应用于数据量分布比较均匀,或比较侧重于区间数量时。
桶排序最关键的建桶,如果桶设计得不好的话桶排序是几乎没有作用的。通常情况下,上下界有两种取法,第一种是取一个10^n或者是2^n的数,方便实现。另一种是取数列的最大值和最小值然后均分作桶.
基数排序
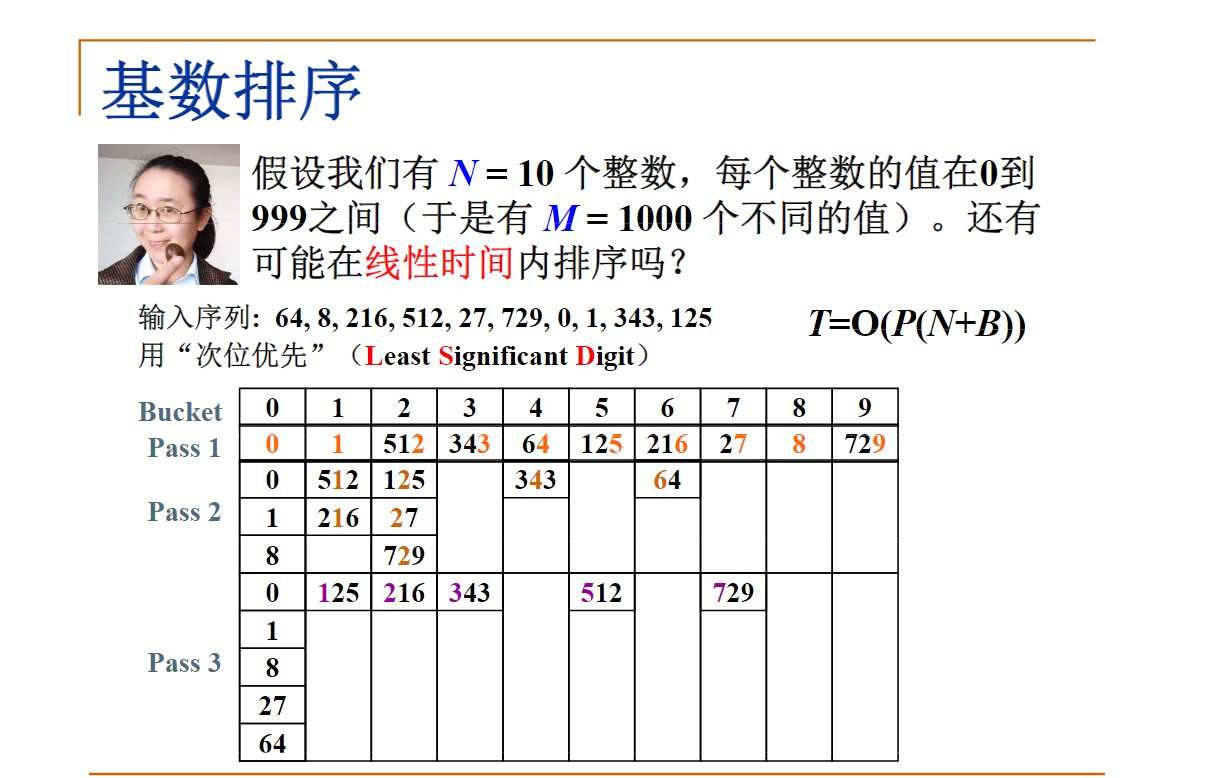
基数排序是稳定的算法。
10个基数就建立10个桶
基数排序(Radix sort)是一种非比较型整数排序算法。
1. 基本思想
原理是将整数按位数切割成不同的数字,然后按每个位数分别比较。基数排序的方式可以采用LSD(Least significant digital)或MSD(Most significant digital),LSD的排序方式由键值的最右边开始,而MSD则相反,由键值的最左边开始。
- MSD:先从高位开始进行排序,在每个关键字上,可采用计数排序
- LSD:先从低位开始进行排序,在每个关键字上,可采用桶排序
2. 实现逻辑
① 将所有待比较数值(正整数)统一为同样的数位长度,数位较短的数前面补零。
② 从最低位开始,依次进行一次排序。
③ 这样从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列。
3. 动图演示
分步图示说明:设有数组 array = {53, 3, 542, 748, 14, 214, 154, 63, 616},对其进行基数排序:
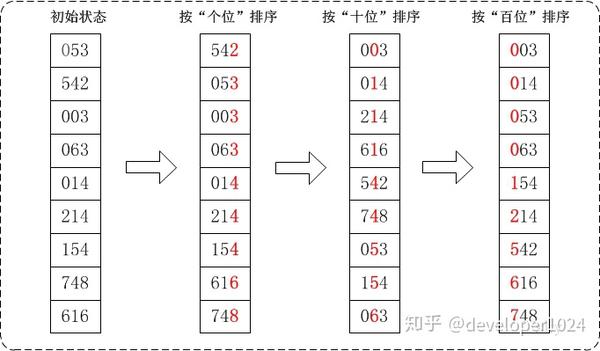
在上图中,首先将所有待比较数字统一为统一位数长度,接着从最低位开始,依次进行排序。
- 按照个位数进行排序。
- 按照十位数进行排序。
- 按照百位数进行排序。
排序后,数列就变成了一个有序序列。
4. 复杂度分析
时间复杂度:O(k*N)
空间复杂度:O(k + N)
稳定性:稳定
设待排序的数组R[1..n],数组中最大的数是d位数,基数为r(如基数为10,即10进制,最大有10种可能,即最多需要10个桶来映射数组元素)。
处理一位数,需要将数组元素映射到r个桶中,映射完成后还需要收集,相当于遍历数组一遍,最多元素数为n,则时间复杂度为O(n+r)。所以,总的时间复杂度为O(d*(n+r))。
基数排序过程中,用到一个计数器数组,长度为r,还用到一个r_n的二位数组来做为桶,所以空间复杂度为O(r_n)。
基数排序基于分别排序,分别收集,所以是稳定的。
5.基数排序 - 次位优先代码实现
/* 基数排序 - 次位优先 */
/* 假设元素最多有MaxDigit个关键字,基数全是同样的Radix */
#define MaxDigit 4
#define Radix 10
/* 桶元素结点 */
typedef struct Node *PtrToNode;
struct Node {
int key;
PtrToNode next;
};
/* 桶头结点 */
struct HeadNode {
PtrToNode head, tail;
};
typedef struct HeadNode Bucket[Radix];
int GetDigit ( int X, int D )
{ /* 默认次位D=1, 主位D<=MaxDigit */
int d, i;
for (i=1; i<=D; i++) {
d = X % Radix;
X /= Radix;
}
return d;
}
void LSDRadixSort( ElementType A[], int N )
{ /* 基数排序 - 次位优先 */
int D, Di, i;
Bucket B;
PtrToNode tmp, p, List = NULL;
for (i=0; i<Radix; i++) /* 初始化每个桶为空链表 */
B[i].head = B[i].tail = NULL;
for (i=0; i<N; i++) { /* 将原始序列逆序存入初始链表List */
tmp = (PtrToNode)malloc(sizeof(struct Node));
tmp->key = A[i];
tmp->next = List;
List = tmp;
}
/* 下面开始排序 */
for (D=1; D<=MaxDigit; D++) { /* 对数据的每一位循环处理 */
/* 下面是分配的过程 */
p = List;
while (p) {
Di = GetDigit(p->key, D); /* 获得当前元素的当前位数字 */
/* 从List中摘除 */
tmp = p; p = p->next;
/* 插入B[Di]号桶尾 */
tmp->next = NULL;
if (B[Di].head == NULL)
B[Di].head = B[Di].tail = tmp;
else {
B[Di].tail->next = tmp;
B[Di].tail = tmp;
}
}
/* 下面是收集的过程 */
List = NULL;
for (Di=Radix-1; Di>=0; Di--) { /* 将每个桶的元素顺序收集入List */
if (B[Di].head) { /* 如果桶不为空 */
/* 整桶插入List表头 */
B[Di].tail->next = List;
List = B[Di].head;
B[Di].head = B[Di].tail = NULL; /* 清空桶 */
}
}
}
/* 将List倒入A[]并释放空间 */
for (i=0; i<N; i++) {
tmp = List;
List = List->next;
A[i] = tmp->key;
free(tmp);
}
}
5.基数排序 - 主位优先代码实现
/* 基数排序 - 主位优先 */
/* 假设元素最多有MaxDigit个关键字,基数全是同样的Radix */
#define MaxDigit 4
#define Radix 10
/* 桶元素结点 */
typedef struct Node *PtrToNode;
struct Node{
int key;
PtrToNode next;
};
/* 桶头结点 */
struct HeadNode {
PtrToNode head, tail;
};
typedef struct HeadNode Bucket[Radix];
int GetDigit ( int X, int D )
{ /* 默认次位D=1, 主位D<=MaxDigit */
int d, i;
for (i=1; i<=D; i++) {
d = X%Radix;
X /= Radix;
}
return d;
}
void MSD( ElementType A[], int L, int R, int D )
{ /* 核心递归函数: 对A[L]...A[R]的第D位数进行排序 */
int Di, i, j;
Bucket B;
PtrToNode tmp, p, List = NULL;
if (D==0) return; /* 递归终止条件 */
for (i=0; i<Radix; i++) /* 初始化每个桶为空链表 */
B[i].head = B[i].tail = NULL;
for (i=L; i<=R; i++) { /* 将原始序列逆序存入初始链表List */
tmp = (PtrToNode)malloc(sizeof(struct Node));
tmp->key = A[i];
tmp->next = List;
List = tmp;
}
/* 下面是分配的过程 */
p = List;
while (p) {
Di = GetDigit(p->key, D); /* 获得当前元素的当前位数字 */
/* 从List中摘除 */
tmp = p; p = p->next;
/* 插入B[Di]号桶 */
if (B[Di].head == NULL) B[Di].tail = tmp;
tmp->next = B[Di].head;
B[Di].head = tmp;
}
/* 下面是收集的过程 */
i = j = L; /* i, j记录当前要处理的A[]的左右端下标 */
for (Di=0; Di<Radix; Di++) { /* 对于每个桶 */
if (B[Di].head) { /* 将非空的桶整桶倒入A[], 递归排序 */
p = B[Di].head;
while (p) {
tmp = p;
p = p->next;
A[j++] = tmp->key;
free(tmp);
}
/* 递归对该桶数据排序, 位数减1 */
MSD(A, i, j-1, D-1);
i = j; /* 为下一个桶对应的A[]左端 */
}
}
}
void MSDRadixSort( ElementType A[], int N )
{ /* 统一接口 */
MSD(A, 0, N-1, MaxDigit);
}
基数排序与计数排序、桶排序这三种排序算法都利用了桶的概念,但对桶的使用方法上有明显差异:
- 基数排序:根据键值的每位数字来分配桶;
- 计数排序:每个桶只存储单一键值;
- 桶排序:每个桶存储一定范围的数值;
基数排序不是直接根据元素整体的大小进行元素比较,而是将原始列表元素分成多个部分,对每一部分按一定的规则进行排序,进而形成最终的有序列表。
多关键字排序
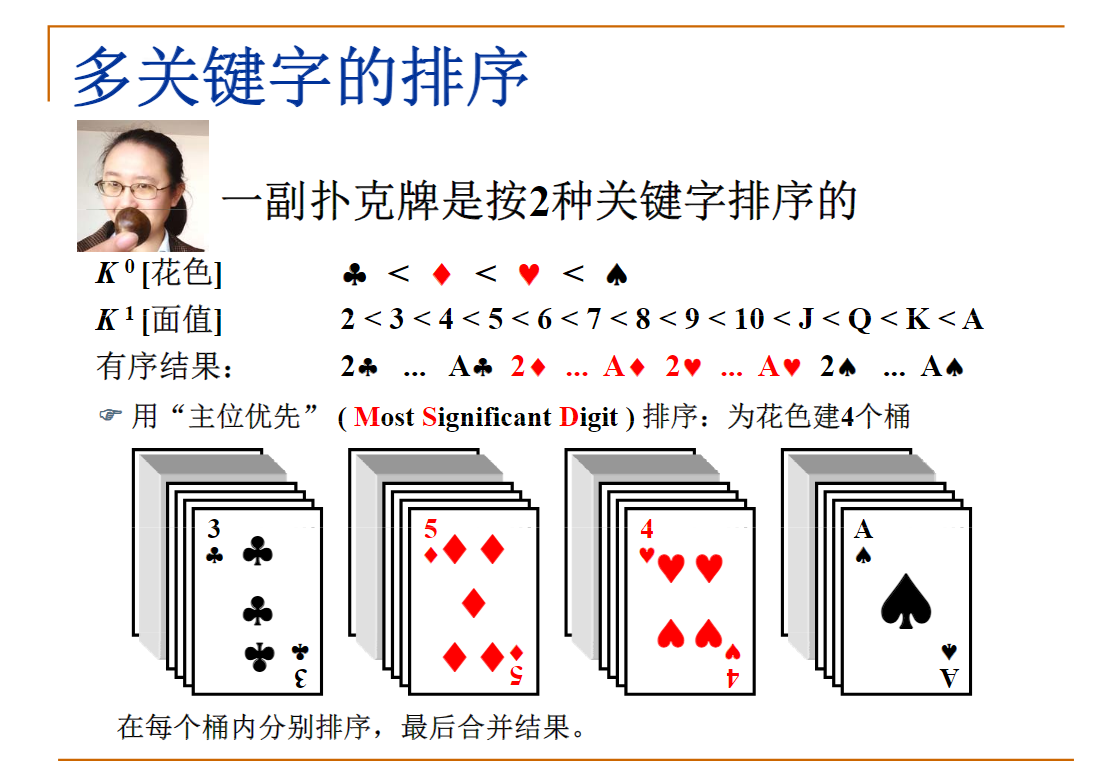
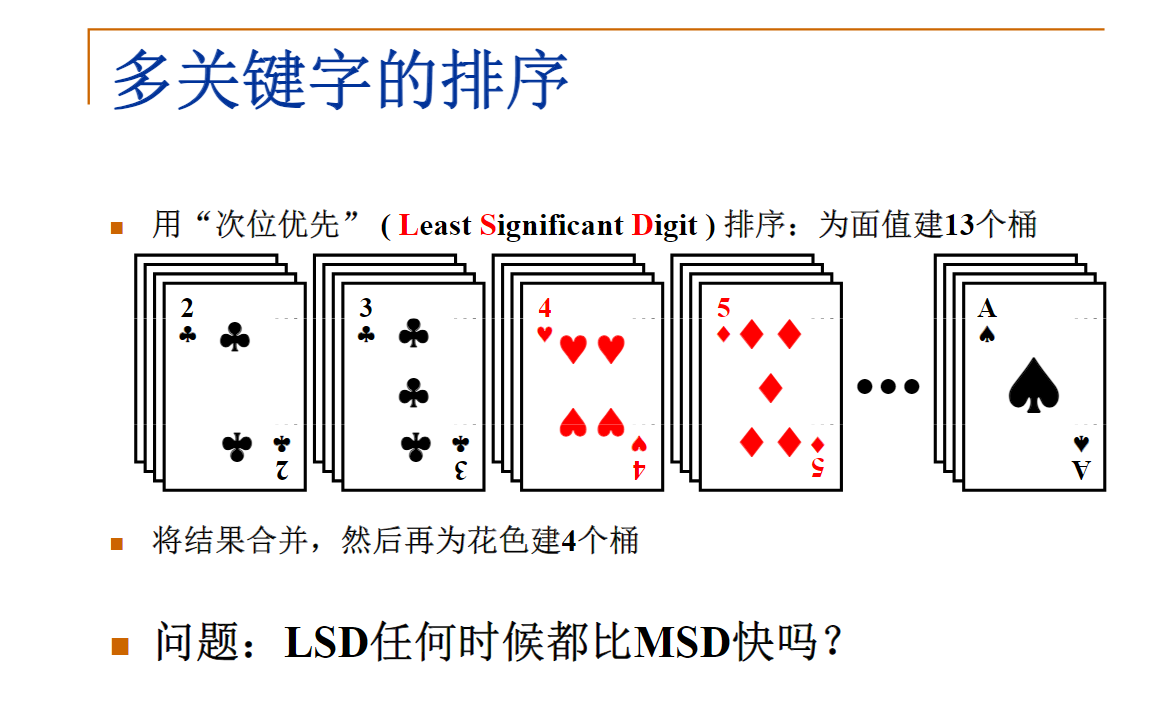
MOOC-PTA排序题目
- PTA 09-排序1 排序
- PTA 09-排序2 Insert or Merge
- PTA 09-排序3 Insertion or Heap Sort
- PTA 10-排序4 统计工龄
- PTA 10-排序5 PAT Judge
- PTA 10-排序6 Sort with Swap(0, i)
PTA 09-排序1 排序
略
PTA 09-排序2 Insert or Merge
According to Wikipedia:
Insertion sort iterates, consuming one input element each repetition, and growing a sorted output list. Each iteration, insertion sort removes one element from the input data, finds the location it belongs within the sorted list, and inserts it there. It repeats until no input elements remain.
Merge sort works as follows: Divide the unsorted list into N sublists, each containing 1 element (a list of 1 element is considered sorted). Then repeatedly merge two adjacent sublists to produce new sorted sublists until there is only 1 sublist remaining.
Now given the initial sequence of integers, together with a sequence which is a result of several iterations of some sorting method, can you tell which sorting method we are using?
Input Specification:
Each input file contains one test case. For each case, the first line gives a positive integer N (≤100). Then in the next line, N integers are given as the initial sequence. The last line contains the partially sorted sequence of the N numbers. It is assumed that the target sequence is always ascending. All the numbers in a line are separated by a space.
Output Specification:
For each test case, print in the first line either "Insertion Sort" or "Merge Sort" to indicate the method used to obtain the partial result. Then run this method for one more iteration and output in the second line the resuling sequence. It is guaranteed that the answer is unique for each test case. All the numbers in a line must be separated by a space, and there must be no extra space at the end of the line.
Sample Input 1:
10
3 1 2 8 7 5 9 4 6 0
1 2 3 7 8 5 9 4 6 0
Sample Output 1:
Insertion Sort
1 2 3 5 7 8 9 4 6 0
Sample Input 2:
10
3 1 2 8 7 5 9 4 0 6
1 3 2 8 5 7 4 9 0 6
Sample Output 2:
Merge Sort
1 2 3 8 4 5 7 9 0 6

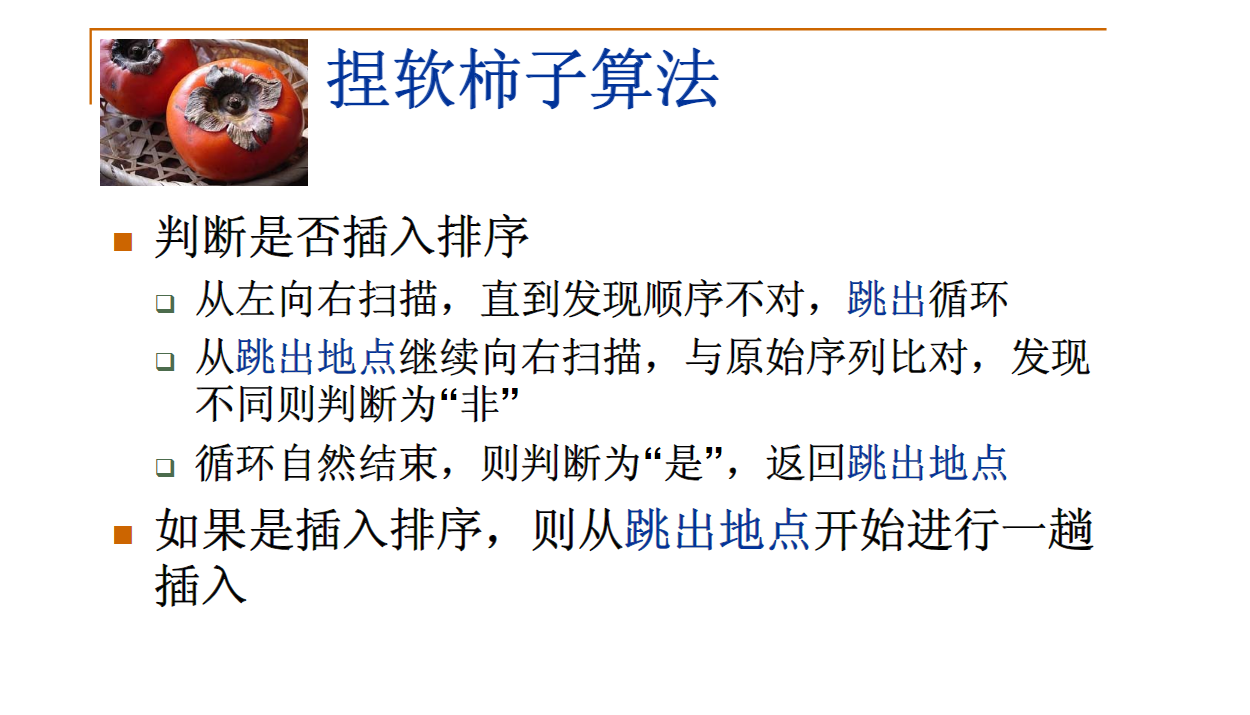


#include <stdio.h>
#include <stdlib.h>
typedef int ElementType;
int Compare_Array(ElementType A[], ElementType B[], int N)
{
int flag = 1;
for(int i=0; i<N; i++)
{
if(A[i] != B[i])
{
flag = 0;
break;
}
}
return flag;
}
void Merge(ElementType A[], ElementType TmpA[], int L, int R, int RightEnd)
{
int LeftEnd, NumElements, Tmp;
int i;
LeftEnd = R - 1;
Tmp = L;
NumElements = RightEnd - L + 1;
while(L <= LeftEnd && R <= RightEnd)
{
if(A[L] < A[R])
TmpA[Tmp++] = A[L++];
else
TmpA[Tmp++] = A[R++];
}
while(L <= LeftEnd)
TmpA[Tmp++] = A[L++];
while(R <= RightEnd)
TmpA[Tmp++] = A[R++];
for(i=0; i<NumElements; i++, RightEnd--)
A[RightEnd] = TmpA[RightEnd];
}
void MSort(ElementType A[], ElementType TmpA[], int L, int RightEnd)
{
int Center;
if(L < RightEnd)
{
Center = (L + RightEnd)/2;
MSort(A, TmpA, L, Center);
MSort(A, TmpA, Center+1, RightEnd);
Merge(A, TmpA, L, Center+1, RightEnd);
}
}
void Merge_pass( ElementType A[], ElementType TmpA[], int N, int length )
{ /* 两两归并相邻有序子列 */
int i, j;
for ( i=0; i <= N-2*length; i += 2*length )
Merge( A, TmpA, i, i+length, i+2*length-1 );
if ( i+length < N ) /* 归并最后2个子列*/
Merge( A, TmpA, i, i+length, N-1);
else /* 最后只剩1个子列*/
for ( j = i; j < N; j++ ) TmpA[j] = A[j];
}
void PrintA(ElementType A[], int N)
{
int First = 1;
for(int i=0; i<N; i++)
{
if(First)
{
printf("%d", A[i]);
First = 0;
}
else
printf(" %d", A[i]);
}
}
void Merge_Or_Insertion( ElementType A[], ElementType Temp[], int N )
{
int length;
ElementType *TmpA;
int flag = 0;
length = 1; /* 初始化子序列长度*/
TmpA = malloc( N * sizeof( ElementType ) );
if ( TmpA != NULL ) {
while( length < N ) {
Merge_pass( A, TmpA, N, length );
length *= 2;
if(flag == 1) {
PrintA(A,N);
flag = 0;
}
if(Compare_Array(A,Temp,N)) {
flag = 1;
printf("Merge Sort\n");
}
Merge_pass( TmpA, A, N, length );
length *= 2;
if(flag == 1) {
PrintA(A,N);
flag = 0;
}
if(Compare_Array(A,Temp,N)) {
flag = 1;
printf("Merge Sort\n");
}
}
free( TmpA );
}
else printf( "空间不足" );
}
void CopyArr(int A[],int B[],int N)
{
int i;
for(i=0;i<N;i++)
B[i] = A[i];
}
void Insertion_Or_Merge(ElementType A[], ElementType B[], int N)
{
int flag = 0;
for(int P=1; P<N; P++)
{
ElementType temp = A[P];
int i;
for(i=P; i>0&&A[i-1]>temp; i--)
A[i] = A[i-1];
A[i] = temp;
if(Compare_Array(A,B,N))
{
printf("Insertion Sort\n");
flag = 1;
continue;
}
if(flag)
{
PrintA(A,N);
return;
}
}
return;
}
int main()
{
int N;
scanf("%d", &N);
ElementType A[N];
for(int i=0; i<N; i++)
{
scanf("%d", &A[i]);
}
ElementType Temp[N];
for(int i=0; i<N; i++)
{
scanf("%d", &Temp[i]);
}
ElementType *A2 = (ElementType*)malloc(N*sizeof(ElementType));
ElementType *Temp2 = (ElementType*)malloc(N*sizeof(ElementType));
CopyArr(A,A2,N);
CopyArr(Temp,Temp2,N);
Insertion_Or_Merge(A,Temp,N);
Merge_Or_Insertion(A2, Temp2, N);
return 0;
}
PTA 09-排序3 Insertion or Heap Sort
According to Wikipedia:
Insertion sort iterates, consuming one input element each repetition, and growing a sorted output list. Each iteration, insertion sort removes one element from the input data, finds the location it belongs within the sorted list, and inserts it there. It repeats until no input elements remain.
Heap sort divides its input into a sorted and an unsorted region, and it iteratively shrinks the unsorted region by extracting the largest element and moving that to the sorted region. it involves the use of a heap data structure rather than a linear-time search to find the maximum.
Now given the initial sequence of integers, together with a sequence which is a result of several iterations of some sorting method, can you tell which sorting method we are using?
Input Specification:
Each input file contains one test case. For each case, the first line gives a positive integer N (≤100). Then in the next line, N integers are given as the initial sequence. The last line contains the partially sorted sequence of the N numbers. It is assumed that the target sequence is always ascending. All the numbers in a line are separated by a space.
Output Specification:
For each test case, print in the first line either "Insertion Sort" or "Heap Sort" to indicate the method used to obtain the partial result. Then run this method for one more iteration and output in the second line the resulting sequence. It is guaranteed that the answer is unique for each test case. All the numbers in a line must be separated by a space, and there must be no extra space at the end of the line.
Sample Input 1:
10
3 1 2 8 7 5 9 4 6 0
1 2 3 7 8 5 9 4 6 0
Sample Output 1:
Insertion Sort
1 2 3 5 7 8 9 4 6 0
Sample Input 2:
10
3 1 2 8 7 5 9 4 6 0
6 4 5 1 0 3 2 7 8 9
Sample Output 2:
Heap Sort
5 4 3 1 0 2 6 7 8 9
要点:增加标志,控制输出时机
#include <stdio.h>
#include <stdlib.h>
typedef int ElementType;
void Swap(ElementType *a, ElementType *b)
{
ElementType temp = *a;
*a = *b;
*b = temp;
}
void PercDown(ElementType A[], int p, int N)
{
int Parent,Child;
ElementType X;
X = A[p];
for(Parent=p; (Parent*2+1)<N; Parent=Child)
{
Child = Parent*2+1;
if(Child!=N-1 && A[Child]<A[Child+1])
Child++;
if(X>=A[Child])
break;
else
A[Parent] = A[Child];
}
A[Parent] = X;
}
void Heap_Sort(ElementType A[], int N)
{
for(int i=N/2-1; i>=0; i--)
{
PercDown(A,i,N);
}
for(int i=N-1; i>0; i--)
{
Swap(&A[0],&A[i]);
PercDown(A, 0, i);
}
}
int Compare_Array(ElementType A[], ElementType B[], int N)
{
int flag = 1;
for(int i=0; i<N; i++)
{
if(A[i] != B[i])
{
flag = 0;
break;
}
}
return flag;
}
void PrintA(ElementType A[], int N)
{
int First = 1;
for(int i=0; i<N; i++)
{
if(First)
{
printf("%d", A[i]);
First = 0;
}
else
printf(" %d", A[i]);
}
}
void CopyArr(int A[],int B[],int N)
{
int i;
for(i=0;i<N;i++)
B[i] = A[i];
}
void Insertion_Or_Merge(ElementType A[], ElementType B[], int N)
{
int flag = 0;
for(int P=1; P<N; P++)
{
ElementType temp = A[P];
int i;
for(i=P; i>0&&A[i-1]>temp; i--)
A[i] = A[i-1];
A[i] = temp;
if(Compare_Array(A,B,N))
{
printf("Insertion Sort\n");
flag = 1;
continue;
}
if(flag)
{
PrintA(A,N);
return;
}
}
return;
}
void Heap_Or_Insertion(ElementType A[], ElementType B[], int N)
{
for(int i=N/2-1; i>=0; i--)
{
PercDown(A,i,N);
}
int flag = 0;
for(int i=N-1; i>0; i--)
{
Swap(&A[0],&A[i]);
PercDown(A, 0, i);
if(Compare_Array(A,B,N))
{
printf("Heap Sort\n");
flag = 1;
continue;
}
if(flag)
{
PrintA(A,N);
return;
}
}
}
int main()
{
int N;
scanf("%d", &N);
ElementType A[N];
for(int i=0; i<N; i++)
{
scanf("%d", &A[i]);
}
ElementType Temp[N];
for(int i=0; i<N; i++)
{
scanf("%d", &Temp[i]);
}
ElementType *A2 = (ElementType*)malloc(N*sizeof(ElementType));
ElementType *Temp2 = (ElementType*)malloc(N*sizeof(ElementType));
CopyArr(A,A2,N);
CopyArr(Temp,Temp2,N);
Insertion_Or_Merge(A,Temp,N);
Heap_Or_Insertion(A2, Temp2, N);
return 0;
}
PTA 10-排序4 统计工龄
给定公司N名员工的工龄,要求按工龄增序输出每个工龄段有多少员工。
输入格式:
输入首先给出正整数N(≤105),即员工总人数;随后给出N个整数,即每个员工的工龄,范围在[0, 50]。
输出格式:
按工龄的递增顺序输出每个工龄的员工个数,格式为:“工龄:人数”。每项占一行。如果人数为0则不输出该项。
输入样例:
8
10 2 0 5 7 2 5 2
输出样例:
0:1
2:3
5:2
7:1
10:1
#include <stdio.h>
typedef int ElementType;
int main()
{
int N;
scanf("%d", &N);
ElementType Result[51]={0};
ElementType temp;
for(int i=0; i<N; i++)
{
scanf("%d", &temp);
Result[temp]++;
}
for(int i=0; i<51; i++)
{
if(Result[i]==0)
continue;
else
printf("%d:%d\n",i,Result[i]);
}
return 0;
}
PTA 10-排序5 PAT Judge
The ranklist of PAT is generated from the status list, which shows the scores of the submissions. This time you are supposed to generate the ranklist for PAT.
Input Specification:
Each input file contains one test case. For each case, the first line contains 3 positive integers, N (≤104), the total number of users, K (≤5), the total number of problems, and M (≤105), the total number of submissions. It is then assumed that the user id's are 5-digit numbers from 00001 to N, and the problem id's are from 1 to K. The next line contains K positive integers p[i] (i=1, ..., K), where p[i] corresponds to the full mark of the i-th problem. Then M lines follow, each gives the information of a submission in the following format:
user_id problem_id partial_score_obtained
where partial_score_obtained is either −1 if the submission cannot even pass the compiler, or is an integer in the range [0, p[problem_id]]. All the numbers in a line are separated by a space.
Output Specification:
For each test case, you are supposed to output the ranklist in the following format:
rank user_id total_score s[1] ... s[K]
where rank is calculated according to the total_score, and all the users with the same total_score obtain the same rank; and s[i] is the partial score obtained for the i-th problem. If a user has never submitted a solution for a problem, then "-" must be printed at the corresponding position. If a user has submitted several solutions to solve one problem, then the highest score will be counted.
The ranklist must be printed in non-decreasing order of the ranks. For those who have the same rank, users must be sorted in nonincreasing order according to the number of perfectly solved problems. And if there is still a tie, then they must be printed in increasing order of their id's. For those who has never submitted any solution that can pass the compiler, or has never submitted any solution, they must NOT be shown on the ranklist. It is guaranteed that at least one user can be shown on the ranklist.
Sample Input:
7 4 20
20 25 25 30
00002 2 12
00007 4 17
00005 1 19
00007 2 25
00005 1 20
00002 2 2
00005 1 15
00001 1 18
00004 3 25
00002 2 25
00005 3 22
00006 4 -1
00001 2 18
00002 1 20
00004 1 15
00002 4 18
00001 3 4
00001 4 2
00005 2 -1
00004 2 0
Sample Output:
1 00002 63 20 25 - 18
2 00005 42 20 0 22 -
2 00007 42 - 25 - 17
2 00001 42 18 18 4 2
5 00004 40 15 0 25 -
PTA 10-排序6 Sort with Swap(0, i)
Given any permutation of the numbers {0, 1, 2,..., N−1}, it is easy to sort them in increasing order. But what if Swap(0, *) is the ONLY operation that is allowed to use? For example, to sort {4, 0, 2, 1, 3} we may apply the swap operations in the following way:
Swap(0, 1) => {4, 1, 2, 0, 3}
Swap(0, 3) => {4, 1, 2, 3, 0}
Swap(0, 4) => {0, 1, 2, 3, 4}
Now you are asked to find the minimum number of swaps need to sort the given permutation of the first N nonnegative integers.
Input Specification:
Each input file contains one test case, which gives a positive N (≤105) followed by a permutation sequence of {0, 1, ..., N−1}. All the numbers in a line are separated by a space.
Output Specification:
For each case, simply print in a line the minimum number of swaps need to sort the given permutation.
Sample Input:
10
3 5 7 2 6 4 9 0 8 1
Sample Output:
9
查找算法
普通查找算法
顺序查找
- 被查找的数存放在一个数组中
- 从数组的第一个元素开始,依次往下比较,直到找到要找的元素为止
下面程序能在一整数数组中查找元素x的存储位置
#include <iostream>
using namespace std;
int main() {
int k,x;
int array[]={2,3,1,7,5,8,9,0,4,6};
cout<<"输入要查找的元素值:";
cin>>x;
for(k=0;k<10;k++)
{
if(x==array[k])
{
cout<<k;
break;
}
}
if(k==10) cout<<"not found";
return 0;
}
二分查找
前提:数组已排序
#include <iostream>
using namespace std;
int main() {
int x;
int array[]={5,13,19,21,37,56,64,74,80,88,92};
int high,low,mid;
cout<<"输入要查找的元素值:";
cin>>x;
low=0;
high=10;
while(low<=high)
{
mid=(high-low)/2+low;
if(x==array[mid])
{
cout<<x<<"的位置是:"<<mid<<endl;
break;
}
if(x<array[mid]) high=mid-1;
else low=mid+1;
}
if(low>high) cout<<"找不到"<<x<<endl;
return 0;
}
散列查找
散列表




哈希是一种数据按照特定关系存储的存储结构
哈希函数:值与地址的特定关系
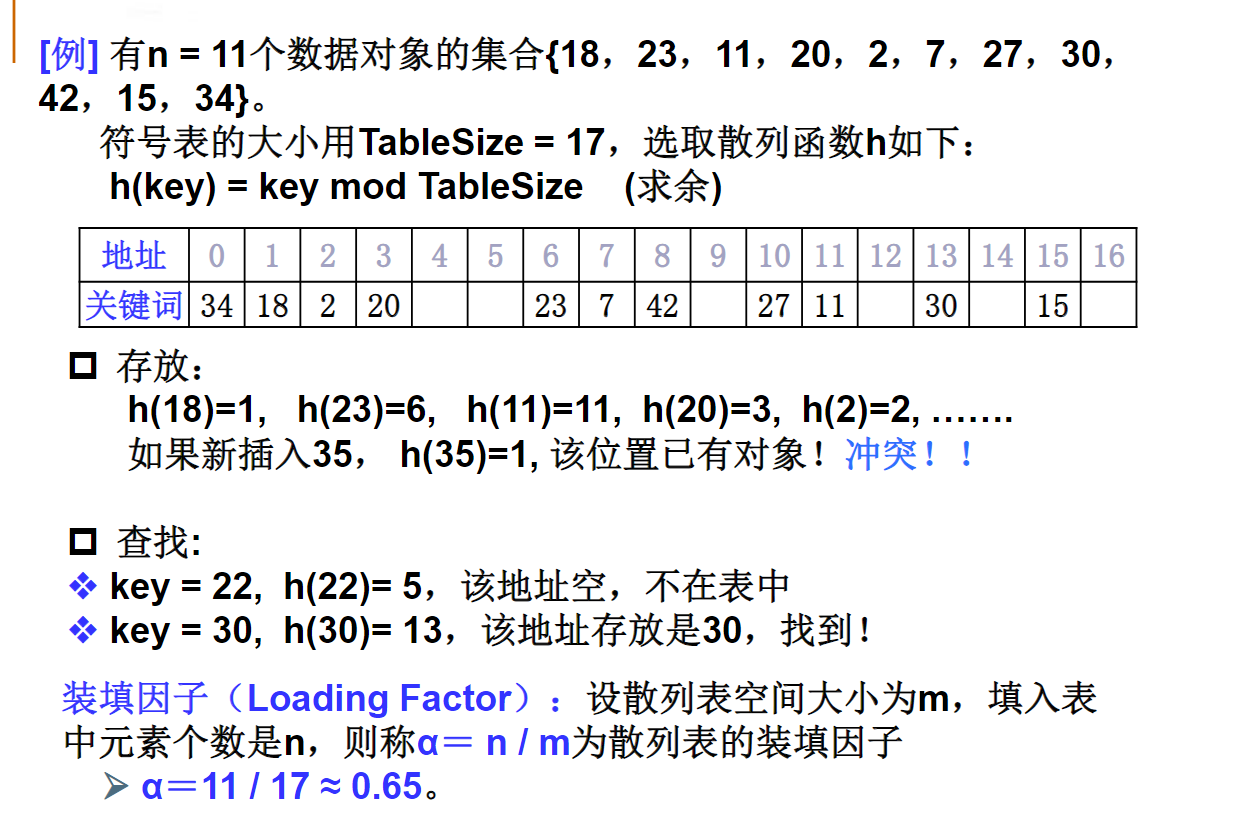
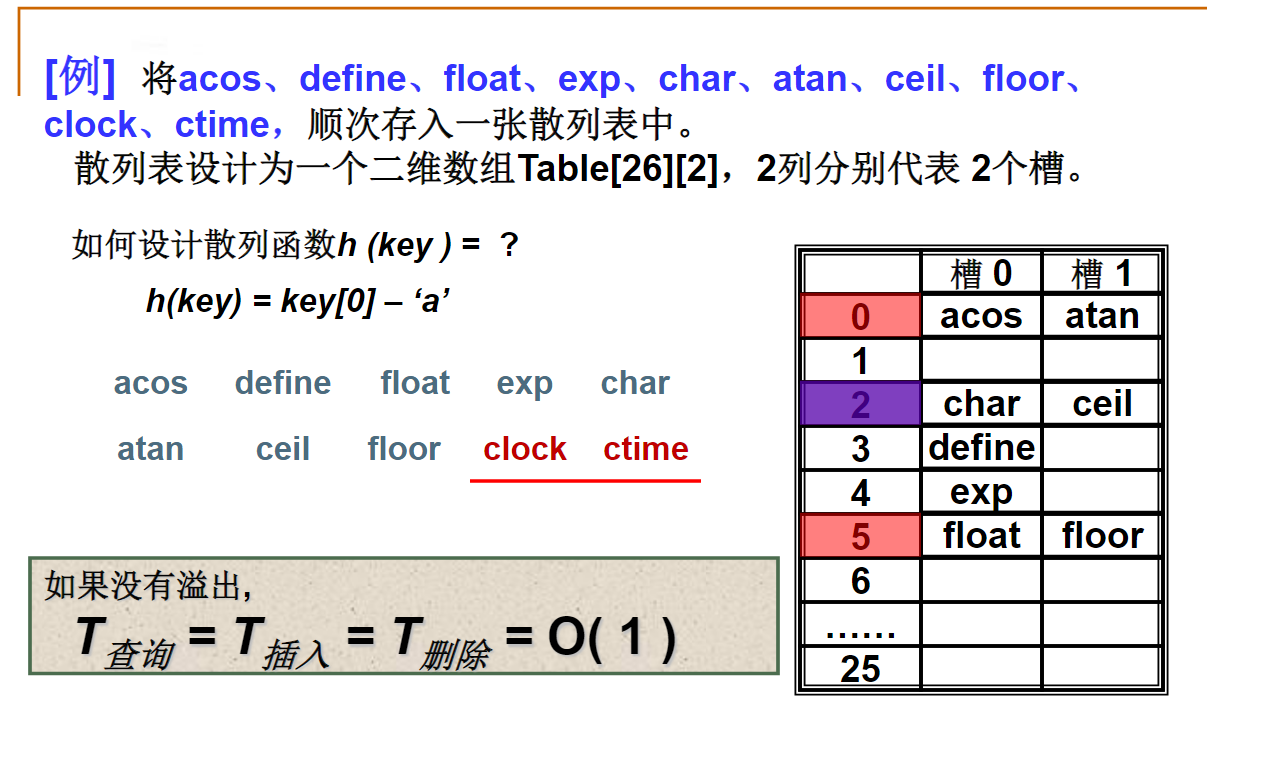
散列函数的构造方法
数字关键词的散列函数构造
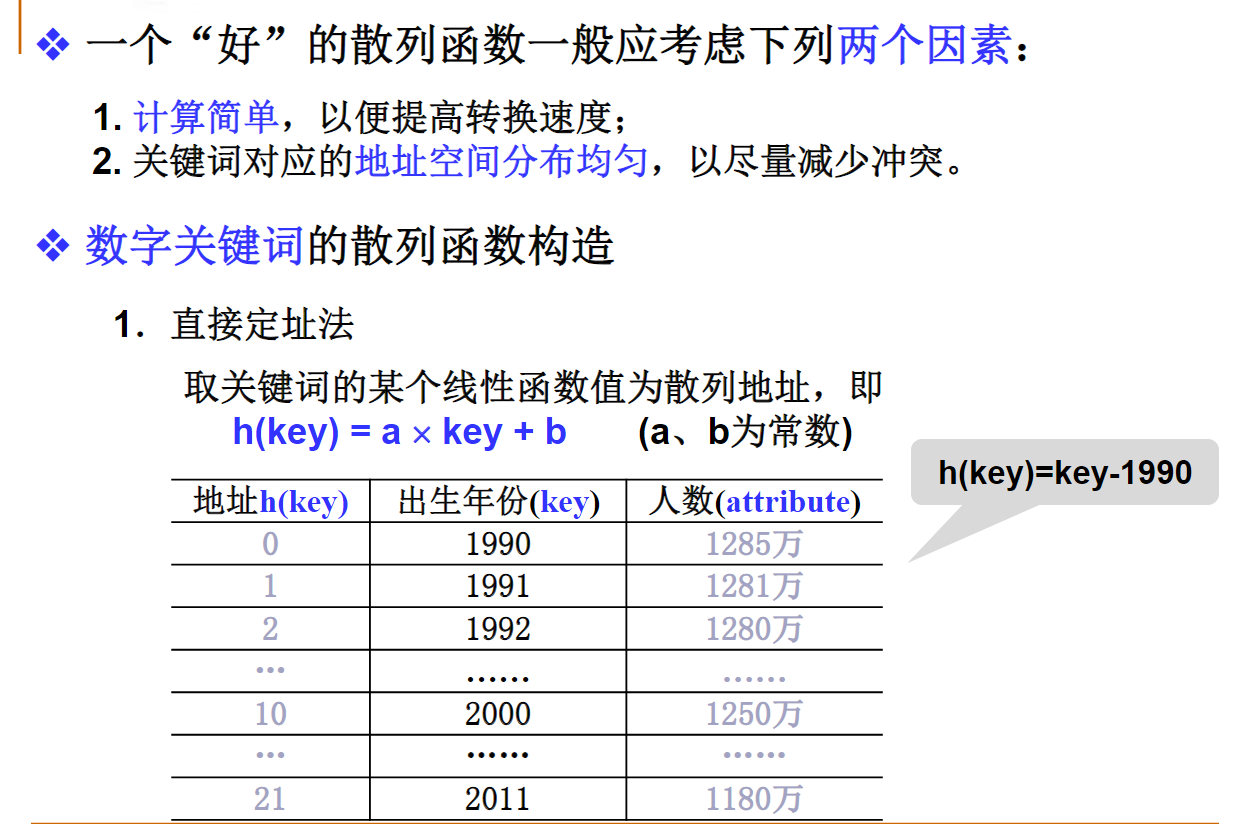
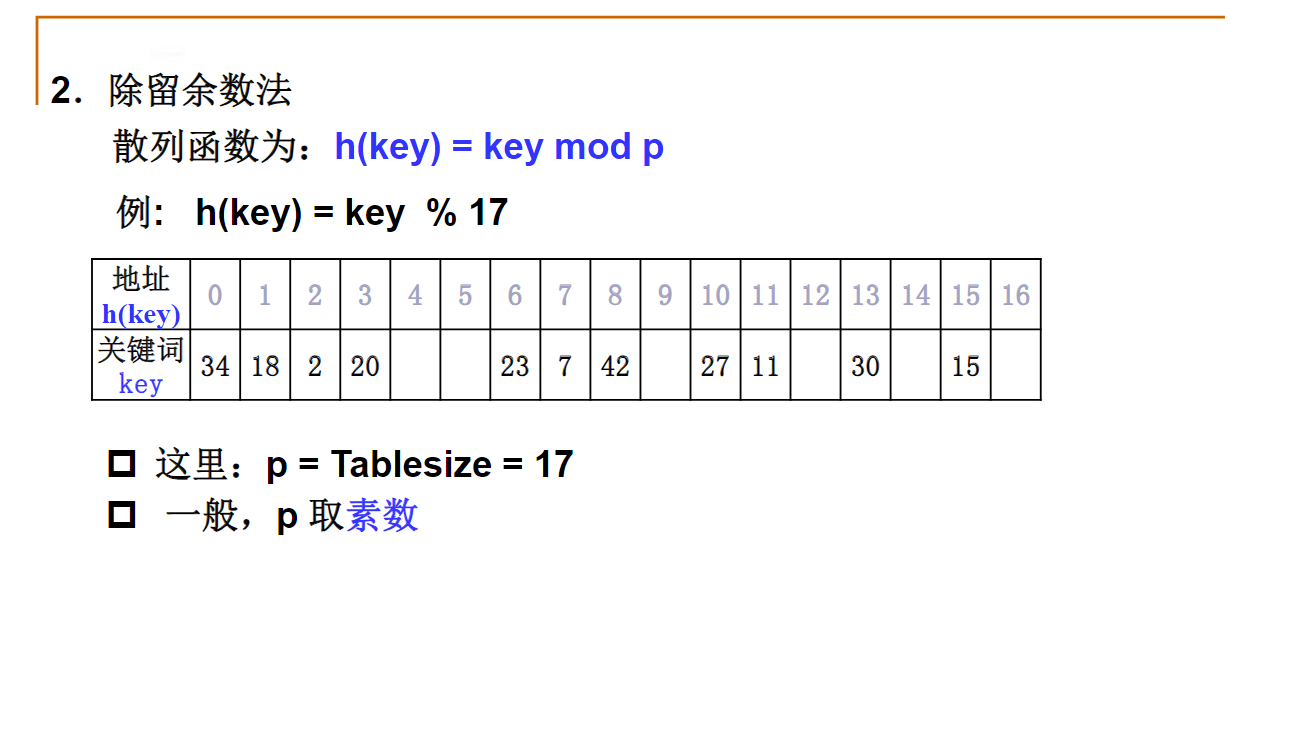


字符串关键词的散列函数构造


如果直接计算'a'*32^4+'b'*32^3+'c'*32^2+'d'*32+'e'所需要的乘法总次数是4+3+2+1=10次。
采用 ((('a'*32+'b')*32+'c')*32+'d')*32+'e'的计算方法,乘法总次数是多少?
(顺便思考一下两者时间效率的差别)
正确答案:4
冲突处理方法
开放定址法

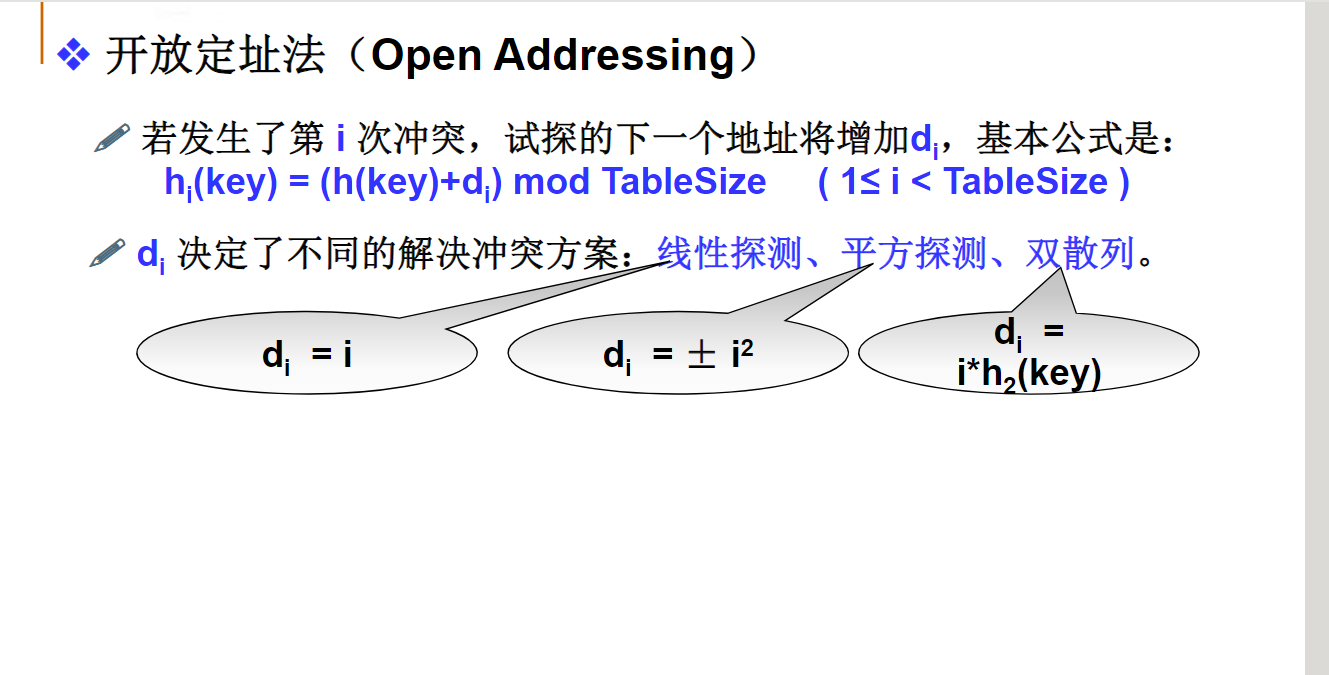
开放地址法代码:
#define MAXTABLESIZE 100000 /* 允许开辟的最大散列表长度 */
typedef int ElementType; /* 关键词类型用整型 */
typedef int Index; /* 散列地址类型 */
typedef Index Position; /* 数据所在位置与散列地址是同一类型 */
/* 散列单元状态类型,分别对应:有合法元素、空单元、有已删除元素 */
typedef enum { Legitimate, Empty, Deleted } EntryType;
typedef struct HashEntry Cell; /* 散列表单元类型 */
struct HashEntry{
ElementType Data; /* 存放元素 */
EntryType Info; /* 单元状态 */
};
typedef struct TblNode *HashTable; /* 散列表类型 */
struct TblNode { /* 散列表结点定义 */
int TableSize; /* 表的最大长度 */
Cell *Cells; /* 存放散列单元数据的数组 */
};
int NextPrime( int N )
{ /* 返回大于N且不超过MAXTABLESIZE的最小素数 */
int i, p = (N%2)? N+2 : N+1; /*从大于N的下一个奇数开始 */
while( p <= MAXTABLESIZE ) {
for( i=(int)sqrt(p); i>2; i-- )
if ( !(p%i) ) break; /* p不是素数 */
if ( i==2 ) break; /* for正常结束,说明p是素数 */
else p += 2; /* 否则试探下一个奇数 */
}
return p;
}
HashTable CreateTable( int TableSize )
{
HashTable H;
int i;
H = (HashTable)malloc(sizeof(struct TblNode));
/* 保证散列表最大长度是素数 */
H->TableSize = NextPrime(TableSize);
/* 声明单元数组 */
H->Cells = (Cell *)malloc(H->TableSize*sizeof(Cell));
/* 初始化单元状态为“空单元” */
for( i=0; i<H->TableSize; i++ )
H->Cells[i].Info = Empty;
return H;
}
线性探测
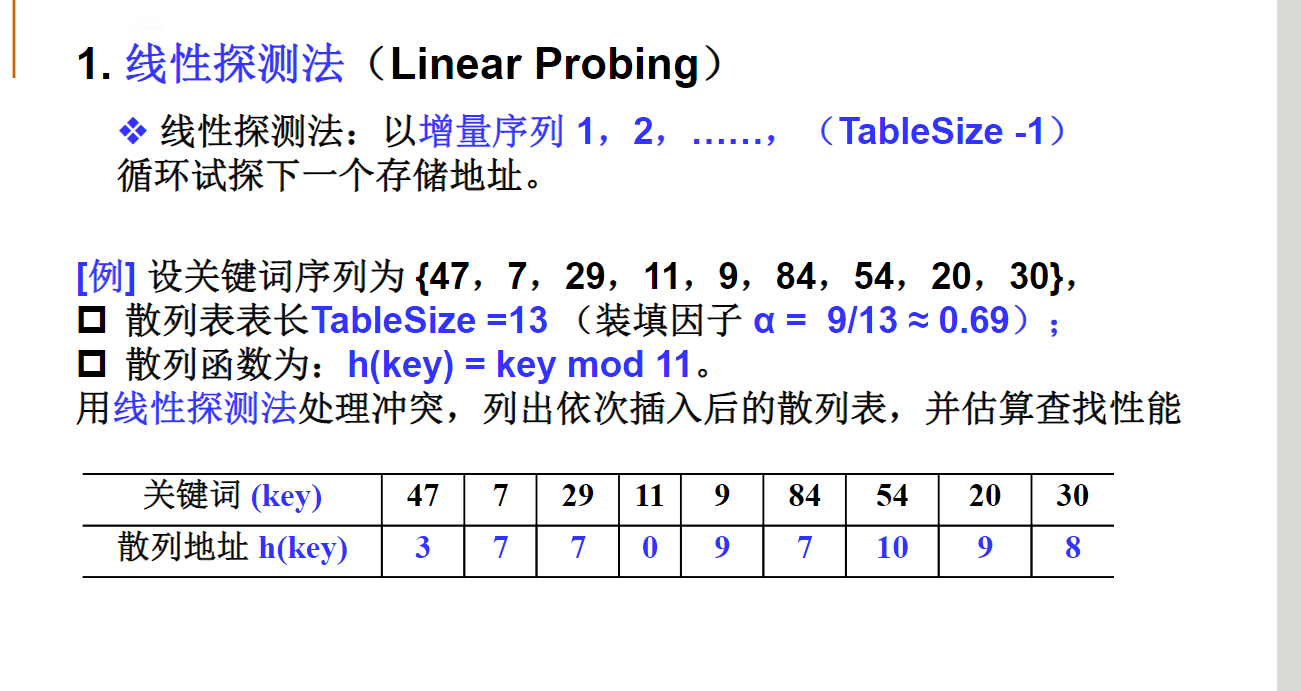
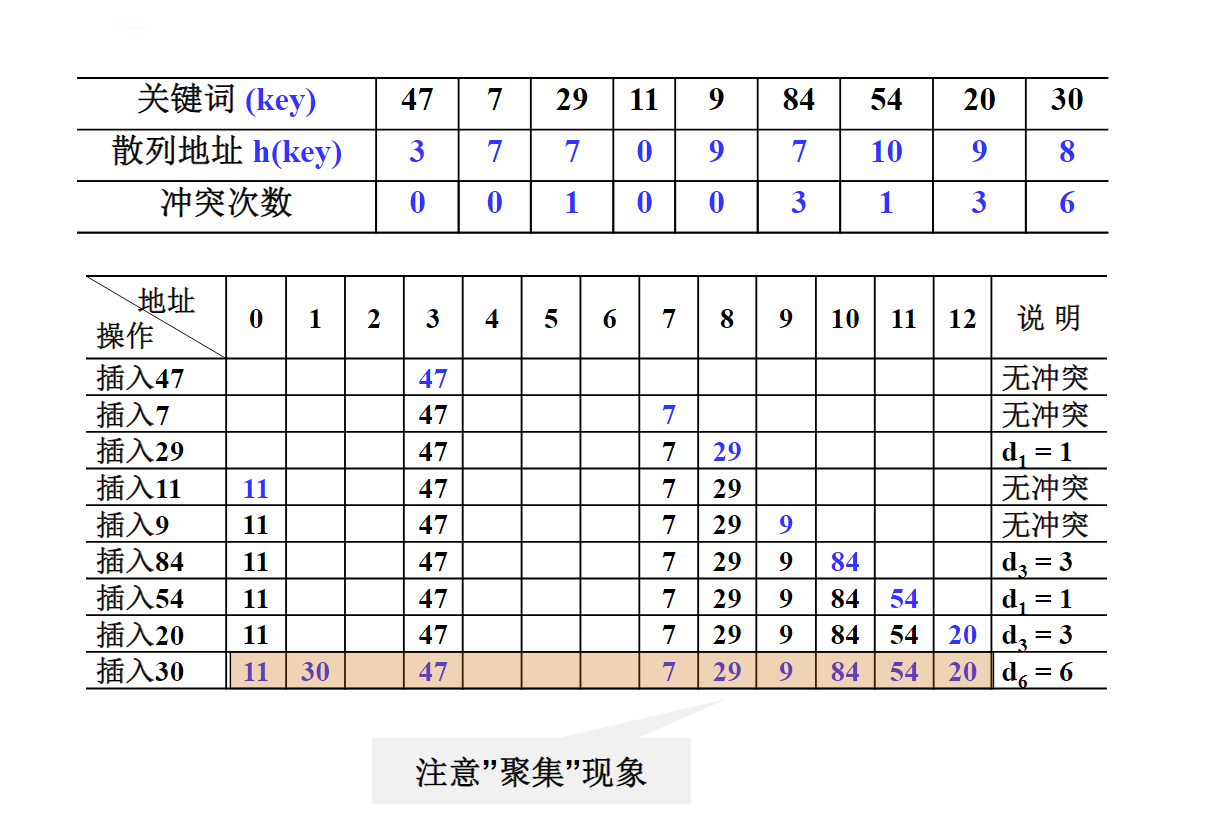
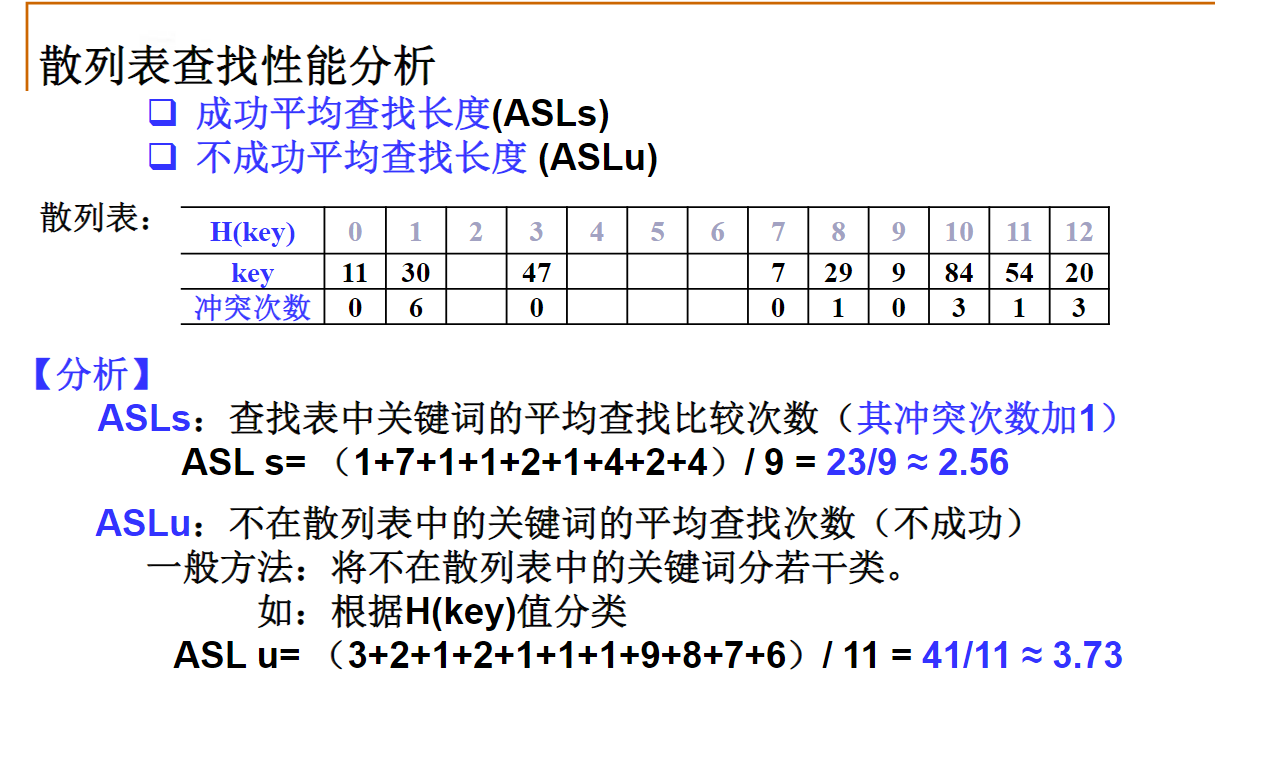
线性探测—字符串的例子
与例子相似,如果已知散列表的前8个位置有元素(但元素内容与例子不一样)而且后面18个位置也全是空位,那么平均不成功查找次数还是一样的.
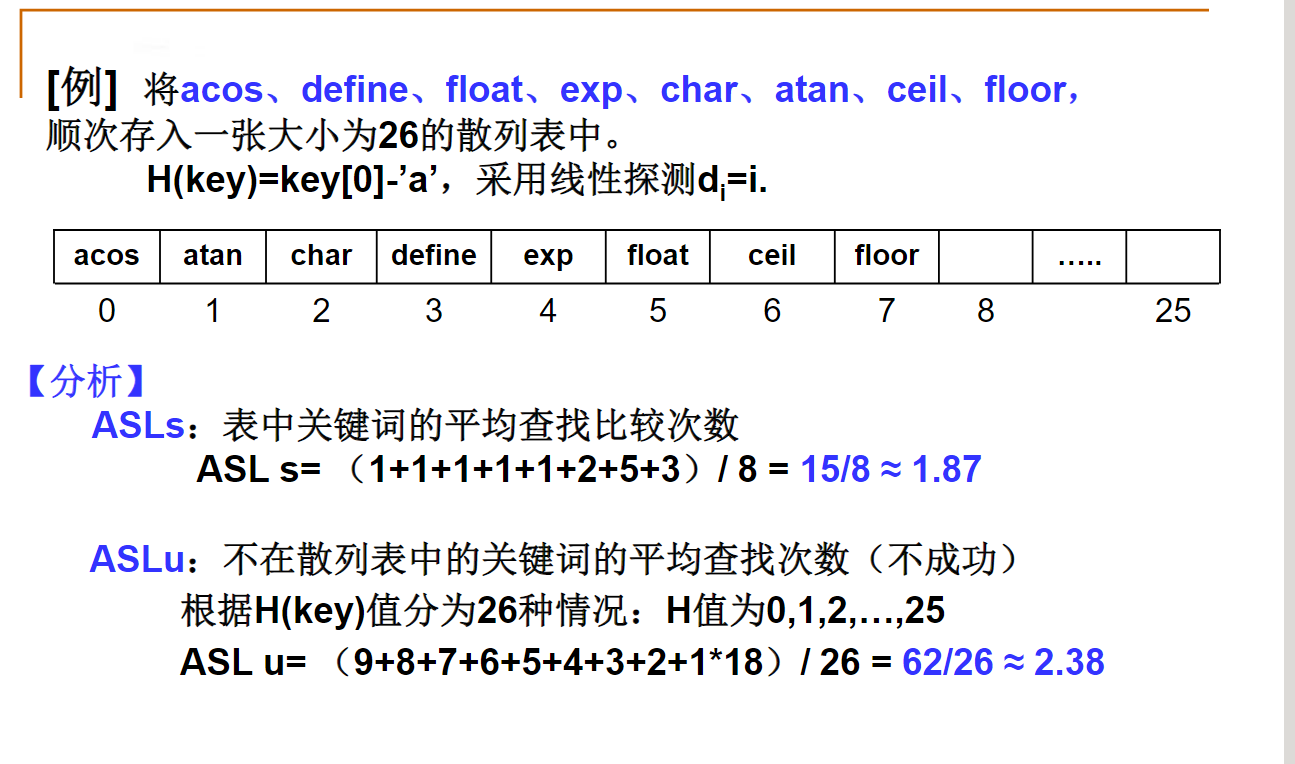
平方探测法
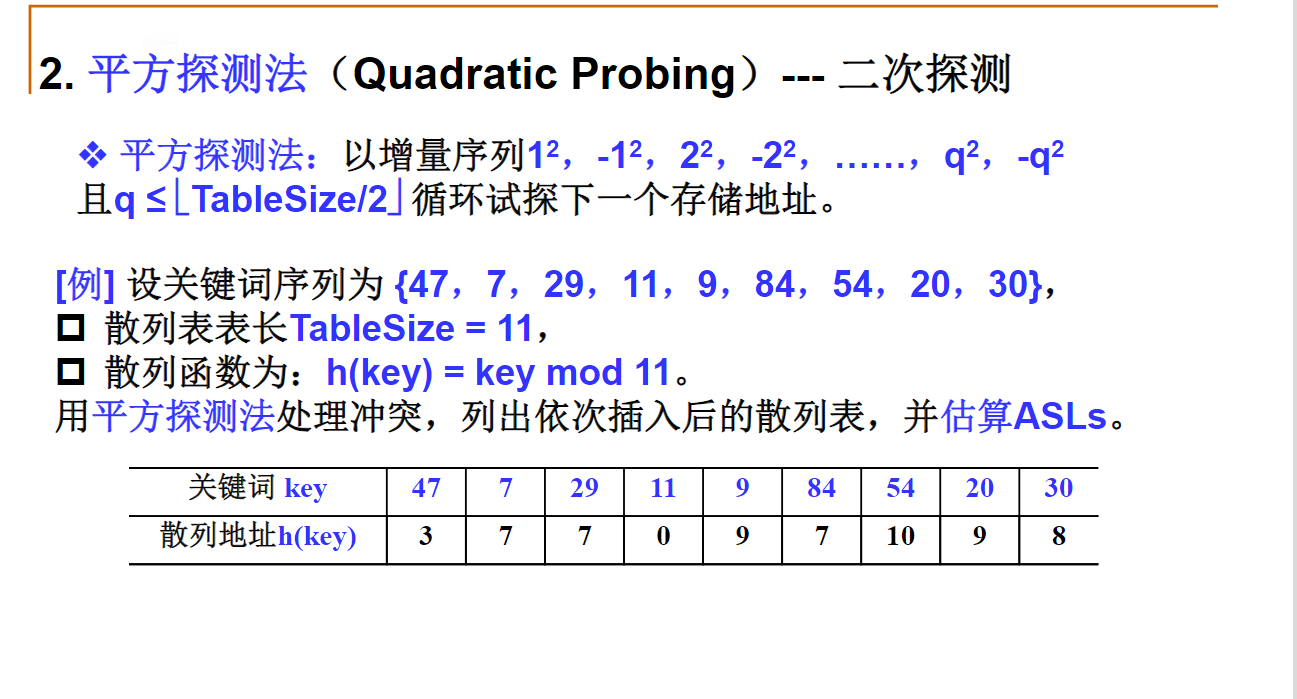
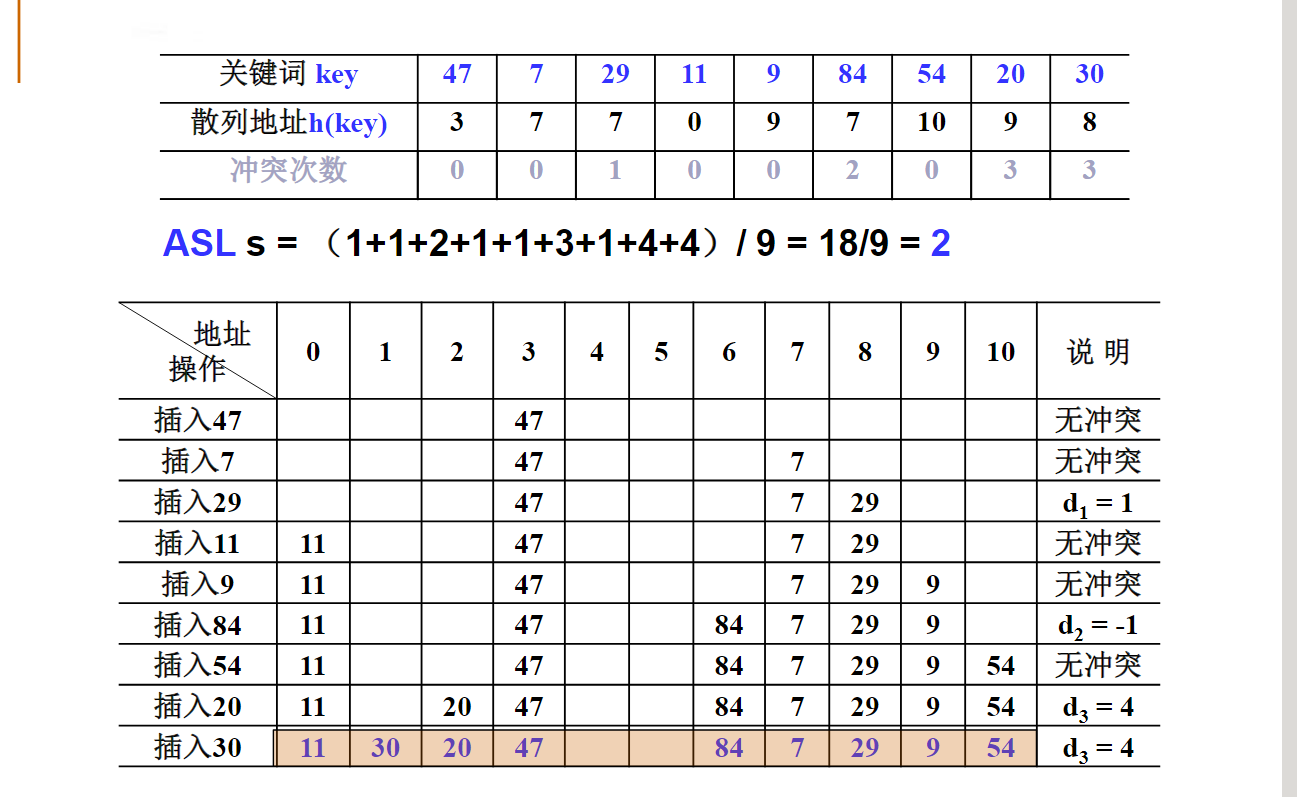
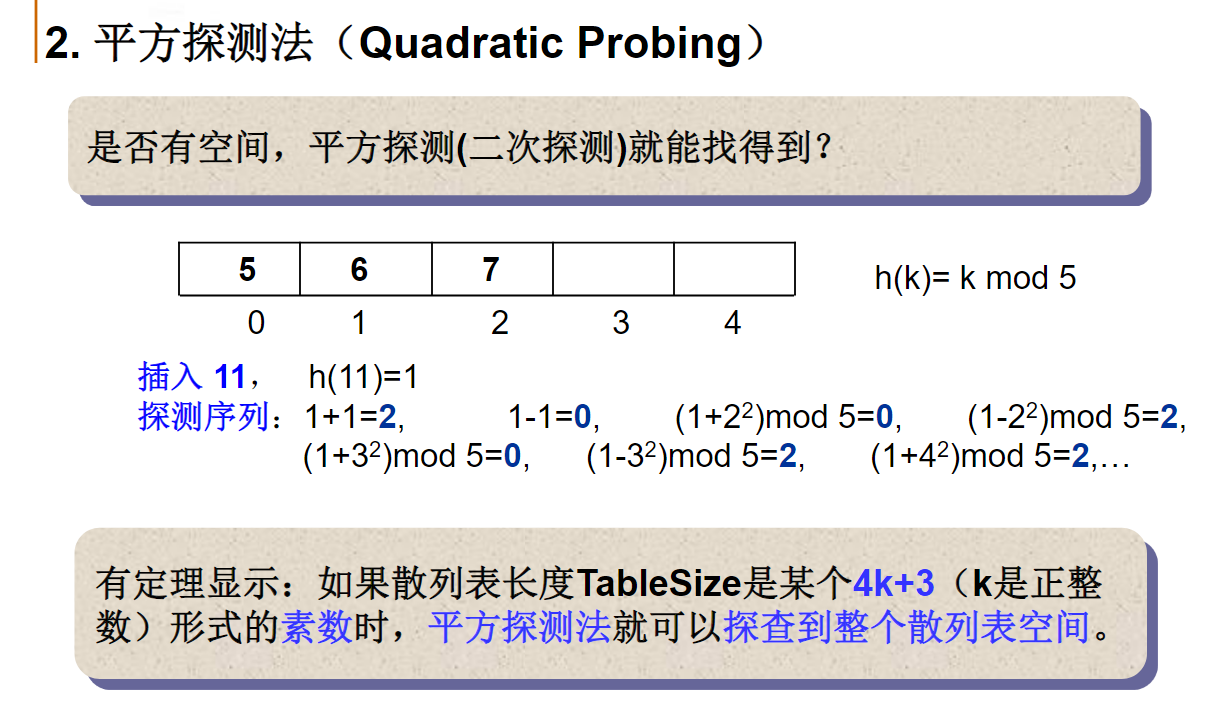
平方探测法的实现
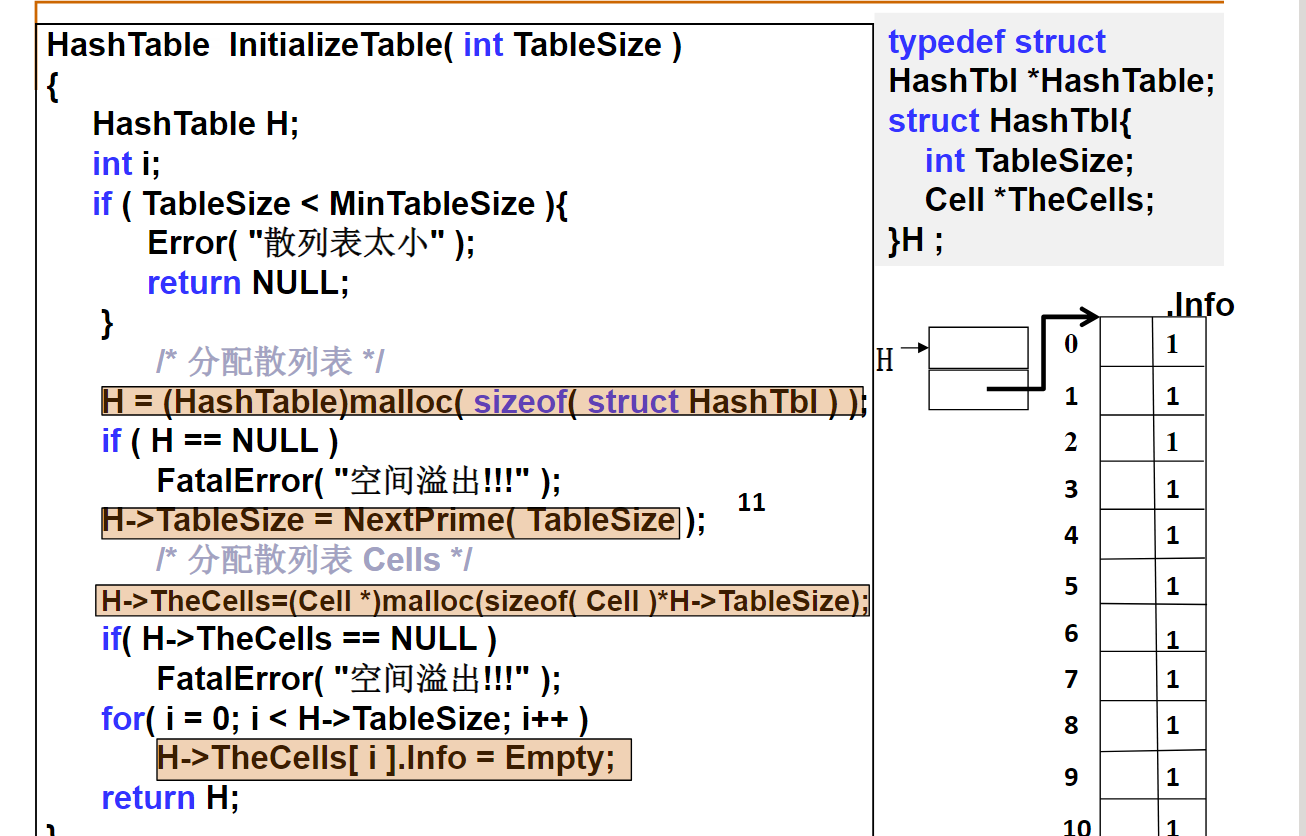
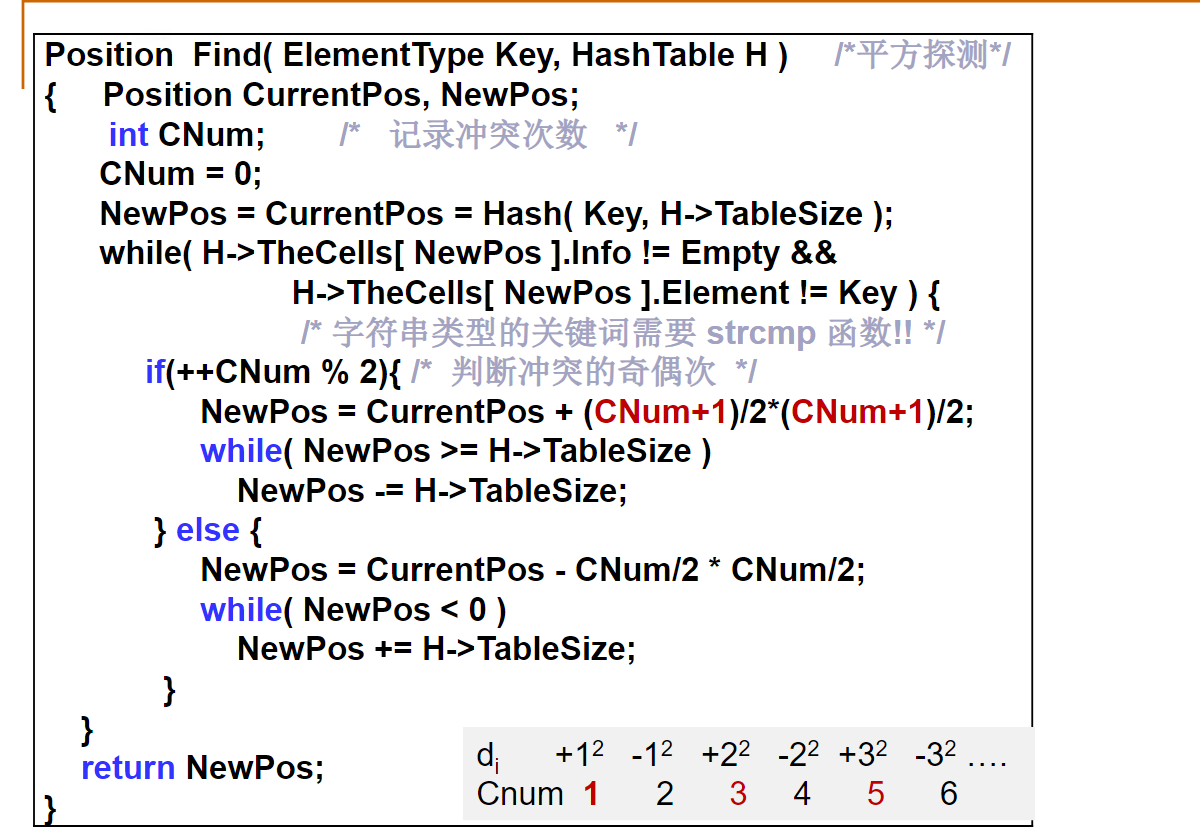



Position Find( HashTable H, ElementType Key )
{
Position CurrentPos, NewPos;
int CNum = 0; /* 记录冲突次数 */
NewPos = CurrentPos = Hash( Key, H->TableSize ); /* 初始散列位置 */
/* 当该位置的单元非空,并且不是要找的元素时,发生冲突 */
while( H->Cells[NewPos].Info!=Empty && H->Cells[NewPos].Data!=Key ) {
/* 字符串类型的关键词需要 strcmp 函数!! */
/* 统计1次冲突,并判断奇偶次 */
if( ++CNum%2 ){ /* 奇数次冲突 */
NewPos = CurrentPos + (CNum+1)*(CNum+1)/4; /* 增量为+[(CNum+1)/2]^2 */
if ( NewPos >= H->TableSize )
NewPos = NewPos % H->TableSize; /* 调整为合法地址 */
}
else { /* 偶数次冲突 */
NewPos = CurrentPos - CNum*CNum/4; /* 增量为-(CNum/2)^2 */
while( NewPos < 0 )
NewPos += H->TableSize; /* 调整为合法地址 */
}
}
return NewPos; /* 此时NewPos或者是Key的位置,或者是一个空单元的位置(表示找不到)*/
}
bool Insert( HashTable H, ElementType Key )
{
Position Pos = Find( H, Key ); /* 先检查Key是否已经存在 */
if( H->Cells[Pos].Info != Legitimate ) { /* 如果这个单元没有被占,说明Key可以插入在此 */
H->Cells[Pos].Info = Legitimate;
H->Cells[Pos].Data = Key;
/*字符串类型的关键词需要 strcpy 函数!! */
return true;
}
else {
printf("键值已存在");
return false;
}
}
分离链接法
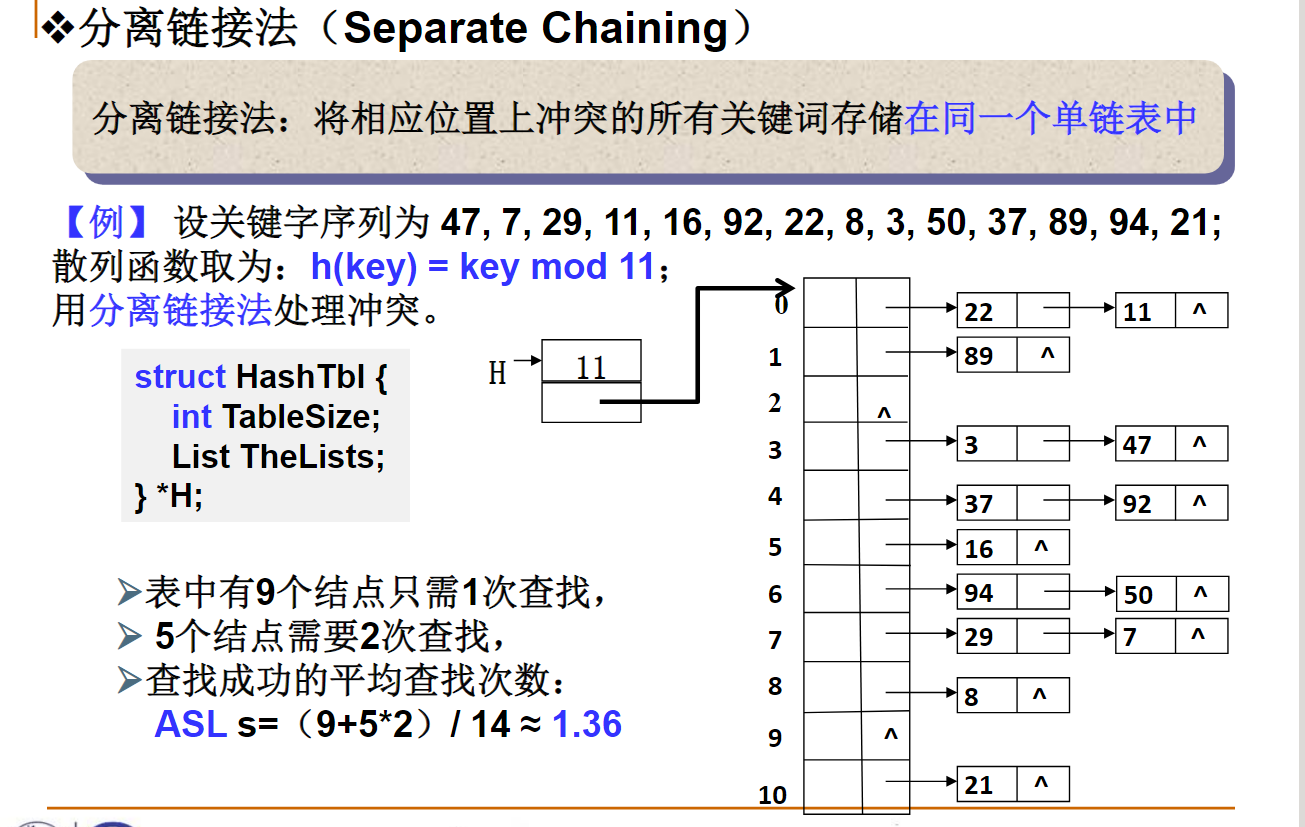
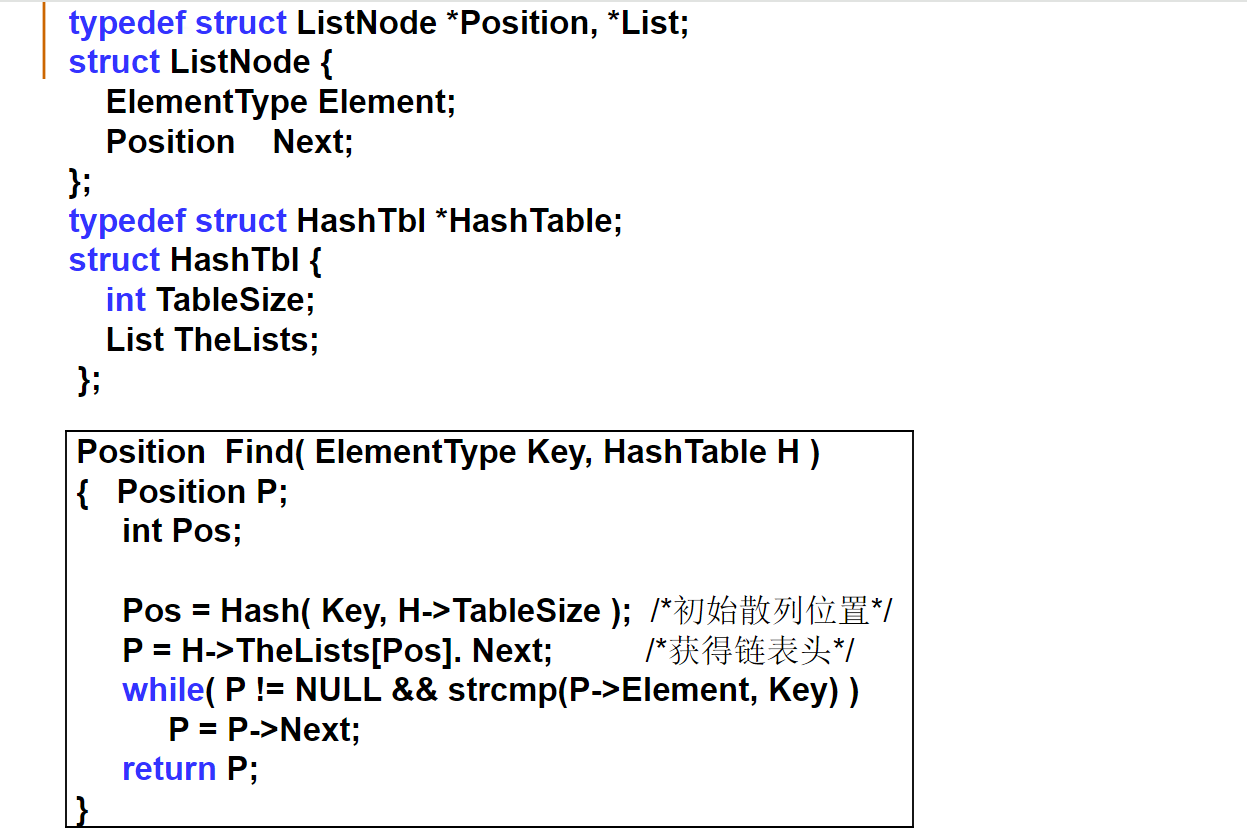
#define KEYLENGTH 15 /* 关键词字符串的最大长度 */
typedef char ElementType[KEYLENGTH+1]; /* 关键词类型用字符串 */
typedef int Index; /* 散列地址类型 */
/******** 以下是单链表的定义 ********/
typedef struct LNode *PtrToLNode;
struct LNode {
ElementType Data;
PtrToLNode Next;
};
typedef PtrToLNode Position;
typedef PtrToLNode List;
/******** 以上是单链表的定义 ********/
typedef struct TblNode *HashTable; /* 散列表类型 */
struct TblNode { /* 散列表结点定义 */
int TableSize; /* 表的最大长度 */
List Heads; /* 指向链表头结点的数组 */
};
HashTable CreateTable( int TableSize )
{
HashTable H;
int i;
H = (HashTable)malloc(sizeof(struct TblNode));
/* 保证散列表最大长度是素数,具体见代码5.3 */
H->TableSize = NextPrime(TableSize);
/* 以下分配链表头结点数组 */
H->Heads = (List)malloc(H->TableSize*sizeof(struct LNode));
/* 初始化表头结点 */
for( i=0; i<H->TableSize; i++ ) {
H->Heads[i].Data[0] = '\0';
H->Heads[i].Next = NULL;
}
return H;
}
Position Find( HashTable H, ElementType Key )
{
Position P;
Index Pos;
Pos = Hash( Key, H->TableSize ); /* 初始散列位置 */
P = H->Heads[Pos].Next; /* 从该链表的第1个结点开始 */
/* 当未到表尾,并且Key未找到时 */
while( P && strcmp(P->Data, Key) )
P = P->Next;
return P; /* 此时P或者指向找到的结点,或者为NULL */
}
bool Insert( HashTable H, ElementType Key )
{
Position P, NewCell;
Index Pos;
P = Find( H, Key );
if ( !P ) { /* 关键词未找到,可以插入 */
NewCell = (Position)malloc(sizeof(struct LNode));
strcpy(NewCell->Data, Key);
Pos = Hash( Key, H->TableSize ); /* 初始散列位置 */
/* 将NewCell插入为H->Heads[Pos]链表的第1个结点 */
NewCell->Next = H->Heads[Pos].Next;
H->Heads[Pos].Next = NewCell;
return true;
}
else { /* 关键词已存在 */
printf("键值已存在");
return false;
}
}
void DestroyTable( HashTable H )
{
int i;
Position P, Tmp;
/* 释放每个链表的结点 */
for( i=0; i<H->TableSize; i++ ) {
P = H->Heads[i].Next;
while( P ) {
Tmp = P->Next;
free( P );
P = Tmp;
}
}
free( H->Heads ); /* 释放头结点数组 */
free( H ); /* 释放散列表结点 */
}
散列表的性能分析

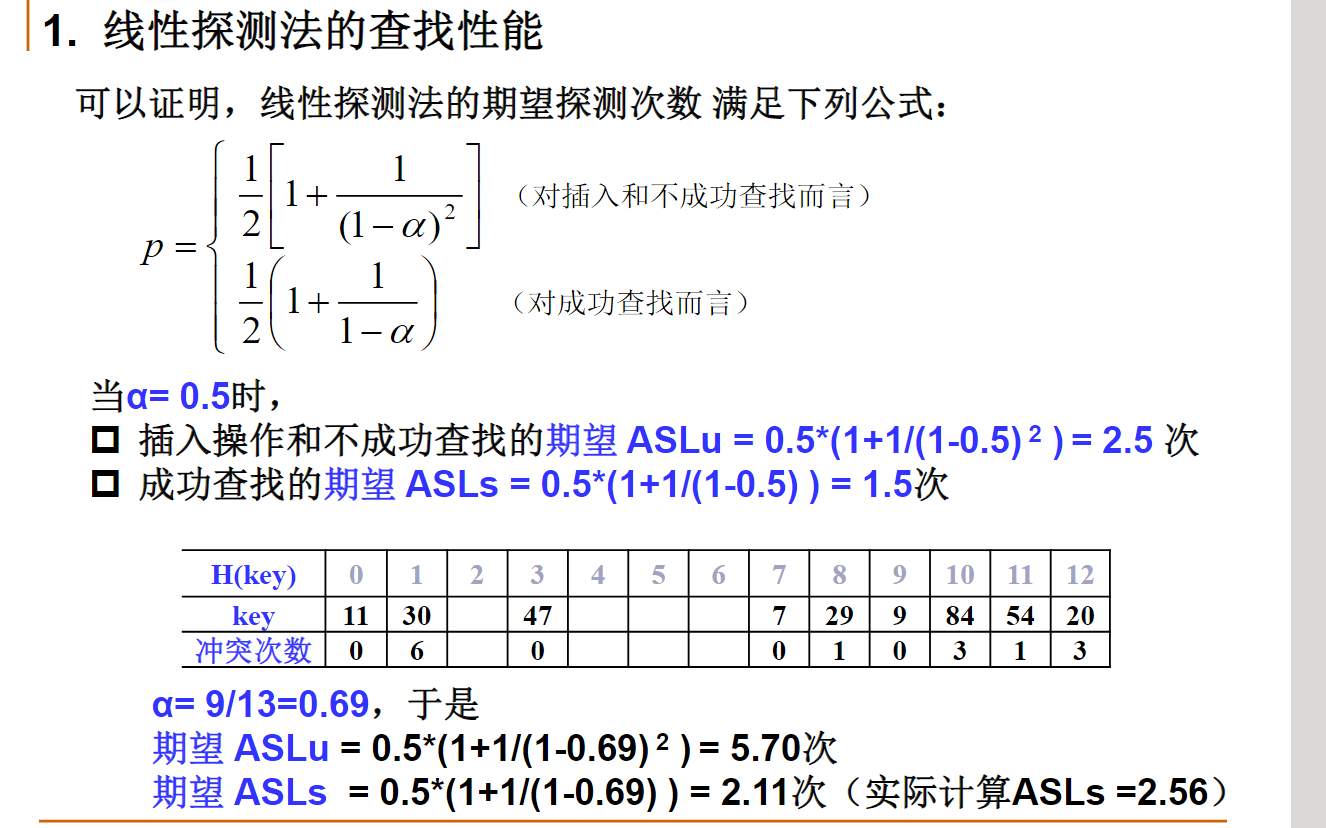
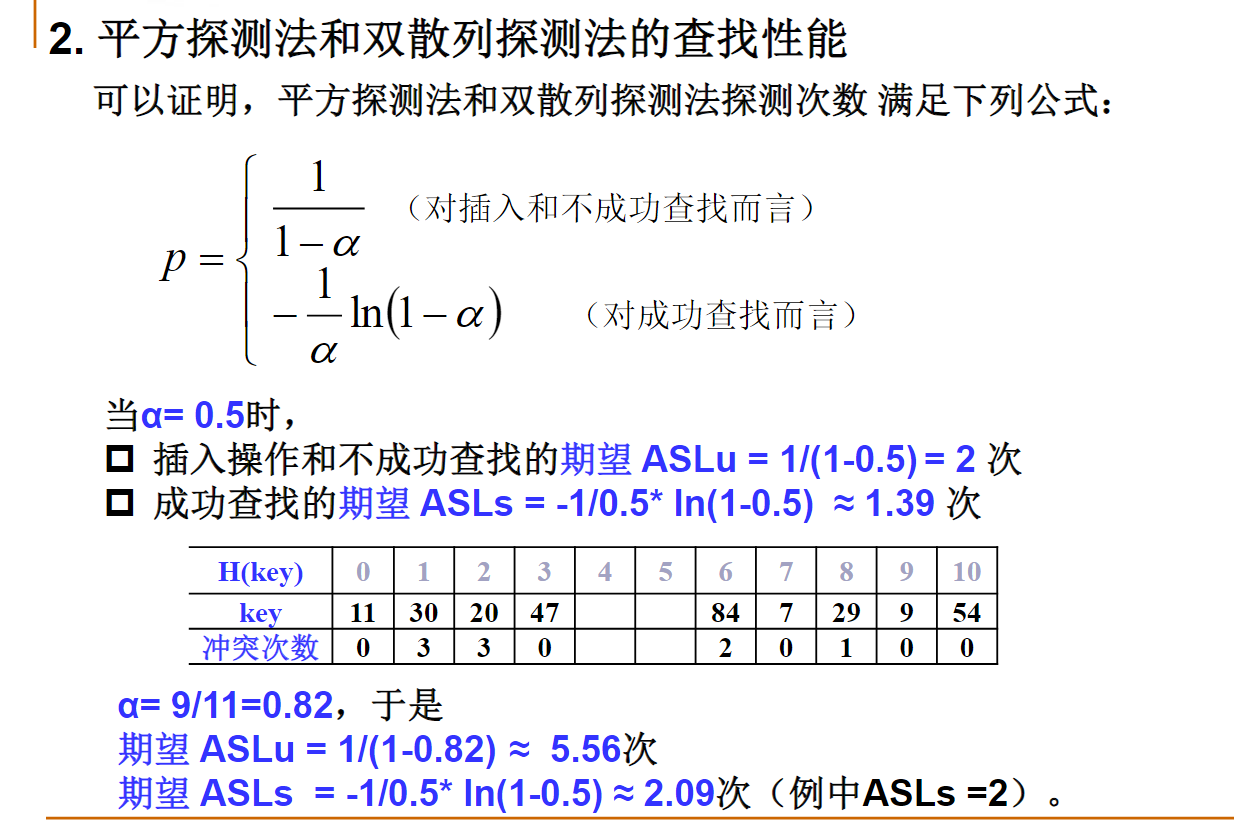
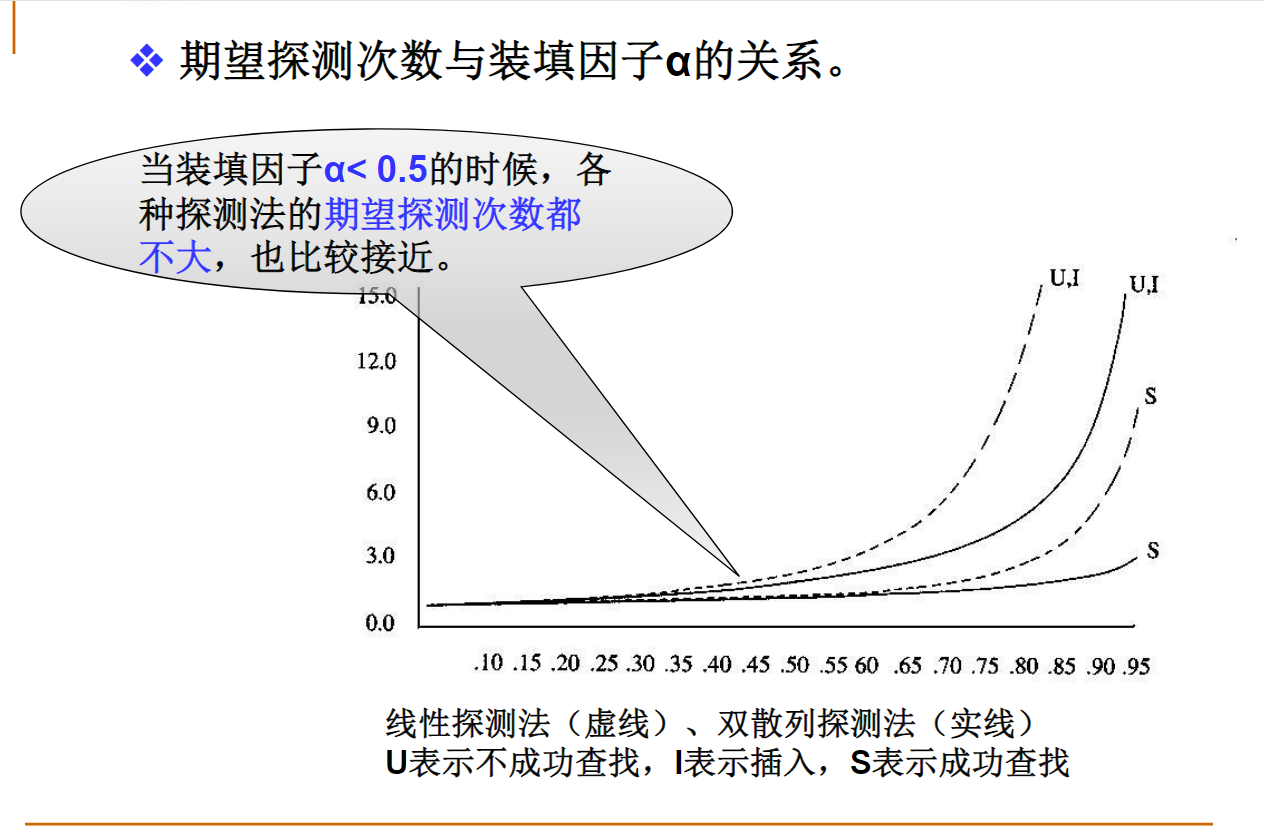
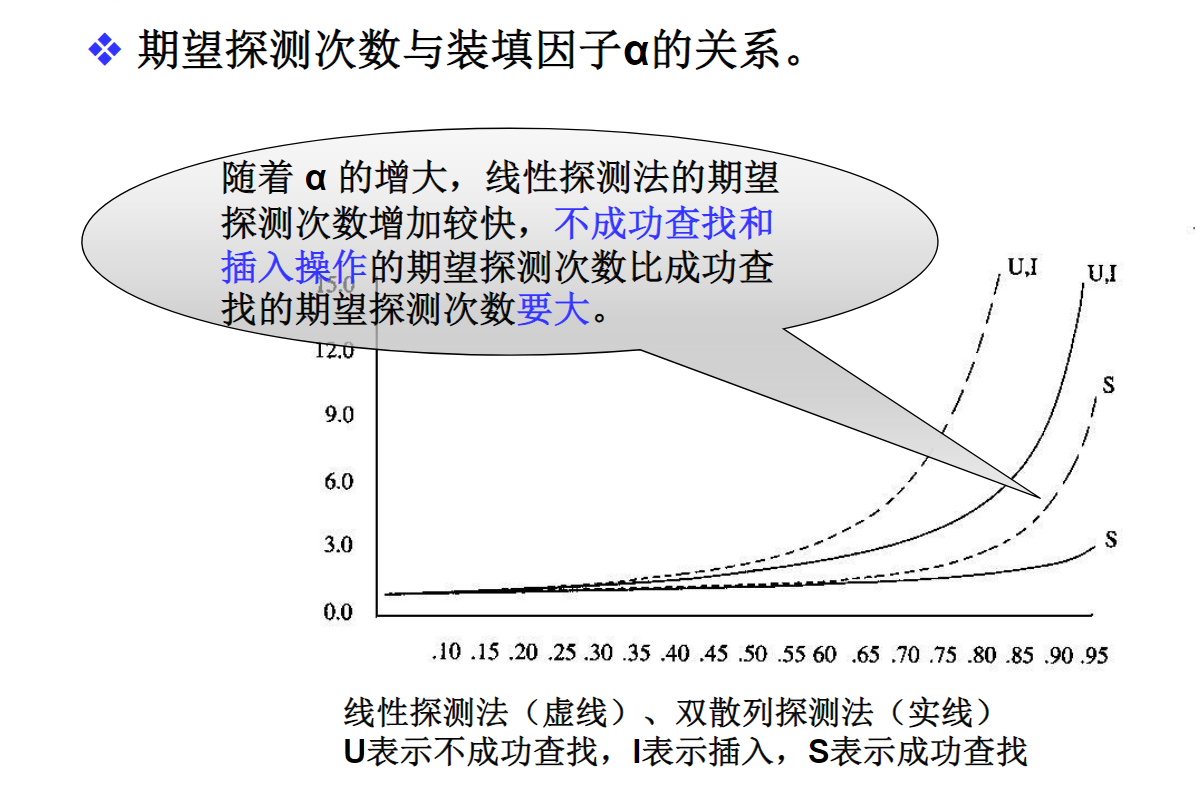
一个大小为11的散列表,散列函数为H(key)=key mod 11,采用线性探测冲突解决策略。如果现有散列表中仅有的5个元素均位于下标为奇数的位置,问:该散列表的平均不成功查找次数是多少?
16/11
在一个大小为K的空散列表中,按照线性探测冲突解决策略连续插入散列值相同的N个元素(N<K)。问:此时,该散列表的平均成功查找次数是多少?(N+1)/2
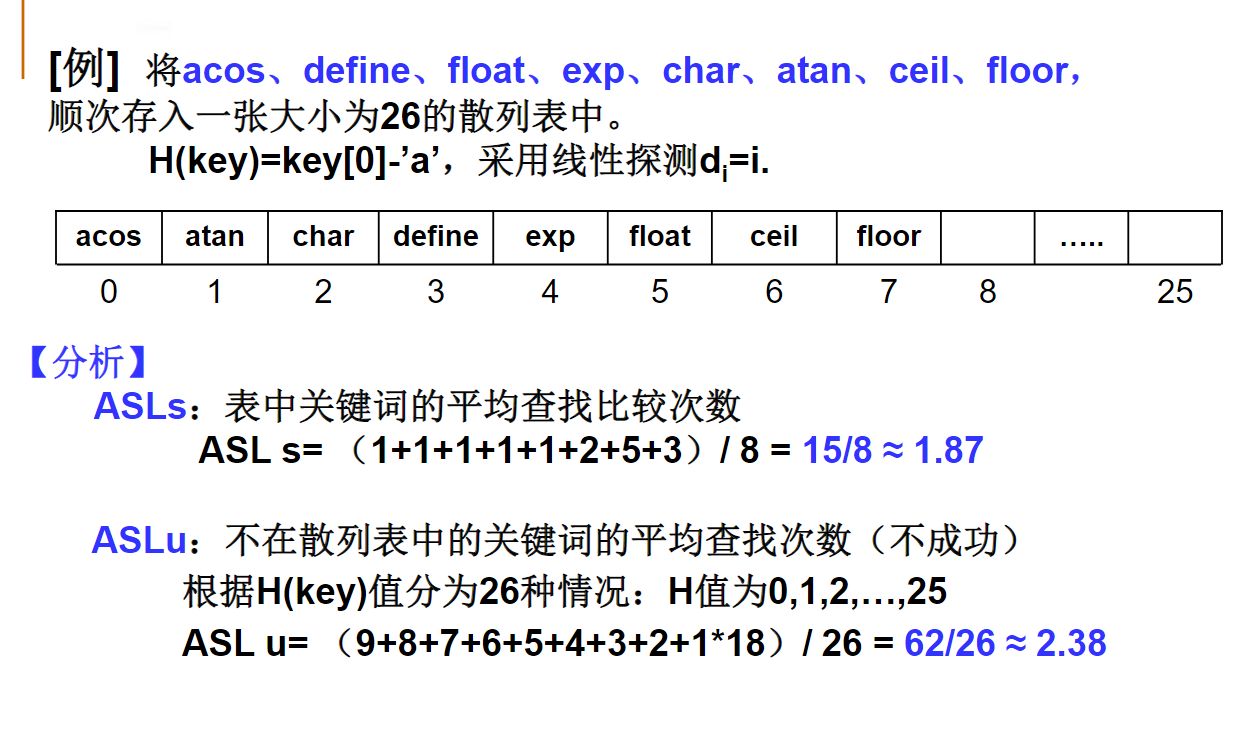
当采用线性探测冲突解决策略时,非空且有空闲空间的散列表中无论有多少元素,不成功情况下的期望查找次数总是大于成功情况下的期望查找次数。




基于数组的哈希表实现
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <assert.h>
typedef struct pair
{
int key;
char element[20];
}DATA, *LPDATA;
typedef struct hashTable
{
int divisor; //哈希表长度
int curSize; //当前元素个数
LPDATA *table; //用二级指针,便于初始化
}HASH, *LPHASH;
LPHASH createHash(int divisor)
{
LPHASH pHash = (LPHASH)malloc(sizeof(struct hashTable));
assert(pHash);
pHash->divisor = divisor;
pHash->curSize = 0;
pHash->table = (LPDATA*)malloc(sizeof(LPDATA) * pHash->divisor);
assert(pHash->table);
for(int i=0; i < pHash->divisor; i++)
{
pHash->table[i] = NULL;
}
return pHash;
}
int searchCorrectPos(LPHASH pHash, int key)
{
int Pos = key % pHash->divisor;
int curPos = Pos;
do
{
if(pHash->table[curPos] == NULL || pHash->table[curPos]->key == key)
return curPos;
curPos = (curPos + 1) % pHash->divisor;
}while(curPos != Pos);
return curPos;
}
void insertHash(LPHASH pHash, DATA data)
{
int pos = searchCorrectPos(pHash, data.key);
if(pHash->table[pos] == NULL)
{
pHash->table[pos] = (LPDATA)malloc(sizeof(DATA));
assert(pHash->table[pos]);
memcpy(pHash->table[pos], &data, sizeof(DATA));
pHash->curSize++;
}
else
{
if(pHash->table[pos]->key == data.key)
{
strcpy(pHash->table[pos]->element, data.element); //遇到冲突,覆盖相同key
}
else
{
printf("表满了,无法插入!\n");
return;
}
}
}
void printHash(LPHASH pHash)
{
for(int i=0; i<pHash->divisor; i++)
{
if(pHash->table[i] == NULL)
{
printf("NULL\n");
}
else
{
printf("%d:%s\n",pHash->table[i]->key,pHash->table[i]->element);
}
}
}
int main()
{
DATA array[3] = {29,"Young",35,"蓬蒿人",39,"哦哦哦"};
LPHASH pHash = createHash(10);
for(int i=0; i<3; i++)
{
insertHash(pHash,array[i]);
}
printHash(pHash);
return 0;
}
39:哦哦哦
NULL
NULL
NULL
NULL
35:蓬蒿人
NULL
NULL
NULL
29:Young
基于链表的哈希表实现
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <assert.h>
typedef struct pair
{
int key;
char element[20];
}DATA, *LPDATA;
typedef struct Node
{
DATA data;
struct Node *Next;
}NODE, *LPNODE;
LPNODE createNode(DATA data)
{
LPNODE newNode = (LPNODE)malloc(sizeof(NODE));
newNode->data = data;
newNode->Next = NULL;
return newNode;
}
typedef struct skipListNode
{
DATA data;
LPNODE fisrtNode;
struct skipListNode *Next;
}SLNODE, *LPSLNODE;
LPSLNODE createSkipListNode(DATA data)
{
LPSLNODE newNode = (LPSLNODE)malloc(sizeof(SLNODE));
newNode->data = data;
newNode->fisrtNode = NULL;
newNode->Next = NULL;
return newNode;
}
typedef struct Hash
{
LPSLNODE headNode;
int curSize;
int divisor;
}HASH, *LPHASH;
LPHASH createHash(int divisor)
{
LPHASH pHash = (LPHASH)malloc(sizeof(HASH));
assert(pHash);
pHash->curSize = 0;
pHash->divisor = divisor;
pHash->headNode = NULL;
return pHash;
}
void insertHash(LPHASH pHash, DATA data)
{
int dataHashPos = data.key % pHash->divisor;
LPSLNODE newSkipNode = createSkipListNode(data);
//第一次插入
if(pHash->headNode == NULL)
{
pHash->headNode = newSkipNode;
pHash->curSize++;
}
else
{
//纵向是要有序的
LPSLNODE pMove = pHash->headNode;
LPSLNODE prePmove = NULL;
//表头元素的地址大于要插入元素的地址,用头插法
if(pMove->data.key % pHash->divisor > dataHashPos)
{
newSkipNode->Next = pHash->headNode;
pHash->headNode = newSkipNode;
pHash->curSize++;
}
else
{
//向下找
while(pMove!=NULL && pMove->data.key%pHash->divisor < dataHashPos)
{
prePmove = pMove;
pMove = prePmove->Next;
}
//结果:找到、没找到
//找到的话,单独分析等于的情况,等于就是哈希冲突
if(pMove!=NULL && pMove->data.key%pHash->divisor == dataHashPos)
{
//相同键采用覆盖方式
//不同键、相同哈希地址插入横向链表
if(pMove->data.key == data.key)
{
strcpy(pMove->data.element, data.element);
}
else
{
LPNODE newNode = createNode(data);
LPNODE ppMove = pMove->fisrtNode;
//横向链表的插入
if(ppMove == NULL)
{
newNode->Next = pMove->fisrtNode;
pMove->fisrtNode = newNode;
pHash->curSize++;
}
else
{
//横向处理相同key的问题
while(ppMove != NULL && ppMove->data.key != data.key)
{
ppMove = ppMove->Next;
}
if(ppMove == NULL)
{
//表头法插入
newNode->Next = pMove->fisrtNode;
pMove->fisrtNode = newNode;
pHash->curSize++;
}
else
{
//相同则覆盖
strcpy(ppMove->data.element, data.element);
}
}
}
}
else
{
prePmove->Next = newSkipNode;
newSkipNode->Next = pMove;
pHash->curSize++;
}
}
}
}
void printHash(LPHASH pHash)
{
LPSLNODE pMove = pHash->headNode;
while(pMove != NULL)
{
printf("%d:%s ",pMove->data.key, pMove->data.element);
LPNODE ppMove = pMove->fisrtNode;
while(ppMove != NULL)
{
printf("%d:%s ",ppMove->data.key, ppMove->data.element);
ppMove = ppMove->Next;
}
pMove = pMove->Next;
printf("\n");
}
}
int main()
{
DATA array[3] = {29,"Young",35,"蓬蒿人",39,"哦哦哦"};
LPHASH pHash = createHash(10);
for(int i=0; i<3; i++)
{
insertHash(pHash,array[i]);
}
printHash(pHash);
return 0;
}
35:蓬蒿人
29:Young 39:哦哦哦
哈希表应用实例:统计词频


字符串匹配


普通字符串匹配实现




#include <stdio.h>
#include <string.h>
#include <stdlib.h>
typedef char* Position;
#define NotFound NULL
int main()
{
char string[] = "This is a simple example.";
char pattern[] = "simple";
Position p = strstr(string, pattern);
if (p==NotFound)
printf("Not Found.\n");
else
printf("%s\n",p);
return 0;
}
simple example.
KMP算法——字符串匹配
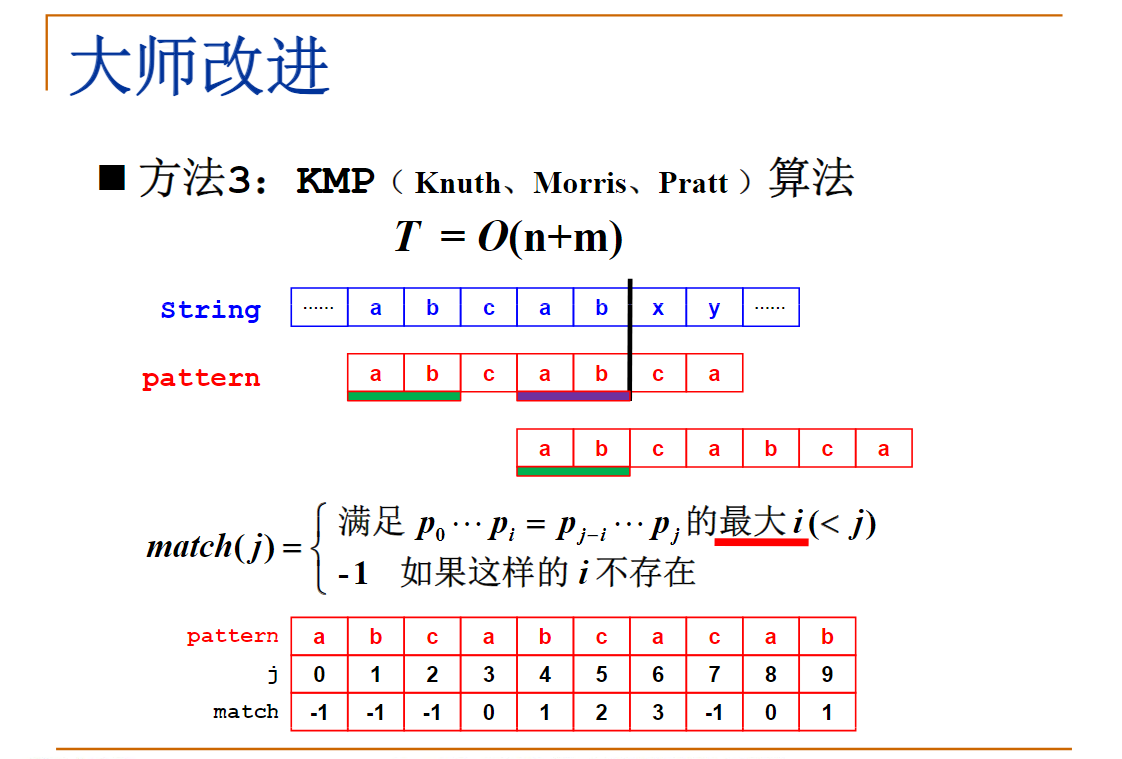




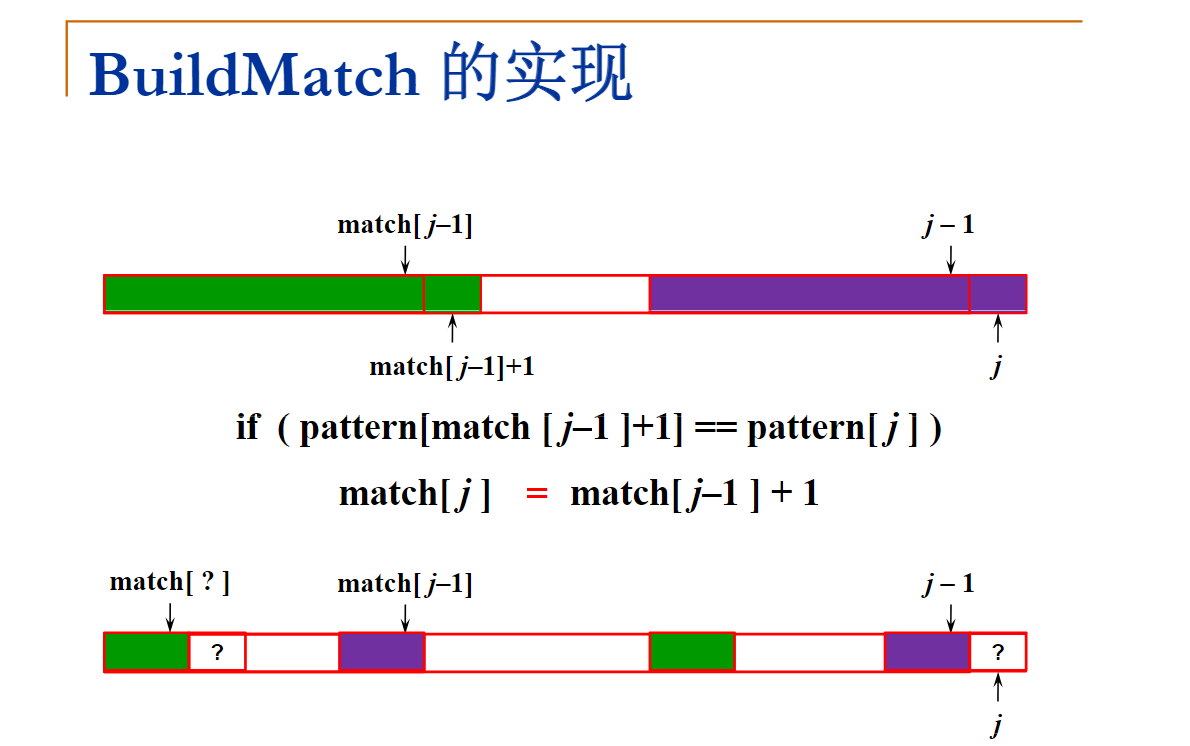
当pattern[match[j-1]+1] != pattern[j] 时,下一个待与 pattern[j] 比较的元素下标是:D
- A.
match[j-2] - B.
match[j-2]+1 - C
.match[match[j-1]] - D.
match[match[j-1]]+1


#include <stdio.h>
#include <string.h>
#include <stdlib.h>
typedef int Position;
#define NotFound -1
void BuildMatch( char *pattern, int *match )
{
Position i, j;
int m = strlen(pattern);
match[0] = -1;
for ( j=1; j<m; j++ ) {
i = match[j-1];
while ( (i>=0) && (pattern[i+1]!=pattern[j]) )
i = match[i];
if ( pattern[i+1]==pattern[j] )
match[j] = i+1;
else match[j] = -1;
}
}
Position KMP( char *string, char *pattern )
{
int n = strlen(string);
int m = strlen(pattern);
Position s, p, *match;
if ( n < m ) return NotFound;
match = (Position *)malloc(sizeof(Position) * m);
BuildMatch(pattern, match);
s = p = 0;
while ( s<n && p<m ) {
if ( string[s]==pattern[p] ) {
s++; p++;
}
else if (p>0) p = match[p-1]+1;
else s++;
}
return ( p==m )? (s-m) : NotFound;
}
int main()
{
char string[] = "This is a simple example.";
char pattern[] = "simple";
Position p = KMP(string, pattern);
if (p==NotFound) printf("Not Found.\n");
else printf("%s\n", string+p);
return 0;
}
实例:PTA KMP 串的模式匹配
给定两个由英文字母组成的字符串 String 和 Pattern,要求找到 Pattern 在 String 中第一次出现的位置,并将此位置后的 String 的子串输出。如果找不到,则输出“Not Found”。
本题旨在测试各种不同的匹配算法在各种数据情况下的表现。各组测试数据特点如下:
- 数据0:小规模字符串,测试基本正确性;
- 数据1:随机数据,String 长度为 105,Pattern 长度为 10;
- 数据2:随机数据,String 长度为 105,Pattern 长度为 102;
- 数据3:随机数据,String 长度为 105,Pattern 长度为 103;
- 数据4:随机数据,String 长度为 105,Pattern 长度为 104;
- 数据5:String 长度为 106,Pattern 长度为 105;测试尾字符不匹配的情形;
- 数据6:String 长度为 106,Pattern 长度为 105;测试首字符不匹配的情形。
输入格式:
输入第一行给出 String,为由英文字母组成的、长度不超过 106 的字符串。第二行给出一个正整数 N(≤10),为待匹配的模式串的个数。随后 N 行,每行给出一个 Pattern,为由英文字母组成的、长度不超过 105 的字符串。每个字符串都非空,以回车结束。
输出格式:
对每个 Pattern,按照题面要求输出匹配结果。
输入样例:
abcabcabcabcacabxy
3
abcabcacab
cabcabcd
abcabcabcabcacabxyz
输出样例:
abcabcacabxy
Not Found
Not Found
使用KMP算法的解法如下:
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
typedef int Position;
#define NotFound -1
void BuildMatch( char *pattern, int *match )
{
Position i, j;
int m = strlen(pattern);
match[0] = -1;
for ( j=1; j<m; j++ ) {
i = match[j-1];
while ( (i>=0) && (pattern[i+1]!=pattern[j]) )
i = match[i];
if ( pattern[i+1]==pattern[j] )
match[j] = i+1;
else match[j] = -1;
}
}
Position KMP( char *string, char *pattern )
{
int n = strlen(string);
int m = strlen(pattern);
Position s, p, *match;
if ( n < m ) return NotFound;
match = (Position *)malloc(sizeof(Position) * m);
BuildMatch(pattern, match);
s = p = 0;
while ( s<n && p<m ) {
if ( string[s]==pattern[p] ) {
s++; p++;
}
else if (p>0) p = match[p-1]+1;
else s++;
}
return ( p==m )? (s-m) : NotFound;
}
int main()
{
char string[1000005];
scanf("%s",string);
int N;
scanf("%d",&N);
for(int i=0; i<N; i++)
{
char pattern[100005];
scanf("%s",pattern);
Position p = KMP(string, pattern);
if (p==NotFound)
printf("Not Found\n");
else
printf("%s\n", string+p);
}
return 0;
}
使用strstr函数的解法如下:
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
typedef char* Position;
#define NotFound NULL
int main()
{
char string[1000005];
scanf("%s",string);
int N;
scanf("%d",&N);
for(int i=0; i<N; i++)
{
char pattern[100005];
scanf("%s",pattern);
Position p = strstr(string, pattern);
if (p==NotFound)
printf("Not Found\n");
else
printf("%s\n", p);
}
return 0;
}
MOOC-PTA查找题目
- PTA 11-散列1 电话聊天狂人
- PTA 11-散列2 Hashing
- PTA 11-散列3 QQ帐户的申请与登陆
- PTA 11-散列4 Hashing - Hard Version
- PTA KMP 串的模式匹配
PTA 11-散列1 电话聊天狂人
给定大量手机用户通话记录,找出其中通话次数最多的聊天狂人。
输入格式:
输入首先给出正整数N(≤105),为通话记录条数。随后N行,每行给出一条通话记录。简单起见,这里只列出拨出方和接收方的11位数字构成的手机号码,其中以空格分隔。
输出格式:
在一行中给出聊天狂人的手机号码及其通话次数,其间以空格分隔。如果这样的人不唯一,则输出狂人中最小的号码及其通话次数,并且附加给出并列狂人的人数。
输入样例:
4
13005711862 13588625832
13505711862 13088625832
13588625832 18087925832
15005713862 13588625832
输出样例:
13588625832 3
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <string.h>
#include <assert.h>
#define KEYLENGTH 11
#define MAXD 5
#define MAXTABLESIZE 1000000
typedef char ElementType[KEYLENGTH+1];
typedef int Index;
typedef struct LNode *PtrToLNode;
struct LNode
{
ElementType Data;
PtrToLNode Next;
int count;
};
typedef PtrToLNode Position;
typedef PtrToLNode List;
typedef struct TblNode *HashTable;
struct TblNode
{
int TableSize;
List Heads;
};
int NextPrime(int N)
{
int i,p = (N%2)?(N+2):(N+1);
while(p<=MAXTABLESIZE)
{
for(i=(int)sqrt(p); i>2; i--)
{
if(!(p%i))
break;
}
if(i==2)
break;
else
p += 2;
}
return p;
}
HashTable CreateTable(int TableSize)
{
HashTable H = (HashTable)malloc(sizeof(struct TblNode));
H->TableSize = NextPrime(TableSize);
H->Heads = (List)malloc(H->TableSize * sizeof(struct LNode));
for(int i=0; i<H->TableSize; i++)
{
H->Heads[i].Data[0] = '\0';
H->Heads[i].Next = NULL;
H->Heads[i].count = 0;
}
return H;
}
int Hash(int Key, int P)
{
return Key%P;
}
Position Find(HashTable H, ElementType Key)
{
Position P;
Index Pos;
Pos = Hash(atoi(Key+KEYLENGTH-MAXD), H->TableSize);
P = H->Heads[Pos].Next;
while(P && strcmp(P->Data,Key))
P = P->Next;
return P;
}
bool Insert(HashTable H, ElementType Key)
{
Position P,NewCell;
Index Pos;
P = Find(H,Key);
if(!P)
{
NewCell = (Position)malloc(sizeof(struct LNode));
strcpy(NewCell->Data, Key);
NewCell->count = 1;
Pos = Hash(atoi(Key+KEYLENGTH-MAXD), H->TableSize);
NewCell->Next = H->Heads[Pos].Next;
H->Heads[Pos].Next = NewCell;
return true;
}
else
{
P->count++;
return false;
}
}
void ScanAndOutput(HashTable H)
{
int MaxCnt = 0;
int pCnt = 0;
ElementType MinPhone;
List Ptr;
MinPhone[0] = '\0';
for(int i=0; i<H->TableSize; i++)
{
Ptr = H->Heads[i].Next;
while(Ptr)
{
if(Ptr->count > MaxCnt)
{
MaxCnt = Ptr->count;
strcpy(MinPhone, Ptr->Data);
pCnt = 1;
}
else if(Ptr->count == MaxCnt)
{
pCnt++;
if(strcmp(MinPhone, Ptr->Data)>0)
{
strcpy(MinPhone, Ptr->Data);
}
}
Ptr = Ptr->Next;
}
}
printf("%s %d",MinPhone,MaxCnt);
if(pCnt > 1)
printf(" %d",pCnt);
printf("\n");
}
void DestroyTable( HashTable H )
{
int i;
Position P, Tmp;
//释放每个链表的结点
for( i=0; i<H->TableSize; i++ ) {
P = H->Heads[i].Next;
while( P ) {
Tmp = P->Next;
free( P );
P = Tmp;
}
}
free( H->Heads ); //释放头结点数组
free( H ); //释放散列表结点
}
int main()
{
int N;
scanf("%d",&N);
ElementType Key;
HashTable H;
H = CreateTable(N*2);
for(int i=0; i<N; i++)
{
scanf("%s",&Key);
Insert(H,Key);
scanf("%s",&Key);
Insert(H,Key);
}
ScanAndOutput(H);
DestroyTable(H);
return 0;
}
下面是Python实现的代码:
dt = {}
N = int(input())
for i in range(N):
number1, number2 = map(int,input().split())
dt[number1] = dt.get(number1,0) + 1
dt[number2] = dt.get(number2,0) + 1
count = 0
maxValue = 0
min_number = 0
for k,v in dt.items():
if v > maxValue:
maxValue = v
min_number = k
for k,v in dt.items():
if v == maxValue:
count += 1
if k < min_number:
min_number = k
if count == 1:
print(min_number,maxValue)
else:
print(min_number,maxValue,count)
PTA 11-散列2 Hashing
The task of this problem is simple: insert a sequence of distinct positive integers into a hash table, and output the positions of the input numbers. The hash function is defined to be H(key)=key%TSize where TSize is the maximum size of the hash table. Quadratic probing (with positive increments only) is used to solve the collisions.
Note that the table size is better to be prime. If the maximum size given by the user is not prime, you must re-define the table size to be the smallest prime number which is larger than the size given by the user.
Input Specification:
Each input file contains one test case. For each case, the first line contains two positive numbers: MSize (≤104) and N (≤MSize) which are the user-defined table size and the number of input numbers, respectively. Then N distinct positive integers are given in the next line. All the numbers in a line are separated by a space.
Output Specification:
For each test case, print the corresponding positions (index starts from 0) of the input numbers in one line. All the numbers in a line are separated by a space, and there must be no extra space at the end of the line. In case it is impossible to insert the number, print "-" instead.
Sample Input:
4 4
10 6 4 15
Sample Output:
0 1 4 -
解题方法: 这道题目只需要用一个数组就可以解决,开始对数组每个元素先初始化为0,然后通过散列映射到数组中去,如果该映射的下标的元素值为0,则把该下标置为我们输入的值,否则就遍历正向的二次探测。这里大家可能会对什么时候才能结束探测循环表示疑问。因此我们循环只需要到TableSize就可以结束。
易错点:
对1来说,他不是素数(质数定义为在大于1的自然数中,除了1和它本身以外不再有其他因数),所以对他而言最小素数为2
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <string.h>
#include <assert.h>
#define MAXTABLESIZE 100000
typedef int ElementType;
typedef int Index;
typedef Index Position;
typedef enum { Legitimate, Empty, Deleted } EntryType;
typedef struct HashEntry Cell;
struct HashEntry
{
ElementType Data;
EntryType Info;
};
typedef struct TblNode *HashTable;
struct TblNode
{
int TableSize;
Cell *Cells;
};
int NextPrime( int N )
{
if(N==1)
return 2;
int i, p = (N%2)? N+2 : N+1;
while( p <= MAXTABLESIZE ) {
for( i=(int)sqrt(p); i>2; i-- )
if ( !(p%i) ) break;
if ( i==2 ) break;
else p += 2;
}
return p;
}
int Hash(ElementType Key, int TableSize)
{
return (Key%TableSize);
}
HashTable CreateTable( int TableSize )
{
HashTable H;
int i;
H = (HashTable)malloc(sizeof(struct TblNode));
H->TableSize = NextPrime(TableSize);
H->Cells = (Cell *)malloc(H->TableSize*sizeof(Cell));
for( i=0; i<H->TableSize; i++ )
H->Cells[i].Info = Empty;
return H;
}
void Insert(HashTable H, int key)
{
int Pos = Hash(key, H->TableSize);
if(H->Cells[Pos].Info == Empty)
{
H->Cells[Pos].Data = key;
H->Cells[Pos].Info = Legitimate;
printf("%d",Pos);
}
else
{
int newp = Pos;
for(int i=0; i<H->TableSize; i++)
{
newp = (Pos + i*i)%(H->TableSize);
if(H->Cells[newp].Info == Empty)
{
H->Cells[newp].Data = key;
H->Cells[newp].Info = Legitimate;
printf("%d",newp);
return;
}
}
printf("-");
}
}
int main()
{
int MSize,N;
scanf("%d %d",&MSize,&N);
HashTable H = CreateTable(MSize);
for(int i=0; i<N; i++)
{
int key;
scanf("%d",&key);
Insert(H,key);
if(i != N-1)
{
printf(" ");
}
else
{
printf("\n");
}
}
}
PTA 11-散列3 QQ帐户的申请与登陆
实现QQ新帐户申请和老帐户登陆的简化版功能。最大挑战是:据说现在的QQ号码已经有10位数了。
输入格式:
输入首先给出一个正整数N(≤105),随后给出N行指令。每行指令的格式为:“命令符(空格)QQ号码(空格)密码”。其中命令符为“N”(代表New)时表示要新申请一个QQ号,后面是新帐户的号码和密码;命令符为“L”(代表Login)时表示是老帐户登陆,后面是登陆信息。QQ号码为一个不超过10位、但大于1000(据说QQ老总的号码是1001)的整数。密码为不小于6位、不超过16位、且不包含空格的字符串。
输出格式:
针对每条指令,给出相应的信息:
1)若新申请帐户成功,则输出“New: OK”;
2)若新申请的号码已经存在,则输出“ERROR: Exist”;
3)若老帐户登陆成功,则输出“Login: OK”;
4)若老帐户QQ号码不存在,则输出“ERROR: Not Exist”;
5)若老帐户密码错误,则输出“ERROR: Wrong PW”。
输入样例:
5
L 1234567890 myQQ@qq.com
N 1234567890 myQQ@qq.com
N 1234567890 myQQ@qq.com
L 1234567890 myQQ@qq
L 1234567890 myQQ@qq.com
输出样例:
ERROR: Not Exist
New: OK
ERROR: Exist
ERROR: Wrong PW
Login: OK
思路:在基本的Cell类型中,增加一个存储密码的字符串类型PWType、Info只需要用来判断账号存在还是不存在,不需要判断是否已删除、此题还是常规的哈希表题,涉及到哈希表的构建,查找(这里采用线性探测的方式),插入的操作。再额外加一个登陆——即字符串的比较操作即可。
易错点:strcpy之前需要对Password中赋值"\0"、读取字符时需要用getchar()函数处理回车符
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define MAXTABLESIZE 100005
#define MAXCHAR 16
typedef long long int ElementType;
typedef char PWType[MAXCHAR+1];
typedef int Index;
typedef Index Position;
typedef enum { Legitimate, Empty, Deleted } EntryType;
typedef struct HashEntry Cell;
struct HashEntry
{
ElementType Data;
PWType Password;
EntryType Info;
};
typedef struct TblNode *HashTable;
struct TblNode
{
int TableSize;
Cell *Cells;
};
int NextPrime( int N )
{
if(N==1)
return 2;
int i, p = (N%2)? N+2 : N+1;
while( p <= MAXTABLESIZE ) {
for( i=(int)sqrt(p); i>2; i-- )
if ( !(p%i) ) break;
if ( i==2 ) break;
else p += 2;
}
return p;
}
int Hash(ElementType Key, HashTable H)
{
return (Key%H->TableSize);
}
HashTable CreateTable( int TableSize )
{
HashTable H;
int i;
H = (HashTable)malloc(sizeof(struct TblNode));
H->TableSize = NextPrime(TableSize);
H->Cells = (Cell *)malloc(H->TableSize*sizeof(Cell));
for( i=0; i<H->TableSize; i++ )
{
H->Cells[i].Info = Empty;
strcpy(H->Cells[i].Password, "\0");
}
return H;
}
int LinearFind(HashTable H, ElementType Key)
{
int curPos = Hash(Key ,H);
int newPos = curPos;
int count = 0;
while(H->Cells[newPos].Info != Empty && H->Cells[newPos].Data != Key)
{
count++;
newPos = (curPos + count) % H->TableSize;
}
return newPos;
}
void Insert(HashTable H, ElementType Key, PWType password)
{
int Pos = LinearFind(H, Key);
if(H->Cells[Pos].Info == Empty)
{
H->Cells[Pos].Data = Key;
strcpy(H->Cells[Pos].Password, password);
H->Cells[Pos].Info = Legitimate;
printf("New: OK\n");
}
else
{
printf("ERROR: Exist\n");
}
}
void LogIn(HashTable H, ElementType Key, PWType password)
{
int Pos = LinearFind(H, Key);
if(H->Cells[Pos].Info == Empty)
{
printf("ERROR: Not Exist\n");
}
else if(H->Cells[Pos].Info == Legitimate && strcmp(H->Cells[Pos].Password, password))
{
printf("ERROR: Wrong PW\n");
}
else
{
printf("Login: OK\n");
}
}
int main()
{
int N;
scanf("%d",&N);
HashTable H = CreateTable(N);
ElementType Key;
PWType Password;
char command;
for(int i=0; i<N; i++)
{
getchar();
scanf("%c",&command);
scanf("%lld",&Key);
scanf("%s", Password);
switch(command)
{
case 'N':
Insert(H, Key, Password);
break;
case 'L':
LogIn(H, Key, Password);
break;
}
}
}
使用C++STL实现:
#include <iostream>
#include <string>
#include <map>
using namespace std;
int main() {
map<string, string> user;//账号密码
int N;
string o, us, pw;
cin >> N;
for(int i = 0; i < N; ++i) {
cin >> o >> us >> pw;
if(o == "L") {//Login
if(user.find(us) == user.end())
cout << "ERROR: Not Exist" << endl;
else if(user[us] == pw)
cout << "Login: OK" << endl;
else cout << "ERROR: Wrong PW" << endl;
} else if(o == "N") {//New
if(user.find(us) != user.end())
cout << "ERROR: Exist" << endl;
else {
user[us] = pw;
cout << "New: OK" << endl;
}
}
}
return 0;
}
PTA 11-散列4 Hashing - Hard Version
Given a hash table of size N, we can define a hash function H(x)=x%N. Suppose that the linear probing is used to solve collisions, we can easily obtain the status of the hash table with a given sequence of input numbers.
However, now you are asked to solve the reversed problem: reconstruct the input sequence from the given status of the hash table. Whenever there are multiple choices, the smallest number is always taken.
Input Specification:
Each input file contains one test case. For each test case, the first line contains a positive integer N (≤1000), which is the size of the hash table. The next line contains N integers, separated by a space. A negative integer represents an empty cell in the hash table. It is guaranteed that all the non-negative integers are distinct in the table.
Output Specification:
For each test case, print a line that contains the input sequence, with the numbers separated by a space. Notice that there must be no extra space at the end of each line.
Sample Input:
11
33 1 13 12 34 38 27 22 32 -1 21
Sample Output:
1 13 12 21 33 34 38 27 22 32

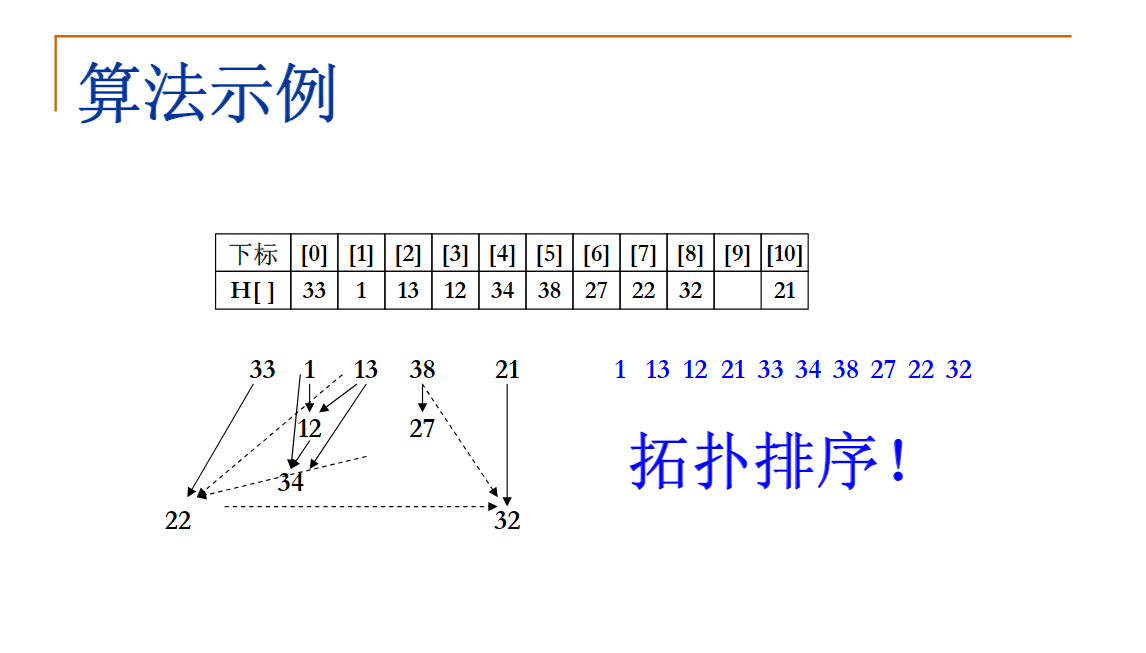
PTA KMP 串的模式匹配
给定两个由英文字母组成的字符串 String 和 Pattern,要求找到 Pattern 在 String 中第一次出现的位置,并将此位置后的 String 的子串输出。如果找不到,则输出“Not Found”。
本题旨在测试各种不同的匹配算法在各种数据情况下的表现。各组测试数据特点如下:
- 数据0:小规模字符串,测试基本正确性;
- 数据1:随机数据,String 长度为 105,Pattern 长度为 10;
- 数据2:随机数据,String 长度为 105,Pattern 长度为 102;
- 数据3:随机数据,String 长度为 105,Pattern 长度为 103;
- 数据4:随机数据,String 长度为 105,Pattern 长度为 104;
- 数据5:String 长度为 106,Pattern 长度为 105;测试尾字符不匹配的情形;
- 数据6:String 长度为 106,Pattern 长度为 105;测试首字符不匹配的情形。
输入格式:
输入第一行给出 String,为由英文字母组成的、长度不超过 106 的字符串。第二行给出一个正整数 N(≤10),为待匹配的模式串的个数。随后 N 行,每行给出一个 Pattern,为由英文字母组成的、长度不超过 105 的字符串。每个字符串都非空,以回车结束。
输出格式:
对每个 Pattern,按照题面要求输出匹配结果。
输入样例:
abcabcabcabcacabxy
3
abcabcacab
cabcabcd
abcabcabcabcacabxyz
输出样例:
abcabcacabxy
Not Found
Not Found
使用KMP算法的解法如下:
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
typedef int Position;
#define NotFound -1
void BuildMatch( char *pattern, int *match )
{
Position i, j;
int m = strlen(pattern);
match[0] = -1;
for ( j=1; j<m; j++ ) {
i = match[j-1];
while ( (i>=0) && (pattern[i+1]!=pattern[j]) )
i = match[i];
if ( pattern[i+1]==pattern[j] )
match[j] = i+1;
else match[j] = -1;
}
}
Position KMP( char *string, char *pattern )
{
int n = strlen(string);
int m = strlen(pattern);
Position s, p, *match;
if ( n < m ) return NotFound;
match = (Position *)malloc(sizeof(Position) * m);
BuildMatch(pattern, match);
s = p = 0;
while ( s<n && p<m ) {
if ( string[s]==pattern[p] ) {
s++; p++;
}
else if (p>0) p = match[p-1]+1;
else s++;
}
return ( p==m )? (s-m) : NotFound;
}
int main()
{
char string[1000005];
scanf("%s",string);
int N;
scanf("%d",&N);
for(int i=0; i<N; i++)
{
char pattern[100005];
scanf("%s",pattern);
Position p = KMP(string, pattern);
if (p==NotFound)
printf("Not Found\n");
else
printf("%s\n", string+p);
}
return 0;
}
使用strstr函数的解法如下:
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
typedef char* Position;
#define NotFound NULL
int main()
{
char string[1000005];
scanf("%s",string);
int N;
scanf("%d",&N);
for(int i=0; i<N; i++)
{
char pattern[100005];
scanf("%s",pattern);
Position p = strstr(string, pattern);
if (p==NotFound)
printf("Not Found\n");
else
printf("%s\n", p);
}
return 0;
}