MOOC-PTA图题目
- PTA 06-图1 列出连通集
- PTA 06-图2 Saving James Bond - Easy Version
- PTA 06-图3 六度空间
- PTA 07-图4 哈利·波特的考试
- PTA 07-图5 Saving James Bond - Hard Version
- PTA 07-图6 旅游规划
- PTA 08-图7 公路村村通
- PTA 08-图8 How Long Does It Take
- PTA 08-图9 关键活动
PTA 06-图1 列出连通集
给定一个有N个顶点和E条边的无向图,请用DFS和BFS分别列出其所有的连通集。假设顶点从0到N−1编号。进行搜索时,假设我们总是从编号最小的顶点出发,按编号递增的顺序访问邻接点。
输入格式:
输入第1行给出2个整数N(0<N≤10)和E,分别是图的顶点数和边数。随后E行,每行给出一条边的两个端点。每行中的数字之间用1空格分隔。
输出格式:
按照"{ v1 v2 ... vk }"的格式,每行输出一个连通集。先输出DFS的结果,再输出BFS的结果。
输入样例:
8 6
0 7
0 1
2 0
4 1
2 4
3 5
输出样例:
{ 0 1 4 2 7 }
{ 3 5 }
{ 6 }
{ 0 1 2 7 4 }
{ 3 5 }
{ 6 }
#include <stdio.h>
#include <stdlib.h>
#define MAXN 100
int G[MAXN][MAXN], Nv, Ne;
void BuildGraph()
{
int i,j,v1,v2,w;
scanf("%d",&Nv);
for(i=0; i<Nv; i++)
{
for(j=0; j<Nv; j++)
{
G[i][j] = 0;
}
}
scanf("%d",&Ne);
for(i=0; i<Ne; i++)
{
scanf("%d %d",&v1,&v2);
G[v1][v2] = 1;
G[v2][v1] = 1;
}
}
void printGraph()
{
for(int i=0;i < Nv; i++)
{
for(int j=0; j<Nv; j++)
{
printf("%d ", G[i][j]);
}
printf("\n");
}
}
typedef int Vertex;
#define TRUE 1
#define FALSE 0
typedef int Boolean;
Boolean visited[MAXN];
Boolean IsFirst = TRUE;
void dfs(Vertex V)
{
visited[V] = TRUE;
if(IsFirst)
{
printf("%d",V);
IsFirst = FALSE;
}
else
printf(" %d",V);
for(int j=0; j<Nv; j++)
{
if(G[V][j]==1 && visited[j] == FALSE)
dfs(j);
}
}
void bfs(Vertex V)
{
int queue[100];
int front = 0;
int tail = 0;
visited[V] = TRUE;
queue[tail++] = V;
int temp;
while(front != tail)
{
temp = queue[front++];
if(IsFirst)
{
printf("%d", temp);
IsFirst = FALSE;
}
else
printf(" %d",temp);
for(int i=0;i <Nv; i++)
{
if(G[temp][i] == 1 && visited[i] == FALSE)
{
visited[i] = TRUE;
queue[tail++] = i;
}
}
}
}
int main()
{
BuildGraph();
//printGraph();
for(int i=0; i<Nv;i++)
{
if(visited[i] == FALSE)
{
printf("{ ");
dfs(i);
printf(" }\n");
}
IsFirst = TRUE;
}
for(int i=0; i<Nv; i++)
visited[i] = FALSE;
for(int i=0; i<Nv;i++)
{
if(visited[i] == FALSE)
{
printf("{ ");
bfs(i);
printf(" }\n");
}
IsFirst = TRUE;
}
return 0;
}
PTA 06-图2 Saving James Bond - Easy Version
This time let us consider the situation in the movie "Live and Let Die" in which James Bond, the world's most famous spy, was captured by a group of drug dealers. He was sent to a small piece of land at the center of a lake filled with crocodiles. There he performed the most daring action to escape -- he jumped onto the head of the nearest crocodile! Before the animal realized what was happening, James jumped again onto the next big head... Finally he reached the bank before the last crocodile could bite him (actually the stunt man was caught by the big mouth and barely escaped with his extra thick boot).
Assume that the lake is a 100 by 100 square one. Assume that the center of the lake is at (0,0) and the northeast corner at (50,50). The central island is a disk centered at (0,0) with the diameter of 15. A number of crocodiles are in the lake at various positions. Given the coordinates of each crocodile and the distance that James could jump, you must tell him whether or not he can escape.
Input Specification:
Each input file contains one test case. Each case starts with a line containing two positive integers N (≤100), the number of crocodiles, and D, the maximum distance that James could jump. Then N lines follow, each containing the (x,y) location of a crocodile. Note that no two crocodiles are staying at the same position.
Output Specification:
For each test case, print in a line "Yes" if James can escape, or "No" if not.
Sample Input 1:
14 20
25 -15
-25 28
8 49
29 15
-35 -2
5 28
27 -29
-8 -28
-20 -35
-25 -20
-13 29
-30 15
-35 40
12 12
Sample Output 1:
Yes
Sample Input 2:
4 13
-12 12
12 12
-12 -12
12 -12
Sample Output 2:
No


#include <stdio.h>
#include <stdlib.h>
#define MAXN 100
#define TRUE 1
#define FALSE 0
typedef int Boolean;
Boolean visited[MAXN];
struct coordinate
{
int x;
int y;
}Points[MAXN];
int D = 0;
/*初始化标记矩阵*/
void ResetVisit()
{
for(int i=0;i<MAXN;i++)
visited[i]=0;
}
Boolean FirstJump(int i)
{
int x = Points[i].x;
int y = Points[i].y;
if((7.5+D)*(7.5+D) >= (x*x + y*y))
{
return TRUE;
}
else
{
return FALSE;
}
}
Boolean Jump(int i, int j)
{
int x1 = Points[i].x;
int y1 = Points[i].y;
int x2 = Points[j].x;
int y2 = Points[j].y;
if(D*D >= ((x1-x2)*(x1-x2) + (y1-y2)*(y1-y2)))
{
return TRUE;
}
else
{
return FALSE;
}
}
Boolean IsSafe(int i)
{
int x = Points[i].x;
int y = Points[i].y;
if(x<0)
x = -x;
if(y<0)
y = -y;
if(50-x<=D || 50-y<=D)
return TRUE;
else
return FALSE;
}
Boolean dfs(int i)
{
visited[i] = TRUE;
int answer;
if(IsSafe(i))
answer = TRUE;
else
{
for(int j=0; j<MAXN; j++)
{
//如果j节点未被访问,且能从j结点跳至j结点
if(Jump(i,j) && visited[j]!=TRUE)
{
answer = dfs(j);
if(answer == TRUE)
break;
}
}
}
return answer;
}
void Save007()
{
int answer;
ResetVisit();
for(int i=0; i<MAXN; i++)
{
if(FirstJump(i) && visited[i]!=TRUE)
{
answer = dfs(i);
if(answer==TRUE)
break;
}
}
if(answer==TRUE)
printf("Yes\n");
else
printf("No\n");
}
int main()
{
int N;
scanf("%d %d",&N,&D);
for(int i=0; i<N; i++)
{
scanf("%d %d",&(Points[i].x),&(Points[i].y));
}
Save007();
return 0;
}
PTA 06-图3 六度空间
“六度空间”理论又称作“六度分隔(Six Degrees of Separation)”理论。这个理论可以通俗地阐述为:“你和任何一个陌生人之间所间隔的人不会超过六个,也就是说,最多通过五个人你就能够认识任何一个陌生人。”如图1所示。
图1 六度空间示意图
“六度空间”理论虽然得到广泛的认同,并且正在得到越来越多的应用。但是数十年来,试图验证这个理论始终是许多社会学家努力追求的目标。然而由于历史的原因,这样的研究具有太大的局限性和困难。随着当代人的联络主要依赖于电话、短信、微信以及因特网上即时通信等工具,能够体现社交网络关系的一手数据已经逐渐使得“六度空间”理论的验证成为可能。
假如给你一个社交网络图,请你对每个节点计算符合“六度空间”理论的结点占结点总数的百分比。
输入格式:
输入第1行给出两个正整数,分别表示社交网络图的结点数N(1<N≤10^3,表示人数)、边数M(≤33×N,表示社交关系数)。随后的M行对应M条边,每行给出一对正整数,分别是该条边直接连通的两个结点的编号(节点从1到N编号)。
输出格式:
对每个结点输出与该结点距离不超过6的结点数占结点总数的百分比,精确到小数点后2位。每个结节点输出一行,格式为“结点编号:(空格)百分比%”。
输入样例:
10 9
1 2
2 3
3 4
4 5
5 6
6 7
7 8
8 9
9 10
输出样例:
1: 70.00%
2: 80.00%
3: 90.00%
4: 100.00%
5: 100.00%
6: 100.00%
7: 100.00%
8: 90.00%
9: 80.00%
10: 70.00%

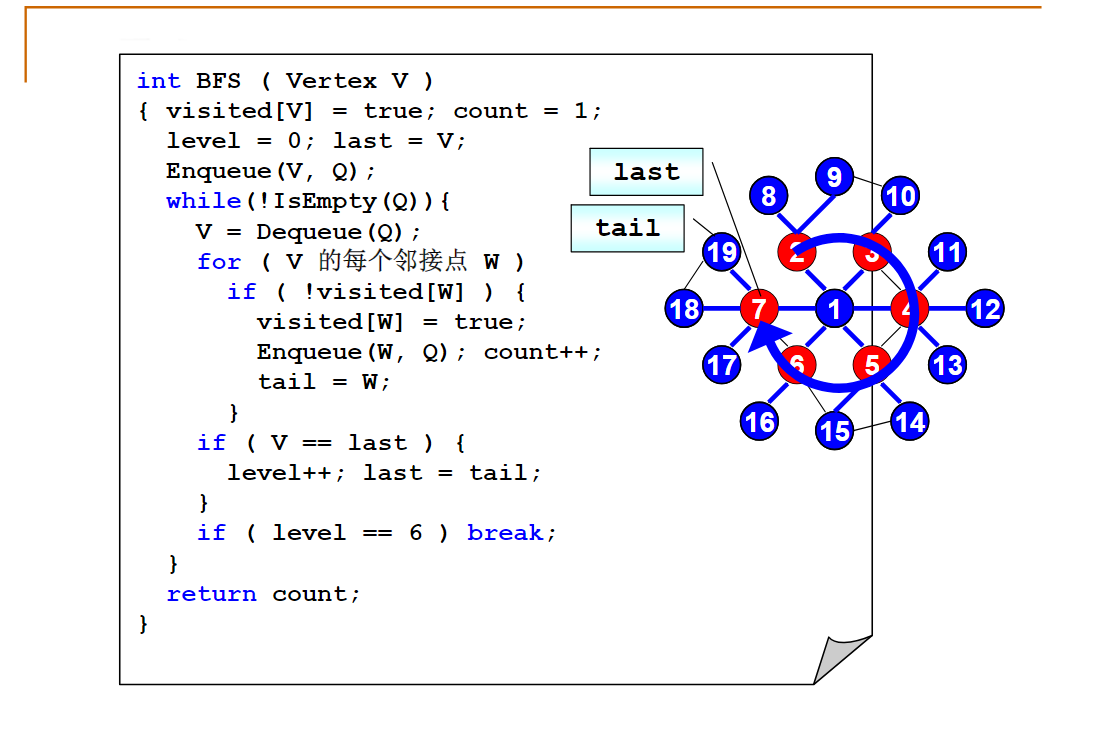
注意:
- 不要忘记初始化,每个顶点统计完毕后都需要进行 /(ㄒoㄒ)/~~
- 统计结果的变量count需要设定初始值为1,因为该节点也满足统计要求
#include <stdio.h>
#include <stdlib.h>
#define TRUE 1
#define FALSE 0
int G[1001][1001];
int visited[1001];
int N = 0;
int last = 0;
int tail = 0;
void ResetVisited()
{
for(int i=0; i<1001; i++)
visited[i] = 0;
}
int bfs(int v)
{
visited[v] = TRUE;
int count = 1;
int level = 0;
last = v;
tail = 0;
int queue[1001];
int front = 0;
int rear = 0;
queue[rear++] = v;
while(rear != front)
{
int temp = queue[front++];
for(int i=1; i<=N; i++)
{
if(visited[i]==FALSE && G[temp][i]==1)
{
visited[i] = TRUE;
queue[rear++] = i;
tail = i;
count++;
}
}
if(temp == last)
{
level++;
last = tail;
}
if(level == 6)
break;
}
return count;
}
int main()
{
int M,v1,v2;
scanf("%d %d",&N,&M);
for(int i=0; i<N; i++)
{
for(int j=0; j<N; j++)
G[i][j] = 0;
}
for(int i=0; i<M; i++)
{
scanf("%d %d",&v1, &v2);
G[v1][v2] = 1;
G[v2][v1] = 1;
}
for(int i=1; i<=N; i++)
{
ResetVisited();
int count = bfs(i);
printf("%d: %.2f%%\n",i, count*1.0*100/N);
}
}
PTA 07-图4 哈利·波特的考试
哈利·波特要考试了,他需要你的帮助。这门课学的是用魔咒将一种动物变成另一种动物的本事。例如将猫变成老鼠的魔咒是haha,将老鼠变成鱼的魔咒是hehe等等。反方向变化的魔咒就是简单地将原来的魔咒倒过来念,例如ahah可以将老鼠变成猫。另外,如果想把猫变成鱼,可以通过念一个直接魔咒lalala,也可以将猫变老鼠、老鼠变鱼的魔咒连起来念:hahahehe。
现在哈利·波特的手里有一本教材,里面列出了所有的变形魔咒和能变的动物。老师允许他自己带一只动物去考场,要考察他把这只动物变成任意一只指定动物的本事。于是他来问你:带什么动物去可以让最难变的那种动物(即该动物变为哈利·波特自己带去的动物所需要的魔咒最长)需要的魔咒最短?例如:如果只有猫、鼠、鱼,则显然哈利·波特应该带鼠去,因为鼠变成另外两种动物都只需要念4个字符;而如果带猫去,则至少需要念6个字符才能把猫变成鱼;同理,带鱼去也不是最好的选择。
输入格式:
输入说明:输入第1行给出两个正整数N (≤100)和M,其中N是考试涉及的动物总数,M是用于直接变形的魔咒条数。为简单起见,我们将动物按1~N编号。随后M行,每行给出了3个正整数,分别是两种动物的编号、以及它们之间变形需要的魔咒的长度(≤100),数字之间用空格分隔。
输出格式:
输出哈利·波特应该带去考场的动物的编号、以及最长的变形魔咒的长度,中间以空格分隔。如果只带1只动物是不可能完成所有变形要求的,则输出0。如果有若干只动物都可以备选,则输出编号最小的那只。
输入样例:
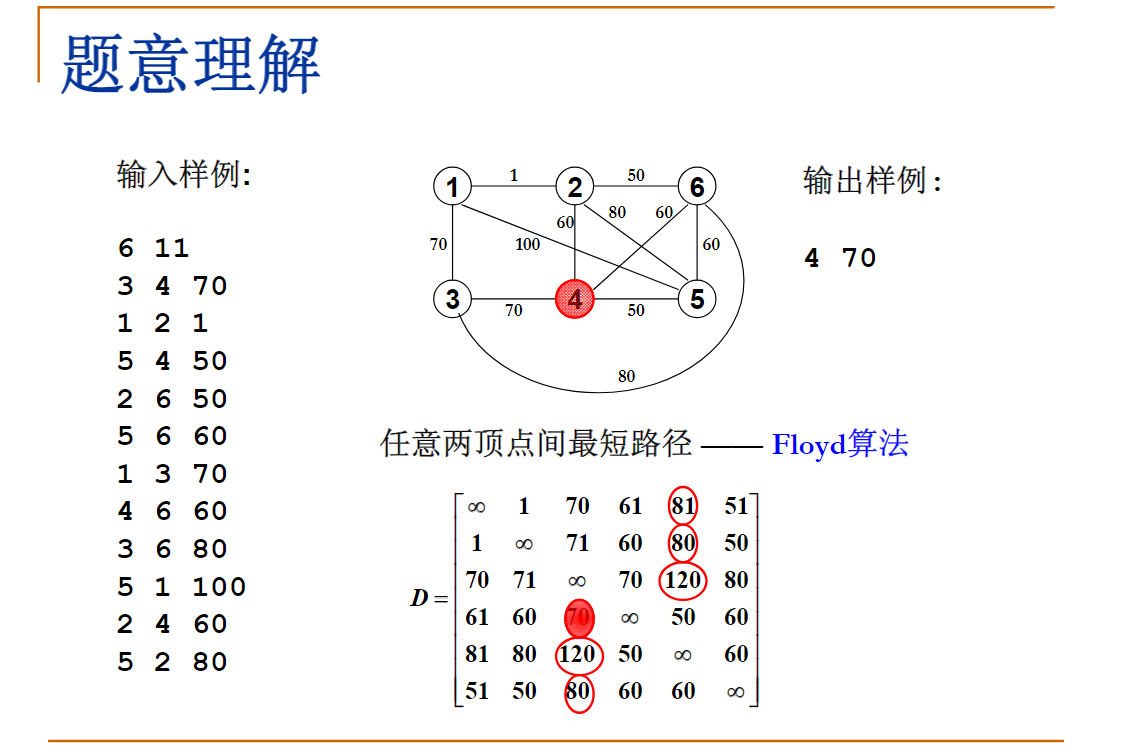
6 11
3 4 70
1 2 1
5 4 50
2 6 50
5 6 60
1 3 70
4 6 60
3 6 80
5 1 100
2 4 60
5 2 80
输出样例:
4 70
#include <stdio.h>
#include <stdlib.h>
#define MaxVertexNum 100
#define INFINITY 65535
typedef int Vertex;
typedef int WeightType;
typedef struct ENode *PtrToENode;
struct ENode
{
Vertex V1;
Vertex V2;
WeightType Weight;
};
typedef PtrToENode Edge;
typedef struct GNode *PtrToGNode;
struct GNode
{
int Nv;
int Ne;
WeightType G[MaxVertexNum][MaxVertexNum];
};
typedef PtrToGNode MGraph;
MGraph CreateGraph(int VertexNum)
{
MGraph Graph = (MGraph)malloc(sizeof(struct GNode));
Graph->Nv = VertexNum;
Graph->Ne = 0;
Vertex V1,V2;
for(Vertex V1=0; V1<Graph->Nv; V1++)
for(Vertex V2=0; V2<Graph->Nv; V2++)
Graph->G[V1][V2] = INFINITY;
return Graph;
}
void InsertEdge(MGraph Graph, Edge E)
{
Graph->G[E->V1][E->V2] = E->Weight;
Graph->G[E->V2][E->V1] = E->Weight;
}
MGraph BuildGraph()
{
int Nv;
Edge E;
scanf("%d", &Nv);
MGraph Graph = CreateGraph(Nv);
scanf("%d", &(Graph->Ne));
if((Graph->Ne) != 0)
{
E = (Edge)malloc(sizeof(struct ENode));
for(int i=0; i<Graph->Ne; i++)
{
scanf("%d %d %d",&E->V1,&E->V2,&E->Weight);
E->V1--;
E->V2--;
InsertEdge(Graph, E);
}
}
return Graph;
}
void Floyd(MGraph Graph, WeightType D[][MaxVertexNum])
{
Vertex i,j,k;
//初始化
for(i=0; i<Graph->Nv; i++)
for(j=0; j<Graph->Nv; j++)
D[i][j] = Graph->G[i][j];
for(k = 0; k < Graph->Nv; ++k){
for(i = 0; i < Graph->Nv; ++i){
for(j = 0; j < Graph->Nv; ++j){
if(D[i][k] + D[k][j] < D[i][j]){
D[i][j] = D[i][k] + D[k][j];
}
}
}
}
}
WeightType FindMaxDist(WeightType D[MaxVertexNum][MaxVertexNum], Vertex i, int N)
{
WeightType MaxDist = 0;
for(Vertex j=0; j<N; j++)
{
if(i!=j && D[i][j]>MaxDist)
MaxDist = D[i][j];
}
return MaxDist;
}
void FindAnimal(MGraph Graph)
{
WeightType D[MaxVertexNum][MaxVertexNum], MaxDist, MinDist;
Vertex Animal, i;
Floyd(Graph, D);
MinDist = INFINITY;
for(i=0; i<Graph->Nv; i++)
{
MaxDist = FindMaxDist(D, i, Graph->Nv);
if(MaxDist == INFINITY)
{
printf("0\n");
return;
}
if(MaxDist < MinDist)
{
MinDist = MaxDist;
Animal = i + 1;
}
}
printf("%d %d\n", Animal, MinDist);
}
int main()
{
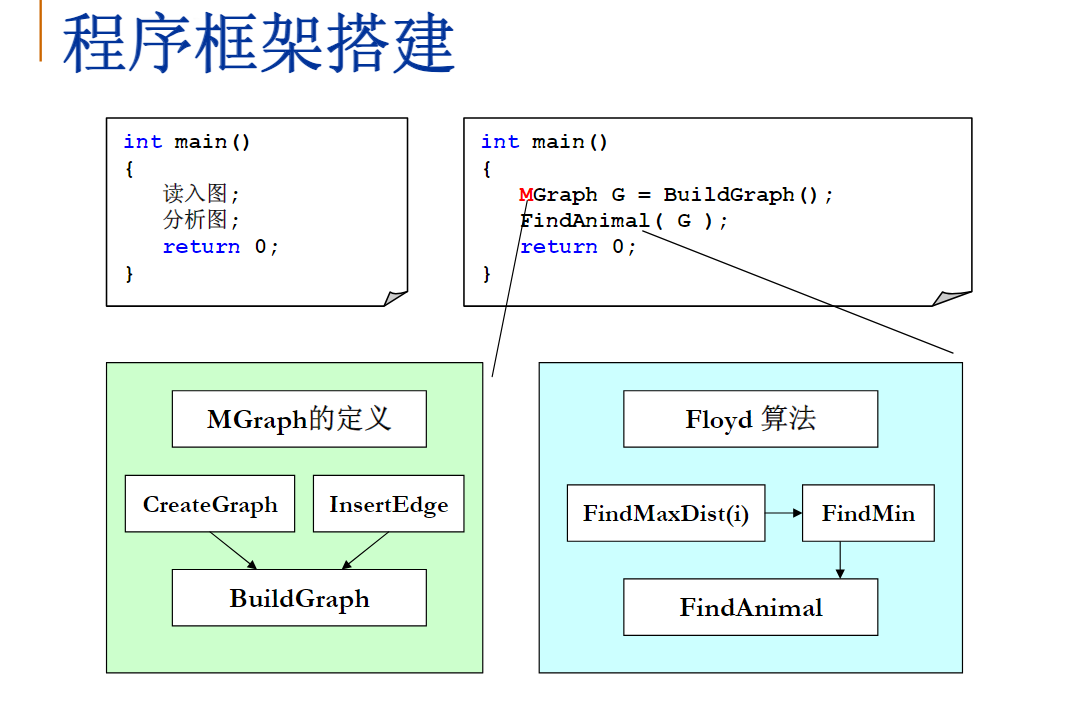
MGraph Graph = BuildGraph();
FindAnimal(Graph);
return 0;
}
注意:Floyd算法中的三重循环顺序不能更改,写成下面这样就无法通过部分测试用例。
for(i=0; i<Graph->Nv; i++)
{
for(j=0; j<Graph->Nv; j++)
{
for(k=0; k<Graph->Nv; k++)
{
if(D[i][k] + D[k][j] < D[i][j])
{
D[i][j] = D[i][k] + D[k][j];
}
}
}
PTA 07-图5 Saving James Bond - Hard Version
This time let us consider the situation in the movie "Live and Let Die" in which James Bond, the world's most famous spy, was captured by a group of drug dealers. He was sent to a small piece of land at the center of a lake filled with crocodiles. There he performed the most daring action to escape -- he jumped onto the head of the nearest crocodile! Before the animal realized what was happening, James jumped again onto the next big head... Finally he reached the bank before the last crocodile could bite him (actually the stunt man was caught by the big mouth and barely escaped with his extra thick boot).
Assume that the lake is a 100 by 100 square one. Assume that the center of the lake is at (0,0) and the northeast corner at (50,50). The central island is a disk centered at (0,0) with the diameter of 15. A number of crocodiles are in the lake at various positions. Given the coordinates of each crocodile and the distance that James could jump, you must tell him a shortest path to reach one of the banks. The length of a path is the number of jumps that James has to make.
Input Specification:
Each input file contains one test case. Each case starts with a line containing two positive integers N (≤100), the number of crocodiles, and D, the maximum distance that James could jump. Then N lines follow, each containing the (x,y) location of a crocodile. Note that no two crocodiles are staying at the same position.
Output Specification:
For each test case, if James can escape, output in one line the minimum number of jumps he must make. Then starting from the next line, output the position (x,y) of each crocodile on the path, each pair in one line, from the island to the bank. If it is impossible for James to escape that way, simply give him 0 as the number of jumps. If there are many shortest paths, just output the one with the minimum first jump, which is guaranteed to be unique.
Sample Input 1:
17 15
10 -21
10 21
-40 10
30 -50
20 40
35 10
0 -10
-25 22
40 -40
-30 30
-10 22
0 11
25 21
25 10
10 10
10 35
-30 10
Sample Output 1:
4
0 11
10 21
10 35
Sample Input 2:
4 13
-12 12
12 12
-12 -12
12 -12
Sample Output 2:
0
思路:
单源无权图最短路径问题
我们可以看到 If there are many shortest paths, just output the one with the minimum first jump, which is guaranteed to be unique.(当有多条最短路时,输出第一跳最小的最短路) 首先需要对图中的相关顶点(鳄鱼坐标),按第一跳的距离从小到大排序。
从岛中心开始进行BFS,按第一跳从小到大的顺序收入顶点,在遍历顶点的过程中,实时记录各顶点到源点的距离(dist数组) 以及当前顶点的前一跳顶点(path数组),这样才能满足题目的输出要求。
PTA 07-图6 旅游规划
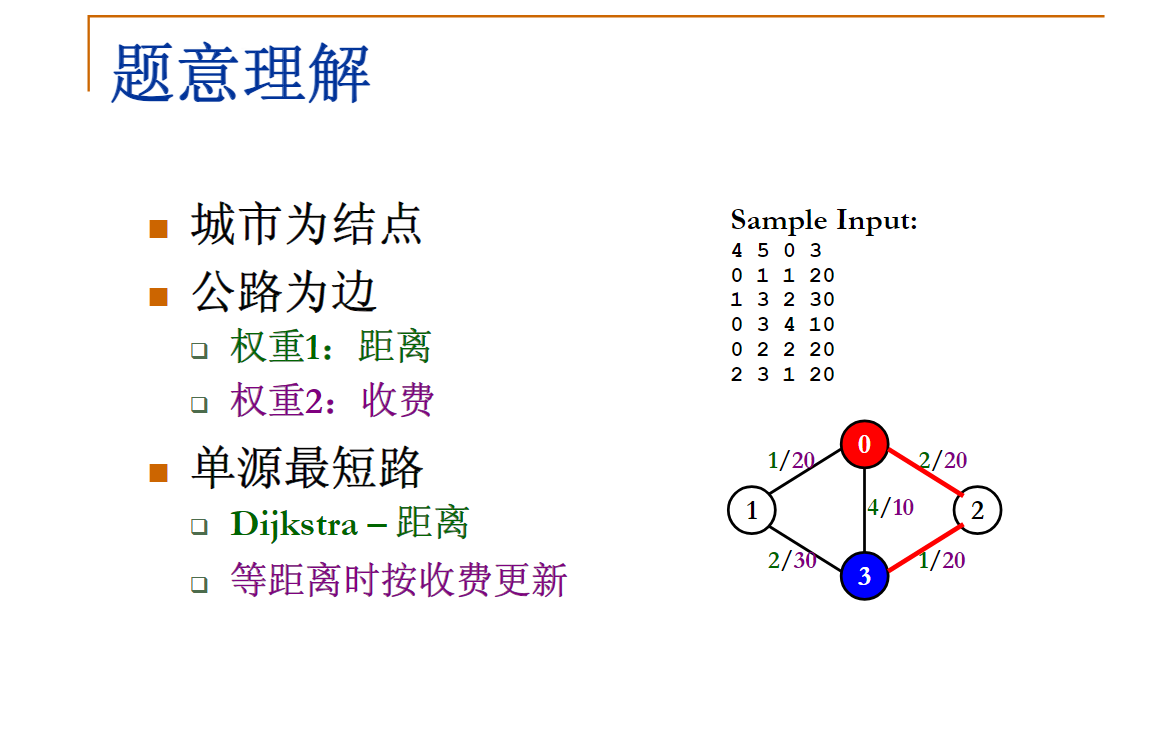
有了一张自驾旅游路线图,你会知道城市间的高速公路长度、以及该公路要收取的过路费。现在需要你写一个程序,帮助前来咨询的游客找一条出发地和目的地之间的最短路径。如果有若干条路径都是最短的,那么需要输出最便宜的一条路径。
输入格式:
输入说明:输入数据的第1行给出4个正整数N、M、S、D,其中N(2≤N≤500)是城市的个数,顺便假设城市的编号为0~(N−1);M是高速公路的条数;S是出发地的城市编号;D是目的地的城市编号。随后的M行中,每行给出一条高速公路的信息,分别是:城市1、城市2、高速公路长度、收费额,中间用空格分开,数字均为整数且不超过500。输入保证解的存在。
输出格式:
在一行里输出路径的长度和收费总额,数字间以空格分隔,输出结尾不能有多余空格。
输入样例:
4 5 0 3
0 1 1 20
1 3 2 30
0 3 4 10
0 2 2 20
2 3 1 20
输出样例:
3 40


#include <iostream>
#include <vector>
using namespace std;
class vertexNode{
public:
int s;//源城市
int d;//目的城市
int weight;//路程长 权值
int charge;//收费
vertexNode()=default;
vertexNode(int s_,int d_,int w_,int c_):s{s_},d{d_},weight{w_},charge{c_}{};
};
class AdjacencyLinkGraphic{
public:
vector<vector<vertexNode*>> vertexs;//二维数组, 存的值是结点 包含该点的路径和收费 vertexs[i][j] i是起点 j是终点
int cityNum{0};
int highwayNum{0};
int s;//出发城市
int d;//目的城市
AdjacencyLinkGraphic()=default;
AdjacencyLinkGraphic(int n_,int m_,int s_,int d_):cityNum{n_},highwayNum{m_},s{s_},d{d_}{};
void build(){
vertexs=vector<vector<vertexNode*>>(cityNum,vector<vertexNode*>(cityNum,nullptr));
int s,d,w,c;
for(int i=0;i<highwayNum;i++){
scanf("%d %d %d %d",&s,&d,&w,&c);
vertexs[s][d]=new vertexNode{s,d,w,c};
vertexs[d][s]=new vertexNode{d,s,w,c};
}
}
void dijkstra(){
vector<int> visited(cityNum);
visited[s]=1;
int u;//起点 的 未访问的 最小权值的 邻接点
// 先将s的访问位置为1,
// 1.找到u 然后将u的访问位置为1
// 2.先由起点的最小权值邻接点 u 开始, 寻找起点s 经由 u 到u的邻接点 j 的总权值是否小于 s到j的权值
// 3.如果经由 s 经由 u 到 j 的的路径权值小于s到j的权值 ,就更新s到j的权值为 (s到u的权值)+(u到j的权值)
// 循环直到s的邻接点全部遍历完毕,这时就得到了s到任意连通点的最小路径长 和 对应的收费
//直接输出 vertexs[s][d]的路径长 和 收费
for(int i=0;i<cityNum;i++){
int min=999999;
for(int j=0;j<cityNum;j++){
if( vertexs[s][j] && !visited[j] && vertexs[s][j]->weight < min){
min= vertexs[s][j]->weight;
u = j;
}
}
visited[u]=1;
for(int j=0; j<cityNum; j++){
if( vertexs[u][j] && vertexs[u][j]->weight <= 99999 ){
if( vertexs[u][j] && vertexs[s][u] && vertexs[s][j] ){//确认为连通点
if(vertexs[s][j]->weight == vertexs[s][u]->weight + vertexs[u][j]->weight){
if(vertexs[s][j]->charge > vertexs[s][u]->charge + vertexs[u][j]->charge)
vertexs[s][j]->charge=vertexs[s][u]->charge+vertexs[u][j]->charge;
}else if(vertexs[s][j]->weight > vertexs[s][u]->weight + vertexs[u][j]->weight){
//更新由s到j的最小权值和对应的路费
vertexs[s][j]->weight = vertexs[s][u]->weight + vertexs[u][j]->weight;
vertexs[s][j]->charge = vertexs[s][u]->charge + vertexs[u][j]->charge;
}
}
}
}
}
cout << vertexs[s][d]->weight <<" "<< vertexs[s][d]->charge<<endl;
}
};
int main(){
int n,m,s,d;
cin >> n >> m >> s >> d ;
AdjacencyLinkGraphic ALG{n,m,s,d};
ALG.build();
ALG.dijkstra();
return 0;
}
注:下面是我自己写的,只通过了第一个测试样例,过几天考完试接着搞!!
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#define MaxVertexNum 10000
#define INFINITY 65535
#define INT_MAX 65535
int visited[MaxVertexNum];
int dist[MaxVertexNum];
int path[MaxVertexNum];
int cost[MaxVertexNum];
typedef int Vertex;
typedef int WeightType;
typedef struct ENode *PtrToENode;
struct ENode
{
Vertex V1;
Vertex V2;
WeightType Weight;
WeightType Charge;
};
typedef PtrToENode Edge;
typedef struct GNode *PtrToGNode;
struct GNode
{
int Nv;
int Ne;
WeightType G[MaxVertexNum][MaxVertexNum];
WeightType Cost[MaxVertexNum][MaxVertexNum];
};
typedef PtrToGNode MGraph;
MGraph CreateGraph(int VertexNum)
{
MGraph Graph = (MGraph)malloc(sizeof(struct GNode));
Graph->Nv = VertexNum;
Graph->Ne = 0;
for(Vertex V1=0; V1<Graph->Nv; V1++)
for(Vertex V2=0; V2<Graph->Nv; V2++)
{
Graph->G[V1][V2] = 0;
Graph->Cost[V1][V2] = 0;
}
return Graph;
}
void InsertEdge(MGraph Graph, Edge E)
{
Graph->G[E->V1][E->V2] = E->Weight;
Graph->Cost[E->V1][E->V2] = E->Charge;
}
void ResetVisited()
{
for(int i=0; i<MaxVertexNum; i++)
visited[i] = 0;
}
void Dijkstra(MGraph Graph, Vertex V, Vertex dest)
{
ResetVisited();
for(int i=0; i<Graph->Nv; i++)
{
if(Graph->G[V][i]>0 && V!=i)
{
dist[i] = Graph->G[V][i];
path[i] = V;
cost[i] = Graph->Cost[V][i];
}
else
{
dist[i] = INFINITY;
path[i] = -1;
cost[i] = 0;
}
}
dist[V] = 0;
path[V] = V;
cost[V] = 0;
visited[V] = 1;
for(int i=1; i<Graph->Nv; i++)
{
int minDist = INT_MAX;
int index;
for(int j=0; j<Graph->Nv; j++)
{
if(visited[j]==0 && dist[j]<minDist)
{
minDist = dist[j];
index = j;
}
}
visited[index] = 1;
for(int k=0; k<Graph->Nv; k++)
{
if(visited[k]==0)
{
if(Graph->G[index][k]>0 && minDist+Graph->G[index][k]<dist[k])
{
dist[k] = minDist+Graph->G[index][k];
path[k] = index;
cost[k] = cost[index] + Graph->Cost[index][k];
}
else if(Graph->G[index][k]>0 && minDist+Graph->G[index][k]==dist[k] && cost[V] + Graph->Cost[index][k]<cost[k])
{
cost[k] = cost[index] + Graph->Cost[index][k];
}
}
}
}
printf("%d %d\n",dist[dest],cost[dest]);
}
int main()
{
int Nv;
Edge E;
scanf("%d", &Nv);
MGraph Graph = CreateGraph(Nv);
scanf("%d", &(Graph->Ne));
int src, dest;
scanf("%d %d",&src,&dest);
int fee;
if((Graph->Ne) != 0)
{
E = (Edge)malloc(sizeof(struct ENode));
for(int i=0; i<Graph->Ne; i++)
{
scanf("%d %d %d %d",&E->V1,&E->V2,&E->Weight,&E->Charge);
InsertEdge(Graph, E);
}
}
Dijkstra(Graph, src, dest);
return 0;
}
PTA 08-图7 公路村村通
现有村落间道路的统计数据表中,列出了有可能建设成标准公路的若干条道路的成本,求使每个村落都有公路连通所需要的最低成本。
输入格式:
输入数据包括城镇数目正整数N(≤1000)和候选道路数目M(≤3N);随后的M行对应M条道路,每行给出3个正整数,分别是该条道路直接连通的两个城镇的编号以及该道路改建的预算成本。为简单起见,城镇从1到N编号。
输出格式:
输出村村通需要的最低成本。如果输入数据不足以保证畅通,则输出−1,表示需要建设更多公路。
输入样例:
6 15
1 2 5
1 3 3
1 4 7
1 5 4
1 6 2
2 3 4
2 4 6
2 5 2
2 6 6
3 4 6
3 5 1
3 6 1
4 5 10
4 6 8
5 6 3
输出样例:
12
PTA 08-图8 How Long Does It Take
Given the relations of all the activities of a project, you are supposed to find the earliest completion time of the project.
Input Specification:
Each input file contains one test case. Each case starts with a line containing two positive integers N (≤100), the number of activity check points (hence it is assumed that the check points are numbered from 0 to N−1), and M, the number of activities. Then M lines follow, each gives the description of an activity. For the i-th activity, three non-negative numbers are given: S[i], E[i], and L[i], where S[i] is the index of the starting check point, E[i] of the ending check point, and L[i] the lasting time of the activity. The numbers in a line are separated by a space.
Output Specification:
For each test case, if the scheduling is possible, print in a line its earliest completion time; or simply output "Impossible".
Sample Input 1:
9 12
0 1 6
0 2 4
0 3 5
1 4 1
2 4 1
3 5 2
5 4 0
4 6 9
4 7 7
5 7 4
6 8 2
7 8 4
Sample Output 1:
18
Sample Input 2:
4 5
0 1 1
0 2 2
2 1 3
1 3 4
3 2 5
Sample Output 2:
Impossible
PTA 08-图9 关键活动
假定一个工程项目由一组子任务构成,子任务之间有的可以并行执行,有的必须在完成了其它一些子任务后才能执行。“任务调度”包括一组子任务、以及每个子任务可以执行所依赖的子任务集。
比如完成一个专业的所有课程学习和毕业设计可以看成一个本科生要完成的一项工程,各门课程可以看成是子任务。有些课程可以同时开设,比如英语和C程序设计,它们没有必须先修哪门的约束;有些课程则不可以同时开设,因为它们有先后的依赖关系,比如C程序设计和数据结构两门课,必须先学习前者。
但是需要注意的是,对一组子任务,并不是任意的任务调度都是一个可行的方案。比如方案中存在“子任务A依赖于子任务B,子任务B依赖于子任务C,子任务C又依赖于子任务A”,那么这三个任务哪个都不能先执行,这就是一个不可行的方案。
任务调度问题中,如果还给出了完成每个子任务需要的时间,则我们可以算出完成整个工程需要的最短时间。在这些子任务中,有些任务即使推迟几天完成,也不会影响全局的工期;但是有些任务必须准时完成,否则整个项目的工期就要因此延误,这种任务就叫“关键活动”。
请编写程序判定一个给定的工程项目的任务调度是否可行;如果该调度方案可行,则计算完成整个工程项目需要的最短时间,并输出所有的关键活动。
输入格式:
输入第1行给出两个正整数N(≤100)和M,其中N是任务交接点(即衔接相互依赖的两个子任务的节点,例如:若任务2要在任务1完成后才开始,则两任务之间必有一个交接点)的数量。交接点按1N编号,M是子任务的数量,依次编号为1M。随后M行,每行给出了3个正整数,分别是该任务开始和完成涉及的交接点编号以及该任务所需的时间,整数间用空格分隔。
输出格式:
如果任务调度不可行,则输出0;否则第1行输出完成整个工程项目需要的时间,第2行开始输出所有关键活动,每个关键活动占一行,按格式“V->W”输出,其中V和W为该任务开始和完成涉及的交接点编号。关键活动输出的顺序规则是:任务开始的交接点编号小者优先,起点编号相同时,与输入时任务的顺序相反。
输入样例:
7 8
1 2 4
1 3 3
2 4 5
3 4 3
4 5 1
4 6 6
5 7 5
6 7 2
输出样例:
17
1->2
2->4
4->6
6->7