拓扑排序和关键路径

AOV网络和拓扑排序
AOE网络和关键路径

AOV网络和拓扑排序

定义

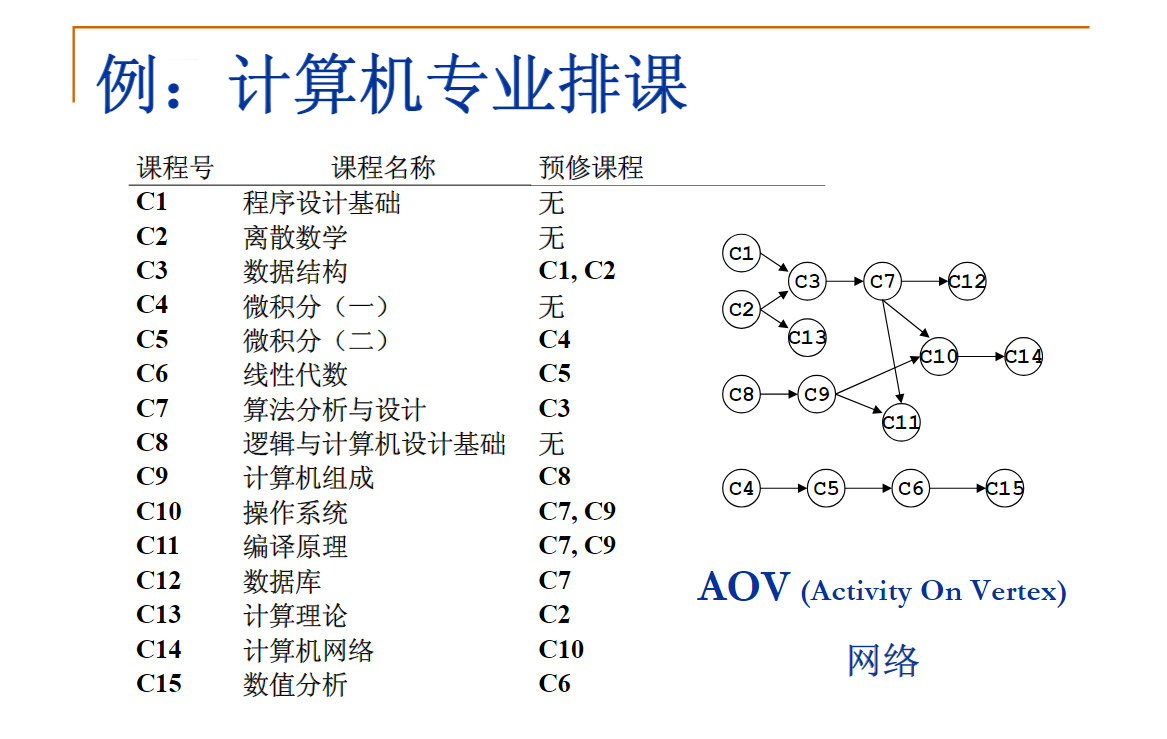
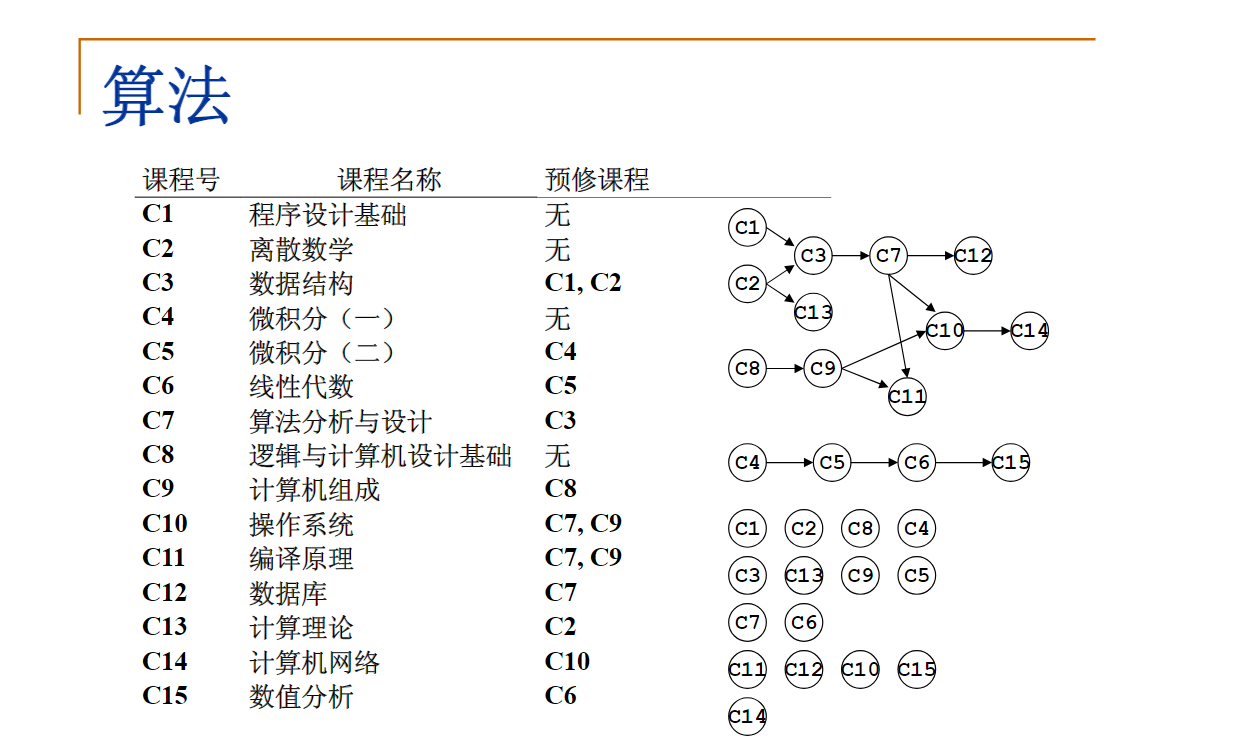
在TopSort函数中，如果外循环还没结束，就已经找不到“未输出的入度为0的顶点”，则说明图中必定存在回路。

容器的影响

分别用队列和堆栈作为容器，对计算机专业课程进行拓扑排序，得到的序列有什么区别？用哪种容器排课更合理？

队列拓扑排序得到的结果是从上到下的顺序，类似于一层一层地拓扑排序。堆栈拓扑排序得到的结果是从下到上的顺序，类似于逆序的拓扑排序。选择合理的容器：如果你希望按照正常的学习顺序，从基础课程开始，逐渐深入，那么队列拓扑排序更合理。如果你更关注最终课程的先修条件，或者希望从高级课程逆向推导，那么堆栈拓扑排序更合理。

分别用队列和堆栈作为容器，对计算机专业课程进行拓扑排序，得到的序列有什么区别？用哪种容器排课更合理？

在进行拓扑排序时，可以使用队列或堆栈作为辅助容器。这两种方法都能够正确地产生拓扑排序，但得到的序列可能会不同，这取决于容器的数据结构特性。

使用队列进行拓扑排序

当使用队列进行拓扑排序时，通常是实现了所谓的Kahn算法。这种方法是基于入度（指向某个顶点的边的数量）的概念：

首先将所有入度为0的顶点加入队列。

然后依次从队列中取出一个顶点，将其添加到排序结果中，并移除所有从该顶点出发的边，更新相关顶点的入度。

如果某个顶点的入度变为0，则将其加入队列。

重复步骤2和3，直到队列为空。

使用队列的拓扑排序通常产生多种合法的排序结果，对于同一张图，不同的顶点加入队列的顺序可能会产生不同的拓扑排序序列。

使用堆栈进行拓扑排序

使用堆栈进行拓扑排序通常是基于深度优先搜索（DFS）：

对每个尚未访问的顶点，执行DFS。

在DFS的过程中，当从某个顶点出发的所有边都被探索过后，将该顶点压入堆栈。

DFS完成后，依次从堆栈中弹出顶点，这个顺序就是拓扑排序的结果。

这种方法也可能产生多种拓扑排序，具体结果取决于DFS的顺序。

哪种方法更合理？

在排课程时，选择哪种方法取决于具体的需求：

如果你想要的是一种可能的顺序，并且希望尽快开始没有先决条件的课程（即入度为0的课程），那么使用基于队列的Kahn算法更合适。

如果你对课程之间的依赖关系有更深入的探究，或者对课程的探索顺序有特定需求，使用基于DFS的堆栈方法可能更合适。

在大多数情况下，使用队列的方法更直观，因为它直接处理了课程之间的依赖关系。然而，最终的选择应该基于具体场景和需求。

邻接表存储——拓扑排序算法

/* 邻接表存储 - 拓扑排序算法 */

bool TopSort( LGraph Graph, Vertex TopOrder[] )
{ /* 对Graph进行拓扑排序,  TopOrder[]顺序存储排序后的顶点下标 */
    int Indegree[MaxVertexNum], cnt;
    Vertex V;
    PtrToAdjVNode W;
       Queue Q = CreateQueue( Graph->Nv );
 
    /* 初始化Indegree[] */
    for (V=0; V<Graph->Nv; V++)
        Indegree[V] = 0;
        
    /* 遍历图，得到Indegree[] */
    for (V=0; V<Graph->Nv; V++)
        for (W=Graph->G[V].FirstEdge; W; W=W->Next)
            Indegree[W->AdjV]++; /* 对有向边<V, W->AdjV>累计终点的入度 */
            
    /* 将所有入度为0的顶点入列 */
    for (V=0; V<Graph->Nv; V++)
        if ( Indegree[V]==0 )
            AddQ(Q, V);
            
    /* 下面进入拓扑排序 */ 
    cnt = 0; 
    while( !IsEmpty(Q) ){
        V = DeleteQ(Q); /* 弹出一个入度为0的顶点 */
        TopOrder[cnt++] = V; /* 将之存为结果序列的下一个元素 */
        /* 对V的每个邻接点W->AdjV */
        for ( W=Graph->G[V].FirstEdge; W; W=W->Next )
            if ( --Indegree[W->AdjV] == 0 )/* 若删除V使得W->AdjV入度为0 */
                AddQ(Q, W->AdjV); /* 则该顶点入列 */ 
    } /* while结束*/
    
    if ( cnt != Graph->Nv )
        return false; /* 说明图中有回路, 返回不成功标志 */ 
    else
        return true;
}

邻接表存储——拓扑排序算法实例

#include <stdio.h>
#include <stdlib.h>

#define MaxVertexNum 100
typedef int WeightType;
typedef int Vertex;

typedef struct ENode *PtrToENode;
struct ENode
{
    Vertex V1;
    Vertex V2;
    WeightType Weight;
};
typedef PtrToENode Edge;

typedef struct AdjVNode *PtrToAdjVNode;
struct AdjVNode
{
    PtrToAdjVNode Next;
    Vertex AdjV;
    WeightType Weight;
};

typedef struct VNode
{
    PtrToAdjVNode FirstEdge;
}AdjList[MaxVertexNum];


typedef struct GNode *PtrToGNode;
struct GNode
{
    int Ne;
    int Nv;
    AdjList G;
};
typedef PtrToGNode LGraph;

void InsertEdge(LGraph Graph, Edge E)
{
    PtrToAdjVNode newNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
    newNode->AdjV = E->V2;
    newNode->Weight = E->Weight;
    newNode->Next = Graph->G[E->V1].FirstEdge;
    Graph->G[E->V1].FirstEdge = newNode;

    //newNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
    //newNode->AdjV = E->V1;
    //newNode->Weight = E->Weight;
    //newNode->Next = Graph->G[E->V2].FirstEdge;
    //Graph->G[E->V2].FirstEdge = newNode;
}

LGraph CreateGraph(int VertexNum)
{
    LGraph Graph = (LGraph)malloc(sizeof(struct GNode));
    Graph->Nv = VertexNum;
    Graph->Ne = 0;
    for(int i=0; i<Graph->Nv; i++)
        Graph->G[i].FirstEdge = NULL;
    return Graph;
}

LGraph BuildGraph()
{
    int N;
    Edge E;
    scanf("%d",&N);
    LGraph Graph = CreateGraph(N);
    scanf("%d",&Graph->Ne);
    if(Graph->Ne != 0)
    {
        for(int i=0; i<Graph->Ne; i++)
        {
            E = (Edge)malloc(sizeof(struct ENode));
            scanf("%d %d %d",&E->V1,&E->V2,&E->Weight);
            InsertEdge(Graph, E);
        }
    }
    return Graph;
}

void TopSort(LGraph Graph, int TopOrder[])
{
    int Indegree[MaxVertexNum], count;
    Vertex V;
    PtrToAdjVNode W;
    //Queue Q = CreateQueue( Graph->Nv );
    Vertex queue[Graph->Nv];
    int front = 0;
    int rear = 0;
    for (V=0; V<Graph->Nv; V++)
        Indegree[V] = 0;

    for(V=0; V<Graph->Nv; V++)
    {
        for(W=Graph->G[V].FirstEdge; W; W=W->Next)
        {
            Indegree[W->AdjV]++;
        }
    }
    for(V=0; V<Graph->Nv; V++)
    {
        if(Indegree[V] == 0)
        {
            queue[rear++] = V;
        }
    }
    //下面进入拓扑排序
    count = 0;
    while(front != rear)
    {
        V = queue[front++];
        TopOrder[count++] = V;
        for(W=Graph->G[V].FirstEdge; W; W=W->Next)
        {
            if(--Indegree[W->AdjV] == 0)
            {
                queue[rear++] = W->AdjV;
            }
        }
    }
    if(count != Graph->Nv)
    {
        printf("图中存在循环路径！\n");
    }
    else
    {
        for(int i=0; i<count; i++)
            printf("%d ",TopOrder[i]);
    }

}

int main()
{
    LGraph Graph = BuildGraph();
    Vertex TopOrder[MaxVertexNum];
    TopSort(Graph, TopOrder);
    return 0;
}

输入数据：

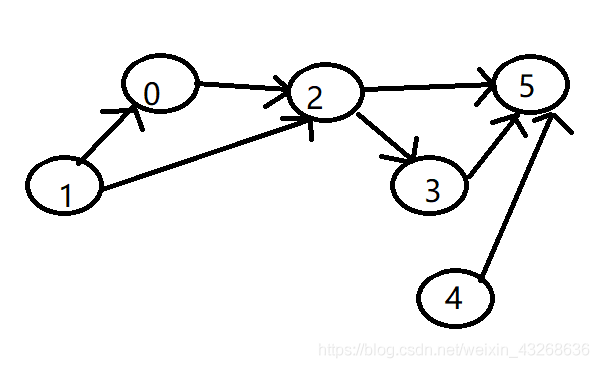
输出结果：

1 4 0 2 3 5

说明一下，拓扑排序可能有多种结果。

另一种结果可以是4 1 0 2 3 5。

#include <stdio.h>
#include <stdlib.h>

#define MaxVertexNum 100
typedef int WeightType;
typedef int Vertex;

typedef struct ENode *PtrToENode;
struct ENode
{
    Vertex V1;
    Vertex V2;
    WeightType Weight;
};
typedef PtrToENode Edge;

typedef struct AdjVNode *PtrToAdjVNode;
struct AdjVNode
{
    PtrToAdjVNode Next;
    Vertex AdjV;
    WeightType Weight;
};

typedef struct VNode
{
    PtrToAdjVNode FirstEdge;
}AdjList[MaxVertexNum];


typedef struct GNode *PtrToGNode;
struct GNode
{
    int Ne;
    int Nv;
    AdjList G;
};
typedef PtrToGNode LGraph;

void InsertEdge(LGraph Graph, Edge E)
{
    PtrToAdjVNode newNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
    newNode->AdjV = E->V2;
    newNode->Weight = E->Weight;
    newNode->Next = Graph->G[E->V1].FirstEdge;
    Graph->G[E->V1].FirstEdge = newNode;

    //newNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
    //newNode->AdjV = E->V1;
    //newNode->Weight = E->Weight;
    //newNode->Next = Graph->G[E->V2].FirstEdge;
    //Graph->G[E->V2].FirstEdge = newNode;
}

LGraph CreateGraph(int VertexNum)
{
    LGraph Graph = (LGraph)malloc(sizeof(struct GNode));
    Graph->Nv = VertexNum;
    Graph->Ne = 0;
    for(int i=0; i<Graph->Nv; i++)
        Graph->G[i].FirstEdge = NULL;
    return Graph;
}

LGraph BuildGraph()
{
    int N;
    Edge E;
    scanf("%d",&N);
    LGraph Graph = CreateGraph(N);
    scanf("%d",&Graph->Ne);
    if(Graph->Ne != 0)
    {
        for(int i=0; i<Graph->Ne; i++)
        {
            E = (Edge)malloc(sizeof(struct ENode));
            scanf("%d %d %d",&E->V1,&E->V2,&E->Weight);
            InsertEdge(Graph, E);
        }
    }
    return Graph;
}

void PrintList(LGraph Graph)
{
    for(int i=0; i<Graph->Nv; i++)
    {
        PtrToAdjVNode W = Graph->G[i].FirstEdge;
        printf("G[%d]:", i);
        int IsFirst = 1;
        while(W)
        {
            if(IsFirst)
            {
                printf("%d", W->AdjV);
                IsFirst = 0;
            }
            else
                printf("->%d", W->AdjV);
            W = W->Next;
        }
        printf("\n");
    }
}

void TopSort(LGraph Graph, int TopOrder[])
{
    int Indegree[MaxVertexNum], count;
    Vertex V;
    PtrToAdjVNode W;
    //Queue Q = CreateQueue( Graph->Nv );
    Vertex queue[Graph->Nv];
    int front = 0;
    int rear = 0;
    for (V=0; V<Graph->Nv; V++)
        Indegree[V] = 0;

    for(V=0; V<Graph->Nv; V++)
    {
        for(W=Graph->G[V].FirstEdge; W; W=W->Next)
        {
            Indegree[W->AdjV]++;
        }
    }
    for(V=0; V<Graph->Nv; V++)
    {
        if(Indegree[V] == 0)
        {
            queue[rear++] = V;
        }
    }
    //下面进入拓扑排序
    count = 0;
    while(front != rear)
    {
        V = queue[front++];
        TopOrder[count++] = V;
        for(W=Graph->G[V].FirstEdge; W; W=W->Next)
        {
            if(--Indegree[W->AdjV] == 0)
            {
                queue[rear++] = W->AdjV;
            }
        }
    }
    if(count != Graph->Nv)
    {
        printf("图中存在循环路径！\n");
    }
    else
    {
        for(int i=0; i<count; i++)
            printf("%d ",TopOrder[i]);
    }

}

int main()
{
    LGraph Graph = BuildGraph();
    PrintList(Graph);
    Vertex TopOrder[MaxVertexNum];
    TopSort(Graph, TopOrder);
    return 0;
}

输入数据：

输出结果：

G[0]:2
G[1]:0
G[2]:3->5->1
G[3]:5
G[4]:5
G[5]:
图中存在循环路径！

AOE网络和关键路径

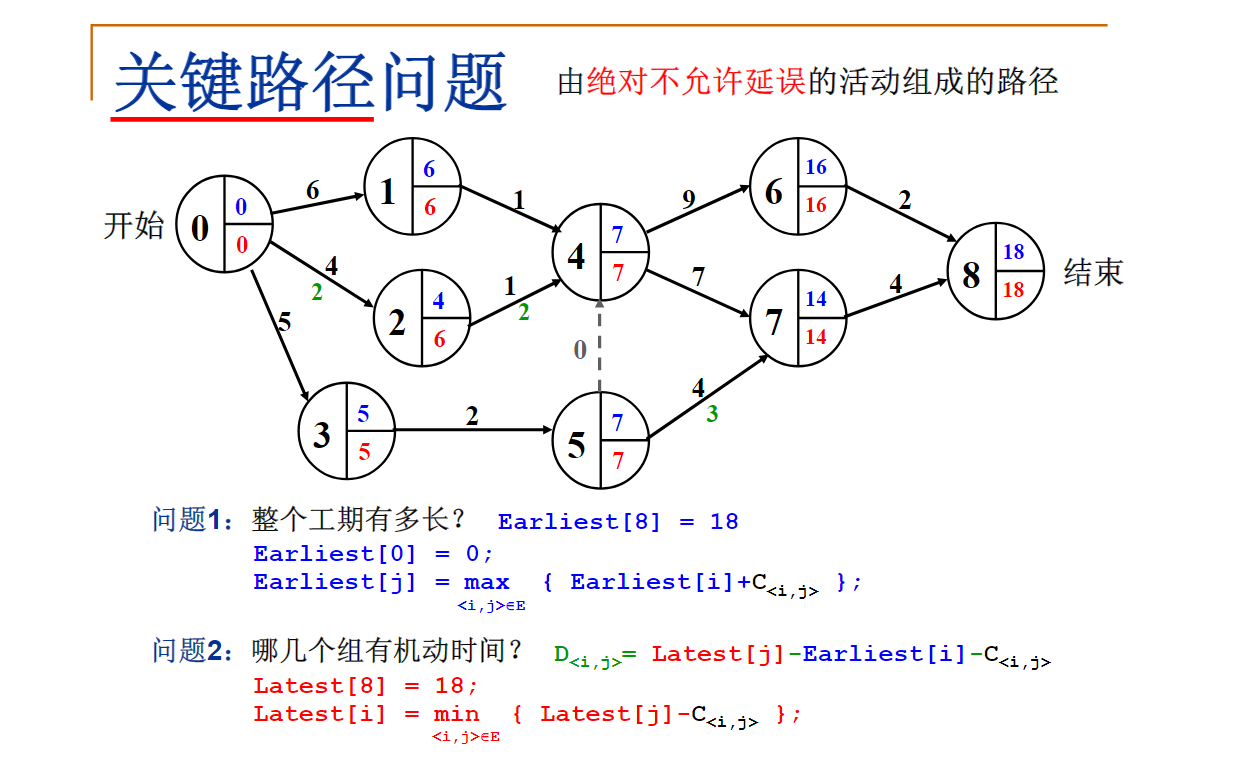
下图给定了一个项目的AOE。整个项目最早完工需要的时间是

A.17
B.19
C.20
D.23

正确答案：D你选对了

2在上图中，如果<0,2>组能加快进度，整个项目就能提前完工。

✔

正确答案：A你选对了

资料结构与演算法