并查集
集合表示
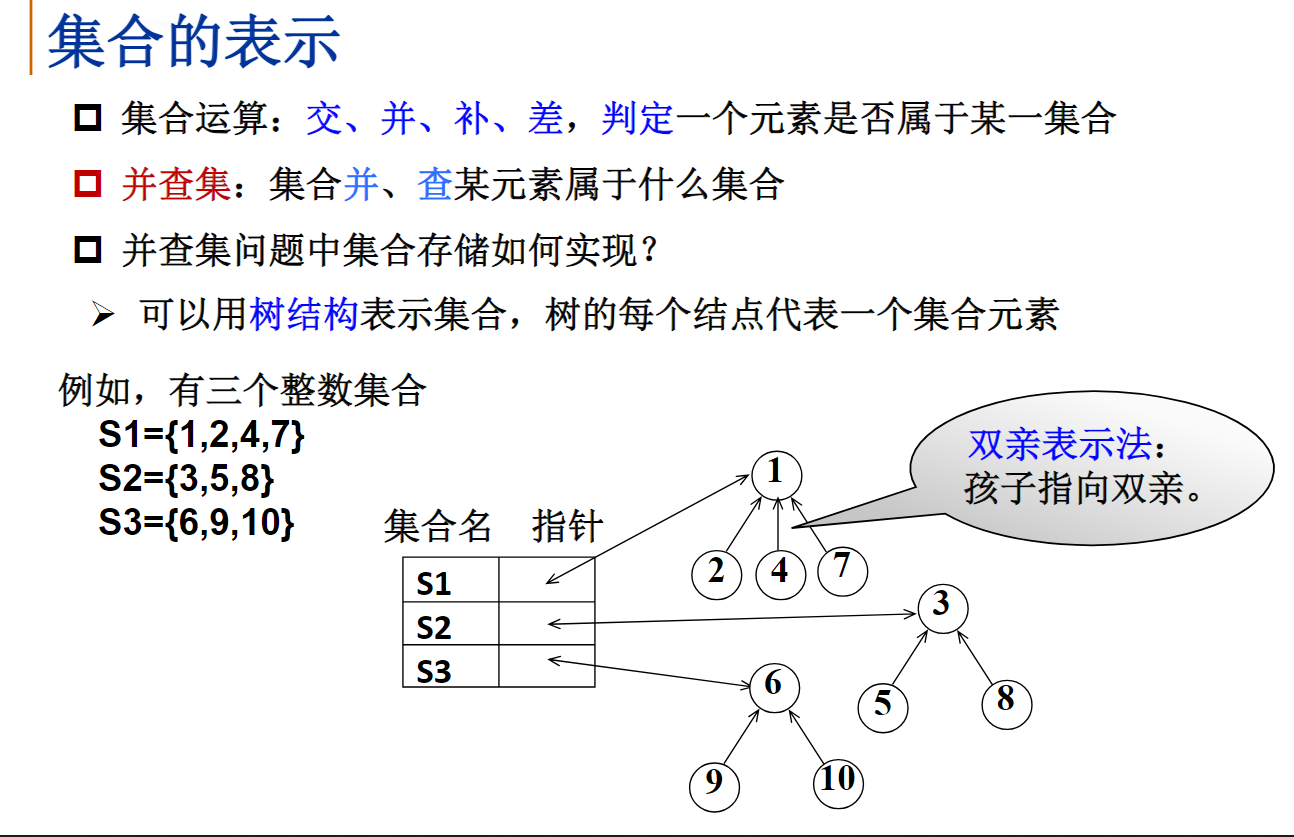
如果有10台电脑{1,2,3,4,...,9,10},已知下列电脑之间实现了连接:1和2,2和4,3和5,4和7,5和8,6和9,6和10问:2和7,5和9之间是否可以连通?2和7是连通的,5和9不连通
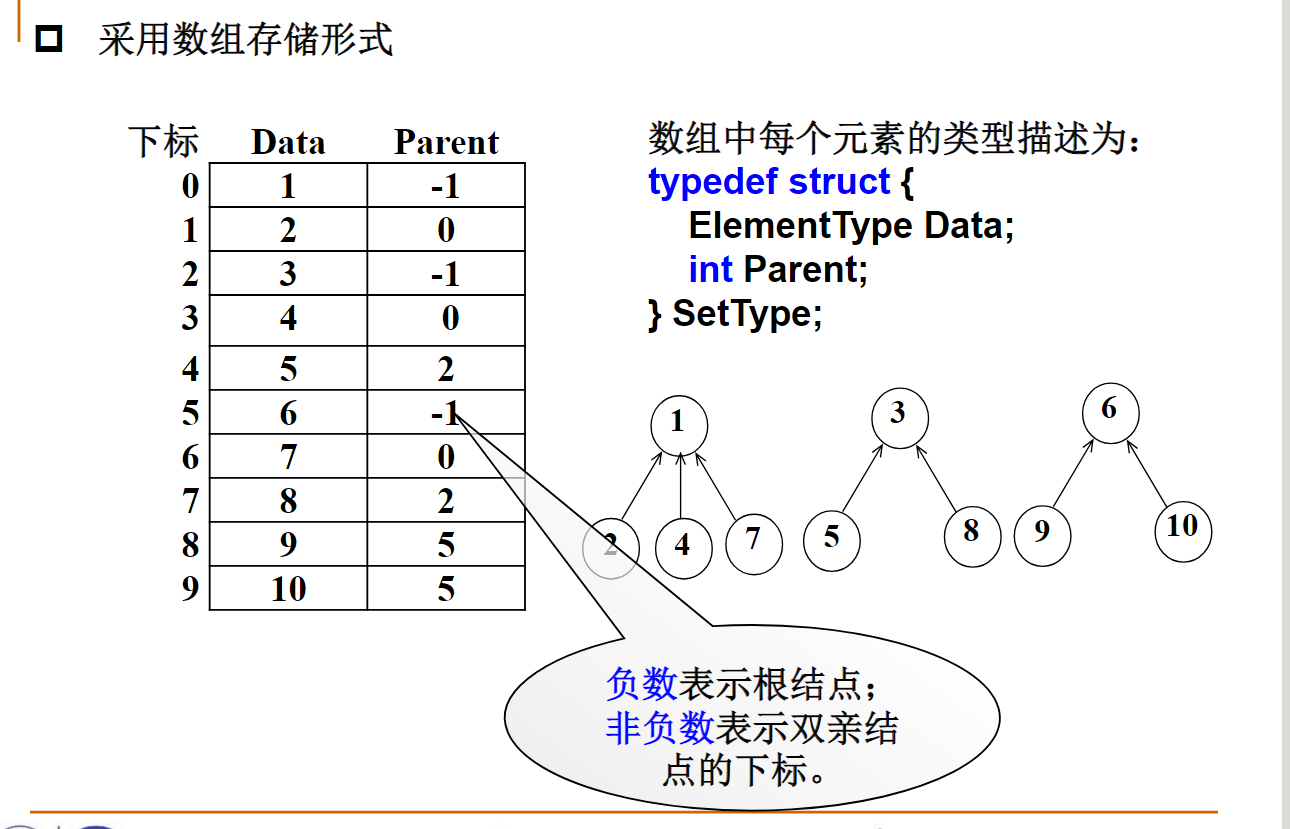
集合运算


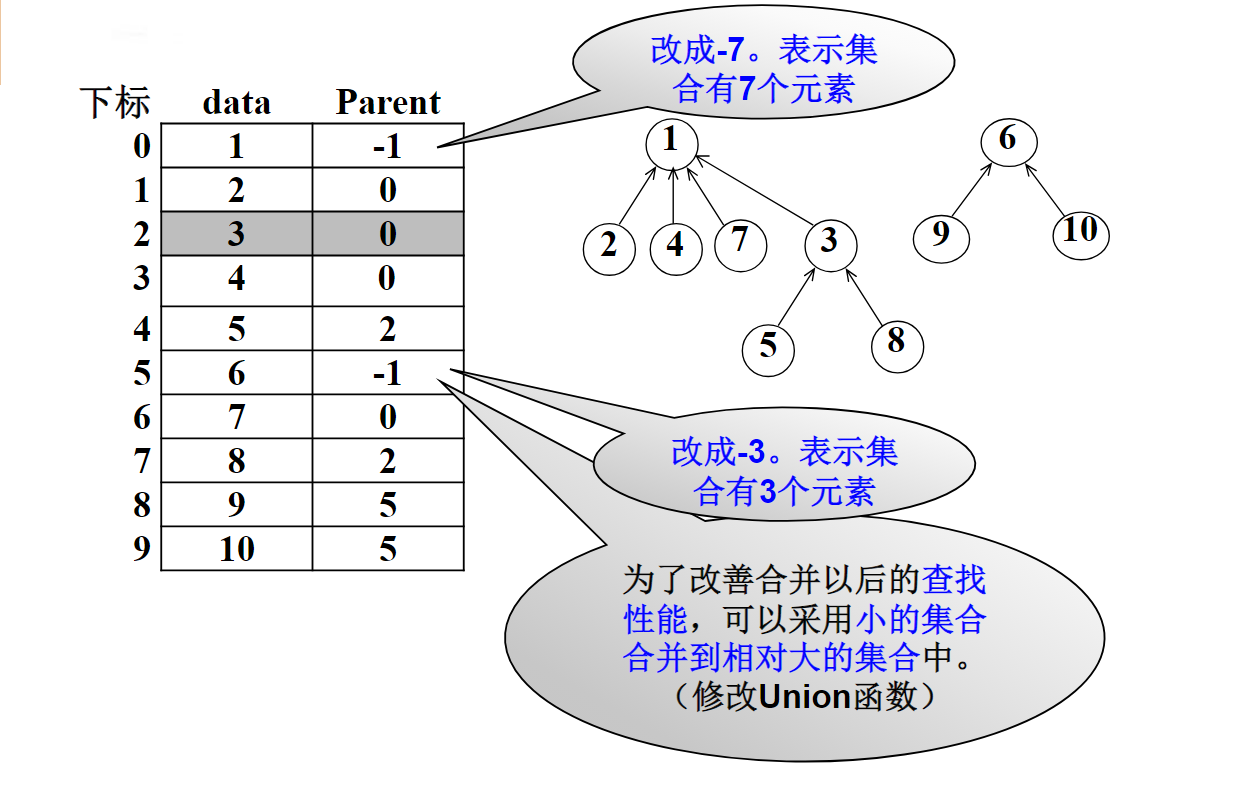
已知a、b两个元素均是所在集合的根结点,且分别位于数组分量3和2位置上,其parent值分别为-3,-2。问:将这两个集合按集合大小合并后,a和b的parent值分别是多少?-5,3
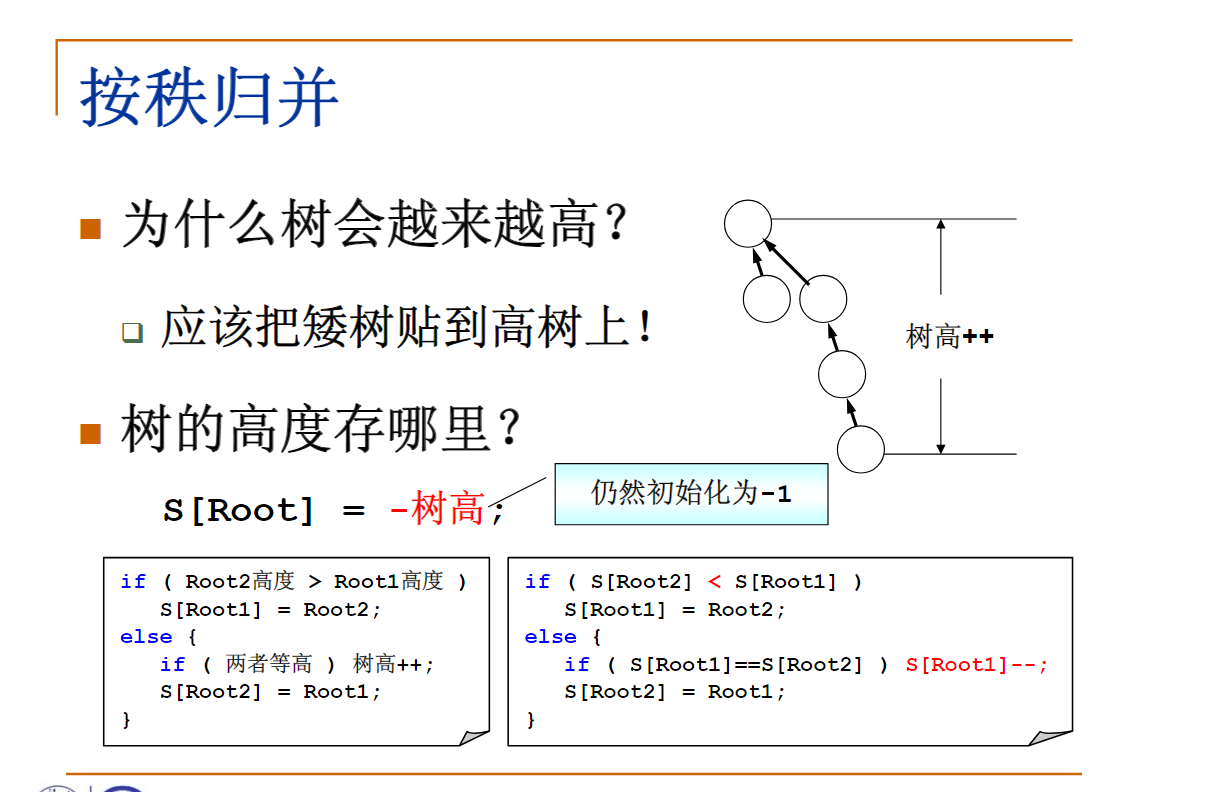
集合的定义与并查操作(已加入按秩归并方法):
#define MAXN 1000 /* 集合最大元素个数 */
typedef int ElementType; /* 默认元素可以用非负整数表示 */
typedef int SetName; /* 默认用根结点的下标作为集合名称 */
typedef ElementType SetType[MAXN]; /* 假设集合元素下标从0开始 */
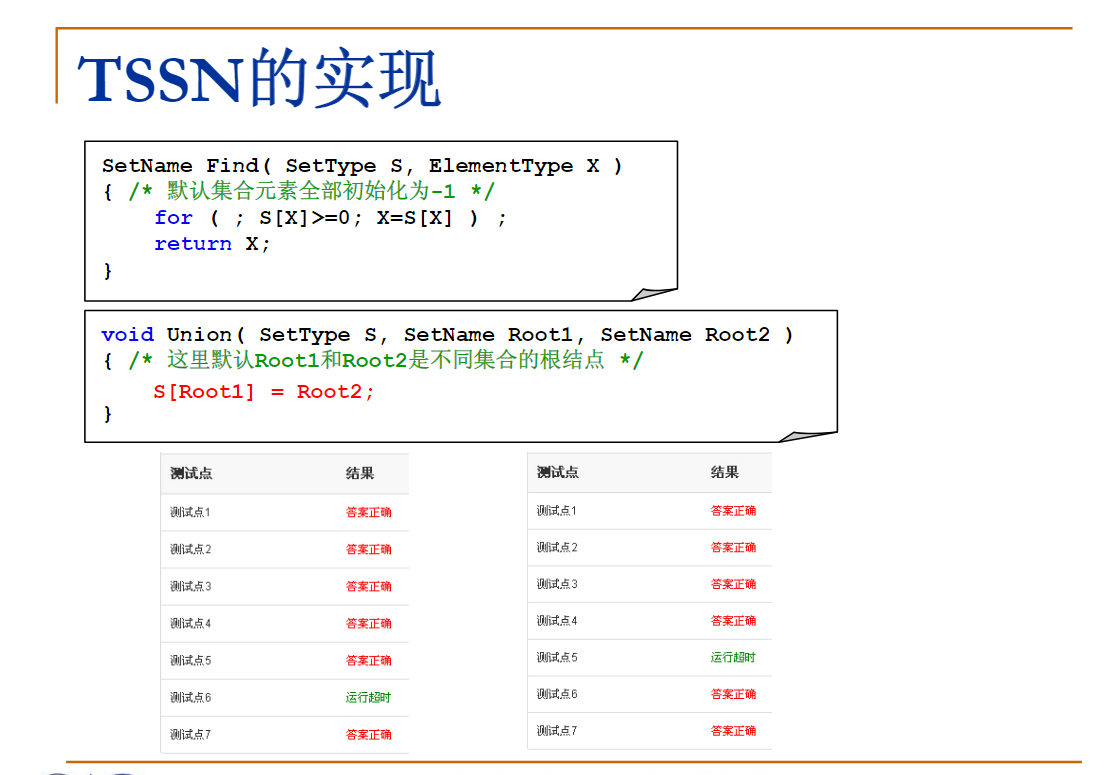
void Union( SetType S, SetName Root1, SetName Root2 )
{ /* 这里默认Root1和Root2是不同集合的根结点 */
/* 保证小集合并入大集合 */
if ( S[Root2] < S[Root1] ) { /* 如果集合2比较大 */
S[Root2] += S[Root1]; /* 集合1并入集合2 */
S[Root1] = Root2;
}
else { /* 如果集合1比较大 */
S[Root1] += S[Root2]; /* 集合2并入集合1 */
S[Root2] = Root1;
}
}
SetName Find( SetType S, ElementType X )
{ /* 默认集合元素全部初始化为-1 */
if ( S[X] < 0 ) /* 找到集合的根 */
return X;
else
return S[X] = Find( S, S[X] ); /* 路径压缩 */
}
并查集实例PTA 05-树8 File Transfer
We have a network of computers and a list of bi-directional connections. Each of these connections allows a file transfer from one computer to another. Is it possible to send a file from any computer on the network to any other?
Input Specification:
Each input file contains one test case. For each test case, the first line contains N (2≤N≤104), the total number of computers in a network. Each computer in the network is then represented by a positive integer between 1 and N. Then in the following lines, the input is given in the format:
I c1 c2
where I stands for inputting a connection between c1 and c2; or
C c1 c2
where C stands for checking if it is possible to transfer files between c1 and c2; or
S
where S stands for stopping this case.
Output Specification:
For each C case, print in one line the word "yes" or "no" if it is possible or impossible to transfer files between c1 and c2, respectively. At the end of each case, print in one line "The network is connected." if there is a path between any pair of computers; or "There are k components." where k is the number of connected components in this network.
Sample Input 1:
5
C 3 2
I 3 2
C 1 5
I 4 5
I 2 4
C 3 5
S
Sample Output 1:
no
no
yes
There are 2 components.
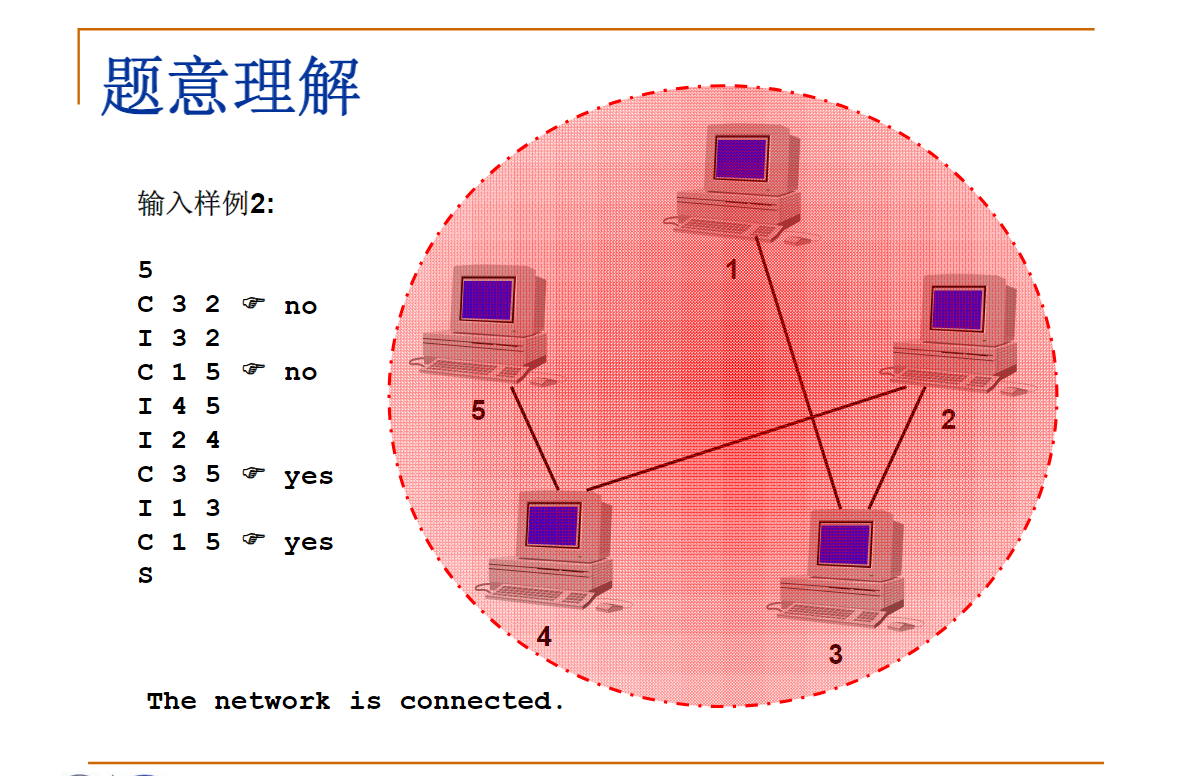
Sample Input 2:
5
C 3 2
I 3 2
C 1 5
I 4 5
I 2 4
C 3 5
I 1 3
C 1 5
S
Sample Output 2:
no
no
yes
yes
The network is connected.

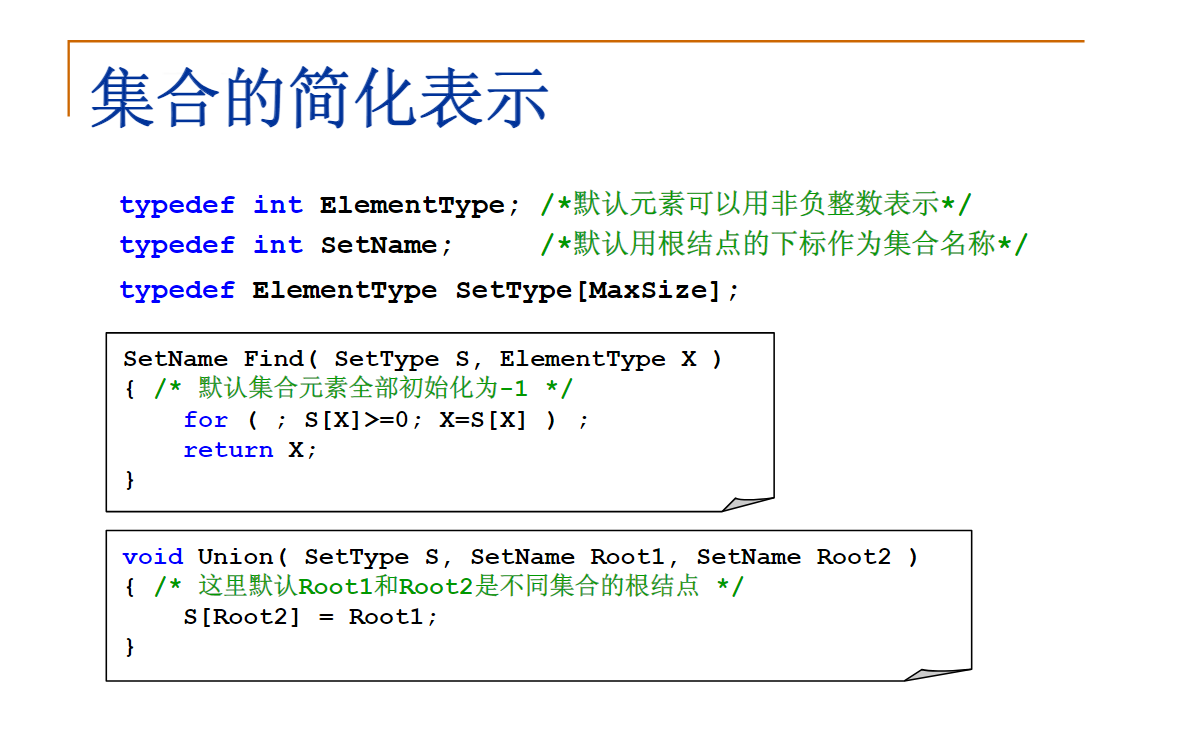



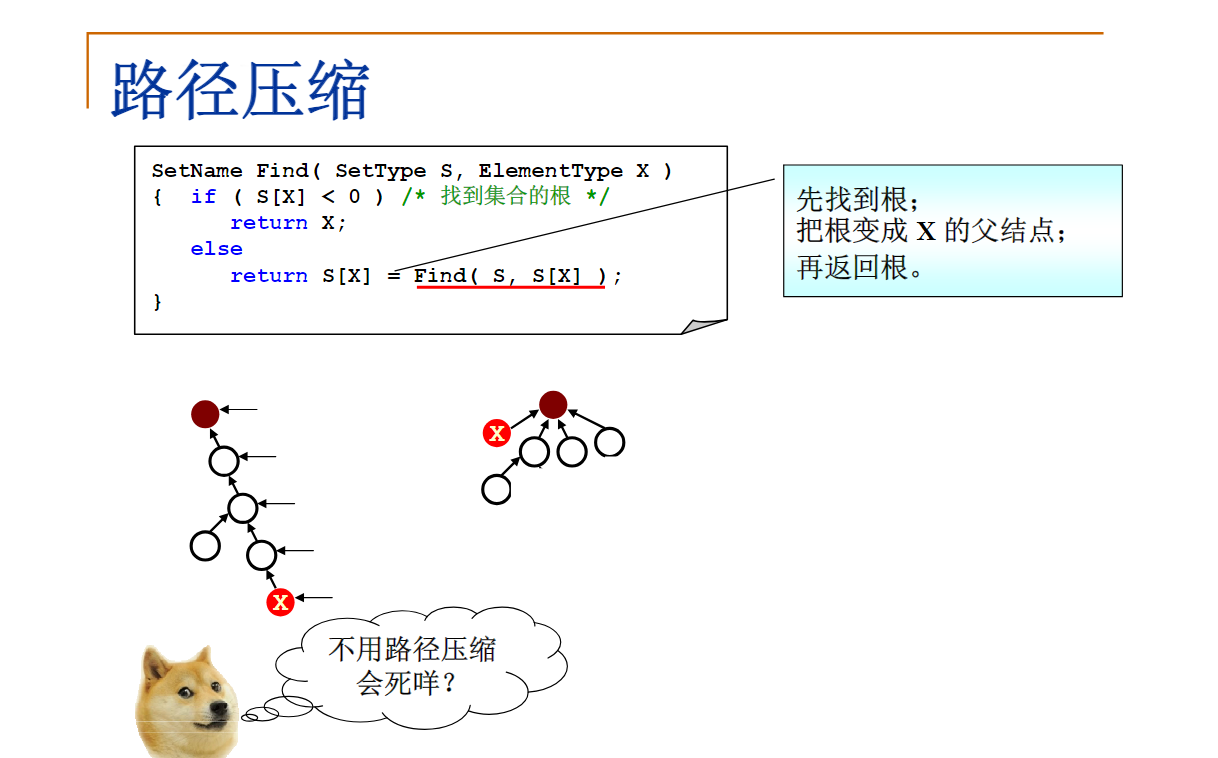
这里代码是伪递归形式的,会被编译器优化成循环形式。

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAXN 10001 /* 集合最大元素个数 */
typedef int ElementType; /* 默认元素可以用非负整数表示 */
typedef int SetName; /* 默认用根结点的下标作为集合名称 */
typedef ElementType SetType[MAXN]; /* 假设集合元素下标从0开始 */
void Union( SetType S, SetName Root1, SetName Root2 )
{ /* 这里默认Root1和Root2是不同集合的根结点 */
/* 保证小集合并入大集合 */
if ( S[Root2] < S[Root1] ) { /* 如果集合2比较大 */
S[Root2] += S[Root1]; /* 集合1并入集合2 */
S[Root1] = Root2;
}
else { /* 如果集合1比较大 */
S[Root1] += S[Root2]; /* 集合2并入集合1 */
S[Root2] = Root1;
}
}
SetName Find( SetType S, ElementType X )
{ /* 默认集合元素全部初始化为-1 */
if ( S[X] < 0 ) /* 找到集合的根 */
return X;
else
return S[X] = Find( S, S[X] ); /* 路径压缩 */
}
void Initialization(SetType S, int N)
{
for(int i=0; i<N; i++)
S[i] = -1;
}
void Input_connection(SetType S)
{
ElementType u,v;
SetName Root1, Root2;
scanf("%d %d\n",&u,&v);
Root1 = Find(S, u-1);
Root2 = Find(S, v-1);
if(Root1 != Root2)
Union(S, Root1, Root2);
}
void Check_connection(SetType S)
{
ElementType u,v;
SetName Root1,Root2;
scanf("%d %d\n",&u,&v);
Root1 = Find(S, u-1);
Root2 = Find(S, v-1);
if(Root1 == Root2)
printf("yes\n");
else
printf("no\n");
}
void Check_network(SetType S, int n)
{
int i,counter = 0;
for(i=0; i<n; i++)
{
if(S[i] < 0)
counter++;
}
if(counter == 1)
printf("The network is connected.\n");
else
printf("There are %d components.\n",counter);
}
int main()
{
int N;
scanf("%d",&N);
SetType S;
char in;
Initialization(S, N);
do
{
scanf("%c",&in);
switch(in)
{
case 'I':
Input_connection(S);
break;
case 'C':
Check_connection(S);
break;
case 'S':
Check_network(S, N);
break;
}
}while(in != 'S');
return 0;
}