堆

• 定义
• 最大堆
• 最小堆
• 实例 PTA 05-树7 堆中的路径

定义

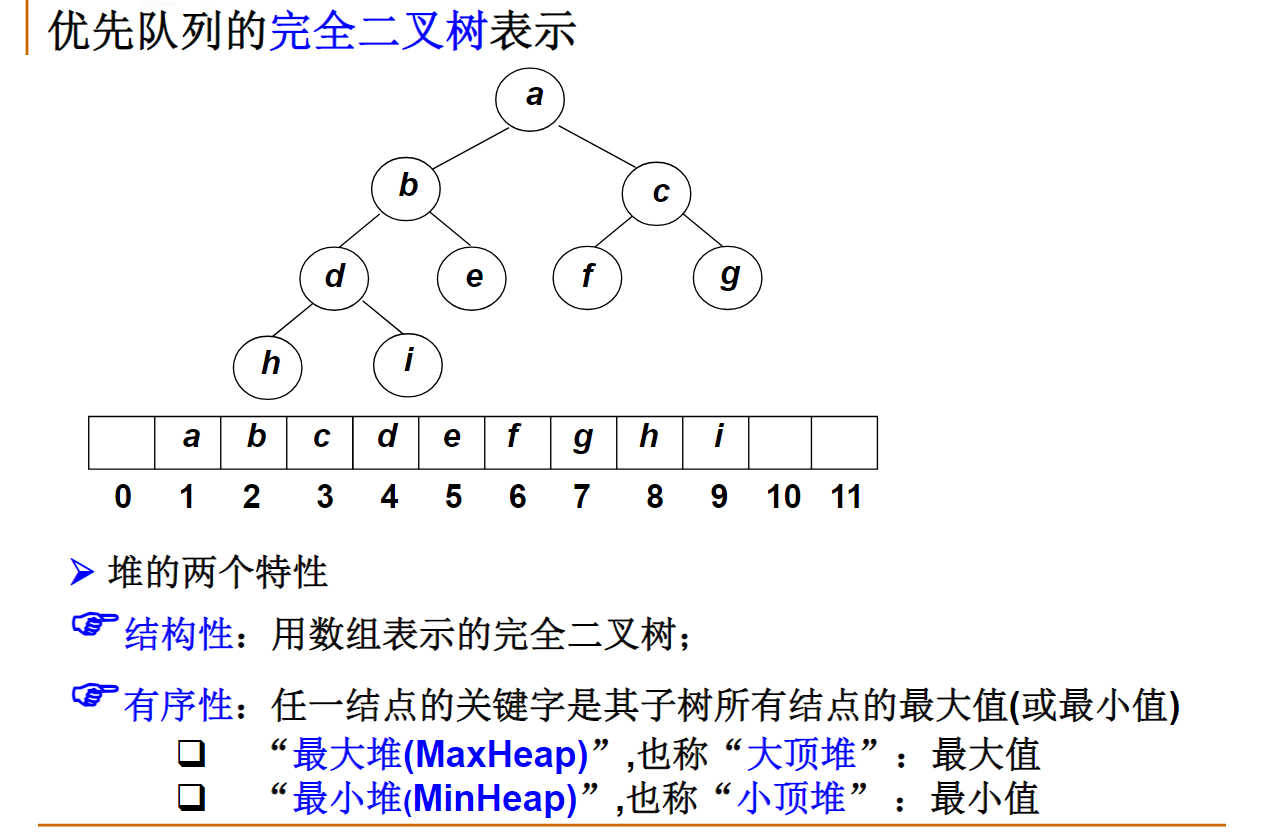
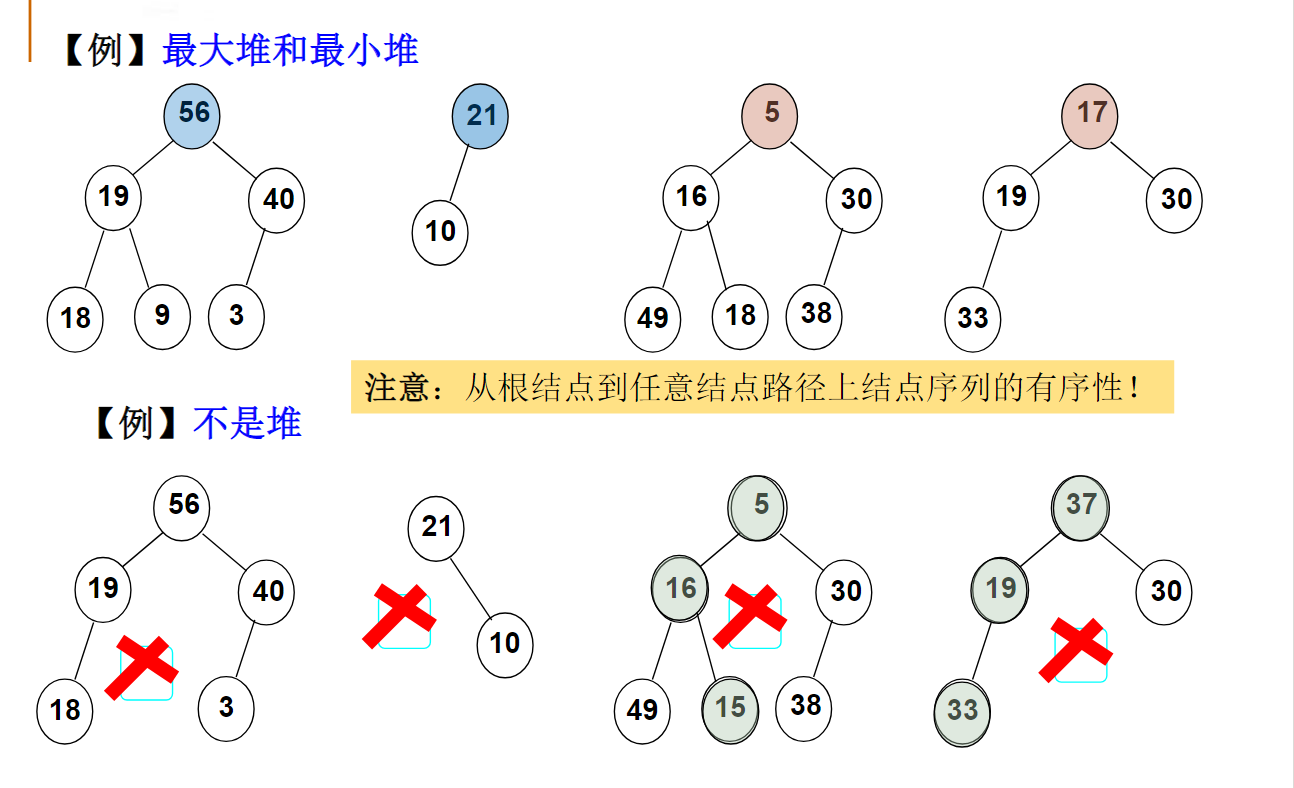
堆的定义与操作代码：

typedef struct HNode *Heap; /* 堆的类型定义 */
struct HNode {
    ElementType *Data; /* 存储元素的数组 */
    int Size;          /* 堆中当前元素个数 */
    int Capacity;      /* 堆的最大容量 */
};
typedef Heap MaxHeap; /* 最大堆 */
typedef Heap MinHeap; /* 最小堆 */

#define MAXDATA 1000  /* 该值应根据具体情况定义为大于堆中所有可能元素的值 */

MaxHeap CreateHeap( int MaxSize )
{ /* 创建容量为MaxSize的空的最大堆 */

    MaxHeap H = (MaxHeap)malloc(sizeof(struct HNode));
    H->Data = (ElementType *)malloc((MaxSize+1)*sizeof(ElementType));
    H->Size = 0;
    H->Capacity = MaxSize;
    H->Data[0] = MAXDATA; /* 定义"哨兵"为大于堆中所有可能元素的值*/

    return H;
}

bool IsFull( MaxHeap H )
{
    return (H->Size == H->Capacity);
}

bool Insert( MaxHeap H, ElementType X )
{ /* 将元素X插入最大堆H，其中H->Data[0]已经定义为哨兵 */
    int i;
 
    if ( IsFull(H) ) { 
        printf("最大堆已满");
        return false;
    }
    i = ++H->Size; /* i指向插入后堆中的最后一个元素的位置 */
    for ( ; H->Data[i/2] < X; i/=2 )
        H->Data[i] = H->Data[i/2]; /* 上滤X */
    H->Data[i] = X; /* 将X插入 */
    return true;
}

#define ERROR -1 /* 错误标识应根据具体情况定义为堆中不可能出现的元素值 */

bool IsEmpty( MaxHeap H )
{
    return (H->Size == 0);
}

ElementType DeleteMax( MaxHeap H )
{ /* 从最大堆H中取出键值为最大的元素，并删除一个结点 */
    int Parent, Child;
    ElementType MaxItem, X;

    if ( IsEmpty(H) ) {
        printf("最大堆已为空");
        return ERROR;
    }

    MaxItem = H->Data[1]; /* 取出根结点存放的最大值 */
    /* 用最大堆中最后一个元素从根结点开始向上过滤下层结点 */
    X = H->Data[H->Size--]; /* 注意当前堆的规模要减小 */
    for( Parent=1; Parent*2<=H->Size; Parent=Child ) {
        Child = Parent * 2;
        if( (Child!=H->Size) && (H->Data[Child]<H->Data[Child+1]) )
            Child++;  /* Child指向左右子结点的较大者 */
        if( X >= H->Data[Child] ) break; /* 找到了合适位置 */
        else  /* 下滤X */
            H->Data[Parent] = H->Data[Child];
    }
    H->Data[Parent] = X;

    return MaxItem;
} 

/*----------- 建造最大堆 -----------*/
void PercDown( MaxHeap H, int p )
{ /* 下滤：将H中以H->Data[p]为根的子堆调整为最大堆 */
    int Parent, Child;
    ElementType X;

    X = H->Data[p]; /* 取出根结点存放的值 */
    for( Parent=p; Parent*2<=H->Size; Parent=Child ) {
        Child = Parent * 2;
        if( (Child!=H->Size) && (H->Data[Child]<H->Data[Child+1]) )
            Child++;  /* Child指向左右子结点的较大者 */
        if( X >= H->Data[Child] ) break; /* 找到了合适位置 */
        else  /* 下滤X */
            H->Data[Parent] = H->Data[Child];
    }
    H->Data[Parent] = X;
}

void BuildHeap( MaxHeap H )
{ /* 调整H->Data[]中的元素，使满足最大堆的有序性  */
  /* 这里假设所有H->Size个元素已经存在H->Data[]中 */

    int i;

    /* 从最后一个结点的父节点开始，到根结点1 */
    for( i = H->Size/2; i>0; i-- )
        PercDown( H, i );
}

最大堆

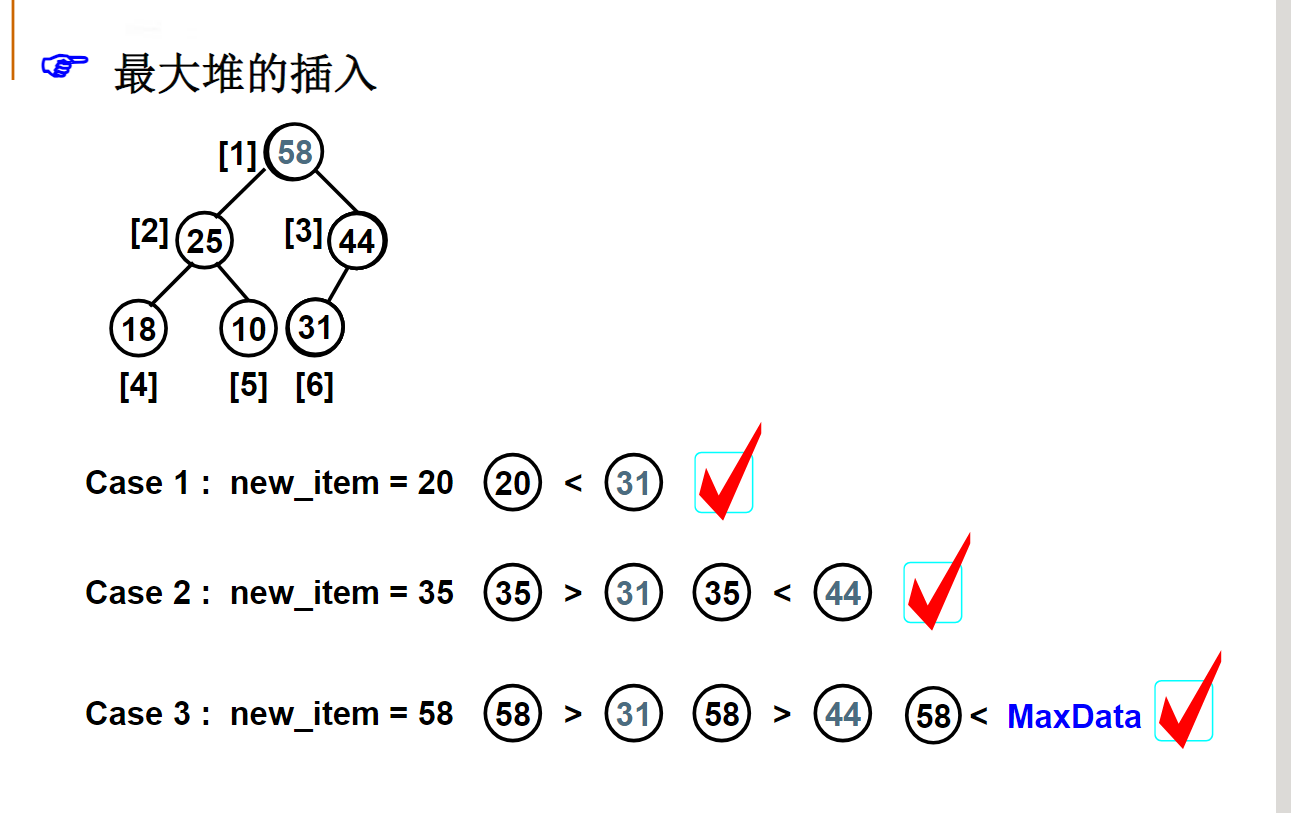
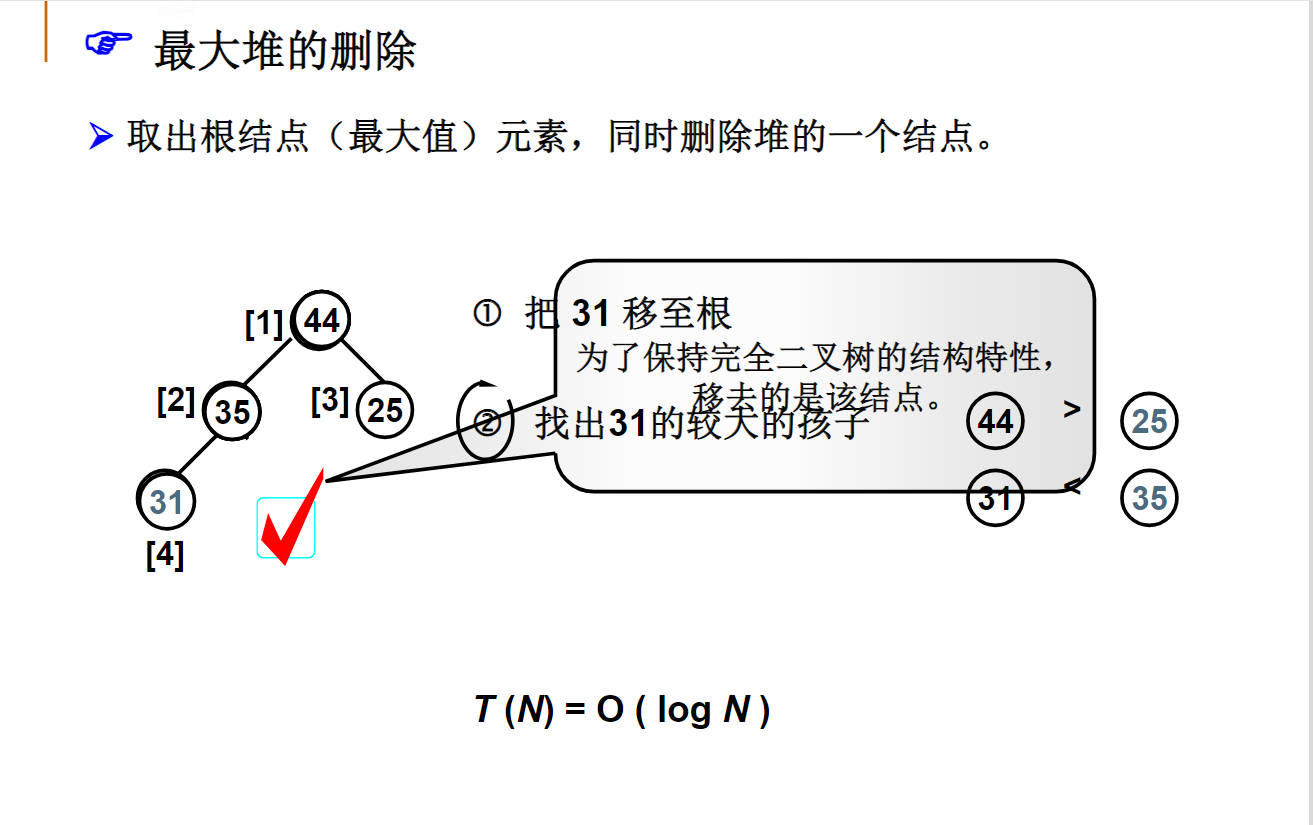
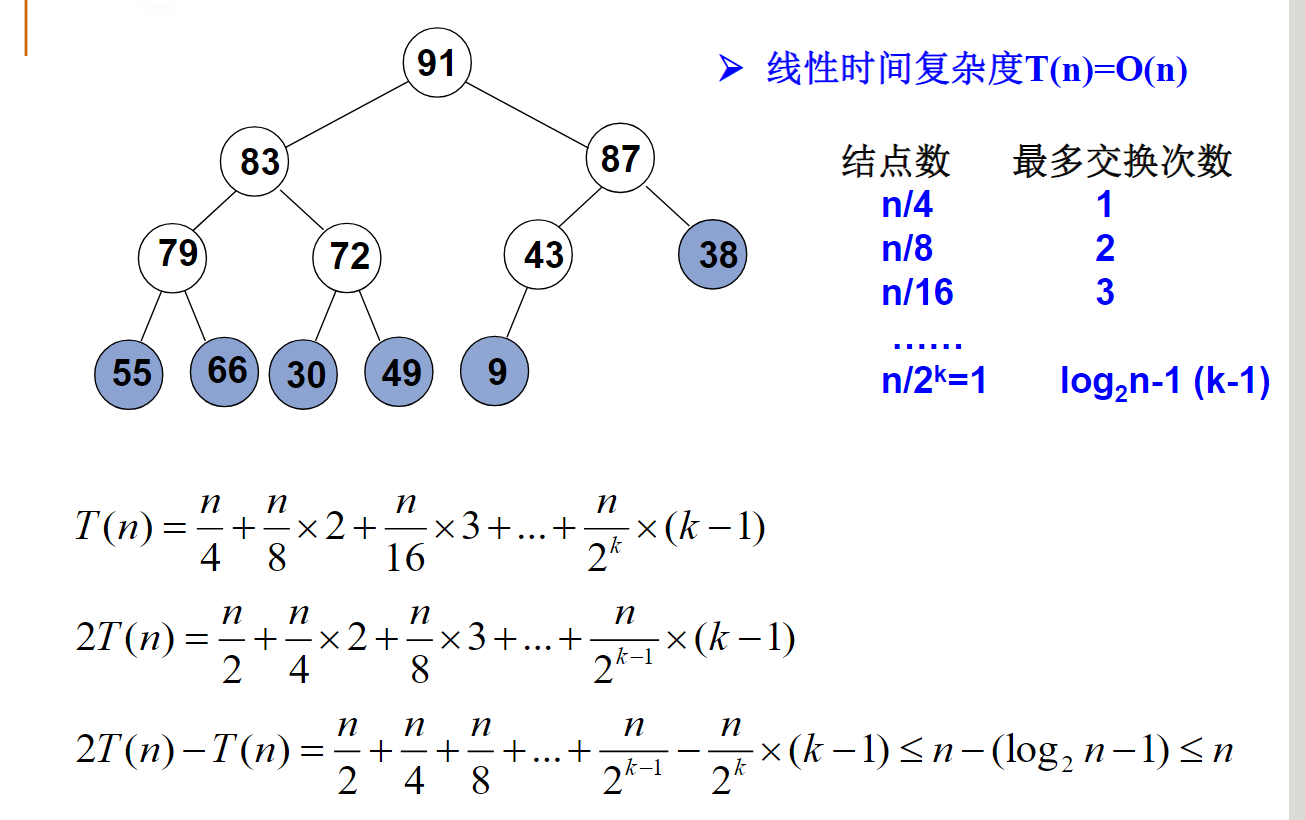
建堆时，最坏情况下需要挪动元素次数是等于树中各结点的高度和。问：对于元素个数为12的堆，其各结点的高度之和是多少？10

在最大堆 {97,76,65,50,49,13,27}中插入83后，该最大堆为： {97,83,65,76,49,13,27,50}

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>

typedef int ElementType;
typedef struct HNode *Heap;

struct HNode
{
    ElementType *Data;  //存储元素的数组
    int Size;           //堆中当前元素个数
    int Capacity;       //堆的最大容量
};

typedef Heap MaxHeap;
typedef Heap MinHeap;

#define MAXDATA  1000  //该值应根据具体情况定义为大于堆中所有可能元素的值

MaxHeap CreateHeap(int MaxSize)  //创建容量为MaxSize的空的最大堆
{
    MaxHeap H = (Heap)malloc(sizeof(struct HNode));
    H->Data = (ElementType *)malloc(sizeof(ElementType) * (MaxSize+1));
    H->Capacity = MaxSize;
    H->Size = 0;
    H->Data[0] = MAXDATA;    //定义"哨兵"为大于堆中所有可能元素的值
    return H;
}

bool IsFull(MaxHeap H)
{
    return (H->Size == H->Capacity);
}

bool Insert(MaxHeap H, ElementType X)  //将元素X插入最大堆H，其中H->Data[0]已经定义为哨兵
{
    if(IsFull(H))
    {
        printf("The heap is full!\n");
        return false;
    }
    int i = ++H->Size;                  //i指向插入后堆中的最后一个元素的位置
    for(;H->Data[i/2] < X;i/=2)
    {
        H->Data[i] = H->Data[i/2];       //上滤X
    }
    H->Data[i] = X;
    return true;
}

bool IsEmpty(MaxHeap H)
{
    return (H->Size == 0);
}

#define ERROR -1

ElementType Delete(MaxHeap H)   //从最大堆H中取出键值为最大的元素，并删除一个结点
{
    if(IsEmpty(H))
    {
        printf("The heap is empty!\n");
        return ERROR;
    }
    ElementType MaxItem = H->Data[1];  //取出根结点存放的最大值
    //用最大堆中最后一个元素从根结点开始向上过滤下层结点
    ElementType X = H->Data[H->Size--];  //注意当前堆的规模要减小
    int Parent, Child;
    for(Parent=1; Parent*2<=H->Size; Parent=Child)
    {
        Child = Parent*2;
        if((Child!=H->Size)&&(H->Data[Child]<H->Data[Child+1]))
            Child++;      //Child指向左右子结点的较大者
        if(X > H->Data[Child])    //找到了合适位置
            break;
        else
            H->Data[Parent] = H->Data[Child]; //下滤X
    }
    H->Data[Parent] = X;
    return MaxItem;
}

int main()
{
    int MaxSize = 100;
    MaxHeap H = CreateHeap(MaxSize);
    Insert(H,97);
    Insert(H,76);
    Insert(H,65);
    Insert(H,50);
    Insert(H,49);
    Insert(H,13);
    Insert(H,27);
    Insert(H,83);
    for(int i=1; i<=H->Size;i++)
        printf("%d ",H->Data[i]);
    printf("\n");
    Delete(H);
    for(int i=1; i<=H->Size;i++)
        printf("%d ",H->Data[i]);
    printf("\n");
    Delete(H);
    for(int i=1; i<=H->Size;i++)
        printf("%d ",H->Data[i]);
    return 0;
}

97 83 65 76 49 13 27 50
83 76 65 50 49 13 27
76 50 65 27 49 13

有个堆其元素在数组中的序列为：58，25，44，18，10，26，20，12。如果调用DeleteMax函数删除最大值元素，请猜猜看：程序中的for循环刚退出时变量parent的值是多少？6

最小堆

对由同样的n个整数构成的二叉搜索树（查找树）和最小堆，下面说法中D是 不正确 的:

A.二叉搜索树（查找树）高度大于等于最小堆高度

B.对该二叉搜索树（查找树）进行中序遍历可得到从小到大的序列

C.从最小堆根节点到其任何叶结点的路径上的结点值构成从小到大的序列

D.对该最小堆进行按层序（level order）遍历可得到从小到大的序列

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>

#define ERROR -1

typedef int ElementType;
typedef struct HNode *Heap;
typedef Heap MaxHeap;
typedef Heap MinHeap;

struct HNode
{
    ElementType *Data;
    int Size;
    int Capacity;
};

MinHeap CreateHeap(int MaxSize)
{
    MinHeap H = (MinHeap)malloc(sizeof(struct HNode));
    H->Data = (ElementType*)malloc(sizeof(ElementType)*MaxSize);
    H->Size = 0;
    H->Capacity = MaxSize;
    H->Data[0] = -100;
    return H;
}

bool IsFull(MinHeap H)
{
    return (H->Size == H->Capacity);
}

bool Insert(MinHeap H, ElementType X)
{
    if(IsFull(H))
    {
        printf("The heap is full!\n");
        return false;
    }
    int i = ++H->Size;
    for(; H->Data[i/2] >= X; i /= 2)
    {
        H->Data[i] = H->Data[i/2];
    }
    H->Data[i] = X;
    return true;
}



bool IsEmpty(MinHeap H)
{
    return (H->Size == 0);
}



ElementType Delete(MinHeap H)
{
    if(IsEmpty(H))
    {
        printf("The heap is empty!\n");
        return ERROR;
    }
    int Parent, Child;
    ElementType MinItem,X;
    MinItem = H->Data[1];
    X = H->Data[H->Size--];
    for(Parent = 1; Parent * 2 <= H->Size; Parent = Child)
    {
        Child = Parent * 2;
        if((Child!=H->Size)&&(H->Data[Child] > H->Data[Child + 1]))
            Child++;
        if(X < H->Data[Child])
            break;
        else
            H->Data[Parent] = H->Data[Child];
    }
    H->Data[Parent] = X;
    return MinItem;
}

int main()
{
    int MaxSize = 100;
    MinHeap H = CreateHeap(MaxSize);
    Insert(H,97);
    Insert(H,76);
    Insert(H,65);
    Insert(H,50);
    Insert(H,49);
    Insert(H,13);
    Insert(H,27);
    Insert(H,83);
    for(int i=1; i<=H->Size;i++)
        printf("%d ",H->Data[i]);
    printf("\n");
    Delete(H);
    for(int i=1; i<=H->Size;i++)
        printf("%d ",H->Data[i]);
    printf("\n");
    Delete(H);
    for(int i=1; i<=H->Size;i++)
        printf("%d ",H->Data[i]);
    return 0;
}

13 50 27 83 65 76 49 97
27 50 49 83 65 76 97
49 50 76 83 65 97

实例 PTA 05-树7 堆中的路径

将一系列给定数字依次插入一个初始为空的小顶堆H[]。随后对任意给定的下标i，打印从H[i]到根结点的路径。

输入格式:

每组测试第1行包含2个正整数N和M(≤1000)，分别是插入元素的个数、以及需要打印的路径条数。下一行给出区间[-10000, 10000]内的N个要被插入一个初始为空的小顶堆的整数。最后一行给出M个下标。

输出格式:

对输入中给出的每个下标i，在一行中输出从H[i]到根结点的路径上的数据。数字间以1个空格分隔，行末不得有多余空格。

输入样例:

5 3
46 23 26 24 10
5 4 3

输出样例:

24 23 10
46 23 10
26 10

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>

#define ERROR -1

typedef int ElementType;
typedef struct HNode *Heap;
typedef Heap MaxHeap;
typedef Heap MinHeap;

struct HNode
{
    ElementType *Data;
    int Size;
    int Capacity;
};

MinHeap CreateHeap(int MaxSize)
{
    MinHeap H = (MinHeap)malloc(sizeof(struct HNode));
    H->Data = (ElementType*)malloc(sizeof(ElementType)*MaxSize);
    H->Size = 0;
    H->Capacity = MaxSize;
    H->Data[0] = -10001;
    return H;
}

bool IsFull(MinHeap H)
{
    return (H->Size == H->Capacity);
}

bool Insert(MinHeap H, ElementType X)
{
    if(IsFull(H))
    {
        printf("The heap is full!\n");
        return false;
    }
    int i = ++H->Size;
    for(; H->Data[i/2] >= X; i /= 2)
    {
        H->Data[i] = H->Data[i/2];
    }
    H->Data[i] = X;
    return true;
}



bool IsEmpty(MinHeap H)
{
    return (H->Size == 0);
}



ElementType Delete(MinHeap H)
{
    if(IsEmpty(H))
    {
        printf("The heap is empty!\n");
        return ERROR;
    }
    int Parent, Child;
    ElementType MinItem,X;
    MinItem = H->Data[1];
    X = H->Data[H->Size--];
    for(Parent = 1; Parent * 2 <= H->Size; Parent = Child)
    {
        Child = Parent * 2;
        if((Child!=H->Size)&&(H->Data[Child] > H->Data[Child + 1]))
            Child++;
        if(X < H->Data[Child])
            break;
        else
            H->Data[Parent] = H->Data[Child];
    }
    H->Data[Parent] = X;
    return MinItem;
}

int main()
{
    int MaxSize = 1001;
    MinHeap H = CreateHeap(MaxSize);
    int N,M;
    scanf("%d %d",&N,&M);
    for(int i=0; i<N; i++)
    {
        int num;
        scanf("%d",&num);
        Insert(H,num);
    }
    for(int i=0; i<M; i++)
    {
        int idx;
        scanf("%d",&idx);
        int Fisrt = 1;
        for(int j=idx; j>=1; j/=2)
        {
            if(Fisrt)
            {
                printf("%d",H->Data[j]);
                Fisrt = 0;
            }
            else
            {
                printf(" %d",H->Data[j]);
            }
        }
        printf("\n");
    }
    return 0;
}