资料结构与演算法

• 引子：二分查找
• 树的定义

引子：二分查找

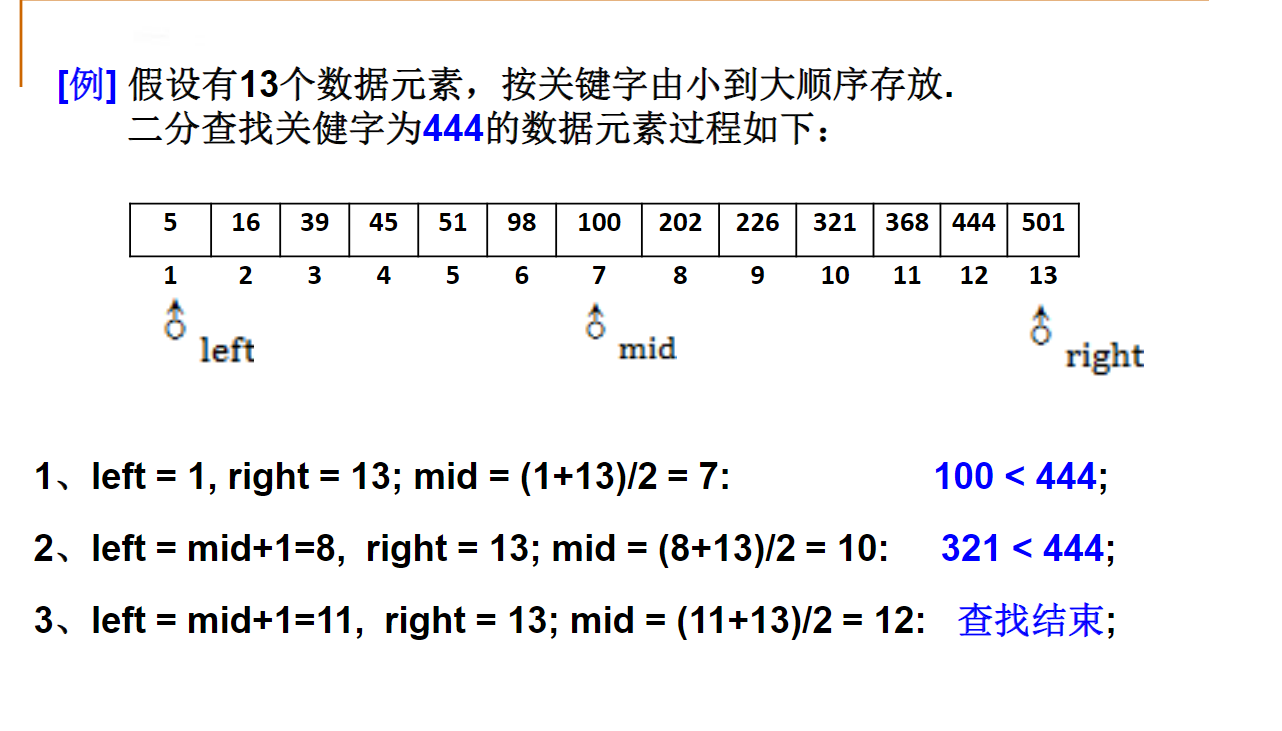
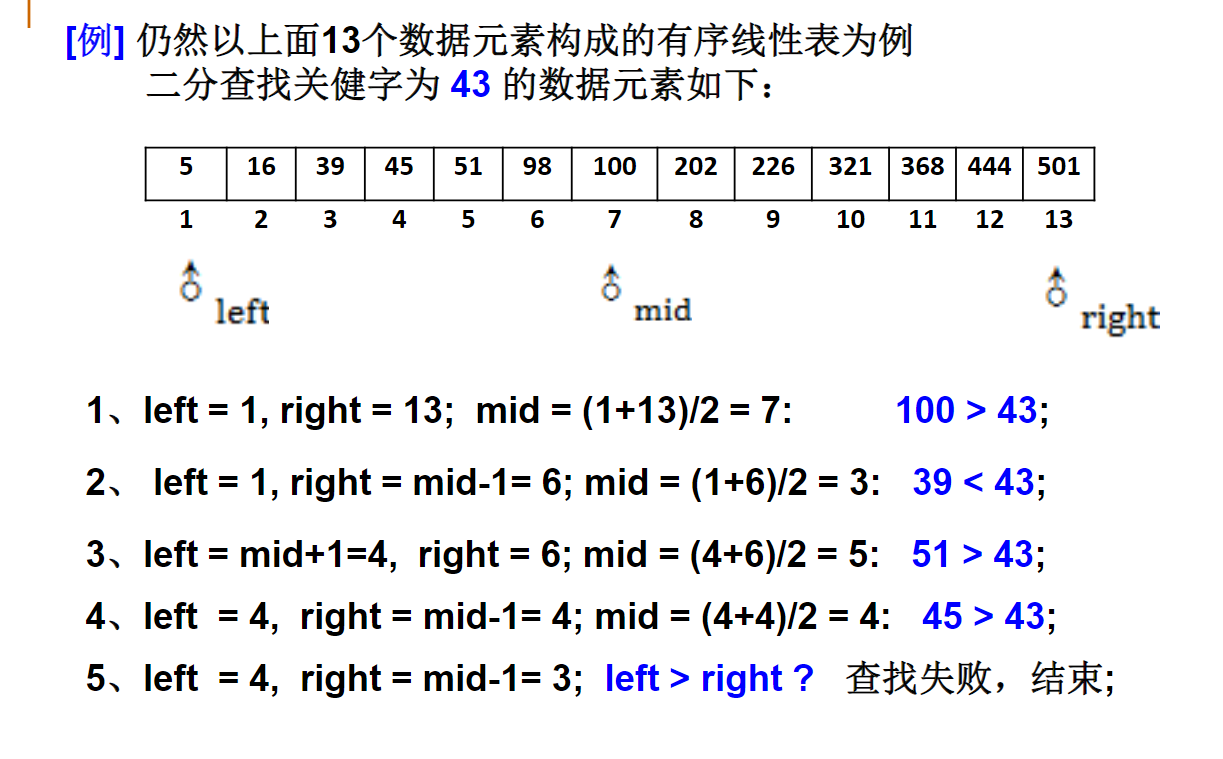
int BinarySearch(StaticTable *Tbl,ElementType K)
{
    int left,right,mid,NotFound = -1;
    left = 1;
    right = Tbl->Length;

    while(left <= right)
    {
        mid = (left + right) / 2;
        if(K > Tbl->Element[mid])
            left = mid + 1;
        else if(K < Tbl->Element[mid])
            right = mid - 1;
        else
            return mid;
    }
    return NotFound;
}

在分量1~11的数组中按从小到大顺序存放11个元素，如果用顺序查找和二分查找分别查找这11个元素，哪个位置的元素在这两种方法的查找中总次数最少？1

在分量1~11的数组中按从小到大顺序存放11个元素，如果进行二分查找，查找次数最少的元素位于什么位置？6

测试程序如下：

#include <stdio.h>

int OrderSearch(int arr[],int n,int x)
{
    for(int i = 0 ; i < n; i++)
    {
        if(x == arr[i])
            return i;
    }
    return -1;
}

int BinarySearch(int arr[],int n,int x)
{
    int left = 0;
    int right = n-1;
    int mid;
    while(left <= right)
    {
        mid = (left + right) / 2;
        if(arr[mid] < x)
            left = mid + 1;
        else if(arr[mid] > x)
            right = mid - 1;
        else
            return mid;
    }
    return -1;
}

int main()
{
    int n = 10;
    int arr[10] = {1,2,3,4,5,6,7,8,9,10};
    int x = 3;
    printf("%d\n",BinarySearch(arr,n,x));
    printf("%d\n",OrderSearch(arr,n,x));
    return 0;
}

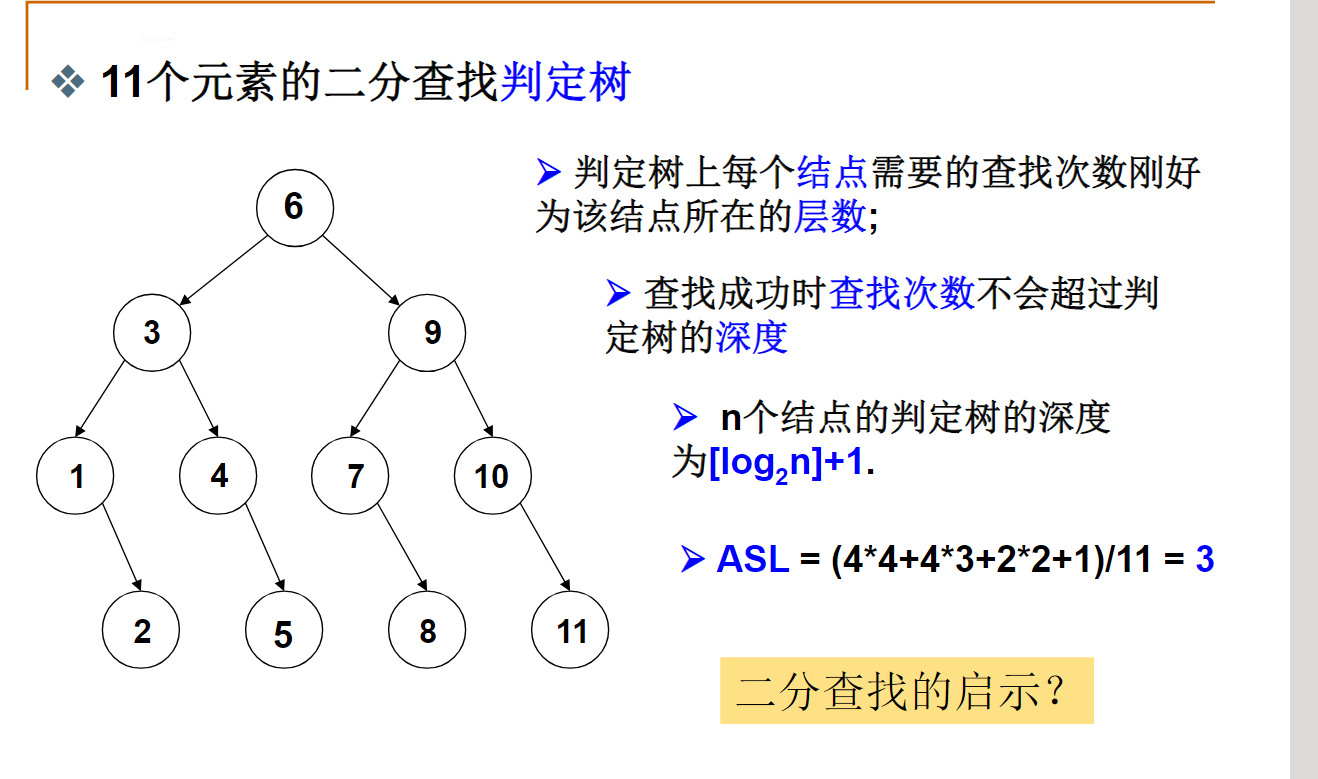
ASL：Average Search Length平均查找长度

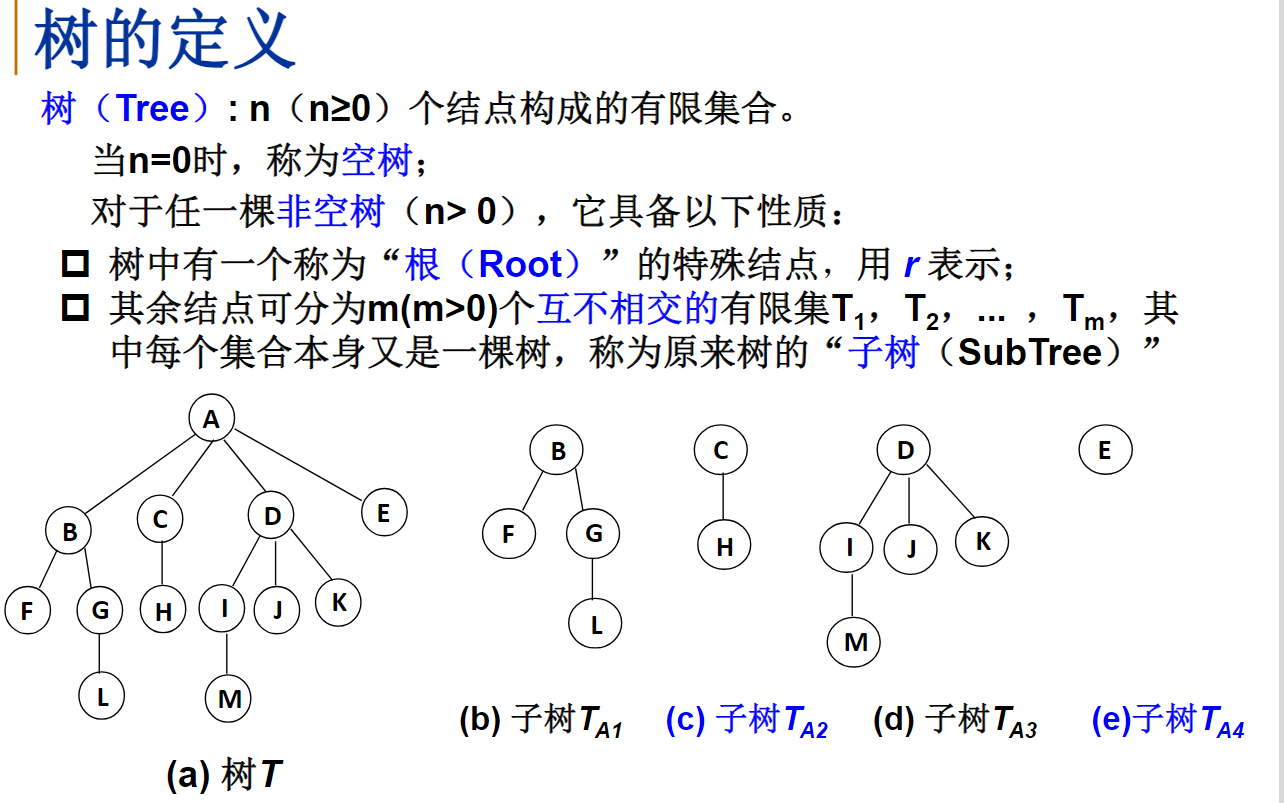
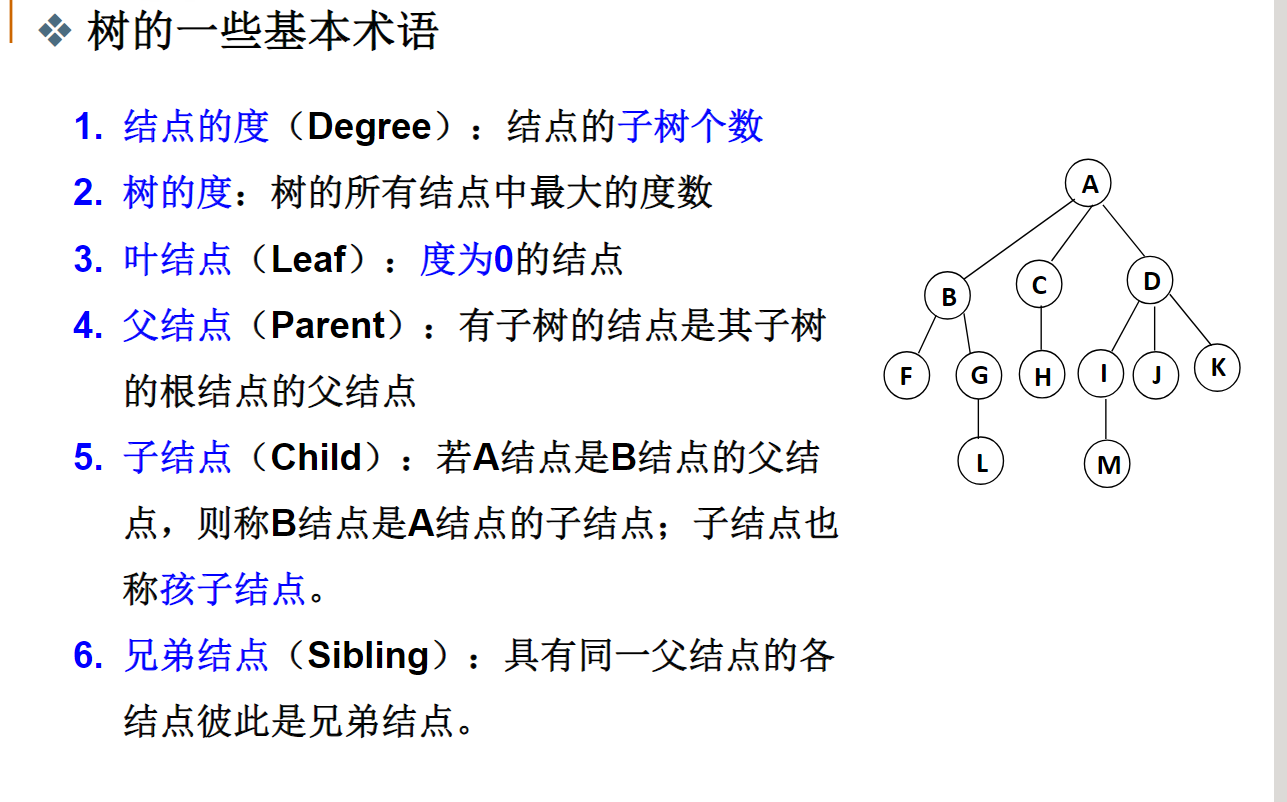
树的定义

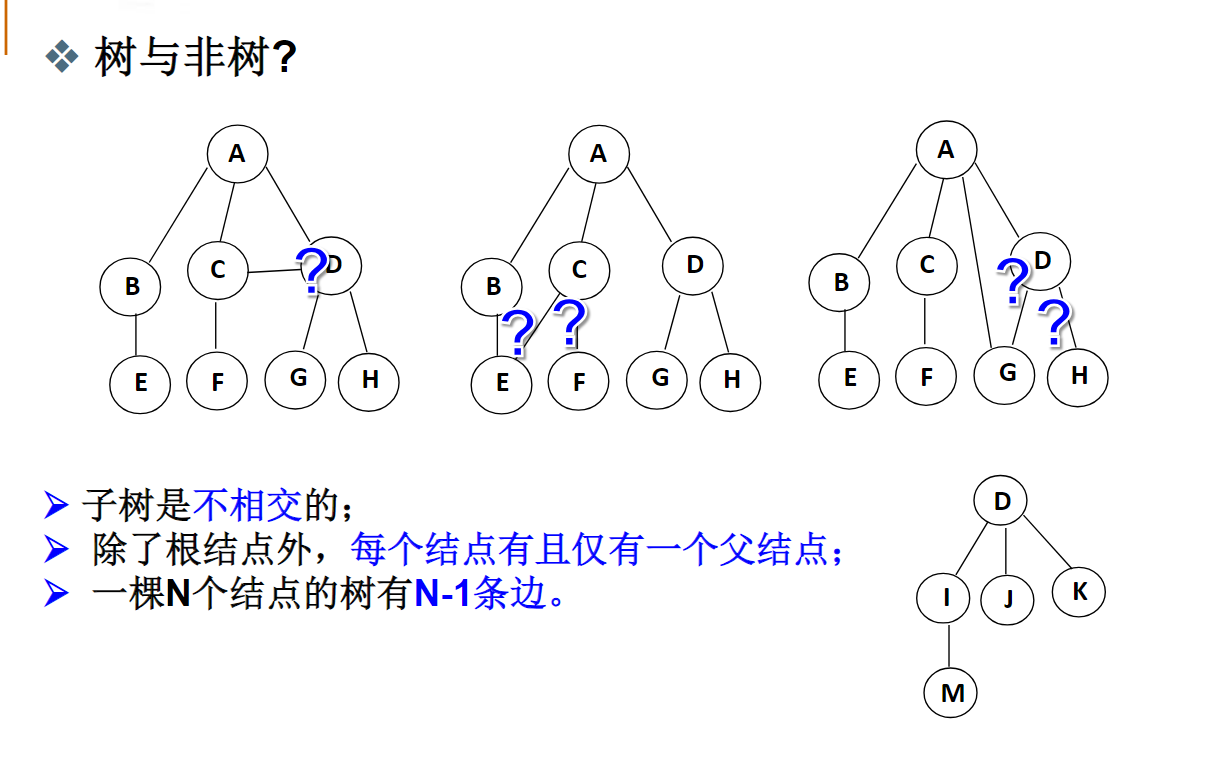
有一个m棵树的集合（也叫森林）共有k条边，问这m颗树共有多少个结点？k+m

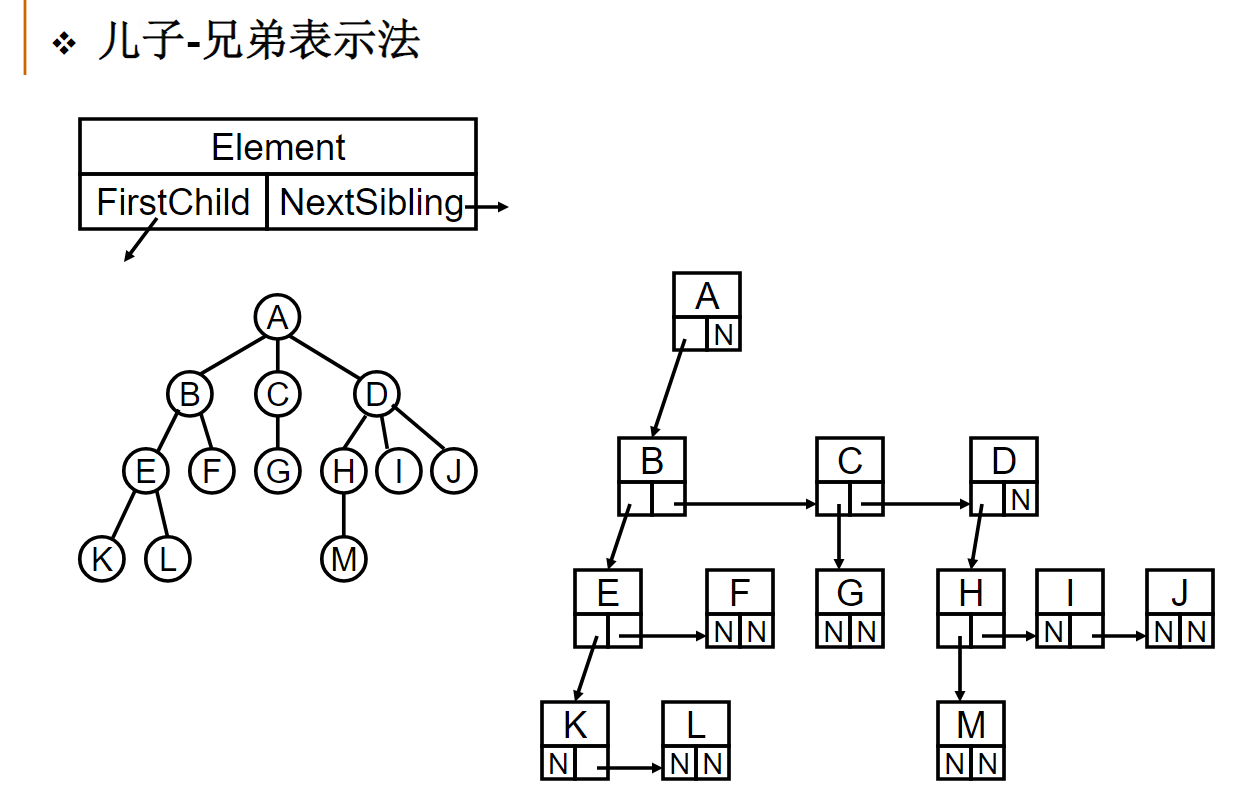
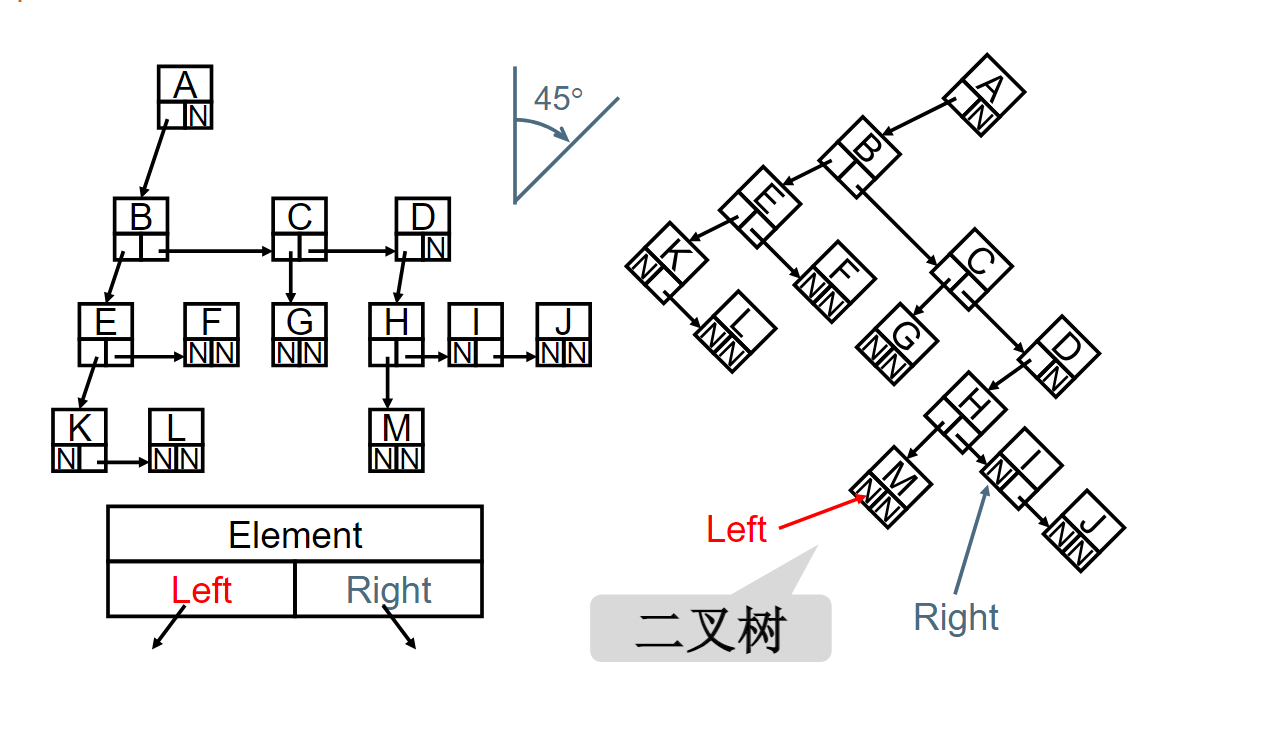
在用“儿子-兄弟”法表示的树中，如果从根结点开始访问其“次子”的“次子”，所经过的结点数与从根结点开始访问其“长子”的“长子”的“长子”的“长子”一样。(注意:比较的是结点数,而不是路径)

一棵度为 m的树有n个节点。若每个节点直接用m个链指向相应的儿子，则表示这个树所需要的总空间是n*(m+1) (假定每个链以及表示节点的数据域都是一个单位空间).。当采用儿子/兄弟（First Child/Next Sibling）表示法时，所需的总空间是：3n

树的集合称为森林。是否也可以使用“儿子-兄弟”表示法存储森林？如何实现？

是的，可以使用"儿子-兄弟"表示法（又称作"左孩子-右兄弟"表示法或"孩子兄弟链表"）来存储森林，其中每个节点表示一棵树。这种表示法适用于多叉树和森林结构，它使用两个指针来表示树中的节点之间的关系：左孩子指针和右兄弟指针。左孩子指针指向当前节点的第一个子节点，而右兄弟指针指向当前节点的兄弟节点。