二叉搜索树

查找分为静态查找和动态查找。静态查找可以使用二分查找方式。

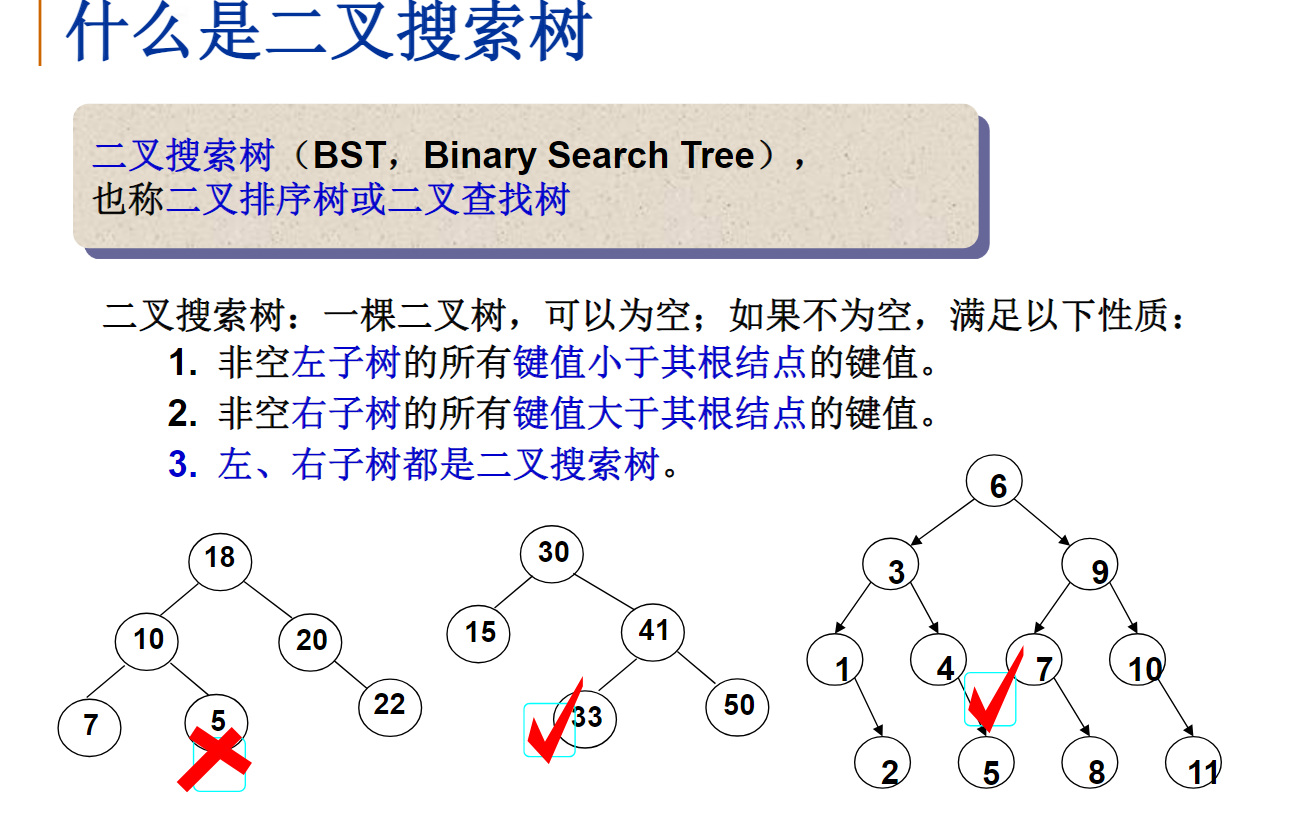
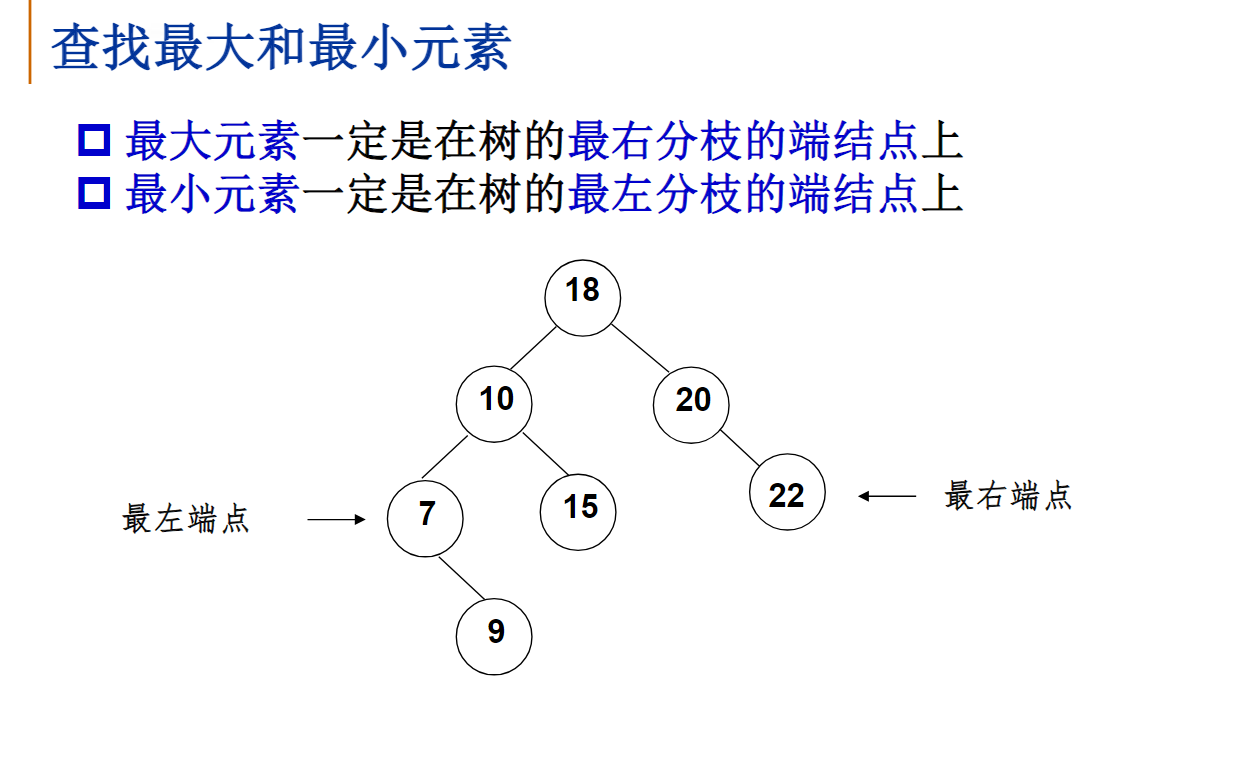
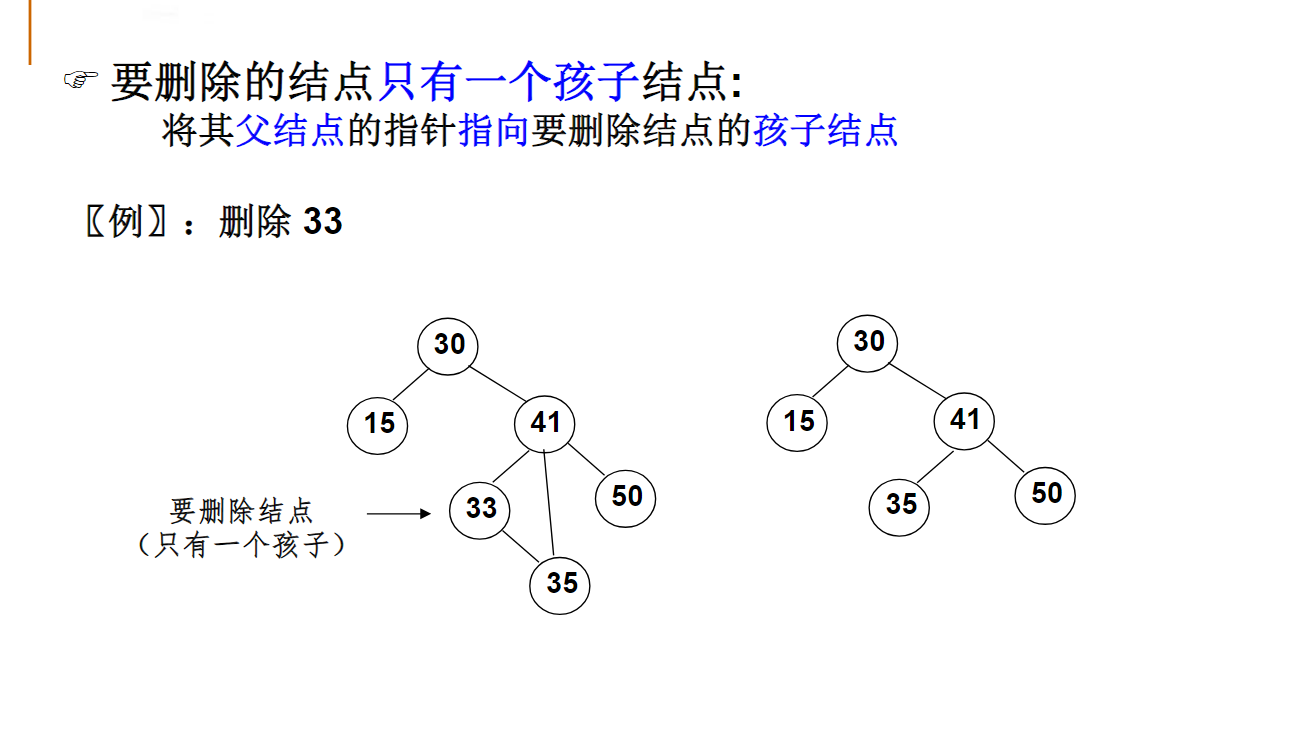
若一搜索树（查找树）是一个有n个结点的完全二叉树，则该树的最大值一定在叶结点上

错误

若一搜索树（查找树）是一个有n个结点的完全二叉树，则该树的最小值一定在叶结点上

正确

#include <stdio.h>
#include <stdlib.h>

typedef int ElementType;

typedef struct TreeNode *BinTree;

typedef BinTree Position;

typedef struct TreeNode
{
    ElementType Data;
    BinTree Left;
    BinTree Right;
}*LPNODE;

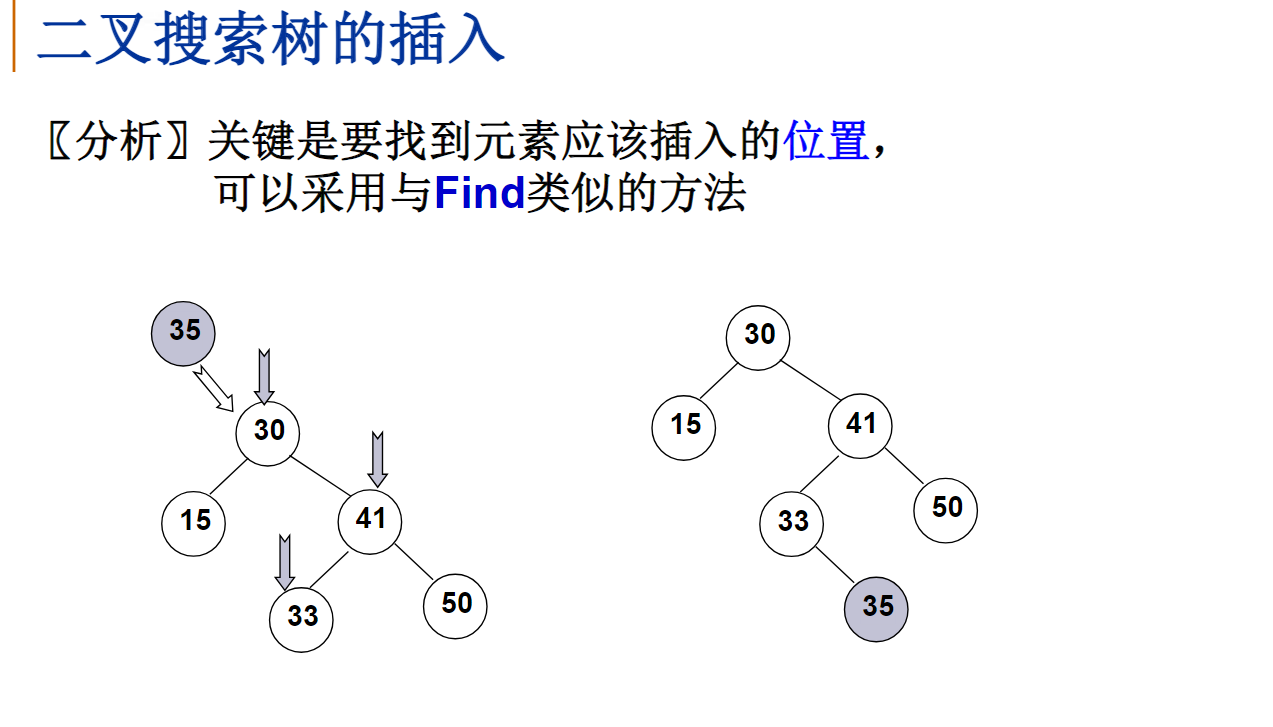
BinTree Insert(ElementType X,BinTree BST)
{
    if(!BST)
    {
        /*若原树为空，生成并返回一个结点的二叉搜索树*/
        BST = (BinTree)malloc(sizeof(struct TreeNode));
        BST->Data = X;
        BST->Left = NULL;
        BST->Right = NULL;
    }
    else   /*开始找要插入元素的位置*/
    {
        if(BST->Data < X)
            BST->Right = Insert(X,BST->Right);
        else if(BST->Data > X)
            BST->Left = Insert(X,BST->Left);
        /*else X已经存在，什么都不做 */
    }
    return BST;
}


/*尾递归方式查找*/
ElementType Find(ElementType X,BinTree BST)
{
    if(!BST)
        return NULL;
    if(BST->Data < X)
        return Find(X,BST->Right);
    else if(BST->Data > X)
        return Find(X,BST->Left);
    else       /*X == BST->Data*/
        return BST; /*查找成功，返回找到结点的地址*/
}

/*迭代、非递归方式*/
Position FindMax(BinTree BST)
{
    if(BST)
        while(BST->Right)
            BST = BST->Right;
    return BST;
}



Position FindMin(BinTree BST)
{
    if(!BST)
        return NULL;
    else if(!BST->Left)  /*有根结点，但没有左子树，直接返回根*/
            return BST;
    else
        return FindMin(BST->Left);
}

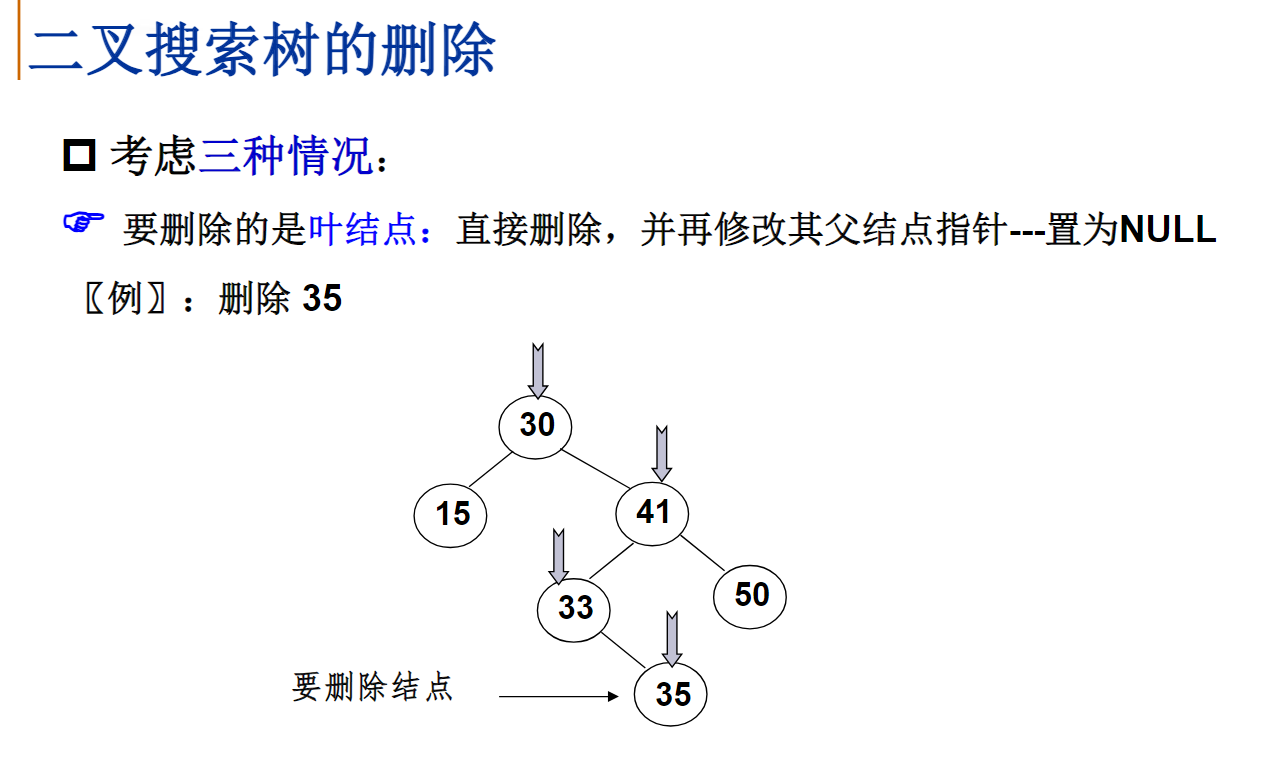
BinTree Delete(ElementType X,BinTree BST)
{
    Position Tmp;
    if(!BST)
        printf("找不到要删除的元素！\n");
    else if(X < BST->Data)
        BST->Left = Delete(X,BST->Left);
    else if(X > BST->Data)
        BST->Right = Delete(X,BST->Right);
    else
    {
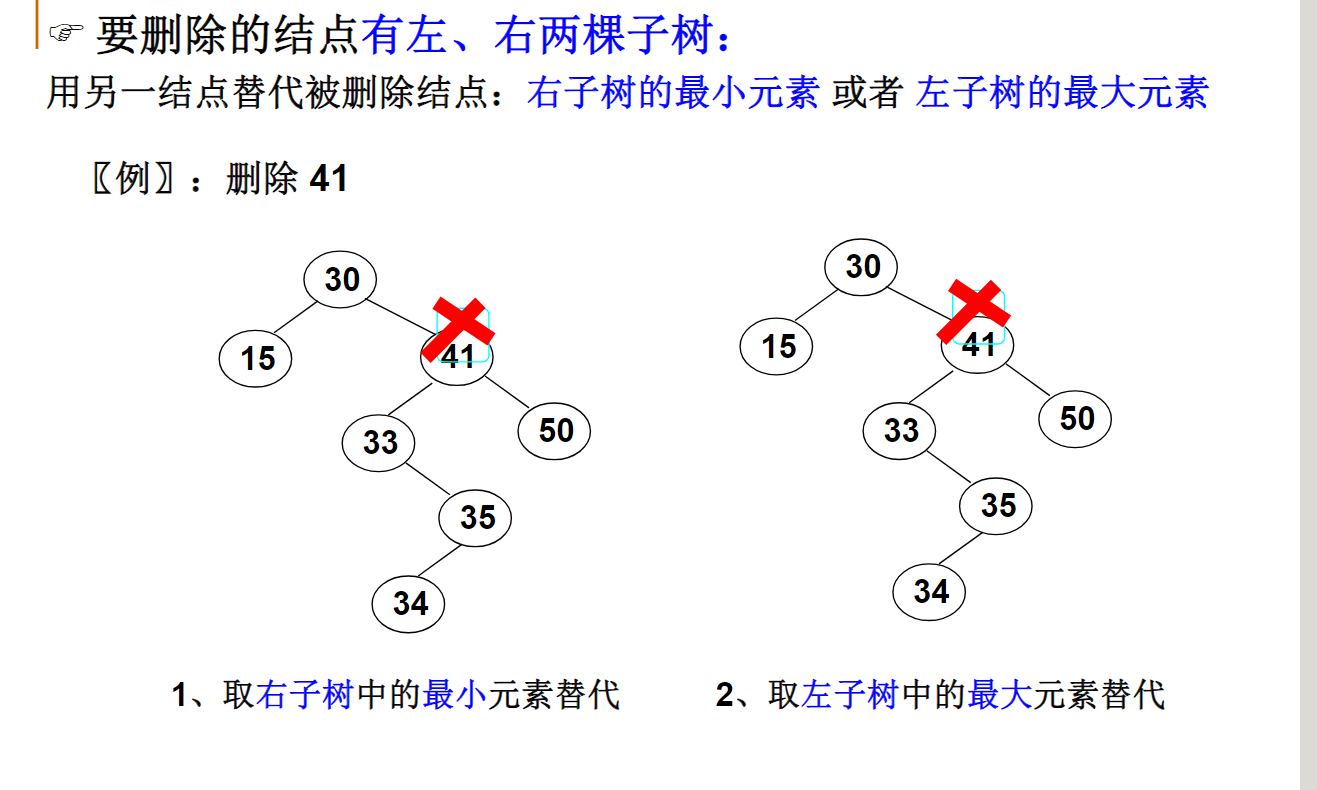
        if(BST->Left && BST->Right)
        {
            Tmp = FindMin(BST->Right);
            BST->Data = Tmp->Data;
            BST->Right = Delete(BST->Data,BST->Right);
        }
        else
        {
            Tmp = BST;
            if(!BST->Left)
                BST = BST->Right;
            else if(!BST->Right)
                BST = BST->Left;
            free(Tmp);
        }
    }
    return BST;

}

void PreOrderTraversalByStack(BinTree BST)
{
    if(!BST)
        return;
    BinTree pMove = BST;
    BinTree stack[100];
    int stackTop = -1;

    while(pMove || stackTop != -1 )
    {
        while(pMove)
        {
            printf("%d ",pMove->Data);
            stack[++stackTop] = pMove;
            pMove = pMove->Left;
        }
        if(stackTop != -1)
        {
            pMove = stack[stackTop--];
            pMove = pMove->Right;
            while(pMove)
            {
                printf("%d ",pMove->Data);
                stack[++stackTop] = pMove;
                pMove = pMove->Left;
            }
        }
    }
}

void InOrderTraversalByStack(BinTree BST)
{
    if(!BST)
        return;
    BinTree pMove = BST;
    BinTree stack[100];
    int stackTop = -1;

    while(pMove || stackTop != -1 )
    {
        while(pMove)
        {
            stack[++stackTop] = pMove;
            pMove = pMove->Left;
        }
        if(stackTop != -1)
        {
            pMove = stack[stackTop--];
            printf("%d ",pMove->Data);
            pMove = pMove->Right;
            while(pMove)
            {
                stack[++stackTop] = pMove;
                pMove = pMove->Left;
            }
        }
    }
}


void LevelTraversal(BinTree BT)
{
    LPNODE pMove = BT;
    LPNODE queue[100];
    int front = 0;
    int tail = 0;
    queue[tail++] = pMove;
    printf("%d ",pMove->Data);
    while(front != tail)
    {
        pMove = queue[front++];
        if(pMove->Left != NULL)
        {
            queue[tail++] = pMove->Left;
            printf("%d ",pMove->Left->Data);
        }
        if(pMove->Right != NULL)
        {
            queue[tail++] = pMove->Right;
            printf("%d ",pMove->Right->Data);
        }

    }

}

int main()
{
    BinTree BST = NULL;
    BST = Insert(5,BST);
    BST = Insert(3,BST);
    BST = Insert(4,BST);
    BST = Insert(9,BST);
    BST = Insert(20,BST);
    BST = Insert(30,BST);
    BST = Insert(40,BST);
    BST = Insert(43,BST);
    BST = Insert(34,BST);
    BST = Insert(6,BST);
    BST = Insert(7,BST);
    BST = Insert(8,BST);
    LevelTraversal(BST);
    printf("\n%d",FindMax(BST)->Data);
    printf("\n%d",FindMin(BST)->Data);
    BST = Delete(43,BST);
    BST = Delete(3,BST);
    printf("\n");
    LevelTraversal(BST);
    printf("\n%d",FindMax(BST)->Data);
    printf("\n%d",FindMin(BST)->Data);
    BinTree Tmp = Find(100,BST);
    if(!Tmp)
        printf("\nNULL\n");
    else
        printf("\n%d\n",Find(100,BST));
        //printf("\n%d\n",Tmp->Data);
    return 0;

}

5 3 9 4 6 20 7 30 8 40 34 43
43
3
5 4 9 6 20 7 30 8 40 34
40
4
NULL