最短路径算法

单源无权图最短路算法
- 邻接表存储 - 无权图的单源最短路算法
单源有权图最短路径算法——Dijkstra算法
- 邻接矩阵存储 - 有权图的单源最短路算法
- 邻接矩阵存储 - 有权图的单源最短路算法实例
多源最短路算法——Floyd算法
- 邻接矩阵存储 - 多源最短路算法
分支限界法
Bellman-Ford算法

单源无权图最短路算法

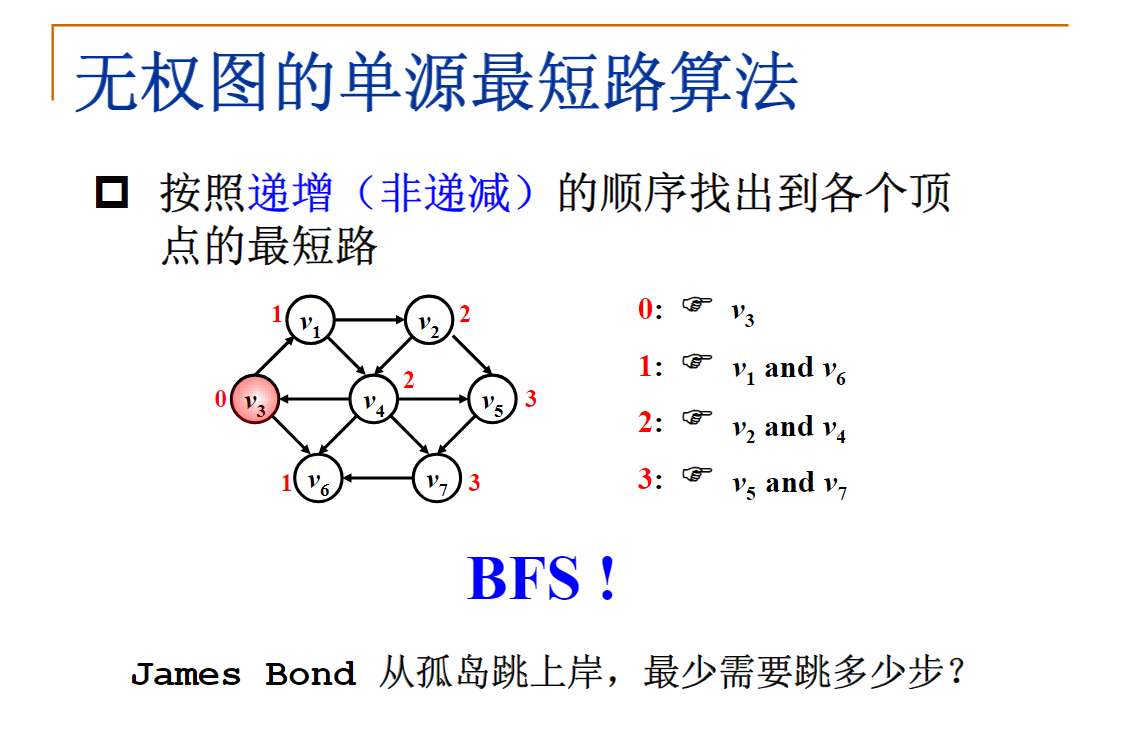
dist[W] = V 到 W 的最短距离；那么dist[W]应该被初始化为多少呢？D

A.正无穷
B.负无穷
C.-1
D.这三种都可以

随便一个不可能的数字即可表示没被访问，注意这里是无权图。

如果有|V|个顶点和|E|条边的图用邻接表存储，则算法的时间复杂度是多少？

void Unweighted ( Vertex S ) 
{ 
	Enqueue(S, Q);
	while(!IsEmpty(Q)){
	    V = Dequeue(Q); 
	    for ( V 的每个邻接点 W )
	      if ( dist[W] == -1  ) {
	        dist[W] = dist[V]+1;
	        path[W] = V;
	        Enqueue(W, Q);
      }
  }
}

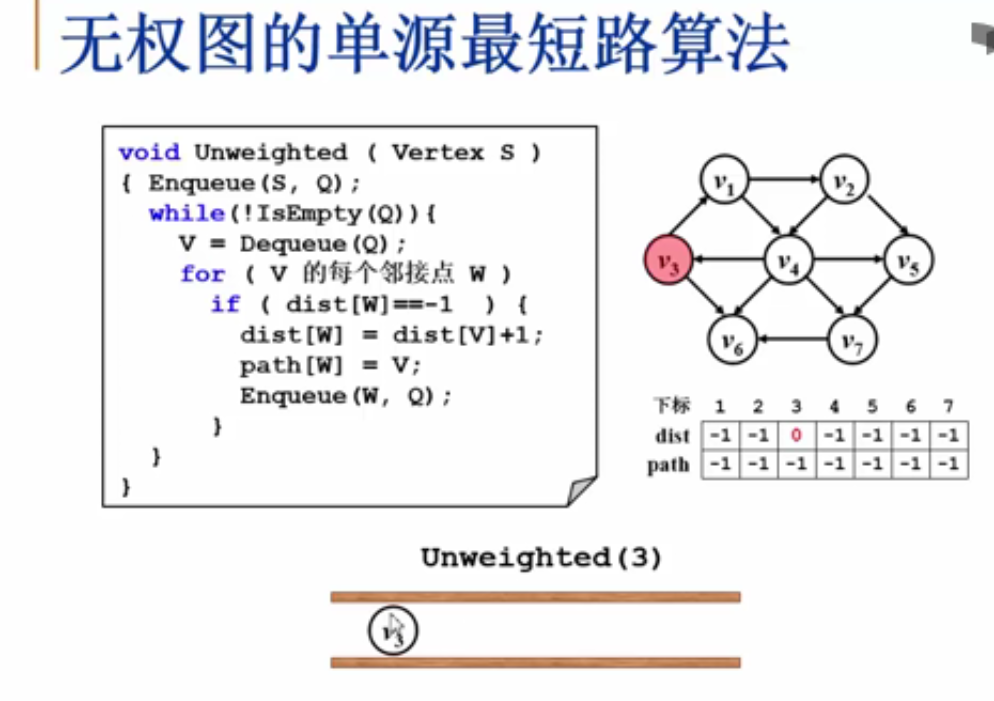
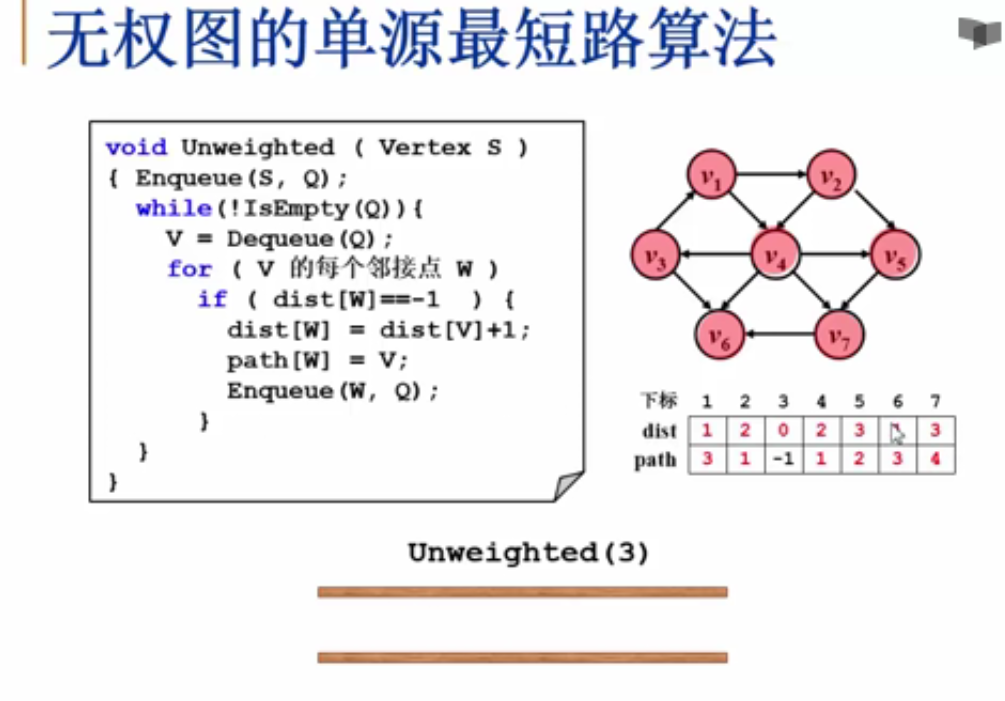
邻接表存储 - 无权图的单源最短路算法

/* 邻接表存储 - 无权图的单源最短路算法 */

/* dist[]和path[]全部初始化为-1 */
void Unweighted ( LGraph Graph, int dist[], int path[], Vertex S )
{
    Queue Q;
    Vertex V;
    PtrToAdjVNode W;
    
    Q = CreateQueue( Graph->Nv ); /* 创建空队列, MaxSize为外部定义的常数 */
    dist[S] = 0; /* 初始化源点 */
    AddQ (Q, S);

    while( !IsEmpty(Q) ){
        V = DeleteQ(Q);
        for ( W=Graph->G[V].FirstEdge; W; W=W->Next ) /* 对V的每个邻接点W->AdjV */
            if ( dist[W->AdjV]==-1 ) { /* 若W->AdjV未被访问过 */
                dist[W->AdjV] = dist[V]+1; /* W->AdjV到S的距离更新 */
                path[W->AdjV] = V; /* 将V记录在S到W->AdjV的路径上 */
                AddQ(Q, W->AdjV);
            }
    } /* while结束*/
}

单源有权图最短路径算法——Dijkstra算法

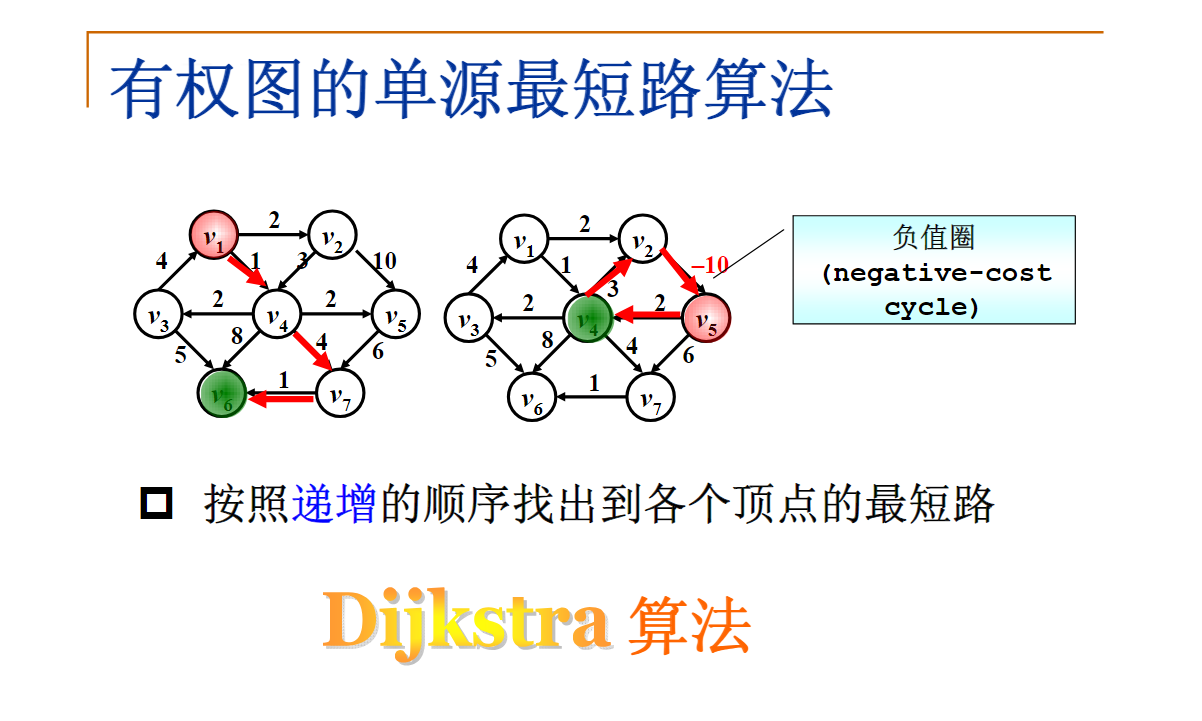
如果收录v使得s到w的路径变短，则：s到w的路径一定经过v，并且v到w有一条边

Dijkstra算法中的dist应该如何初始化？如果s到w有直接的边，则dist[w]=<s,w>的权重；否则dist[w]定义为A

A.正无穷
B.负无穷
C. -1
D.这三种都可以

注：这里是根据不等式结果更新dist数组的，不能随便初始化

void Dijkstra( Vertex s )
{ while (1) {
    V = 未收录顶点中dist最小者;
    if ( 这样的V不存在 )
      break; 
    collected[V] = true;
    for ( V 的每个邻接点 W )
      if ( collected[W] == false ) 
    if ( dist[V]+E<V,W> < dist[W] ) {
         dist[W] = dist[V] + E<V,W> ;
         path[W] = V;
    }
  }
}

算法的时间复杂度是多少？

不好计算，取决于如何从未收录顶点中选出dist最小者

邻接矩阵存储 - 有权图的单源最短路算法

/* 邻接矩阵存储 - 有权图的单源最短路算法 */

Vertex FindMinDist( MGraph Graph, int dist[], int collected[] )
{ /* 返回未被收录顶点中dist最小者 */
    Vertex MinV, V;
    int MinDist = INFINITY;

    for (V=0; V<Graph->Nv; V++) {
        if ( collected[V]==false && dist[V]<MinDist) {
            /* 若V未被收录，且dist[V]更小 */
            MinDist = dist[V]; /* 更新最小距离 */
            MinV = V; /* 更新对应顶点 */
        }
    }
    if (MinDist < INFINITY) /* 若找到最小dist */
        return MinV; /* 返回对应的顶点下标 */
    else return ERROR;  /* 若这样的顶点不存在，返回错误标记 */
}

bool Dijkstra( MGraph Graph, int dist[], int path[], Vertex S )
{
    int collected[MaxVertexNum];
    Vertex V, W;

    /* 初始化：此处默认邻接矩阵中不存在的边用INFINITY表示 */
    for ( V=0; V<Graph->Nv; V++ ) {
        dist[V] = Graph->G[S][V];
        if ( dist[V]<INFINITY )
            path[V] = S;
        else
            path[V] = -1;
        collected[V] = false;
    }
    /* 先将起点收入集合 */
    dist[S] = 0;
    collected[S] = true;

    while (1) {
        /* V = 未被收录顶点中dist最小者 */
        V = FindMinDist( Graph, dist, collected );
        if ( V==ERROR ) /* 若这样的V不存在 */
            break;      /* 算法结束 */
        collected[V] = true;  /* 收录V */
        for( W=0; W<Graph->Nv; W++ ) /* 对图中的每个顶点W */
            /* 若W是V的邻接点并且未被收录 */
            if ( collected[W]==false && Graph->G[V][W]<INFINITY ) {
                if ( Graph->G[V][W]<0 ) /* 若有负边 */
                    return false; /* 不能正确解决，返回错误标记 */
                /* 若收录V使得dist[W]变小 */
                if ( dist[V]+Graph->G[V][W] < dist[W] ) {
                    dist[W] = dist[V]+Graph->G[V][W]; /* 更新dist[W] */
                    path[W] = V; /* 更新S到W的路径 */
                }
            }
    } /* while结束*/
    return true; /* 算法执行完毕，返回正确标记 */
}

邻接矩阵存储 - 有权图的单源最短路算法实例

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>

#define MaxVertexNum 100
#define INFINITY 65535

int visited[MaxVertexNum];
int dist[MaxVertexNum];
int path[MaxVertexNum];

typedef int Vertex;
typedef int WeightType;

typedef struct ENode *PtrToENode;
struct ENode
{
    Vertex V1;
    Vertex V2;
    WeightType Weight;
};
typedef PtrToENode Edge;

typedef struct GNode *PtrToGNode;
struct GNode
{
    int Nv;
    int Ne;
    WeightType G[MaxVertexNum][MaxVertexNum];
};
typedef PtrToGNode MGraph;

MGraph CreateGraph(int VertexNum)
{
    MGraph Graph = (MGraph)malloc(sizeof(struct GNode));
    Graph->Nv = VertexNum;
    Graph->Ne = 0;
    Vertex V1,V2;
    for(Vertex V1=0; V1<Graph->Nv; V1++)
        for(Vertex V2=0; V2<Graph->Nv; V2++)
            Graph->G[V1][V2] = 0;

    return Graph;
}

void InsertEdge(MGraph Graph, Edge E)
{
    Graph->G[E->V1][E->V2] = E->Weight;
}

MGraph BuildGraph()
{
    int Nv;
    Edge E;
    scanf("%d", &Nv);
    MGraph Graph = CreateGraph(Nv);
    scanf("%d", &(Graph->Ne));
    if((Graph->Ne) != 0)
    {
        E = (Edge)malloc(sizeof(struct ENode));
        for(int i=0; i<Graph->Ne; i++)
        {
            scanf("%d %d %d",&E->V1,&E->V2,&E->Weight);
            InsertEdge(Graph, E);
        }
    }
    return Graph;
}

void ResetVisited()
{
    for(int i=0; i<MaxVertexNum; i++)
        visited[i] = 0;
}

void Dijkstra(MGraph Graph, Vertex V)
{
    ResetVisited();
    for(int i=0; i<Graph->Nv; i++)
    {
        if(Graph->G[V][i]>0 && V!=i)
        {
            dist[i] = Graph->G[V][i];
            path[i] = V;
        }
        else
        {
            dist[i] = INFINITY;
            path[i] = -1;
        }
    }
    dist[V] = 0;
    path[V] = V;
    visited[V] = 1;
    for(int i=1; i<Graph->Nv; i++)
    {
        int minDist = INT_MAX;
        int index;
        for(int j=0; j<Graph->Nv; j++)
        {
            if(visited[j]==0 && dist[j]<minDist)
            {
                minDist = dist[j];
                index = j;
            }
        }
        visited[index] = 1;
        for(int k=0; k<Graph->Nv; k++)
        {
            if(visited[k]==0 && Graph->G[index][k]>0 && minDist+Graph->G[index][k]<dist[k])
            {
                dist[k] = minDist+Graph->G[index][k];
                path[k] = index;
            }
        }
    }

}

void PrintPath(int path[], int distance)
{
    int temp = distance;
    int count = 1;
    int collected[MaxVertexNum] = {0};

    while(path[temp]!=0)
    {
        collected[count] = path[temp];
        count++;
        temp = path[temp];
    }
    collected[count] = path[temp];
    while(count!=0)
    {
        printf("v%d->", collected[count]);
        count--;
    }
    printf("v%d",distance);
}

int main()
{
    MGraph Graph = BuildGraph();
    Dijkstra(Graph, 0);
    int distance = 5;
    PrintPath(path, distance);
    printf("\ncost distance :%d",dist[distance]);
    return 0;
}

输入数据：

输出结果：

v0->v3->v6->v5
cost distance :6

多源最短路算法——Floyd算法

D矩阵应该初始化为什么？

A.带权的邻接矩阵，对角元是0
B.带权的邻接矩阵，对角元是无穷大
C.全是0的矩阵
D.全是无穷大的矩阵

正确答案：A你选对了

如果i和j之间没有直接的边，D[i][j]应该定义为什么？

A.正无穷
B.0
C.负无穷
D.这三种都可以

正确答案：A你选对了

邻接矩阵存储 - 多源最短路算法

/* 邻接矩阵存储 - 多源最短路算法 */

bool Floyd( MGraph Graph, WeightType D[][MaxVertexNum], Vertex path[][MaxVertexNum] )
{
    Vertex i, j, k;

    /* 初始化 */
    for ( i=0; i<Graph->Nv; i++ )
        for( j=0; j<Graph->Nv; j++ ) {
            D[i][j] = Graph->G[i][j];
            path[i][j] = -1;
        }

    for( k=0; k<Graph->Nv; k++ )
        for( i=0; i<Graph->Nv; i++ )
            for( j=0; j<Graph->Nv; j++ )
                if( D[i][k] + D[k][j] < D[i][j] ) {
                    D[i][j] = D[i][k] + D[k][j];
                    if ( i==j && D[i][j]<0 ) /* 若发现负值圈 */
                        return false; /* 不能正确解决，返回错误标记 */
                    path[i][j] = k;
                }
    return true; /* 算法执行完毕，返回正确标记 */
}

分支限界法

https://blog.csdn.net/lcw_2015/article/details/52892501

资料结构与演算法