MOOC-PTA查找题目
- PTA 11-散列1 电话聊天狂人
- PTA 11-散列2 Hashing
- PTA 11-散列3 QQ帐户的申请与登陆
- PTA 11-散列4 Hashing - Hard Version
- PTA KMP 串的模式匹配
PTA 11-散列1 电话聊天狂人
给定大量手机用户通话记录,找出其中通话次数最多的聊天狂人。
输入格式:
输入首先给出正整数N(≤105),为通话记录条数。随后N行,每行给出一条通话记录。简单起见,这里只列出拨出方和接收方的11位数字构成的手机号码,其中以空格分隔。
输出格式:
在一行中给出聊天狂人的手机号码及其通话次数,其间以空格分隔。如果这样的人不唯一,则输出狂人中最小的号码及其通话次数,并且附加给出并列狂人的人数。
输入样例:
4
13005711862 13588625832
13505711862 13088625832
13588625832 18087925832
15005713862 13588625832
输出样例:
13588625832 3
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <string.h>
#include <assert.h>
#define KEYLENGTH 11
#define MAXD 5
#define MAXTABLESIZE 1000000
typedef char ElementType[KEYLENGTH+1];
typedef int Index;
typedef struct LNode *PtrToLNode;
struct LNode
{
ElementType Data;
PtrToLNode Next;
int count;
};
typedef PtrToLNode Position;
typedef PtrToLNode List;
typedef struct TblNode *HashTable;
struct TblNode
{
int TableSize;
List Heads;
};
int NextPrime(int N)
{
int i,p = (N%2)?(N+2):(N+1);
while(p<=MAXTABLESIZE)
{
for(i=(int)sqrt(p); i>2; i--)
{
if(!(p%i))
break;
}
if(i==2)
break;
else
p += 2;
}
return p;
}
HashTable CreateTable(int TableSize)
{
HashTable H = (HashTable)malloc(sizeof(struct TblNode));
H->TableSize = NextPrime(TableSize);
H->Heads = (List)malloc(H->TableSize * sizeof(struct LNode));
for(int i=0; i<H->TableSize; i++)
{
H->Heads[i].Data[0] = '\0';
H->Heads[i].Next = NULL;
H->Heads[i].count = 0;
}
return H;
}
int Hash(int Key, int P)
{
return Key%P;
}
Position Find(HashTable H, ElementType Key)
{
Position P;
Index Pos;
Pos = Hash(atoi(Key+KEYLENGTH-MAXD), H->TableSize);
P = H->Heads[Pos].Next;
while(P && strcmp(P->Data,Key))
P = P->Next;
return P;
}
bool Insert(HashTable H, ElementType Key)
{
Position P,NewCell;
Index Pos;
P = Find(H,Key);
if(!P)
{
NewCell = (Position)malloc(sizeof(struct LNode));
strcpy(NewCell->Data, Key);
NewCell->count = 1;
Pos = Hash(atoi(Key+KEYLENGTH-MAXD), H->TableSize);
NewCell->Next = H->Heads[Pos].Next;
H->Heads[Pos].Next = NewCell;
return true;
}
else
{
P->count++;
return false;
}
}
void ScanAndOutput(HashTable H)
{
int MaxCnt = 0;
int pCnt = 0;
ElementType MinPhone;
List Ptr;
MinPhone[0] = '\0';
for(int i=0; i<H->TableSize; i++)
{
Ptr = H->Heads[i].Next;
while(Ptr)
{
if(Ptr->count > MaxCnt)
{
MaxCnt = Ptr->count;
strcpy(MinPhone, Ptr->Data);
pCnt = 1;
}
else if(Ptr->count == MaxCnt)
{
pCnt++;
if(strcmp(MinPhone, Ptr->Data)>0)
{
strcpy(MinPhone, Ptr->Data);
}
}
Ptr = Ptr->Next;
}
}
printf("%s %d",MinPhone,MaxCnt);
if(pCnt > 1)
printf(" %d",pCnt);
printf("\n");
}
void DestroyTable( HashTable H )
{
int i;
Position P, Tmp;
//释放每个链表的结点
for( i=0; i<H->TableSize; i++ ) {
P = H->Heads[i].Next;
while( P ) {
Tmp = P->Next;
free( P );
P = Tmp;
}
}
free( H->Heads ); //释放头结点数组
free( H ); //释放散列表结点
}
int main()
{
int N;
scanf("%d",&N);
ElementType Key;
HashTable H;
H = CreateTable(N*2);
for(int i=0; i<N; i++)
{
scanf("%s",&Key);
Insert(H,Key);
scanf("%s",&Key);
Insert(H,Key);
}
ScanAndOutput(H);
DestroyTable(H);
return 0;
}
下面是Python实现的代码:
dt = {}
N = int(input())
for i in range(N):
number1, number2 = map(int,input().split())
dt[number1] = dt.get(number1,0) + 1
dt[number2] = dt.get(number2,0) + 1
count = 0
maxValue = 0
min_number = 0
for k,v in dt.items():
if v > maxValue:
maxValue = v
min_number = k
for k,v in dt.items():
if v == maxValue:
count += 1
if k < min_number:
min_number = k
if count == 1:
print(min_number,maxValue)
else:
print(min_number,maxValue,count)
PTA 11-散列2 Hashing
The task of this problem is simple: insert a sequence of distinct positive integers into a hash table, and output the positions of the input numbers. The hash function is defined to be H(key)=key%TSize where TSize is the maximum size of the hash table. Quadratic probing (with positive increments only) is used to solve the collisions.
Note that the table size is better to be prime. If the maximum size given by the user is not prime, you must re-define the table size to be the smallest prime number which is larger than the size given by the user.
Input Specification:
Each input file contains one test case. For each case, the first line contains two positive numbers: MSize (≤104) and N (≤MSize) which are the user-defined table size and the number of input numbers, respectively. Then N distinct positive integers are given in the next line. All the numbers in a line are separated by a space.
Output Specification:
For each test case, print the corresponding positions (index starts from 0) of the input numbers in one line. All the numbers in a line are separated by a space, and there must be no extra space at the end of the line. In case it is impossible to insert the number, print "-" instead.
Sample Input:
4 4
10 6 4 15
Sample Output:
0 1 4 -
解题方法: 这道题目只需要用一个数组就可以解决,开始对数组每个元素先初始化为0,然后通过散列映射到数组中去,如果该映射的下标的元素值为0,则把该下标置为我们输入的值,否则就遍历正向的二次探测。这里大家可能会对什么时候才能结束探测循环表示疑问。因此我们循环只需要到TableSize就可以结束。
易错点:
对1来说,他不是素数(质数定义为在大于1的自然数中,除了1和它本身以外不再有其他因数),所以对他而言最小素数为2
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <string.h>
#include <assert.h>
#define MAXTABLESIZE 100000
typedef int ElementType;
typedef int Index;
typedef Index Position;
typedef enum { Legitimate, Empty, Deleted } EntryType;
typedef struct HashEntry Cell;
struct HashEntry
{
ElementType Data;
EntryType Info;
};
typedef struct TblNode *HashTable;
struct TblNode
{
int TableSize;
Cell *Cells;
};
int NextPrime( int N )
{
if(N==1)
return 2;
int i, p = (N%2)? N+2 : N+1;
while( p <= MAXTABLESIZE ) {
for( i=(int)sqrt(p); i>2; i-- )
if ( !(p%i) ) break;
if ( i==2 ) break;
else p += 2;
}
return p;
}
int Hash(ElementType Key, int TableSize)
{
return (Key%TableSize);
}
HashTable CreateTable( int TableSize )
{
HashTable H;
int i;
H = (HashTable)malloc(sizeof(struct TblNode));
H->TableSize = NextPrime(TableSize);
H->Cells = (Cell *)malloc(H->TableSize*sizeof(Cell));
for( i=0; i<H->TableSize; i++ )
H->Cells[i].Info = Empty;
return H;
}
void Insert(HashTable H, int key)
{
int Pos = Hash(key, H->TableSize);
if(H->Cells[Pos].Info == Empty)
{
H->Cells[Pos].Data = key;
H->Cells[Pos].Info = Legitimate;
printf("%d",Pos);
}
else
{
int newp = Pos;
for(int i=0; i<H->TableSize; i++)
{
newp = (Pos + i*i)%(H->TableSize);
if(H->Cells[newp].Info == Empty)
{
H->Cells[newp].Data = key;
H->Cells[newp].Info = Legitimate;
printf("%d",newp);
return;
}
}
printf("-");
}
}
int main()
{
int MSize,N;
scanf("%d %d",&MSize,&N);
HashTable H = CreateTable(MSize);
for(int i=0; i<N; i++)
{
int key;
scanf("%d",&key);
Insert(H,key);
if(i != N-1)
{
printf(" ");
}
else
{
printf("\n");
}
}
}
PTA 11-散列3 QQ帐户的申请与登陆
实现QQ新帐户申请和老帐户登陆的简化版功能。最大挑战是:据说现在的QQ号码已经有10位数了。
输入格式:
输入首先给出一个正整数N(≤105),随后给出N行指令。每行指令的格式为:“命令符(空格)QQ号码(空格)密码”。其中命令符为“N”(代表New)时表示要新申请一个QQ号,后面是新帐户的号码和密码;命令符为“L”(代表Login)时表示是老帐户登陆,后面是登陆信息。QQ号码为一个不超过10位、但大于1000(据说QQ老总的号码是1001)的整数。密码为不小于6位、不超过16位、且不包含空格的字符串。
输出格式:
针对每条指令,给出相应的信息:
1)若新申请帐户成功,则输出“New: OK”;
2)若新申请的号码已经存在,则输出“ERROR: Exist”;
3)若老帐户登陆成功,则输出“Login: OK”;
4)若老帐户QQ号码不存在,则输出“ERROR: Not Exist”;
5)若老帐户密码错误,则输出“ERROR: Wrong PW”。
输入样例:
5
L 1234567890 myQQ@qq.com
N 1234567890 myQQ@qq.com
N 1234567890 myQQ@qq.com
L 1234567890 myQQ@qq
L 1234567890 myQQ@qq.com
输出样例:
ERROR: Not Exist
New: OK
ERROR: Exist
ERROR: Wrong PW
Login: OK
思路:在基本的Cell类型中,增加一个存储密码的字符串类型PWType、Info只需要用来判断账号存在还是不存在,不需要判断是否已删除、此题还是常规的哈希表题,涉及到哈希表的构建,查找(这里采用线性探测的方式),插入的操作。再额外加一个登陆——即字符串的比较操作即可。
易错点:strcpy之前需要对Password中赋值"\0"、读取字符时需要用getchar()函数处理回车符
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define MAXTABLESIZE 100005
#define MAXCHAR 16
typedef long long int ElementType;
typedef char PWType[MAXCHAR+1];
typedef int Index;
typedef Index Position;
typedef enum { Legitimate, Empty, Deleted } EntryType;
typedef struct HashEntry Cell;
struct HashEntry
{
ElementType Data;
PWType Password;
EntryType Info;
};
typedef struct TblNode *HashTable;
struct TblNode
{
int TableSize;
Cell *Cells;
};
int NextPrime( int N )
{
if(N==1)
return 2;
int i, p = (N%2)? N+2 : N+1;
while( p <= MAXTABLESIZE ) {
for( i=(int)sqrt(p); i>2; i-- )
if ( !(p%i) ) break;
if ( i==2 ) break;
else p += 2;
}
return p;
}
int Hash(ElementType Key, HashTable H)
{
return (Key%H->TableSize);
}
HashTable CreateTable( int TableSize )
{
HashTable H;
int i;
H = (HashTable)malloc(sizeof(struct TblNode));
H->TableSize = NextPrime(TableSize);
H->Cells = (Cell *)malloc(H->TableSize*sizeof(Cell));
for( i=0; i<H->TableSize; i++ )
{
H->Cells[i].Info = Empty;
strcpy(H->Cells[i].Password, "\0");
}
return H;
}
int LinearFind(HashTable H, ElementType Key)
{
int curPos = Hash(Key ,H);
int newPos = curPos;
int count = 0;
while(H->Cells[newPos].Info != Empty && H->Cells[newPos].Data != Key)
{
count++;
newPos = (curPos + count) % H->TableSize;
}
return newPos;
}
void Insert(HashTable H, ElementType Key, PWType password)
{
int Pos = LinearFind(H, Key);
if(H->Cells[Pos].Info == Empty)
{
H->Cells[Pos].Data = Key;
strcpy(H->Cells[Pos].Password, password);
H->Cells[Pos].Info = Legitimate;
printf("New: OK\n");
}
else
{
printf("ERROR: Exist\n");
}
}
void LogIn(HashTable H, ElementType Key, PWType password)
{
int Pos = LinearFind(H, Key);
if(H->Cells[Pos].Info == Empty)
{
printf("ERROR: Not Exist\n");
}
else if(H->Cells[Pos].Info == Legitimate && strcmp(H->Cells[Pos].Password, password))
{
printf("ERROR: Wrong PW\n");
}
else
{
printf("Login: OK\n");
}
}
int main()
{
int N;
scanf("%d",&N);
HashTable H = CreateTable(N);
ElementType Key;
PWType Password;
char command;
for(int i=0; i<N; i++)
{
getchar();
scanf("%c",&command);
scanf("%lld",&Key);
scanf("%s", Password);
switch(command)
{
case 'N':
Insert(H, Key, Password);
break;
case 'L':
LogIn(H, Key, Password);
break;
}
}
}
使用C++STL实现:
#include <iostream>
#include <string>
#include <map>
using namespace std;
int main() {
map<string, string> user;//账号密码
int N;
string o, us, pw;
cin >> N;
for(int i = 0; i < N; ++i) {
cin >> o >> us >> pw;
if(o == "L") {//Login
if(user.find(us) == user.end())
cout << "ERROR: Not Exist" << endl;
else if(user[us] == pw)
cout << "Login: OK" << endl;
else cout << "ERROR: Wrong PW" << endl;
} else if(o == "N") {//New
if(user.find(us) != user.end())
cout << "ERROR: Exist" << endl;
else {
user[us] = pw;
cout << "New: OK" << endl;
}
}
}
return 0;
}
PTA 11-散列4 Hashing - Hard Version
Given a hash table of size N, we can define a hash function H(x)=x%N. Suppose that the linear probing is used to solve collisions, we can easily obtain the status of the hash table with a given sequence of input numbers.
However, now you are asked to solve the reversed problem: reconstruct the input sequence from the given status of the hash table. Whenever there are multiple choices, the smallest number is always taken.
Input Specification:
Each input file contains one test case. For each test case, the first line contains a positive integer N (≤1000), which is the size of the hash table. The next line contains N integers, separated by a space. A negative integer represents an empty cell in the hash table. It is guaranteed that all the non-negative integers are distinct in the table.
Output Specification:
For each test case, print a line that contains the input sequence, with the numbers separated by a space. Notice that there must be no extra space at the end of each line.
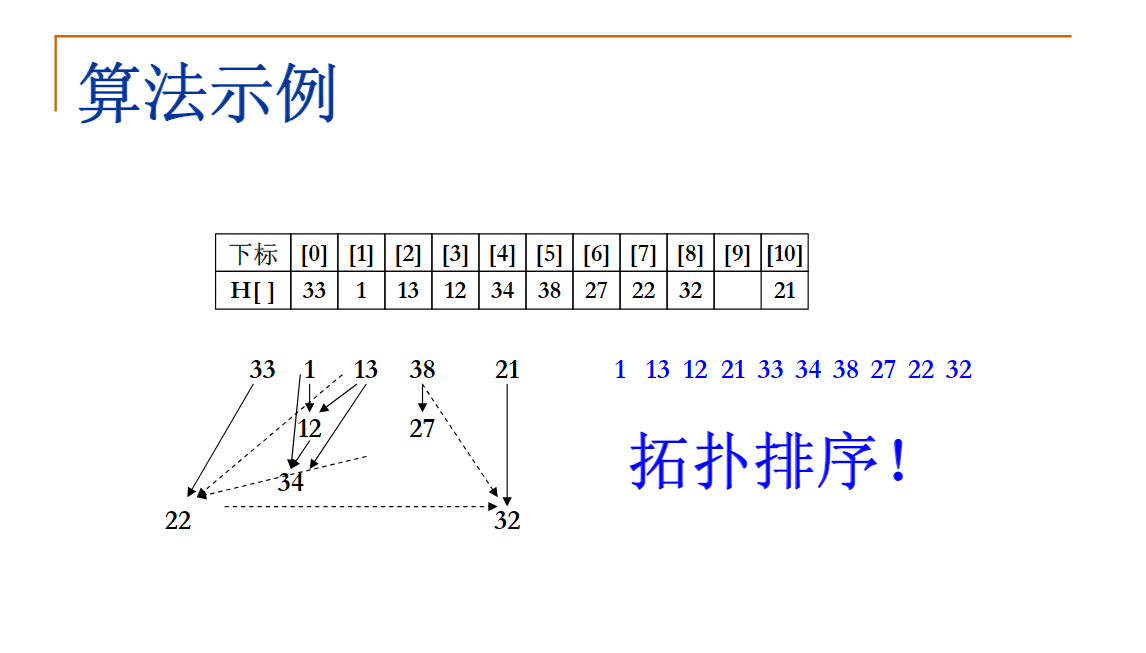
Sample Input:
11
33 1 13 12 34 38 27 22 32 -1 21
Sample Output:
1 13 12 21 33 34 38 27 22 32

PTA KMP 串的模式匹配
给定两个由英文字母组成的字符串 String 和 Pattern,要求找到 Pattern 在 String 中第一次出现的位置,并将此位置后的 String 的子串输出。如果找不到,则输出“Not Found”。
本题旨在测试各种不同的匹配算法在各种数据情况下的表现。各组测试数据特点如下:
- 数据0:小规模字符串,测试基本正确性;
- 数据1:随机数据,String 长度为 105,Pattern 长度为 10;
- 数据2:随机数据,String 长度为 105,Pattern 长度为 102;
- 数据3:随机数据,String 长度为 105,Pattern 长度为 103;
- 数据4:随机数据,String 长度为 105,Pattern 长度为 104;
- 数据5:String 长度为 106,Pattern 长度为 105;测试尾字符不匹配的情形;
- 数据6:String 长度为 106,Pattern 长度为 105;测试首字符不匹配的情形。
输入格式:
输入第一行给出 String,为由英文字母组成的、长度不超过 106 的字符串。第二行给出一个正整数 N(≤10),为待匹配的模式串的个数。随后 N 行,每行给出一个 Pattern,为由英文字母组成的、长度不超过 105 的字符串。每个字符串都非空,以回车结束。
输出格式:
对每个 Pattern,按照题面要求输出匹配结果。
输入样例:
abcabcabcabcacabxy
3
abcabcacab
cabcabcd
abcabcabcabcacabxyz
输出样例:
abcabcacabxy
Not Found
Not Found
使用KMP算法的解法如下:
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
typedef int Position;
#define NotFound -1
void BuildMatch( char *pattern, int *match )
{
Position i, j;
int m = strlen(pattern);
match[0] = -1;
for ( j=1; j<m; j++ ) {
i = match[j-1];
while ( (i>=0) && (pattern[i+1]!=pattern[j]) )
i = match[i];
if ( pattern[i+1]==pattern[j] )
match[j] = i+1;
else match[j] = -1;
}
}
Position KMP( char *string, char *pattern )
{
int n = strlen(string);
int m = strlen(pattern);
Position s, p, *match;
if ( n < m ) return NotFound;
match = (Position *)malloc(sizeof(Position) * m);
BuildMatch(pattern, match);
s = p = 0;
while ( s<n && p<m ) {
if ( string[s]==pattern[p] ) {
s++; p++;
}
else if (p>0) p = match[p-1]+1;
else s++;
}
return ( p==m )? (s-m) : NotFound;
}
int main()
{
char string[1000005];
scanf("%s",string);
int N;
scanf("%d",&N);
for(int i=0; i<N; i++)
{
char pattern[100005];
scanf("%s",pattern);
Position p = KMP(string, pattern);
if (p==NotFound)
printf("Not Found\n");
else
printf("%s\n", string+p);
}
return 0;
}
使用strstr函数的解法如下:
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
typedef char* Position;
#define NotFound NULL
int main()
{
char string[1000005];
scanf("%s",string);
int N;
scanf("%d",&N);
for(int i=0; i<N; i++)
{
char pattern[100005];
scanf("%s",pattern);
Position p = strstr(string, pattern);
if (p==NotFound)
printf("Not Found\n");
else
printf("%s\n", p);
}
return 0;
}