二叉树

• 二叉树的定义
• 二叉树的存储结构
• 二叉树的创建
  • 非递归方式
  • 递归方式
• 二叉树的遍历

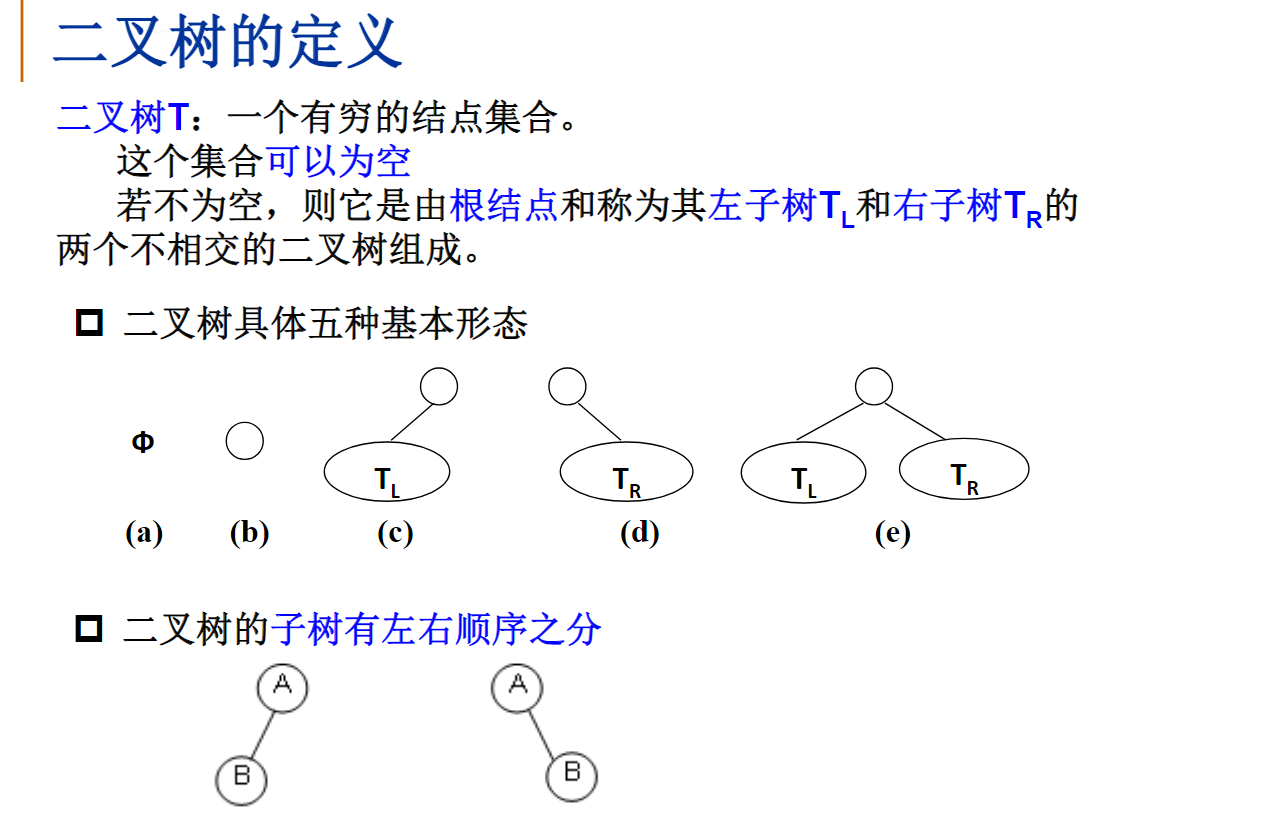
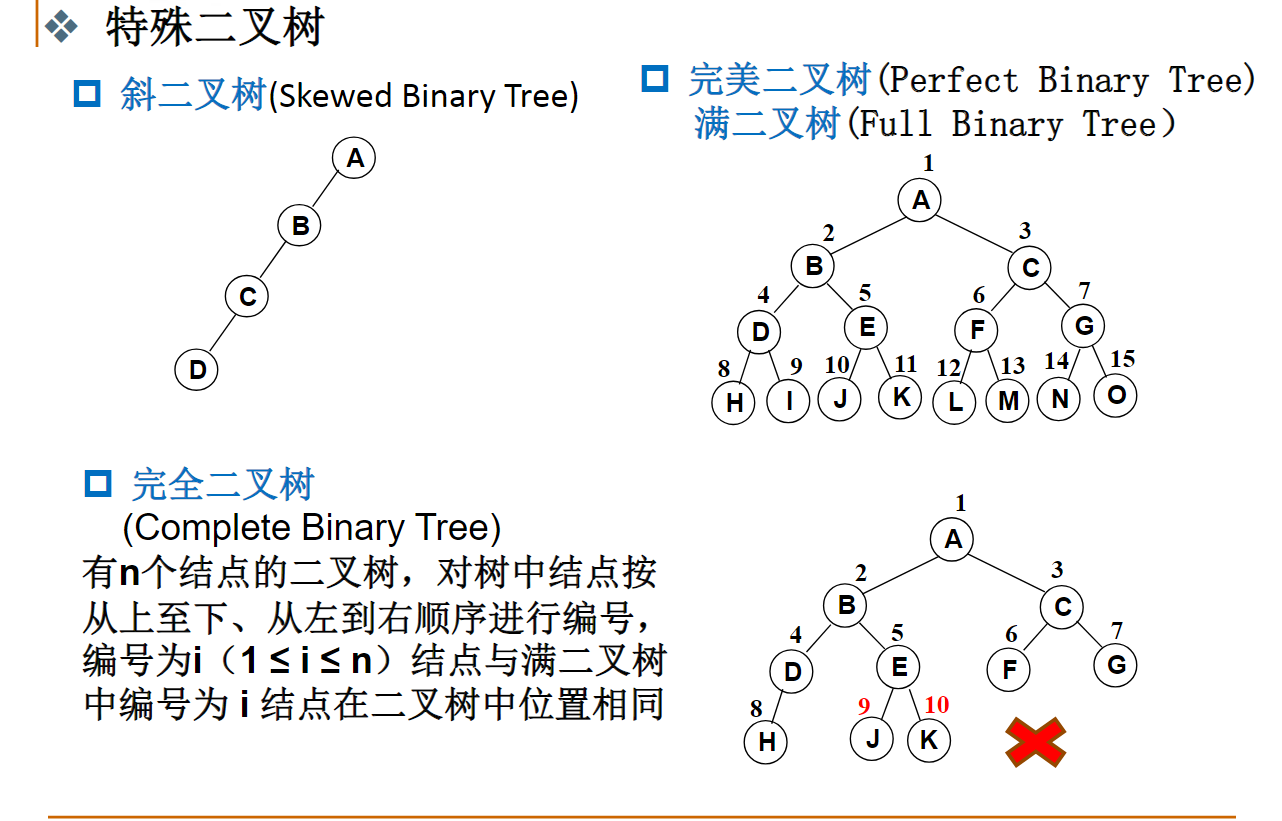
二叉树的定义

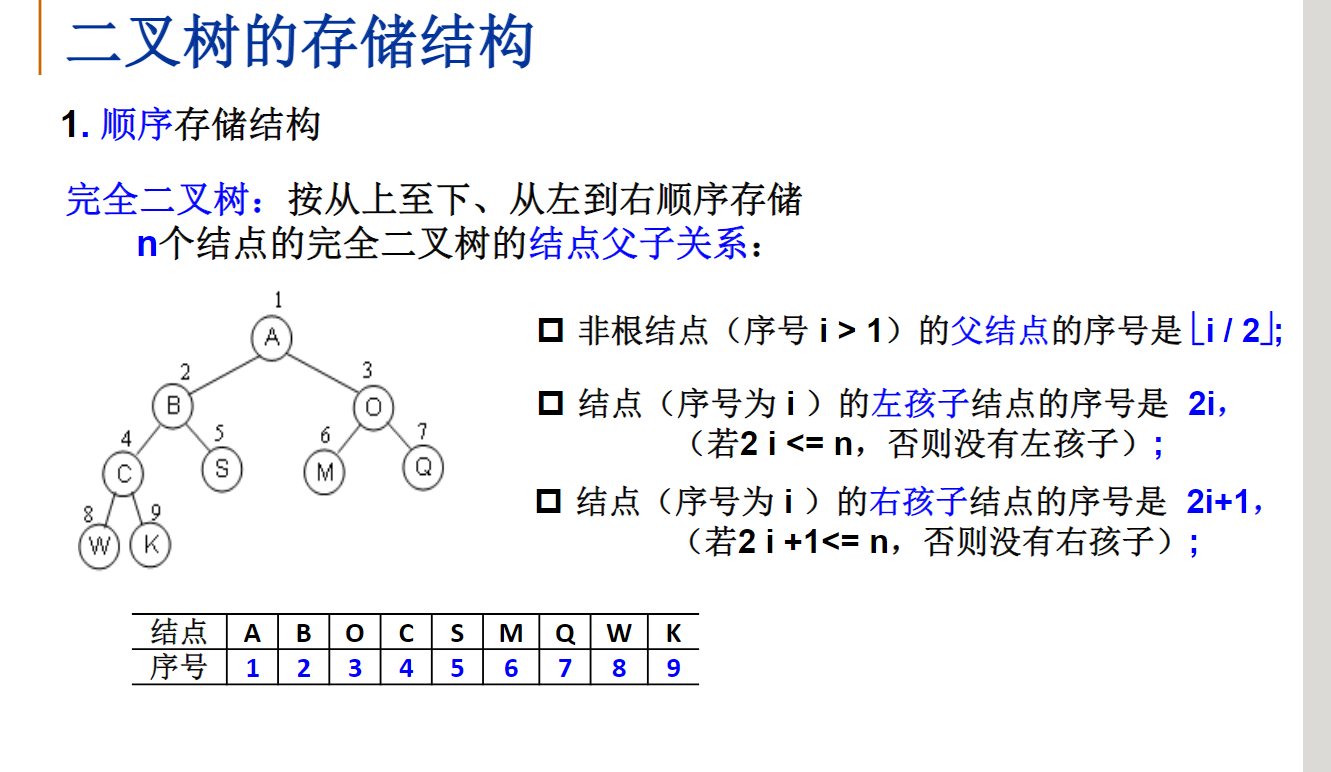
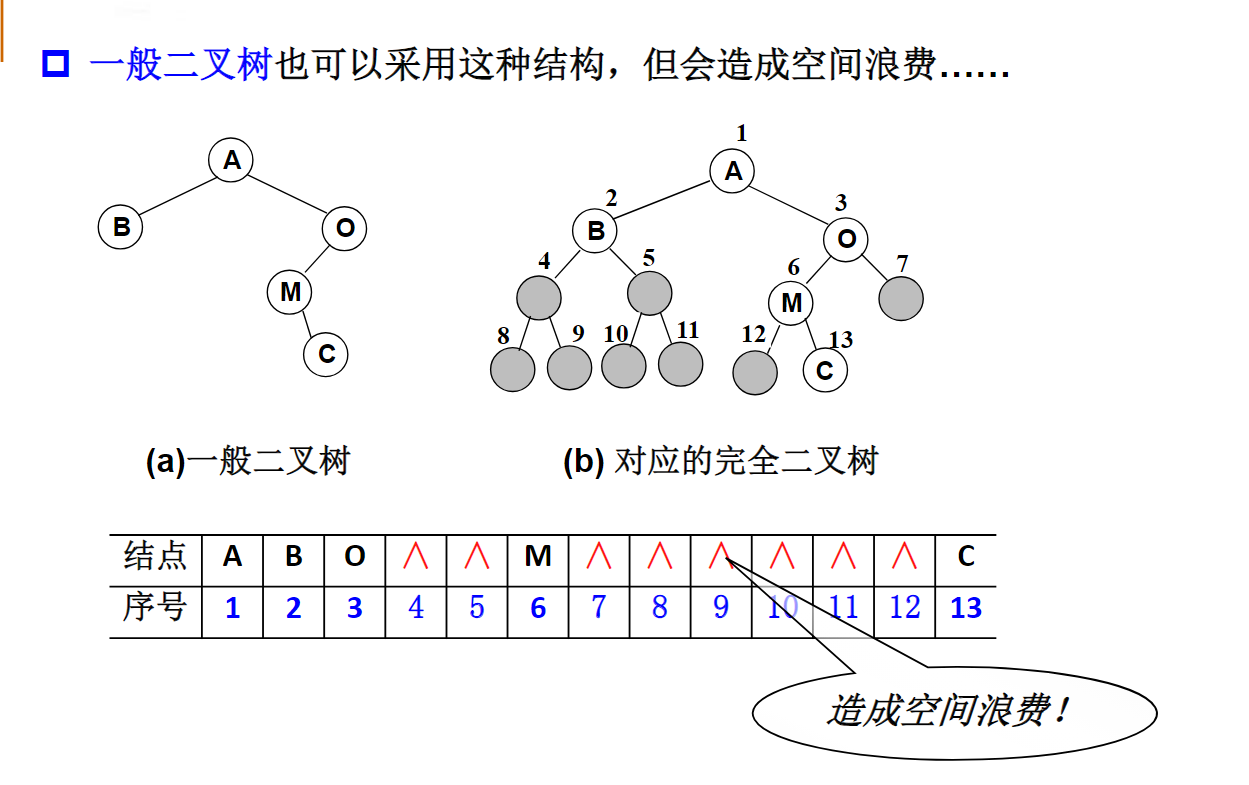
二叉树的存储结构

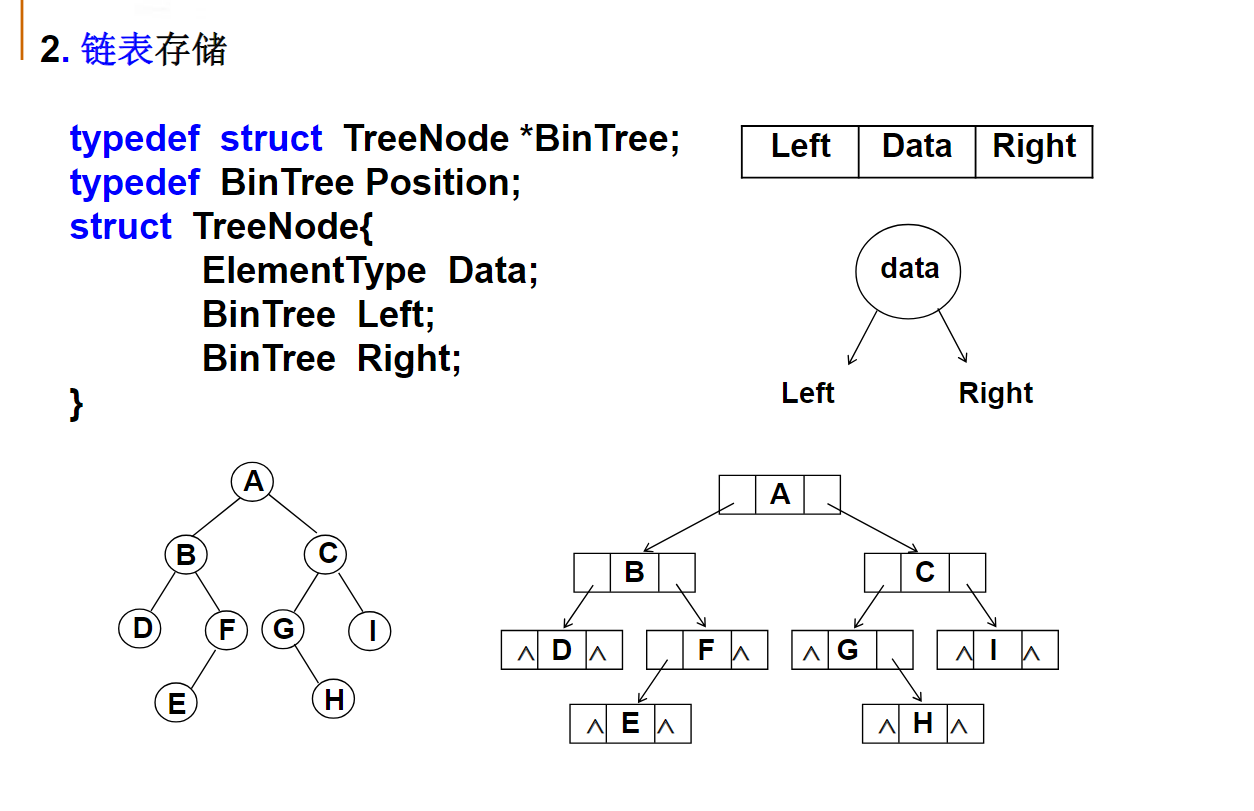
链表结构：

typedef struct TNode *Position;
typedef Position BinTree; /* 二叉树类型 */
struct TNode{ /* 树结点定义 */
    ElementType Data; /* 结点数据 */
    BinTree Left;     /* 指向左子树 */
    BinTree Right;    /* 指向右子树 */
};

包含较多别名的写法如下：

typedef struct treenode
{
    char data;
    struct treenode* LChild;
    struct treenode* RChild;
}NODE,*LPNODE,*LPTREE;

//struct treenode : NODE
//struct treenode* : LPNODE或LPTREE
NODE node1;
struct treenode* p = NULL;
LPNODE p1 = NULL;

二叉树的创建

非递归方式

实现代码如下：

#include <stdio.h>
#include <stdlib.h>

typedef struct TreeNode *LPNODE;
typedef LPNODE BinTree;
typedef char ElementType;

struct TreeNode
{
    ElementType Data;
    BinTree Left;
    BinTree Right;
};

LPNODE CreateNode(ElementType Data)
{
    LPNODE newNode = (LPNODE)malloc(sizeof(struct TreeNode));
    newNode->Left = NULL;
    newNode->Right = NULL;
    newNode->Data = Data;
    return newNode;
}

/* 非递归创建树 */
void InsertNode(BinTree parent, LPNODE Left, LPNODE Right)
{
    parent->Left = Left;
    parent->Right = Right;
}

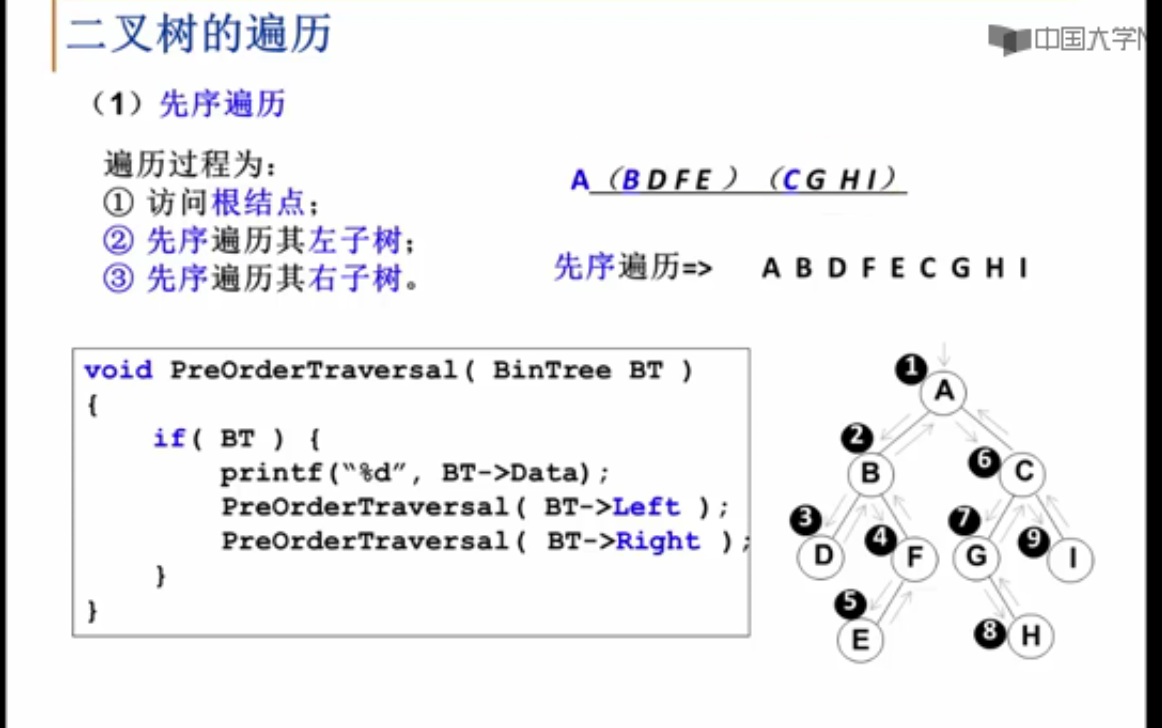
void PreOrderTraversal(BinTree BT)
{
    if(BT)
    {
        printf("%c ",BT->Data);
        PreOrderTraversal(BT->Left);
        PreOrderTraversal(BT->Right);
    }
}

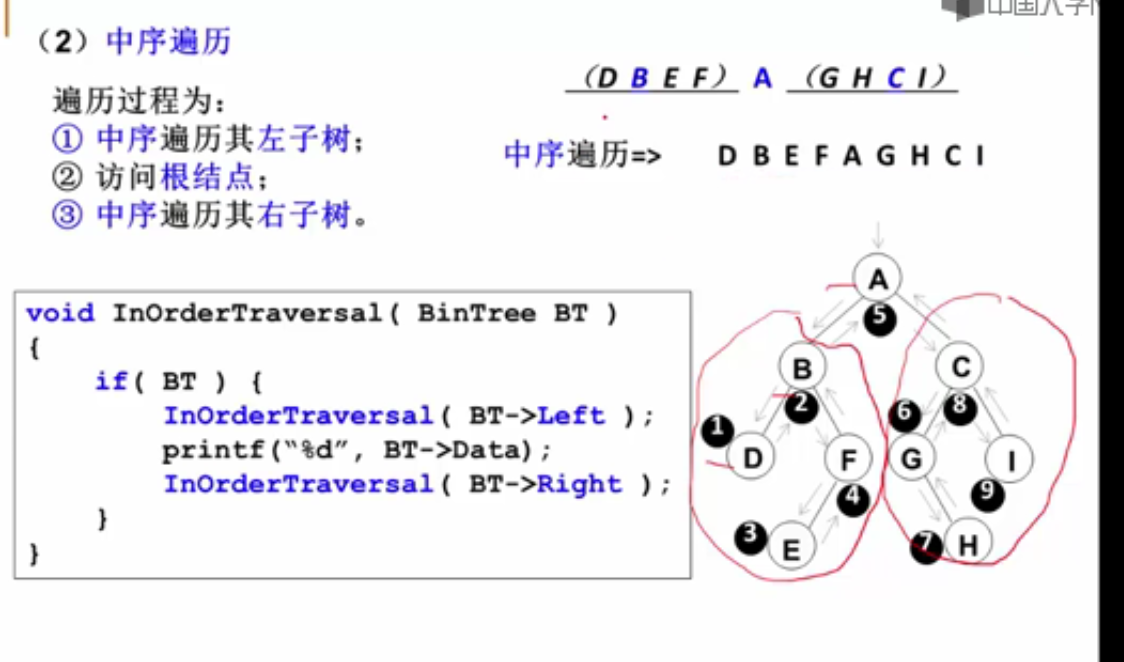
void InOrderTraversal(BinTree BT)
{
    if(BT)
    {
        InOrderTraversal(BT->Left);
        printf("%c ",BT->Data);
        InOrderTraversal(BT->Right);
    }
}

void PostOrderTraversal(BinTree BT)
{
    if(BT)
    {
        PostOrderTraversal(BT->Left);
        PostOrderTraversal(BT->Right);
        printf("%c ",BT->Data);
    }
}

int main()
{
    LPNODE A = CreateNode('A');
    LPNODE B = CreateNode('B');
    LPNODE C = CreateNode('C');
    LPNODE D = CreateNode('D');
    LPNODE E = CreateNode('E');
    LPNODE F = CreateNode('F');
    InsertNode(A,B,C);
    InsertNode(B,D,NULL);
    InsertNode(C,E,NULL);
    InsertNode(E,NULL,F);
    PreOrderTraversal(A);
    printf("\n");
    InOrderTraversal(A);
    printf("\n");
    PostOrderTraversal(A);
    printf("\n");
    return 0;
}

A B D C E F
D B A E F C
D B F E C A

递归方式

实现代码如下：

#include <stdio.h>
#include <stdlib.h>

typedef char ElementType;

typedef struct TreeNode
{
    ElementType Data;
    struct TreeNode* Left;
    struct TreeNode* Right;
}NODE,*LPNODE,*LPTREE;

/* 递归创建树 */
void createTree(LPTREE* root)
{
    char userKey = '\0';
    scanf_s("%c",&userKey,1);
    if(userKey == '#')
    {
        *root = NULL;
    }
    else
    {
        *root = (LPTREE)malloc(sizeof(struct TreeNode));
        (*root)->Data = userKey;
        createTree(&(*root)->Left);
        createTree(&(*root)->Right);
    }
}

void PreOrderTraversal(LPTREE BT)
{
    if(BT)
    {
        printf("%c ",BT->Data);
        PreOrderTraversal(BT->Left);
        PreOrderTraversal(BT->Right);
    }
}

int main()
{
    LPTREE root = NULL;
    createTree(&root);
    printf("PreOrderTraversal:\n");
    PreOrderTraversal(root);
    printf("\n");
    return 0;
}

ABD###CE#F###
PreOrderTraversal:
A B D C E F

二叉树的遍历

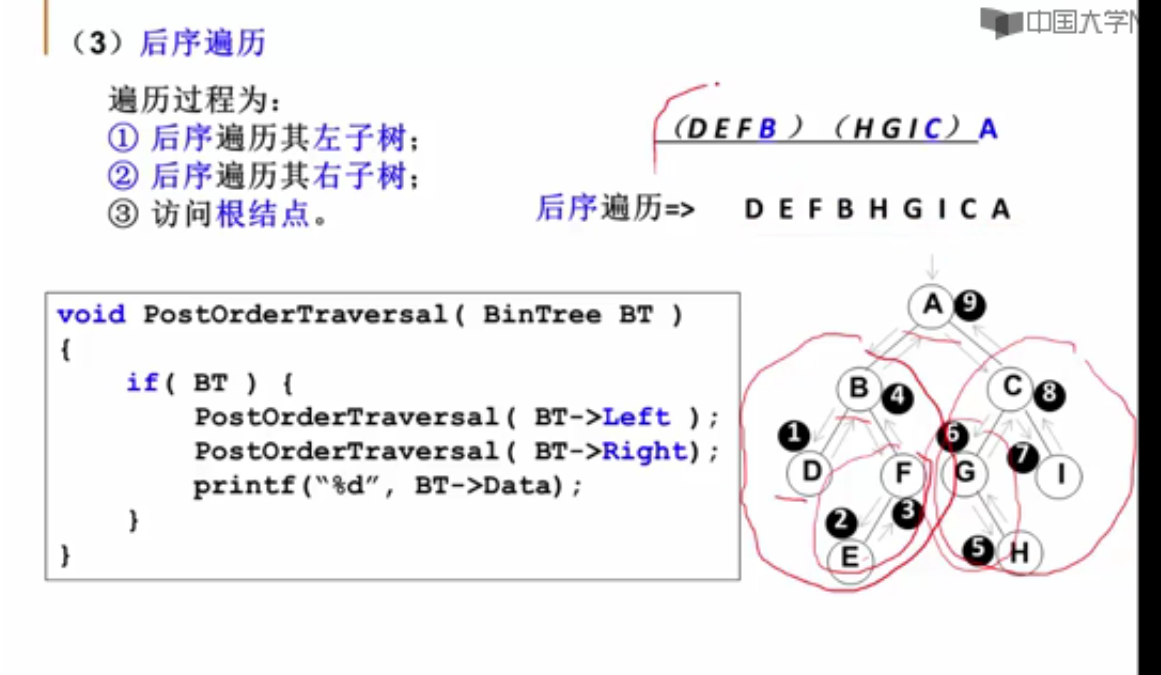
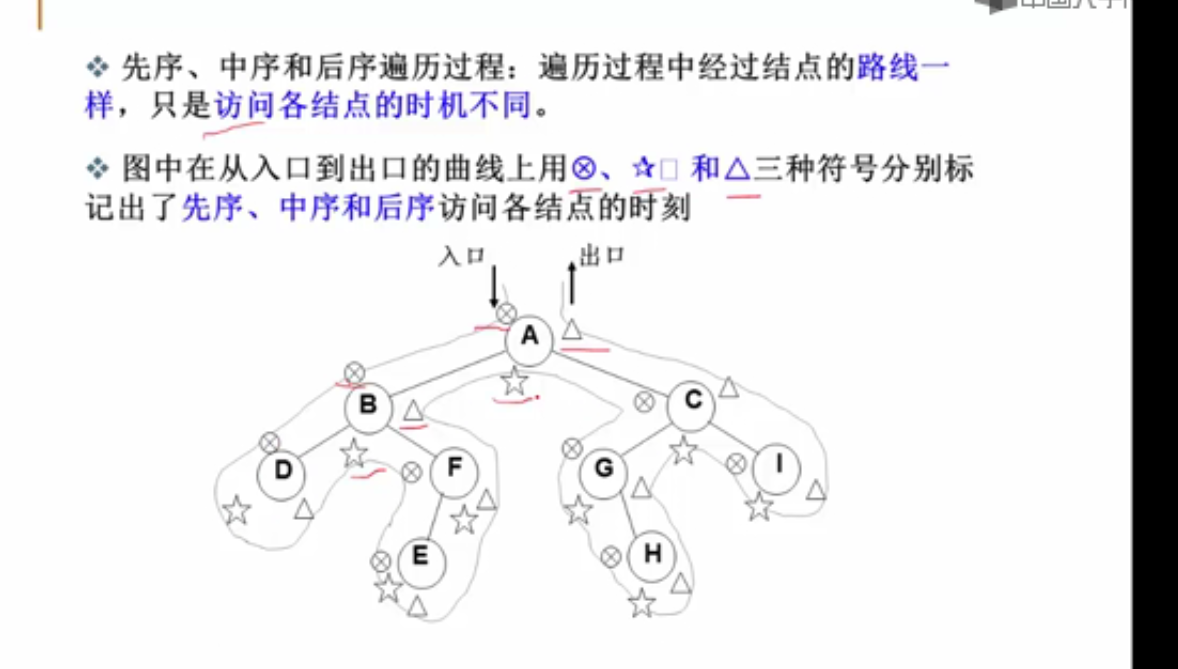
#include <stdio.h>
#include <stdlib.h>

typedef struct TreeNode *LPNODE;
typedef LPNODE BinTree;
typedef char ElementType;

struct TreeNode
{
    ElementType Data;
    BinTree Left;
    BinTree Right;
};

LPNODE CreateNode(ElementType Data)
{
    LPNODE newNode = (LPNODE)malloc(sizeof(struct TreeNode));
    newNode->Left = NULL;
    newNode->Right = NULL;
    newNode->Data = Data;
    return newNode;
}

void InsertNode(BinTree parent, LPNODE Left, LPNODE Right)
{
    parent->Left = Left;
    parent->Right = Right;
}

void PreOrderTraversal(BinTree BT)
{
    if(BT)
    {
        printf("%c ",BT->Data);
        PreOrderTraversal(BT->Left);
        PreOrderTraversal(BT->Right);
    }
}

void PreOrderTraversalByStack(BinTree BT)
{
    if(BT == NULL)
        return;
    LPNODE pMove = BT;
    LPNODE stack[100];
    int stackTop = -1;
    while(stackTop != -1 || pMove)
    {
        while(pMove)
        {
            printf("%c ",pMove->Data);
            stack[++stackTop] = pMove;
            pMove = pMove->Left;
        }
        if(stackTop != -1)
        {
            pMove = stack[stackTop--];
            pMove = pMove->Right;
        }
    }

}

void InOrderTraversal(BinTree BT)
{
    if(BT)
    {
        InOrderTraversal(BT->Left);
        printf("%c ",BT->Data);
        InOrderTraversal(BT->Right);
    }
}

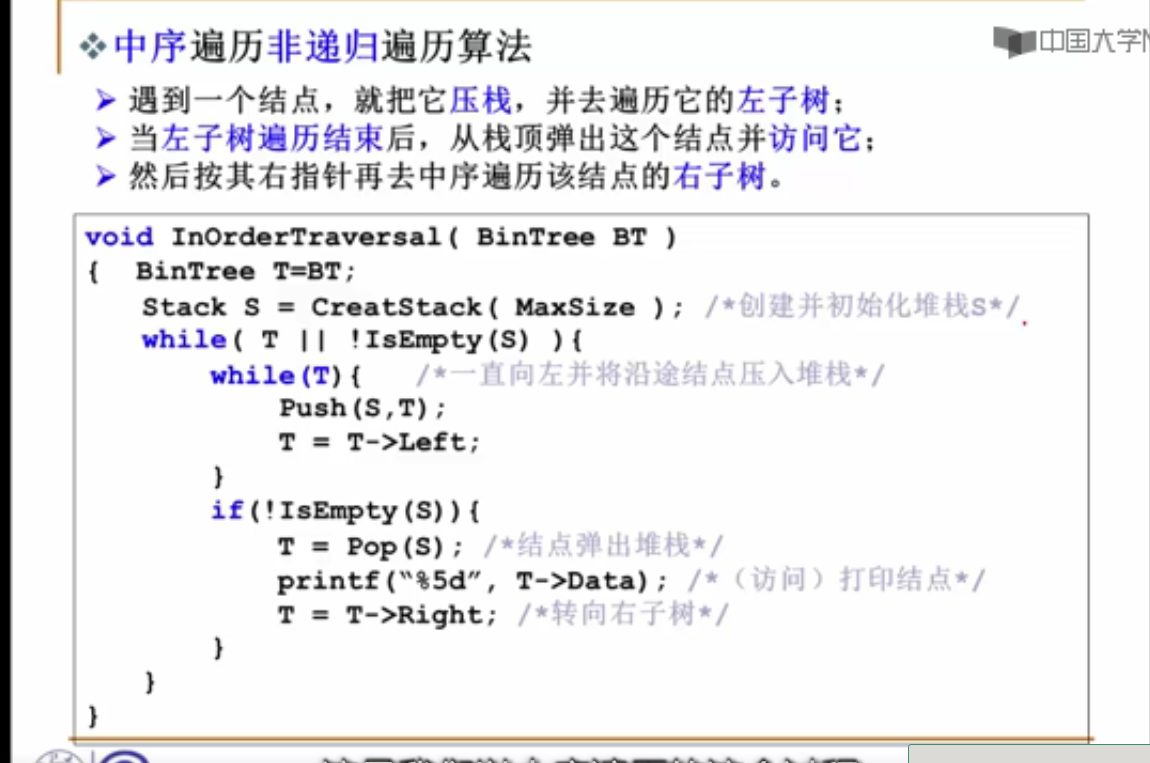
void InOrderTraversalByStack(BinTree BT)
{
    if(BT == NULL)
        return;
    LPNODE pMove = BT;
    LPNODE stack[100];
    int stackTop = -1;
    while(stackTop != -1 || pMove)
    {
        while(pMove)
        {
            stack[++stackTop] = pMove;
            pMove = pMove->Left;
        }
        if(stackTop != -1)
        {
            pMove = stack[stackTop--];
            printf("%c ",pMove->Data);
            pMove = pMove->Right;
        }
    }

}

void PostOrderTraversal(BinTree BT)
{
    if(BT)
    {
        PostOrderTraversal(BT->Left);
        PostOrderTraversal(BT->Right);
        printf("%c ",BT->Data);
    }
}

void PostOrderTraversalByStack(BinTree BT)
{
    if(BT == NULL)
        return;
    LPNODE pMove = BT;
    LPNODE stack[100];
    int stackTop = -1;
    LPNODE placeVisited = NULL;

    while(pMove)
    {
        stack[++stackTop] = pMove;
        pMove = pMove->Left;
    }

    while(stackTop != -1)
    {
        pMove = stack[stackTop--];
        if(pMove->Right == NULL || pMove->Right == placeVisited)
        {
            printf("%c ",pMove->Data);
            placeVisited = pMove;
        }
        else
        {
            stack[++stackTop] = pMove;
            pMove = pMove->Right;
            while(pMove)
            {
                stack[++stackTop] = pMove;
                pMove = pMove->Left;
            }
        }
    }

}

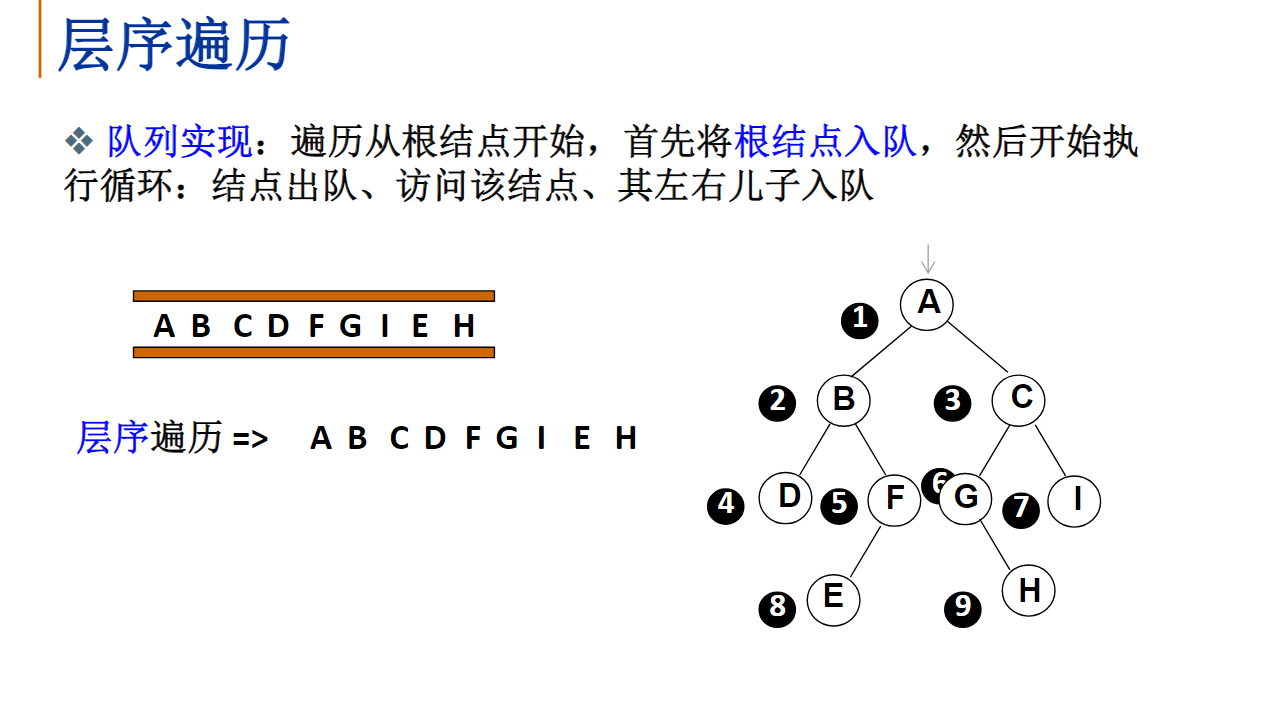
void LevelTraversal(BinTree BT)
{
    LPNODE pMove = BT;
    LPNODE queue[100];
    int front = 0;
    int tail = 0;
    queue[tail++] = pMove;
    printf("%c ",pMove->Data);
    while(front != tail)
    {
        pMove = queue[front++];
        if(pMove->Left != NULL)
        {
            queue[tail++] = pMove->Left;
            printf("%c ",pMove->Left->Data);
        }
        if(pMove->Right != NULL)
        {
            queue[tail++] = pMove->Right;
            printf("%c ",pMove->Right->Data);
        }

    }

}

int main()
{
    LPNODE A = CreateNode('A');
    LPNODE B = CreateNode('B');
    LPNODE C = CreateNode('C');
    LPNODE D = CreateNode('D');
    LPNODE E = CreateNode('E');
    LPNODE F = CreateNode('F');
    InsertNode(A,B,C);
    InsertNode(B,D,NULL);
    InsertNode(C,E,NULL);
    InsertNode(E,NULL,F);
    printf("PreOrderTraversal:\n");
    PreOrderTraversal(A);
    printf("\nPreOrderTraversalByStack:\n");
    PreOrderTraversalByStack(A);
    printf("\nInOrderTraversal:\n");
    InOrderTraversal(A);
    printf("\nInOrderTraversalByStack:\n");
    InOrderTraversalByStack(A);
    printf("\nPostOrderTraversal:\n");
    PostOrderTraversal(A);
    printf("\nPostOrderTraversalByStack:\n");
    PostOrderTraversalByStack(A);
    printf("\nLevelTraversal:\n");
    LevelTraversal(A);
    printf("\n");
    return 0;
}

PreOrderTraversal:
A B D C E F
PreOrderTraversalByStack:
A B D C E F
InOrderTraversal:
D B A E F C
InOrderTraversalByStack:
D B A E F C
PostOrderTraversal:
D B F E C A
PostOrderTraversalByStack:
D B F E C A
LevelTraversal:
A B C D E F

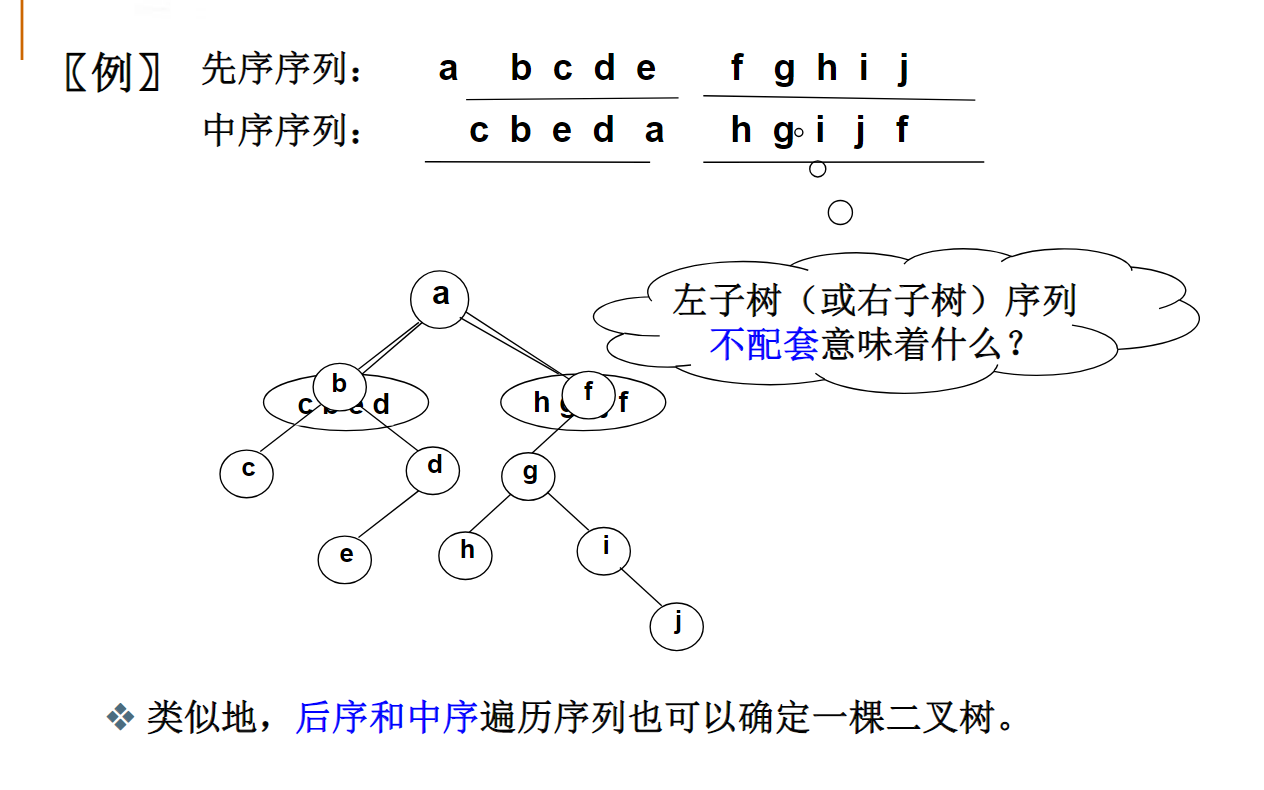
1.假定只有四个结点A、B、C、D的二叉树，其前序遍历序列为ABCD，则下面哪个序列是不可能的中序遍历序列？

A.ABCD

B.ACDB

C.DCBA

D.DABC

正确答案：D你选对了

2对于二叉树，如果其中序遍历结果与前序遍历结果一样，那么可以断定该二叉树________

A.是完全二叉树

B.所有结点都没有左儿子

C.所有结点都没有右儿子

D.这样的树不存在

正确答案：B你选对了

3已知一二叉树的后序和中序遍历的结果分别是FDEBGCA 和FDBEACG,那么该二叉树的前序遍历结果是什么？

A.ABDFECG

B.ABDEFCG

C.ABDFEGC

D.ABCDEFG

正确答案：A你选对了