MOOC-PTA线性结构题目
- PTA 02-线性结构1 两个有序链表序列的合并
- PTA02-线性结构2 一元多项式的乘法与加法运算
- PTA 02-线性结构3 Reversing Linked List
- PTA 02-线性结构4 Pop Sequence
PTA 02-线性结构1 两个有序链表序列的合并
本题要求实现一个函数,将两个链表表示的递增整数序列合并为一个非递减的整数序列。
函数接口定义:
List Merge( List L1, List L2 );
其中List结构定义如下:
typedef struct Node *PtrToNode;
struct Node {
ElementType Data; /* 存储结点数据 */
PtrToNode Next; /* 指向下一个结点的指针 */
};
typedef PtrToNode List; /* 定义单链表类型 */
L1和L2是给定的带头结点的单链表,其结点存储的数据是递增有序的;函数Merge要将L1和L2合并为一个非递减的整数序列。应直接使用原序列中的结点,返回归并后的带头结点的链表头指针。
裁判测试程序样例:
#include <stdio.h>
#include <stdlib.h>
typedef int ElementType;
typedef struct Node *PtrToNode;
struct Node {
ElementType Data;
PtrToNode Next;
};
typedef PtrToNode List;
List Read(); /* 细节在此不表 */
void Print( List L ); /* 细节在此不表;空链表将输出NULL */
List Merge( List L1, List L2 );
int main()
{
List L1, L2, L;
L1 = Read();
L2 = Read();
L = Merge(L1, L2);
Print(L);
Print(L1);
Print(L2);
return 0;
}
/* 你的代码将被嵌在这里 */
输入样例:
3
1 3 5
5
2 4 6 8 10
输出样例:
1 2 3 4 5 6 8 10
NULL
NULL
能AC的代码如下:
List Merge( List L1, List L2 )
{
if(L1 == NULL || L2 == NULL)
return (L1 == NULL)?L2:L1;
List head = (List)malloc(sizeof(struct Node));
List cur1 = L1->Next;
List cur2 = L2->Next;
List pre = head;
while(cur1 != NULL && cur2 != NULL)
{
if(cur1->Data <= cur2->Data)
{
pre->Next = cur1;
cur1 = cur1->Next;
}
else
{
pre->Next = cur2;
cur2 = cur2->Next;
}
pre = pre->Next;
}
pre->Next = (cur1 != NULL)?cur1:cur2;
L1->Next = NULL;
L2->Next = NULL;
return head;
}
PTA02-线性结构2 一元多项式的乘法与加法运算
设计函数分别求两个一元多项式的乘积与和。
输入格式:
输入分2行,每行分别先给出多项式非零项的个数,再以指数递降方式输入一个多项式非零项系数和指数(绝对值均为不超过1000的整数)。数字间以空格分隔。
输出格式:
输出分2行,分别以指数递降方式输出乘积多项式以及和多项式非零项的系数和指数。数字间以空格分隔,但结尾不能有多余空格。零多项式应输出0 0。
输入样例:
4 3 4 -5 2 6 1 -2 0
3 5 20 -7 4 3 1
输出样例:
15 24 -25 22 30 21 -10 20 -21 8 35 6 -33 5 14 4 -15 3 18 2 -6 1
5 20 -4 4 -5 2 9 1 -2 0




如果当前p1指向项的(系数,指数)为(2,4),同时P2指向项为(2,6),那么循环中的switch是执行case -1。


#include <stdio.h>
#include <stdlib.h>
typedef struct PolyNode *Polynomial;
struct PolyNode
{
int coef;
int expon;
Polynomial link;
};
Polynomial ReadPoly()
{
Polynomial P,Rear,temp;
int n,e,c;
scanf("%d",&n);
P = (Polynomial)malloc(sizeof(struct PolyNode));
P->link = NULL;
Rear = P;
while(n--)
{
scanf("%d %d",&c,&e);
Attach(c,e,&Rear);
}
temp = P;
P = P->link;
free(temp);
return P;
}
void Attach(int c,int e,Polynomial *pRear)
{
Polynomial P = (Polynomial)malloc(sizeof(struct PolyNode));
P->coef = c;
P->expon = e;
P->link = NULL;
(*pRear)->link = P;
*pRear = P;
}
int Compare(int a,int b)
{
if(a>b)
return 1;
else if(a<b)
return -1;
else
return 0;
}
/*
Polynomial AddPoly(Polynomial P1,Polynomial P2)
{
Polynomial front,rear,temp;
int sum = 0;
rear = (Polynomial)malloc(sizeof(struct PolyNode));
front = rear;
while(P1&&P2)
{
switch(Compare(P1->expon,P2->expon))
{
case 1:
Attach(P1->coef,P1->expon,&rear);
P1 = P1->link;
break;
case -1:
Attach(P2->coef,P2->expon,&rear);
P2 = P2->link;
break;
case 0:
sum = P1->coef + P2->coef;
if(sum)
Attach(sum,P1->expon,&rear);
P1 = P1->link;
P2 = P2->link;
break;
}
for(;P1;P1 = P1->link)
Attach(P1->coef,P1->expon,&rear);
for(;P2;P2 = P2->link)
Attach(P2->coef,P2->expon,&rear);
rear->link = NULL;
temp = front;
front = front->link;
free(temp);
return front;
}
}
*/
Polynomial AddPoly(Polynomial P1,Polynomial P2)
{
Polynomial t1,t2,P,Rear,temp;
int sum;
t1 = P1;
t2 = P2;
P = (Polynomial)malloc(sizeof(struct PolyNode));
P->link = NULL;
Rear = P;
while(t1&&t2)
{
if(t1->expon == t2->expon)
{
sum = t1->coef + t2->coef;
if(sum)
Attach(sum,t1->expon,&Rear);
t1 = t1->link;
t2 = t2->link;
}
else if(t1->expon > t2->expon)
{
Attach(t1->coef,t1->expon,&Rear);
t1 = t1->link;
}
else
{
Attach(t2->coef,t2->expon,&Rear);
t2 = t2->link;
}
}
while(t1)
{
Attach(t1->coef,t1->expon,&Rear);
t1 = t1->link;
}
while(t2)
{
Attach(t2->coef,t2->expon,&Rear);
t2 = t2->link;
}
Rear->link = NULL;
temp = P;
P = P->link;
free(temp);
return P;
}
Polynomial MultPoly(Polynomial P1,Polynomial P2)
{
Polynomial t1,t2,temp,P,Rear;
int c,e;
if(!P1 || !P2)
return NULL;
t1 = P1;
t2 = P2;
P = (Polynomial)malloc(sizeof(struct PolyNode));
P->link = NULL;
Rear = P;
while(t2)
{
Attach(t1->coef * t2->coef,t1->expon + t2->expon,&Rear);
t2 = t2->link;
}
t1 = t1->link;
while(t1)
{
t2 = P2;
Rear = P;
while(t2)
{
e = t1->expon + t2->expon;
c = t1->coef * t2->coef;
while(Rear->link && Rear->link->expon > e)
Rear = Rear->link;
if(Rear->link && Rear->link->expon == e)
{
if(Rear->link->coef + c)
Rear->link->coef += c;
else
{
temp = Rear->link;
Rear->link = temp->link;
free(temp);
}
}
else
{
temp = (Polynomial)malloc(sizeof(struct PolyNode));
temp->coef = c;
temp->expon = e;
temp->link = Rear->link;
Rear->link = temp;
Rear = Rear->link;
}
t2 = t2->link;
}
t1 = t1->link;
}
t2 = P;
P = P->link;
free(t2);
return P;
}
void PrintPoly(Polynomial P)
{
int flag = 0;
if(!P)
{
printf("0 0\n");
return;
}
while(P)
{
if(!flag)
flag = 1;
else
printf(" ");
printf("%d %d",P->coef,P->expon);
P = P->link;
}
printf("\n");
}
int main()
{
Polynomial P1,P2,PP,PS;
P1 = ReadPoly();
P2 = ReadPoly();
PP = MultPoly(P1,P2);
PrintPoly(PP);
PS = AddPoly(P1,P2);
PrintPoly(PS);
return 0;
}
PTA 02-线性结构3 Reversing Linked List
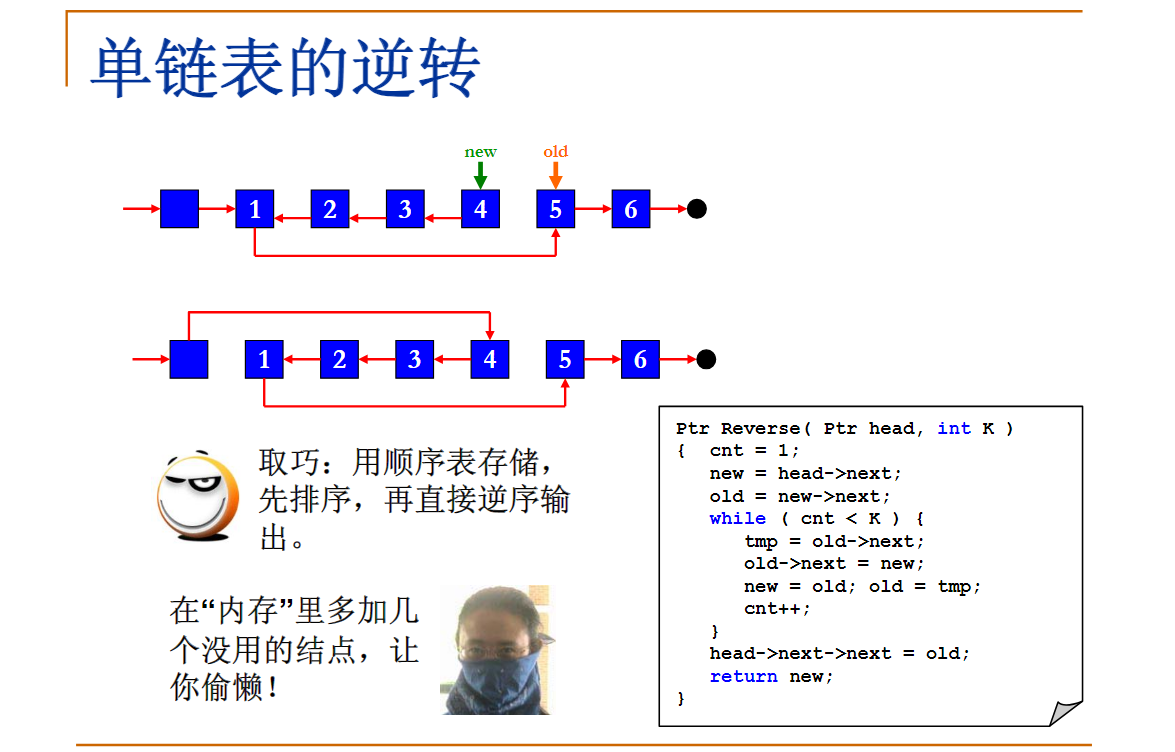
Given a constant K and a singly linked list L, you are supposed to reverse the links of every K elements on L. For example, given L being 1→2→3→4→5→6, if K=3, then you must output 3→2→1→6→5→4; if K=4, you must output 4→3→2→1→5→6.
Input Specification:
Each input file contains one test case. For each case, the first line contains the address of the first node, a positive N (≤105) which is the total number of nodes, and a positive K (≤N) which is the length of the sublist to be reversed. The address of a node is a 5-digit nonnegative integer, and NULL is represented by -1.
Then N lines follow, each describes a node in the format:
Address Data Next
where Address is the position of the node, Data is an integer, and Next is the position of the next node.
Output Specification:
For each case, output the resulting ordered linked list. Each node occupies a line, and is printed in the same format as in the input.
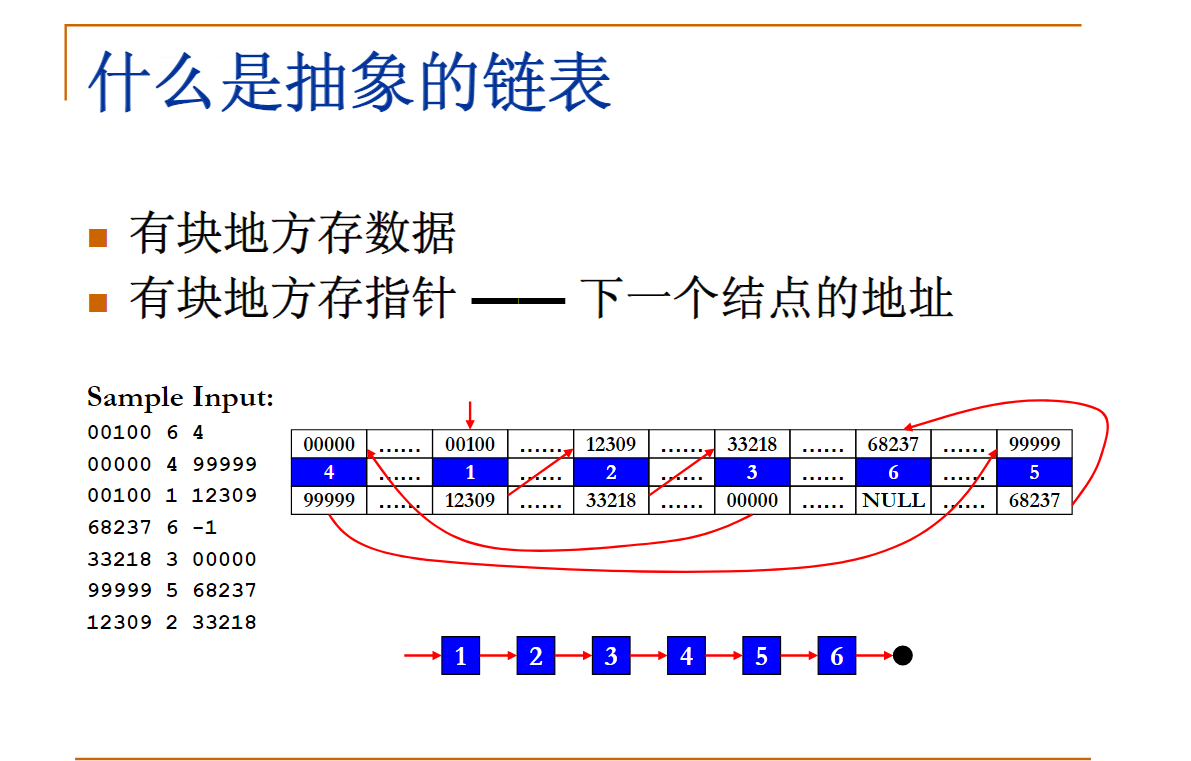
Sample Input:
00100 6 4
00000 4 99999
00100 1 12309
68237 6 -1
33218 3 00000
99999 5 68237
12309 2 33218
Sample Output:
00000 4 33218
33218 3 12309
12309 2 00100
00100 1 99999
99999 5 68237
68237 6 -1

#include <stdio.h>
#include <stdlib.h>
typedef int Address;
typedef int Data;
typedef struct Node *Ptr;
#define MaxSize 100001
struct Node
{
Data data;
Address next;
}Nodes[MaxSize];
int List[MaxSize];
void Reverse(Address head, Address tail)
{
int tempHead = head;
int tempTail = tail;
int list;
while(tempTail > tempHead)
{
list = List[tempHead];
List[tempHead] = List[tempTail];
List[tempTail] = list;
tempHead++;
tempTail--;
}
}
int main()
{
int n;
Address root;
int K;
scanf("%d %d %d",&root,&n,&K);
Address address;
Data data;
Address next;
for(int i=0; i<n; i++)
{
scanf("%d %d %d", &address,&data,&next);
Nodes[address].data = data;
Nodes[address].next = next;
}
int maxn = 0;
int pMove = root;
while(pMove != -1)
{
List[maxn++] = pMove;
pMove = Nodes[pMove].next;
}
int i = 0;
while(i + K < maxn)
{
Reverse(i,i+K-1);
i = i + K;
}
for(i=0;i<maxn-1;i++)
printf("%05d %d %05d\n",List[i],Nodes[List[i]].data,List[i+1]);
printf("%05d %d -1\n",List[i],Nodes[List[i]].data);
return 0;
}
使用C++的reverse函数解法如下:
#include<iostream>
#include<stdio.h>
#include<algorithm> ///使用到reverse 翻转函数
using namespace std;
#define MAXSIZE 1000010 ///最大为五位数的地址
struct node ///使用顺序表存储data和下一地址next
{
int data;
int next;
}node[MAXSIZE];
int List[MAXSIZE]; ///存储可以连接上的顺序表
int main()
{
int First, n, k;
cin>>First>>n>>k; ///输入头地址 和 n,k;
int Address,Data,Next;
for(int i=0;i<n;i++)
{
cin>>Address>>Data>>Next;
node[Address].data=Data;
node[Address].next=Next;
}
int j=0; ///j用来存储能够首尾相连的节点数
int p=First; ///p指示当前结点
while(p!=-1)
{
List[j++]=p;
p=node[p].next;
}
int i=0;
while(i+k<=j) ///每k个节点做一次翻转
{
reverse(&List[i],&List[i+k]);
i=i+k;
}
for(i=0;i<j-1;i++)
printf("%05d %d %05d\n",List[i],node[List[i]].data,List[i+1]);
printf("%05d %d -1\n",List[i],node[List[i]].data);
return 0;
}
PTA 02-线性结构4 Pop Sequence
Given a stack which can keep M numbers at most. Push N numbers in the order of 1, 2, 3, ..., N and pop randomly. You are supposed to tell if a given sequence of numbers is a possible pop sequence of the stack. For example, if M is 5 and N is 7, we can obtain 1, 2, 3, 4, 5, 6, 7 from the stack, but not 3, 2, 1, 7, 5, 6, 4.
Input Specification:
Each input file contains one test case. For each case, the first line contains 3 numbers (all no more than 1000): M (the maximum capacity of the stack), N (the length of push sequence), and K (the number of pop sequences to be checked). Then K lines follow, each contains a pop sequence of N numbers. All the numbers in a line are separated by a space.
Output Specification:
For each pop sequence, print in one line "YES" if it is indeed a possible pop sequence of the stack, or "NO" if not.
Sample Input:
5 7 5 1 2 3 4 5 6 7 3 2 1 7 5 6 4 7 6 5 4 3 2 1 5 6 4 3 7 2 1 1 7 6 5 4 3 2
Sample Output:
YES
NO
NO
YES
NO
#include <stdio.h>
#include <stdlib.h>
#define Maxsize 1000//最大容量
typedef struct Node
{
int Top;//栈顶
int Data[Maxsize];//元素
int Capacity;//容量
}*Stack;
int Test(int Array[],int M,int N)
{
int count = 0;
Stack Pile = (Stack)malloc(sizeof(struct Node));//申请并初始化一个空栈
Pile->Capacity = M;
Pile->Top = -1;
for(int i = 1;i <= N;i++)
{
if(Pile->Capacity == Pile->Top+1)//栈满
return 0;
else
Pile->Data[++Pile->Top] = i;//入栈
while(Pile->Data[Pile->Top] == Array[count])
{//比较栈顶是否与某数相等
Pile->Top--;//出栈
count++;//数组往后移位
}
}
if(count == N)//全部找到并且输出时
return 1;
else
return 0;
}
int main()
{
int M,N,K;
scanf("%d %d %d",&M,&N,&K);
int Array[N];
for(int i=0; i<K; i++)
{
for(int j=0; j<N; j++)
{
scanf("%d",&Array[j]);
}
if(Test(Array,M,N))
printf("YES\n");
else
printf("NO\n");
}
return 0;
}