MOOC-PTA树题目
- PTA 03-树1 树的同构
- PTA 03-树2 List Leaves
- PTA 03-树3 Tree Traversals Again
- PTA 04-树4 是否同一棵二叉搜索树
- PTA 04-树5 Root of AVL Tree
- PTA 04-树6 Complete Binary Search Tree
- PTA 04-树7 二叉搜索树的操作集
- PTA 05-树7 堆中的路径
- PTA 05-树8 File Transfer
- PTA 05-树9 Huffman Codes
PTA 03-树1 树的同构
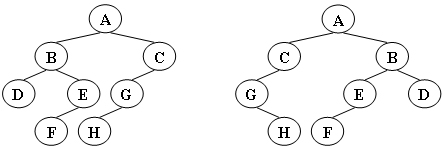
给定两棵树T1和T2。如果T1可以通过若干次左右孩子互换就变成T2,则我们称两棵树是“同构”的。例如图1给出的两棵树就是同构的,因为我们把其中一棵树的结点A、B、G的左右孩子互换后,就得到另外一棵树。而图2就不是同构的。
 |
|---|
| 图1 |
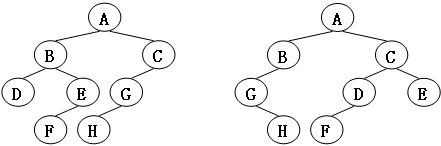 |
| 图2 |
现给定两棵树,请你判断它们是否是同构的。
输入格式:
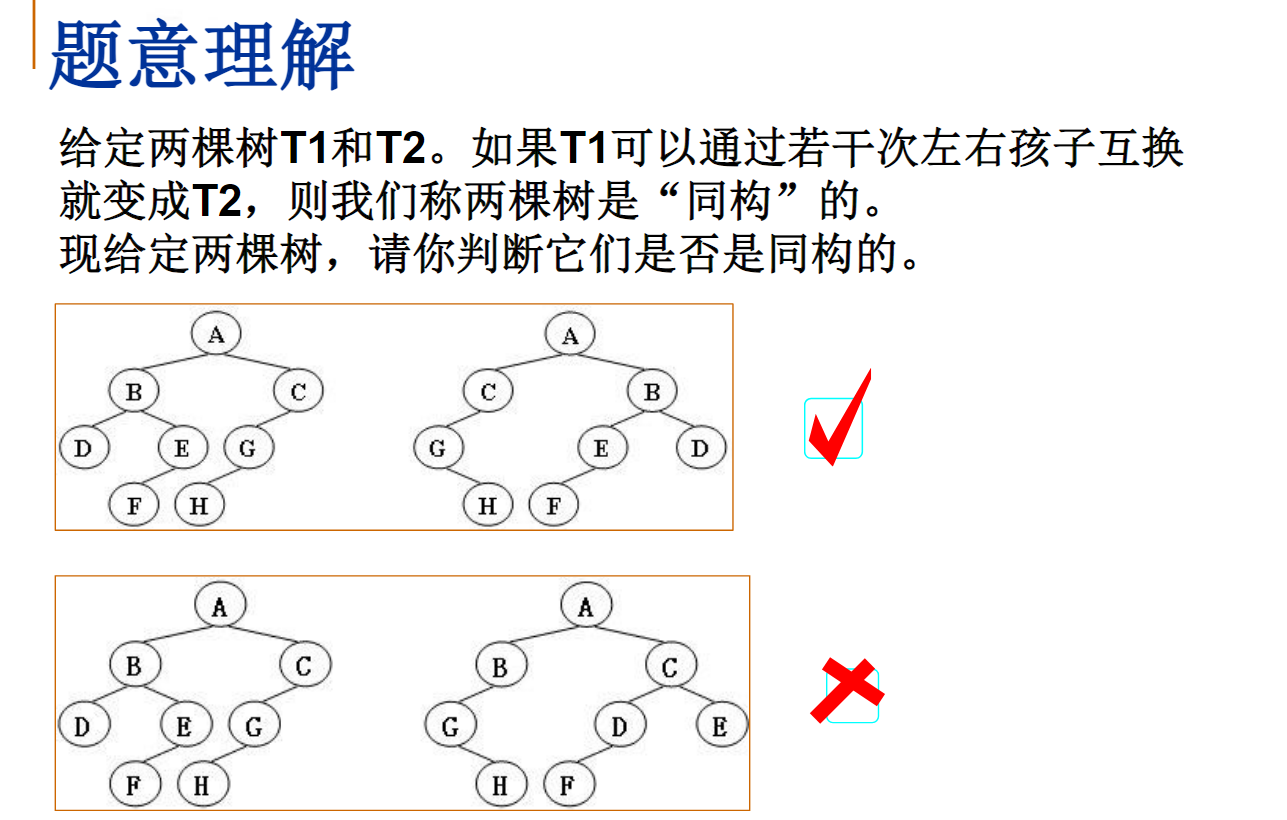
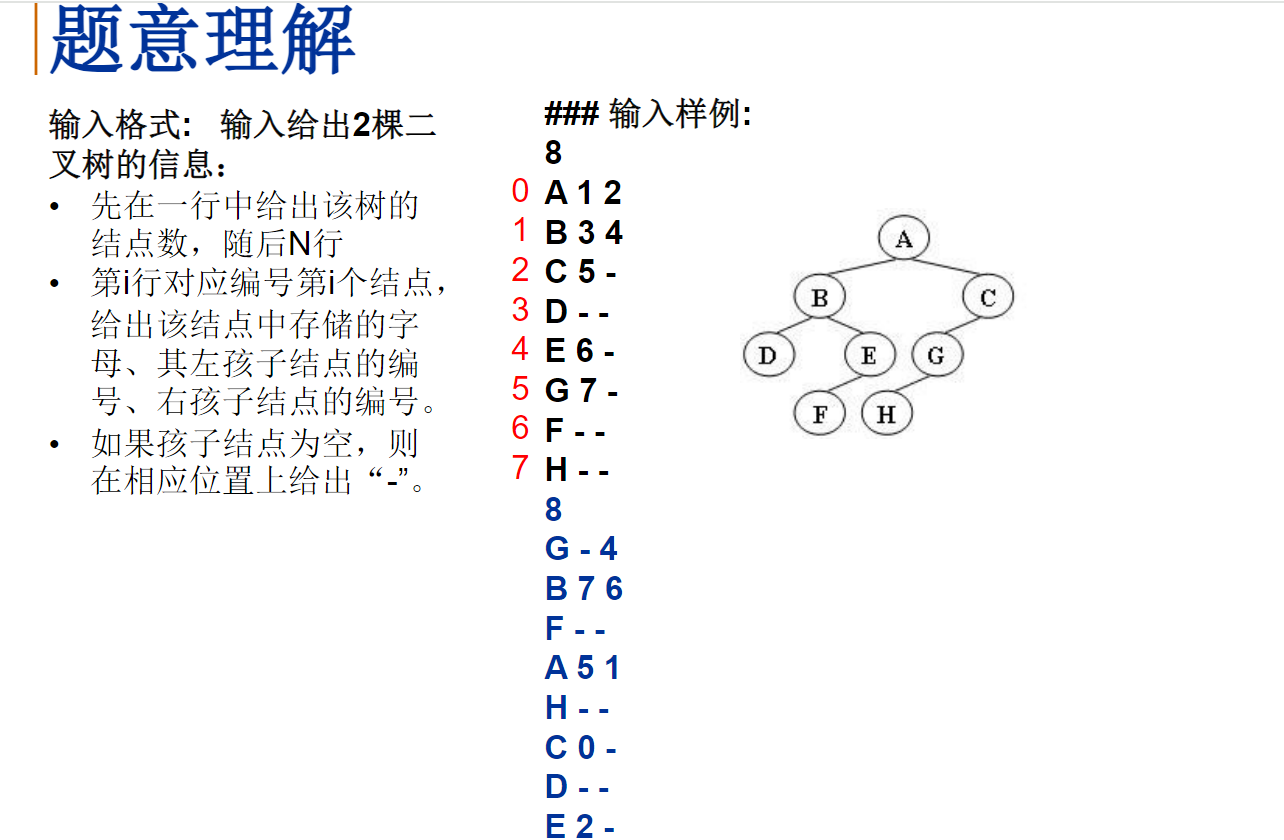
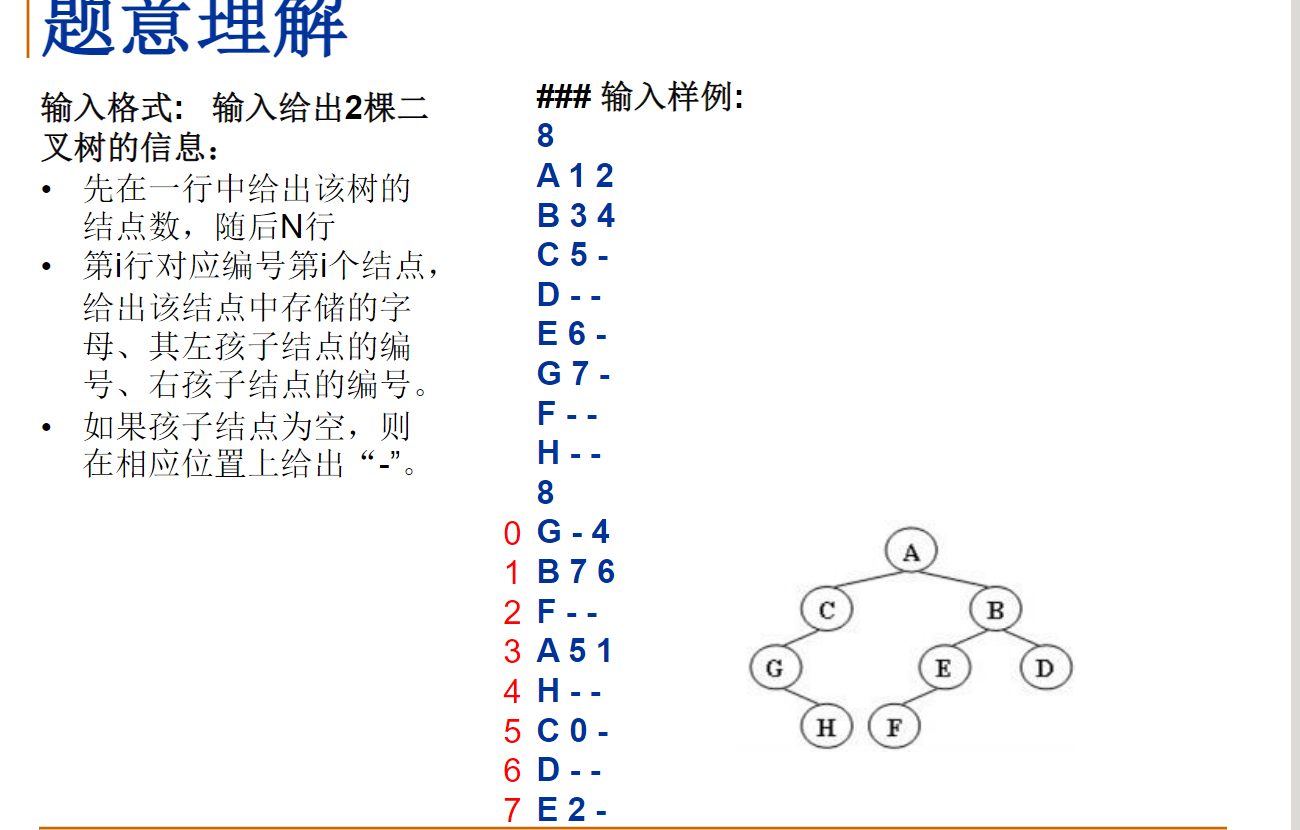
输入给出2棵二叉树树的信息。对于每棵树,首先在一行中给出一个非负整数N (≤10),即该树的结点数(此时假设结点从0到N−1编号);随后N行,第i行对应编号第i个结点,给出该结点中存储的1个英文大写字母、其左孩子结点的编号、右孩子结点的编号。如果孩子结点为空,则在相应位置上给出“-”。给出的数据间用一个空格分隔。注意:题目保证每个结点中存储的字母是不同的。
输出格式:
如果两棵树是同构的,输出“Yes”,否则输出“No”。
输入样例1(对应图1):
8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -
输出样例1:
Yes
输入样例2(对应图2):
8
B 5 7
F - -
A 0 3
C 6 -
H - -
D - -
G 4 -
E 1 -
8
D 6 -
B 5 -
E - -
H - -
C 0 2
G - 3
F - -
A 1 4
输出样例2:
No
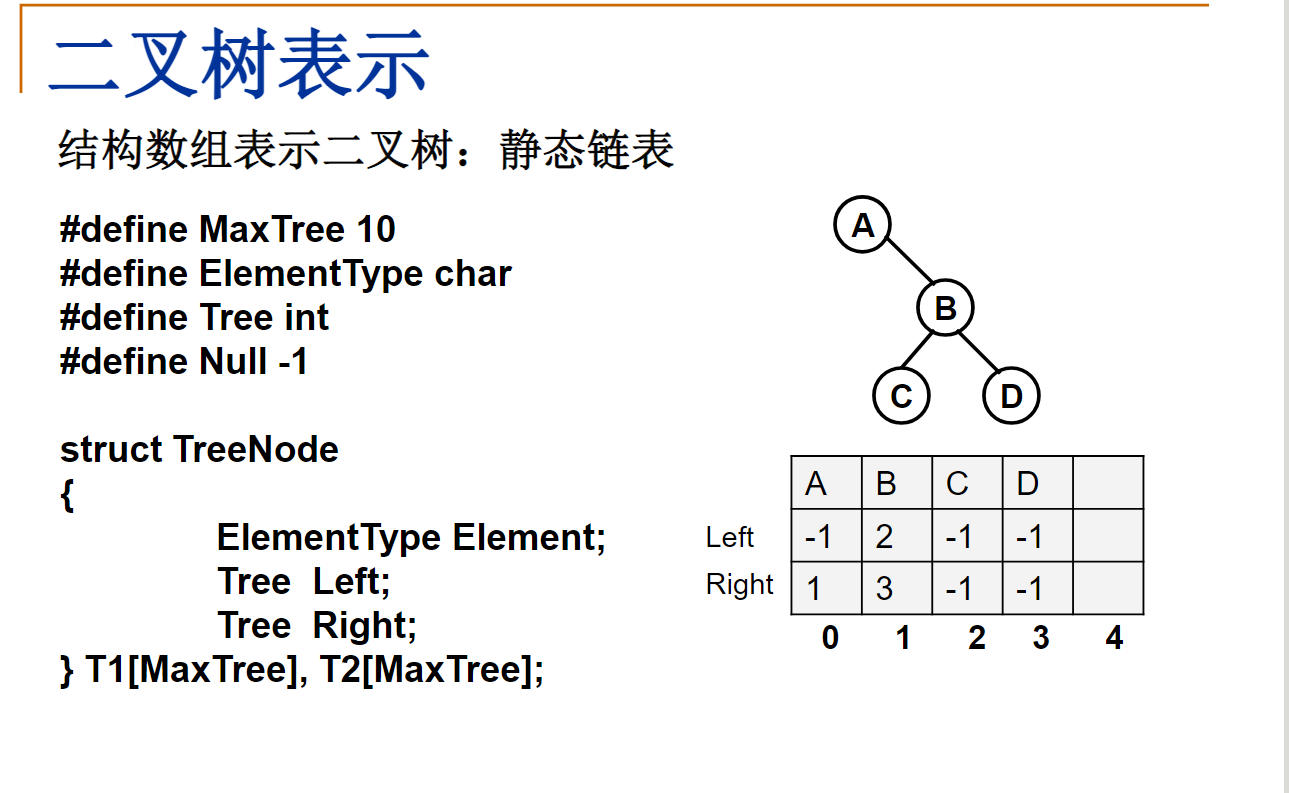






#include <stdio.h>
#include <stdlib.h>
#define MaxSize 10
#define Null -1
#define ElementType char
#define Tree int
struct TreeNode
{
ElementType Element;
Tree Left;
Tree Right;
}T1[MaxSize],T2[MaxSize];
Tree BuildTree(struct TreeNode T[])
{
int N;
int Root = 0;
scanf("%d",&N);
getchar();
if(N)
{
int check[MaxSize];
char cl,cr;
for(int i = 0;i < N;i++)
check[i] = 0;
for(int i = 0;i < N;i++)
{
scanf("%c %c %c\n",&T[i].Element,&cl,&cr);
if(cl != '-')
{
T[i].Left = cl - '0';
check[T[i].Left] = 1;
}
else
T[i].Left = Null;
if(cr != '-')
{
T[i].Right = cr - '0';
check[T[i].Right] = 1;
}
else
T[i].Right = Null;
//getchar();
}
for(int i = 0;i < N;i++)
if(!check[i])
{
Root = i;
break;
}
}
else
return Null;
return Root;
}
int Isomorphic(Tree R1,Tree R2)
{
if(R1 == Null && R2 == Null)
return 1;
if((R1 != Null && R2 == Null)||(R1 == Null && R2 != Null))
return 0;
if(T1[R1].Element != T2[R2].Element)
return 0;
if((T1[R1].Left == Null)&&T2[R2].Left == Null)
Isomorphic(T1[R1].Right,T2[R2].Right);
if((T1[R1].Left != Null)&&T2[R2].Left != Null && (T1[T1[R1].Left].Element) == (T2[T2[R2].Left].Element))
return Isomorphic(T1[R1].Right,T2[R2].Right) && Isomorphic(T1[R1].Left,T2[R2].Left);
else
Isomorphic(T1[R1].Left,T2[R2].Right) && Isomorphic(T1[R1].Right,T2[R2].Left);
}
int main()
{
Tree R1,R2;
R1 = BuildTree(T1);
R2 = BuildTree(T2);
if(Isomorphic(R1,R2))
printf("Yes\n");
else
printf("No\n");
return 0;
}
PTA 03-树2 List Leaves
Given a tree, you are supposed to list all the leaves in the order of top down, and left to right.
Input Specification:
Each input file contains one test case. For each case, the first line gives a positive integer N (≤10) which is the total number of nodes in the tree -- and hence the nodes are numbered from 0 to N−1. Then N lines follow, each corresponds to a node, and gives the indices of the left and right children of the node. If the child does not exist, a "-" will be put at the position. Any pair of children are separated by a space.
Output Specification:
For each test case, print in one line all the leaves' indices in the order of top down, and left to right. There must be exactly one space between any adjacent numbers, and no extra space at the end of the line.
Sample Input:
8
1 -
- -
0 -
2 7
- -
- -
5 -
4 6
Sample Output:
4 1 5
#include <stdio.h>
#include <stdlib.h>
#define MAXTREE 10
typedef int Tree;
#define Null -1
struct TreeNode
{
Tree id;
Tree left;
Tree right;
}T[MAXTREE];
Tree BuildTree(struct TreeNode T[])
{
for(int i=0; i<MAXTREE; i++)
T[i].left = T[i].right = 0;
int N;
scanf("%d",&N);
getchar();
int check[MAXTREE];
for(int i=0; i<N; i++)
check[i] = 0;
char cl,cr;
for(int i=0; i<N; i++)
{
T[i].id = i;
scanf("%c %c\n",&cl,&cr);
if(cl != '-')
{
T[i].left = cl - '0';
check[T[i].left] = 1;
}
else
T[i].left = Null;
if(cr != '-')
{
T[i].right = cr - '0';
check[T[i].right] = 1;
}
else
T[i].right = Null;
}
Tree root;
for(int i=0; i<N; i++)
{
if(check[i] == 0)
{
root = i;
break;
}
}
return root;
}
void Traversal(struct TreeNode T[], Tree root)
{
Tree pMove = root;
Tree queue[MAXTREE];
int front = 0;
int rear = 0;
queue[rear++] = pMove;
int IsFirst = 1;
while(front != rear)
{
pMove = queue[front++];
if(T[pMove].left == Null && T[pMove].right == Null)
{
if(IsFirst)
{
printf("%d",T[pMove].id);
IsFirst = 0;
}
else
printf(" %d",T[pMove].id);
}
if(T[pMove].left != Null)
{
queue[rear++] = T[pMove].left;
}
if(T[pMove].right != Null)
{
queue[rear++] = T[pMove].right;
}
}
}
int main()
{
struct TreeNode T[MAXTREE];
Tree root = BuildTree(T);
Traversal(T, root);
return 0;
}
核心要点:
- 静态链表存储
- 读入数据创建相应的树,并找到相应的根节点
- 改造层次遍历
PTA 03-树3 Tree Traversals Again
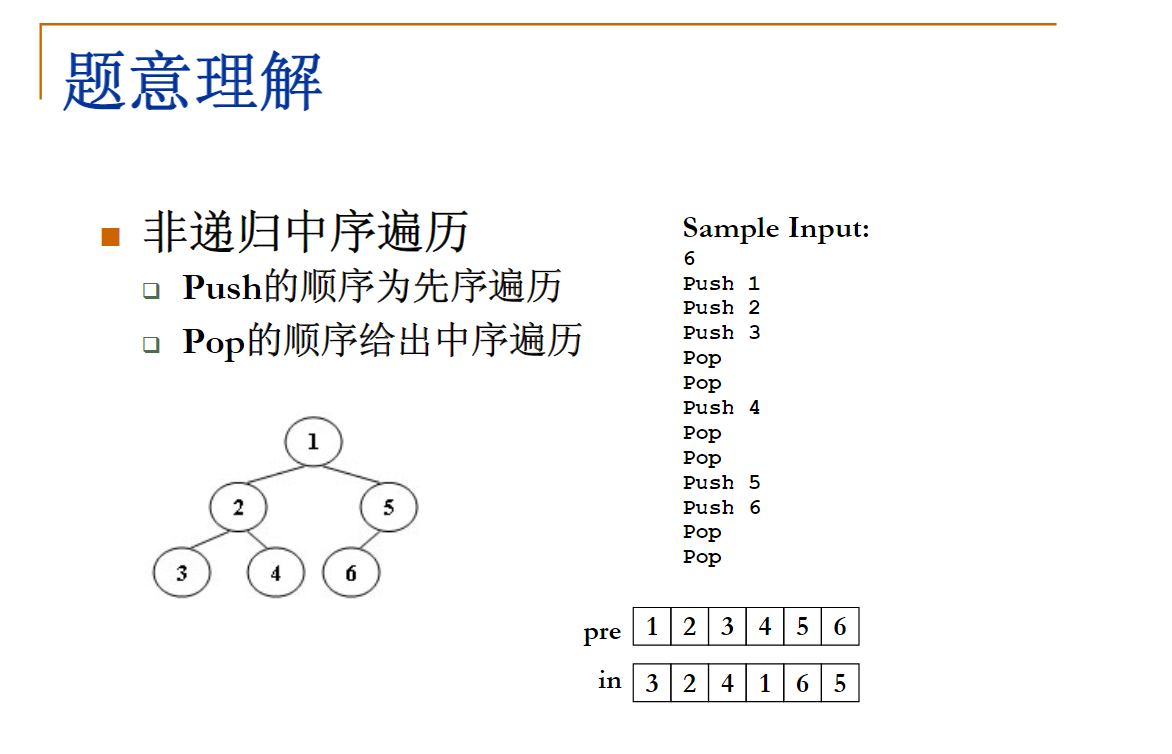
An inorder binary tree traversal can be implemented in a non-recursive way with a stack. For example, suppose that when a 6-node binary tree (with the keys numbered from 1 to 6) is traversed, the stack operations are: push(1); push(2); push(3); pop(); pop(); push(4); pop(); pop(); push(5); push(6); pop(); pop(). Then a unique binary tree (shown in Figure 1) can be generated from this sequence of operations. Your task is to give the postorder traversal sequence of this tree.
Input Specification:
Each input file contains one test case. For each case, the first line contains a positive integer N (≤30) which is the total number of nodes in a tree (and hence the nodes are numbered from 1 to N). Then 2N lines follow, each describes a stack operation in the format: "Push X" where X is the index of the node being pushed onto the stack; or "Pop" meaning to pop one node from the stack.
Output Specification:
For each test case, print the postorder traversal sequence of the corresponding tree in one line. A solution is guaranteed to exist. All the numbers must be separated by exactly one space, and there must be no extra space at the end of the line.
Sample Input:
6
Push 1
Push 2
Push 3
Pop
Pop
Push 4
Pop
Pop
Push 5
Push 6
Pop
Pop
Sample Output:
3 4 2 6 5 1
在这一道题里面,把树的三种遍历——前序遍历、中序遍历和后序遍历全部都包括了,而且最重要的是,你根本就不需要建一棵树。
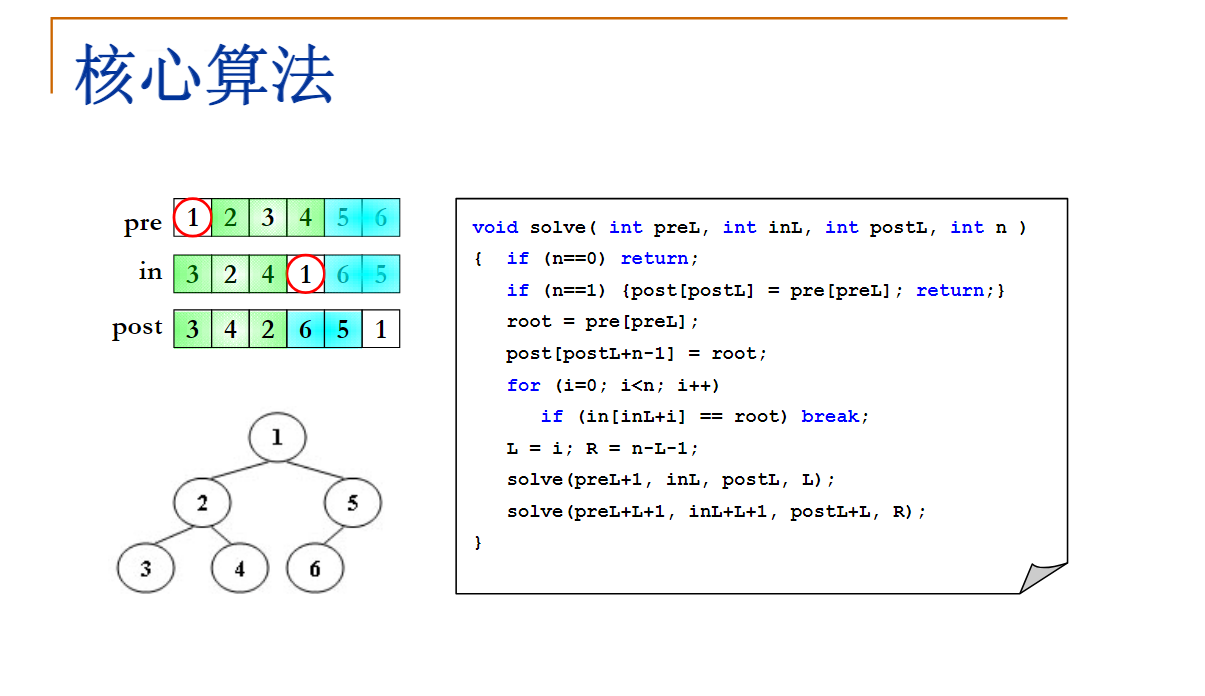
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define MAXSIZE 30
int pre[MAXSIZE];
int in[MAXSIZE];
int post[MAXSIZE];
void Solve(int preIndex, int inIndex, int postIndex, int N)
{
if(N == 0)
return;
if(N == 1)
{
post[postIndex] = pre[preIndex];
return;
}
int root = pre[preIndex];
post[postIndex+N-1] = root;
int L,R,i;
for(i=0; i<N; i++)
{
if(in[inIndex+i] == root)
break;
}
L = i;
R = N - L -1;
Solve(preIndex+1, inIndex, postIndex, L);
Solve(preIndex+1+L, inIndex+L+1, postIndex+L, R);
}
int main()
{
int N;
scanf("%d", &N);
for(int i=0; i<N; i++)
{
pre[i] = 0;
in[i] = 0;
post[i] = 0;
}
int preIndex = 0, inIndex = 0, postIndex = 0;
int stack[6];
int count = 0;
for(int i=0; i<N*2; i++)
{
char str[5];
scanf("%s",str);
if(strcmp(str,"Push") == 0)
{
int num;
scanf("%d\n",&num);
count++;
stack[count] = num;
pre[preIndex] = num;
preIndex++;
}
else if(strcmp(str,"Pop") == 0)
{
in[inIndex] = stack[count];
count--;
inIndex++;
}
}
Solve(0, 0, 0, N);
int First = 1;
for(int i=0; i<N; i++)
{
if(First)
{
printf("%d", post[i]);
First = 0;
}
else
printf(" %d", post[i]);
}
return 0;
}
核心要点:
- 读入字符串并比较
- 使用栈获得中序遍历相应数组
- 分治算法
- 递归结束条件要有n=0
PTA 04-树4 是否同一棵二叉搜索树
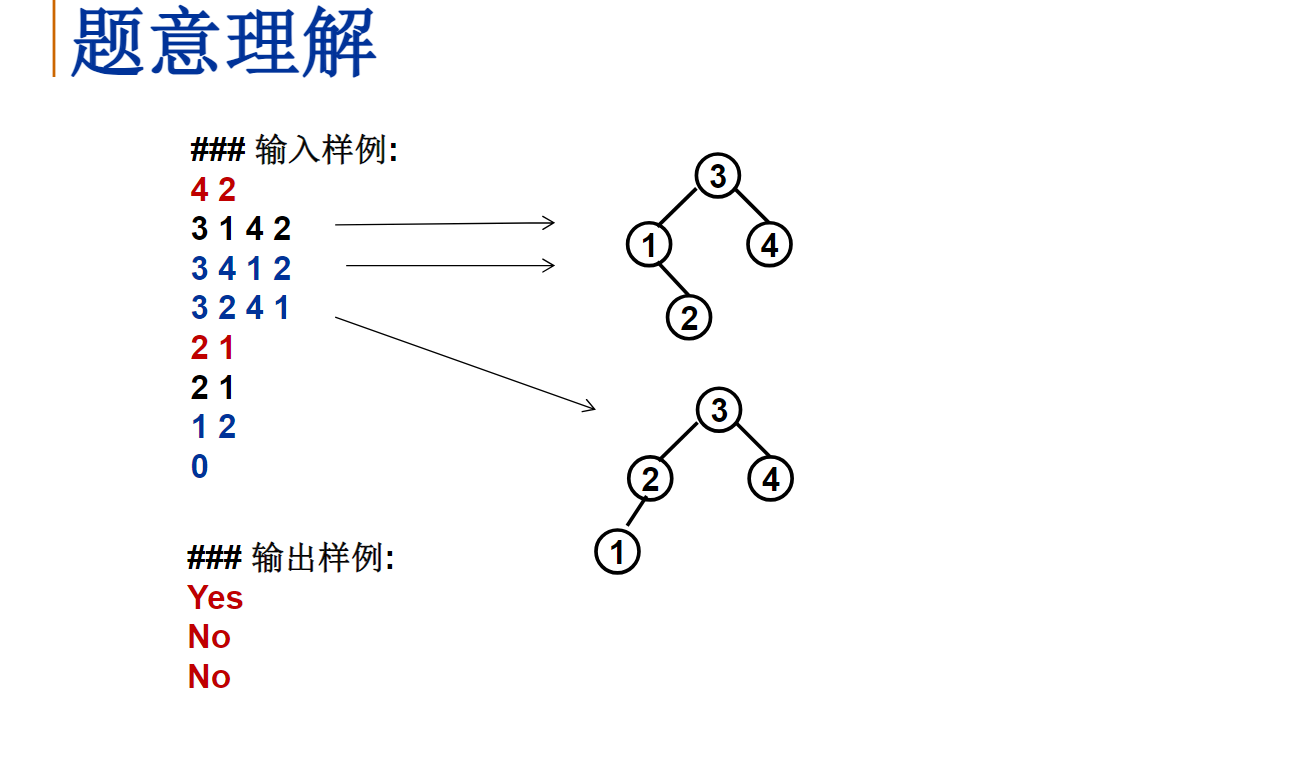
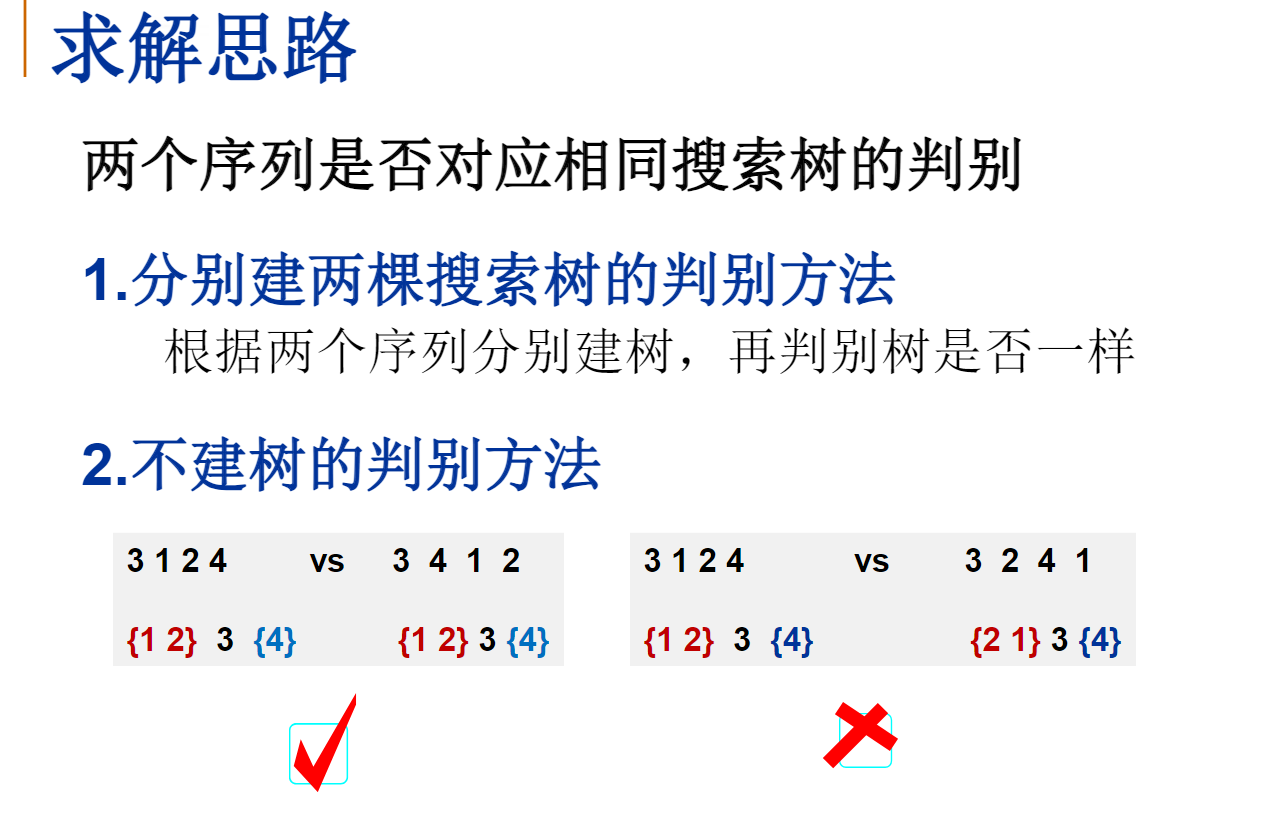
给定一个插入序列就可以唯一确定一棵二叉搜索树。然而,一棵给定的二叉搜索树却可以由多种不同的插入序列得到。例如分别按照序列{2, 1, 3}和{2, 3, 1}插入初始为空的二叉搜索树,都得到一样的结果。于是对于输入的各种插入序列,你需要判断它们是否能生成一样的二叉搜索树。
输入格式:
输入包含若干组测试数据。每组数据的第1行给出两个正整数N (≤10)和L,分别是每个序列插入元素的个数和需要检查的序列个数。第2行给出N个以空格分隔的正整数,作为初始插入序列。随后L行,每行给出N个插入的元素,属于L个需要检查的序列。
简单起见,我们保证每个插入序列都是1到N的一个排列。当读到N为0时,标志输入结束,这组数据不要处理。
输出格式:
对每一组需要检查的序列,如果其生成的二叉搜索树跟对应的初始序列生成的一样,输出“Yes”,否则输出“No”。
输入样例:
4 2
3 1 4 2
3 4 1 2
3 2 4 1
2 1
2 1
1 2
0
输出样例:
Yes
No
No







#include <stdio.h>
#include <stdlib.h>
typedef int ElementType;
typedef struct TreeNode *Tree;
struct TreeNode
{
ElementType Data;
Tree Left;
Tree Right;
int flag;
};
Tree NewNode(ElementType v)
{
Tree T = (Tree)malloc(sizeof(struct TreeNode));
T->Data = v;
T->Left = NULL;
T->Right = NULL;
T->flag = 0;
return T;
}
Tree Insert(Tree T,ElementType v)
{
if(!T)
T = NewNode(v);
else
{
if(T->Data < v)
T->Right = Insert(T->Right,v);
else
T->Left = Insert(T->Left,v);
}
return T;
}
Tree MakeTree(int N)
{
Tree T;
int i,v;
scanf("%d",&v);
T = NewNode(v);
for(i = 1;i < N;i++)
{
scanf("%d",&v);
T = Insert(T,v);
}
return T;
}
void ResetT(Tree T)
{
if(T->Left)
ResetT(T->Left);
if(T->Right)
ResetT(T->Right);
T->flag = 0;
}
void FreeTree(Tree T)
{
if(T->Left)
FreeTree(T->Left);
if(T->Right)
FreeTree(T->Right);
free(T);
}
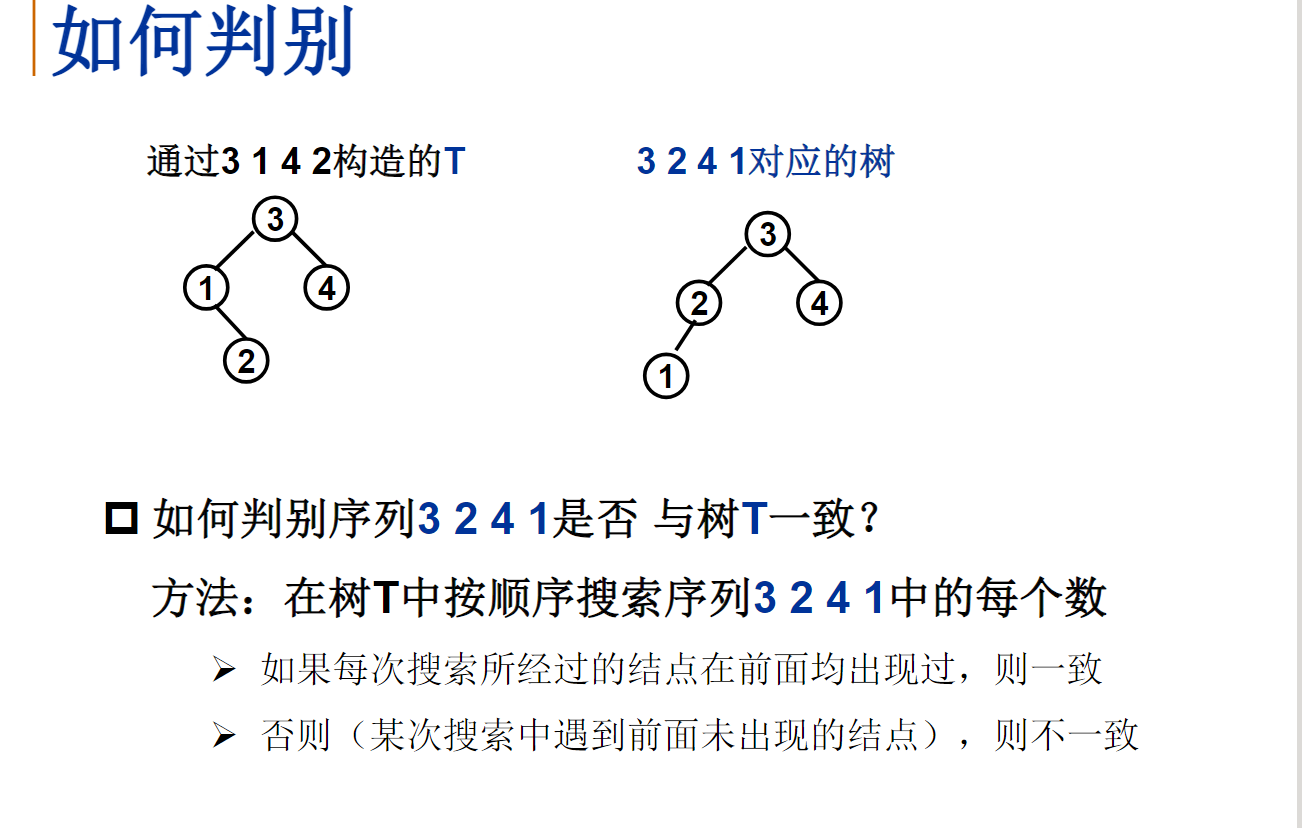
int check(Tree T, ElementType v)
{
if(T->flag)
{
if(v > T->Data)
return check(T->Right, v);
else if(v < T->Data)
return check(T->Left,v);
else
return 0;
}
else
{
if(v == T->Data)
{
T->flag = 1;
return 1;
}
else
return 0;
}
}
int Judge(Tree T, int N)
{
int i, V, flag = 0;
scanf("%d",&V);
if(T->Data != V)
flag = 1;
else
T->flag = 1;
for(i = 1;i < N;i++)
{
scanf("%d",&V);
if((!flag)&&(!check(T,V)))
flag = 1;
}
if(flag)
return 0;
else
return 1;
}
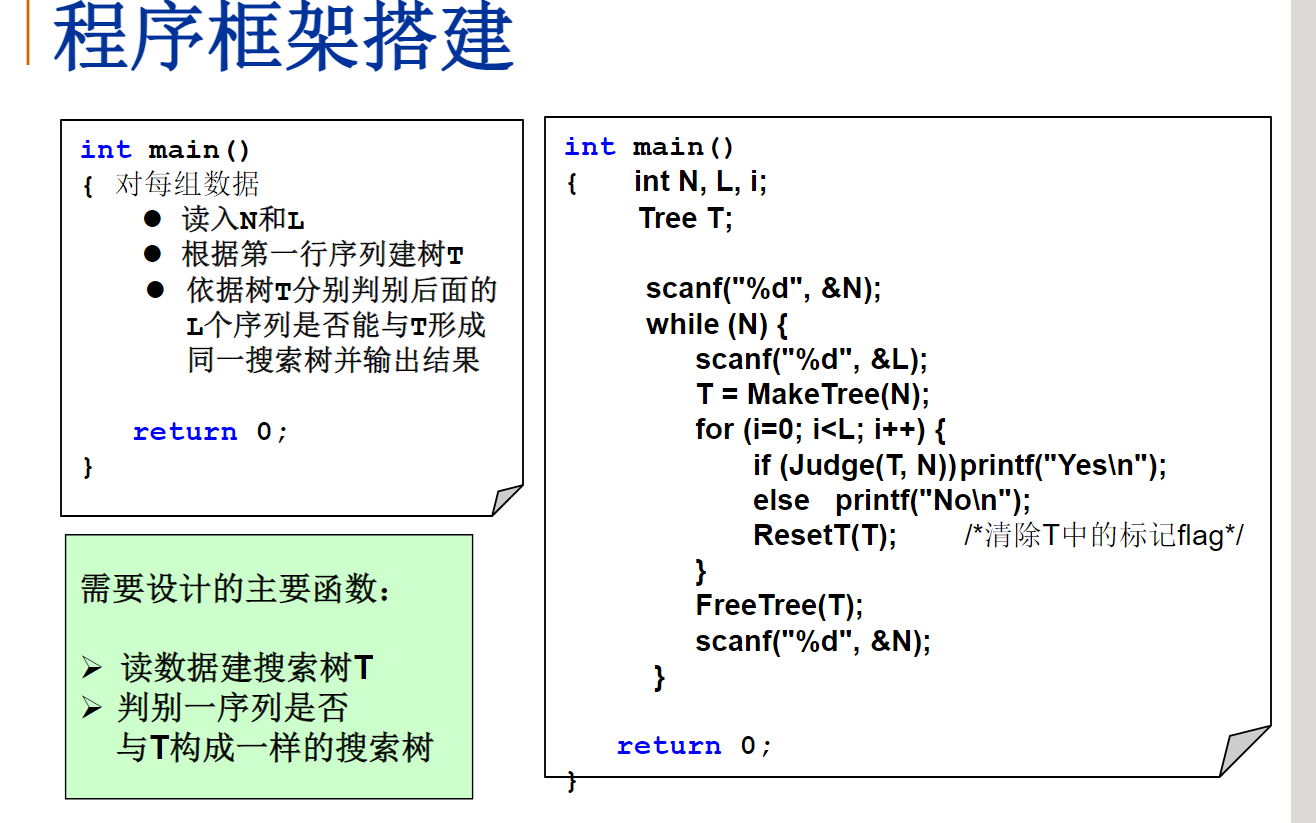
int main()
{
int N,L,i;
Tree T;
scanf("%d",&N);
while(N != 0)
{
scanf("%d",&L);
T = MakeTree(N);
for(i = 0;i < L;i++)
{
if(Judge(T,N))
printf("Yes\n");
else
printf("No\n");
ResetT(T);
}
FreeTree(T);
scanf("%d",&N);
}
return 0;
}
PTA 04-树5 Root of AVL Tree
An AVL tree is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Figures 1-4 illustrate the rotation rules.
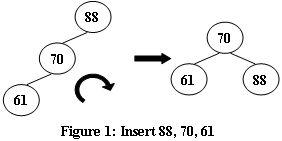
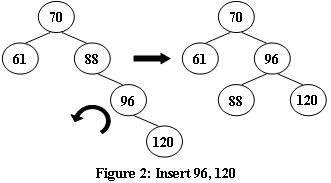
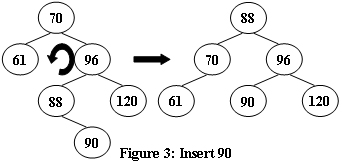
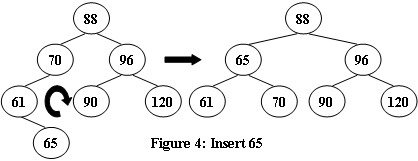
Now given a sequence of insertions, you are supposed to tell the root of the resulting AVL tree.
Input Specification:
Each input file contains one test case. For each case, the first line contains a positive integer N (≤20) which is the total number of keys to be inserted. Then N distinct integer keys are given in the next line. All the numbers in a line are separated by a space.
Output Specification:
For each test case, print the root of the resulting AVL tree in one line.
Sample Input 1:
5
88 70 61 96 120
Sample Output 1:
70
Sample Input 2:
7
88 70 61 96 120 90 65
Sample Output 2:
88
#include <stdio.h>
#include <stdlib.h>
typedef int ElementType;
typedef struct AVLNode *Position;
typedef Position AVLTree; /* AVL树类型 */
struct AVLNode{
ElementType Data; /* 结点数据 */
AVLTree Left; /* 指向左子树 */
AVLTree Right; /* 指向右子树 */
int Height; /* 树高 */
};
int Max ( int a, int b )
{
return a > b ? a : b;
}
int GetHeight(AVLTree T)
{
if (!T)
return -1;
else
return T->Height;
}
AVLTree SingleLeftRotation ( AVLTree A )
{ /* 注意:A必须有一个左子结点B */
/* 将A与B做左单旋,更新A与B的高度,返回新的根结点B */
AVLTree B = A->Left;
A->Left = B->Right;
B->Right = A;
A->Height = Max( GetHeight(A->Left), GetHeight(A->Right) ) + 1;
B->Height = Max( GetHeight(B->Left), A->Height ) + 1;
return B;
}
AVLTree SingleRightRotation(AVLTree A)//麻烦结点存在右子树的右边
{
AVLTree B=A->Right;
A->Right=B->Left;//右子树的左儿子赋给A的右子树
B->Left=A;//B变成A的父结点
A->Height=Max(GetHeight(A->Left),GetHeight(A->Right))+1;
B->Height=Max(A->Height,GetHeight(B->Right))+1;
return B;
}
AVLTree DoubleRightLeftRotation(AVLTree A)//麻烦结点存在右子树的左边
{
A->Right=SingleLeftRotation(A->Right);
return SingleRightRotation(A);
}
AVLTree DoubleLeftRightRotation ( AVLTree A )
{ /* 注意:A必须有一个左子结点B,且B必须有一个右子结点C */
/* 将A、B与C做两次单旋,返回新的根结点C */
/* 将B与C做右单旋,C被返回 */
A->Left = SingleRightRotation(A->Left);
/* 将A与C做左单旋,C被返回 */
return SingleLeftRotation(A);
}
AVLTree Insert( AVLTree T, ElementType X )
{ /* 将X插入AVL树T中,并且返回调整后的AVL树 */
if ( !T ) { /* 若插入空树,则新建包含一个结点的树 */
T = (AVLTree)malloc(sizeof(struct AVLNode));
T->Data = X;
T->Height = 0;
T->Left = T->Right = NULL;
} /* if (插入空树) 结束 */
else if ( X < T->Data ) {
/* 插入T的左子树 */
T->Left = Insert( T->Left, X);
/* 如果需要左旋 */
if ( GetHeight(T->Left)-GetHeight(T->Right) == 2 )
if ( X < T->Left->Data )
T = SingleLeftRotation(T); /* 左单旋 */
else
T = DoubleLeftRightRotation(T); /* 左-右双旋 */
} /* else if (插入左子树) 结束 */
else if ( X > T->Data ) {
/* 插入T的右子树 */
T->Right = Insert( T->Right, X );
/* 如果需要右旋 */
if ( GetHeight(T->Left)-GetHeight(T->Right) == -2 )
if ( X > T->Right->Data )
T = SingleRightRotation(T); /* 右单旋 */
else
T = DoubleRightLeftRotation(T); /* 右-左双旋 */
} /* else if (插入右子树) 结束 */
/* else X == T->Data,无须插入 */
/* 别忘了更新树高 */
T->Height = Max( GetHeight(T->Left), GetHeight(T->Right) ) + 1;
return T;
}
int main()
{
int n;
scanf("%d",&n);
ElementType X;
AVLTree T = NULL;
for(int i=0; i<n; i++)
{
scanf("%d", &X);
T = Insert(T,X);
}
if(T)
printf("%d",T->Data);
return 0;
}
PTA 04-树6 Complete Binary Search Tree
A Binary Search Tree (BST) is recursively defined as a binary tree which has the following properties:
- The left subtree of a node contains only nodes with keys less than the node's key.
- The right subtree of a node contains only nodes with keys greater than or equal to the node's key.
- Both the left and right subtrees must also be binary search trees.
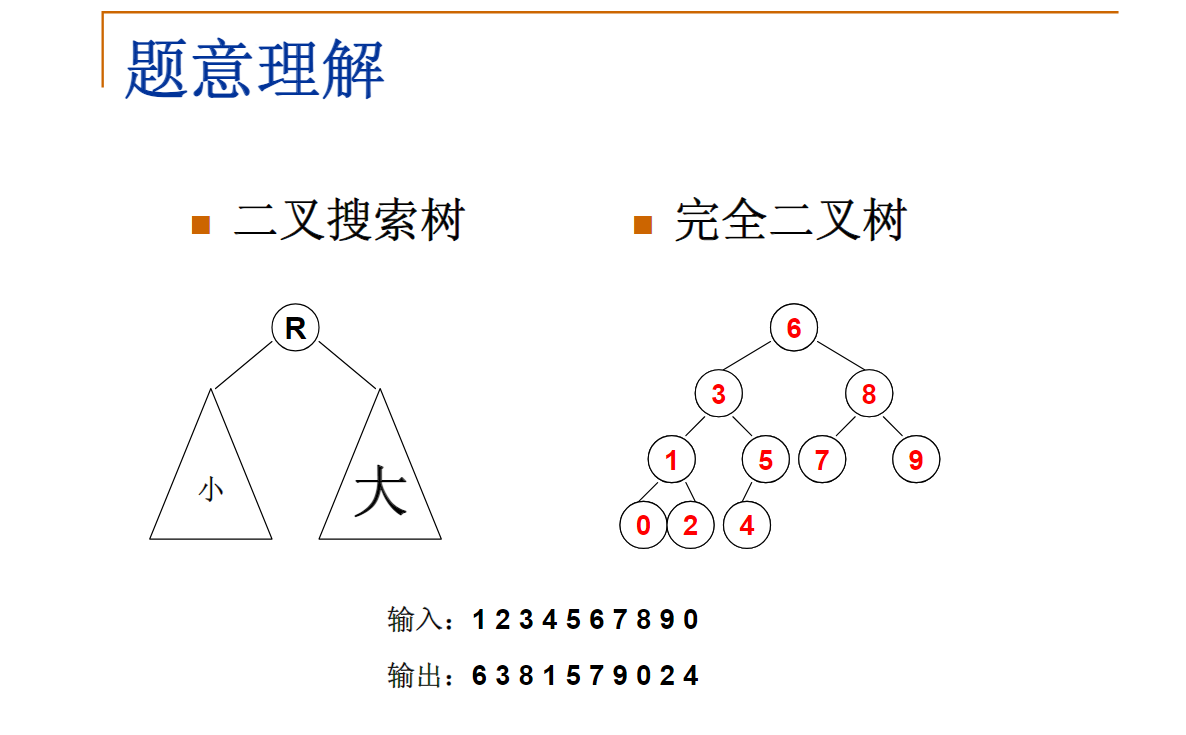
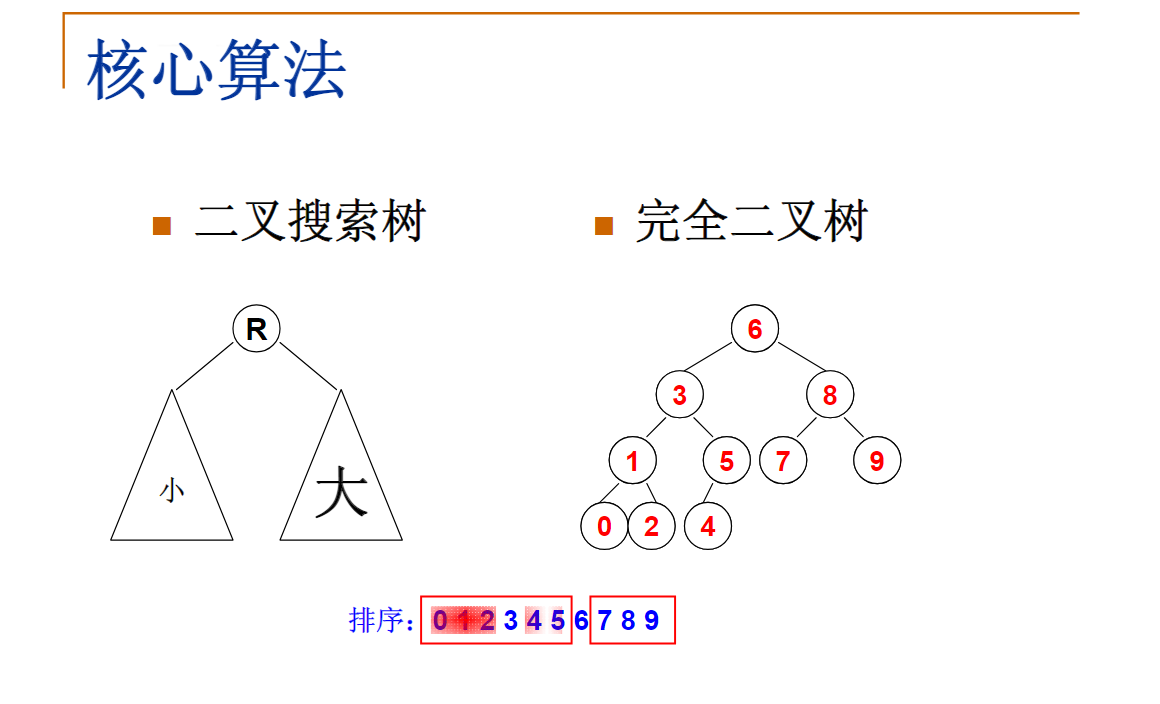
A Complete Binary Tree (CBT) is a tree that is completely filled, with the possible exception of the bottom level, which is filled from left to right.
Now given a sequence of distinct non-negative integer keys, a unique BST can be constructed if it is required that the tree must also be a CBT. You are supposed to output the level order traversal sequence of this BST.
Input Specification:
Each input file contains one test case. For each case, the first line contains a positive integer N (≤1000). Then N distinct non-negative integer keys are given in the next line. All the numbers in a line are separated by a space and are no greater than 2000.
Output Specification:
For each test case, print in one line the level order traversal sequence of the corresponding complete binary search tree. All the numbers in a line must be separated by a space, and there must be no extra space at the end of the line.
Sample Input:
10
1 2 3 4 5 6 7 8 9 0
Sample Output:
6 3 8 1 5 7 9 0 2 4


#include <stdio.h>
#include <stdlib.h>
#include <math.h>
int Nodes[1005] = {0};
int T[1005] = {0};
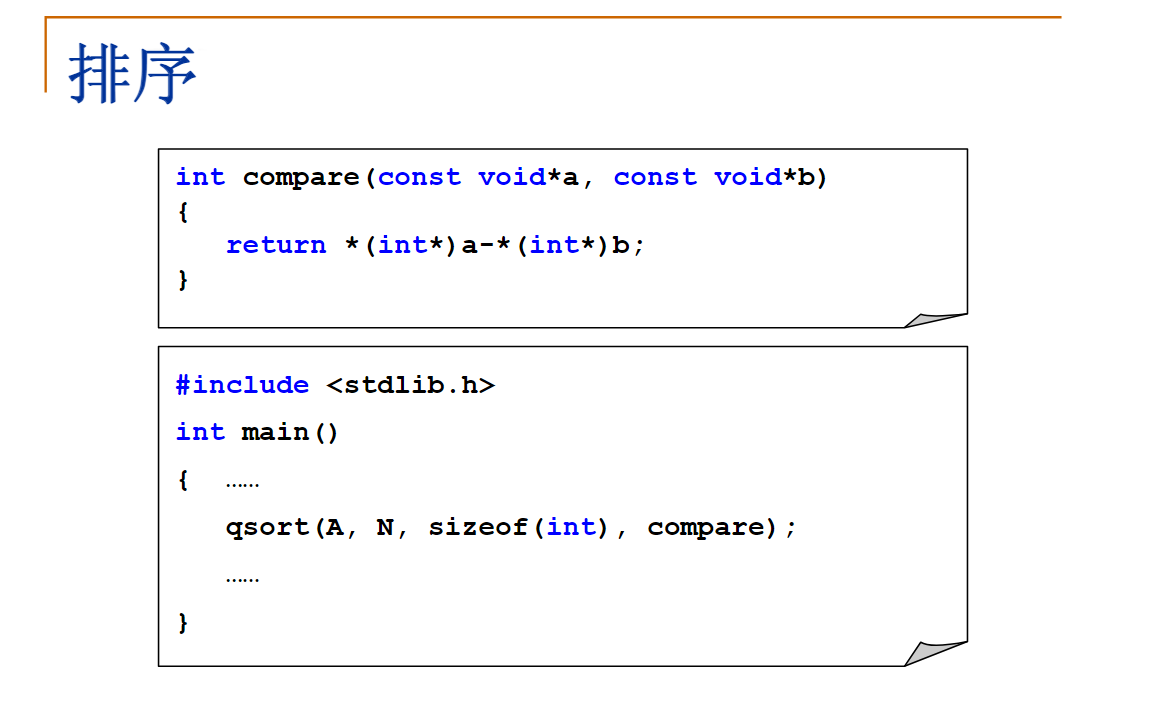
int compare(const void * a, const void * b)
{
return *(int *)a - *(int *)b;
}
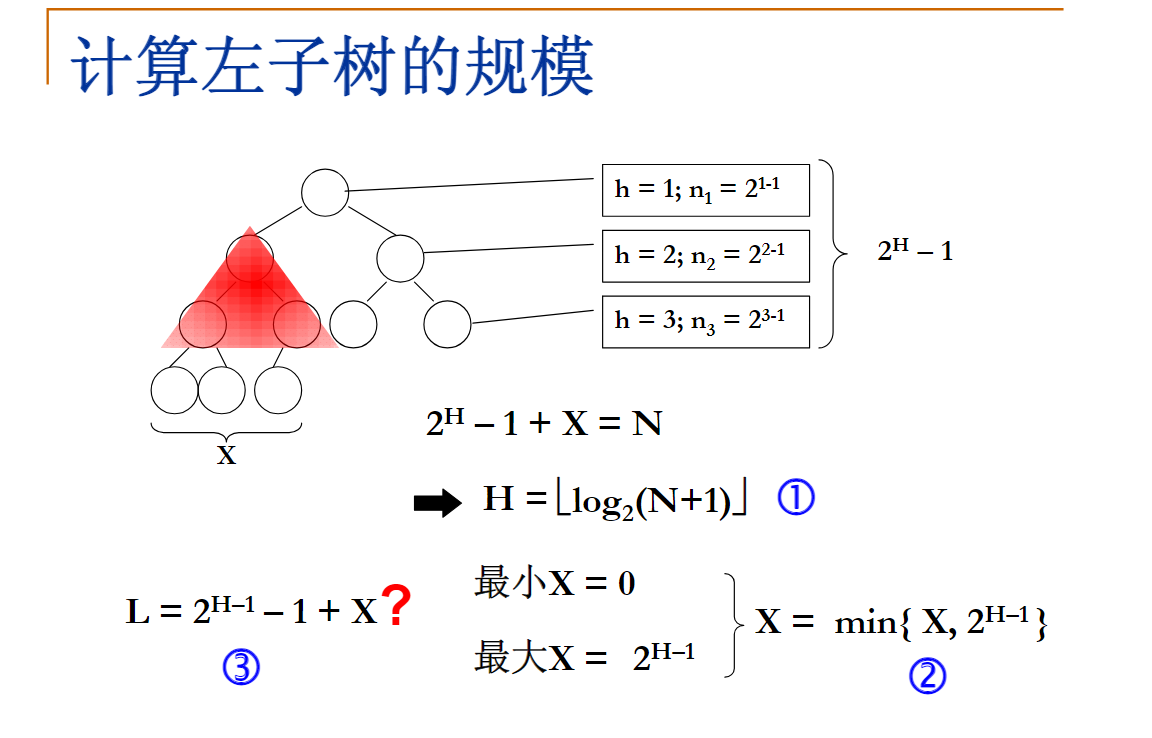
int GetLeftLength(int N)
{
int L;
int H = (int)(log(N+1)/log(2));
int X = (N+1-pow(2,H));
X = X<pow(2,H-1)?X:pow(2,H-1);
L = pow(2,H-1) - 1 + X;
return L;
}
void solve(int ALeft, int ARight, int TRoot)
{
int n = ARight - ALeft + 1;
if(n==0)
return;
int L = GetLeftLength(n);
T[TRoot] = Nodes[ALeft+L];
int LeftRoot = TRoot * 2 + 1;
int RightRoot = TRoot * 2 + 2;
solve(ALeft, ALeft+L-1, LeftRoot);
solve(ALeft+L+1, ARight,RightRoot);
}
int main()
{
int n;
scanf("%d",&n);
for(int i=0; i<n; i++)
{
scanf("%d", &Nodes[i]);
}
qsort(Nodes,n,sizeof(int),compare);
solve(0, n-1, 0);
int First = 1;
for(int i=0; i<n; i++)
{
if(First)
{
printf("%d", T[i]);
First = 0;
}
else
{
printf(" %d",T[i]);
}
}
return 0;
}
柳婼cpp题解:
题目大意:给一串构成树的序列,已知该树是完全二叉搜索树,求它的层序遍历的序列 分析:总得概括来说,已知中序,从根节点开始中序遍历,按中序数组给出的顺序依次将值填入level数组对应的下标中,输出level数组可得层序遍历。 1. 因为二叉搜索树的中序满足:是一组序列的从小到大排列,所以只需将所给序列排序即可得到中序数组in 2. 假设把树按从左到右、从上到下的顺序依次编号,根节点为0,则从根结点root = 0开始中序遍历,root结点的左孩子下标是root_2+1,右孩子下标是root_2+2 3. 因为是中序遍历,所以遍历结果与中序数组in中的值从0开始依次递增的结果相同,即in[t++](t从0开始),将in[t++]赋值给level[root]数组 4. 因为树是按从左到右、从上到下的顺序依次编号的,所以level数组从0到n-1的值即所求的层序遍历的值,输出level数组即可~
#include <iostream>
#include <algorithm>
using namespace std;
int in[1010], level[1010], n, t = 0;
void inOrder(int root) {
if (root >= n) return ;
inOrder(root * 2 + 1);
level[root] = in[t++];
inOrder(root * 2 + 2);
}
int main() {
scanf("%d", &n);
for (int i = 0; i < n; i++)
scanf("%d", &in[i]);
sort(in, in + n);
inOrder(0);
printf("%d", level[0]);
for (int i = 1; i < n; i++)
printf(" %d", level[i]);
return 0;
}
PTA 04-树7 二叉搜索树的操作集
本题要求实现给定二叉搜索树的5种常用操作。
函数接口定义:
BinTree Insert( BinTree BST, ElementType X );
BinTree Delete( BinTree BST, ElementType X );
Position Find( BinTree BST, ElementType X );
Position FindMin( BinTree BST );
Position FindMax( BinTree BST );
其中BinTree结构定义如下:
typedef struct TNode *Position;
typedef Position BinTree;
struct TNode{
ElementType Data;
BinTree Left;
BinTree Right;
};
- 函数
Insert将X插入二叉搜索树BST并返回结果树的根结点指针; - 函数
Delete将X从二叉搜索树BST中删除,并返回结果树的根结点指针;如果X不在树中,则打印一行Not Found并返回原树的根结点指针; - 函数
Find在二叉搜索树BST中找到X,返回该结点的指针;如果找不到则返回空指针; - 函数
FindMin返回二叉搜索树BST中最小元结点的指针; - 函数
FindMax返回二叉搜索树BST中最大元结点的指针。
裁判测试程序样例:
#include <stdio.h>
#include <stdlib.h>
typedef int ElementType;
typedef struct TNode *Position;
typedef Position BinTree;
struct TNode{
ElementType Data;
BinTree Left;
BinTree Right;
};
void PreorderTraversal( BinTree BT ); /* 先序遍历,由裁判实现,细节不表 */
void InorderTraversal( BinTree BT ); /* 中序遍历,由裁判实现,细节不表 */
BinTree Insert( BinTree BST, ElementType X );
BinTree Delete( BinTree BST, ElementType X );
Position Find( BinTree BST, ElementType X );
Position FindMin( BinTree BST );
Position FindMax( BinTree BST );
int main()
{
BinTree BST, MinP, MaxP, Tmp;
ElementType X;
int N, i;
BST = NULL;
scanf("%d", &N);
for ( i=0; i<N; i++ ) {
scanf("%d", &X);
BST = Insert(BST, X);
}
printf("Preorder:"); PreorderTraversal(BST); printf("\n");
MinP = FindMin(BST);
MaxP = FindMax(BST);
scanf("%d", &N);
for( i=0; i<N; i++ ) {
scanf("%d", &X);
Tmp = Find(BST, X);
if (Tmp == NULL) printf("%d is not found\n", X);
else {
printf("%d is found\n", Tmp->Data);
if (Tmp==MinP) printf("%d is the smallest key\n", Tmp->Data);
if (Tmp==MaxP) printf("%d is the largest key\n", Tmp->Data);
}
}
scanf("%d", &N);
for( i=0; i<N; i++ ) {
scanf("%d", &X);
BST = Delete(BST, X);
}
printf("Inorder:"); InorderTraversal(BST); printf("\n");
return 0;
}
/* 你的代码将被嵌在这里 */
输入样例:
10
5 8 6 2 4 1 0 10 9 7
5
6 3 10 0 5
5
5 7 0 10 3
输出样例:
Preorder: 5 2 1 0 4 8 6 7 10 9
6 is found
3 is not found
10 is found
10 is the largest key
0 is found
0 is the smallest key
5 is found
Not Found
Inorder: 1 2 4 6 8 9
BinTree Insert(BinTree BST, ElementType X)
{
if(!BST)
{
/*若原树为空,生成并返回一个结点的二叉搜索树*/
BST = (BinTree)malloc(sizeof(struct TNode));
BST->Data = X;
BST->Left = NULL;
BST->Right = NULL;
}
else /*开始找要插入元素的位置*/
{
if(BST->Data < X)
BST->Right = Insert(BST->Right, X);
else if(BST->Data > X)
BST->Left = Insert(BST->Left, X);
/*else X已经存在,什么都不做 */
}
return BST;
}
BinTree Delete(BinTree BST, ElementType X)
{
Position Tmp;
if(!BST)
printf("Not Found\n");
else if(X < BST->Data)
BST->Left = Delete(BST->Left,X);
else if(X > BST->Data)
BST->Right = Delete(BST->Right,X);
else
{
if(BST->Left && BST->Right)
{
Tmp = FindMin(BST->Right);
BST->Data = Tmp->Data;
BST->Right = Delete(BST->Right,BST->Data);
}
else
{
Tmp = BST;
if(!BST->Left)
BST = BST->Right;
else if(!BST->Right)
BST = BST->Left;
free(Tmp);
}
}
return BST;
}
Position Find(BinTree BST,ElementType X)
{
if(!BST)
return NULL;
else
{
if(BST->Data == X)
return BST; /*查找成功,返回找到结点的地址*/
else if(BST->Data > X)
return Find(BST->Left, X);
else
return Find(BST->Right, X);
}
return NULL;
}
/*迭代、非递归方式*/
Position FindMax(BinTree BST)
{
if(BST)
while(BST->Right)
BST = BST->Right;
return BST;
}
Position FindMin(BinTree BST)
{
if(!BST)
return NULL;
else if(!BST->Left) /*有根结点,但没有左子树,直接返回根*/
return BST;
else
return FindMin(BST->Left);
}
PTA 05-树7 堆中的路径
将一系列给定数字依次插入一个初始为空的小顶堆H[]。随后对任意给定的下标i,打印从H[i]到根结点的路径。
输入格式:
每组测试第1行包含2个正整数N和M(≤1000),分别是插入元素的个数、以及需要打印的路径条数。下一行给出区间[-10000, 10000]内的N个要被插入一个初始为空的小顶堆的整数。最后一行给出M个下标。
输出格式:
对输入中给出的每个下标i,在一行中输出从H[i]到根结点的路径上的数据。数字间以1个空格分隔,行末不得有多余空格。
输入样例:
5 3
46 23 26 24 10
5 4 3
输出样例:
24 23 10
46 23 10
26 10
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#define ERROR -1
typedef int ElementType;
typedef struct HNode *Heap;
typedef Heap MaxHeap;
typedef Heap MinHeap;
struct HNode
{
ElementType *Data;
int Size;
int Capacity;
};
MinHeap CreateHeap(int MaxSize)
{
MinHeap H = (MinHeap)malloc(sizeof(struct HNode));
H->Data = (ElementType*)malloc(sizeof(ElementType)*MaxSize);
H->Size = 0;
H->Capacity = MaxSize;
H->Data[0] = -10001;
return H;
}
bool IsFull(MinHeap H)
{
return (H->Size == H->Capacity);
}
bool Insert(MinHeap H, ElementType X)
{
if(IsFull(H))
{
printf("The heap is full!\n");
return false;
}
int i = ++H->Size;
for(; H->Data[i/2] >= X; i /= 2)
{
H->Data[i] = H->Data[i/2];
}
H->Data[i] = X;
return true;
}
bool IsEmpty(MinHeap H)
{
return (H->Size == 0);
}
ElementType Delete(MinHeap H)
{
if(IsEmpty(H))
{
printf("The heap is empty!\n");
return ERROR;
}
int Parent, Child;
ElementType MinItem,X;
MinItem = H->Data[1];
X = H->Data[H->Size--];
for(Parent = 1; Parent * 2 <= H->Size; Parent = Child)
{
Child = Parent * 2;
if((Child!=H->Size)&&(H->Data[Child] > H->Data[Child + 1]))
Child++;
if(X < H->Data[Child])
break;
else
H->Data[Parent] = H->Data[Child];
}
H->Data[Parent] = X;
return MinItem;
}
int main()
{
int MaxSize = 1001;
MinHeap H = CreateHeap(MaxSize);
int N,M;
scanf("%d %d",&N,&M);
for(int i=0; i<N; i++)
{
int num;
scanf("%d",&num);
Insert(H,num);
}
for(int i=0; i<M; i++)
{
int idx;
scanf("%d",&idx);
int Fisrt = 1;
for(int j=idx; j>=1; j/=2)
{
if(Fisrt)
{
printf("%d",H->Data[j]);
Fisrt = 0;
}
else
{
printf(" %d",H->Data[j]);
}
}
printf("\n");
}
return 0;
}
PTA 05-树8 File Transfer
We have a network of computers and a list of bi-directional connections. Each of these connections allows a file transfer from one computer to another. Is it possible to send a file from any computer on the network to any other?
Input Specification:
Each input file contains one test case. For each test case, the first line contains N (2≤N≤104), the total number of computers in a network. Each computer in the network is then represented by a positive integer between 1 and N. Then in the following lines, the input is given in the format:
I c1 c2
where I stands for inputting a connection between c1 and c2; or
C c1 c2
where C stands for checking if it is possible to transfer files between c1 and c2; or
S
where S stands for stopping this case.
Output Specification:
For each C case, print in one line the word "yes" or "no" if it is possible or impossible to transfer files between c1 and c2, respectively. At the end of each case, print in one line "The network is connected." if there is a path between any pair of computers; or "There are k components." where k is the number of connected components in this network.
Sample Input 1:
5
C 3 2
I 3 2
C 1 5
I 4 5
I 2 4
C 3 5
S
Sample Output 1:
no
no
yes
There are 2 components.
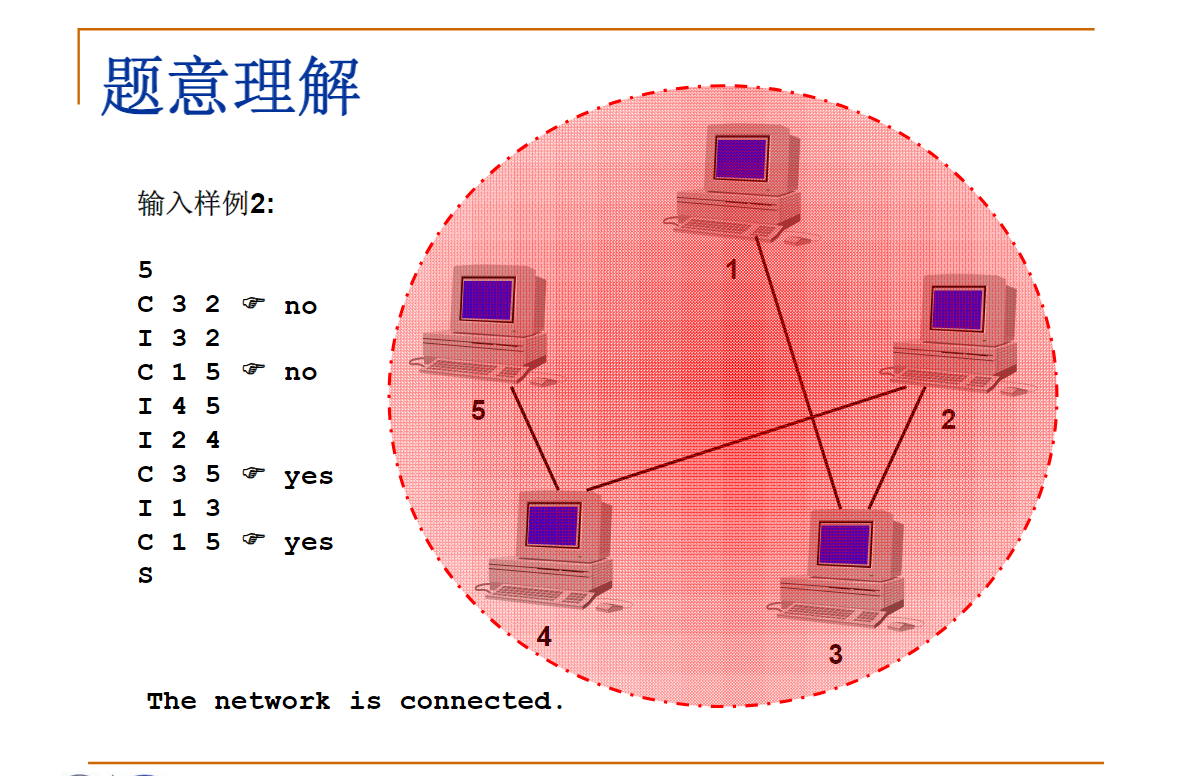
Sample Input 2:
5
C 3 2
I 3 2
C 1 5
I 4 5
I 2 4
C 3 5
I 1 3
C 1 5
S
Sample Output 2:
no
no
yes
yes
The network is connected.



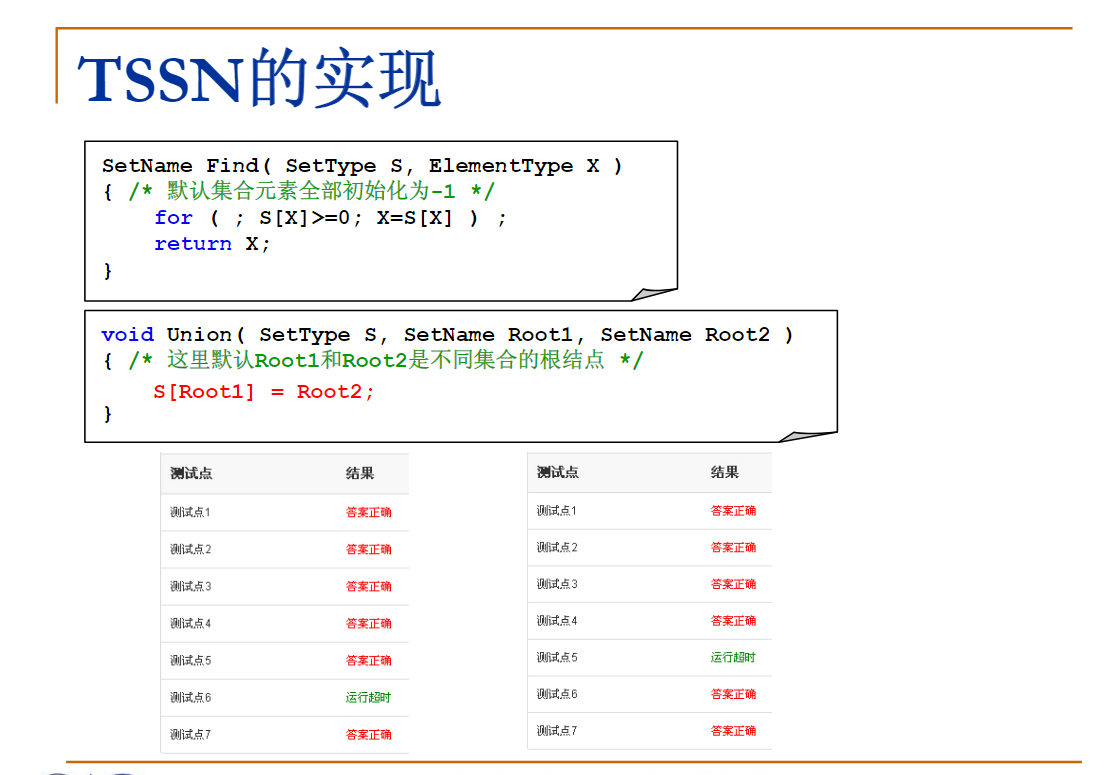

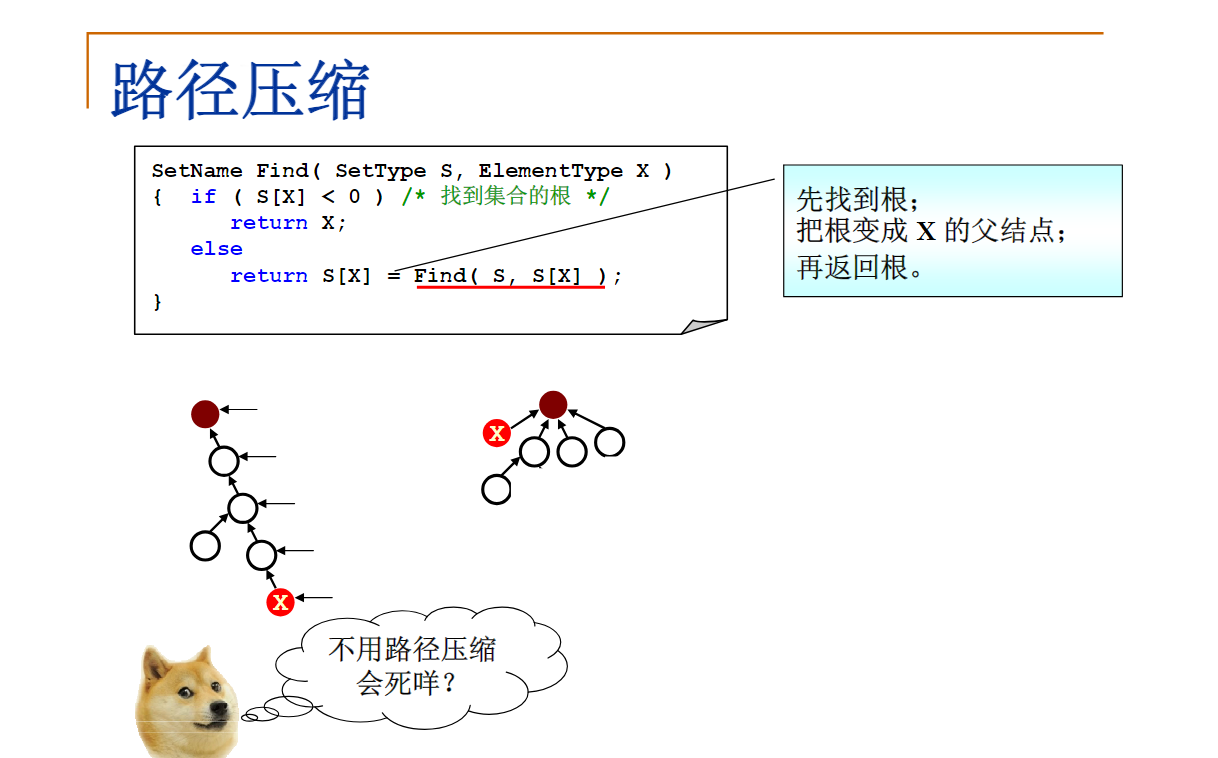
这里代码是伪递归形式的,会被编译器优化成循环形式。

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAXN 10001 /* 集合最大元素个数 */
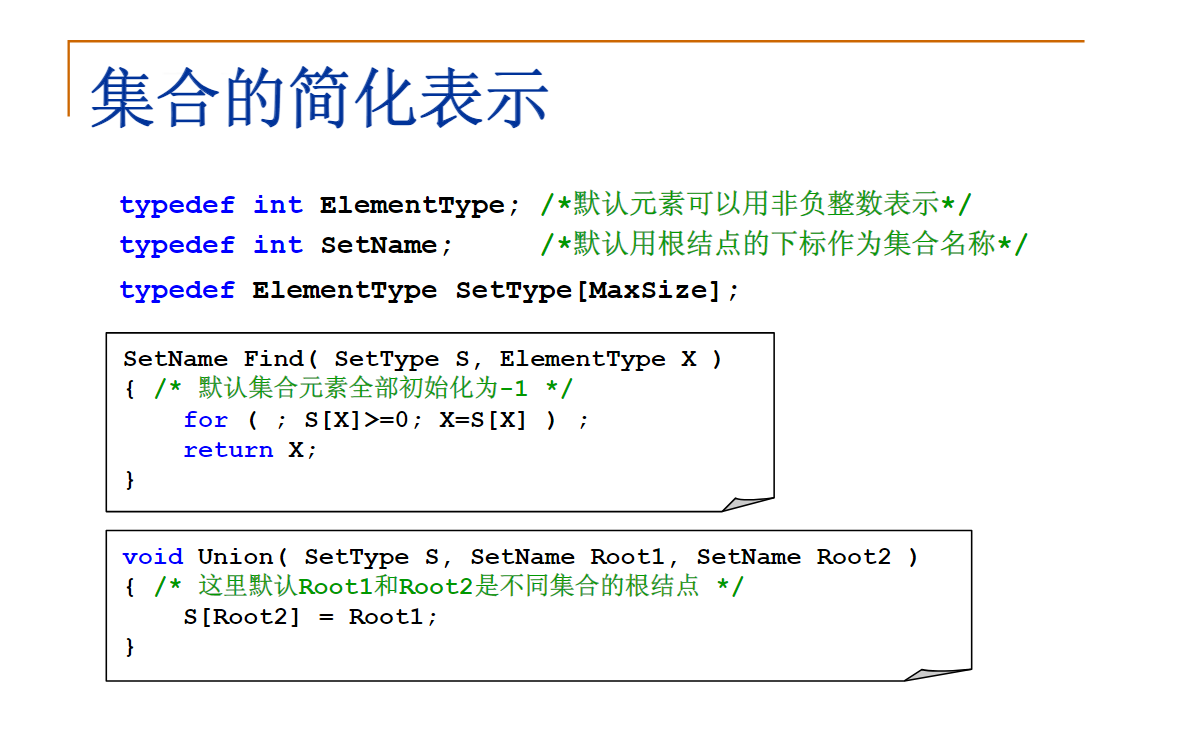
typedef int ElementType; /* 默认元素可以用非负整数表示 */
typedef int SetName; /* 默认用根结点的下标作为集合名称 */
typedef ElementType SetType[MAXN]; /* 假设集合元素下标从0开始 */
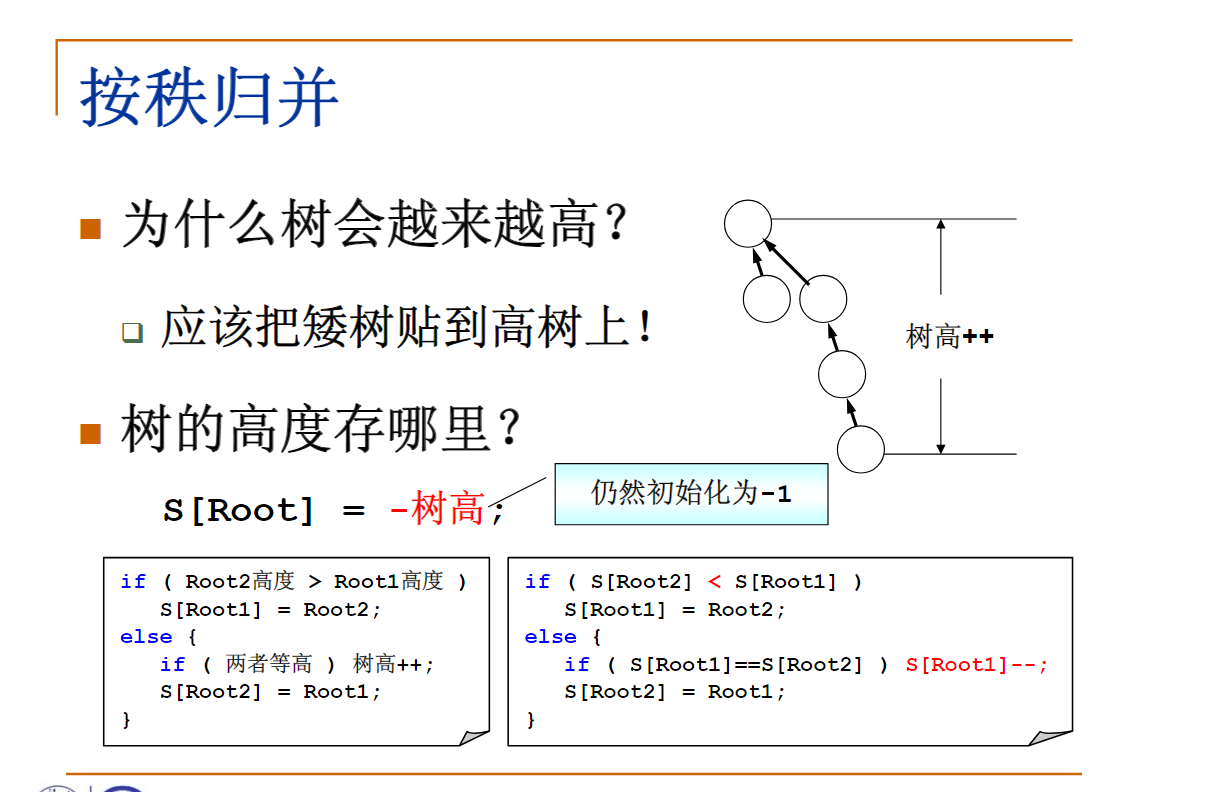
void Union( SetType S, SetName Root1, SetName Root2 )
{ /* 这里默认Root1和Root2是不同集合的根结点 */
/* 保证小集合并入大集合 */
if ( S[Root2] < S[Root1] ) { /* 如果集合2比较大 */
S[Root2] += S[Root1]; /* 集合1并入集合2 */
S[Root1] = Root2;
}
else { /* 如果集合1比较大 */
S[Root1] += S[Root2]; /* 集合2并入集合1 */
S[Root2] = Root1;
}
}
SetName Find( SetType S, ElementType X )
{ /* 默认集合元素全部初始化为-1 */
if ( S[X] < 0 ) /* 找到集合的根 */
return X;
else
return S[X] = Find( S, S[X] ); /* 路径压缩 */
}
void Initialization(SetType S, int N)
{
for(int i=0; i<N; i++)
S[i] = -1;
}
void Input_connection(SetType S)
{
ElementType u,v;
SetName Root1, Root2;
scanf("%d %d\n",&u,&v);
Root1 = Find(S, u-1);
Root2 = Find(S, v-1);
if(Root1 != Root2)
Union(S, Root1, Root2);
}
void Check_connection(SetType S)
{
ElementType u,v;
SetName Root1,Root2;
scanf("%d %d\n",&u,&v);
Root1 = Find(S, u-1);
Root2 = Find(S, v-1);
if(Root1 == Root2)
printf("yes\n");
else
printf("no\n");
}
void Check_network(SetType S, int n)
{
int i,counter = 0;
for(i=0; i<n; i++)
{
if(S[i] < 0)
counter++;
}
if(counter == 1)
printf("The network is connected.\n");
else
printf("There are %d components.\n",counter);
}
int main()
{
int N;
scanf("%d",&N);
SetType S;
char in;
Initialization(S, N);
do
{
scanf("%c",&in);
switch(in)
{
case 'I':
Input_connection(S);
break;
case 'C':
Check_connection(S);
break;
case 'S':
Check_network(S, N);
break;
}
}while(in != 'S');
return 0;
}
PTA 05-树9 Huffman Codes
In 1953, David A. Huffman published his paper "A Method for the Construction of Minimum-Redundancy Codes", and hence printed his name in the history of computer science. As a professor who gives the final exam problem on Huffman codes, I am encountering a big problem: the Huffman codes are NOT unique. For example, given a string "aaaxuaxz", we can observe that the frequencies of the characters 'a', 'x', 'u' and 'z' are 4, 2, 1 and 1, respectively. We may either encode the symbols as {'a'=0, 'x'=10, 'u'=110, 'z'=111}, or in another way as {'a'=1, 'x'=01, 'u'=001, 'z'=000}, both compress the string into 14 bits. Another set of code can be given as {'a'=0, 'x'=11, 'u'=100, 'z'=101}, but {'a'=0, 'x'=01, 'u'=011, 'z'=001} is NOT correct since "aaaxuaxz" and "aazuaxax" can both be decoded from the code 00001011001001. The students are submitting all kinds of codes, and I need a computer program to help me determine which ones are correct and which ones are not.
Input Specification:
Each input file contains one test case. For each case, the first line gives an integer N (2≤N≤63), then followed by a line that contains all the N distinct characters and their frequencies in the following format:
c[1] f[1] c[2] f[2] ... c[N] f[N]
where c[i] is a character chosen from {'0' - '9', 'a' - 'z', 'A' - 'Z', '_'}, and f[i] is the frequency of c[i] and is an integer no more than 1000. The next line gives a positive integer M (≤1000), then followed by M student submissions. Each student submission consists of N lines, each in the format:
c[i] code[i]
where c[i] is the i-th character and code[i] is an non-empty string of no more than 63 '0's and '1's.
Output Specification:
For each test case, print in each line either "Yes" if the student's submission is correct, or "No" if not.
Note: The optimal solution is not necessarily generated by Huffman algorithm. Any prefix code with code length being optimal is considered correct.
Sample Input:
7
A 1 B 1 C 1 D 3 E 3 F 6 G 6
4
A 00000
B 00001
C 0001
D 001
E 01
F 10
G 11
A 01010
B 01011
C 0100
D 011
E 10
F 11
G 00
A 000
B 001
C 010
D 011
E 100
F 101
G 110
A 00000
B 00001
C 0001
D 001
E 00
F 10
G 11
Sample Output:
Yes
Yes
No
No
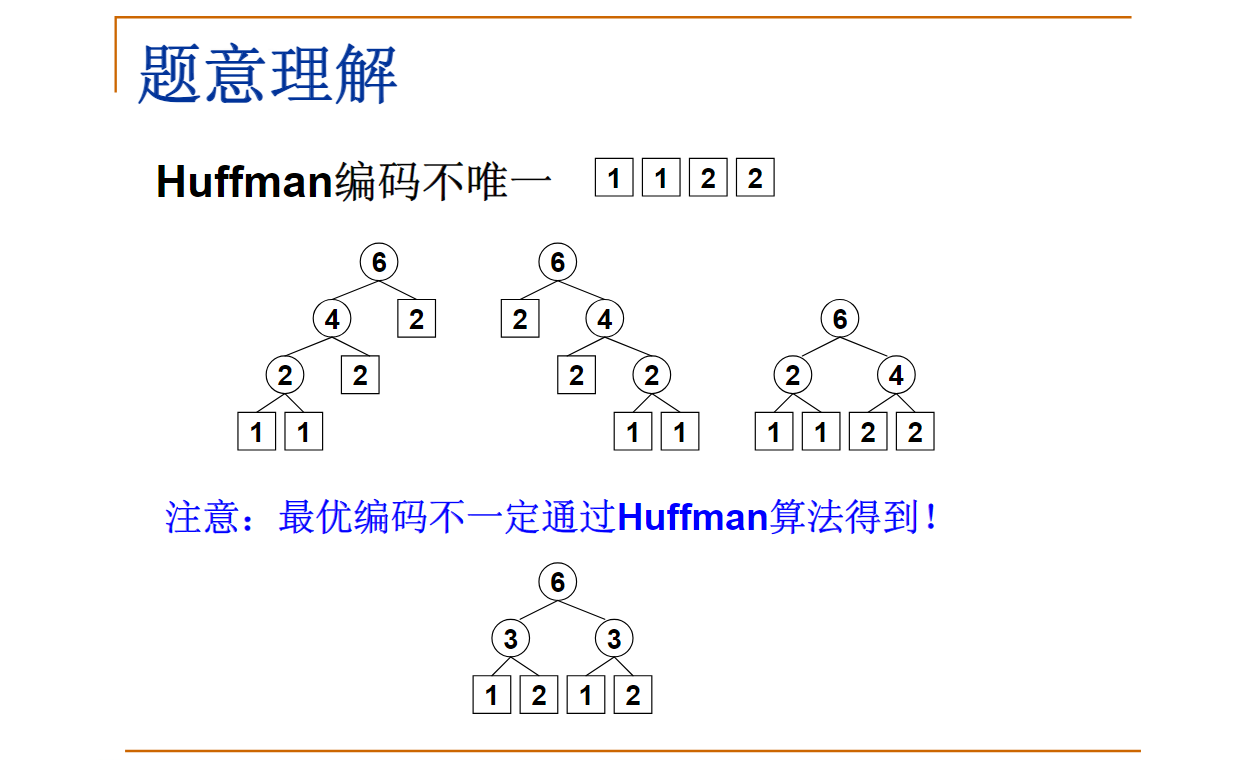

最优编码不一定通过Huffman算法得到。给定4个字符及其出现频率: A:1; B:1; C:2; D:2
下面哪一套不是用Huffman算法得到的正确的编码?
A.A:000; B:001; C:01; D:1
B.A:10; B:11; C:00; D:01
C.A:00; B:10; C:01; D:11
D.A:111; B:001; C:10; D:1
正确答案:C你选对了

这道题主要利用哈夫曼编码的两个性质:
- 哈夫曼编码可能不唯一,但是哈夫曼编码的长度是唯一的。字符串编码成01串后的长度实际上就是其以频率为权值所构成的任意一颗哈夫曼树的带权路径长度。
- 对于任何一个叶子结点,其编号一定不会成为其他任何一个结点编号的前缀—也就是说,题目中给出需要判断的的每个字符的编码,它不会是其他字符编码的前缀。
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#define ERROR -1
typedef HuffmanTree ElementType;
typedef struct HNode *Heap;
typedef Heap MinHeap;
typedef struct TreeNode* HuffmanTree;
struct TreeNode
{ //A 1 B 1 C 1 D 3 E 3 F 6 G 6
int Weight;//为什么不记录A B C 只记录频率1 1 1? 因为根据哈夫曼树的特点,待计算WPL的结点都位于叶结点(知道出现频率就可以了)
HuffmanTree Left;
HuffmanTree Right;
};
struct HNode
{
ElementType *Data;
int Size;
int Capacity;
};
MinHeap CreateHeap(int MaxSize)
{
MinHeap H = (MinHeap)malloc(sizeof(struct HNode));
H->Data = (ElementType*)malloc(sizeof(ElementType)*MaxSize);
H->Size = 0;
H->Capacity = MaxSize;
H->Data[0] = -10001;
return H;
}
bool IsFull(MinHeap H)
{
return (H->Size == H->Capacity);
}
bool Insert(MinHeap H, ElementType X)
{
if(IsFull(H))
{
printf("The heap is full!\n");
return false;
}
int i = ++H->Size;
for(; H->Data[i/2] >= X; i /= 2)
{
H->Data[i] = H->Data[i/2];
}
H->Data[i] = X;
return true;
}
bool IsEmpty(MinHeap H)
{
return (H->Size == 0);
}
ElementType Delete(MinHeap H)
{
if(IsEmpty(H))
{
printf("The heap is empty!\n");
return ERROR;
}
int Parent, Child;
ElementType MinItem,X;
MinItem = H->Data[1];
X = H->Data[H->Size--];
for(Parent = 1; Parent * 2 <= H->Size; Parent = Child)
{
Child = Parent * 2;
if((Child!=H->Size)&&(H->Data[Child] > H->Data[Child + 1]))
Child++;
if(X < H->Data[Child])
break;
else
H->Data[Parent] = H->Data[Child];
}
H->Data[Parent] = X;
return MinItem;
}
MinHeap ReadData(int N)
{
MinHeap H = CreateHeap(N);
char Symbol;
int Weight;
for(int i=0; i<N; i++)
{
scanf("%c %d",&Symbol,&Weight);
HuffmanTree HTree = (HuffmanTree)malloc(sizeof(struct TreeNode));
HTree->Weight = Weight;
HTree->Left = NULL;
HTree->Right = NULL;
}
}
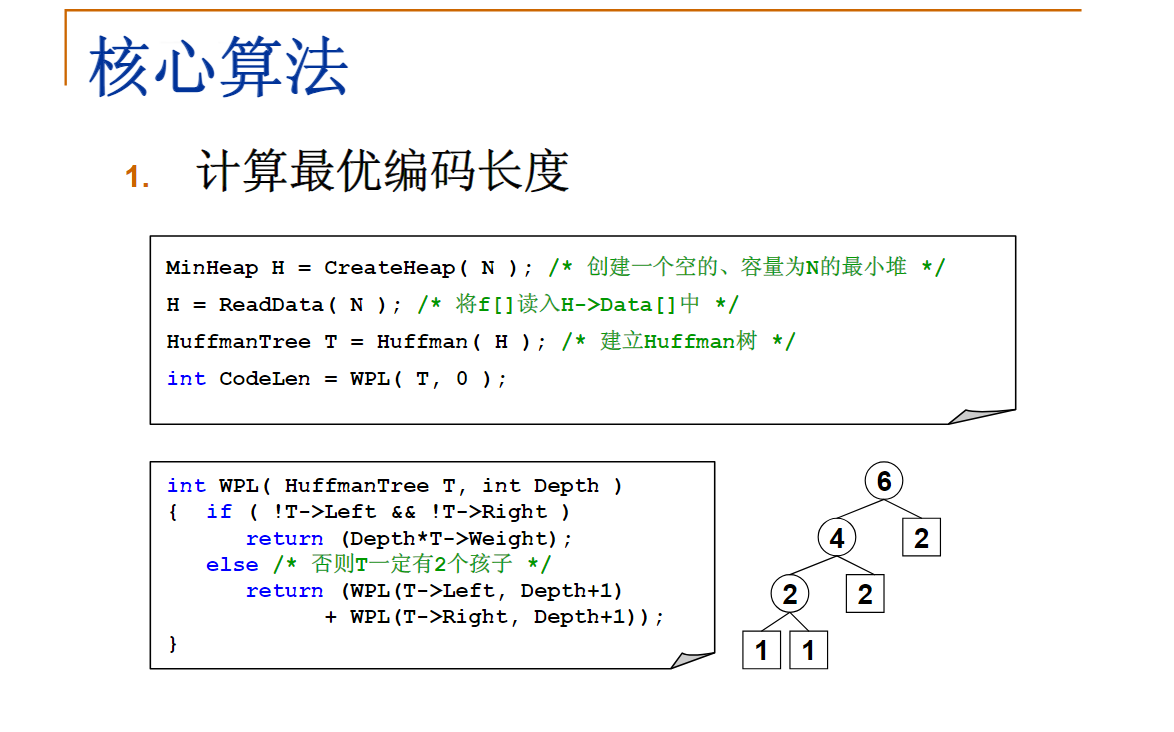
int WPL(HuffmanTree T, int Depth)
{
if (!T->Left && !T->Right) //叶结点就是待计算的结点
return T->Weight * Depth;
else
return WPL(T->Left, Depth + 1) + WPL(T->Right, Depth + 1);
}
int main()
{
int N;
scanf("%d",&N);
MinHeap H = CreateHeap(N);
H = ReadData(N);
HuffmanTree T = Huffman(H);
int CodeLen = WPL(T, 0);
int N,M;
scanf("%d %d",&N,&M);
for(int i=0; i<N; i++)
{
int num;
scanf("%d",&num);
Insert(H,num);
}
for(int i=0; i<M; i++)
{
int idx;
scanf("%d",&idx);
int Fisrt = 1;
for(int j=idx; j>=1; j/=2)
{
if(Fisrt)
{
printf("%d",H->Data[j]);
Fisrt = 0;
}
else
{
printf(" %d",H->Data[j]);
}
}
printf("\n");
}
return 0;
}
未完待续
C++实现代码如下:
#include<bits/stdc++.h>
using namespace std;
int main(){
int s = 0, n, m, x, a[100];
char ch;
priority_queue<int,vector<int>,greater<int> > q; //优先队列
cin>>n;getchar();
for(int i = 0; i < n; i++) {
cin>>ch>>x;
a[i] = x;
q.push(x);
}
while(q.size() > 1) {
int x = q.top();
q.pop();
int y = q.top();
q.pop();
s = s + x + y;
q.push(x + y);
}
cin>>m;
while(m--) {
int s1 = 0;
string str[100];
for(int i = 0; i < n; i++) {
cin>>ch>>str[i];
s1 = s1 + str[i].size() * a[i];
}
if(s == s1) {
bool jdg = true;
for (int i = 0; i < n-1; i++) {
for (int j = i+1; j < n; j++) {
int flag = 0;
int size = str[i].size() > str[j].size() ? str[j].size() : str[i].size();
for(int k = 0; k < size; k++)
if(str[i][k] != str[j][k])
flag = 1;
if (!flag)
jdg = false;
}
}
if(jdg)
cout<<"Yes\n";
else
cout<<"No\n";
}
else
cout<<"No\n";
}
return 0;
}
