图的遍历
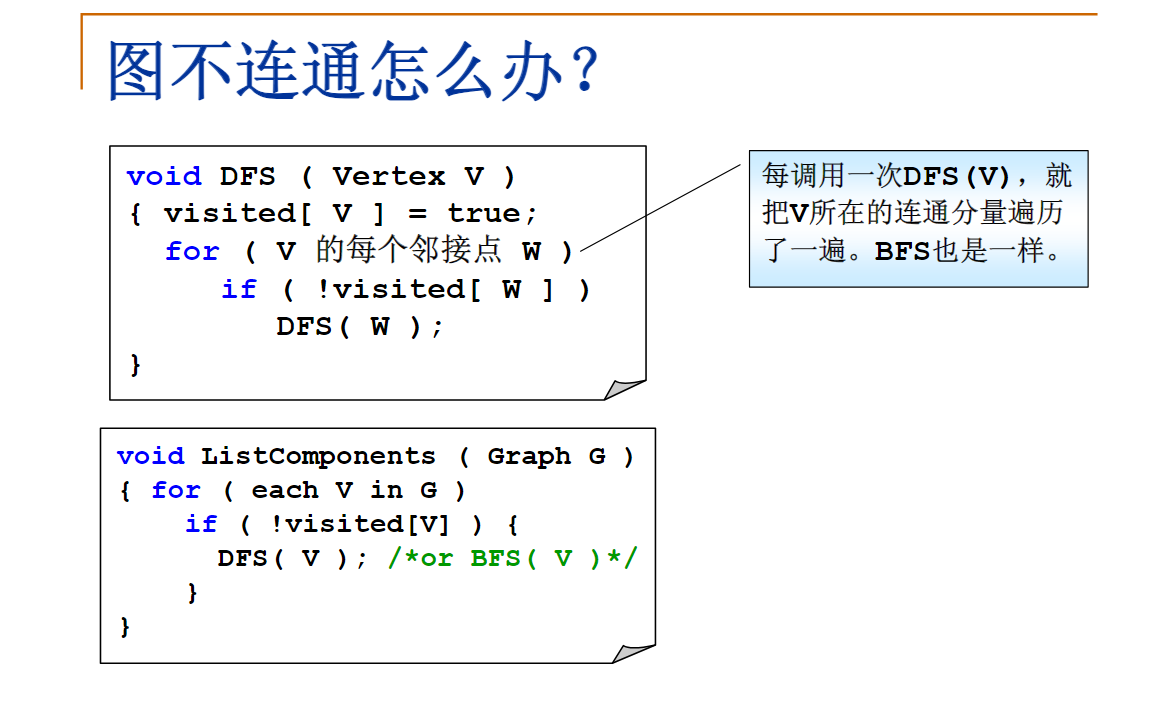
深度优先搜索DFS

邻接矩阵存储
#include <stdio.h>
#include <stdlib.h>
#define MAXN 100
int G[MAXN][MAXN], Nv, Ne;
void BuildGraph()
{
int i,j,v1,v2,w;
scanf("%d",&Nv);
for(i=0; i<Nv; i++)
{
for(j=0; j<Nv; j++)
{
G[i][j] = 0;
}
}
scanf("%d",&Ne);
for(i=0; i<Ne; i++)
{
scanf("%d %d %d",&v1,&v2,&w);
G[v1][v2] = w;
G[v2][v1] = w;
}
}
void printGraph()
{
for(int i=0;i < Nv; i++)
{
for(int j=0; j<Nv; j++)
{
printf("%d ", G[i][j]);
}
printf("\n");
}
}
typedef int Vertex;
#define TRUE 1
#define FALSE 0
typedef int Boolean;
Boolean visited[MAXN];
Boolean IsFirst = TRUE;
void dfs(Vertex V)
{
visited[V] = TRUE;
if(IsFirst)
{
printf("%c",(char)(97 + V));
IsFirst = FALSE;
}
else
printf("->%c",(char)(97 + V));
for(int j=0; j<Nv; j++)
{
if(G[V][j]==1 && visited[j] == FALSE)
dfs(j);
}
}
int main()
{
BuildGraph();
printGraph();
bfs(0);
return 0;
}
6
7
0 1 1
0 2 1
0 4 1
1 4 1
2 5 1
3 4 1
3 5 1
0 1 1 0 1 0
1 0 0 0 1 0
1 0 0 0 0 1
0 0 0 0 1 1
1 1 0 1 0 0
0 0 1 1 0 0
a->b->e->d->f->c
邻接表存储
/* 邻接表存储的图 - DFS */
void Visit( Vertex V )
{
printf("正在访问顶点%d\n", V);
}
/* Visited[]为全局变量,已经初始化为false */
void DFS( LGraph Graph, Vertex V, void (*Visit)(Vertex) )
{ /* 以V为出发点对邻接表存储的图Graph进行DFS搜索 */
PtrToAdjVNode W;
Visit( V ); /* 访问第V个顶点 */
Visited[V] = true; /* 标记V已访问 */
for( W=Graph->G[V].FirstEdge; W; W=W->Next ) /* 对V的每个邻接点W->AdjV */
if ( !Visited[W->AdjV] ) /* 若W->AdjV未被访问 */
DFS( Graph, W->AdjV, Visit ); /* 则递归访问之 */
}
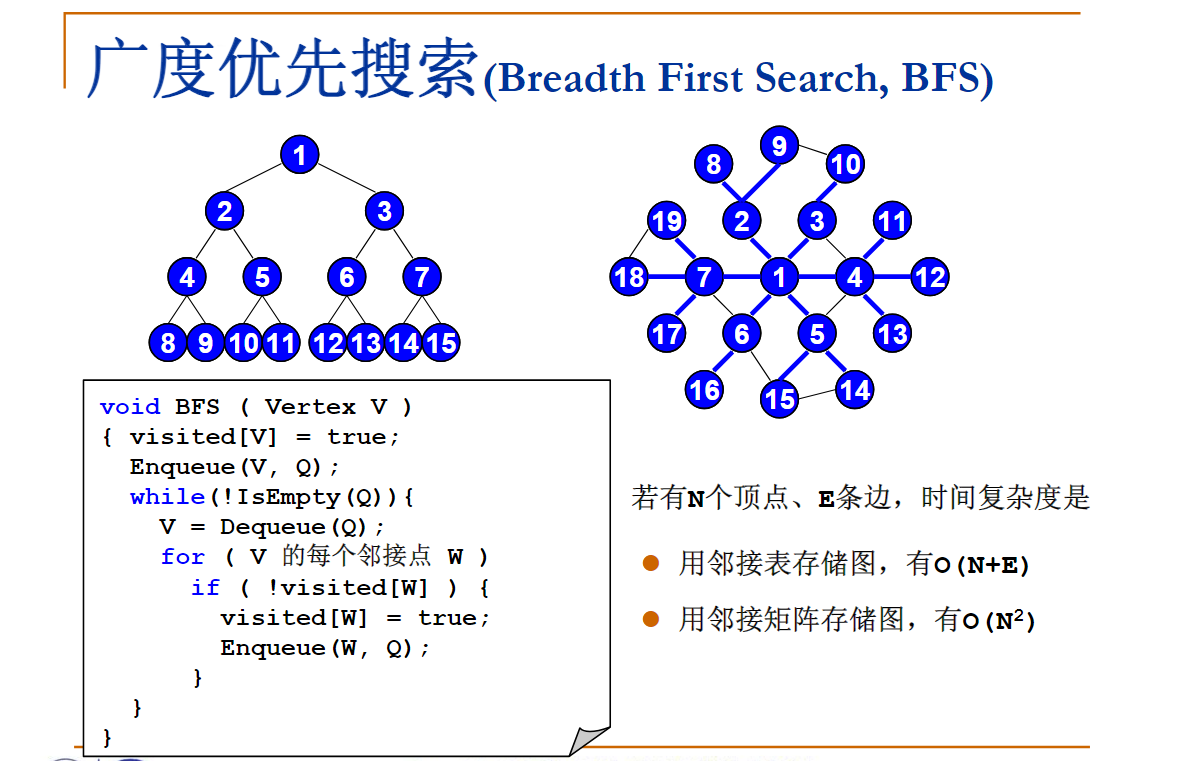
广度优先搜索BFS
邻接矩阵存储
/* 邻接矩阵存储的图 - BFS */
/* IsEdge(Graph, V, W)检查<V, W>是否图Graph中的一条边,即W是否V的邻接点。 */
/* 此函数根据图的不同类型要做不同的实现,关键取决于对不存在的边的表示方法。*/
/* 例如对有权图, 如果不存在的边被初始化为INFINITY, 则函数实现如下: */
bool IsEdge( MGraph Graph, Vertex V, Vertex W )
{
return Graph->G[V][W]<INFINITY ? true : false;
}
/* Visited[]为全局变量,已经初始化为false */
void BFS ( MGraph Graph, Vertex S, void (*Visit)(Vertex) )
{ /* 以S为出发点对邻接矩阵存储的图Graph进行BFS搜索 */
Queue Q;
Vertex V, W;
Q = CreateQueue( MaxSize ); /* 创建空队列, MaxSize为外部定义的常数 */
/* 访问顶点S:此处可根据具体访问需要改写 */
Visit( S );
Visited[S] = true; /* 标记S已访问 */
AddQ(Q, S); /* S入队列 */
while ( !IsEmpty(Q) ) {
V = DeleteQ(Q); /* 弹出V */
for( W=0; W<Graph->Nv; W++ ) /* 对图中的每个顶点W */
/* 若W是V的邻接点并且未访问过 */
if ( !Visited[W] && IsEdge(Graph, V, W) ) {
/* 访问顶点W */
Visit( W );
Visited[W] = true; /* 标记W已访问 */
AddQ(Q, W); /* W入队列 */
}
} /* while结束*/
}
邻接矩阵存储、BFS实例
#include <stdio.h>
#include <stdlib.h>
#define MAXN 100
int G[MAXN][MAXN], Nv, Ne;
void BuildGraph()
{
int i,j,v1,v2,w;
scanf("%d",&Nv);
for(i=0; i<Nv; i++)
{
for(j=0; j<Nv; j++)
{
G[i][j] = 0;
}
}
scanf("%d",&Ne);
for(i=0; i<Ne; i++)
{
scanf("%d %d %d",&v1,&v2,&w);
G[v1][v2] = w;
G[v2][v1] = w;
}
}
void printGraph()
{
for(int i=0;i < Nv; i++)
{
for(int j=0; j<Nv; j++)
{
printf("%d ", G[i][j]);
}
printf("\n");
}
}
typedef int Vertex;
#define TRUE 1
#define FALSE 0
typedef int Boolean;
Boolean visited[MAXN];
Boolean IsFirst = TRUE;
void bfs(Vertex V)
{
int queue[100];
int front = 0;
int tail = 0;
visited[V] = TRUE;
queue[tail++] = V;
int temp;
while(front != tail)
{
temp = queue[front++];
if(IsFirst)
{
printf("%c",(char)(97 + temp));
IsFirst = FALSE;
}
else
printf("->%c",(char)(97 + temp));
for(int i=0;i <Nv; i++)
{
if(G[temp][i] == 1 && visited[i] == FALSE)
{
visited[i] = TRUE;
queue[tail++] = i;
}
}
}
}
int main()
{
BuildGraph();
printGraph();
bfs(0);
return 0;
}
0 1 1 0 1 0
1 0 0 0 1 0
1 0 0 0 0 1
0 0 0 0 1 1
1 1 0 1 0 0
0 0 1 1 0 0
a->b->c->e->f->d
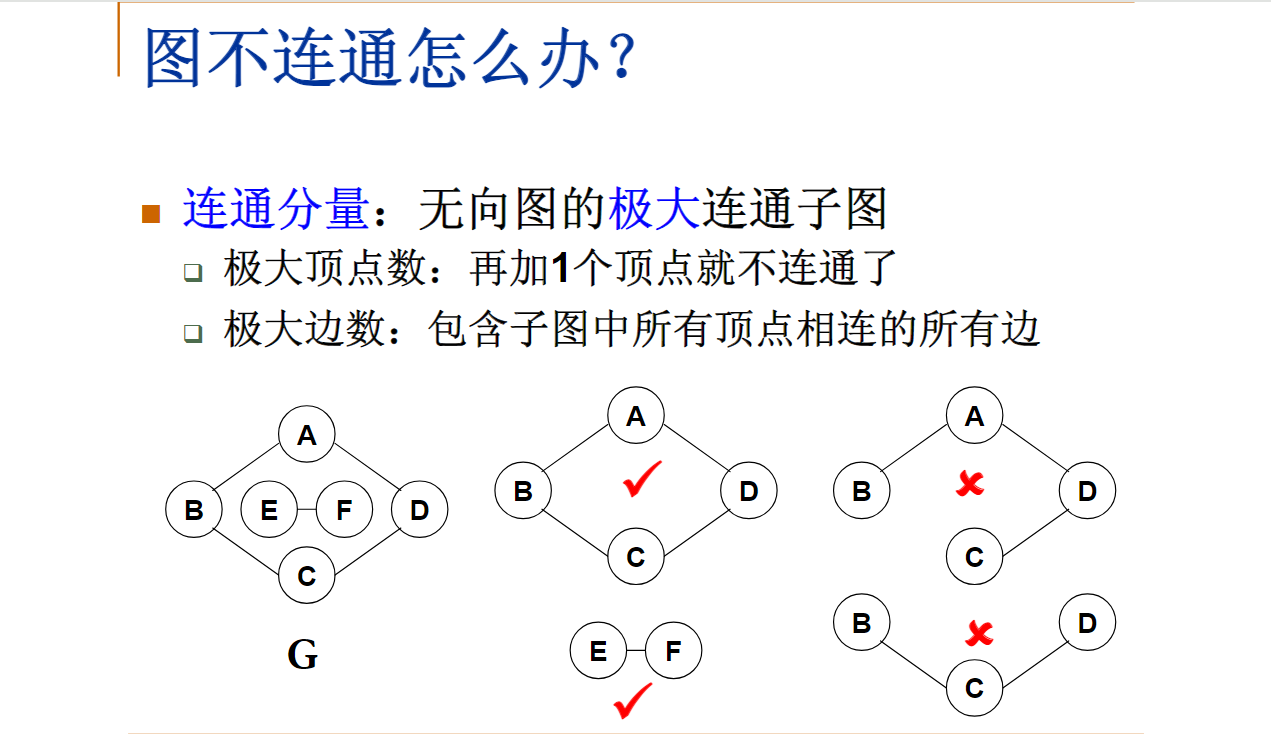
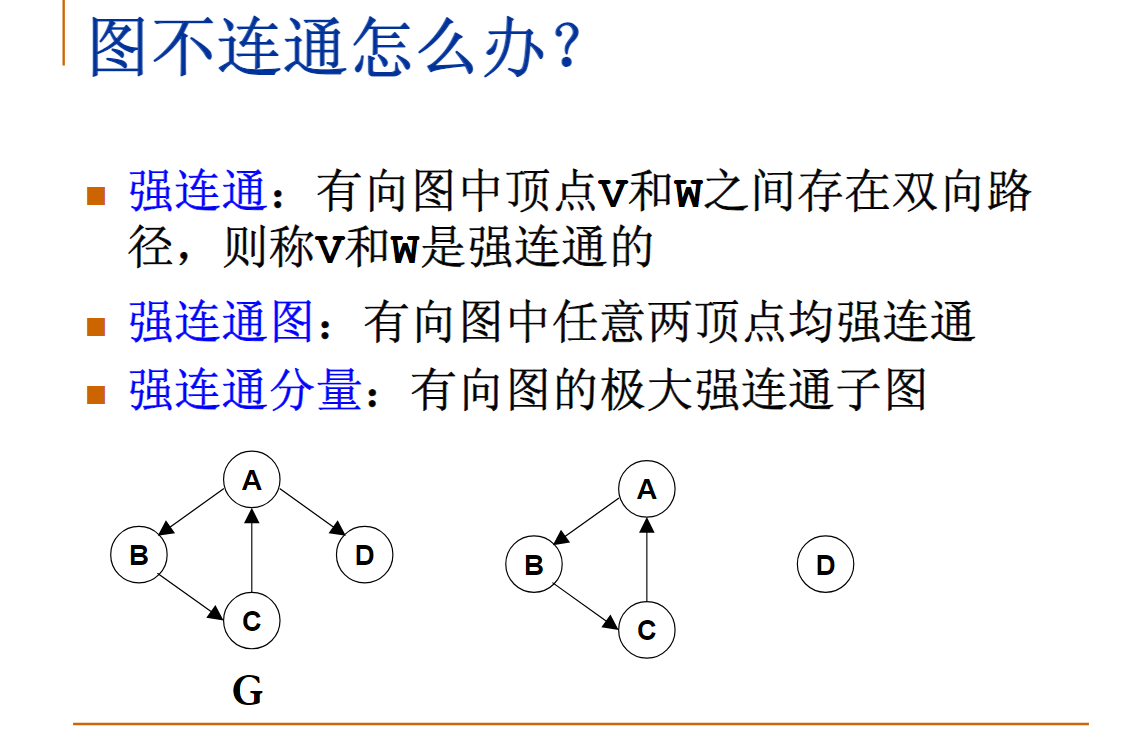
连通图

具有N个顶点的无向图至多有多少个连通分量?N
如果从无向图的任一顶点出发进行一次深度优先搜索可访问所有顶点,则该图一定是连通图
具有N个顶点的无向图至少有多少个连通分量?1