图的存储
邻接矩阵
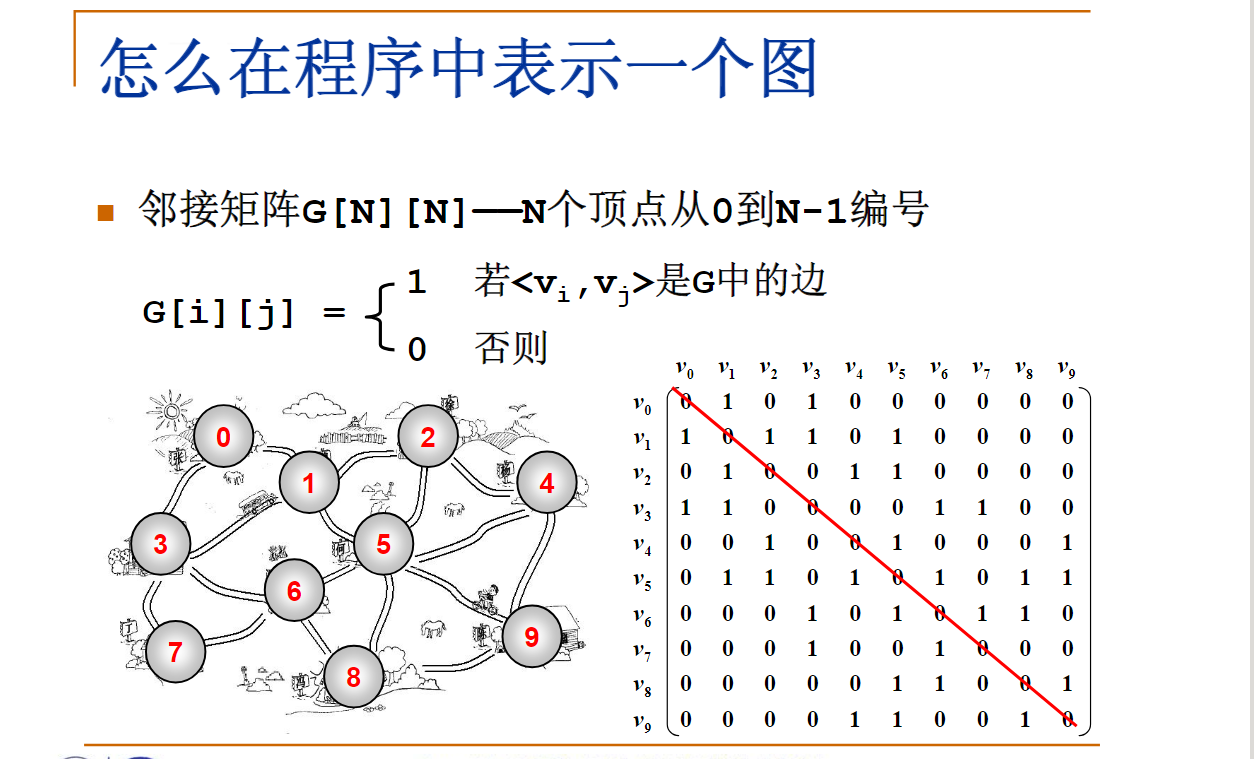
对于有N个顶点的无向图,怎样存储可以省一半空间?
正确答案:用一个长度为N(N+1)/2的1维数组
用一维数组G[ ]存储有4个顶点的无向图如下:G[ ] = { 0, 1, 0, 1, 1, 0, 0, 0, 1, 0 }
则顶点2和顶点0之间是有边的。 ✔
有N个顶点的无向完全图有多少条边?N(N-1)/2



完整版本代码
#include <stdio.h>
#include <stdlib.h>
/* 图的邻接矩阵表示法 */
#define MaxVertexNum 100 /* 最大顶点数设为100 */
#define INFINITY 65535 /* ∞设为双字节无符号整数的最大值65535*/
typedef int Vertex; /* 用顶点下标表示顶点,为整型 */
typedef int WeightType; /* 边的权值设为整型 */
typedef char DataType; /* 顶点存储的数据类型设为字符型 */
/* 边的定义 */
typedef struct ENode *PtrToENode;
struct ENode{
Vertex V1, V2; /* 有向边<V1, V2> */
WeightType Weight; /* 权重 */
};
typedef PtrToENode Edge;
/* 图结点的定义 */
typedef struct GNode *PtrToGNode;
struct GNode{
int Nv; /* 顶点数 */
int Ne; /* 边数 */
WeightType G[MaxVertexNum][MaxVertexNum]; /* 邻接矩阵 */
DataType Data[MaxVertexNum]; /* 存顶点的数据 */
/* 注意:很多情况下,顶点无数据,此时Data[]可以不用出现 */
};
typedef PtrToGNode MGraph; /* 以邻接矩阵存储的图类型 */
MGraph CreateGraph( int VertexNum )
{ /* 初始化一个有VertexNum个顶点但没有边的图 */
Vertex V, W;
MGraph Graph;
Graph = (MGraph)malloc(sizeof(struct GNode)); /* 建立图 */
Graph->Nv = VertexNum;
Graph->Ne = 0;
/* 初始化邻接矩阵 */
/* 注意:这里默认顶点编号从0开始,到(Graph->Nv - 1) */
for (V=0; V<Graph->Nv; V++)
for (W=0; W<Graph->Nv; W++)
Graph->G[V][W] = INFINITY;
return Graph;
}
void InsertEdge( MGraph Graph, Edge E )
{
/* 插入边 <V1, V2> */
Graph->G[E->V1][E->V2] = E->Weight;
/* 若是无向图,还要插入边<V2, V1> */
Graph->G[E->V2][E->V1] = E->Weight;
}
MGraph BuildGraph()
{
MGraph Graph;
Edge E;
Vertex V;
int Nv, i;
scanf("%d", &Nv); /* 读入顶点个数 */
Graph = CreateGraph(Nv); /* 初始化有Nv个顶点但没有边的图 */
scanf("%d", &(Graph->Ne)); /* 读入边数 */
if ( Graph->Ne != 0 ) { /* 如果有边 */
E = (Edge)malloc(sizeof(struct ENode)); /* 建立边结点 */
/* 读入边,格式为"起点 终点 权重",插入邻接矩阵 */
for (i=0; i<Graph->Ne; i++) {
scanf("%d %d %d", &E->V1, &E->V2, &E->Weight);
/* 注意:如果权重不是整型,Weight的读入格式要改 */
InsertEdge( Graph, E );
}
}
/* 如果顶点有数据的话,读入数据 */
for (V=0; V<Graph->Nv; V++)
scanf(" %c", &(Graph->Data[V]));
return Graph;
}
简化版本代码
#include <stdio.h>
#include <stdlib.h>
#define MAXN 100
int G[MAXN][MAXN];
int visited[MAXN];
int Ne,Nv;
void InitVisited()
{
for(int i=0; i<MAXN; i++)
visited[i] = 0;
}
void BuildGraph()
{
for(int i=0; i<MAXN; i++)
{
for(int j=0; j<MAXN; j++)
{
G[i][j] = 0;
}
}
scanf("%d %d",&Nv, &Ne);
if(Ne)
{
for(int i=0; i<Ne; i++)
{
int v1,v2,weight;
scanf("%d %d %d",&v1,&v2,&weight);
G[v1][v2] = weight;
G[v2][v1] = weight;
}
}
}
void dfs(int v)
{
visited[v] = 1;
printf("%d ",v);
for(int i=0; i<Nv; i++)
{
if(visited[i]==0 &&G[v][i]!=0)
{
dfs(i);
}
}
}
int main()
{
BuildGraph();
InitVisited();
dfs(0);
return 0;
}
输入数据:
6 7
0 1 1
0 2 1
0 4 1
1 4 1
2 5 1
3 4 1
3 5 1
输出结果:
0 1 4 3 5 2
邻接表
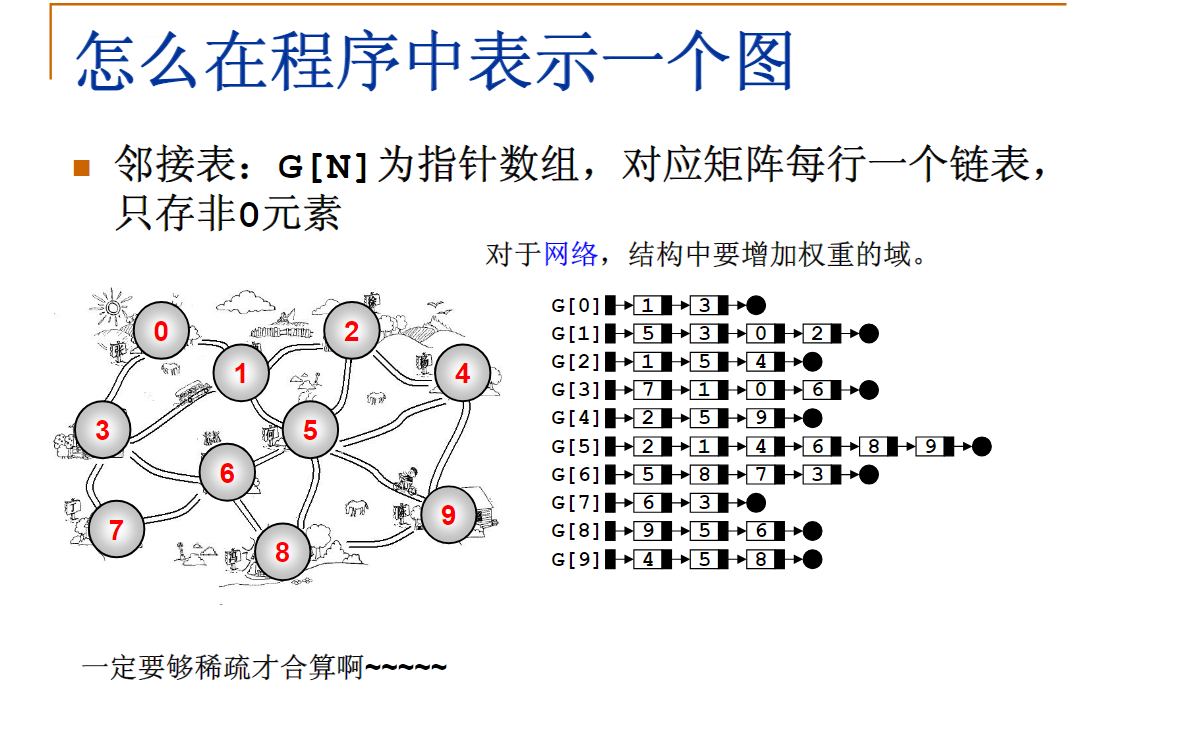

用邻接表表示有N个顶点、E条边的图,则遍历图中所有边的时间复杂度为:O(N+E)
需要N个头指针 + 2E个结点(每个结点至少2个域),则E小于多少是省空间的?
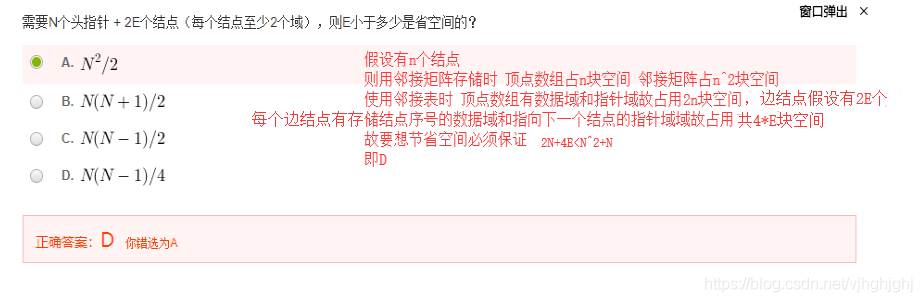
《数据结构》课程给出的图的邻接表表示法如下:
完整版本代码
/* 图的邻接表表示法 */
#define MaxVertexNum 100 /* 最大顶点数设为100 */
typedef int Vertex; /* 用顶点下标表示顶点,为整型 */
typedef int WeightType; /* 边的权值设为整型 */
typedef char DataType; /* 顶点存储的数据类型设为字符型 */
/* 边的定义 */
typedef struct ENode *PtrToENode;
struct ENode{
Vertex V1, V2; /* 有向边<V1, V2> */
WeightType Weight; /* 权重 */
};
typedef PtrToENode Edge;
/* 邻接点的定义 */
typedef struct AdjVNode *PtrToAdjVNode;
struct AdjVNode{
Vertex AdjV; /* 邻接点下标 */
WeightType Weight; /* 边权重 */
PtrToAdjVNode Next; /* 指向下一个邻接点的指针 */
};
/* 顶点表头结点的定义 */
typedef struct Vnode{
PtrToAdjVNode FirstEdge;/* 边表头指针 */
DataType Data; /* 存顶点的数据 */
/* 注意:很多情况下,顶点无数据,此时Data可以不用出现 */
} AdjList[MaxVertexNum]; /* AdjList是邻接表类型 */
/* 图结点的定义 */
typedef struct GNode *PtrToGNode;
struct GNode{
int Nv; /* 顶点数 */
int Ne; /* 边数 */
AdjList G; /* 邻接表 */
};
typedef PtrToGNode LGraph; /* 以邻接表方式存储的图类型 */
LGraph CreateGraph( int VertexNum )
{ /* 初始化一个有VertexNum个顶点但没有边的图 */
Vertex V;
LGraph Graph;
Graph = (LGraph)malloc( sizeof(struct GNode) ); /* 建立图 */
Graph->Nv = VertexNum;
Graph->Ne = 0;
/* 初始化邻接表头指针 */
/* 注意:这里默认顶点编号从0开始,到(Graph->Nv - 1) */
for (V=0; V<Graph->Nv; V++)
Graph->G[V].FirstEdge = NULL;
return Graph;
}
void InsertEdge( LGraph Graph, Edge E )
{
PtrToAdjVNode NewNode;
/* 插入边 <V1, V2> */
/* 为V2建立新的邻接点 */
NewNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
NewNode->AdjV = E->V2;
NewNode->Weight = E->Weight;
/* 将V2插入V1的表头 */
NewNode->Next = Graph->G[E->V1].FirstEdge;
Graph->G[E->V1].FirstEdge = NewNode;
/* 若是无向图,还要插入边 <V2, V1> */
/* 为V1建立新的邻接点 */
NewNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
NewNode->AdjV = E->V1;
NewNode->Weight = E->Weight;
/* 将V1插入V2的表头 */
NewNode->Next = Graph->G[E->V2].FirstEdge;
Graph->G[E->V2].FirstEdge = NewNode;
}
LGraph BuildGraph()
{
LGraph Graph;
Edge E;
Vertex V;
int Nv, i;
scanf("%d", &Nv); /* 读入顶点个数 */
Graph = CreateGraph(Nv); /* 初始化有Nv个顶点但没有边的图 */
scanf("%d", &(Graph->Ne)); /* 读入边数 */
if ( Graph->Ne != 0 ) { /* 如果有边 */
E = (Edge)malloc( sizeof(struct ENode) ); /* 建立边结点 */
/* 读入边,格式为"起点 终点 权重",插入邻接矩阵 */
for (i=0; i<Graph->Ne; i++) {
scanf("%d %d %d", &E->V1, &E->V2, &E->Weight);
/* 注意:如果权重不是整型,Weight的读入格式要改 */
InsertEdge( Graph, E );
}
}
/* 如果顶点有数据的话,读入数据 */
for (V=0; V<Graph->Nv; V++)
scanf(" %c", &(Graph->G[V].Data));
return Graph;
}
邻接表存储、DFS遍历实例
#include <stdio.h>
#include <stdlib.h>
#define MaxVertexNum 100 /* 最大顶点数设为100 */
typedef int Vertex; /* 用顶点下标表示顶点,为整型 */
typedef int WeightType; /* 边的权值设为整型 */
typedef char DataType; /* 顶点存储的数据类型设为字符型 */
int Visited[MaxVertexNum];
void InitVisited()
{
for(int i=0; i<MaxVertexNum; i++)
Visited[i] = 0;
}
/* 边的定义 */
typedef struct ENode *PtrToENode;
struct ENode{
Vertex V1, V2; /* 有向边<V1, V2> */
WeightType Weight; /* 权重 */
};
typedef PtrToENode Edge;
typedef struct AdjVNode *PtrToAdjVNode;
struct AdjVNode
{
Vertex AdjV;
WeightType Weight;
PtrToAdjVNode Next;
};
typedef struct VNode
{
PtrToAdjVNode FirstEdge;
}AdjList[MaxVertexNum];
typedef struct GNode *PtrToGNode;
struct GNode
{
int Ne;
int Nv;
AdjList G;
};
typedef PtrToGNode LGraph;
LGraph CreateGraph(int VertexNum)
{
LGraph Graph = (LGraph)malloc(sizeof(struct GNode));
Graph->Nv = VertexNum;
Graph->Ne = 0;
for(int i=0; i<Graph->Nv; i++)
{
Graph->G[i].FirstEdge = NULL;
}
return Graph;
}
void InsertEdge(LGraph Graph, Edge E)
{
PtrToAdjVNode newNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
newNode->AdjV = E->V2;
newNode->Weight = E->Weight;
newNode->Next = Graph->G[E->V1].FirstEdge;
Graph->G[E->V1].FirstEdge = newNode;
newNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
newNode->AdjV = E->V1;
newNode->Weight = E->Weight;
newNode->Next = Graph->G[E->V2].FirstEdge;
Graph->G[E->V2].FirstEdge = newNode;
}
LGraph BuildGraph()
{
LGraph Graph = (LGraph)malloc(sizeof(struct GNode));
Edge E;
int Nv;
scanf("%d", &Nv);
Graph = CreateGraph(Nv);
scanf("%d", &(Graph->Ne));
if(Graph->Ne != 0)
{
for(int i=0; i<Graph->Ne; i++)
{
E = (Edge)malloc(sizeof(struct ENode));
scanf("%d %d %d",&E->V1,&E->V2,&E->Weight);
InsertEdge(Graph, E);
}
}
return Graph;
}
/* 邻接表存储的图 - DFS */
void Visit( Vertex V )
{
printf("正在访问顶点%d\n", V);
}
/* Visited[]为全局变量,已经初始化为false */
void DFS( LGraph Graph, Vertex V, void (*Visit)(Vertex) )
{ /* 以V为出发点对邻接表存储的图Graph进行DFS搜索 */
PtrToAdjVNode W;
Visit( V ); /* 访问第V个顶点 */
Visited[V] = 1; /* 标记V已访问 */
for( W=Graph->G[V].FirstEdge; W; W=W->Next ) /* 对V的每个邻接点W->AdjV */
if ( !Visited[W->AdjV] ) /* 若W->AdjV未被访问 */
DFS( Graph, W->AdjV, Visit ); /* 则递归访问之 */
}
void PrintList(LGraph Graph)
{
for(int i=0; i<Graph->Nv; i++)
{
PtrToAdjVNode W = Graph->G[i].FirstEdge;
printf("G[%d]:", i);
int IsFirst = 1;
while(W)
{
if(IsFirst)
{
printf("%d", W->AdjV);
IsFirst = 0;
}
else
printf("->%d", W->AdjV);
W = W->Next;
}
printf("\n");
}
}
int main()
{
LGraph Graph = BuildGraph();
InitVisited();
DFS(Graph, 0, Visit);
PrintList(Graph);
return 0;
}
输入数据:
6
7
0 1 1
0 2 1
0 4 1
1 4 1
2 5 1
3 4 1
3 5 1
输出结果:
正在访问顶点0
正在访问顶点4
正在访问顶点3
正在访问顶点5
正在访问顶点2
正在访问顶点1
G[0]:4->2->1
G[1]:4->0
G[2]:5->0
G[3]:5->4
G[4]:3->1->0
G[5]:3->2