查找算法
普通查找算法
顺序查找
- 被查找的数存放在一个数组中
- 从数组的第一个元素开始,依次往下比较,直到找到要找的元素为止
下面程序能在一整数数组中查找元素x的存储位置
#include <iostream>
using namespace std;
int main() {
int k,x;
int array[]={2,3,1,7,5,8,9,0,4,6};
cout<<"输入要查找的元素值:";
cin>>x;
for(k=0;k<10;k++)
{
if(x==array[k])
{
cout<<k;
break;
}
}
if(k==10) cout<<"not found";
return 0;
}
二分查找
前提:数组已排序
#include <iostream>
using namespace std;
int main() {
int x;
int array[]={5,13,19,21,37,56,64,74,80,88,92};
int high,low,mid;
cout<<"输入要查找的元素值:";
cin>>x;
low=0;
high=10;
while(low<=high)
{
mid=(high-low)/2+low;
if(x==array[mid])
{
cout<<x<<"的位置是:"<<mid<<endl;
break;
}
if(x<array[mid]) high=mid-1;
else low=mid+1;
}
if(low>high) cout<<"找不到"<<x<<endl;
return 0;
}
散列查找
散列表




哈希是一种数据按照特定关系存储的存储结构
哈希函数:值与地址的特定关系
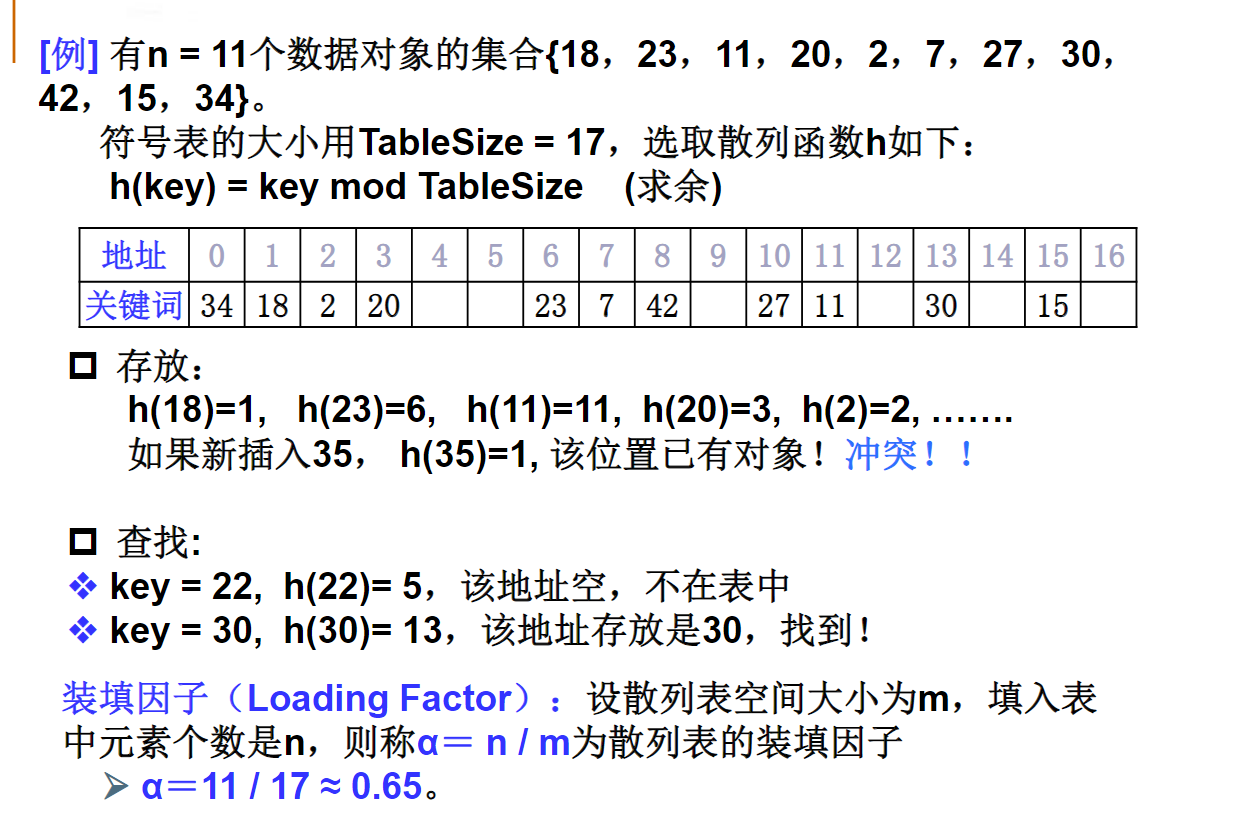
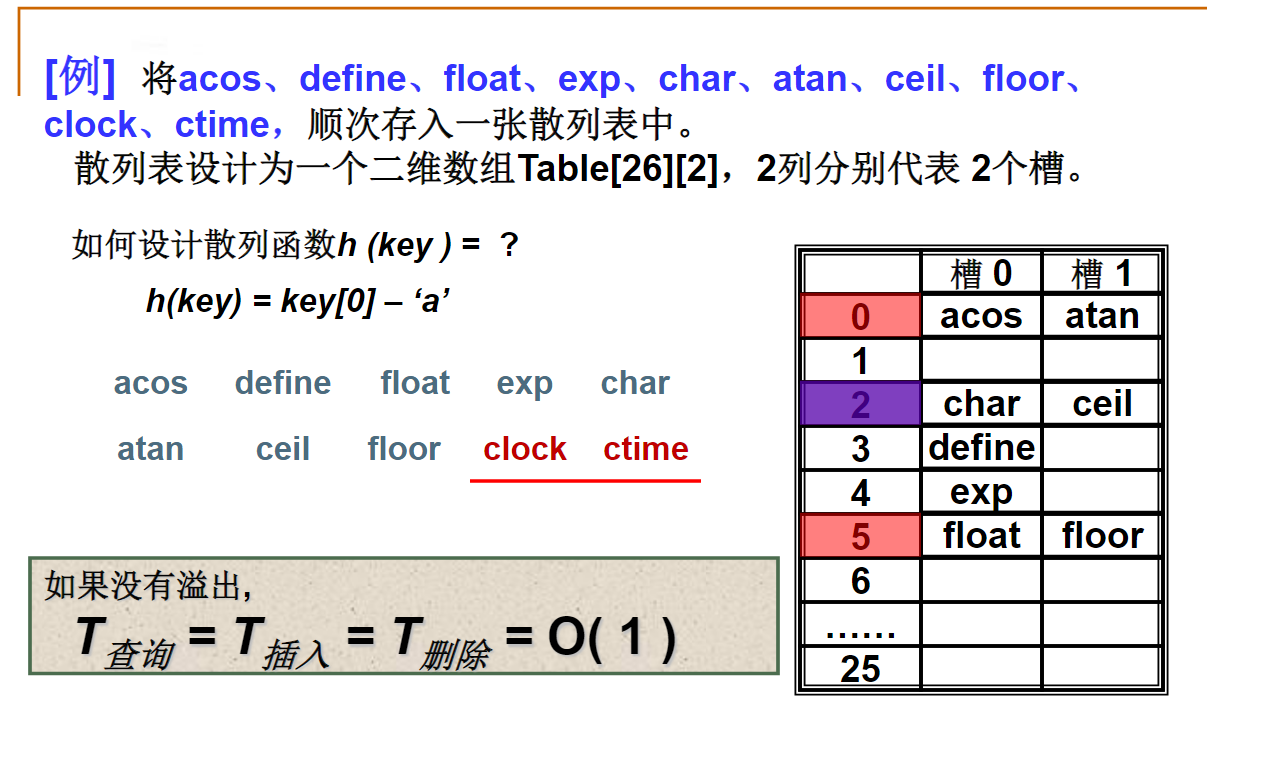
散列函数的构造方法
数字关键词的散列函数构造
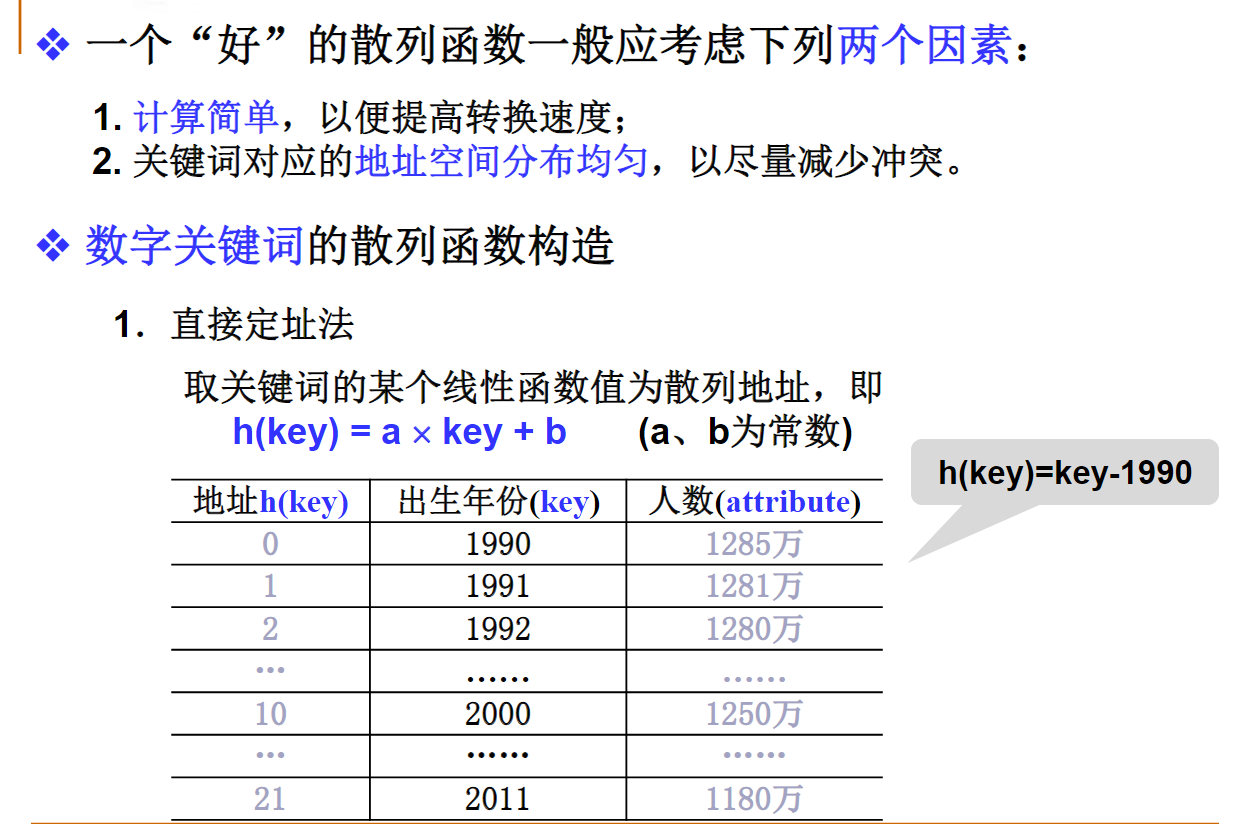
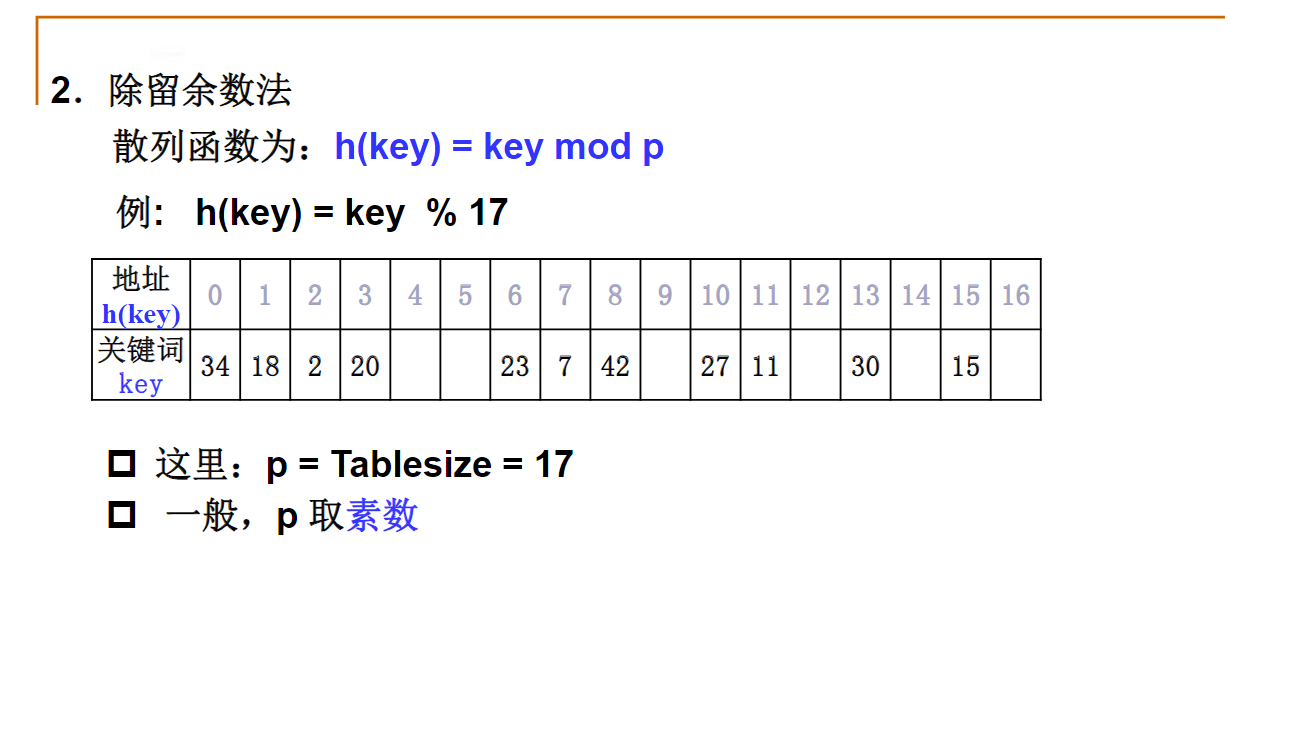


字符串关键词的散列函数构造


如果直接计算'a'*32^4+'b'*32^3+'c'*32^2+'d'*32+'e'所需要的乘法总次数是4+3+2+1=10次。
采用 ((('a'*32+'b')*32+'c')*32+'d')*32+'e'的计算方法,乘法总次数是多少?
(顺便思考一下两者时间效率的差别)
正确答案:4
冲突处理方法
开放定址法

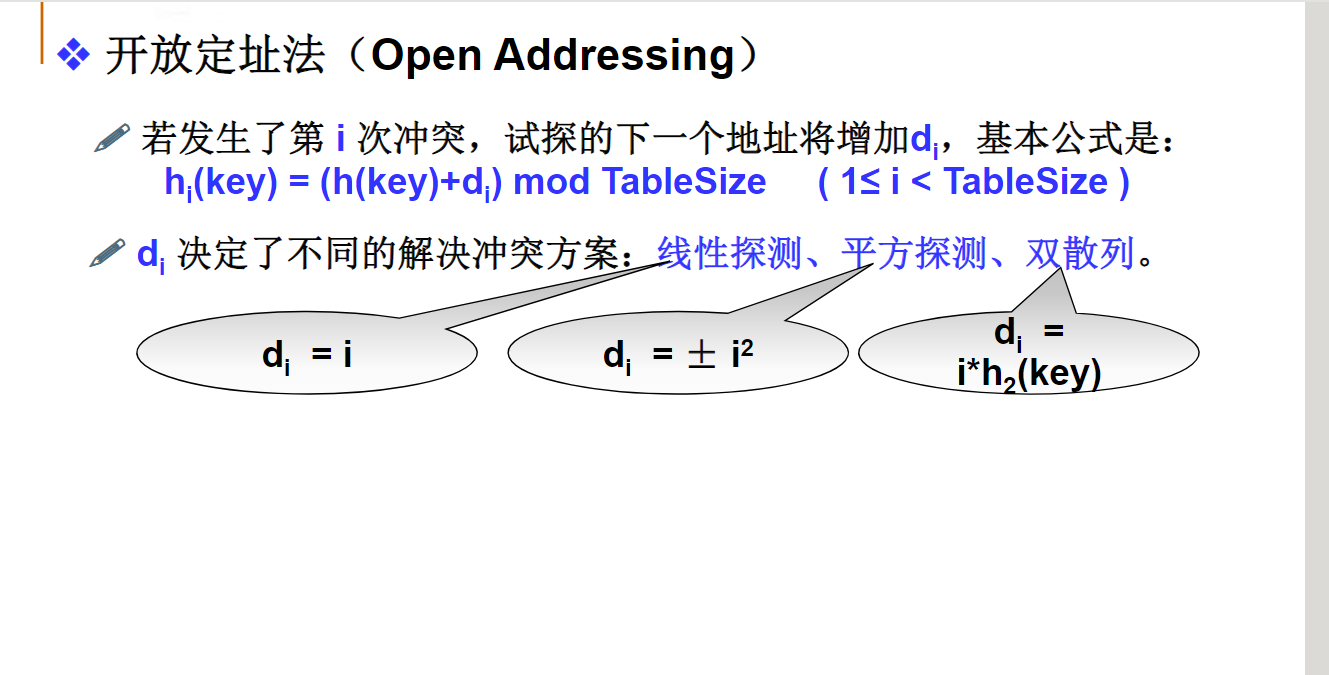
开放地址法代码:
#define MAXTABLESIZE 100000 /* 允许开辟的最大散列表长度 */
typedef int ElementType; /* 关键词类型用整型 */
typedef int Index; /* 散列地址类型 */
typedef Index Position; /* 数据所在位置与散列地址是同一类型 */
/* 散列单元状态类型,分别对应:有合法元素、空单元、有已删除元素 */
typedef enum { Legitimate, Empty, Deleted } EntryType;
typedef struct HashEntry Cell; /* 散列表单元类型 */
struct HashEntry{
ElementType Data; /* 存放元素 */
EntryType Info; /* 单元状态 */
};
typedef struct TblNode *HashTable; /* 散列表类型 */
struct TblNode { /* 散列表结点定义 */
int TableSize; /* 表的最大长度 */
Cell *Cells; /* 存放散列单元数据的数组 */
};
int NextPrime( int N )
{ /* 返回大于N且不超过MAXTABLESIZE的最小素数 */
int i, p = (N%2)? N+2 : N+1; /*从大于N的下一个奇数开始 */
while( p <= MAXTABLESIZE ) {
for( i=(int)sqrt(p); i>2; i-- )
if ( !(p%i) ) break; /* p不是素数 */
if ( i==2 ) break; /* for正常结束,说明p是素数 */
else p += 2; /* 否则试探下一个奇数 */
}
return p;
}
HashTable CreateTable( int TableSize )
{
HashTable H;
int i;
H = (HashTable)malloc(sizeof(struct TblNode));
/* 保证散列表最大长度是素数 */
H->TableSize = NextPrime(TableSize);
/* 声明单元数组 */
H->Cells = (Cell *)malloc(H->TableSize*sizeof(Cell));
/* 初始化单元状态为“空单元” */
for( i=0; i<H->TableSize; i++ )
H->Cells[i].Info = Empty;
return H;
}
线性探测
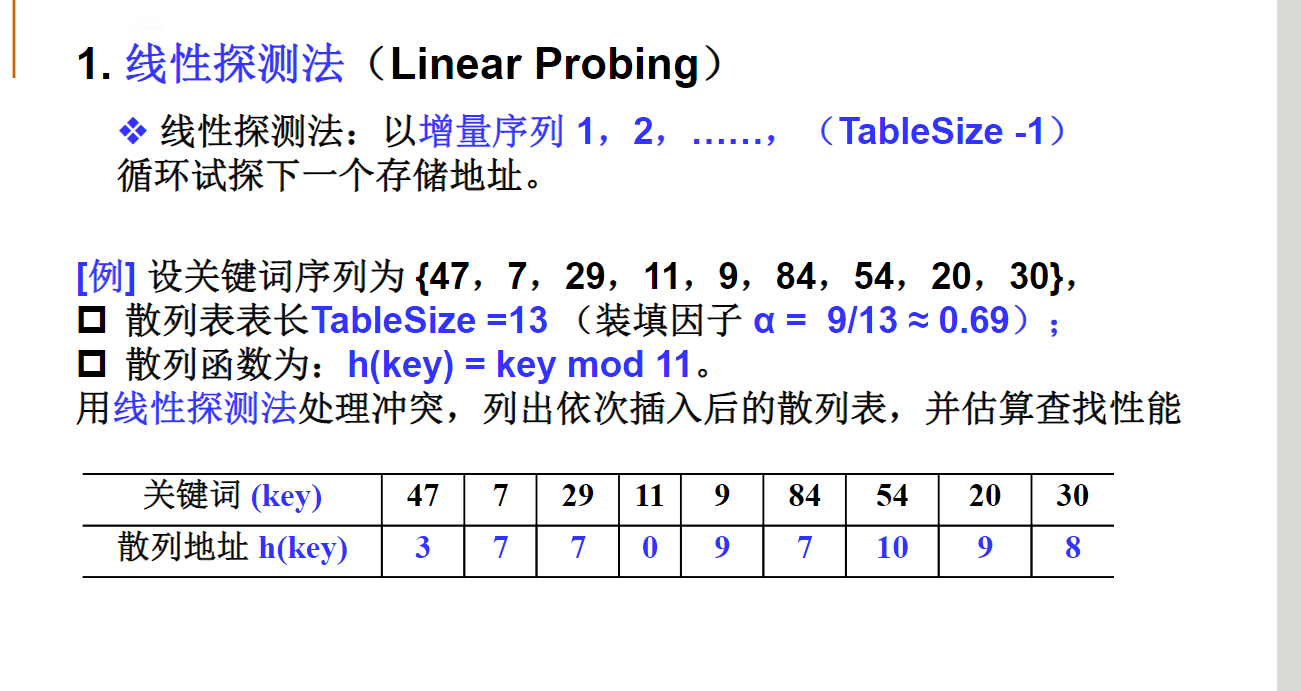
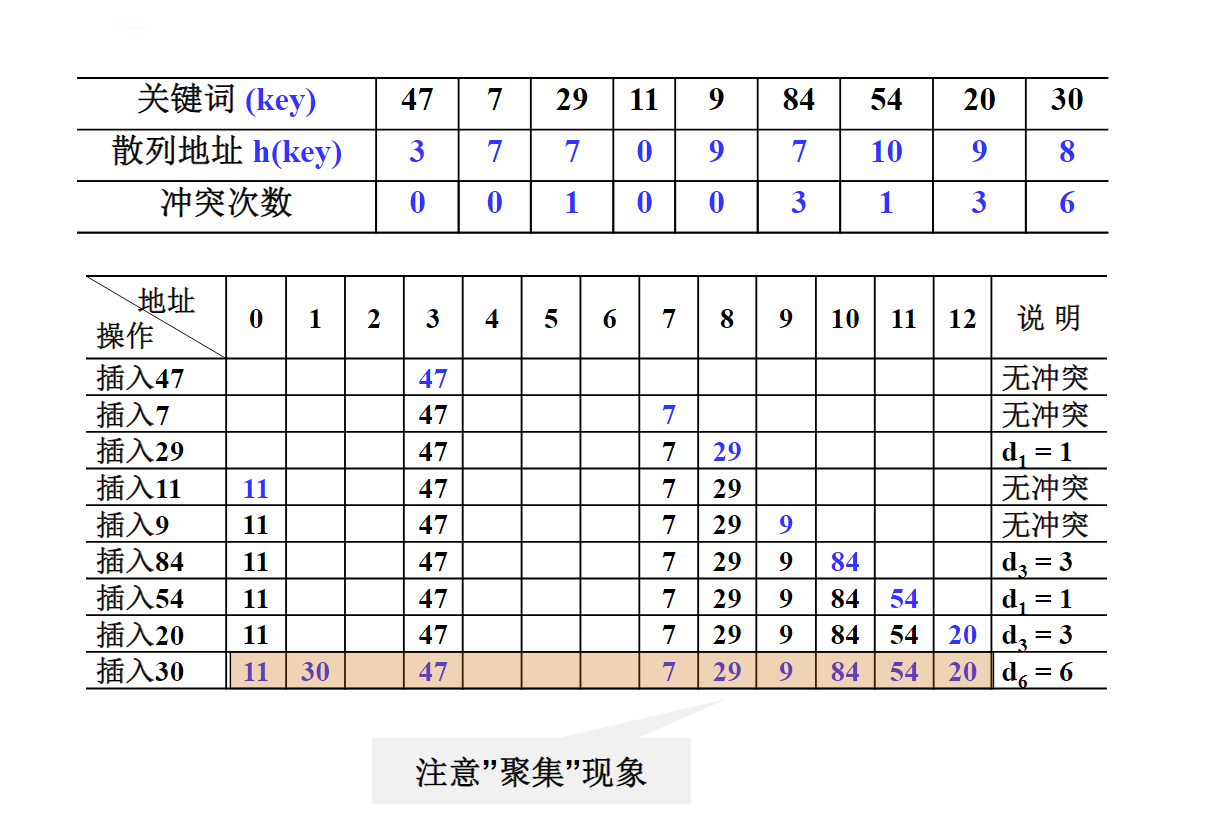
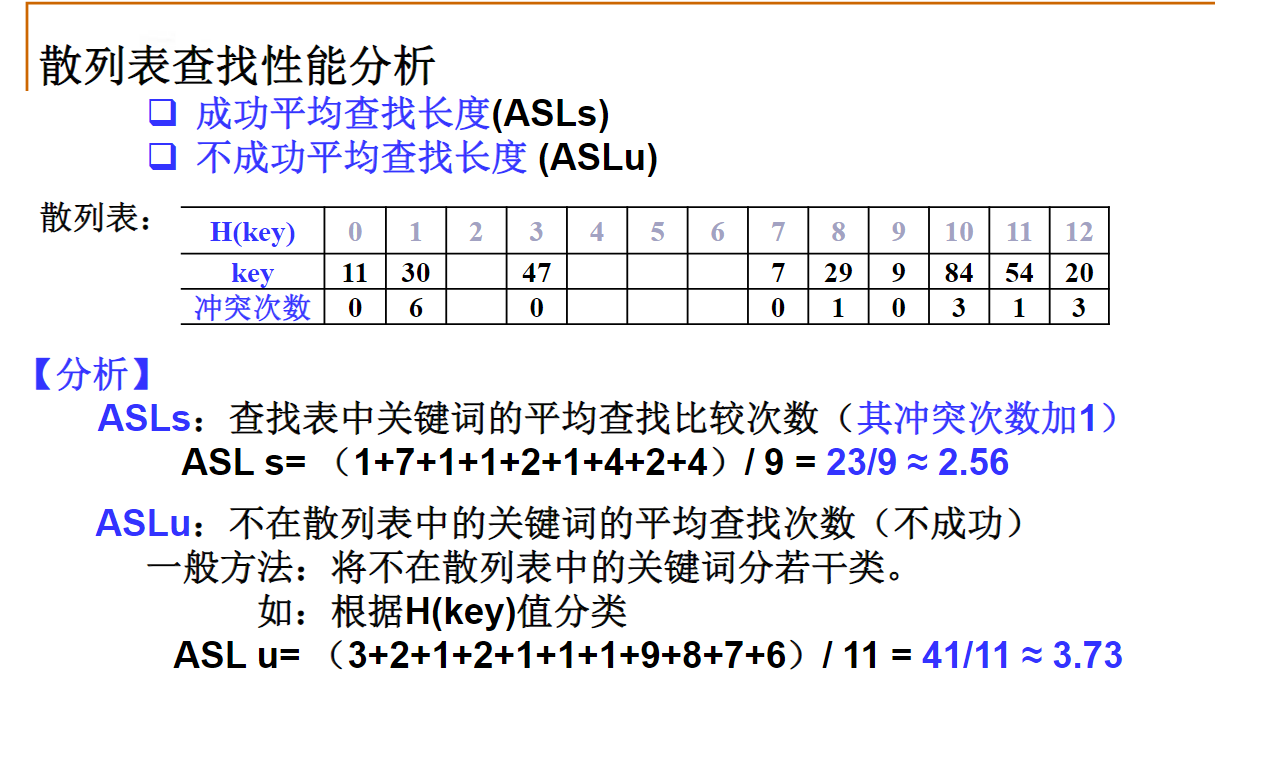
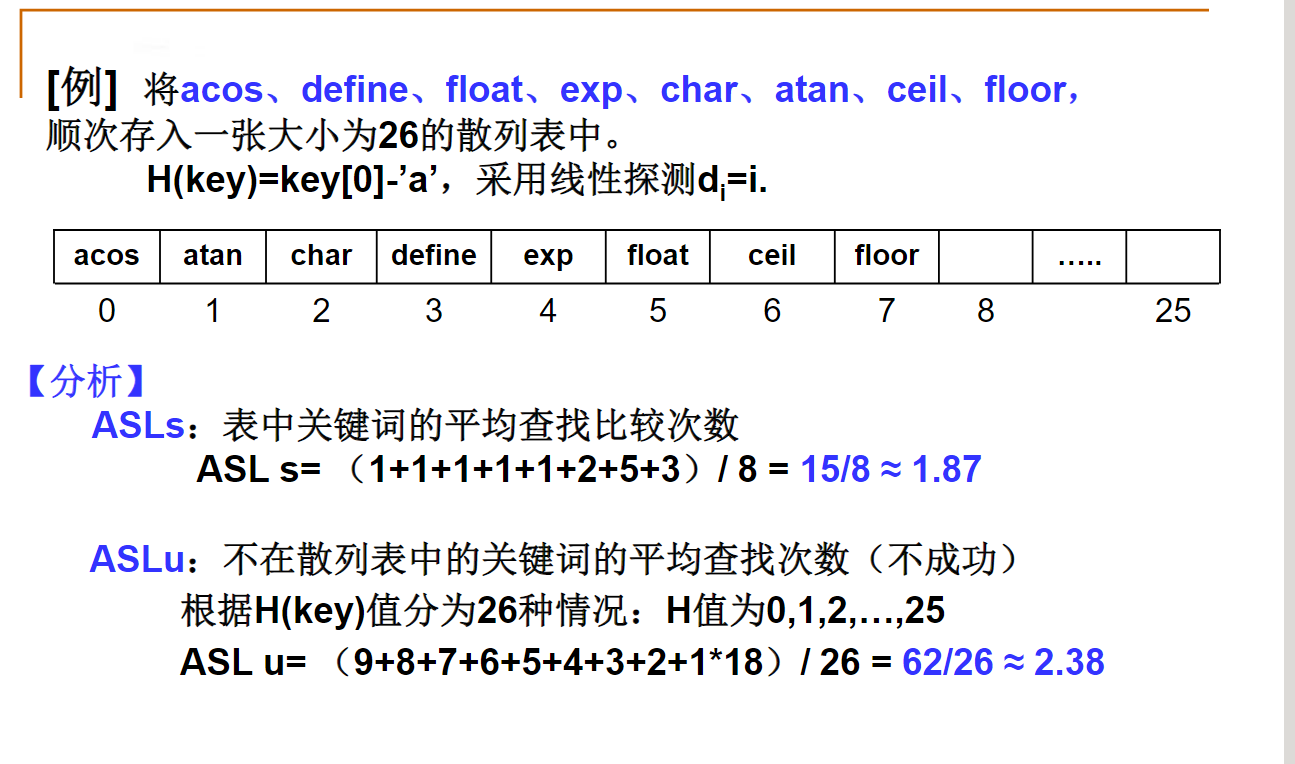
线性探测—字符串的例子
与例子相似,如果已知散列表的前8个位置有元素(但元素内容与例子不一样)而且后面18个位置也全是空位,那么平均不成功查找次数还是一样的.
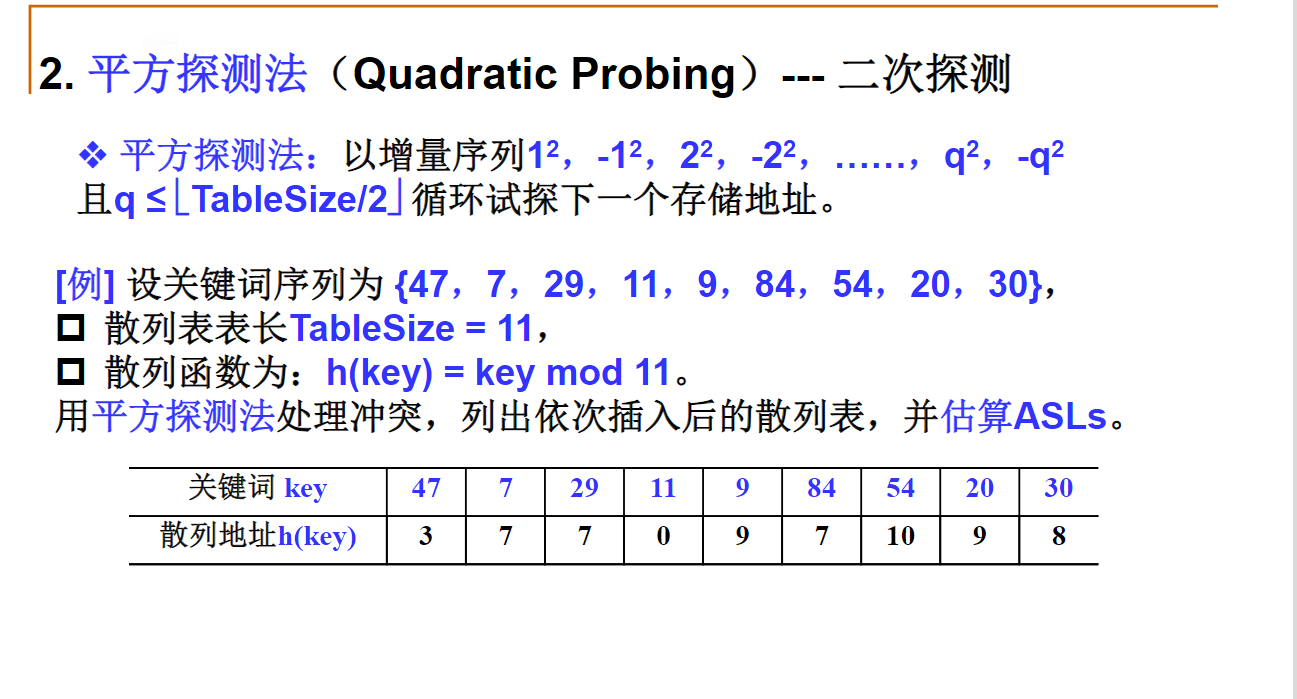
平方探测法
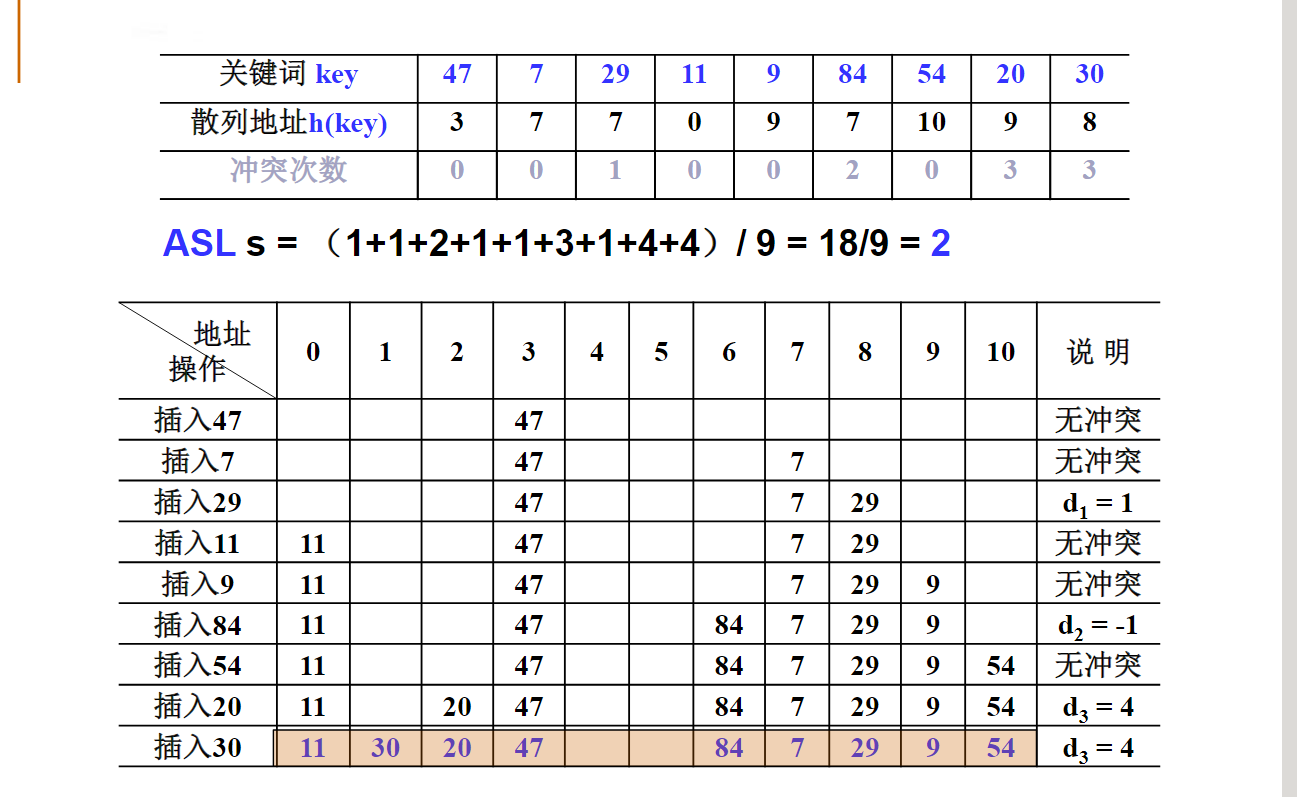
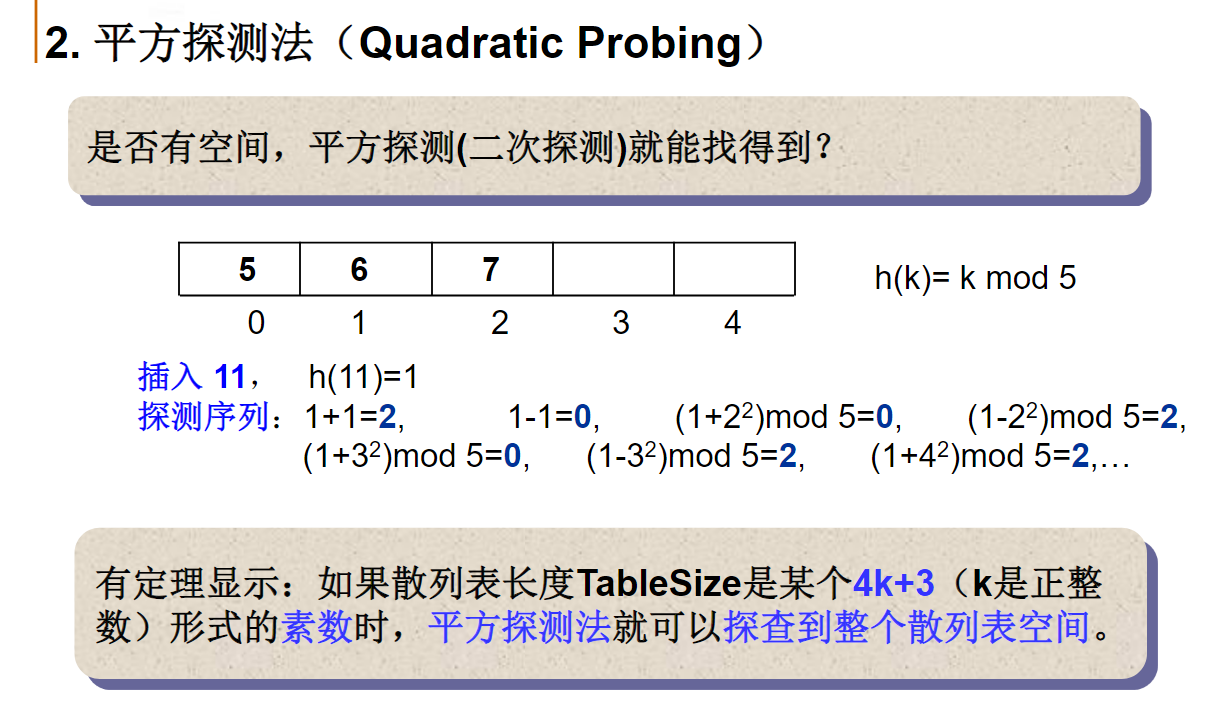
平方探测法的实现
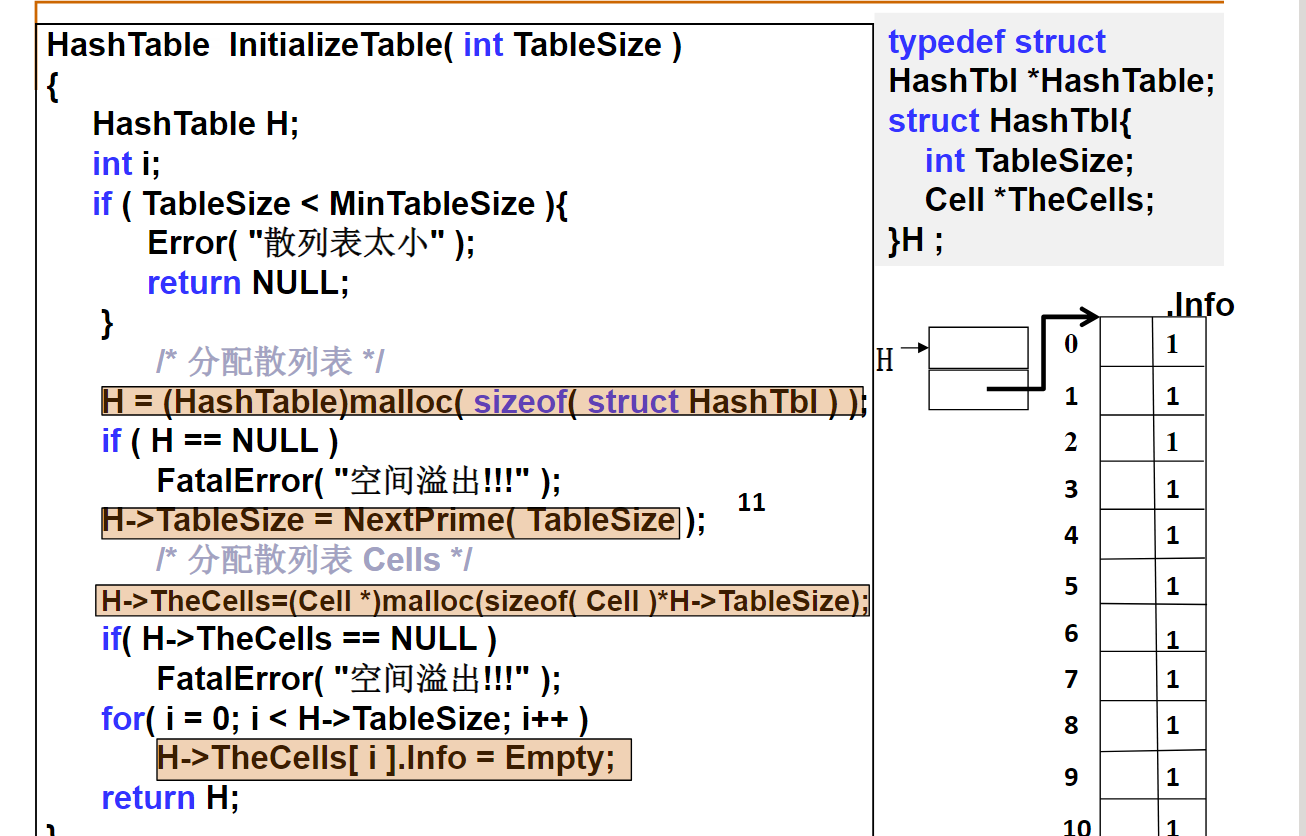
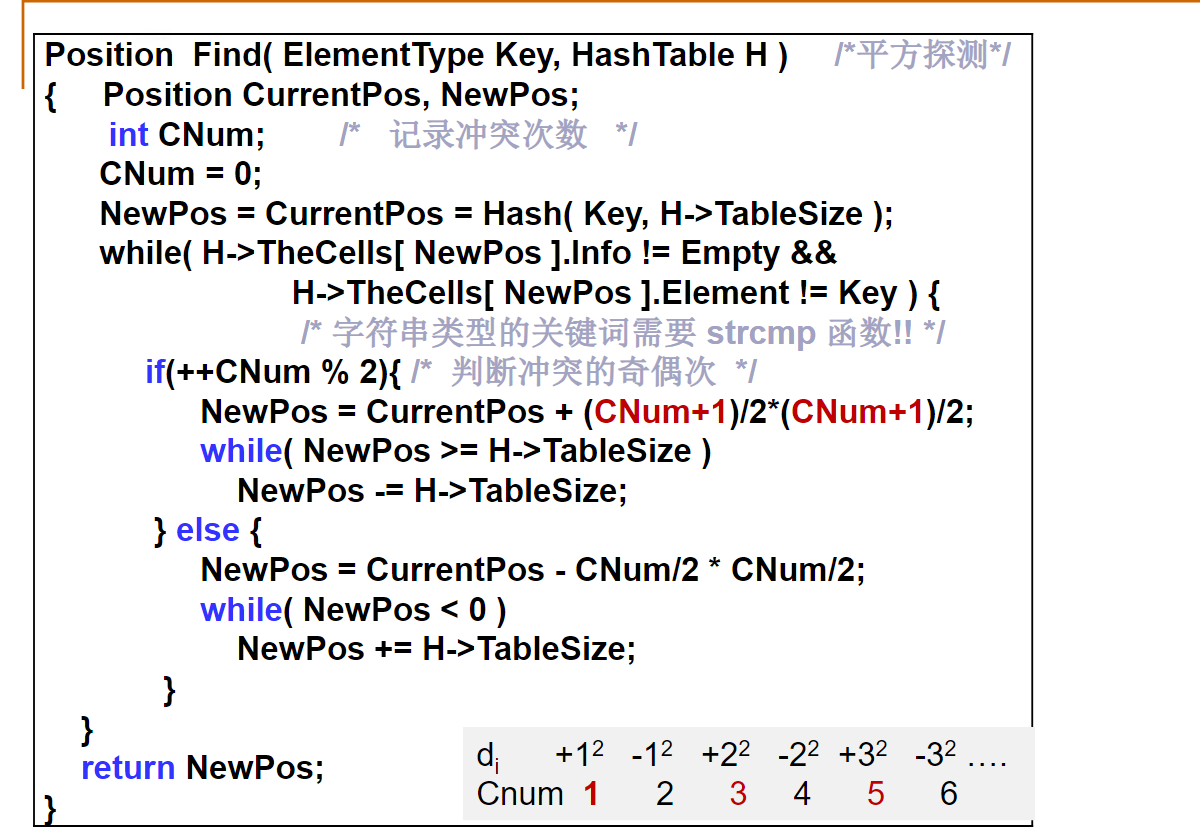



Position Find( HashTable H, ElementType Key )
{
Position CurrentPos, NewPos;
int CNum = 0; /* 记录冲突次数 */
NewPos = CurrentPos = Hash( Key, H->TableSize ); /* 初始散列位置 */
/* 当该位置的单元非空,并且不是要找的元素时,发生冲突 */
while( H->Cells[NewPos].Info!=Empty && H->Cells[NewPos].Data!=Key ) {
/* 字符串类型的关键词需要 strcmp 函数!! */
/* 统计1次冲突,并判断奇偶次 */
if( ++CNum%2 ){ /* 奇数次冲突 */
NewPos = CurrentPos + (CNum+1)*(CNum+1)/4; /* 增量为+[(CNum+1)/2]^2 */
if ( NewPos >= H->TableSize )
NewPos = NewPos % H->TableSize; /* 调整为合法地址 */
}
else { /* 偶数次冲突 */
NewPos = CurrentPos - CNum*CNum/4; /* 增量为-(CNum/2)^2 */
while( NewPos < 0 )
NewPos += H->TableSize; /* 调整为合法地址 */
}
}
return NewPos; /* 此时NewPos或者是Key的位置,或者是一个空单元的位置(表示找不到)*/
}
bool Insert( HashTable H, ElementType Key )
{
Position Pos = Find( H, Key ); /* 先检查Key是否已经存在 */
if( H->Cells[Pos].Info != Legitimate ) { /* 如果这个单元没有被占,说明Key可以插入在此 */
H->Cells[Pos].Info = Legitimate;
H->Cells[Pos].Data = Key;
/*字符串类型的关键词需要 strcpy 函数!! */
return true;
}
else {
printf("键值已存在");
return false;
}
}
分离链接法
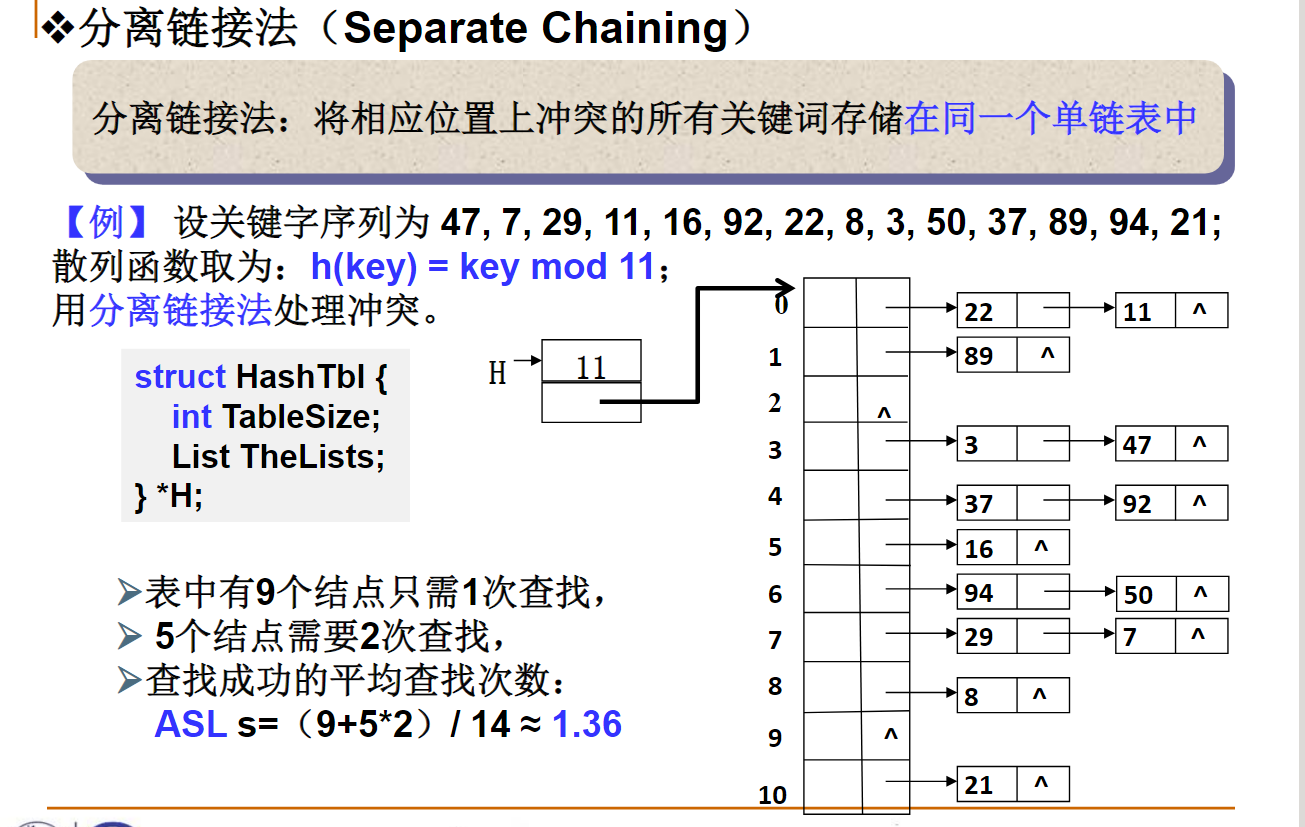
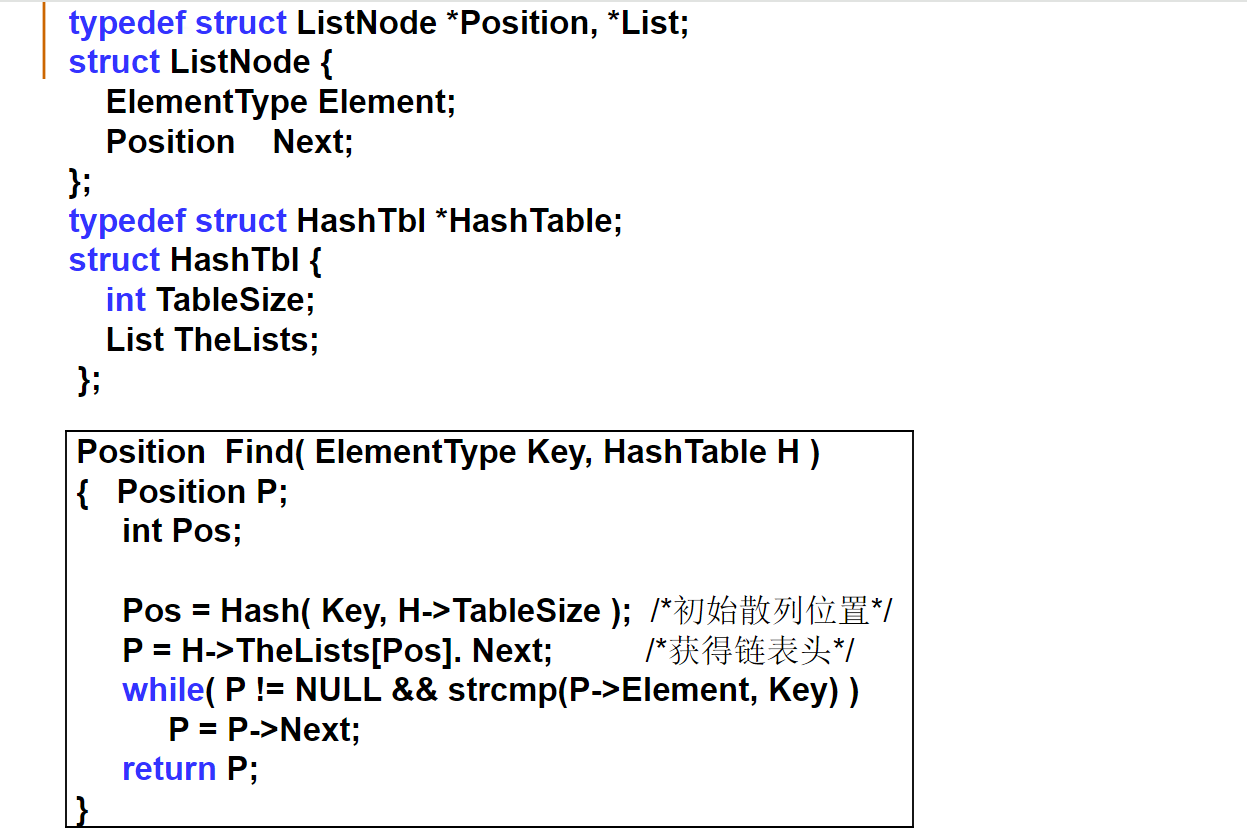
#define KEYLENGTH 15 /* 关键词字符串的最大长度 */
typedef char ElementType[KEYLENGTH+1]; /* 关键词类型用字符串 */
typedef int Index; /* 散列地址类型 */
/******** 以下是单链表的定义 ********/
typedef struct LNode *PtrToLNode;
struct LNode {
ElementType Data;
PtrToLNode Next;
};
typedef PtrToLNode Position;
typedef PtrToLNode List;
/******** 以上是单链表的定义 ********/
typedef struct TblNode *HashTable; /* 散列表类型 */
struct TblNode { /* 散列表结点定义 */
int TableSize; /* 表的最大长度 */
List Heads; /* 指向链表头结点的数组 */
};
HashTable CreateTable( int TableSize )
{
HashTable H;
int i;
H = (HashTable)malloc(sizeof(struct TblNode));
/* 保证散列表最大长度是素数,具体见代码5.3 */
H->TableSize = NextPrime(TableSize);
/* 以下分配链表头结点数组 */
H->Heads = (List)malloc(H->TableSize*sizeof(struct LNode));
/* 初始化表头结点 */
for( i=0; i<H->TableSize; i++ ) {
H->Heads[i].Data[0] = '\0';
H->Heads[i].Next = NULL;
}
return H;
}
Position Find( HashTable H, ElementType Key )
{
Position P;
Index Pos;
Pos = Hash( Key, H->TableSize ); /* 初始散列位置 */
P = H->Heads[Pos].Next; /* 从该链表的第1个结点开始 */
/* 当未到表尾,并且Key未找到时 */
while( P && strcmp(P->Data, Key) )
P = P->Next;
return P; /* 此时P或者指向找到的结点,或者为NULL */
}
bool Insert( HashTable H, ElementType Key )
{
Position P, NewCell;
Index Pos;
P = Find( H, Key );
if ( !P ) { /* 关键词未找到,可以插入 */
NewCell = (Position)malloc(sizeof(struct LNode));
strcpy(NewCell->Data, Key);
Pos = Hash( Key, H->TableSize ); /* 初始散列位置 */
/* 将NewCell插入为H->Heads[Pos]链表的第1个结点 */
NewCell->Next = H->Heads[Pos].Next;
H->Heads[Pos].Next = NewCell;
return true;
}
else { /* 关键词已存在 */
printf("键值已存在");
return false;
}
}
void DestroyTable( HashTable H )
{
int i;
Position P, Tmp;
/* 释放每个链表的结点 */
for( i=0; i<H->TableSize; i++ ) {
P = H->Heads[i].Next;
while( P ) {
Tmp = P->Next;
free( P );
P = Tmp;
}
}
free( H->Heads ); /* 释放头结点数组 */
free( H ); /* 释放散列表结点 */
}
散列表的性能分析

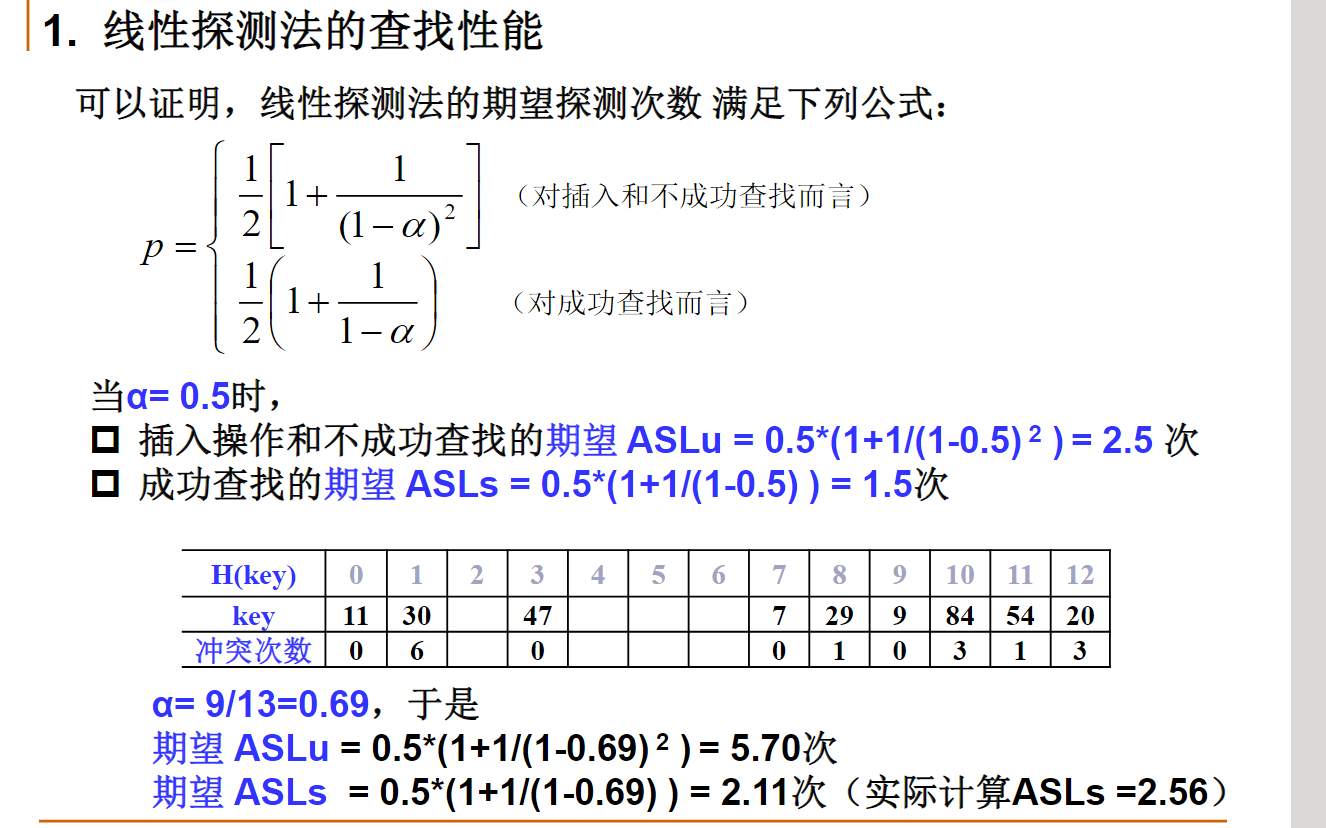
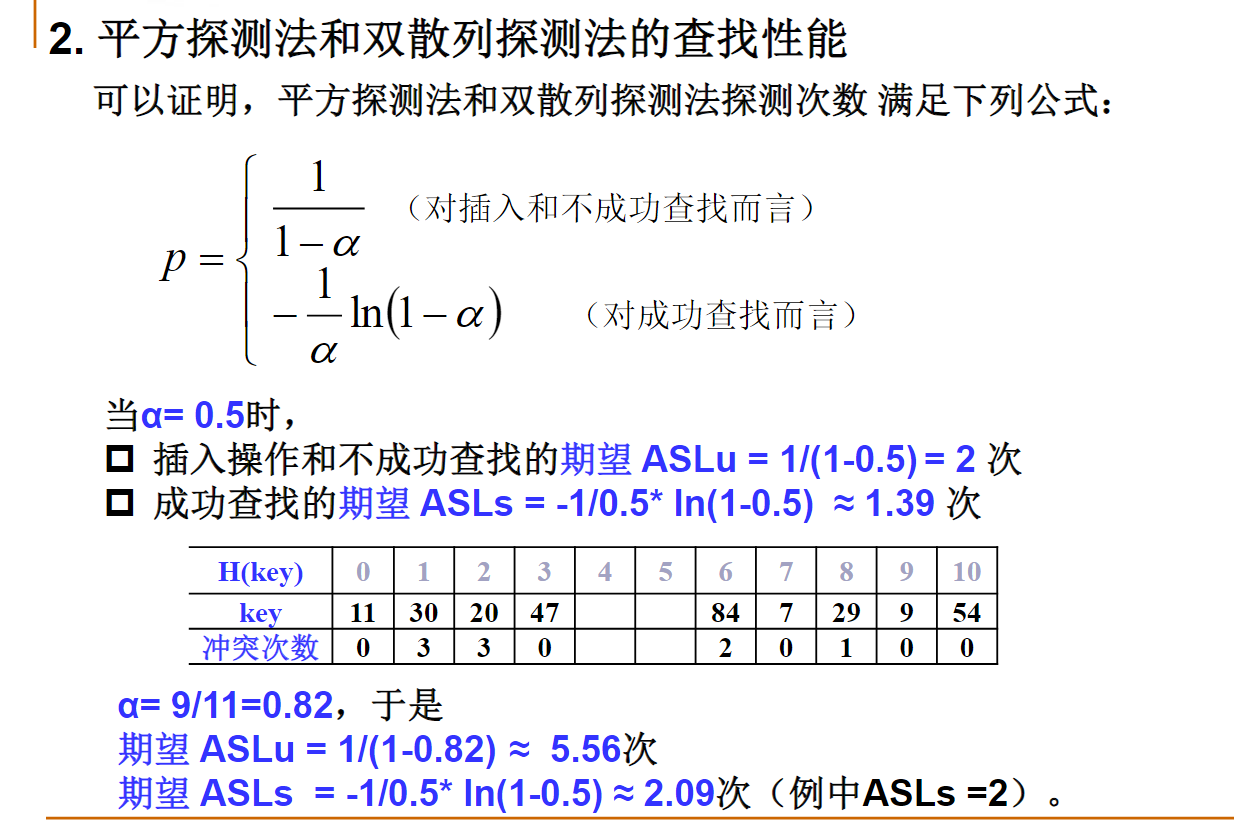
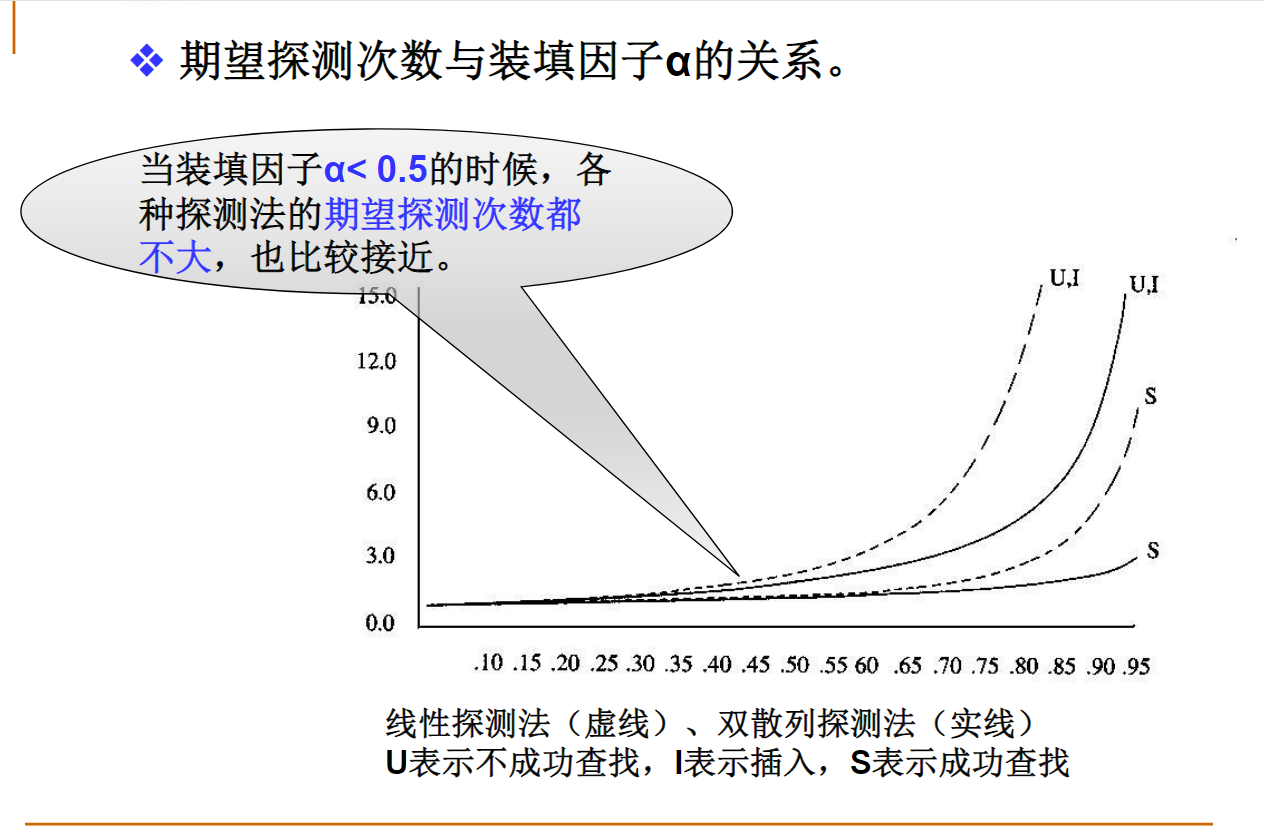
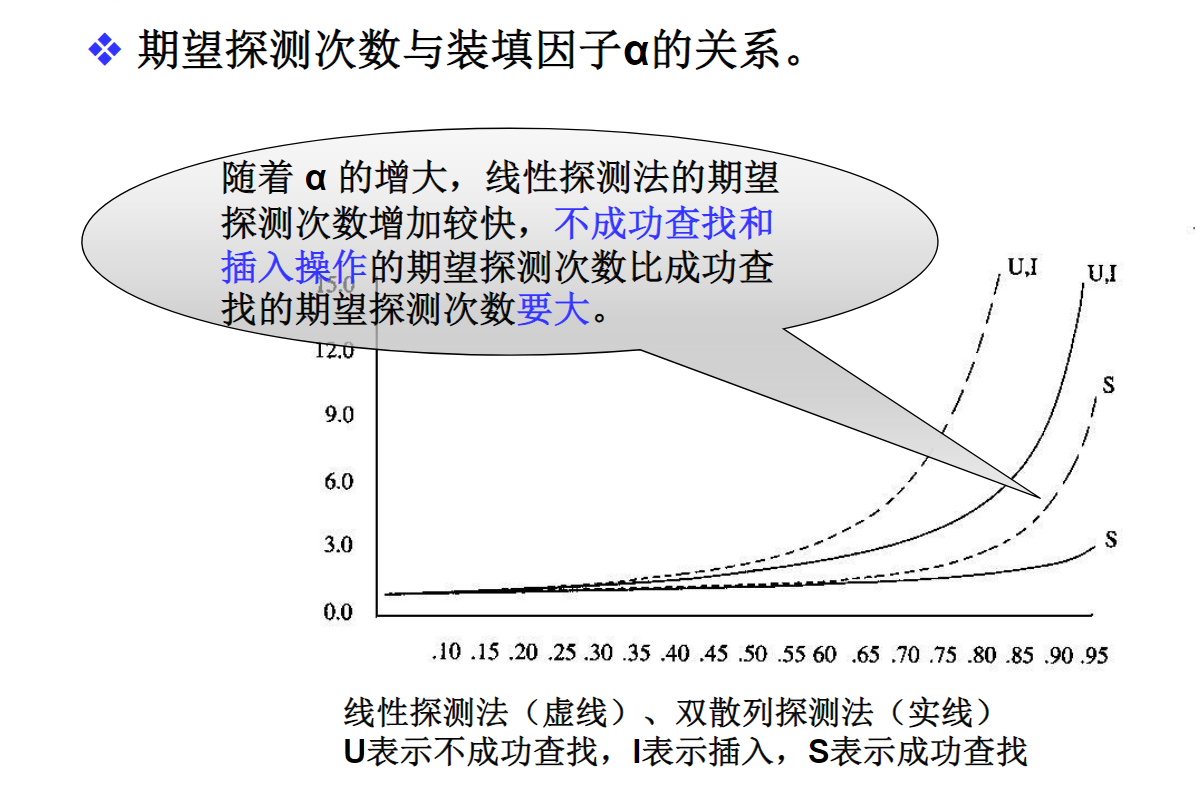
一个大小为11的散列表,散列函数为H(key)=key mod 11,采用线性探测冲突解决策略。如果现有散列表中仅有的5个元素均位于下标为奇数的位置,问:该散列表的平均不成功查找次数是多少?
16/11
在一个大小为K的空散列表中,按照线性探测冲突解决策略连续插入散列值相同的N个元素(N<K)。问:此时,该散列表的平均成功查找次数是多少?(N+1)/2
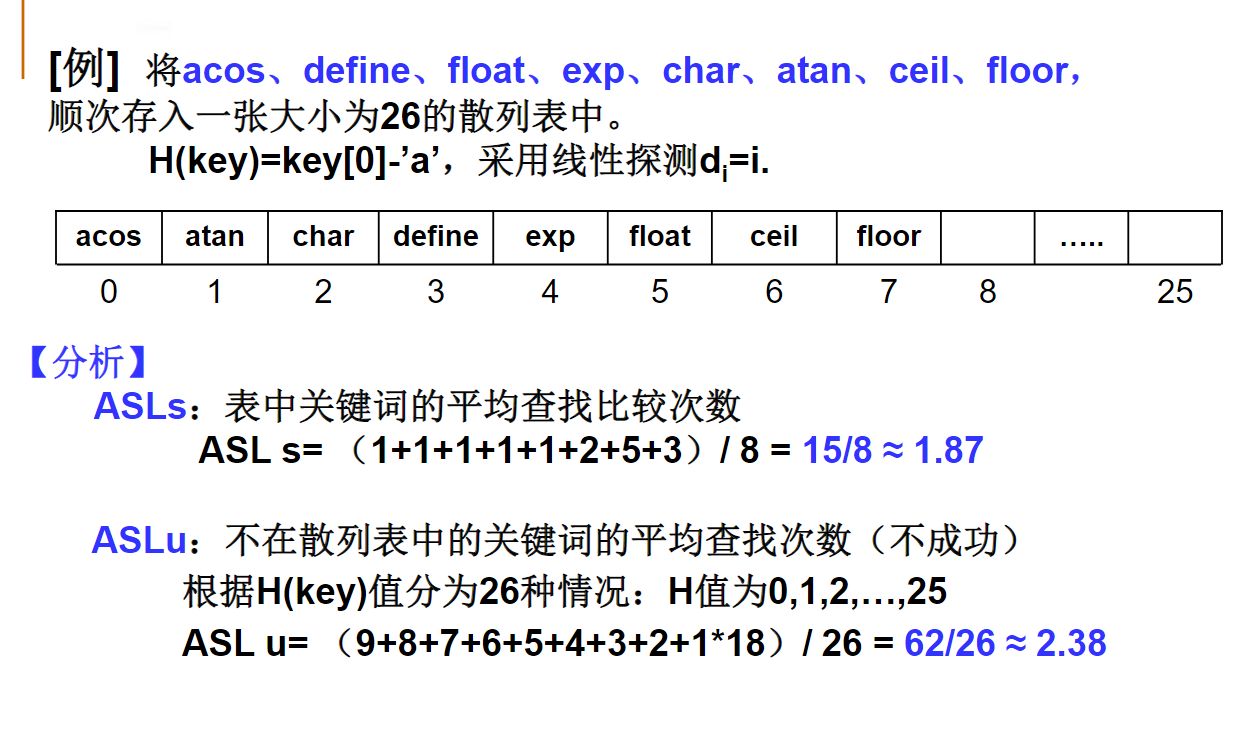
当采用线性探测冲突解决策略时,非空且有空闲空间的散列表中无论有多少元素,不成功情况下的期望查找次数总是大于成功情况下的期望查找次数。




基于数组的哈希表实现
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <assert.h>
typedef struct pair
{
int key;
char element[20];
}DATA, *LPDATA;
typedef struct hashTable
{
int divisor; //哈希表长度
int curSize; //当前元素个数
LPDATA *table; //用二级指针,便于初始化
}HASH, *LPHASH;
LPHASH createHash(int divisor)
{
LPHASH pHash = (LPHASH)malloc(sizeof(struct hashTable));
assert(pHash);
pHash->divisor = divisor;
pHash->curSize = 0;
pHash->table = (LPDATA*)malloc(sizeof(LPDATA) * pHash->divisor);
assert(pHash->table);
for(int i=0; i < pHash->divisor; i++)
{
pHash->table[i] = NULL;
}
return pHash;
}
int searchCorrectPos(LPHASH pHash, int key)
{
int Pos = key % pHash->divisor;
int curPos = Pos;
do
{
if(pHash->table[curPos] == NULL || pHash->table[curPos]->key == key)
return curPos;
curPos = (curPos + 1) % pHash->divisor;
}while(curPos != Pos);
return curPos;
}
void insertHash(LPHASH pHash, DATA data)
{
int pos = searchCorrectPos(pHash, data.key);
if(pHash->table[pos] == NULL)
{
pHash->table[pos] = (LPDATA)malloc(sizeof(DATA));
assert(pHash->table[pos]);
memcpy(pHash->table[pos], &data, sizeof(DATA));
pHash->curSize++;
}
else
{
if(pHash->table[pos]->key == data.key)
{
strcpy(pHash->table[pos]->element, data.element); //遇到冲突,覆盖相同key
}
else
{
printf("表满了,无法插入!\n");
return;
}
}
}
void printHash(LPHASH pHash)
{
for(int i=0; i<pHash->divisor; i++)
{
if(pHash->table[i] == NULL)
{
printf("NULL\n");
}
else
{
printf("%d:%s\n",pHash->table[i]->key,pHash->table[i]->element);
}
}
}
int main()
{
DATA array[3] = {29,"Young",35,"蓬蒿人",39,"哦哦哦"};
LPHASH pHash = createHash(10);
for(int i=0; i<3; i++)
{
insertHash(pHash,array[i]);
}
printHash(pHash);
return 0;
}
39:哦哦哦
NULL
NULL
NULL
NULL
35:蓬蒿人
NULL
NULL
NULL
29:Young
基于链表的哈希表实现
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <assert.h>
typedef struct pair
{
int key;
char element[20];
}DATA, *LPDATA;
typedef struct Node
{
DATA data;
struct Node *Next;
}NODE, *LPNODE;
LPNODE createNode(DATA data)
{
LPNODE newNode = (LPNODE)malloc(sizeof(NODE));
newNode->data = data;
newNode->Next = NULL;
return newNode;
}
typedef struct skipListNode
{
DATA data;
LPNODE fisrtNode;
struct skipListNode *Next;
}SLNODE, *LPSLNODE;
LPSLNODE createSkipListNode(DATA data)
{
LPSLNODE newNode = (LPSLNODE)malloc(sizeof(SLNODE));
newNode->data = data;
newNode->fisrtNode = NULL;
newNode->Next = NULL;
return newNode;
}
typedef struct Hash
{
LPSLNODE headNode;
int curSize;
int divisor;
}HASH, *LPHASH;
LPHASH createHash(int divisor)
{
LPHASH pHash = (LPHASH)malloc(sizeof(HASH));
assert(pHash);
pHash->curSize = 0;
pHash->divisor = divisor;
pHash->headNode = NULL;
return pHash;
}
void insertHash(LPHASH pHash, DATA data)
{
int dataHashPos = data.key % pHash->divisor;
LPSLNODE newSkipNode = createSkipListNode(data);
//第一次插入
if(pHash->headNode == NULL)
{
pHash->headNode = newSkipNode;
pHash->curSize++;
}
else
{
//纵向是要有序的
LPSLNODE pMove = pHash->headNode;
LPSLNODE prePmove = NULL;
//表头元素的地址大于要插入元素的地址,用头插法
if(pMove->data.key % pHash->divisor > dataHashPos)
{
newSkipNode->Next = pHash->headNode;
pHash->headNode = newSkipNode;
pHash->curSize++;
}
else
{
//向下找
while(pMove!=NULL && pMove->data.key%pHash->divisor < dataHashPos)
{
prePmove = pMove;
pMove = prePmove->Next;
}
//结果:找到、没找到
//找到的话,单独分析等于的情况,等于就是哈希冲突
if(pMove!=NULL && pMove->data.key%pHash->divisor == dataHashPos)
{
//相同键采用覆盖方式
//不同键、相同哈希地址插入横向链表
if(pMove->data.key == data.key)
{
strcpy(pMove->data.element, data.element);
}
else
{
LPNODE newNode = createNode(data);
LPNODE ppMove = pMove->fisrtNode;
//横向链表的插入
if(ppMove == NULL)
{
newNode->Next = pMove->fisrtNode;
pMove->fisrtNode = newNode;
pHash->curSize++;
}
else
{
//横向处理相同key的问题
while(ppMove != NULL && ppMove->data.key != data.key)
{
ppMove = ppMove->Next;
}
if(ppMove == NULL)
{
//表头法插入
newNode->Next = pMove->fisrtNode;
pMove->fisrtNode = newNode;
pHash->curSize++;
}
else
{
//相同则覆盖
strcpy(ppMove->data.element, data.element);
}
}
}
}
else
{
prePmove->Next = newSkipNode;
newSkipNode->Next = pMove;
pHash->curSize++;
}
}
}
}
void printHash(LPHASH pHash)
{
LPSLNODE pMove = pHash->headNode;
while(pMove != NULL)
{
printf("%d:%s ",pMove->data.key, pMove->data.element);
LPNODE ppMove = pMove->fisrtNode;
while(ppMove != NULL)
{
printf("%d:%s ",ppMove->data.key, ppMove->data.element);
ppMove = ppMove->Next;
}
pMove = pMove->Next;
printf("\n");
}
}
int main()
{
DATA array[3] = {29,"Young",35,"蓬蒿人",39,"哦哦哦"};
LPHASH pHash = createHash(10);
for(int i=0; i<3; i++)
{
insertHash(pHash,array[i]);
}
printHash(pHash);
return 0;
}
35:蓬蒿人
29:Young 39:哦哦哦
哈希表应用实例:统计词频


字符串匹配


普通字符串匹配实现




#include <stdio.h>
#include <string.h>
#include <stdlib.h>
typedef char* Position;
#define NotFound NULL
int main()
{
char string[] = "This is a simple example.";
char pattern[] = "simple";
Position p = strstr(string, pattern);
if (p==NotFound)
printf("Not Found.\n");
else
printf("%s\n",p);
return 0;
}
simple example.
KMP算法——字符串匹配
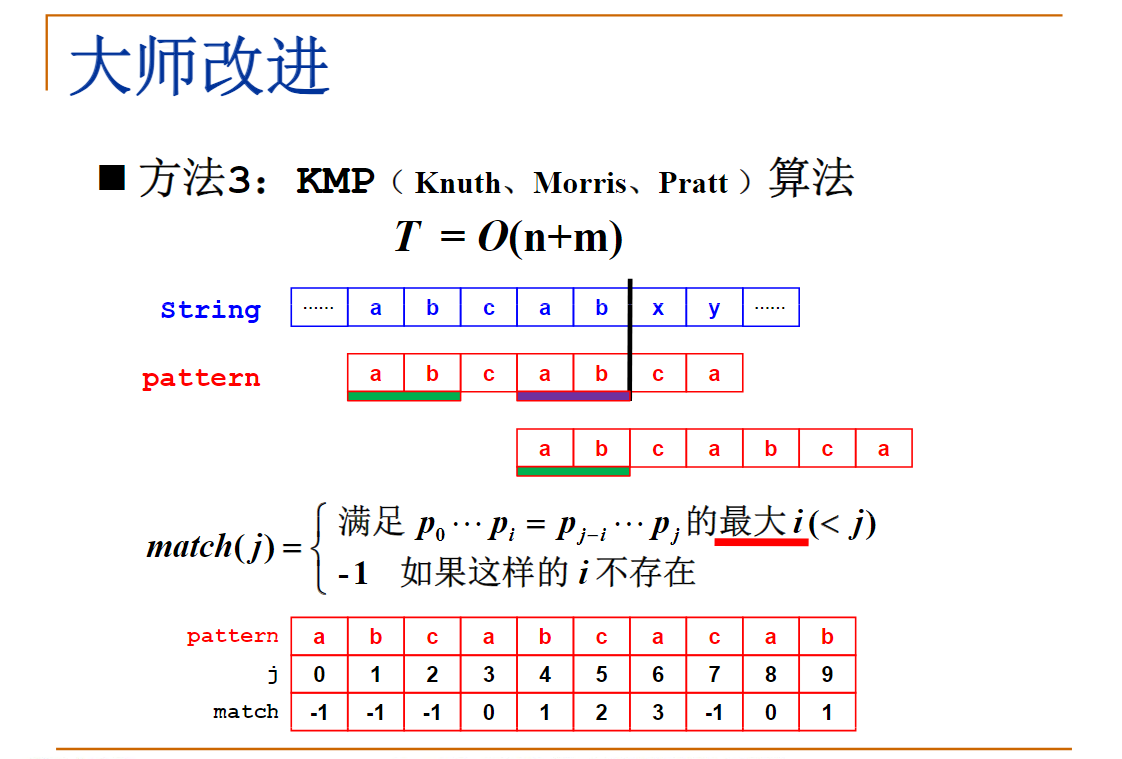




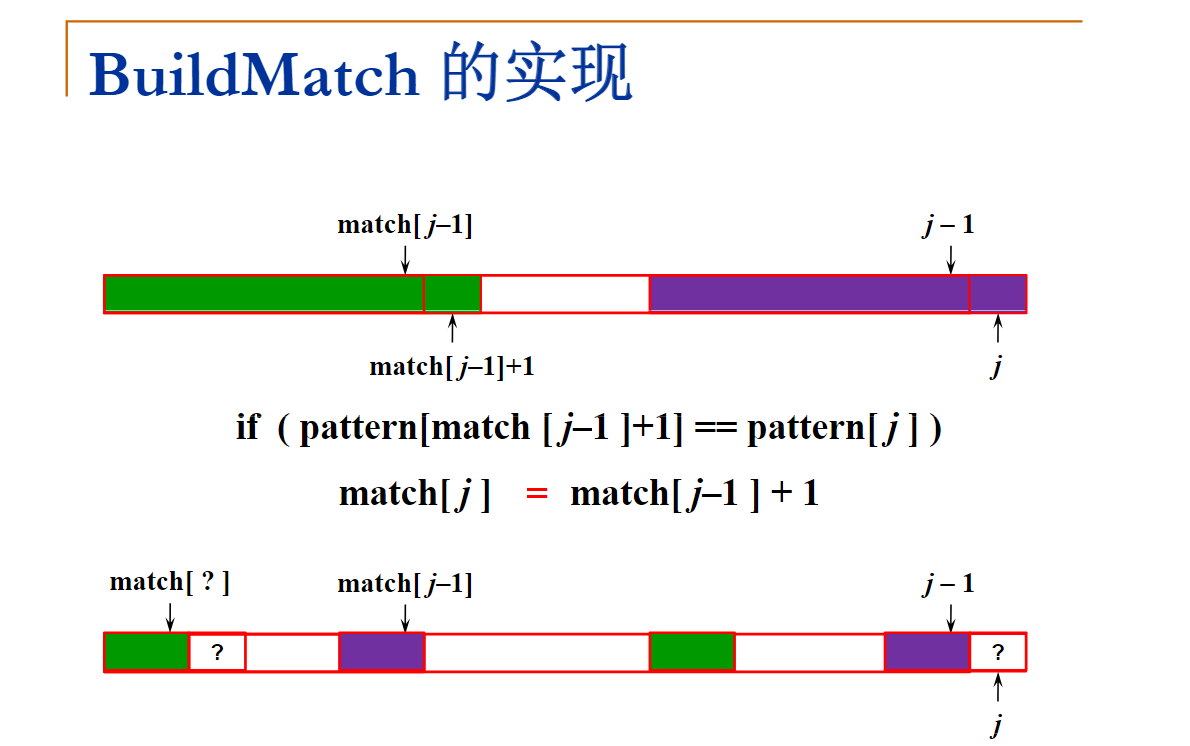
当pattern[match[j-1]+1] != pattern[j] 时,下一个待与 pattern[j] 比较的元素下标是:D
- A.
match[j-2] - B.
match[j-2]+1 - C
.match[match[j-1]] - D.
match[match[j-1]]+1


#include <stdio.h>
#include <string.h>
#include <stdlib.h>
typedef int Position;
#define NotFound -1
void BuildMatch( char *pattern, int *match )
{
Position i, j;
int m = strlen(pattern);
match[0] = -1;
for ( j=1; j<m; j++ ) {
i = match[j-1];
while ( (i>=0) && (pattern[i+1]!=pattern[j]) )
i = match[i];
if ( pattern[i+1]==pattern[j] )
match[j] = i+1;
else match[j] = -1;
}
}
Position KMP( char *string, char *pattern )
{
int n = strlen(string);
int m = strlen(pattern);
Position s, p, *match;
if ( n < m ) return NotFound;
match = (Position *)malloc(sizeof(Position) * m);
BuildMatch(pattern, match);
s = p = 0;
while ( s<n && p<m ) {
if ( string[s]==pattern[p] ) {
s++; p++;
}
else if (p>0) p = match[p-1]+1;
else s++;
}
return ( p==m )? (s-m) : NotFound;
}
int main()
{
char string[] = "This is a simple example.";
char pattern[] = "simple";
Position p = KMP(string, pattern);
if (p==NotFound) printf("Not Found.\n");
else printf("%s\n", string+p);
return 0;
}
实例:PTA KMP 串的模式匹配
给定两个由英文字母组成的字符串 String 和 Pattern,要求找到 Pattern 在 String 中第一次出现的位置,并将此位置后的 String 的子串输出。如果找不到,则输出“Not Found”。
本题旨在测试各种不同的匹配算法在各种数据情况下的表现。各组测试数据特点如下:
- 数据0:小规模字符串,测试基本正确性;
- 数据1:随机数据,String 长度为 105,Pattern 长度为 10;
- 数据2:随机数据,String 长度为 105,Pattern 长度为 102;
- 数据3:随机数据,String 长度为 105,Pattern 长度为 103;
- 数据4:随机数据,String 长度为 105,Pattern 长度为 104;
- 数据5:String 长度为 106,Pattern 长度为 105;测试尾字符不匹配的情形;
- 数据6:String 长度为 106,Pattern 长度为 105;测试首字符不匹配的情形。
输入格式:
输入第一行给出 String,为由英文字母组成的、长度不超过 106 的字符串。第二行给出一个正整数 N(≤10),为待匹配的模式串的个数。随后 N 行,每行给出一个 Pattern,为由英文字母组成的、长度不超过 105 的字符串。每个字符串都非空,以回车结束。
输出格式:
对每个 Pattern,按照题面要求输出匹配结果。
输入样例:
abcabcabcabcacabxy
3
abcabcacab
cabcabcd
abcabcabcabcacabxyz
输出样例:
abcabcacabxy
Not Found
Not Found
使用KMP算法的解法如下:
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
typedef int Position;
#define NotFound -1
void BuildMatch( char *pattern, int *match )
{
Position i, j;
int m = strlen(pattern);
match[0] = -1;
for ( j=1; j<m; j++ ) {
i = match[j-1];
while ( (i>=0) && (pattern[i+1]!=pattern[j]) )
i = match[i];
if ( pattern[i+1]==pattern[j] )
match[j] = i+1;
else match[j] = -1;
}
}
Position KMP( char *string, char *pattern )
{
int n = strlen(string);
int m = strlen(pattern);
Position s, p, *match;
if ( n < m ) return NotFound;
match = (Position *)malloc(sizeof(Position) * m);
BuildMatch(pattern, match);
s = p = 0;
while ( s<n && p<m ) {
if ( string[s]==pattern[p] ) {
s++; p++;
}
else if (p>0) p = match[p-1]+1;
else s++;
}
return ( p==m )? (s-m) : NotFound;
}
int main()
{
char string[1000005];
scanf("%s",string);
int N;
scanf("%d",&N);
for(int i=0; i<N; i++)
{
char pattern[100005];
scanf("%s",pattern);
Position p = KMP(string, pattern);
if (p==NotFound)
printf("Not Found\n");
else
printf("%s\n", string+p);
}
return 0;
}
使用strstr函数的解法如下:
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
typedef char* Position;
#define NotFound NULL
int main()
{
char string[1000005];
scanf("%s",string);
int N;
scanf("%d",&N);
for(int i=0; i<N; i++)
{
char pattern[100005];
scanf("%s",pattern);
Position p = strstr(string, pattern);
if (p==NotFound)
printf("Not Found\n");
else
printf("%s\n", p);
}
return 0;
}