哈夫曼树
定义
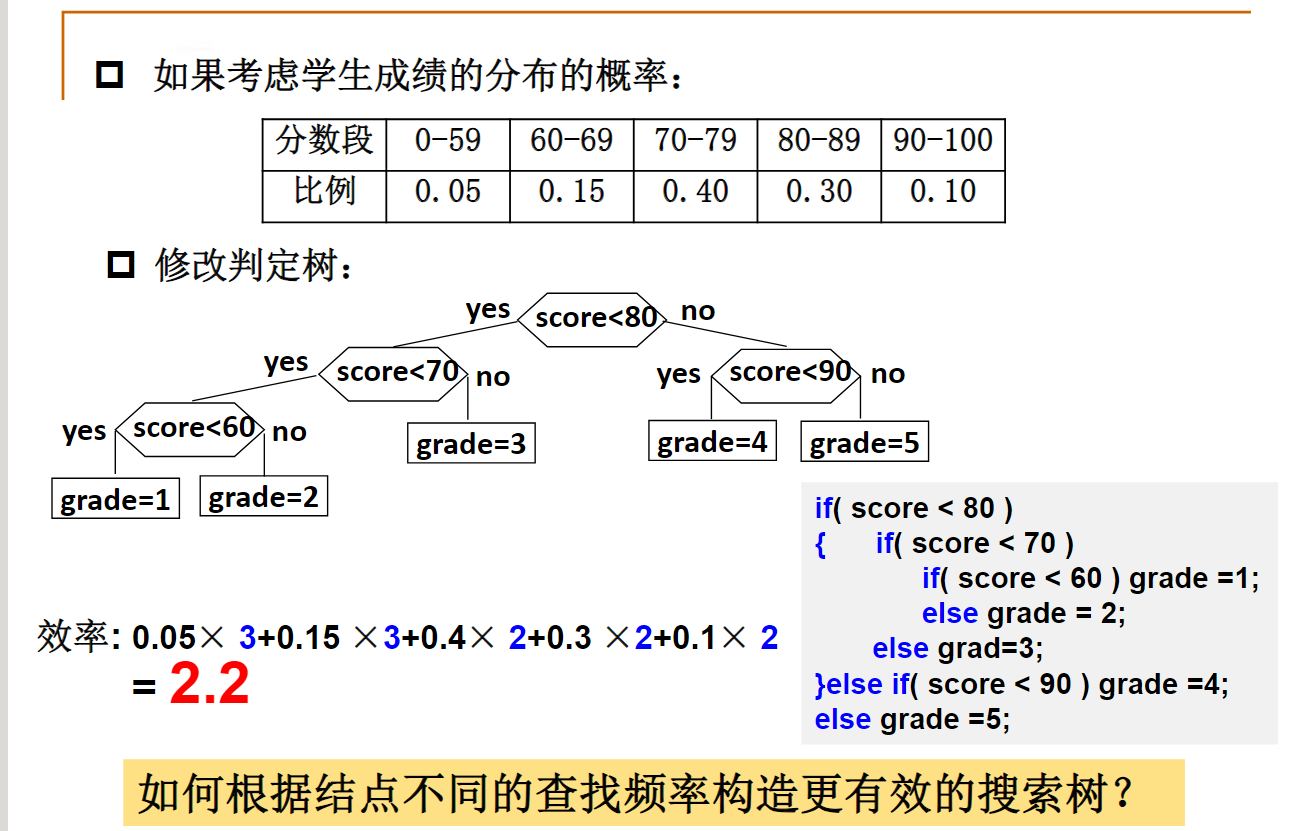
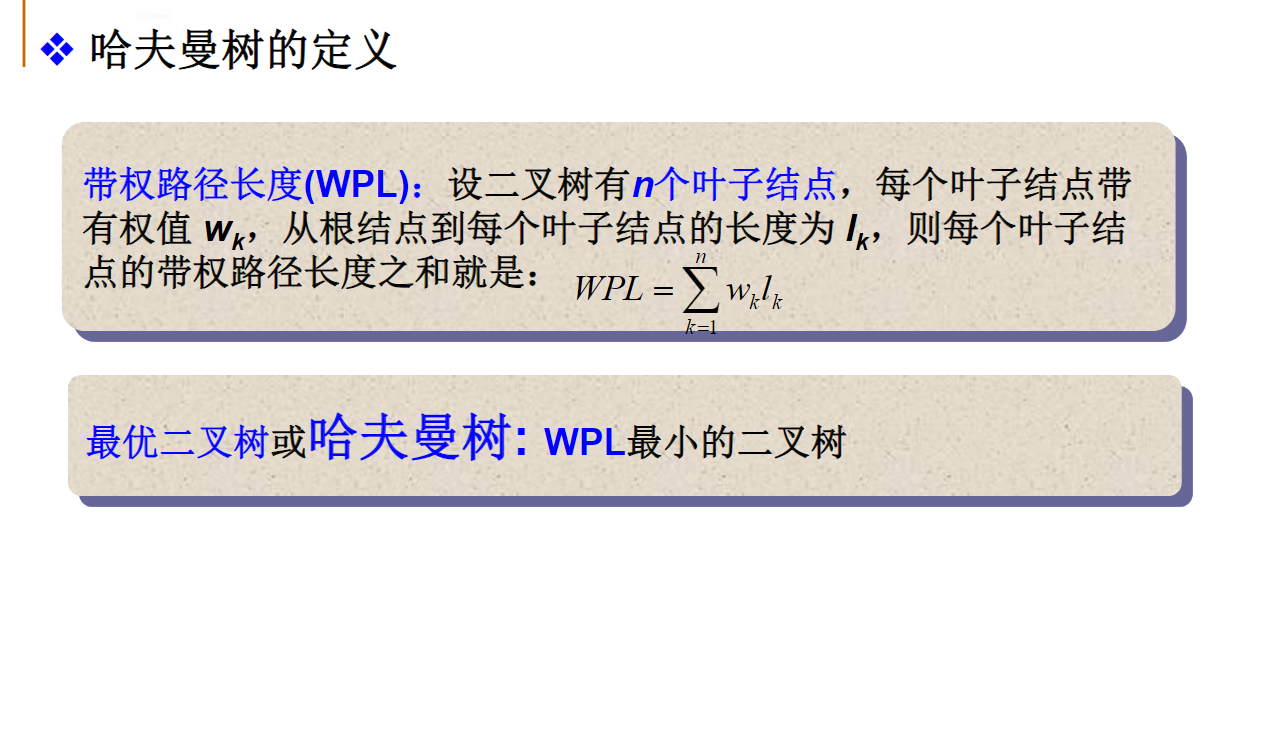
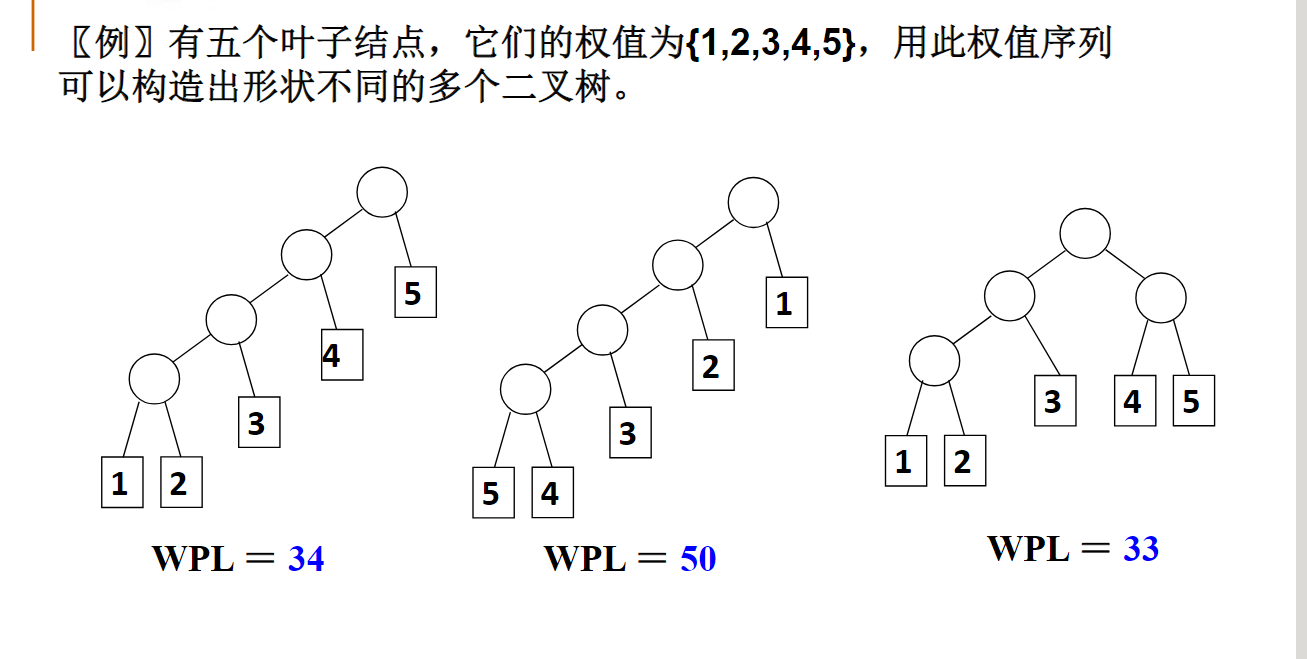

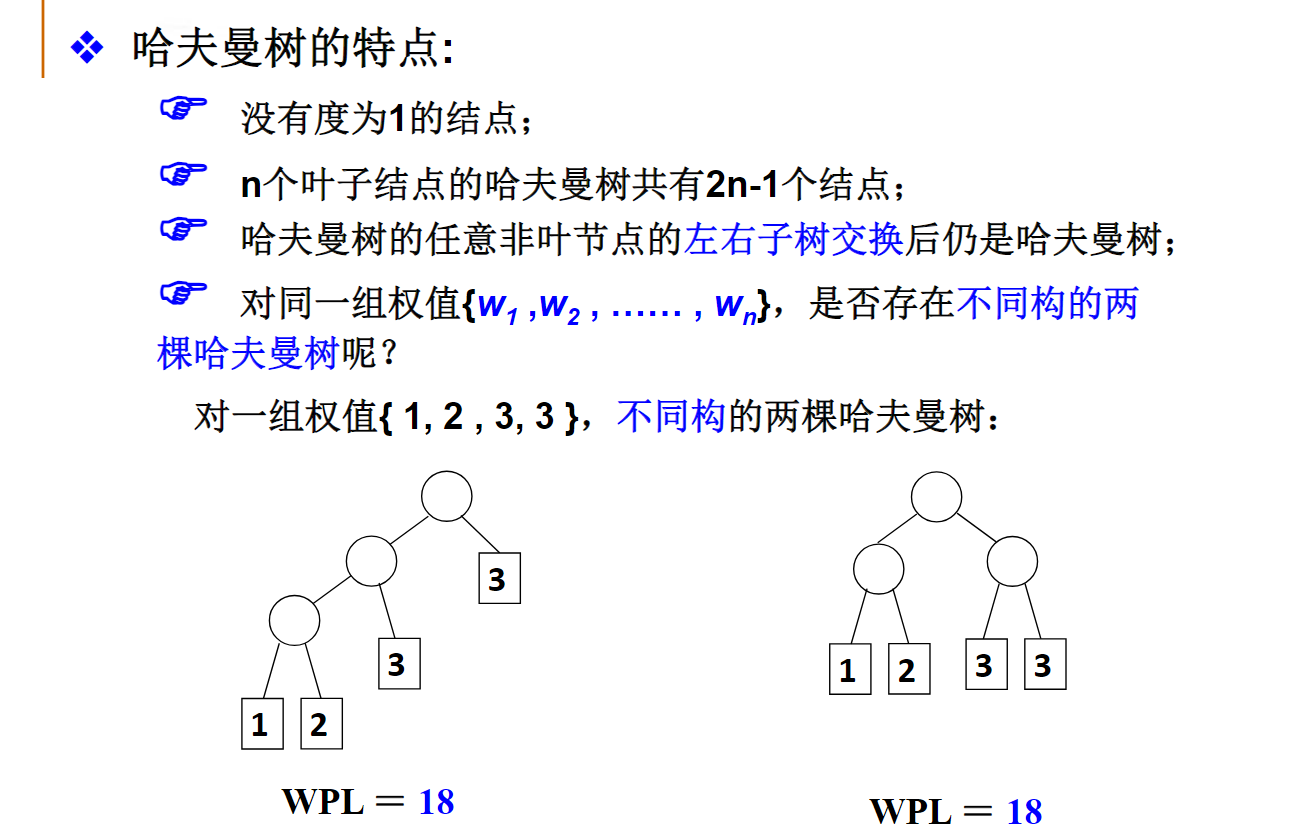
如果哈夫曼树有67个结点,则可知叶结点总数为:34
哈夫曼编码


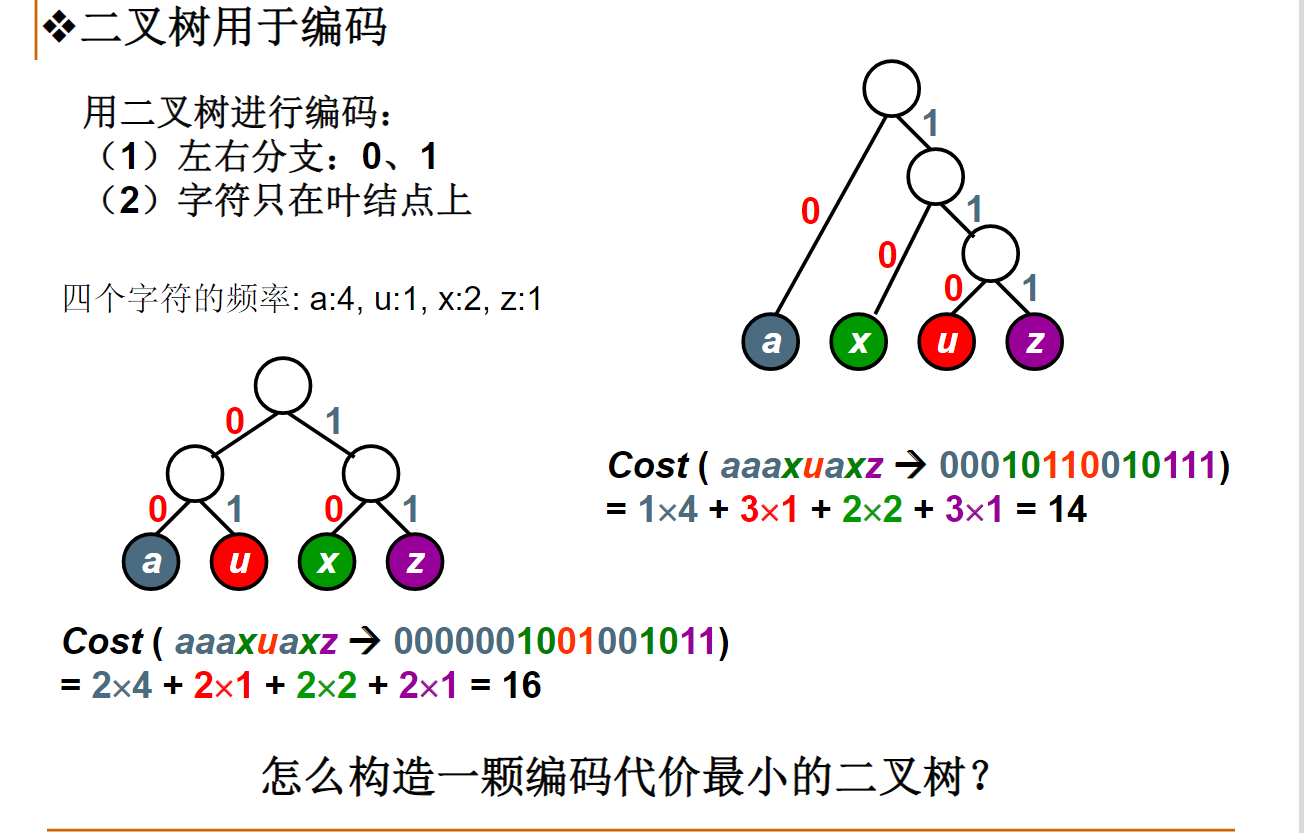
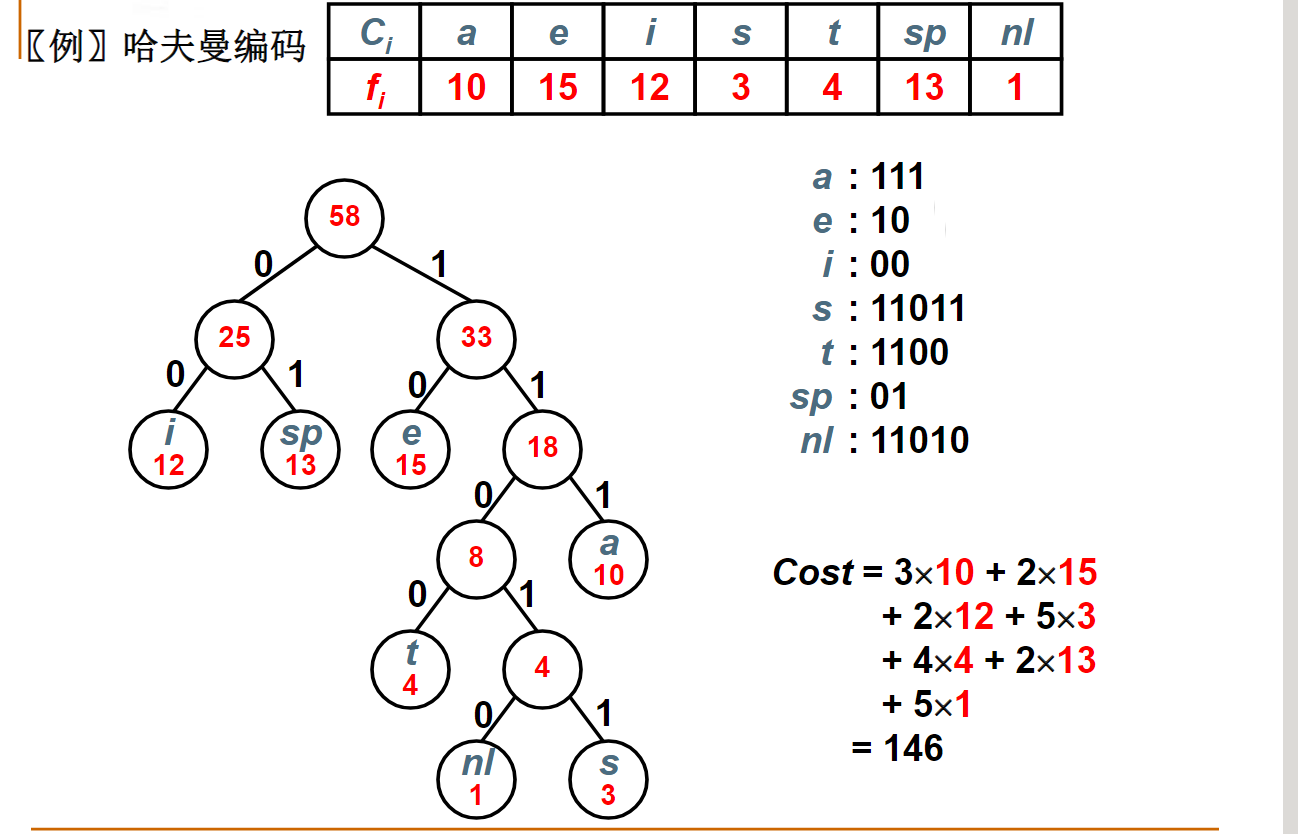
为五个使用频率不同的字符设计哈夫曼编码,下列方案中哪个不可能是哈夫曼编码?A
-
A.00,100,101,110,111
-
B.000,001,01,10,11
-
C.0000,0001,001,01,1
-
D.000,001,010,011,1
哈夫曼树的节点要么是叶子节点,要么是度为2的节点,不可能出现度为1的节点。
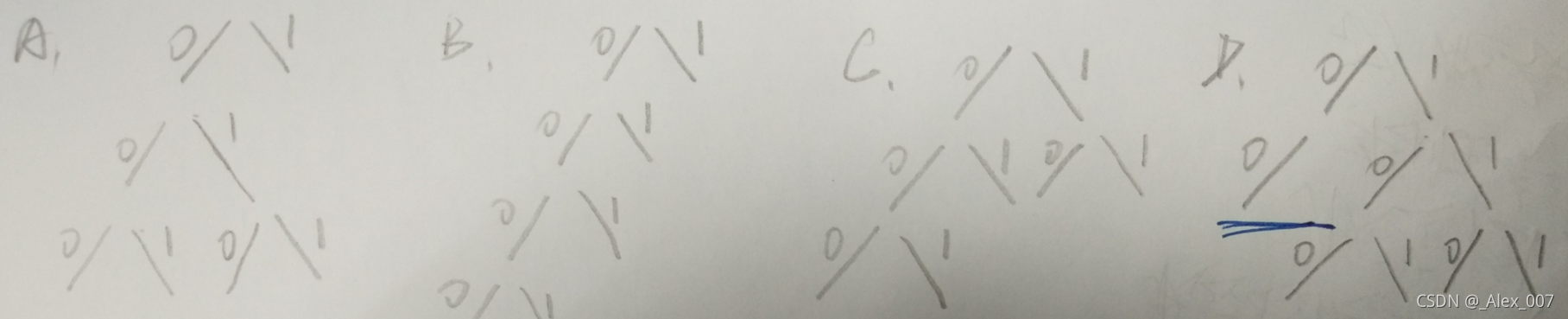
一段文本中包含对象{a,b,c,d,e},其出现次数相应为{3,2,4,2,1},则经过哈夫曼编码后,该文本所占总位数为:27
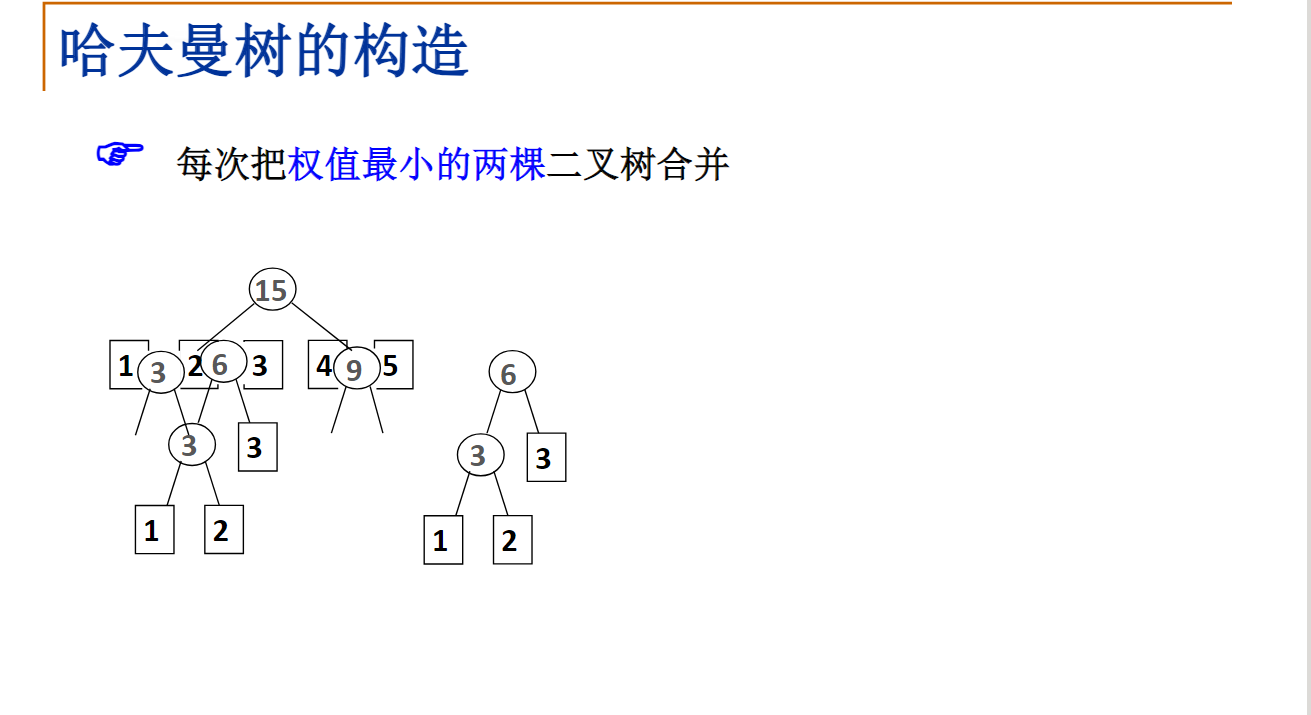
每次把权值最小的两棵二叉树合并
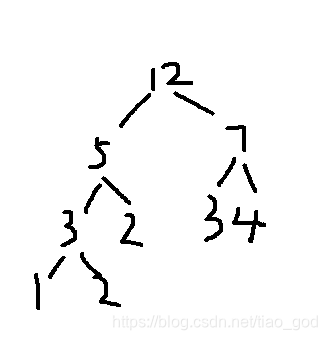
实例PTA 05-树9 Huffman Codes
In 1953, David A. Huffman published his paper "A Method for the Construction of Minimum-Redundancy Codes", and hence printed his name in the history of computer science. As a professor who gives the final exam problem on Huffman codes, I am encountering a big problem: the Huffman codes are NOT unique. For example, given a string "aaaxuaxz", we can observe that the frequencies of the characters 'a', 'x', 'u' and 'z' are 4, 2, 1 and 1, respectively. We may either encode the symbols as {'a'=0, 'x'=10, 'u'=110, 'z'=111}, or in another way as {'a'=1, 'x'=01, 'u'=001, 'z'=000}, both compress the string into 14 bits. Another set of code can be given as {'a'=0, 'x'=11, 'u'=100, 'z'=101}, but {'a'=0, 'x'=01, 'u'=011, 'z'=001} is NOT correct since "aaaxuaxz" and "aazuaxax" can both be decoded from the code 00001011001001. The students are submitting all kinds of codes, and I need a computer program to help me determine which ones are correct and which ones are not.
Input Specification:
Each input file contains one test case. For each case, the first line gives an integer N (2≤N≤63), then followed by a line that contains all the N distinct characters and their frequencies in the following format:
c[1] f[1] c[2] f[2] ... c[N] f[N]
where c[i] is a character chosen from {'0' - '9', 'a' - 'z', 'A' - 'Z', '_'}, and f[i] is the frequency of c[i] and is an integer no more than 1000. The next line gives a positive integer M (≤1000), then followed by M student submissions. Each student submission consists of N lines, each in the format:
c[i] code[i]
where c[i] is the i-th character and code[i] is an non-empty string of no more than 63 '0's and '1's.
Output Specification:
For each test case, print in each line either "Yes" if the student's submission is correct, or "No" if not.
Note: The optimal solution is not necessarily generated by Huffman algorithm. Any prefix code with code length being optimal is considered correct.
Sample Input:
7
A 1 B 1 C 1 D 3 E 3 F 6 G 6
4
A 00000
B 00001
C 0001
D 001
E 01
F 10
G 11
A 01010
B 01011
C 0100
D 011
E 10
F 11
G 00
A 000
B 001
C 010
D 011
E 100
F 101
G 110
A 00000
B 00001
C 0001
D 001
E 00
F 10
G 11
Sample Output:
Yes
Yes
No
No
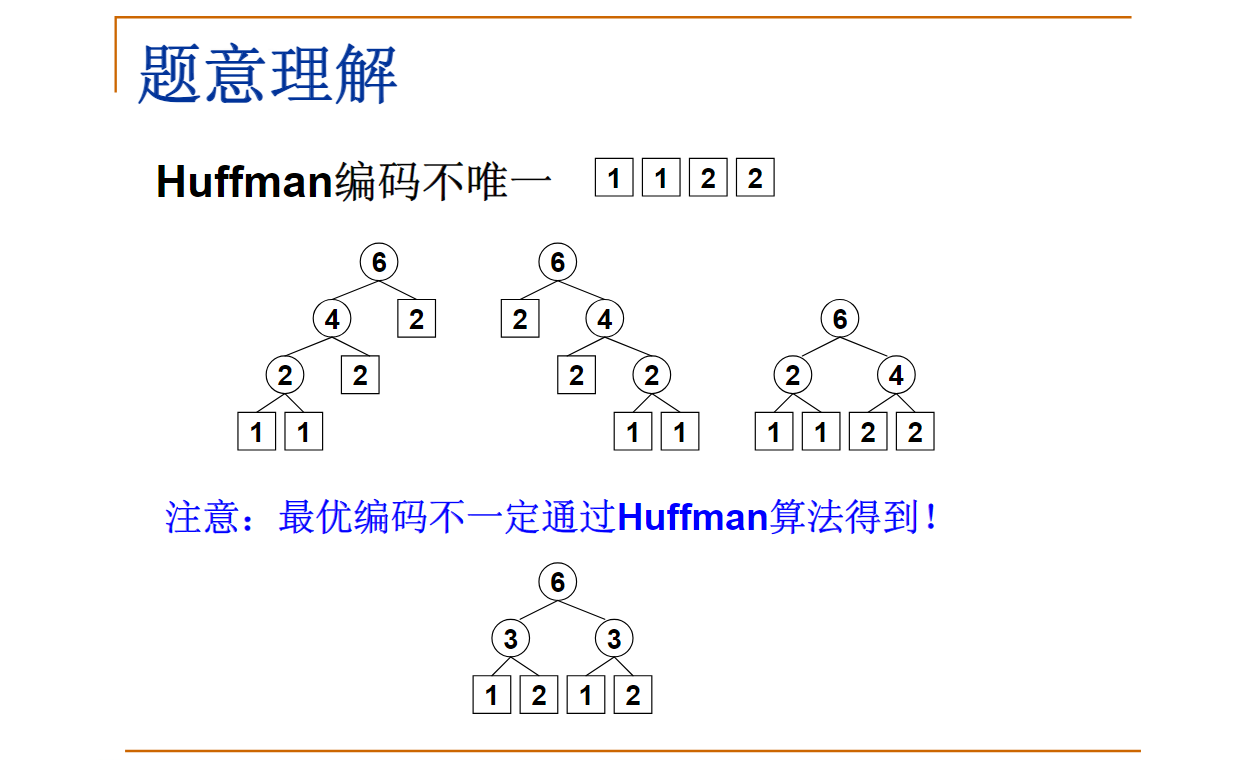

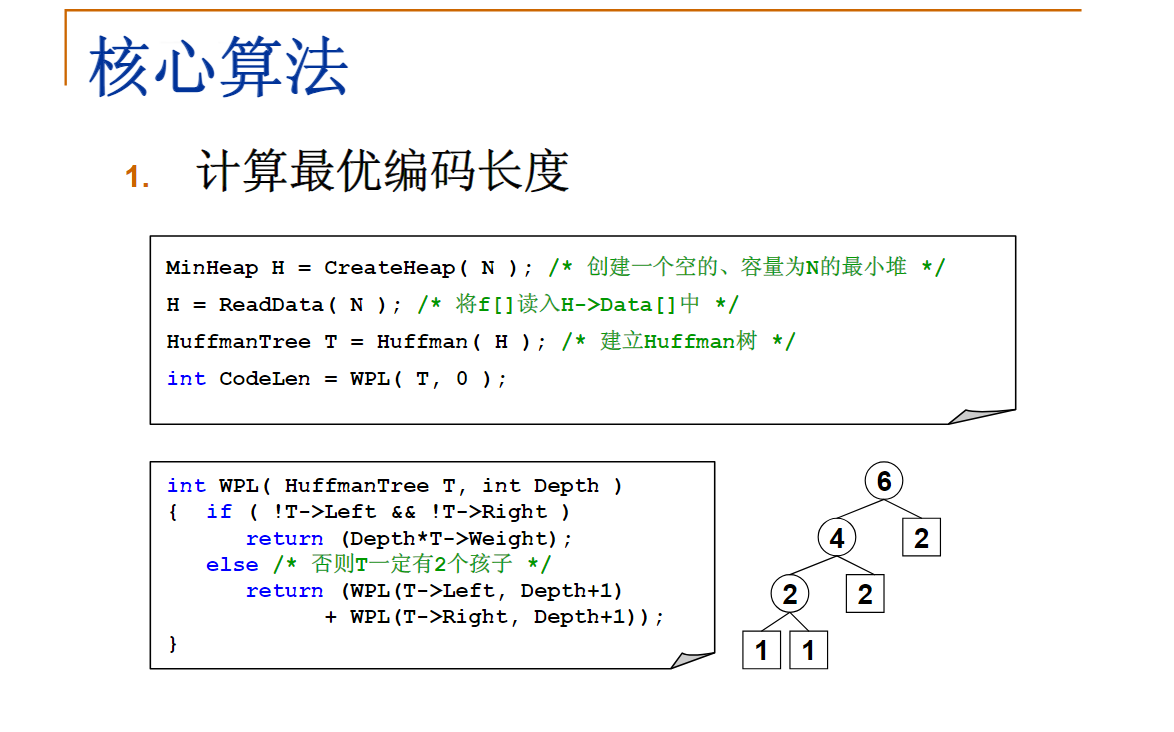
最优编码不一定通过Huffman算法得到。给定4个字符及其出现频率: A:1; B:1; C:2; D:2
下面哪一套不是用Huffman算法得到的正确的编码?
A.A:000; B:001; C:01; D:1
B.A:10; B:11; C:00; D:01
C.A:00; B:10; C:01; D:11
D.A:111; B:001; C:10; D:1
正确答案:C你选对了

这道题主要利用哈夫曼编码的两个性质:
- 哈夫曼编码可能不唯一,但是哈夫曼编码的长度是唯一的。字符串编码成01串后的长度实际上就是其以频率为权值所构成的任意一颗哈夫曼树的带权路径长度。
- 对于任何一个叶子结点,其编号一定不会成为其他任何一个结点编号的前缀—也就是说,题目中给出需要判断的的每个字符的编码,它不会是其他字符编码的前缀。
C++实现代码如下:
#include<bits/stdc++.h>
using namespace std;
int main(){
int s = 0, n, m, x, a[100];
char ch;
priority_queue<int,vector<int>,greater<int> > q; //优先队列
cin>>n;getchar();
for(int i = 0; i < n; i++) {
cin>>ch>>x;
a[i] = x;
q.push(x);
}
while(q.size() > 1) {
int x = q.top();
q.pop();
int y = q.top();
q.pop();
s = s + x + y;
q.push(x + y);
}
cin>>m;
while(m--) {
int s1 = 0;
string str[100];
for(int i = 0; i < n; i++) {
cin>>ch>>str[i];
s1 = s1 + str[i].size() * a[i];
}
if(s == s1) {
bool jdg = true;
for (int i = 0; i < n-1; i++) {
for (int j = i+1; j < n; j++) {
int flag = 0;
int size = str[i].size() > str[j].size() ? str[j].size() : str[i].size();
for(int k = 0; k < size; k++)
if(str[i][k] != str[j][k])
flag = 1;
if (!flag)
jdg = false;
}
}
if(jdg)
cout<<"Yes\n";
else
cout<<"No\n";
}
else
cout<<"No\n";
}
return 0;
}