栈Stack

• 定义
• 栈的顺序存储实现
• 实例PTA6-7 在一个数组中实现两个堆栈
• 栈的链式存储实现
• 栈应用：表达式求值

定义

还有一种表达式叫“前缀表达式”，即运算符号位于运算数之前,比如a+b*c的前缀表达式是+a*bc。

你能写出a+b*c-d/e的前缀表达式吗？-+a*bc/de

栈的顺序存储实现

根据刚才讲的方法，用一个数组来表示双堆栈，如果这两个堆栈的栈顶位置分别是top1和top2，那么可以用top1+top2==MaxSize(数组大小）来判别堆栈是否满？

不可以！！！

《数据结构》课程给出的代码如下：

typedef int Position;
struct SNode {
    ElementType *Data; /* 存储元素的数组 */
    Position Top;      /* 栈顶指针 */
    int MaxSize;       /* 堆栈最大容量 */
};
typedef struct SNode *Stack;

Stack CreateStack( int MaxSize )
{
    Stack S = (Stack)malloc(sizeof(struct SNode));
    S->Data = (ElementType *)malloc(MaxSize * sizeof(ElementType));
    S->Top = -1;
    S->MaxSize = MaxSize;
    return S;
}

bool IsFull( Stack S )
{
    return (S->Top == S->MaxSize-1);
}

bool Push( Stack S, ElementType X )
{
    if ( IsFull(S) ) {
        printf("堆栈满");
        return false;
    }
    else {
        S->Data[++(S->Top)] = X;
        return true;
    }
}

bool IsEmpty( Stack S )
{
    return (S->Top == -1);
}

ElementType Pop( Stack S )
{
    if ( IsEmpty(S) ) {
        printf("堆栈空");
        return ERROR; /* ERROR是ElementType的特殊值，标志错误 */
    }
    else 
        return ( S->Data[(S->Top)--] );
}

测试程序如下：

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>

#define ElementType int
#define ERROR -1
#define OK 0

typedef int Position;
typedef struct SNode *Stack;

struct SNode
{
    ElementType *Data;
    Position Top;
    int MaxSize;
};

Stack CreateStack(int MaxSize)
{
    Stack S = (Stack)malloc(sizeof(struct SNode));
    S->Data = (ElementType*)malloc(MaxSize * sizeof(ElementType));
    S->Top = -1;
    S->MaxSize = MaxSize;
    return S;
}
bool IsFull(Stack S)
{
    return (S->Top == S->MaxSize-1);
}
bool Push(Stack PtrS,ElementType X)
{
    if(IsFull(PtrS))
        return false;
    else
    {
        PtrS->Data[++(PtrS->Top)] = X;
        return true;
    }
}

bool IsEmpty(Stack S)
{
    return (S->Top == -1);
}

ElementType Pop(Stack PtrS)
{

    if(IsEmpty(PtrS))
    {
        printf("栈已空！");
        return ERROR;
    }
    else
    {
        return (PtrS->Data[(PtrS->Top)--]);
    }
}

int main()
{
    Stack S = CreateStack(10);
    int choice;
    while(1)
    {
        printf("（1）进栈 （2）出栈 （3）读栈顶 （4）退出\n");
        scanf("%d",&choice);
        if(choice == 1)
        {
            ElementType X;
            printf("输入进栈元素：");
            scanf("%d",&X);
            if(Push(S,X))
                printf("\n元素进栈成功！\n");
        }
        else if(choice == 2)
        {
            ElementType X;
            X = Pop(S);
            if(X != ERROR)
                printf("出栈元素为%d\n",X);
        }
        else
            return 0;
    }
}

（1）进栈 （2）出栈 （3）读栈顶 （4）退出
1
输入进栈元素：2

元素进栈成功！
（1）进栈 （2）出栈 （3）读栈顶 （4）退出
1
输入进栈元素：4

元素进栈成功！
（1）进栈 （2）出栈 （3）读栈顶 （4）退出
1
输入进栈元素：1

元素进栈成功！
（1）进栈 （2）出栈 （3）读栈顶 （4）退出
2
出栈元素为1
（1）进栈 （2）出栈 （3）读栈顶 （4）退出
2
出栈元素为4
（1）进栈 （2）出栈 （3）读栈顶 （4）退出
2
出栈元素为2
（1）进栈 （2）出栈 （3）读栈顶 （4）退出
2
栈已空！（1）进栈 （2）出栈 （3）读栈顶 （4）退出
4

Process returned 0 (0x0)   execution time : 18.576 s
Press any key to continue.

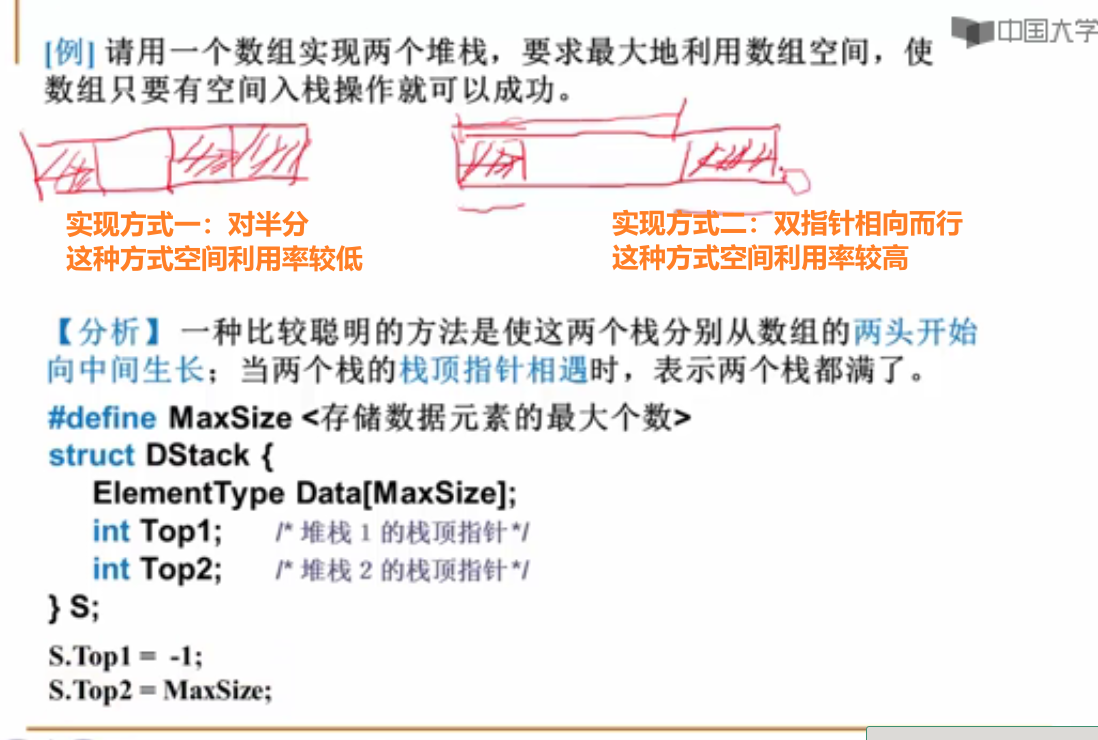
实例PTA6-7 在一个数组中实现两个堆栈

本题要求在一个数组中实现两个堆栈。

函数接口定义：

Stack CreateStack( int MaxSize );
bool Push( Stack S, ElementType X, int Tag );
ElementType Pop( Stack S, int Tag );

其中Tag是堆栈编号，取1或2；MaxSize堆栈数组的规模；Stack结构定义如下：

typedef int Position;
struct SNode {
    ElementType *Data;
    Position Top1, Top2;
    int MaxSize;
};
typedef struct SNode *Stack;

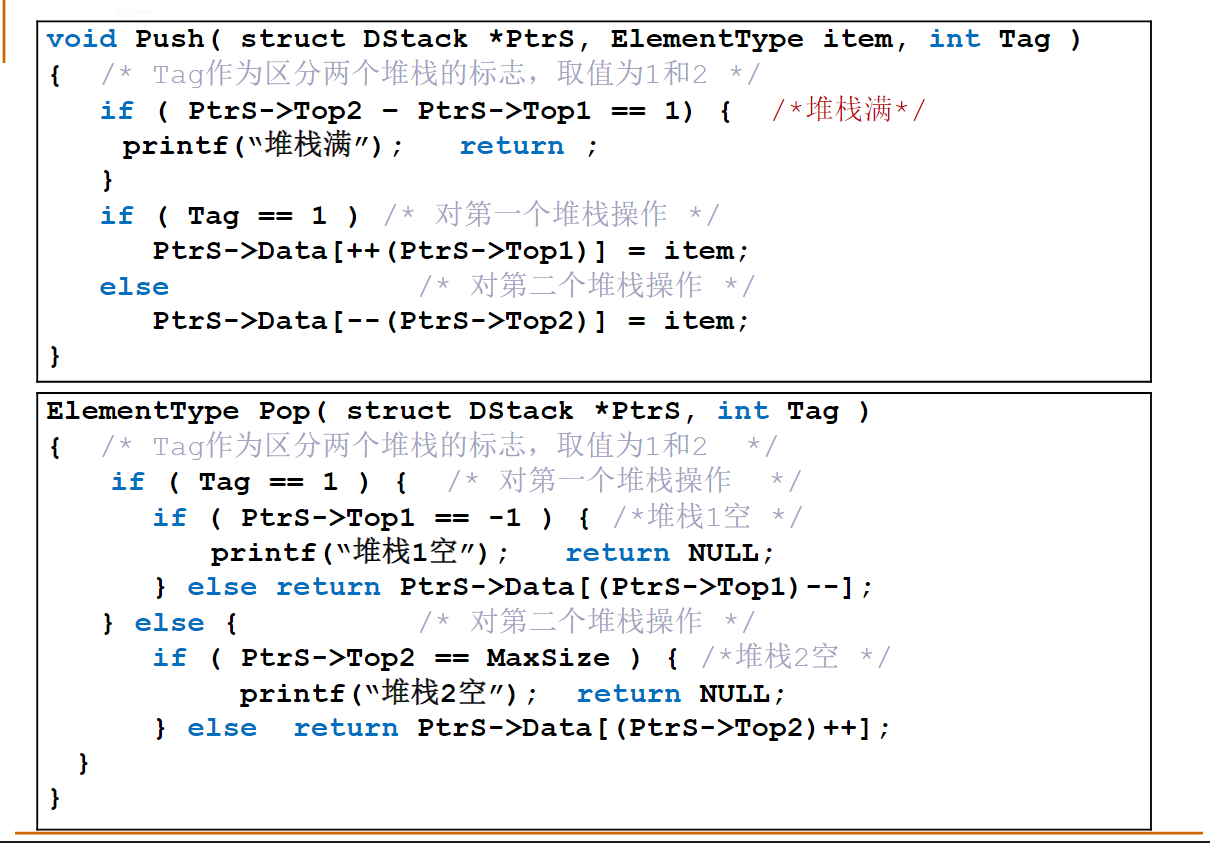
注意：如果堆栈已满，Push函数必须输出“Stack Full”并且返回false；如果某堆栈是空的，则Pop函数必须输出“Stack Tag Empty”（其中Tag是该堆栈的编号），并且返回ERROR。

裁判测试程序样例：

#include <stdio.h>
#include <stdlib.h>

#define ERROR 1e8
typedef int ElementType;
typedef enum { push, pop, end } Operation;
typedef enum { false, true } bool;
typedef int Position;
struct SNode {
    ElementType *Data;
    Position Top1, Top2;
    int MaxSize;
};
typedef struct SNode *Stack;

Stack CreateStack( int MaxSize );
bool Push( Stack S, ElementType X, int Tag );
ElementType Pop( Stack S, int Tag );

Operation GetOp();  /* details omitted */
void PrintStack( Stack S, int Tag ); /* details omitted */

int main()
{
    int N, Tag, X;
    Stack S;
    int done = 0;

    scanf("%d", &N);
    S = CreateStack(N);
    while ( !done ) {
        switch( GetOp() ) {
        case push: 
            scanf("%d %d", &Tag, &X);
            if (!Push(S, X, Tag)) printf("Stack %d is Full!\n", Tag);
            break;
        case pop:
            scanf("%d", &Tag);
            X = Pop(S, Tag);
            if ( X==ERROR ) printf("Stack %d is Empty!\n", Tag);
            break;
        case end:
            PrintStack(S, 1);
            PrintStack(S, 2);
            done = 1;
            break;
        }
    }
    return 0;
}

/* 你的代码将被嵌在这里 */

输入样例：

5
Push 1 1
Pop 2
Push 2 11
Push 1 2
Push 2 12
Pop 1
Push 2 13
Push 2 14
Push 1 3
Pop 2
End

输出样例：

Stack 2 Empty
Stack 2 is Empty!
Stack Full
Stack 1 is Full!
Pop from Stack 1: 1
Pop from Stack 2: 13 12 11

能AC的代码如下：

Stack CreateStack( int MaxSize )
{
    Stack S = (Stack)malloc(sizeof(struct SNode));
    S->Data = (ElementType*)malloc(sizeof(ElementType)*MaxSize);
    S->Top1 = -1;
    S->Top2 = MaxSize;
    S->MaxSize = MaxSize;
    return S;
    
}
bool Push( Stack S, ElementType X, int Tag )
{
    if(S->Top1 + 1 == S->Top2)
    {
        printf("Stack Full\n");
        return false;
    }
    if(Tag == 1)
    {
        S->Data[++(S->Top1)] = X;
        return true;
    }
    else
    {
        S->Data[--(S->Top2)] = X;
        return true;
    }
    
}
ElementType Pop( Stack S, int Tag )
{
    if(Tag == 1)
    {
        if(S->Top1 == -1)
        {
            printf("Stack %d Empty\n",Tag);
            return ERROR;
        }
        else
            return (S->Data[(S->Top1)--]);
    }
    else
    {
        if(S->Top2 == S->MaxSize)
        {
            printf("Stack %d Empty\n",Tag);
            return ERROR;
        }
        else
            return (S->Data[(S->Top2)++]);
    }
}

栈的链式存储实现

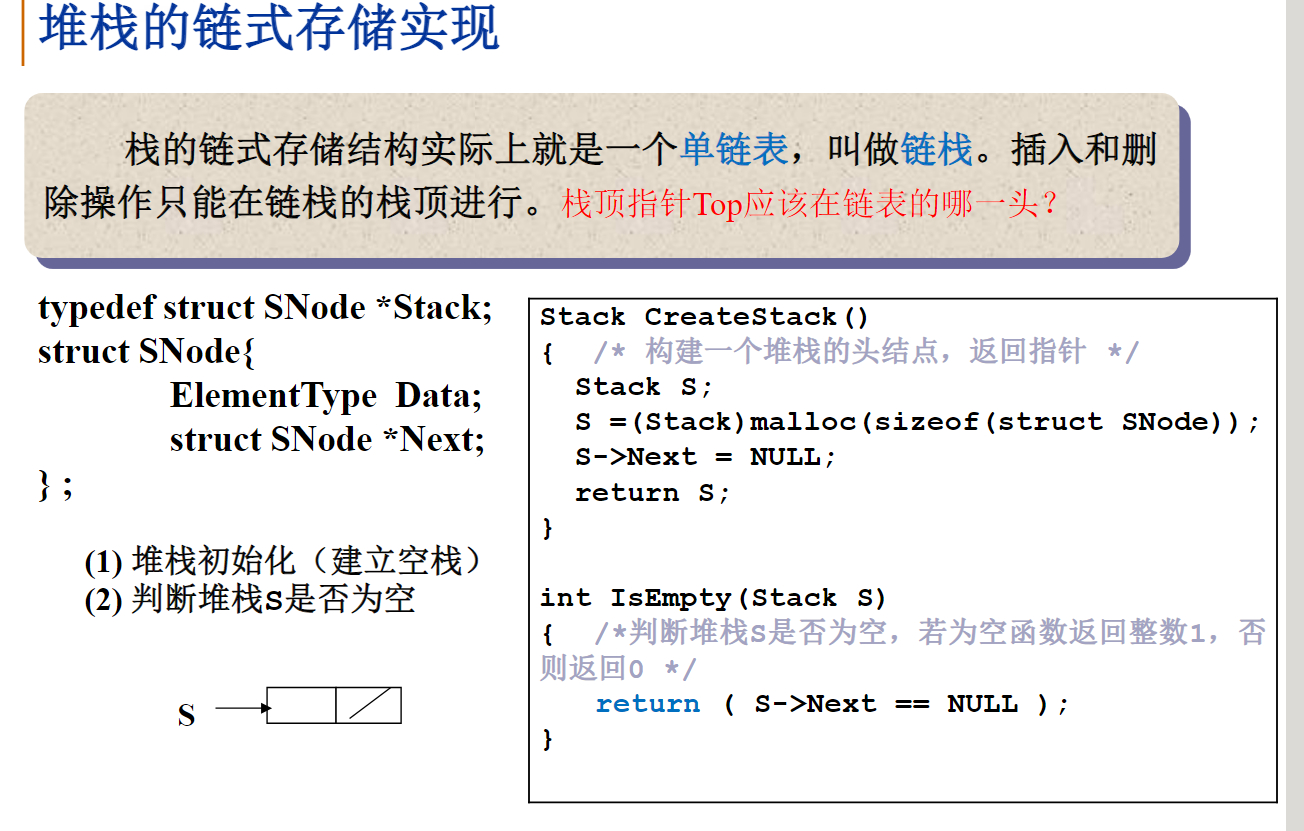
若用单向链表实现一个堆栈，只有链表的头可以作为top。

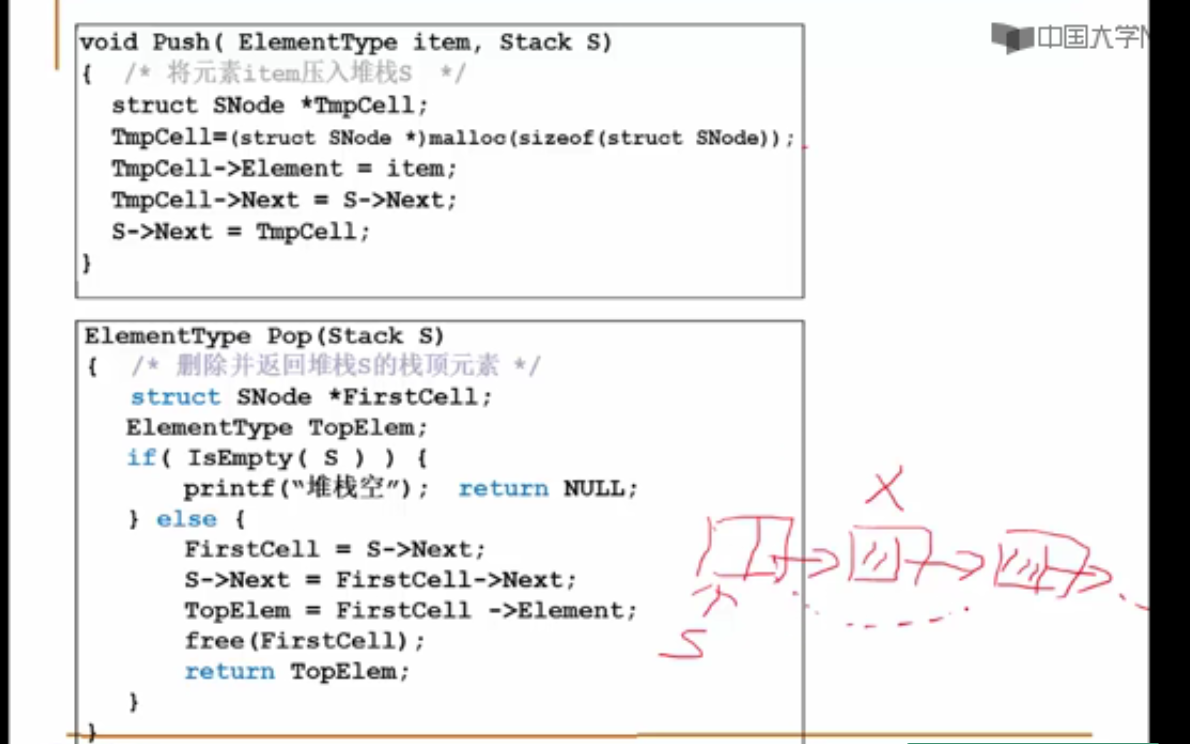
《数据结构》课程给出的代码如下：

typedef struct SNode *PtrToSNode;
struct SNode {
    ElementType Data;
    PtrToSNode Next;
};
typedef PtrToSNode Stack;

Stack CreateStack( ) 
{ /* 构建一个堆栈的头结点，返回该结点指针 */
    Stack S;

    S = (Stack)malloc(sizeof(struct SNode));
    S->Next = NULL;
    return S;
}

bool IsEmpty ( Stack S )
{ /* 判断堆栈S是否为空，若是返回true；否则返回false */
    return ( S->Next == NULL );
}

bool Push( Stack S, ElementType X )
{ /* 将元素X压入堆栈S */
    PtrToSNode TmpCell;

    TmpCell = (PtrToSNode)malloc(sizeof(struct SNode));
    TmpCell->Data = X;
    TmpCell->Next = S->Next;
    S->Next = TmpCell;
    return true;
}

ElementType Pop( Stack S )  
{ /* 删除并返回堆栈S的栈顶元素 */
    PtrToSNode FirstCell;
    ElementType TopElem;

    if( IsEmpty(S) ) {
        printf("堆栈空"); 
        return ERROR;
    }
    else {
        FirstCell = S->Next; 
        TopElem = FirstCell->Data;
        S->Next = FirstCell->Next;
        free(FirstCell);
        return TopElem;
    }
}

测试程序如下：

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>

#define ElementType int
#define ERROR -1
#define OK 0

typedef int Position;
typedef struct SNode *Stack;

struct SNode
{
    ElementType Data;
    Stack Next;
};

Stack CreateStack()
{
    Stack S = (Stack)malloc(sizeof(struct SNode));
    S->Next = NULL;
    return S;
}

bool Push(Stack PtrS,ElementType X)
{
    Stack TempCell = (Stack)malloc(sizeof(struct SNode));
    TempCell->Data = X;
    TempCell->Next = PtrS->Next;
    PtrS->Next = TempCell;
    return true;
}

bool IsEmpty(Stack S)
{
    return (S->Next == NULL);
}

ElementType Pop(Stack PtrS)
{
    Stack FirstCell;
    ElementType TopElem;

    if(IsEmpty(PtrS))
    {
        printf("栈已空！");
        return ERROR;
    }
    else
    {
        FirstCell = PtrS->Next;
        TopElem = FirstCell->Data;
        PtrS->Next = FirstCell->Next;
        free(FirstCell);
        return TopElem;
    }
}

int main()
{
    Stack S = CreateStack();
    int choice;
    while(1)
    {
        printf("（1）进栈 （2）出栈 （3）读栈顶 （4）退出\n");
        scanf("%d",&choice);
        if(choice == 1)
        {
            ElementType X;
            printf("输入进栈元素：");
            scanf("%d",&X);
            if(Push(S,X))
                printf("\n元素进栈成功！\n");
        }
        else if(choice == 2)
        {
            ElementType X;
            X = Pop(S);
            if(X != ERROR)
                printf("出栈元素为%d\n",X);
        }
        else
            return 0;
    }
}

（1）进栈 （2）出栈 （3）读栈顶 （4）退出
1
输入进栈元素：2

元素进栈成功！
（1）进栈 （2）出栈 （3）读栈顶 （4）退出
1
输入进栈元素：3

元素进栈成功！
（1）进栈 （2）出栈 （3）读栈顶 （4）退出
1
输入进栈元素：1

元素进栈成功！
（1）进栈 （2）出栈 （3）读栈顶 （4）退出
2
出栈元素为1
（1）进栈 （2）出栈 （3）读栈顶 （4）退出
2
出栈元素为3
（1）进栈 （2）出栈 （3）读栈顶 （4）退出
2
出栈元素为2
（1）进栈 （2）出栈 （3）读栈顶 （4）退出
2
栈已空！（1）进栈 （2）出栈 （3）读栈顶 （4）退出
4

Process returned 0 (0x0)   execution time : 28.401 s
Press any key to continue.

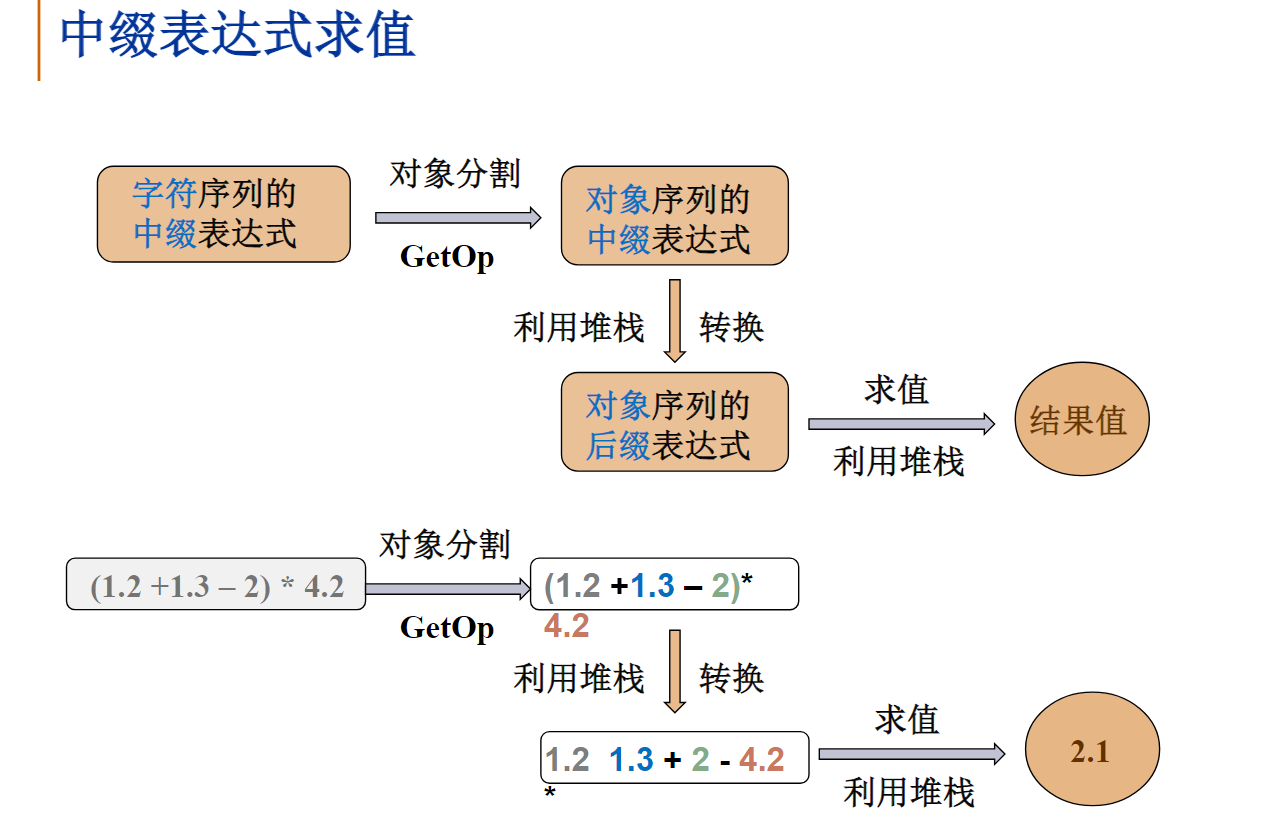
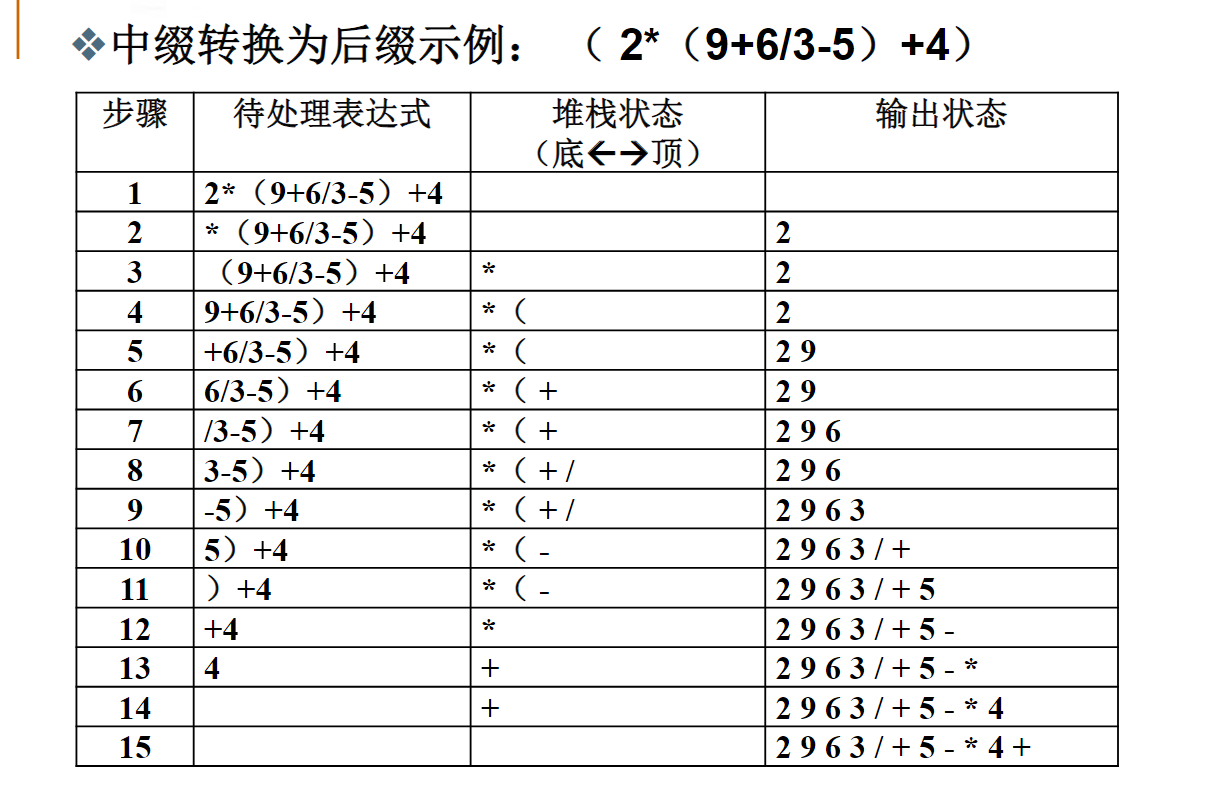
栈应用：表达式求值

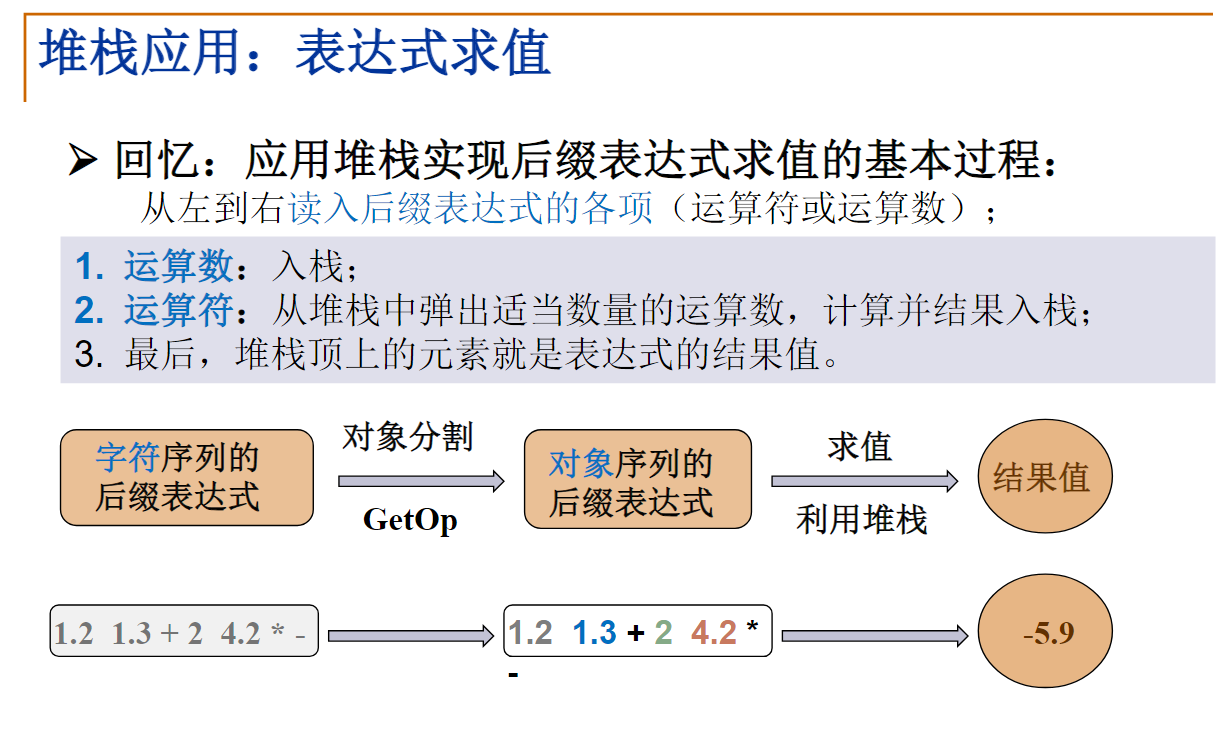
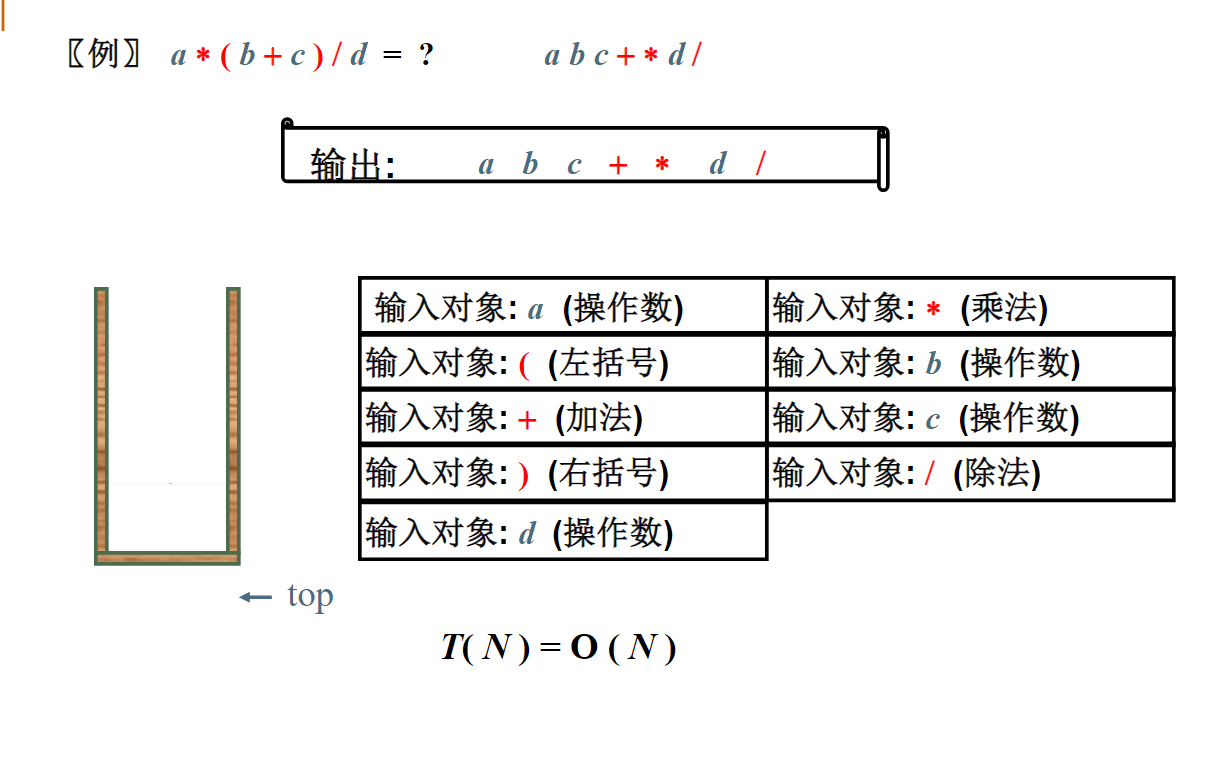
左括号一旦放到堆栈中优先级就变为最低。碰到右括号（右括号不入栈）就把栈顶元素抛出，直到抛出左括号为止。注：括号是不会出现在后缀表达式或前缀表达式中的

请试试应用堆栈将中缀表达式2*(6/3+4)-5转换为后缀表达式。在这个转换过程中，堆栈元素最多时元素个数是3。

借助堆栈将中缀表达式A-(B-C/D)*E转换为后缀表达式，则该堆栈的大小至少为：4

如果一堆栈的输入序列是aAbBc，输出为 abcBA，那么该堆栈所进行的操作序列是什么？ 设P代表入栈，O代表出栈。 POPPOPPOOO