线性回归——正则方程法求解

• Least squares revisited
• 最小二乘法
• 噪声为高斯分布的 MLE
• 权重先验也为高斯分布的 MAP

假设数据集为： $$\mathcal{D}=\{(x_1,y_1),(x_2,y_2),\cdots ,(x_N,y_N)\}$$ 其中$x_i\in R^p,y_i\in R,i=1,2,...,N$

考虑截距的话，则$x_i\in R^{p+1},y_i\in R,i=1,2,...,N$，此时X、W和Y的表达式如下：

$${X=(\begin{array}{cccc}{x}_1& x_2& \cdots & x_N\end{array})}^T=\left(\begin{array}{c}{x}_1^T\\ x_2^T\\ ⋮\\ x_N^T\end{array}\right)={\left(\begin{array}{ccccc}1& x_{11}& x_{12}& \cdots & x_{1p}\\ 1& x_{21}& x_{22}& \cdots & x_{2p}\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ 1& x_{N1}& x_{N2}& \cdots & x_{Np}\end{array}\right)}_{N\ast （p+1）}$$

$$W={\left(\begin{array}{c}{w}_0\\ w_1\\ w_2\\ ⋮\\ w_p\end{array}\right)}_{(p+1)\times 1}$$

$$Y={\left(\begin{array}{c}{y}_1\\ y_2\\ ⋮\\ y_N\end{array}\right)}_{N\times 1}$$

方便起见，后面我们记： $$X=(x_1,x_2,\cdots ,x_N{)}^T,Y=(y_1,y_2,\cdots ,y_N{)}^T$$ 对每一个样本数据，作出如下的线性回归假设： $$f(w)=w^{T}x$$

Least squares revisited

Armed with the tools of matrix derivatives, let us now proceed to find in closed-form the value of θ that minimizes J(θ). We begin by re-writing J in matrix-vectorial notation.

Given a training set, define the design matrix X to be the n-by-d matrix (actually n-by-d + 1, if we include the intercept term) that contains the training examples’ input values in its rows:

$$X=[\begin{array}{c}-(x^{(1)}{)}^T-\\ -(x^{(2)}{)}^T-\\ ⋮\\ -(x^{(n)}{)}^T-\end{array}].$$

Also, let $\vec{y}$ be the $n$-dimensional vector containing all the target values from the training set:

$$\vec{y}=[\begin{array}{c}{y}^{(1)}\\ y^{(2)}\\ ⋮\\ y^{(n)}\end{array}].$$

Now, since $h_{\theta }(x^{(i)})=(x^{(i)}{)}^T\theta ,$ we can easily verify that

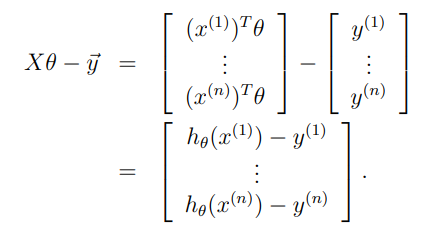
Thus, using the fact that for a vector $z,$ we have that $z^{T}z={\sum }_i{z}_i^2:$

$$\begin{array}{rlrl}\frac{1}{2}(X\theta -\vec{y}{)}^T(X\theta -\vec{y})& & =& \frac{1}{2}\sum _{i=1}^n(h_{\theta }(x^{(i)})-y^{(i)}{)}^2\\ & & =& J(\theta )\end{array}$$

Finally, to minimize $J$ let's find its derivatives with respect to $\theta$. Hence,

$$\begin{array}{rl}{\nabla }_{\theta }J(\theta )& ={\nabla }_{\theta }\frac{1}{2}(X\theta -\vec{y}{)}^T(X\theta -\vec{y})\\ & =\frac{1}{2}{\nabla }_{\theta }((X\theta {)}^{T}X\theta -(X\theta {)}^T\vec{y}-{\vec{y}}^T(X\theta )+{\vec{y}}^T\vec{y})\\ & =\frac{1}{2}{\nabla }_{\theta }\left({\theta }^T(X^{T}X)\theta -{\vec{y}}^T(X\theta )-{\vec{y}}^T(X\theta )\right)\\ & =\begin{array}{rc}\frac{1}{2}{\nabla }_{\theta }& \left({\theta }^T(X^{T}X)\theta -2(X^T\vec{y}{)}^T\theta \right)\end{array}\\ & =\frac{1}{2}\left(2X^{T}X\theta -2X^T\vec{y}\right)\\ & \begin{array}{rc}=& X^{T}X\theta -X^T\vec{y}\end{array}\end{array}$$ In the third step, we used the fact that $a^{T}b=b^{T}a$, and in the fifth step used the facts ${\nabla }_x{b}^{T}x=b$ and ${\nabla }_x{x}^{T}Ax=2Ax$ for symmetric matrix $A$ (fon more details, see Section 4.3 of “Linear Algebra Review and Reference”). To minimize $J,$ we set its derivatives to zero, and obtain the normal equations:

$$X^{T}X\theta =X^T\vec{y}$$

Thus, the value of $\theta$ that minimizes $J(\theta )$ is given in closed form by the equation

$$\theta =(X^{T}X{)}^{-1}{X}^T\vec{y}$$

最小二乘法

对这个问题，采用二范数定义的平方误差来定义损失函数： $$L(w)=\sum _{i=1}^N||w^T{x}_i-y_i|{|}_2^2$$ 展开得到： $$\begin{array}{rl}L(w)& =(w^T{x}_1-y_1,\cdots ,w^T{x}_N-y_N)\cdot (w^T{x}_1-y_1,\cdots ,w^T{x}_N-y_N{)}^T\\ & =(w^T{X}^T-Y^T)\cdot (Xw-Y)=w^T{X}^{T}Xw-Y^{T}Xw-w^T{X}^{T}Y+Y^{T}Y\\ & =w^T{X}^{T}Xw-2w^T{X}^{T}Y+Y^{T}Y\end{array}$$ 最小化这个值的 $\hat{w}$ ： $$\begin{array}{rl}\hat{w}=\underset{w}{\mathrm{argmin}}L(w)& ⟶\frac{\partial }{\partial w}L(w)=0\\ & ⟶2X^{T}X\hat{w}-2X^{T}Y=0\\ & ⟶\hat{w}=(X^{T}X{)}^{-1}{X}^{T}Y=X^{+}Y\end{array}$$ 这个式子中 $(X^{T}X{)}^{-1}{X}^T$ 又被称为伪逆。对于行满秩或者列满秩的 $X$，可以直接求解，但是对于非满秩的样本集合，需要使用奇异值分解（SVD）的方法，对 $X$ 求奇异值分解，得到 $$X=U\Sigma V^T$$ 于是： $$X^{+}=V{\Sigma }^{-1}{U}^T$$ 在几何上，最小二乘法相当于模型（这里就是直线）和试验值的距离的平方求和，假设我们的试验样本张成一个 $p$ 维空间（满秩的情况）：$X=Span(x_1,\cdots ,x_N)$，而模型可以写成 $f(w)=X\beta$，也就是 $x_1,\cdots ,x_N$ 的某种组合，而最小二乘法就是说希望 $Y$ 和这个模型距离越小越好，于是它们的差应该与这个张成的空间垂直： $$X^T\cdot (Y-X\beta )=0⟶\beta =(X^{T}X{)}^{-1}{X}^{T}Y$$

噪声为高斯分布的 MLE

对于一维的情况，记 $y=w^{T}x+ϵ,ϵ\sim \mathcal{N}(0,{\sigma }^2)$，那么 $y\sim \mathcal{N}(w^{T}x,{\sigma }^2)$。代入极大似然估计中： $$\begin{array}{rl}L(w)=\log p(Y|X,w)& =\log \prod _{i=1}^{N}p(y_i|x_i,w)\\ & =\sum _{i=1}^N\log (\frac{1}{\sqrt{2\pi \sigma }}{e}^{-\frac{(y_i-w^T{x}_i{)}^2}{2{\sigma }^2}})\\ \underset{w}{\mathrm{argmax}}L(w)& =\underset{w}{\mathrm{argmin}}\sum _{i=1^N}(y_i-w^T{x}_i{)}^2\end{array}$$ 这个表达式和最小二乘估计得到的结果一样。

权重先验也为高斯分布的 MAP

取先验分布 $w\sim \mathcal{N}(0,{\sigma }_0^2)$。于是：  $$\begin{array}{rl}\hat{w}=\underset{w}{\mathrm{argmax}}p(w|Y)& =\underset{w}{\mathrm{argmax}}p(Y|w)p(w)\\ & =\underset{w}{\mathrm{argmax}}\log p(Y|w)p(w)\\ & =\underset{w}{\mathrm{argmax}}(\log p(Y|w)+\log p(w))\\ & =\underset{w}{\mathrm{argmin}}[(y-w^{T}x{)}^2+\frac{{\sigma }^2}{{\sigma }_0^2}{w}^{T}w]\end{array}$$ 这里省略了 $X$，$p(Y)$和 $w$ 没有关系，同时也利用了上面高斯分布的 MLE的结果。

我们将会看到，超参数 ${\sigma }_0$的存在和下面会介绍的 Ridge 正则项可以对应，同样的如果将先验分布取为 Laplace 分布，那么就会得到和 L1 正则类似的结果。