前言
Machine Learning definition
- Arthur Samuel(1959)Machine Learning: Field of study that gives computers the ability to learn without being explicitly programmed.
- TomMitchell(1998)Well-posed Learning Problem: A computer program is said to learn from experience E with respect to some task T and some performance measure P, if its performance on T, as measured by P, improves with experience E.
机器学习(Machine Learning,ML)是多领域交叉学科,涉及概率论、统计学、逼近论、凸分析、算法复杂度理论等。机器学习专门研究计算机怎样模拟或实现人类的学习行为,以获取新的知识或技能,重新组织已有的知识结构,使之不断改善自身的性能。
机器学习能让我们从数据集中受到启发,换句话说,我们会利用计算机来彰显数据背后的真实含义,这才是机器学习的真实含义。它既不是只会模仿的机器人,也不是具有人类感情的仿生人。
学习资源——在线课程
Stanford CS229: Machine Learning
UCB CS189: Introduction to Machine Learning
学习资源——书籍
《统计学习方法(第2版)》分为监督学习和无监督学习两篇,全面系统地介绍了统计学习的主要方法。包括感知机、k近邻法、朴素贝叶斯法、决策树、逻辑斯谛回归与大熵模型、支持向量机、提升方法、EM算法、隐马尔可夫模型和条件随机场,以及聚类方法、奇异值分解、主成分分析、潜在语义分析、概率潜在语义分析、马尔可夫链蒙特卡罗法、潜在狄利克雷分配和PageRank算法等。
学习路线
以下不是针对回答评论,而是对现在初学者一上来就推荐统计学习方法的回答的评价(来自豆瓣)
初学者不适合看《统计学习方法》,但是从事相关行业的人必定要看,本书精简不啰嗦,面面俱到,从原理上给你整得明明白白的,辅以适当的例子,没有多余的图表,因为人工智能不是什么画图跑demo的专业,你需要有扎实的数学基础。
建议路线,ng课程入门,知道有哪些算法,大致怎么做,然后去kaggle打个入门赛,别做特征工程,把会的算法全用上。然后放下比赛,开始读这本书,同时看机器学习基石或其他比较数学化的进阶课程,这一步不需要你敲代码,你要会的是滚瓜烂熟的推导,做到这一步,再去kaggle参加奖金赛,阅读kernel,学习state of the art 模型,学习特征工程,再在学习过程中阅读最新的论文或者经典的论文,不断迭代这个过程,别淹死在什么机器学习实战上,有现成的轮子不用,非得费那个劲,除非你科班毕业,代码能力扎实,不然你能不能从头实现一遍决策树对你找不找到工作没有任何一毛钱关系。笔试不会考你如何实现hmm,只会考数据结构与算法,面试只会让你推导。
面过一些学过吴恩达公开课和《统计学习方法》之类教材的同学,一方面在实现上,C++水平不行,然后就想要来做算法,说实话,看过这些东西对于机器学习的面有所了解。了解人家转述的算法,连论文都没读过就想要来做研究也是醉了。说PCA,对于SVD分解的方法讲的头头是道,但是问他怎么用基本的特征分解来做,就说自己不了解。说K均值和EM好像很熟悉,问他K均值跟EM什么关系,不知道。说EM熟悉吧,高斯混合模型不了解……说梯度下降很熟悉吧,问他什么是线性最小二乘法什么是非线性最小二乘法,都支支吾吾不懂。一言以蔽之,知其然而不知其所以然,要做算法研究就踏踏实实以书本为纲,找到感兴趣的点去读相关论文。要做算法实现就老老实实地把C++学好,只会一点点python加上读过两本普及教材说真的没有公司要招你。
个人认为各种ML算法(含监督式/非监督式/强化学习)难度从小到大以及学习的顺序应该是这样的:
入门:线性回归/逻辑回归,kNN,k-means,决策树,神经网络(MLP/CNN/LSTM),反向传播,RL的bandit/MDP/动态规划/TD/MC
初级:贝叶斯线性回归/逻辑回归,NLP的Transformer/BERT/GPT, GMM/HMM,EM/Baum-Welch/Viterbi/卡尔曼滤波,概率图模型和BP,Junction tree,SVM/核方法/RKHS,model-based RL/policy gradient/actor-critic
中级:helmholtz/boltzmann machine/RBM/DBN,高斯过程,t-SNE/manifold learning/非线性降维,各种近似推断(平均场,期望传播,变分贝叶斯,loopy BP,kikuchi,stein),各种采样和MCMC方法(MH, Gibb’s, HMC, SMC, AIS, particle filter),各种积分方法(MC/高斯数值求积/无迹变换)。以及一些核方法延伸的主题如MMD,HSIC之类的
高级:统计学习理论(ERM/VC维/PAC/rademacher等),贝叶斯非参(DP/CRP/IBP等)
另外附一份(个人认为)按以上各“等级”的数学要求:
入门:多元微积分,线性代数,基本概率论(随机变量,基本分布,期望和方差)
初级:凸优化(尤其constrained opt/KKT condition),图论,高维概率论(尤其是正态分布,包括正态分布的线性变换,条件概率分布),贝叶斯推断,随机过程
中级:更多的概率论(指数族分布和GLM,skewness, kurtosis,测度论)和凸优化,统计力学(spin glass model),凸分析,泛函分析
Introduction
对概率的诠释有两大学派,一种是频率派另一种是贝叶斯派。后面我们对观测集采用下面记号: 这个记号表示有 个样本,每个样本都是 维向量。其中每个观测都是由 生成的。
频率派的观点
中的 是一个常量。对于 个观测来说观测集的概率为 。为了求 的大小,我们采用最大对数似然MLE的方法:
贝叶斯派的观点
贝叶斯派认为 中的 不是一个常量。这个 满足一个预设的先验的分布 。于是根据贝叶斯定理依赖观测集参数的后验可以写成:
为了求 的值,我们要最大化这个参数后验MAP:
其中第二个等号是由于分母和 没有关系。求解这个 值后计算 ,就得到了参数的后验概率。其中 叫似然,是我们的模型分布。得到了参数的后验分布后,我们可以将这个分布用于预测贝叶斯预测: 其中积分中的被乘数是模型,乘数是后验分布。
小结
频率派和贝叶斯派分别给出了一系列的机器学习算法。频率派的观点导出了一系列的统计机器学习算法而贝叶斯派导出了概率图理论。在应用频率派的 MLE 方法时最优化理论占有重要地位。而贝叶斯派的算法无论是后验概率的建模还是应用这个后验进行推断时积分占有重要地位。因此采样积分方法如 MCMC 有很多应用。
数学基础
线性代数基础
Matrix derivatives
For a function mapping from -by-d matrices to the real numbers, we define the derivative of with respect to to be:
Thus, the gradient is itself an -by- matrix, whose -element is . For example, suppose is a 2-by-2 matrix, and the function is given by
Here, denotes the entry of the matrix . We then have
概率论基础
高斯分布
一维情况 MLE
高斯分布在机器学习中占有举足轻重的作用。在 MLE 方法中:
一般地,高斯分布的概率密度函数PDF写为:
带入 MLE 中我们考虑一维的情况
首先对 的极值可以得到 : 于是: 其次对 中的另一个参数 ,有: 于是: 值得注意的是,上面的推导中,首先对 求 MLE, 然后利用这个结果求 ,因此可以预期的是对数据集求期望时 是无偏差的: 但是当对 求 期望的时候由于使用了单个数据集的 ,因此对所有数据集求期望的时候我们会发现 是 有偏的:
所以:
多维情况
多维高斯分布表达式为: 其中 , 为协方差矩阵,一般而言也是半正定矩阵。这里我们只考虑正定矩阵。首先我们处理指数上的数字,指数上的数字可以记为 和 之间的马氏距离。对于对称的协方差矩阵可进行特征值分解, ,于是:
我们注意到 是 在特征向量 上的投影长度,因此上式子就是 取不同值时的同心椭圆。
下面我们看多维高斯模型在实际应用时的两个问题
-
参数 的自由度为 对于维度很高的数据其自由度太高。解决方案:高自由度的来源是 有 个自由参数,可以假设其是对角矩阵,甚至在各向同性假设中假设其对角线上的元素都相同。前一种的算法有 Factor Analysis,后一种有概率 PCA(p-PCA) 。
-
第二个问题是单个高斯分布是单峰的,对有多个峰的数据分布不能得到好的结果。解决方案:高斯混合GMM 模型。
下面对多维高斯分布的常用定理进行介绍。
我们记 ,已知 。
首先是一个高斯分布的定理:
定理:已知 ,那么 。
证明:,。
下面利用这个定理得到 这四个量。
-
,代入定理中得到: 所以 。
-
同样的,。
-
对于两个条件概率,我们引入三个量: 特别的,最后一个式子叫做 的 Schur Complementary。可以看到: 所以: 利用这三个量可以得到 。因此:
这里同样用到了定理。
-
同样: 所以:
下面利用上边四个量,求解线性模型:
已知:,求解:。
解:令 ,所以 ,,因此: 引入 ,我们可以得到 。对于这个协方差可以直接计算: 注意到协方差矩阵的对称性,所以 。根据之前的公式,我们可以得到:
线性回归
概述
Given data like this, how can we learn to predict the prices of other houses in Portland, as a function of the size of their living areas?
To establish notation for future use, we'll use to denotc the “input” variables (living area in this example), also called input featurcs, and to denote the “output” or target variable that we are trying to predict A pair is called a training example, and the dataset that we'll be using to learn—a list of training examples —is called a training set. Note that the superscript “” in the notation is simply an index into the training set, and has nothing to do with exponentiation. We will also use denote the space of input values, and the space of output values. In this example,
To describe the supervised learning problem slightly more formally, our goal is, given a training set, to learn a function so that is a “good” predictor for the corresponding value of For historical reasons, this function h is called a hypothesis.
When the target variable that we're trying to predict is continuous, such as in our housing example, we call the learning problem a regression problem.When can take on only a small number of discrete values (such as if, given the living area, we wanted to predict if a dwelling is a house or an apartment, say), we call it a classification problem.
Here, the 's are two-dimensional vectors in . For instance, is the living area of the -th house in the training set, and is its number of bedrooms. (In general, when designing a learning problem, it will be up to you to decide what features to choose, so if you are out in Portland gathering housing data, you might also decide to include other features such as whether each house has a fireplace, the number of bathrooms, and so on. We'll say more about feature selection later, but for now let's take the features as given.)
To perform supervised learning, we must decide how we're going to represent functions/hypotheses in a computer. As an initial choice, let's say we decide to approximate as a linear function of
Here, the 's are the parameters (also called weights) parameterizing the space of linear functions mapping from to . When there is no risk of confusion, we will drop the subscript in , and write it more simply as To simplify our notation, we also introduce the convention of letting (this is the intercept term), so that
where on the right-hand side above we are viewing and both as vectors, and here is the number of input variables (not counting
Now, given a training set, how do we pick, or learn, the parameters One reasonable method seems to be to make close to , at least for the training examples we have. To formalize this, we will define a function that measures, for each value of the 's, how close the 's are to the corresponding s. We define the t function:
If you've seen linear regression before, you may recognize this as the familian least-squares cost function that gives rise to the ordinary least squares regression model. Whether or not you have seen it previously, let's keep going, and we'll eventually show this to be a special case of a much broader family of algorithms.
两种求解方式的比较:
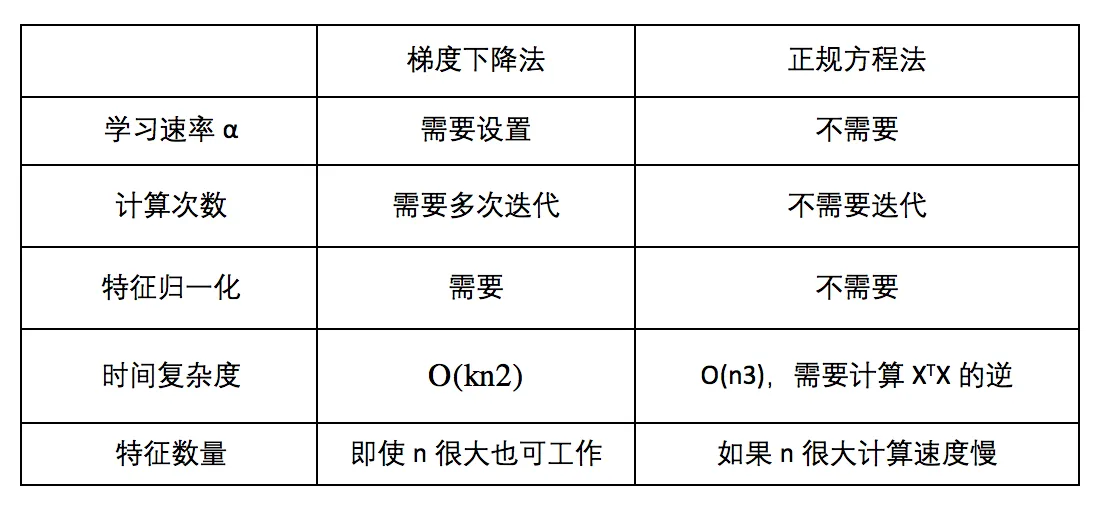
可见特征方程得到的是解析解,无需迭代,也没有设置学习速率的繁琐,需要特征归一化,但是求解正规方程需要求矩阵的逆,然而不是所有的矩阵都可逆,而且有些可逆矩阵的求逆极其耗费时间,所以特征方程法看似简单,其实使用场景并不多。只有当特征值比较小的时候,可以考虑使用特征方程法。
小结
线性回归模型是最简单的模型,但是麻雀虽小,五脏俱全,在这里,我们利用最小二乘误差得到了闭式解。同时也发现,在噪声为高斯分布的时候,MLE 的解等价于最小二乘误差,而增加了正则项后,最小二乘误差加上 L2 正则项等价于高斯噪声先验下的 MAP解,加上 L1 正则项后,等价于 Laplace 噪声先验。
传统的机器学习方法或多或少都有线性回归模型的影子:
- 线性模型往往不能很好地拟合数据,因此有三种方案克服这一劣势:
- 对特征的维数进行变换,例如多项式回归模型就是在线性特征的基础上加入高次项。
- 在线性方程后面加入一个非线性变换,即引入一个非线性的激活函数,典型的有线性分类模型如感知机。
- 对于一致的线性系数,我们进行多次变换,这样同一个特征不仅仅被单个系数影响,例如多层感知机(深度前馈网络)。
- 线性回归在整个样本空间都是线性的,我们修改这个限制,在不同区域引入不同的线性或非线性,例如线性样条回归和决策树模型。
- 线性回归中使用了所有的样本,但是对数据预先进行加工学习的效果可能更好(所谓的维数灾难,高维度数据更难学习),例如 PCA 算法和流形学习。
线性回归——梯度下降法求解
LMS algorithm
We want to choose so as to minimize To do so, let's use a search algorithm that starts with some “initial guess” for , and that repeatedly changes to make smaller, until hopefully we converge to a value of that minimizes Specifically, let's consider the gradient descent algorithm, which starts with some initial , and repeatedly performs the update:
(This update is simultaneously performed for all values of Here, is called the learning rate. This is a very natural algorithm that repeatedly takes a step in the direction of steepest decrease of
In order to implement this algorithm, we have to work out what is the partial derivative term on the right hand side. Let's first work it out for the case of if we have only one training example , so that we can neglect the sum in the definition of . We have:
For a single training example, this gives the update rule:
The rule is called the LMS update rule (LMS stands for “least mean squares”), and is also known as the Widrow-Hoff learning rule. This rule has several properties that seem natural and intuitive. For instance, the magnitude of the update is proportional to the error term thus, for instance, if we are encountering a training example on which our prediction nearly matches the actual value of , then we find that there is little need to change the parameters; in contrast, a larger change to the parameters will be made if our prediction has a large error (i.e., if it is very far from
We'd derived the LMS rule for when there was only a single training example. There are two ways to modify this method for a training set of more than one example.
Batch Gradient Descent
The first is replace it with the following algorithm:
Repeat until convergence
}
By grouping the updates of the coordinates into an update of the vector , we can rewrite update (1.1) in a slightly more succinct way:
The reader can easily verify that the quantity in the summation in the update rule above is just ( for the original definition of ) . So, this is simply gradient descent on the original cost function This method looks at every example in the entire training set on every step, and is called batch gradient descent. Note that, while gradient descent can be susceptible to local minima in general, the optimization problem we have posed here for linear regression has only one global, and no other local, optima; thus gradient descent always converges (assuming the learning rate is not too large) to the global minimum. Indeed, is a convex quadratic function. Here is an example of gradient descent as it is run to minimize a quadratic function.
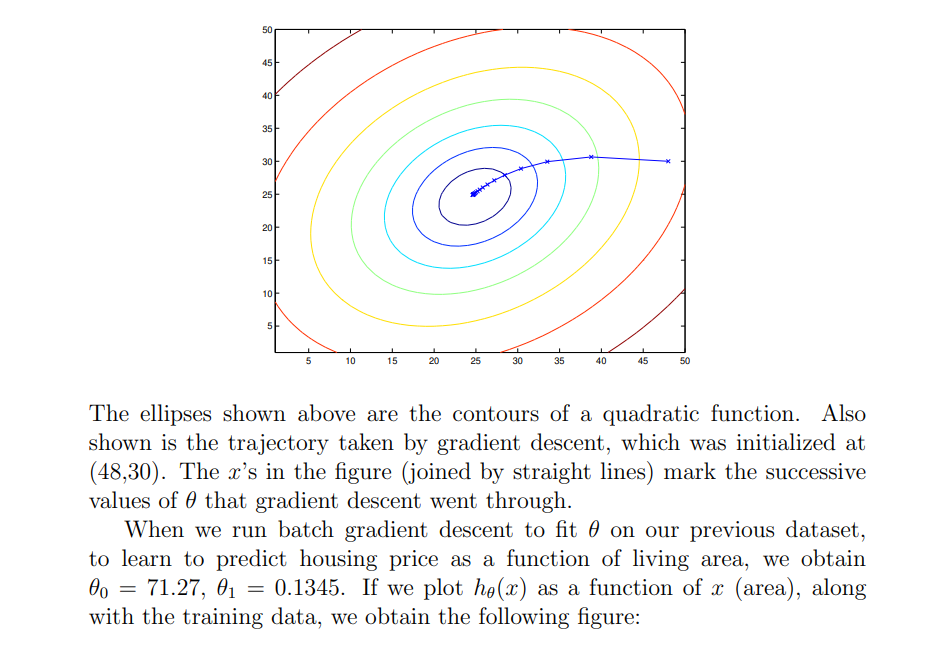
Stochastic Gradient Descent
The above results were obtained with batch gradient descent. There is an alternative to batch gradient descent that also works very well. Consider the following algorithm:
Loop for to
By grouping the updates of the coordinates into an update of the vector , we can rewrite update (1.2) in a slightly more succinct way:
In this algorithm, we repeatedly run through the training set, and each time we encounter a training example, we update the parameters according to the gradient of the error with respect to that single training example only. This algorithm is called stochastic gradient descent (also incremental gradient descent). Whereas batch gradient descent has to scan through the entire training set before taking a single step—a costly operation if is large—stochastic gradient descent can start making progress right away, and continues to make progress with each example it looks at. Often, stochastic gradient descent gets θ “close” to the minimum much faster than batch gradient descent. (Note however that it may never “converge” to the minimum, and the parameters θ will keep oscillating around the minimum of J(θ); but in practice most of the values near the minimum will be reasonably good approximations to the true minimum.)
For these reasons, particularly when the training set is large, stochastic gradient descent is often preferred over batch gradient descent.
线性回归——正则方程法求解
假设数据集为: 其中
考虑截距的话,则,此时X、W和Y的表达式如下:
方便起见,后面我们记: 对每一个样本数据,作出如下的线性回归假设:
Least squares revisited
Armed with the tools of matrix derivatives, let us now proceed to find in closed-form the value of θ that minimizes J(θ). We begin by re-writing J in matrix-vectorial notation.
Given a training set, define the design matrix X to be the n-by-d matrix (actually n-by-d + 1, if we include the intercept term) that contains the training examples’ input values in its rows:
Also, let be the -dimensional vector containing all the target values from the training set:
Now, since we can easily verify that
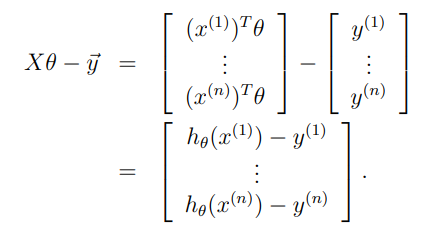
Thus, using the fact that for a vector we have that
Finally, to minimize let's find its derivatives with respect to . Hence,
In the third step, we used the fact that , and in the fifth step used the facts and for symmetric matrix (fon more details, see Section 4.3 of “Linear Algebra Review and Reference”). To minimize we set its derivatives to zero, and obtain the normal equations:
Thus, the value of that minimizes is given in closed form by the equation
最小二乘法
对这个问题,采用二范数定义的平方误差来定义损失函数: 展开得到: 最小化这个值的 : 这个式子中 又被称为伪逆。对于行满秩或者列满秩的 ,可以直接求解,但是对于非满秩的样本集合,需要使用奇异值分解(SVD)的方法,对 求奇异值分解,得到 于是: 在几何上,最小二乘法相当于模型(这里就是直线)和试验值的距离的平方求和,假设我们的试验样本张成一个 维空间(满秩的情况):,而模型可以写成 ,也就是 的某种组合,而最小二乘法就是说希望 和这个模型距离越小越好,于是它们的差应该与这个张成的空间垂直:
噪声为高斯分布的 MLE
对于一维的情况,记 ,那么 。代入极大似然估计中: 这个表达式和最小二乘估计得到的结果一样。
权重先验也为高斯分布的 MAP
取先验分布 。于是: 这里省略了 ,和 没有关系,同时也利用了上面高斯分布的 MLE的结果。
我们将会看到,超参数 的存在和下面会介绍的 Ridge 正则项可以对应,同样的如果将先验分布取为 Laplace 分布,那么就会得到和 L1 正则类似的结果。
线性回归正则化
在实际应用时,如果样本容量不远远大于样本的特征维度,很可能造成过拟合,对这种情况,我们有下面三个解决方式:
- 加数据
- 特征选择(手动删除一些不重要的特征)、特征提取(降维如PCA)
- 正则化
正则化一般是在损失函数(如上面介绍的最小二乘损失)上加入正则化项(表示模型的复杂度对模型的惩罚),下面我们介绍一般情况下的两种正则化框架。 下面对最小二乘误差分别分析这两者的区别。
L1 Lasso
L1正则化可以引起稀疏解。
从最小化损失的角度看,由于 L1 项求导在0附近的左右导数都不是0,因此更容易取到0解。
从另一个方面看,L1 正则化相当于: 我们已经看到平方误差损失函数在 空间是一个椭球,因此上式求解就是椭球和 的切点,因此更容易相切在坐标轴上。
L2 Ridge
可以看到,这个正则化参数和前面的 MAP 结果不谋而合。利用2范数进行正则化不仅可以是模型选择 较小的参数,同时也避免 不可逆的问题。
Linear Classification线性分类
两分类-硬分类-感知机算法

我们选取激活函数为: 这样就可以将线性回归的结果映射到两分类的结果上了。
定义损失函数为错误分类的数目,比较直观的方式是使用指示函数,但是指示函数不可导,因此可以定义: 其中,是错误分类集合,实际在每一次训练的时候,我们采用梯度下降的算法。损失函数对 的偏导为: 但是如果样本非常多的情况下,计算复杂度较高,但是,实际上我们并不需要绝对的损失函数下降的方向,我们只需要损失函数的期望值下降,但是计算期望需要知道真实的概率分布,我们实际只能根据训练数据抽样来估算这个概率分布(经验风险):
\mathbb{E}{\mathcal D}[\mathbb{E}\hat{p}[\nabla_wL(w)]]=\mathbb{E}{\mathcal D}[\frac{1}{N}\sum\limits{i=1}^N\nabla_wL(w)]
我们知道, 越大,样本近似真实分布越准确,但是对于一个标准差为 的数据,可以确定的标准差仅和 成反比,而计算速度却和 成正比。因此可以每次使用较少样本,则在数学期望的意义上损失降低的同时,有可以提高计算速度,如果每次只使用一个错误样本,我们有下面的更新策略(根据泰勒公式,在负方向): 是可以收敛的,同时使用单个观测更新也可以在一定程度上增加不确定度,从而减轻陷入局部最小的可能。在更大规模的数据上,常用的是小批量随机梯度下降法。
两分类-硬分类-线性判别分析 LDA


在 LDA 中,我们的基本想法是选定一个方向,将试验样本顺着这个方向投影,投影后的数据需要满足两个条件,从而可以更好地分类:
- 相同类内部的试验样本距离接近。
- 不同类别之间的距离较大。
首先是投影,我们假定原来的数据是向量 ,那么顺着 方向的投影就是标量: 对第一点,相同类内部的样本更为接近,我们假设属于两类的试验样本数量分别是 和 ,那么我们采用方差矩阵来表征每一个类内的总体分布,这里我们使用了协方差的定义,用 表示原数据的协方差: 所以类内距离可以记为: 对于第二点,我们可以用两类的均值表示这个距离: 综合这两点,由于协方差是一个矩阵,于是我们用将这两个值相除来得到我们的损失函数,并最大化这个值: 这样,我们就把损失函数和原数据集以及参数结合起来了。下面对这个损失函数求偏导,注意我们其实对 的绝对值没有任何要求,只对方向有要求,因此只要一个方程就可以求解了: 于是 就是我们需要寻找的方向。最后可以归一化求得单位的 值。
两分类-软分类-概率判别模型-Logistic 回归

有时候我们只要得到一个类别的概率,那么我们需要一种能输出 区间的值的函数。考虑两分类模型,我们利用判别模型,希望对 建模,利用贝叶斯定理: 取 ,于是: 上面的式子叫 Logistic Sigmoid 函数,其参数表示了两类联合概率比值的对数。在判别式中,不关心这个参数的具体值,模型假设直接对 进行。
Logistic 回归的模型假设是: 于是,通过寻找 的最佳值可以得到在这个模型假设下的最佳模型。概率判别模型常用最大似然估计的方式来确定参数。
对于一次观测,获得分类 的概率为(假定):
那么对于 次独立全同的观测 MLE为: 注意到,这个表达式是交叉熵表达式的相反数乘 ,MLE 中的对数也保证了可以和指数函数相匹配,从而在大的区间汇总获取稳定的梯度。
对这个函数求导数,注意到: 则: 由于概率值的非线性,放在求和符号中时,这个式子无法直接求解。于是在实际训练的时候,和感知机类似,也可以使用不同大小的批量随机梯度上升(对于最小化就是梯度下降)来获得这个函数的极大值。
两分类-软分类-概率生成模型-高斯判别分析 GDA
生成模型中,我们对联合概率分布进行建模,然后采用 MAP 来获得参数的最佳值。两分类的情况,我们采用的假设:
那么独立全同的数据集最大后验概率可以表示为:
-
首先对 进行求解,将式子对 求偏导:
-
然后求解 : 由于:
求微分左边乘以 可以得到:
-
求解 ,由于正反例是对称的,所以:
-
最为困难的是求解 ,我们的模型假设对正反例采用相同的协方差矩阵,当然从上面的求解中我们可以看到,即使采用不同的矩阵也不会影响之前的三个参数。首先我们有: 在这个表达式中,我们在标量上加入迹从而可以交换矩阵的顺序,对于包含绝对值和迹的表达式的导数,我们有: 因此: 其中, 分别为两个类数据内部的协方差矩阵,于是: 这里应用了类协方差矩阵的对称性。
于是我们就利用最大后验的方法求得了我们模型假设里面的所有参数,根据模型,可以得到联合分布,也就可以得到用于推断的条件分布了。



Naive Bayesian Classifier朴素贝叶斯分类器
DimensionReduction降维
Principal Component Analysis主成分分析
支持向量机
支持向量机概览
支撑向量机(SVM)算法在分类问题中有着重要地位,其主要思想是最大化两类之间的间隔。按照数据集的特点:
- 线性可分问题,如之前的感知机算法处理的问题
- 线性可分,只有一点点错误点,如感知机算法发展出来的 Pocket 算法处理的问题
- 非线性问题,完全不可分,如在感知机问题发展出来的多层感知机和深度学习
这三种情况对于 SVM 分别有下面三种处理手段:
- hard-margin SVM
- soft-margin SVM
- kernel Method
L2范数的平方:
若,则
SVM 的求解中,大量用到了 Lagrange 乘子法,首先对这种方法进行介绍。
约束优化问题

一般地,约束优化问题(原问题)可以写成: 定义 Lagrange 函数: 那么原问题可以等价于无约束形式: 这是由于,当满足原问题的不等式约束的时候, 才能取得最大值,直接等价于原问题,如果不满足原问题的不等式约束,那么最大值就为 ,由于需要取最小值,于是不会取到这个情况。
这个问题的对偶形式: 对偶问题是关于 的最大化问题。
由于:
证明:显然有 ,于是显然有 ,且 。
对偶问题的解小于原问题,有两种情况:
- 强对偶:可以取等于号
- 弱对偶:不可以取等于号
其实这一点也可以通过一张图来说明:
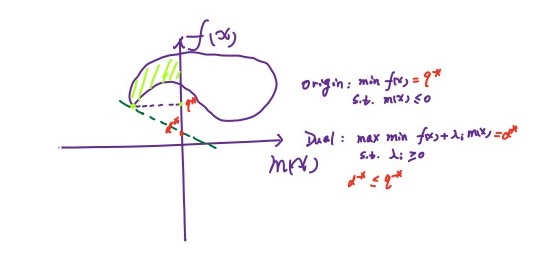
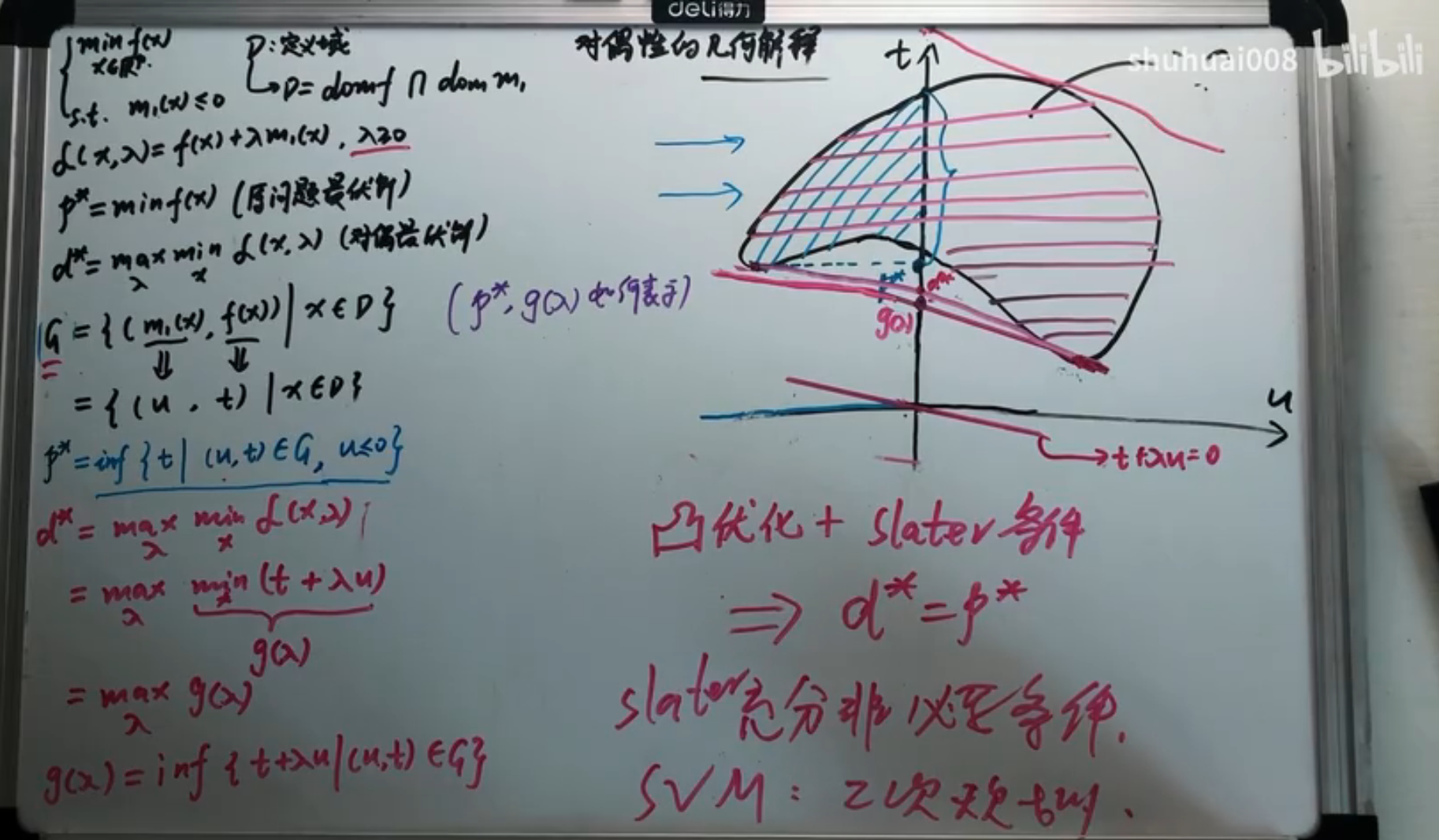
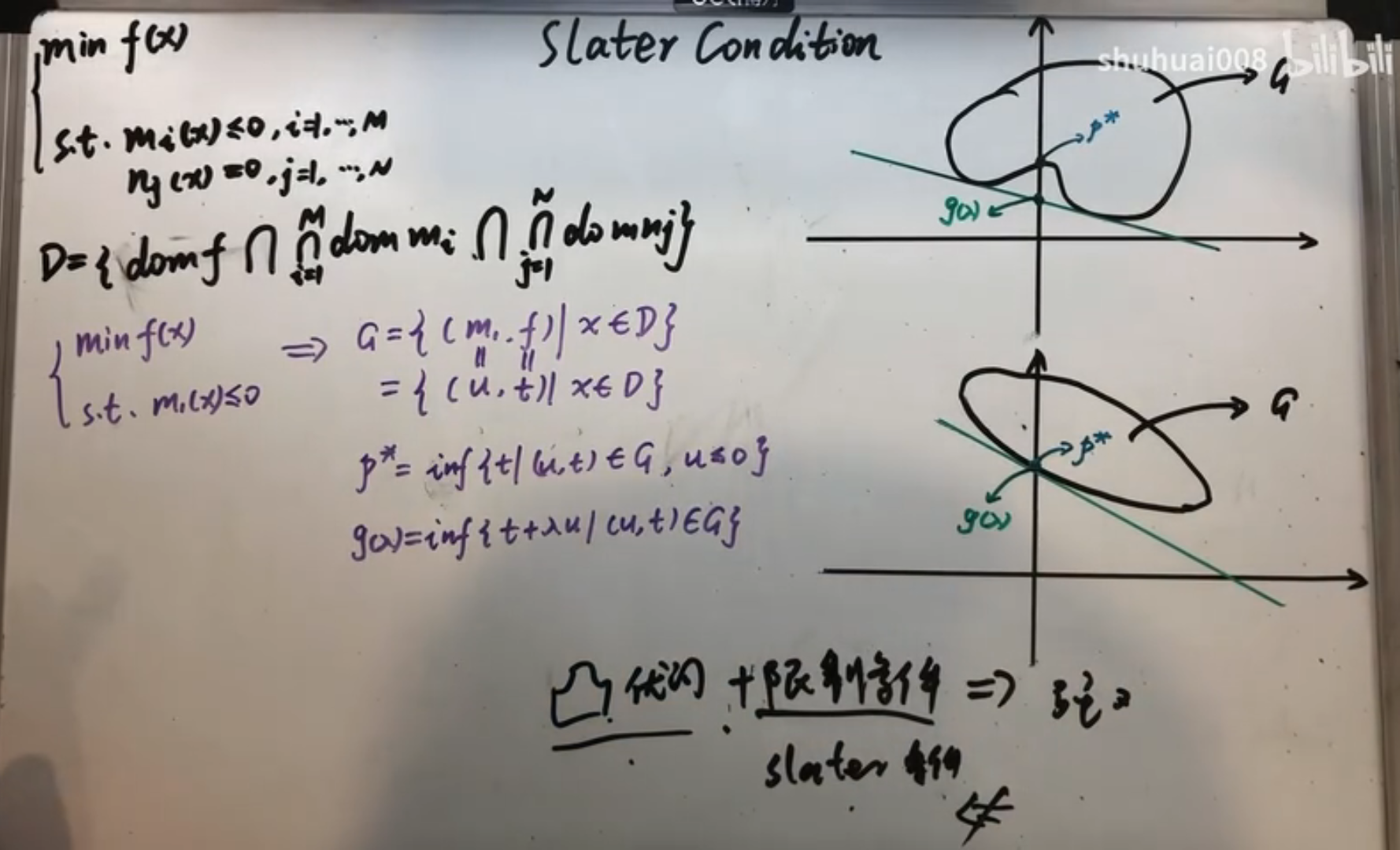

对于一个凸优化问题,有如下定理:
如果凸优化问题满足某些条件如 Slater 条件,那么它和其对偶问题满足强对偶关系。记问题的定义域为:。于是 Slater 条件为: 其中 Relint 表示相对内部(不包含边界的内部)。
- 对于大多数凸优化问题,Slater 条件成立。
- 松弛 Slater 条件,如果 M 个不等式约束中,有 K 个函数为仿射函数,那么只要其余的函数满足 Slater 条件即可。

上面介绍了原问题和对偶问题的对偶关系,但是实际还需要对参数进行求解,求解方法使用 KKT 条件进行:
KKT 条件和强对偶关系是等价关系。KKT 条件对最优解的条件为:
可行域:
互补松弛 ,对偶问题的最佳值为 ,原问题为 为了满足相等,两个不等式必须成立,于是,对于第一个不等于号,需要有梯度为0条件,对于第二个不等于号需要满足互补松弛条件。
梯度为0:
Hard-margin SVM

支撑向量机也是一种硬分类模型,在之前的感知机模型中,我们在线性模型的基础上叠加了符号函数,在几何直观上,可以看到,如果两类分的很开的话,那么其实会存在无穷多条线可以将两类分开。在 SVM 中,我们引入最大化间隔这个概念,间隔指的是数据和直线的距离的最小值,因此最大化这个值反映了我们的模型倾向。
分割的超平面可以写为: 那么最大化间隔(约束为分类任务的要求): 对于这个约束 ,不妨固定 ,这是由于分开两类的超平面的系数经过比例放缩不会改变这个平面,这也相当于给超平面的系数作出了约束。化简后的式子可以表示为: 这就是一个包含 个约束的凸优化问题,有很多求解这种问题的软件。
但是,如果样本数量或维度非常高,直接求解困难甚至不可解,于是需要对这个问题进一步处理。引入 Lagrange 函数: 我们有原问题就等价于: 我们交换最小和最大值的符号得到对偶问题:


由于不等式约束是仿射函数,对偶问题和原问题等价:
-
:
-
:首先将 代入: 所以:
-
将上面两个参数代入:
因此,对偶问题就是:

从 KKT 条件得到超平面的参数:
原问题和对偶问题满足强对偶关系的充要条件为其满足 KKT 条件:
根据这个条件就得到了对应的最佳参数: 于是这个超平面的参数 就是数据点的线性组合,最终的参数值就是部分满足 向量的线性组合(互补松弛条件给出),这些向量也叫支撑向量。
Soft-margin SVM

Hard-margin 的 SVM 只对可分数据可解,如果不可分的情况,我们的基本想法是在损失函数中加入错误分类的可能性。错误分类的个数可以写成: 这个函数不连续,可以将其改写为: 求和符号中的式子又叫做 Hinge Function。
将这个错误加入 Hard-margin SVM 中,于是: 这个式子中,常数 可以看作允许的错误水平,同时上式为了进一步消除 符号,对数据集中的每一个观测,我们可以认为其大部分满足约束,但是其中部分违反约束,因此这部分约束变成 ,其中 ,进一步的化简:
Kernel Method

核方法可以应用在很多问题上,在分类问题中,对于严格不可分问题,我们引入一个特征转换函数将原来的不可分的数据集变为可分的数据集,然后再来应用已有的模型。往往将低维空间的数据集变为高维空间的数据集后,数据会变得可分(数据变得更为稀疏):
Cover theorem:高维空间比低维空间更易线性可分。
应用在 SVM 中时,观察上面的 SVM 对偶问题: 在求解的时候需要求得内积,于是不可分数据在通过特征变换后,需要求得变换后的内积。我们常常很难求得变换函数的内积。于是直接引入内积的变换函数: 称 为一个正定核函数,其中 是 Hilbert 空间(完备的线性内积空间),如果去掉内积这个条件我们简单地称为核函数。
是一个核函数。
证明:


正定核函数有下面的等价定义:
如果核函数满足:
- 对称性
- 正定性(非负性)
那么这个核函数是正定核函数。
证明:
- 对称性 ,显然满足内积的定义
- 正定性 ,对应的 Gram Matrix 是半正定的。
要证: 半正定+对称性。
:首先,对称性是显然的,对于正定性: 任意取 ,即需要证明 : 这个式子就是内积的形式,Hilbert 空间满足线性性,于是正定性的证。
:对于 进行分解,对于对称矩阵 ,那么令 ,其中 是特征向量,于是就构造了
小结
分类问题在很长一段时间都依赖 SVM,对于严格可分的数据集,Hard-margin SVM 选定一个超平面,保证所有数据到这个超平面的距离最大,对这个平面施加约束,固定 ,得到了一个凸优化问题并且所有的约束条件都是仿射函数,于是满足 Slater 条件,将这个问题变换成为对偶的问题,可以得到等价的解,并求出约束参数: 对需要的超平面参数的求解采用强对偶问题的 KKT 条件进行。 解就是: 当允许一点错误的时候,可以在 Hard-margin SVM 中加入错误项。用 Hinge Function 表示错误项的大小,得到: 对于完全不可分的问题,我们采用特征转换的方式,在 SVM 中,我们引入正定核函数来直接对内积进行变换,只要这个变换满足对称性和正定性,那么就可以用做核函数。
SVM实战
支持向量机(Support Vector Machine, SVM)是最受欢迎的机器学习模型之一。它特别适合处理中小型复杂数据集的分类任务。
一、什么是支持向量机
SMV在众多实例中寻找一个最优的决策边界,这个边界上的实例叫做支持向量,它们“支持”(支撑)分离开超平面,所以它叫支持向量机。
那么我们如何保证我们得到的决策边界是最优的呢?
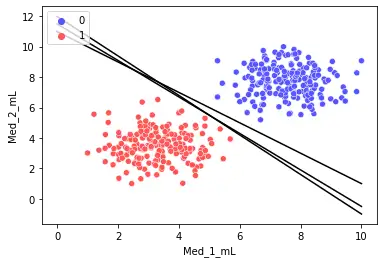
如上图,三条黑色直线都可以完美分割数据集。由此可知,我们仅用单一直线可以得到无数个解。那么,其中怎样的直线是最优的呢?
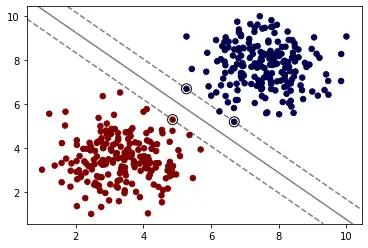
如上图,我们计算直线到分割实例的距离,使得我们的直线与数据集的距离尽可能的远,那么我们就可以得到唯一的解。最大化上图虚线之间的距离就是我们的目标。而上图中重点圈出的实例就叫做支持向量。
这就是支持向量机。
二、观察数据
添加引用:
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
导入数据集(大家不用在意这个域名):
df = pd.read_csv('https://blog.caiyongji.com/assets/mouse_viral_study.csv')
df.head()
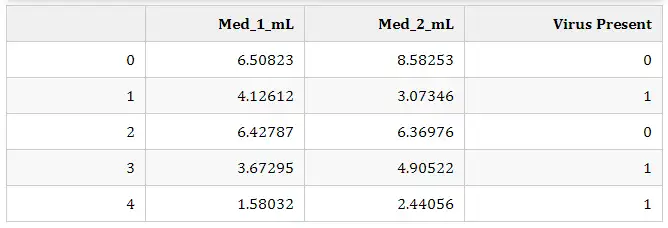
该数据集模拟了一项医学研究,对感染病毒的小白鼠使用不同剂量的两种药物,观察两周后小白鼠是否感染病毒。
- 特征: 1. 药物Med_1_mL 药物Med_2_mL
- 标签:是否感染病毒(1感染/0不感染)
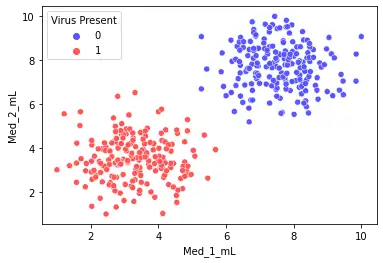
sns.scatterplot(x='Med_1_mL',y='Med_2_mL',hue='Virus Present',data=df)
我们用seaborn绘制两种药物在不同剂量特征对应感染结果的散点图。
sns.pairplot(df,hue='Virus Present')
我们通过pairplot方法绘制特征两两之间的对应关系。
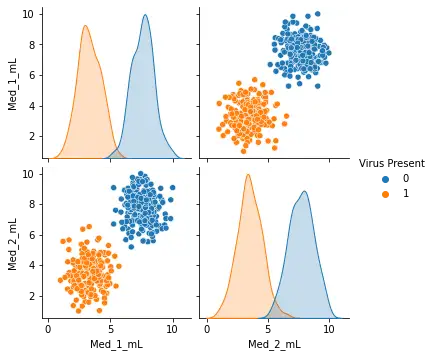
我们可以做出大概的判断,当加大药物剂量可使小白鼠避免被感染。
使用SVM训练数据集
#SVC: Supprt Vector Classifier支持向量分类器
from sklearn.svm import SVC
#准备数据
y = df['Virus Present']
X = df.drop('Virus Present',axis=1)
#定义模型
model = SVC(kernel='linear', C=1000)
#训练模型
model.fit(X, y)
# 绘制图像
# 定义绘制SVM边界方法
def plot_svm_boundary(model,X,y):
X = X.values
y = y.values
# Scatter Plot
plt.scatter(X[:, 0], X[:, 1], c=y, s=30,cmap='coolwarm')
# plot the decision function
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
# create grid to evaluate model
xx = np.linspace(xlim[0], xlim[1], 30)
yy = np.linspace(ylim[0], ylim[1], 30)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = model.decision_function(xy).reshape(XX.shape)
# plot decision boundary and margins
ax.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.5,
linestyles=['--', '-', '--'])
# plot support vectors
ax.scatter(model.support_vectors_[:, 0], model.support_vectors_[:, 1], s=100,
linewidth=1, facecolors='none', edgecolors='k')
plt.show()
plot_svm_boundary(model,X,y)
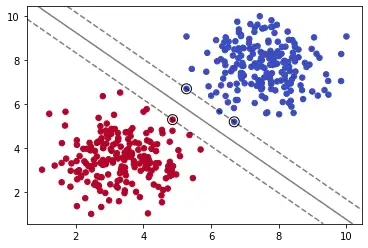 注:这里会报UserWarning: X does not have valid feature names, but SVC was fitted with feature names
注:这里会报UserWarning: X does not have valid feature names, but SVC was fitted with feature names
warnings.warn(
我们导入sklearn下的SVC(Supprt Vector Classifier)分类器,它是SVM的一种实现。
其实在工具 sklearn 中,已经封装了多种 SVM 模型,这里我们重点介绍下 SVC,该模型既可以训练线性可分的数据,也可以训练线性不可分数据。
SVC相关参数
| 参数名 | 含义 |
|---|---|
| C | 惩罚系数,默认为1.0。当 C 越大时,分类器的准确性越高,但是泛化能力越低。反之,泛化能力强,但是准确性会降低。 |
| kernel | 核函数类型,默认为 rbf。主要的核函数类型如下: liner:线性核函数,在数据为线性可分的情况下使用 poly:多项式核函数,可以将数据从低维空间映射到高维空间,但是参数较多,计算量大 rbf:高斯核函数,同样可以将数据从低维空间映射到高维空间,相比 poly,参数较少,通用性较好 sigmoid:当使用 sigmoid 核函数时,SVM 实现的是一个多层神经网络 |
| gamma | 核函数系数,默认为样本特征数的倒数,即 gamma = 1/ n_features |
| max_iter | 最大迭代次数,默认为-1,不做限制 |
| class_weight | 类别权重,dict 类型或 str 类型,可选参数,默认为 None。如果给定参数'balance',则使用 y 的值自动调整为与输入数据中的类频率成反比的权重。 |
SVC参数C
SVC方法参数C代表L2正则化参数,正则化的强度与C的值成反比,即C值越大正则化强度越弱,其必须严格为正。
model = SVC(kernel='linear', C=0.05)
model.fit(X, y)
plot_svm_boundary(model,X,y)
我们减少C的值,可以看到模型拟合数据的程度减弱。
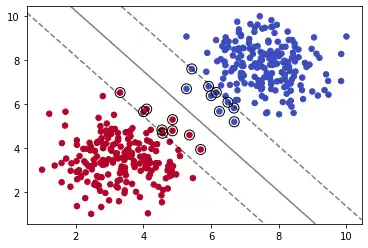
核技巧
SVC方法的kernel参数可取值{'linear', 'poly', 'rbf', 'sigmoid', 'precomputed'}。像前文中所使用的那样,我们可以使kernel='linear'进行线性分类。那么如果我们像进行非线性分类呢?
多项式内核
多项式内核kernel='poly'的原理简单来说就是,用单一特征生成多特征来拟合曲线。比如我们拓展X到y的对应关系如下:
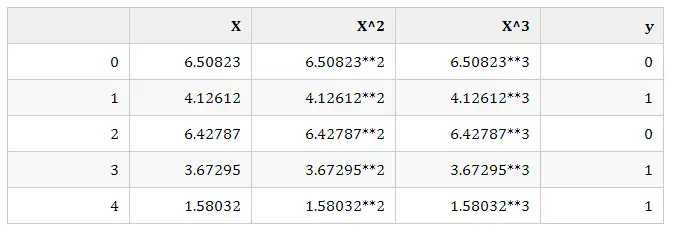
这样我们就可以用曲线来拟合数据集。
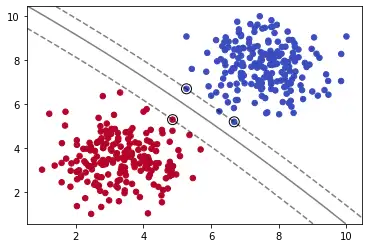
model = SVC(kernel='poly', C=0.05,degree=5)
model.fit(X, y)
plot_svm_boundary(model,X,y)
我们使用多项式内核,并通过degree=5设置多项式的最高次数为5。我们可以看出分割出现了一定的弧度。
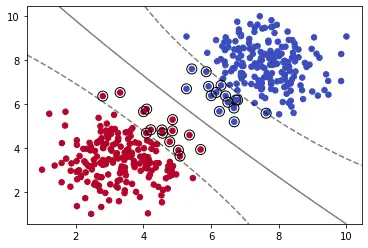
高斯RBF内核
SVC方法默认内核为高斯RBF,即Radial Basis Function(径向基函数)。这时我们需要引入gamma参数来控制钟形函数的形状。增加gamma值会使钟形曲线变得更窄,因此每个实例影响的范围变小,决策边界更不规则。减小gamma值会使钟形曲线变得更宽,因此每个实例的影响范围变大,决策边界更平坦。
model = SVC(kernel='rbf', C=1,gamma=0.01)
model.fit(X, y)
plot_svm_boundary(model,X,y)
调参技巧:网格搜索
from sklearn.model_selection import GridSearchCV
svm = SVC()
param_grid = {'C':[0.01,0.1,1],'kernel':['rbf','poly','linear','sigmoid'],'gamma':[0.01,0.1,1]}
grid = GridSearchCV(svm,param_grid)
grid.fit(X,y)
print("grid.best_params_ = ",grid.best_params_,", grid.best_score_ =" ,grid.best_score_)
我们可以通过GridSearchCV方法来遍历超参数的各种可能性来寻求最优超参数。这是通过算力碾压的方式暴力调参的手段。当然,在分析问题阶段,我们必须限定了各参数的可选范围才能应用此方法。
因为数据集太简单,我们在遍历第一种可能性时就已经得到100%的准确率了,输出如下:
grid.best_params_ = {'C': 0.01, 'gamma': 0.01, 'kernel': 'rbf'} , grid.best_score_ = 1.0
总结
当我们处理线性可分的数据集时,可以使用SVC(kernel='linear')方法来训练数据,当然我们也可以使用更快的方法LinearSVC来训练数据,特别是当训练集特别大或特征非常多的时候。
当我们处理非线性SVM分类时,可以使用高斯RBF内核,多项式内核,sigmoid内核来进行非线性模型的的拟合。当然我们也可以通过GridSearchCV寻找最优参数。