第二周 数据的表示和存储
- 第1讲 数制和编码
- 附录十进制转换为二进制、八进制、十六进制实例
- 第2讲 定点数的编码表示
- 第3讲 C语言中的整数
- 第4讲 浮点数的编码表示
- 第5讲 非数值数据的编码表示
- 第6讲 数据宽度和存储容量的单位
- 第7讲 数据存储时的字节排列
- 第二周小测验
第1讲 数制和编码
1. 10进制数和2进制数(19分钟)
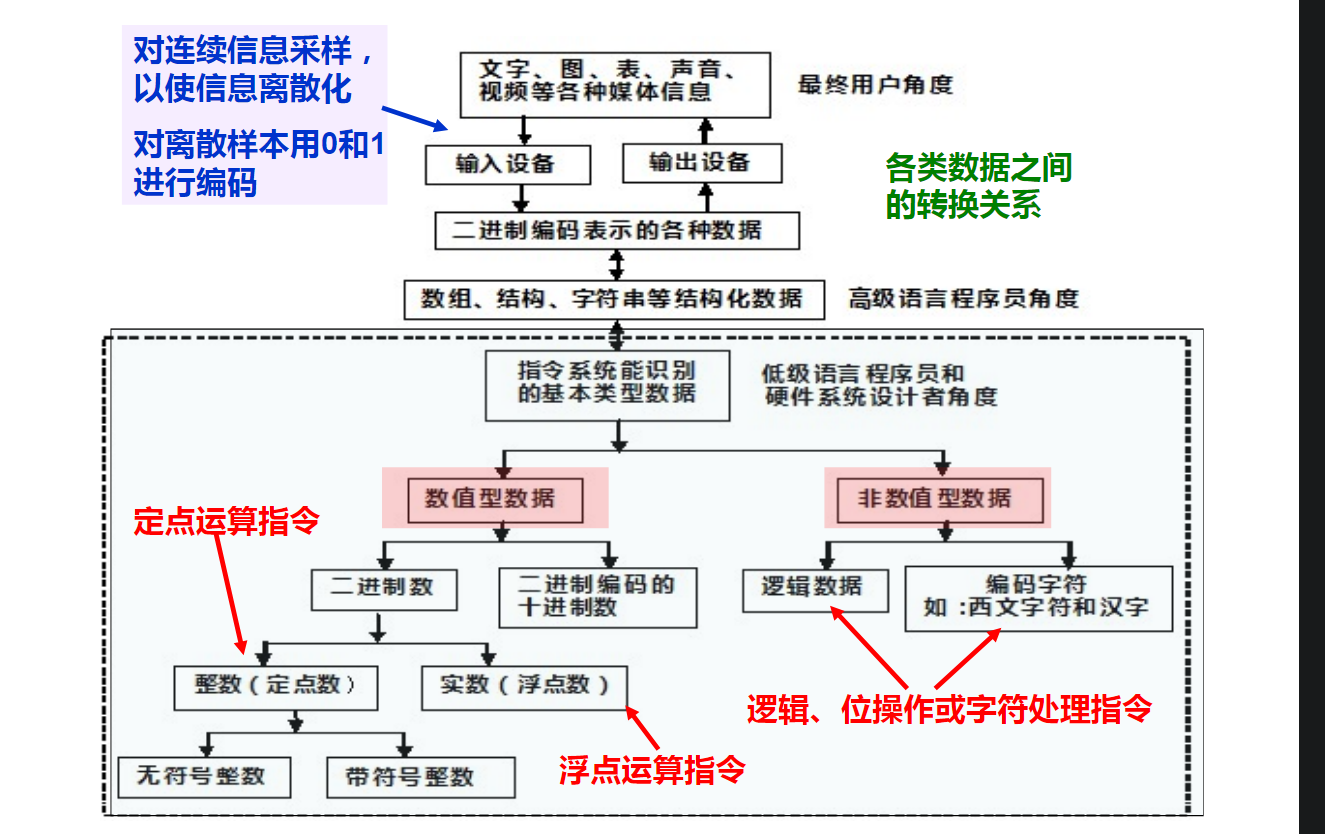
文字、音频和视频等感觉媒体信息通过某种数字化方法被输入到计算机中就变成了用0/1表示的数字信息
在高级语言程序中出现的数据(变量或字面量)都是一种用0/1表示的数字信息
浮点运算指令中的操作数一定是浮点数,定点运算指令中的操作数一定是定点数



2. 2/8/10/16进制数之间的转换(20分钟)

在计算机内部,一个浮点数可以用数的符号和两个定点数来表示。

附录十进制转换为二进制、八进制、十六进制实例
1、十进制转二进制
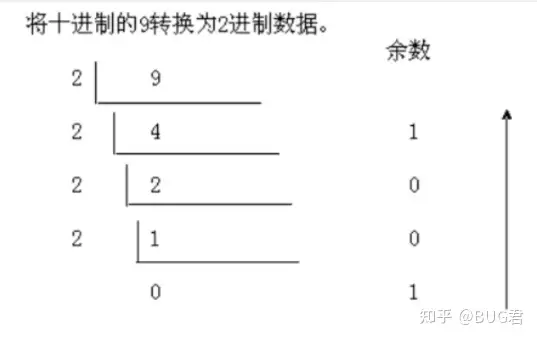
(1)十进制整数转二进制的转换原理:除以2,反向取余数,直到商为0终止。具体做法:
将某个十进制数除2得到的整数部分保留,作为第二次除2时的被除数,得到的余数依次记下,重复上述步骤,直到整数部分为0就结束,将所有得到的余数最终逆序输出,则为该十进制对应的二进制数。
例如:9(十进制)→1001(二进制)
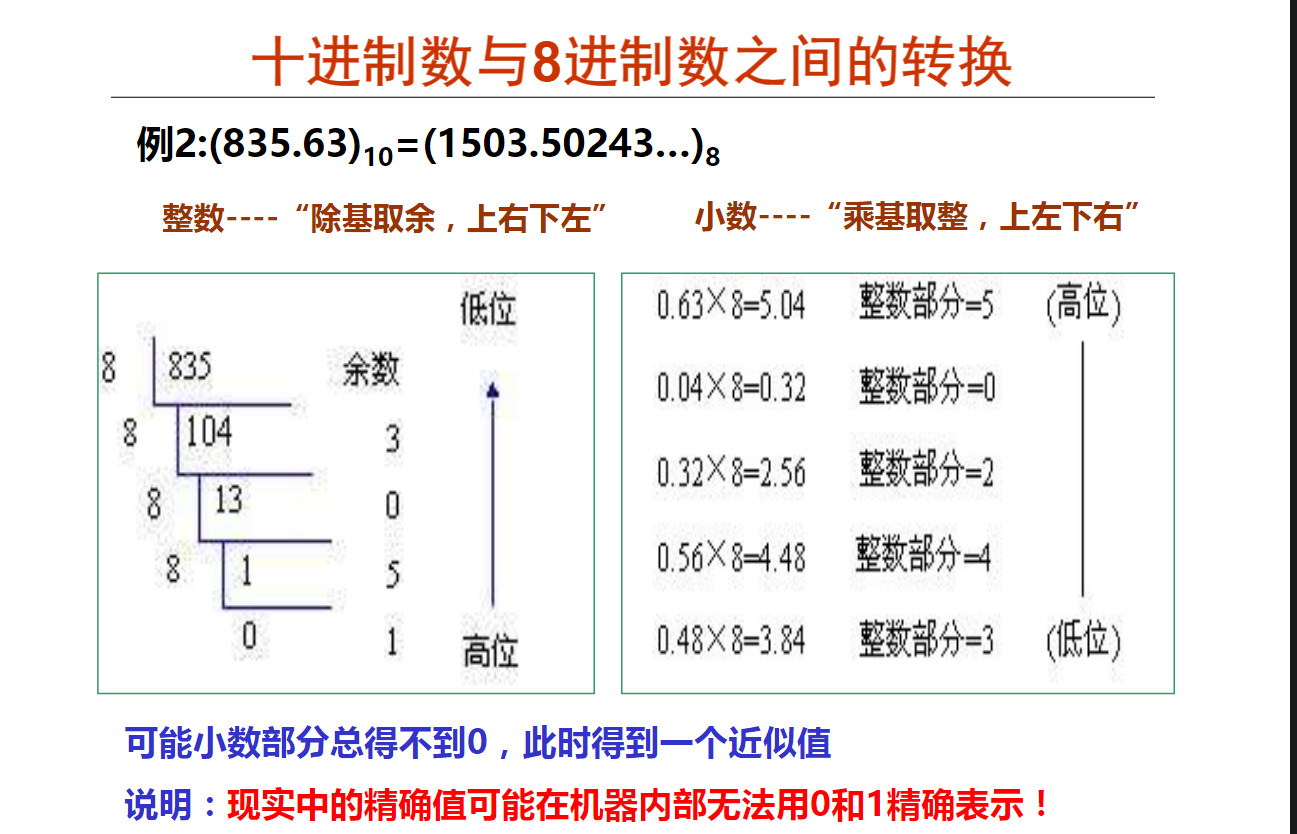
(2)十进制小数转换成二进制小数采用 “乘2取整,顺序输出” 法。
例题: 0.68D = ______ B(精确到小数点后5位)
如下所示,0.68乘以2,取整,然后再将小数乘以2,取整,直到达到题目要求精度。得到结果:0.10101B.
例如:十进制小数0.68转换为二进制数
具体步骤:
0.68* 2=1.36 -->1
0.36* 2=0.72 -->0
0.72* 2=1.44 -->1
0.44* 2=0.88–>0
0.88* 2=1.76 -->1
已经达到了题目要求的精度,最后将取出的整数部分顺序输出即可
则为:0.68D–>0.10101B
2、十进制转八进制
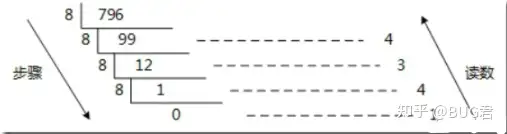
(1)十进制整数转八进制整数原理:除以8,反向取余数,直到商为0终止。具体步骤与二进制一样。例如:十进制数796转换成八进制数:
将796除8取得第一个余数为4,将除8得到的整数部分99作为第二次的被除数,重复上述步骤,直至最终整数部分为0就结束。将取得的所有余数逆序输出
则为:796–>1434
(2)十进制小数转换成八进制小数采用 “乘8取整,顺序输出” 法。思路和十进制转二进制一样,参考如下例题:
例题: 10.68D = ______ Q(精确到小数点后3位)
解析:如下图所示,整数部分除以8取余数,直到无法整除。小数部分0.68乘以8,取整,然后再将小数乘以8,取整,直到达到题目要求精度。得到结果:12.534Q.例如:十进制数10.68转换成八进制数,分为整数部分和小数部分求解
步骤:
(1)整数部分
10/8=1 -->2
1/8=0 -->1
倒序输出为12
(2)小数部分
0.68* 8=5.44 -->5
0.44* 8=3.52 -->3
0.52* 8=4.16 -->4
已经达到了题目要求的精度,即可结束
则小数部分为:0.68–>0.534
因此10.68D -->12.534Q
3、十进制转十六进制
(1)十进制整数转十六进制整数原理:除以16,反向取余数,直到商为0终止。具体步骤也和二进制、八进制一样,重复上述做法即可得到十六进制数。
例如:十进制数796转换为十六进制数,即为:796–>31c
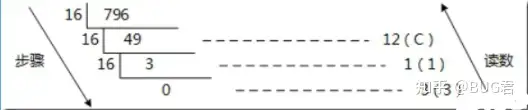
需要注意的是,十六进制数是由0-9和A-F(或者a-f)组成的,A相当于十进制中的10,B相当于11,依次类推,F相当与15,上述事例中取得的余数12即为十六进制中的c
总结:以上几种进制的整数部分转换原理都是除进制数取余数,倒序输出
(2)十进制小数转十六进制小数原理:十进制小数转换成十六进制小数采用 “乘16取整,顺序输出” 法。思路也是一样的,就不重复了。
例题: 25.68D = ______ H(精确到小数点后3位)
解析:如下图所示,整数部分除以16取余数,直到无法整除。小数部分0.68乘以16,取整,然后再将小数乘以16,取整,直到达到题目要求精度。得到结果:19.ae1H.
(1)整数部分
25/16=1 -->9
1/16=0 -->1
倒序输出为:19
(2)小数部分
0.68* 16=10.88 -->a(即十进制中的10)
0.88* 16=14.08 -->e
0.08* 16=1.28 -->1
已经达到了要求的精度,顺序输出为:ae1
则:25.68D -->19.ae1H
总结:小数部分转换原理都是乘进制数取整数部分,再将整数部分顺序输出。
第2讲 定点数的编码表示
1. 原码和移码表示 (10分钟)
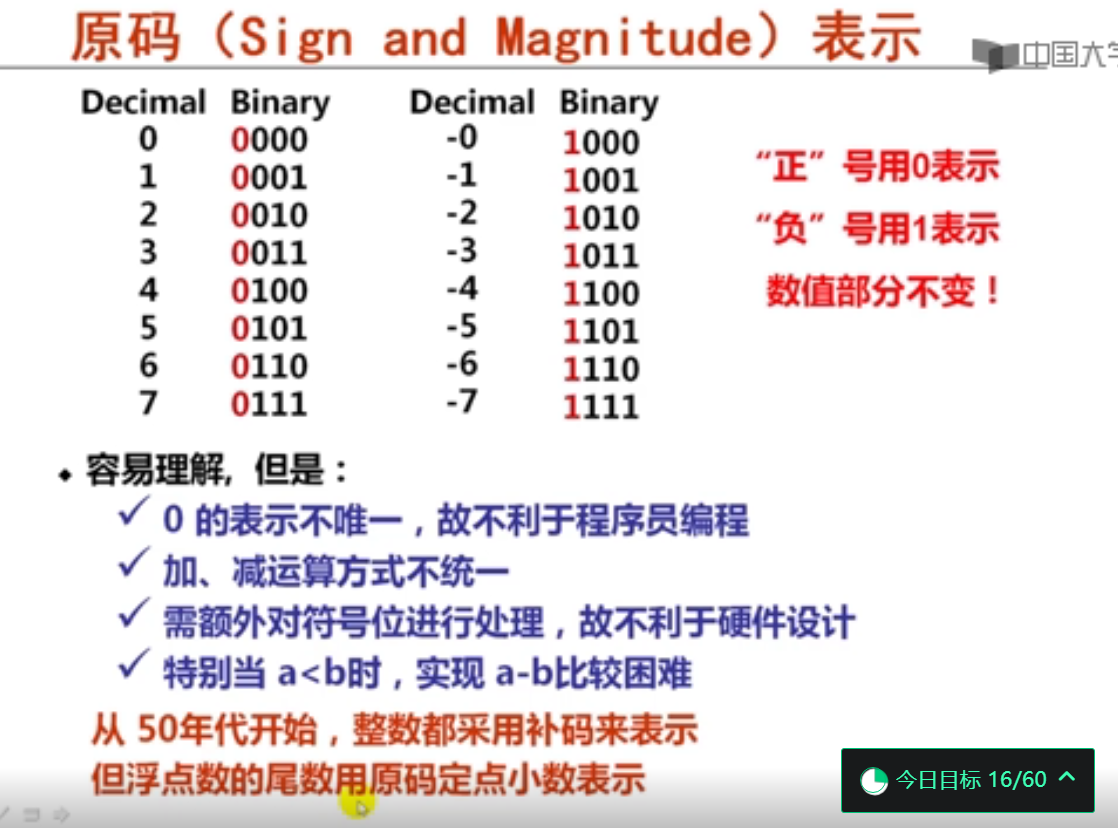

例如:1.01x2^{-5}+1.11x2^3中编码位数为4即阶数要加8
2. 模运算系统和补码表示(17分钟)

钟表系统的模是12,若当前时针指向11点,则顺时针拨动5格与逆时针拨动7格的结果相同,都是指向4点。
在只有4档的算盘中,若用加法实现减法运算的结果,则应该用6823加7044来实现6823-2956,结果为3867。
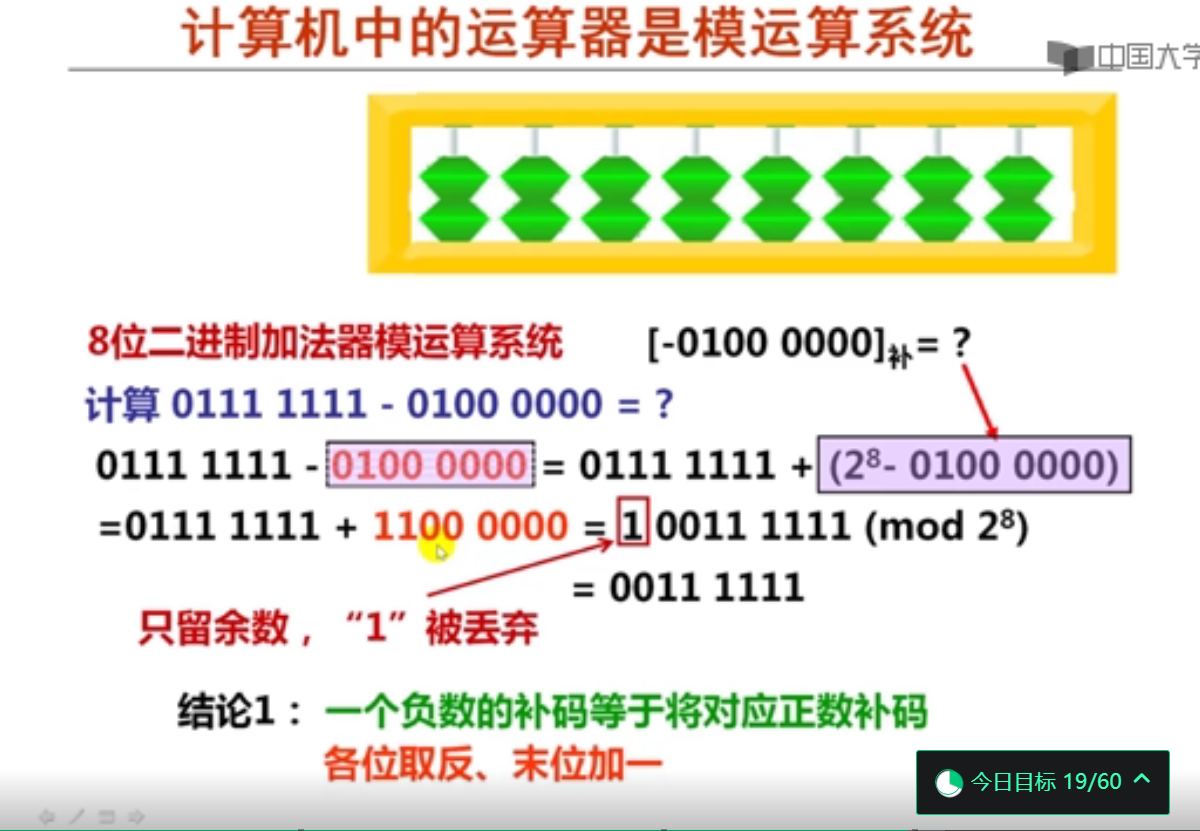
假定补码位数为8,二进制数-1000的补码表示为( 1111 1000 )。
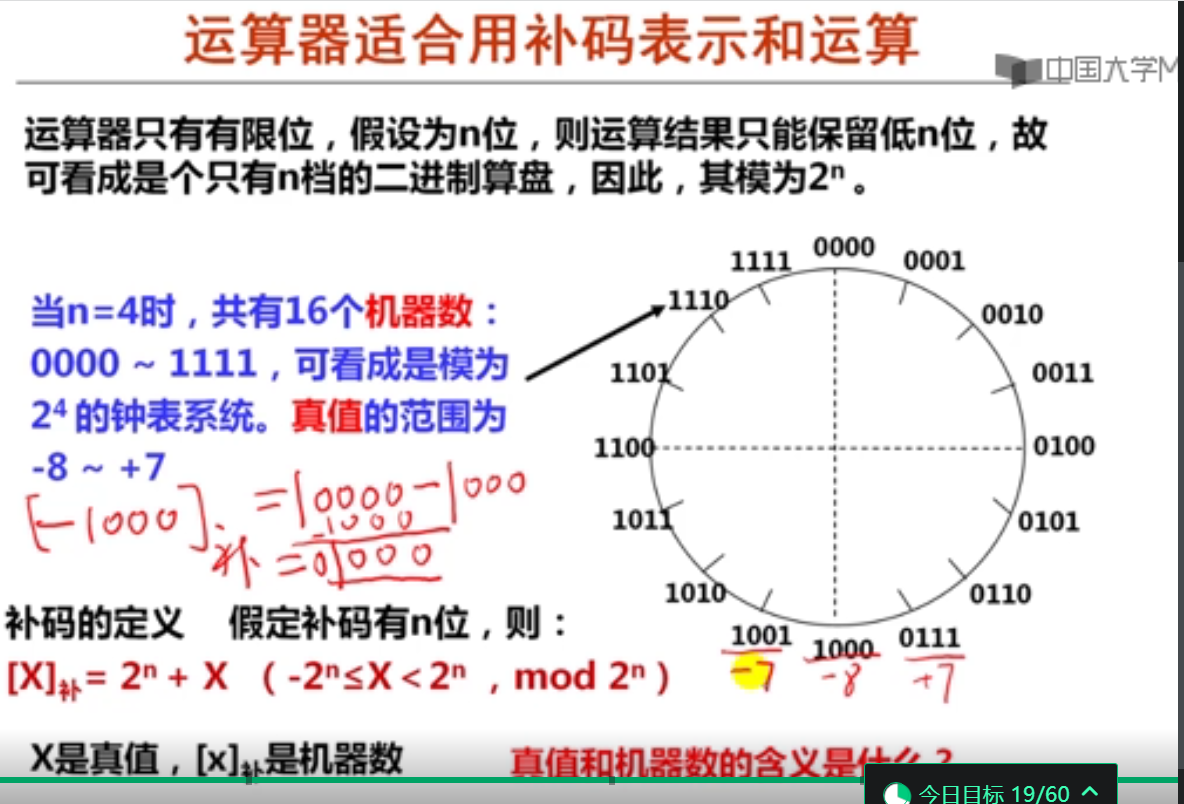
3. 补码和真值的对应关系(19分钟)

在32位机器中,一个int型变量的值为-1,则机器数为( 1111 1111 1111 1111 1111 1111 1111 1111 )。
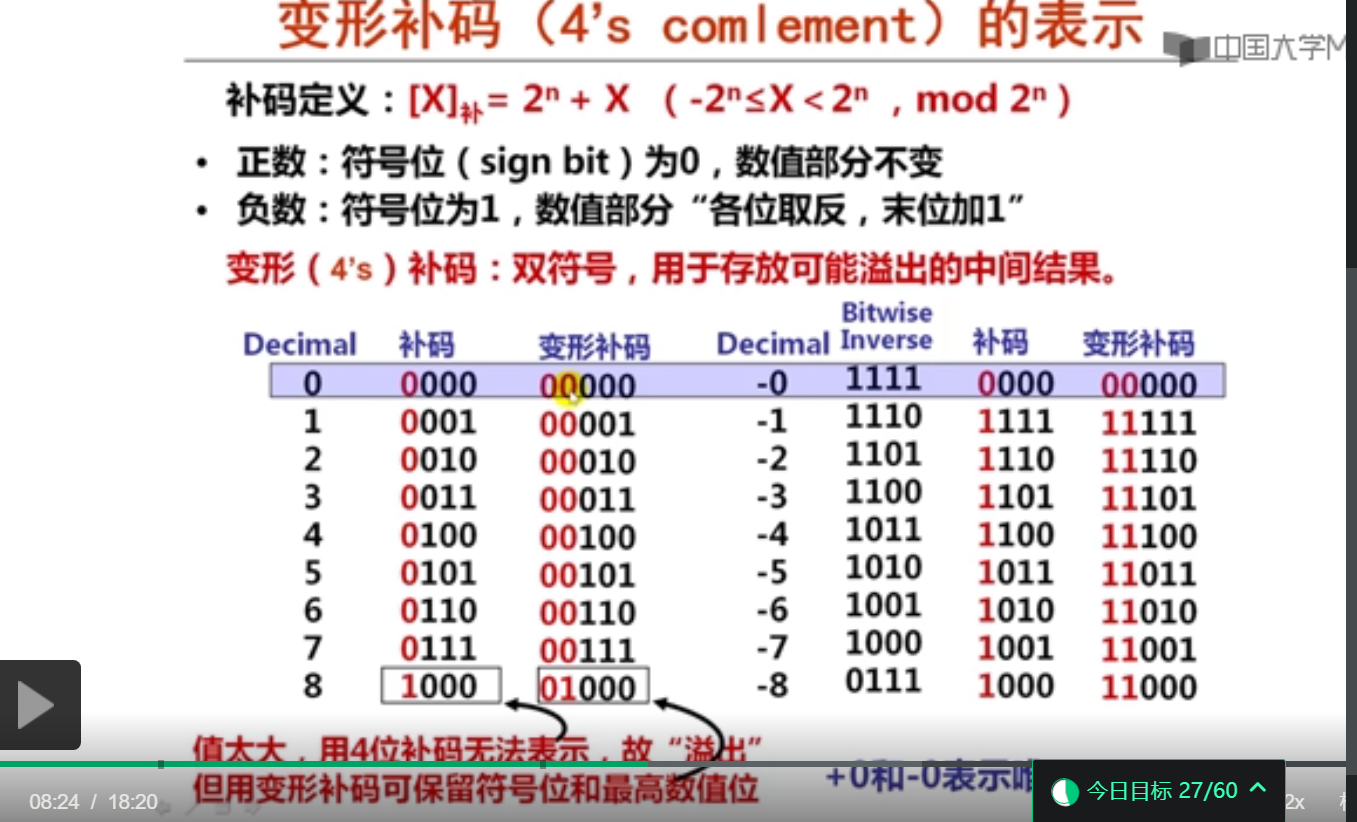
变形补码(4’ complement)采用双符号位表示。例如-100的8位变形补码表示为10011100。-100的8位变形补码高两位不同,是溢出形式。

-123的16位补码表示为( 1111 1111 1000 0101B 或FF85H )。

8位补码表示11010111对应的真值是( -41 )。
第3讲 C语言中的整数
1. 无符号整数和带符号整数 (15分钟)

16位无符号整数中的最大数是( 65535 )。


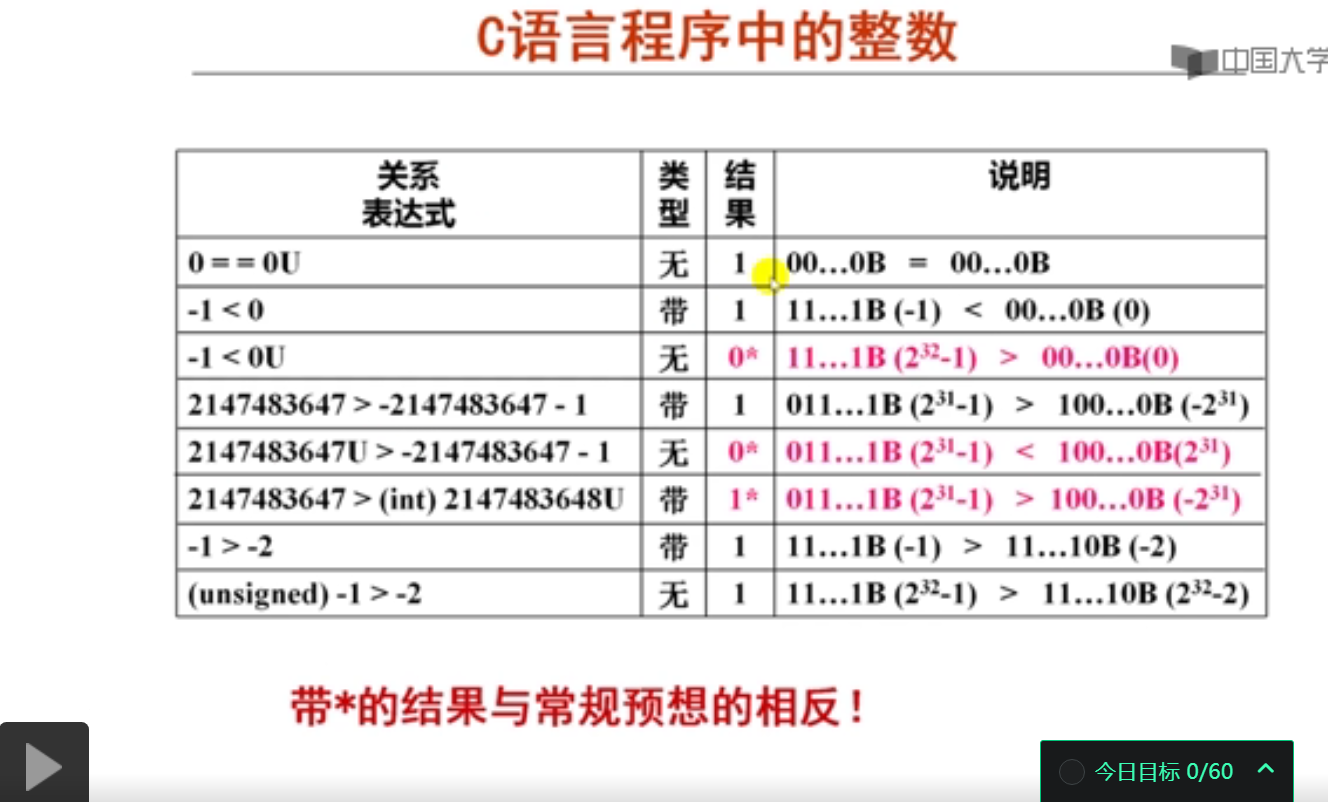
已知2147483647为2^31-1, C语言中的关系表达式"2147483647U>-2147483647-1"的结果是( 假 )。
测试代码:
#include <stdio.h>
int main()
{
printf("%d",(unsigned)-1>-2);//输出1
return 0;
}
#include <stdio.h>
int main()
{
printf("%d",-1<0u);//输出0
return 0;
}
#include <stdio.h>
int main()
{
printf("%d",2147483647>-2147483647-1);//输出1
printf("%d",2147483647u>-2147483647-1);//输出0
printf("%d",2147483647>(int)2147483648u);//输出1
return 0;
}
2. C语言程序中整数举例(16分钟)

4294967295=2^32-1
2147483647=2^31-1
最小负数这里表示需要用到4's complement方式。
测试实例:
#include <stdio.h>
int main()
{
int x=-1;
unsigned u=2147483647;
printf("%d\n",2147483647>-1);
printf("x=%u=%d\n",x,x);
printf("u=%u=%d\n",u,u);
return 0;
}
1
x=4294967295=-1
u=2147483647=2147483647
#include <stdio.h>
int main()
{
int x=-1;
unsigned u=2147483648;
printf("%d\n",2147483648>-1);
printf("%d\n",u>x);
printf("x=%u=%d\n",x,x);
printf("u=%u=%d\n",u,u);
return 0;
}
1
0
x=4294967295=-1
u=2147483648=-2147483648
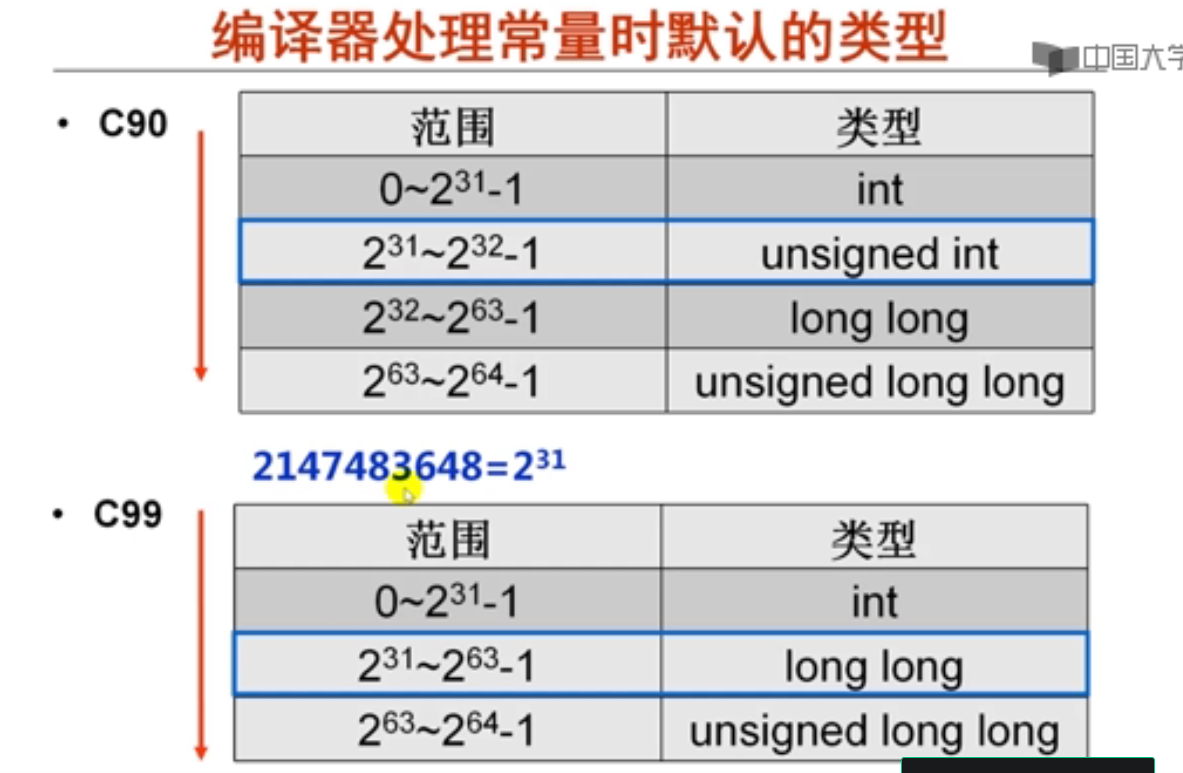

#include <stdio.h>
int main()
{
printf("%d\n",-2147483648>2147483647);//输出0
return 0;
}
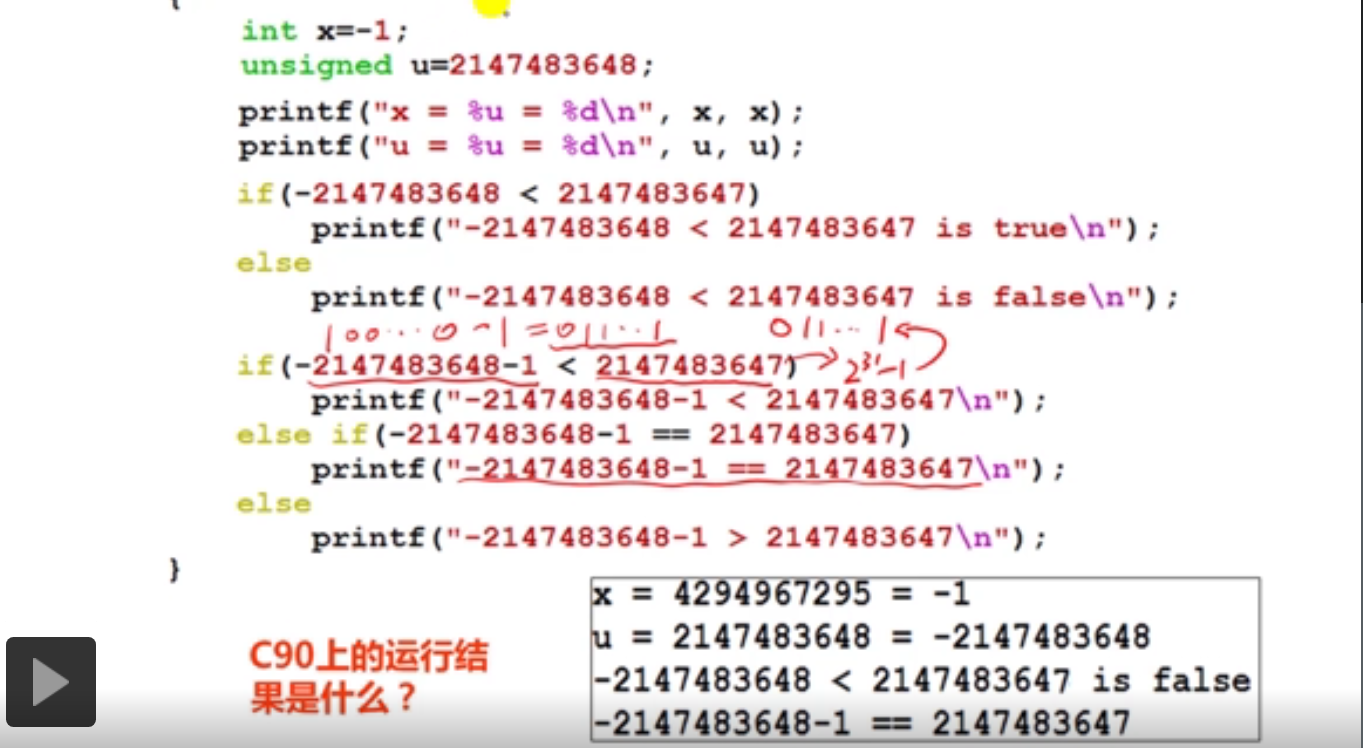
在c99上测试结果如下:
#include <stdio.h>
int main()
{
int x=-1;
unsigned u=2147483648;
printf("x=%u=%d\n",x,x);
printf("u=%u=%d\n",u,u);
if(-2147483648<2147483647)
printf("-2147483648<2147483647 is true\n");
else
printf("-2147483648<2147483647 is false\n");
if(-2147483648-1<2147483647)
printf("-2147483648-1<2147483647 is true\n");
else if(-2147483648-1==2147483647)
printf("-2147483648-1==2147483647 is true\n");
else
printf("-2147483648-1<2147483647 is false\n");
return 0;
}
x=4294967295=-1
u=2147483648=-2147483648
-2147483648<2147483647 is true
-2147483648-1<2147483647 is true
#include <stdio.h>
int main()
{
int x=-2;
unsigned u=2147483648;
printf("x=%u=%d\n",x,x);
printf("u=%u=%d\n",u,u);
return 0;
}
x=4294967294=-2
u=2147483648=-2147483648
产生u=2147483648=-2147483648的原因是2^31的二进制表示为1+31个0,按位取反最后加1,得到的补码也为1+31个0。由补码转为有符号真值时先取出符号位1,数值位按位取反最后加一,结合4's complement表示为1+1+31个0,即为-2^31。
第4讲 浮点数的编码表示
1. 浮点数的表示范围(17分钟)

浮点数由一个定点整数加一个定点小数表示。


以下关于浮点数表示格式的叙述中,错误的是( C )。
A.浮点数的表示范围主要由其阶码E的位数确定
B.浮点数的表示精度主要由其尾数M的位数确定
C.若运算的结果位于浮点数表示的上溢区,则说明其值大于最大可表示数
D.若运算的结果位于浮点数表示的下溢区,则说明其值位于0的附近,可近似表示成0
注:
补码规格化数的符号位和最高有效位相反
补码表示尾数时,“1”而以后各位全为“0”刚好代表 -1/2
为了机器判断方便,往往不把-1/2列入规格化的数,因此,机器只要判断运算结果的尾数最高位(数符)与尾数次高位(第一有效位)是否相同,便可以判断是否是规格化的数。
1.1000是个特例,不把它作为规格化数,是为了方便机器判断。
我们规定负数的补码表示形式为1.0xxxxx的形式,因为这种表示方式便于计算机判断它是否规格化了。
因为浮点数的加减运算都用补码,双符号位比单符号位更加利于检验,所以双符号位的补码形式常用于规格化中。
浮点数的尾数规格化规则
| - | 单符号位 | 双符号位 |
|---|---|---|
| 正数原码 | 0.1xxx | 00.1xxx |
| 正数补码 | 0.1xxx | 00.1xxx |
| 负数原码 | 1.1xxx | 11.1xxx |
| 负数补码 | 1.0xxx | 11.0xxx |
双符号位满足:原码部分第一个数值位都是1,补码的话符号位和第一个数值位都相反。
规格化的尾数必须保证尾数的最高数位必须是一个有效值(除去符号位)
所以按照如下法则判断即可。
原码表示的尾数判断浮点数是否规格化:第一个数值位是否为“1”,是,规格化;否,非规格化
**补码表示的尾数判断浮点数是否规格化:符号位与第一个数值位是否相异,是,规格化;否,非规格化(-1/2除外) **
例题:10、下面尾数(1位符号位)的表示中,不是规格化的尾数的是D 。
A、010011101(原码) B、110011110(原码)
C、010111111 (补码) D、110111001(补码)
由于负数的补码是除符号位其他值按位取反最后加1所以由此可见,D的原码除符号位首位应该是0,并不符合尾数规格化。

早期,不同体系结构计算机所用的浮点数表示格式是不一样的,在不同计算机之间进行程序移植时,需要考虑浮点数格式之间的转换。
2. IEEE 754中规格化数的表示(19分钟)


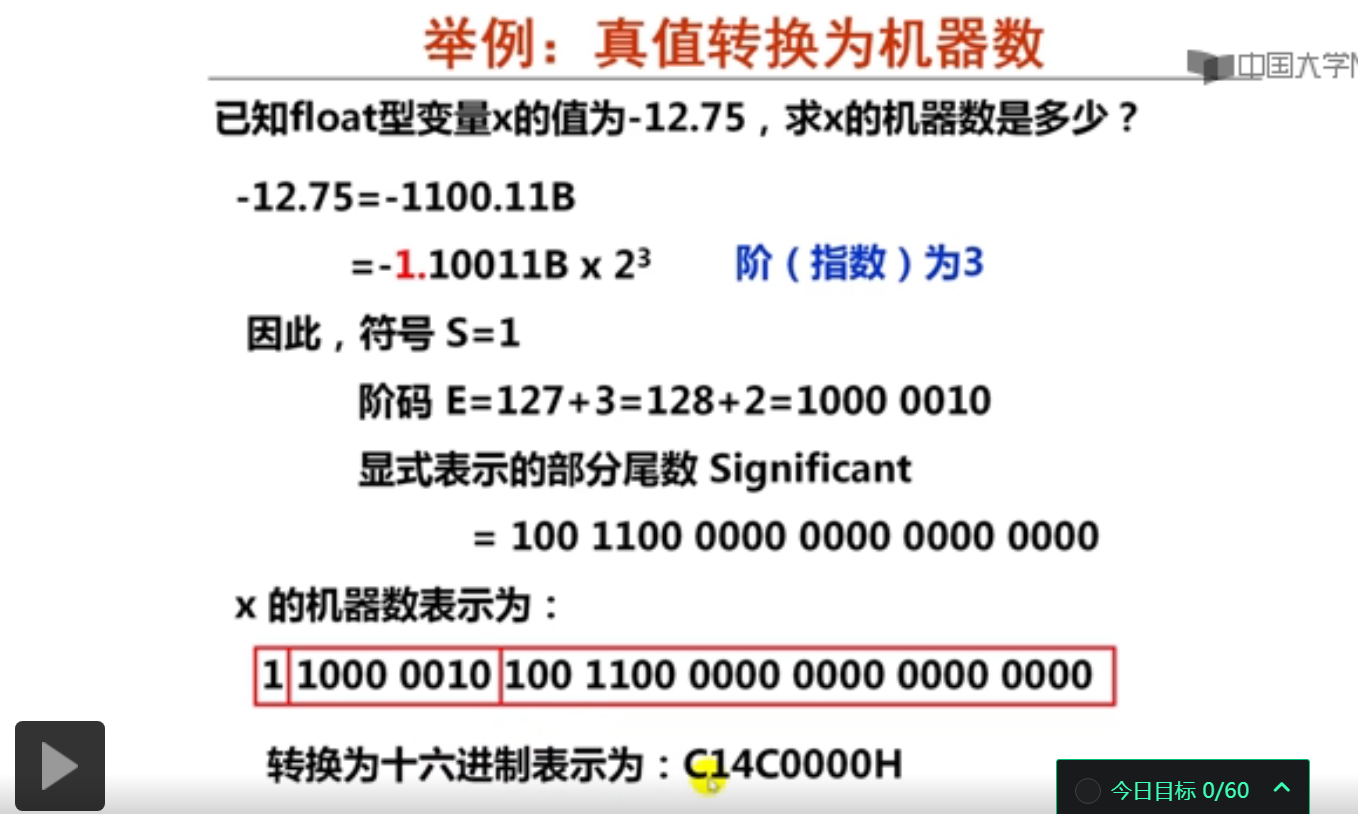
课堂测试:假定某数采用IEEE 754单精度浮点数格式表示为4510 0000H,则该数的值是( 1.125×2^11 )。
实例测试:
#include <stdio.h>
#include <stdlib.h>
void getFloatBin(float num,char bin[])
{
int t=1; //用来进行按位与运算
int *f=(int*)(&num); //将float解释成int,即把float的地址转换成int*
for(int i=0;i<32;i++)
{
//从最高位开始按位与,如果结果为1,则bin[i]=1,如果为0,则bin[i]=0
//这里没有在bin存入字符,而是数字1,0
bin[i]=(*f)&(t<<31-i)?1:0;
}
}
int main()
{
float test=100;
char c[32];
printf("测试的float数为:%f\n",test);
printf("二进制表示为:");
getFloatBin(test,c);
for(int i=0;i<32;i++)
{
printf("%d",c[i]);
if(i==0)
printf(", ");
if(i==8)
printf(", ");
}
return 0;
}
测试的float数为:100.000000
二进制表示为:0, 10000101, 10010000000000000000000
Process returned 0 (0x0) execution time : 0.055 s
当输入数据为-12.75时,输出结果如下:
测试的float数为:-12.750000
二进制表示为:1, 10000010, 10011000000000000000000
Process returned 0 (0x0) execution time : 0.055 s
Press any key to continue.
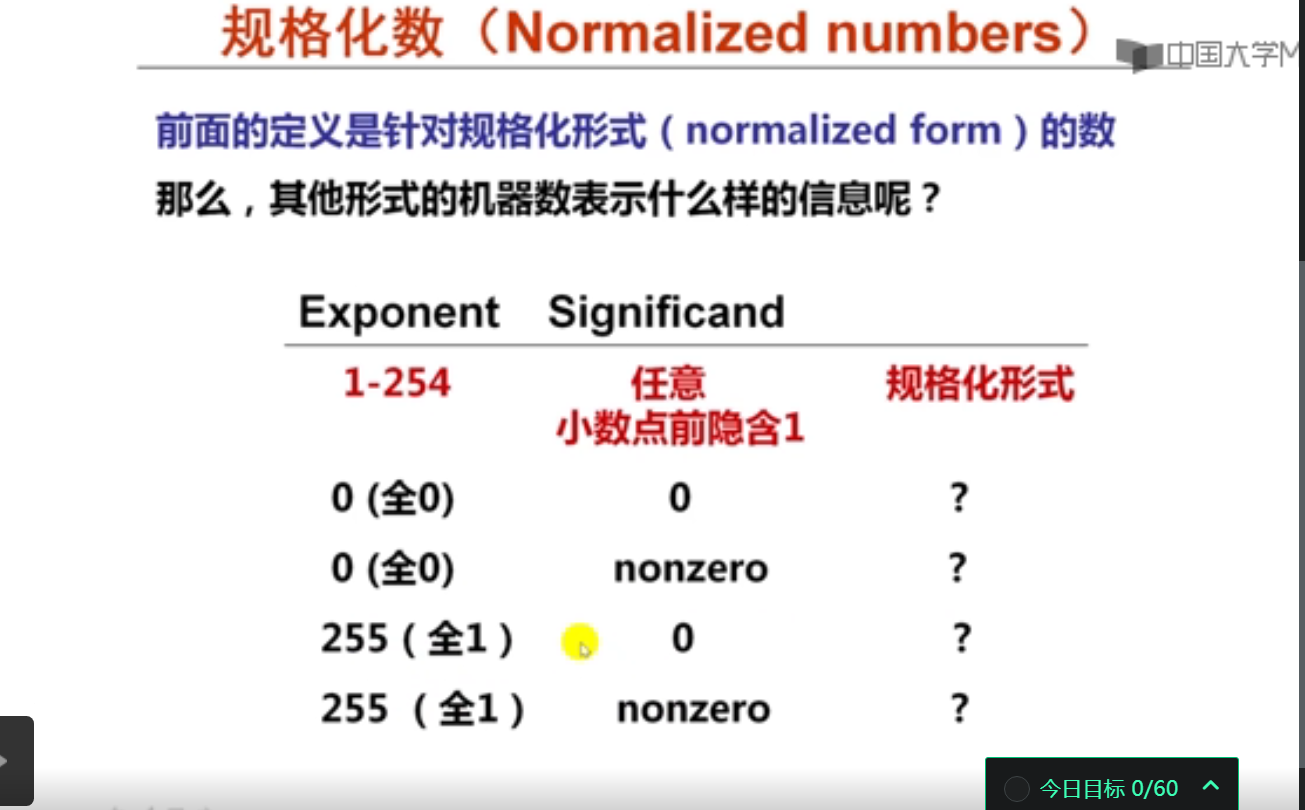
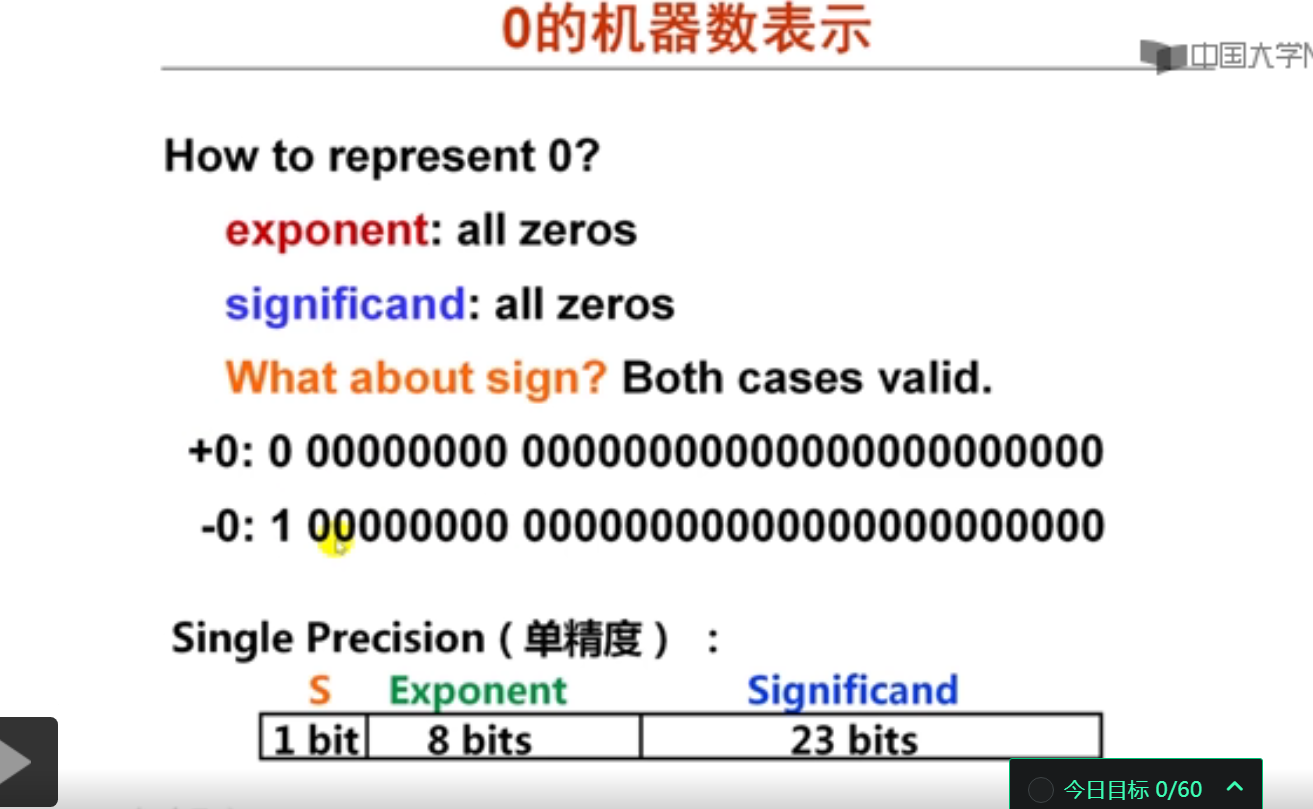
3. IEEE 754中特殊数的表示(15分钟)

实例测试:
#include <stdio.h>
#include <stdlib.h>
int main()
{
float a=1.0,b=1000.0;
printf("%d\n",a/0>b); //输出1
printf("%d\n",a/0<b); //输出0
return 0;
}

若float型变量x=8.0,则x/0.0的值为+∞,若x=0.0,则x/0.0的值为非数(NaN)。
#include <iostream>
#include <cmath>
using namespace std;
int main()
{
cout<<"nan:"<<sqrt(-1)<<endl;
cout<<"nan:"<<log(-1.0)<<endl;
cout<<"nan:"<<0.0/0.0<<endl;
cout<<"nan:"<<0.0*sqrt(-1)<<endl;
cout<<"nan:"<<sqrt(-1)/sqrt(-1)<<endl;
cout<<"nan:"<<sqrt(-1)-sqrt(-1)<<endl;
cout<<"inf:"<<1/0.0<<endl;
cout<<"-inf:"<<-1/0.0<<endl;
cout<<"inf:"<<0.0+1/0.0<<endl;
cout<<"-inf:"<<log(0)<<endl;
cout<<"isfinite:0"<<isfinite(0.0/0.0)<<endl;
cout<<"isfinite:0"<<isfinite(1/0.0)<<endl;
cout<<"isfinite:0"<<isfinite(1.1)<<endl;
cout<<"isnormal:0"<<isnormal(0.0/0.0)<<endl;
cout<<"isnormal:0"<<isnormal(1/0.0)<<endl;
cout<<"isnormal:0"<<isnormal(1.1)<<endl;
cout<<"isinf:0"<<isinf(0.0/0.0)<<endl;
cout<<"isinf:1"<<isinf(1/0.0)<<endl;
cout<<"isinf:0"<<isinf(1.1)<<endl;
return 0;
}
nan:nan
nan:nan
nan:nan
nan:nan
nan:nan
nan:nan
inf:inf
-inf:-inf
inf:inf
-inf:-inf
isfinite:00
isfinite:00
isfinite:01
isnormal:00
isnormal:00
isnormal:01
isinf:00
isinf:11
isinf:00

阶码用移码表示,对于规格化数偏置为127,对于非规格化数偏置为126。
IEEE 754浮点数标准中,对于单精度浮点数(32位)和双精度浮点数(64位),其阶码值(exponent)的范围是一个固定长度的无符号二进制数所能表示的范围。对于单精度,阶码是8位,能表示的值的范围是0~255。对于双精度,阶码是11位,能表示的值的范围是0~2047。
然而,在IEEE 754浮点数中,阶码的0和最大值(对于单精度是255,对于双精度是2047)被保留了出来,用于表示特殊值,如无穷大、零和非规格化数等。所以,实际上,用于表示正常的浮点数的阶码范围是1~254(对于单精度)和1~2046(对于双精度)。
然后,这个范围被设计成了以一个"偏移值"(bias)为中心的负数和正数的范围。对于单精度,偏移值是127,所以实际的阶码范围是-126 ~ 127。对于双精度,偏移值是1023,所以实际的阶码范围是-1022 ~ 1023。
非规格化数是用来表示接近于0的非常小的浮点数的,其阶码被设计为0,然后根据这个偏移值的设计,它实际表示的阶码就是-126(对于单精度)或-1022(对于双精度)。这样设计的目的是为了能表示更接近于0的数。如果阶码是-127或-1023,那么这个范围就会被"浪费"在表示非常接近于0但是又不是非常接近于0的数上,这样就达不到最大化利用阶码范围的目的。
为了让非规格化单精度浮点数能够平缓过渡到规格化单精度浮点数,即,让这两大类单精度浮点数的衔接不至于“突兀”。
如果非规格化数采用-127为阶,那么对于大小在{1.000...(23 个0)~1.111...(23个1)}乘以2^-127之间的数。你就只能把他们归结到规格化的数那里去,但是这样你就发现数的定义出现了歧义,对于阶码是0,尾数非0的数,我们根本不知道他是规格化还是非规格化;同理对于0的表达也出现冲突,所以设计者把不大于【1.111...(23个)乘以2^-127】的数全部归结到非规格化数。这样可以避免阶码为0的情况下不能确定是规格化数还是非规格化数的冲突;同时对于阶码为0,尾数为0的情况,你也能知道它一定是0,而不是一个规格化数1.0000(23个0)乘以2^-127。


关于浮点数精度的一个例子:
#include <iostream>
using namespace std;
int main()
{
float heads;
cout.setf(ios::fixed,ios::floatfield);
while(1)
{
cout<<"Please input a number:";
cin>>heads;
cout<<heads<<endl;
}
}
Please input a number:61.419997
61.419998
Please input a number:61.419998
61.419998
Please input a number:61.419999
61.419998
Please input a number:61.42
61.419998
Please input a number:61.420001
61.420002
Please input a number:
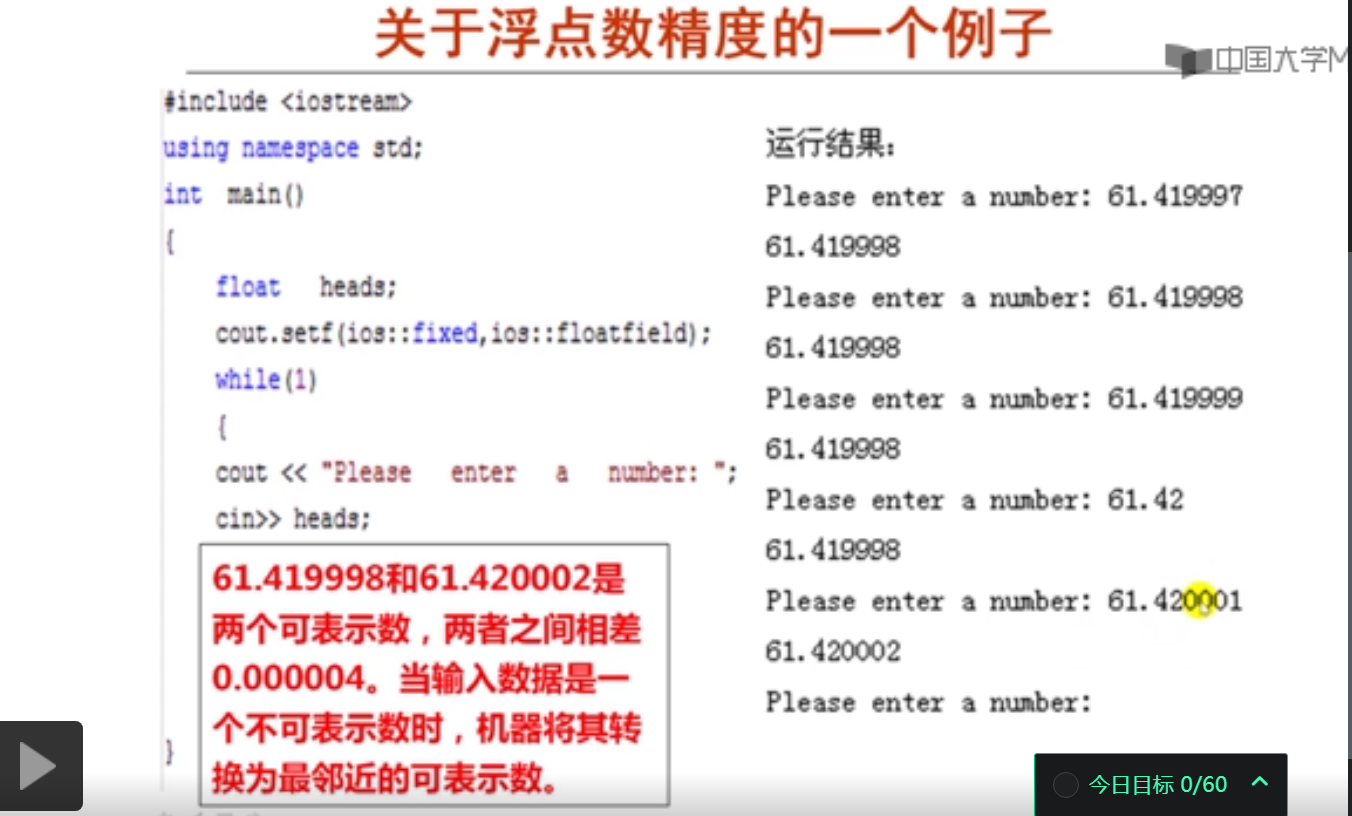
从键盘上输入61.420001赋值给一个float型变量x,再打印输出x时,其结果为61.420002。以下描述的是由此推断出的一些结论,下面三个都是正确结论。
- 由此说明能精确表示的float型数据的有效位数最多为7位。
- 由此说明32位IEEE 754单浮点数格式无法精确表示61.420001。
- 由此说明32位IEEE 754单浮点数格式能精确表示61.420002。
第5讲 非数值数据的编码表示
非数值数据的编码表示(19分钟)



西文字符没有输入码,但有内码(ASCII码),也有字模点阵和轮廓描述。

第6讲 数据宽度和存储容量的单位
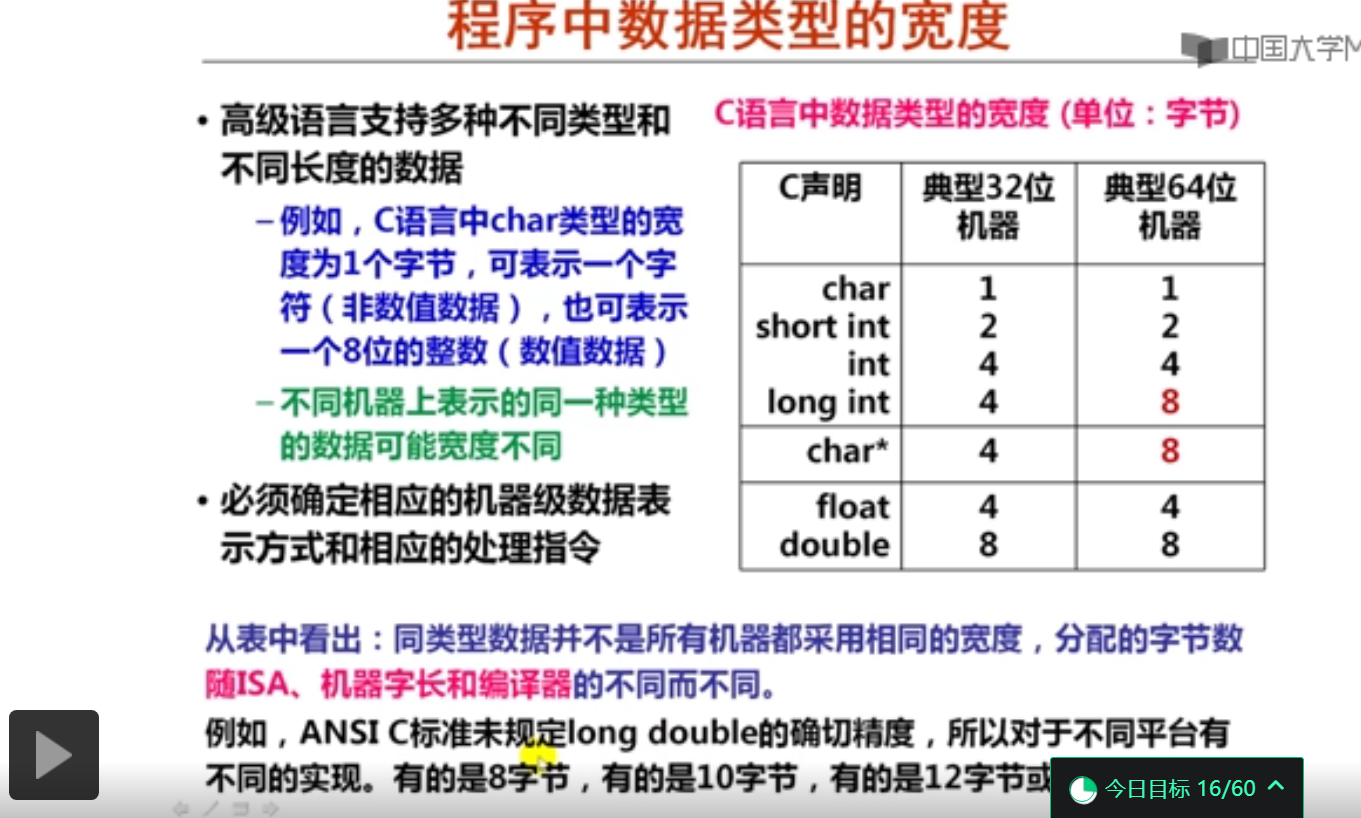
数据宽度和存储容量的单位(12分钟)



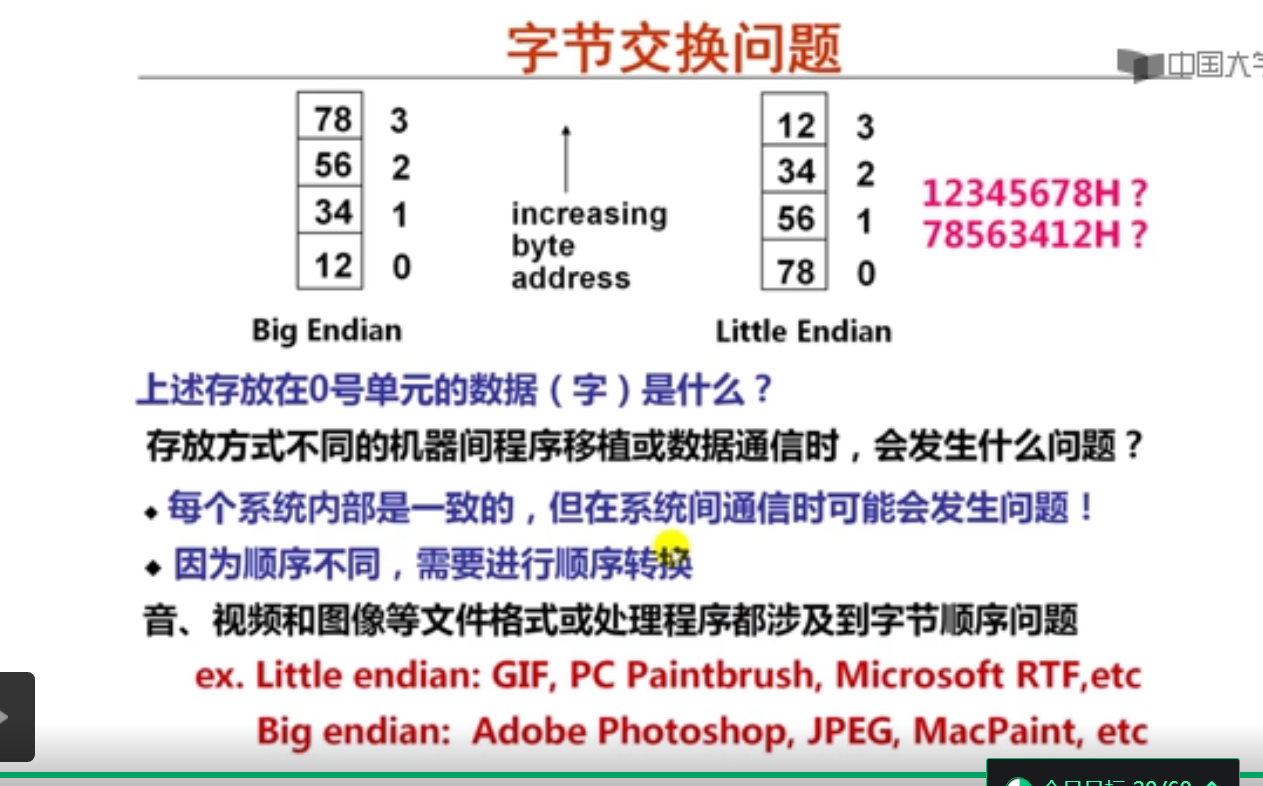
第7讲 数据存储时的字节排列
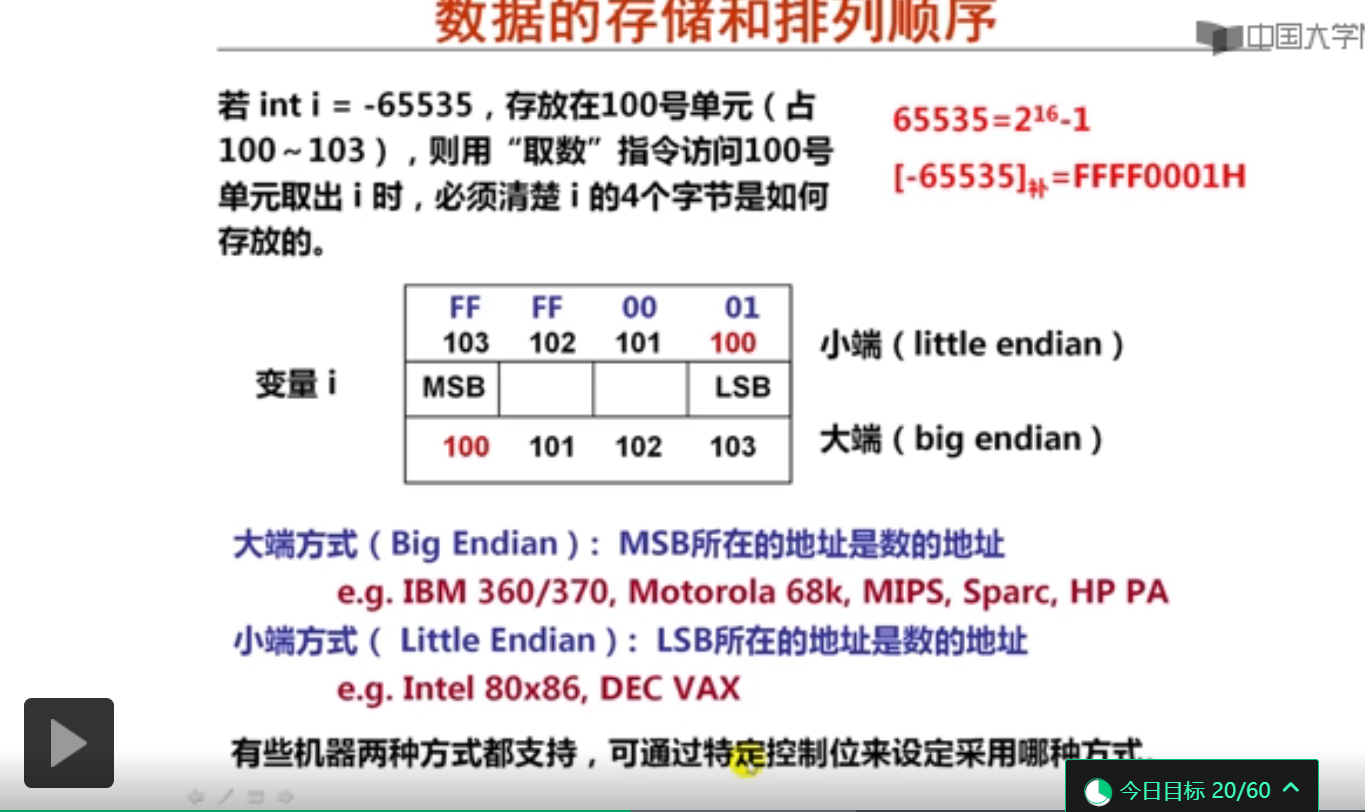
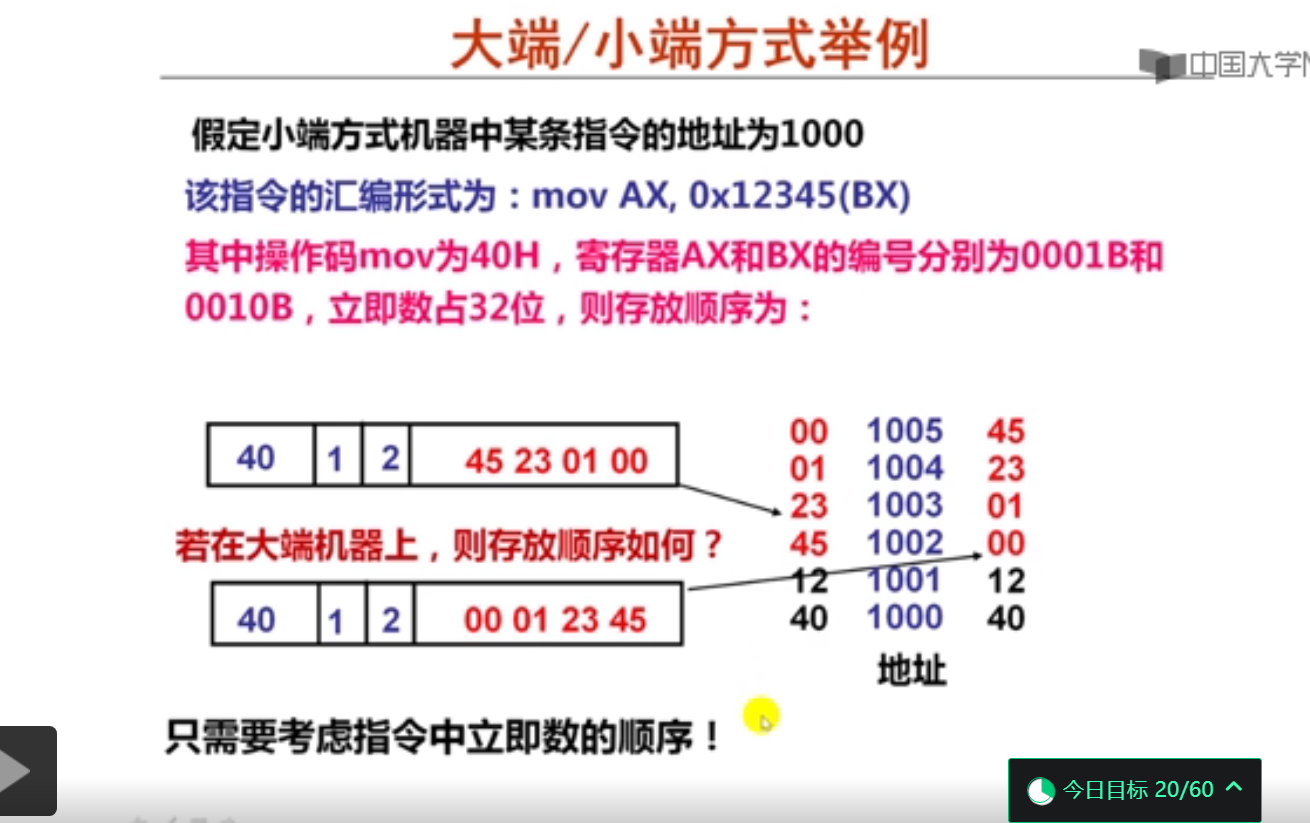
数据存储时的字节排列(20分钟)

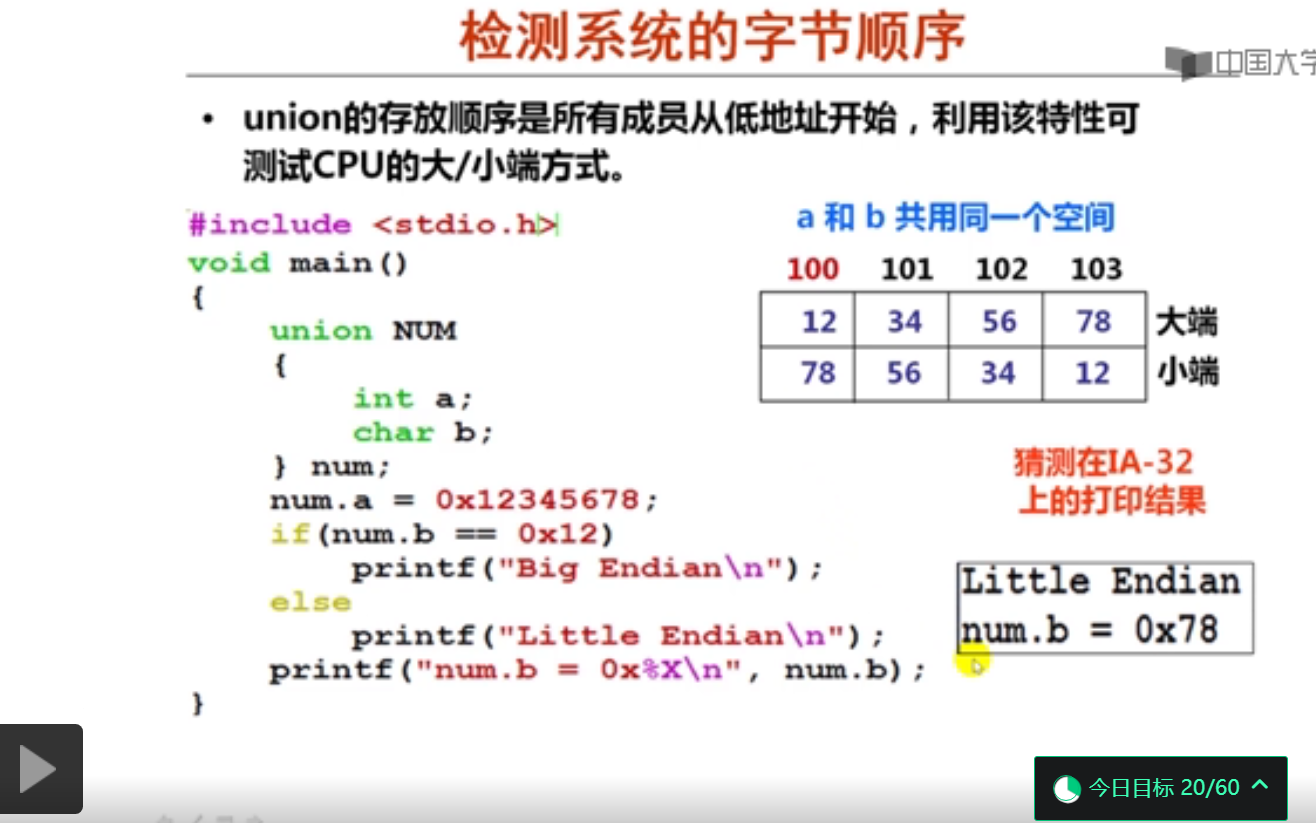
#include <stdio.h>
using namespace std;
int main()
{
union NUM
{
int a;
char b;
} num;
num.a=0x12345678;
if(num.b==0x12)
printf("Big endian!\n");
else
printf("Little endian!\n");
printf("num.b=0x%X\n",num.b);
return 0;
}
Little endian!
num.b=0x78

第二周小测验
1 108对应的十六进制形式是( B )。
A.63H
B.6CH
C.B4H
D.5CH
2 –1029的16位补码用十六进制表示为( C )。
A.0405H
B.7BFBH
C.FBFBH
D.8405H
3考虑以下C语言代码:
short si=–8196;
unsigned short usi=si;
执行上述程序段后,usi的值是( A )。
A.57340
B.8196
C.34572
D.57339
解析: A、-8196=-(8192+4)=-10 0000 0000 0100B,因此,si和usi的机器数都为1101 1111 1111 1100,按无符号整数解释,其值为65535-3-8192=65535-8195=57340。
4考虑以下C语言代码:
short si=–32768;
unsigned short usi=si;
执行上述程序段后,usi的值是( C )。
A.65536
B.–32768
C.32768
D.65535
解析: C、-32768=-1000 0000 0000 0000B,因此,si和usi的机器数都为1000 0000 0000 0000,按无符号整数解释,其值为32768。
5考虑以下C语言代码:
unsigned short usi=65535;
short si=usi;
执行上述程序段后,si的值是( D )。
A.1
B.–65535
C.65535
D.–1
解析: D、65535=1111 1111 1111 1111B,因此,usi和si的机器数都为1111 1111 1111 1111,按带符号整数解释,其值为-1。
6在ISO C90标准下执行以下关系表达式,结果为“真”的是( A )。
A.(unsigned) –1 > –2
B.2147483647 > –2147483648
C.–1 < 0U
D.2147483647 < (int) 2147483648U
解析: A、-1的机器数为全1,-2的机器数为11┅10,按无符号整数比较,显然全1比任何数大,即结果为“真”。 B、2147483647的机器数为011┅1,在C90中为int型;2147483648的机器数为100┅0,在C90中为unsigned型,-2147483648的机器数通过对100┅0各位取反末位加一得到,因此,机器数还是100┅0。011┅1和100┅0按无符号整数比较,显然011┅1比100┅0小,即结果为“假”。 C、-1的机器数为全1,按无符号整数比较,全1是最大的数,显然比0大,即结果为“假”。 D、2147483647的机器数为011┅1,在C90中为int型;2147483648的机器数为100┅0,在C90中为unsigned型,强制类型转换为int后,按带符号整数比较,显然011┅1比100┅0大,即结果为“假”。
7 –1028采用IEEE 754单精度浮点数格式表示的结果(十六进制形式)是( A)。
A.C4808000H
B.44C04000H
C.C4C04000H
D.44808000H
8假定变量i、f的数据类型分别是int、float。已知i=12345,f=1.2345e3,则在一个32位机器中执行下列表达式时,结果为“假”的是( B )。
A.f==(float)(double)f
B.f==(float)(int)f
C.i==(int)(float)i
D.i==(int)(double)i
解析: A、double型数的有效位数比float型数大得多,因而f转换为double类型后不会发生有效数字丢失。 B、f=1234.5,转换为int型数后,小数点后面的数字被丢失,因此与原来的f不相等。 C、12345<1024x16=2^14,因此,12345对应的二进制数的有效位数一定小于14,更小于IEEE 754单精度格式的有效位数24,因而转换为float型后,不会发生有效数字丢失,也即能够精确表示为float型,再转换为int型后,数值是一样的。 D、任何int型数的有效位数不会超过31位,因此都能精确转换为具有53位有效位数的double型。
9假定某计算机按字节编址,采用小端方式,有一个float型变量x的地址为0xffffc000,x=12345678H,则在内存单元0xffffc001中存放的内容是( A )。
A.01010110B
B.0101B
C.0001001000110100B
D.00110100B
解析: A、01010110B=56H,小端方式下,78H存在0xffffc000单元中,56H存在0xffffc001单元中,即结果正确。 B、因为按字节编址,所以某一个单元内存放一个8位数字。 C、因为按字节编址,所以某一个单元内只能存放8位数字。 D、00110100B=34H,小端方式下,78H存在0xffffc000单元中,34H存在0xffffc002单元中,即结果错误。
10下面是关于计算机中存储器容量单位的叙述,其中错误的是( D )。
A.最小的计量单位为位(bit),表示一位“0”或“1”
B.最基本的计量单位是字节(Byte),一个字节等于8bit
C.“主存容量为1KB”的含义是指主存中能存放1024个字节的二进制信息
D.一台计算机的编址单位、指令字长和数据字长都一样,且是字节的整数倍