第四周乘除运算及浮点数运算
第1讲 整数乘法运算
对于C语言程序中的表达式z=x*y,其中x,y和z都是32位的int型整数,z的取值为x*y的64位乘积中的低32位。
在计算机内部,一个整数x的平方可能是负数,这是因为在计算机中其结果取的是x*x的低n位乘积而高n位中的有效数位被丢弃而造成的。

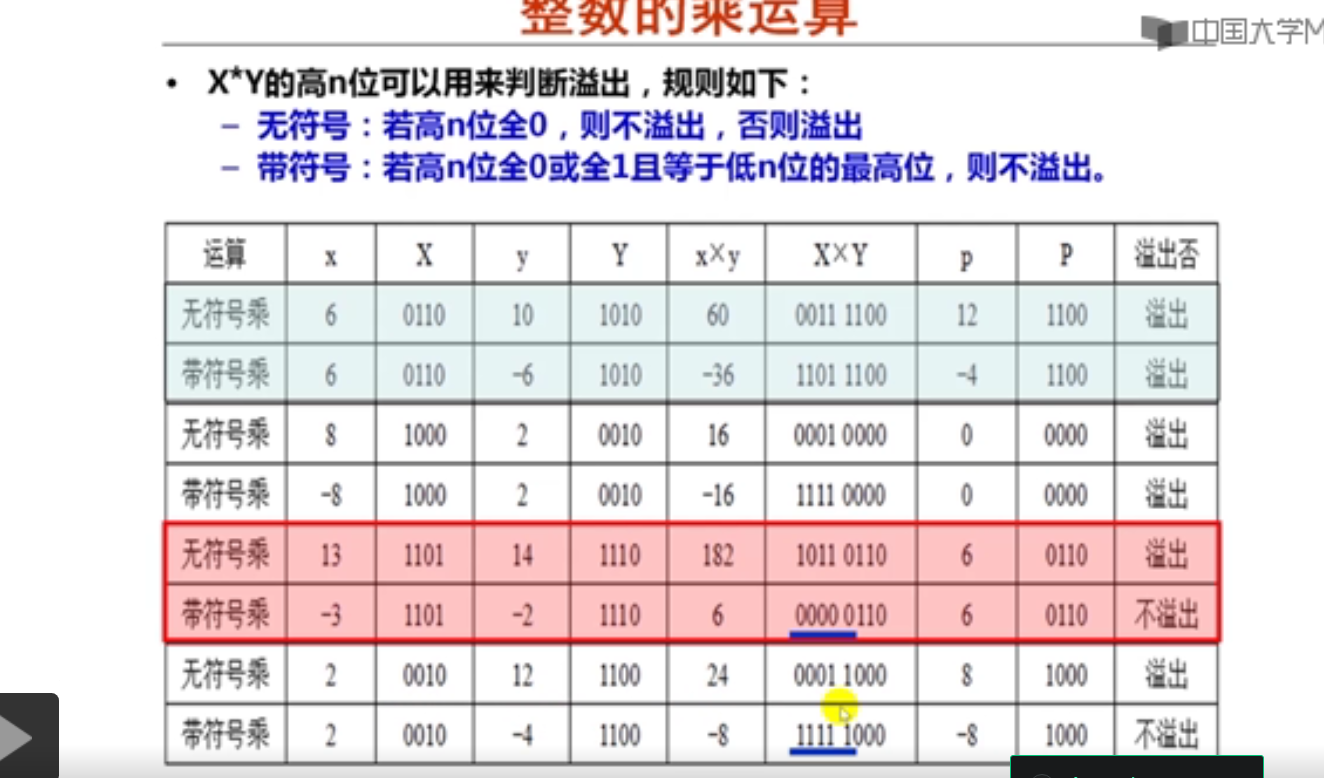
以下是关于整数乘运算(z=x*y)结果溢出判断规则的描述,其中错误的是( A )。
A.如果是C语言程序员,可以采用"若(y!=0 || x==z/y),则结果z不溢出"的规则。
B.若x,y,z为无符号整数,则编译器可以采用"若z的高n为全0,则不溢出,否则溢出"的规则。
C.若x,y,z为带符号整数,则编译器可以采用"若z的高n+1位为全0或全1,则不溢出,否则溢出"的规则。
D.高级语言程序员使用高级语言语句实现溢出判断,而编译器使用若干条指令进行溢出判断。


#include <iostream>
#include <cstdio>
using namespace std;
int is_mul_overflow(int a, int b) {
if( a >= 0 && b >=0 ) {
return INT_MAX / a < b;
}
else if( a < 0 && b < 0 ) {
return INT_MAX / a > b;
}
else if( a * b == INT_MIN ) {
return 0;
}
else {
return a < 0 ? is_mul_overflow(-a, b) : is_mul_overflow(a, -b);
}
}
void check(int n1, int n2, int expect_ret, int case_n) {
int ret = is_mul_overflow(n1, n2);
if( expect_ret == is_mul_overflow(n1, n2) )
printf("test pass case:%d\n",case_n);
else
printf("test fail case:%d\n",case_n);
}
int main() {
int case_n = 0;
check(0x00000001, 0x0000000f, 0x0000000f, ++case_n);
printf("%x\n", INT_MIN);
printf("%x\n", INT_MAX);
int result = -1*1;
printf("%d",result);
return 0;
}
test fail case:1
80000000
7fffffff
-1
-1(1111)乘以+1(0001)结果(00001111)溢出????
取负指令neg:各位取反末位加一
判断两int相乘是否溢出,目前找到的最正确方式:
#include <iostream>
#include <cstdio>
using namespace std;
int is_mul_overflow(int a, int b) {
if( a >= 0 && b >=0 ) {
return INT_MAX / a < b;
}
else if( a < 0 && b < 0 ) {
return INT_MAX / a > b;
}
else if( a * b == INT_MIN ) {
return 0;
}
else {
return a < 0 ? is_mul_overflow(-a, b) : is_mul_overflow(a, -b);
}
}
void check(int n1, int n2, int expect_ret, int case_n) {
int ret = is_mul_overflow(n1, n2);
if( expect_ret == is_mul_overflow(n1, n2) )
printf("test pass case:%d\n",case_n);
else
printf("test fail case:%d\n",case_n);
}
int main() {
int case_n = 0;
check(1, 0x80000000, 0, ++case_n);
check(-1, 0x80000000, 1, ++case_n);
check(0x80000000, -1, 1, ++case_n);
check(-1, 0x80000001, 0, ++case_n);
check(0x80000001, -1, 0, ++case_n);
check(1, 0x7fffffff, 0, ++case_n);
check(0x7fffffff, 1, 0, ++case_n);
check(2, 0x7fffffff, 1, ++case_n);
check(0x7fffffff, 2, 1, ++case_n);
check(0x7fffffff, -1, 0, ++case_n);
check(-1, 0x7fffffff, 0, ++case_n);
check(2, 0xc0000000, 0, ++case_n);
check(0xc0000000, 2, 0, ++case_n);
check(0x70000000, 2, 1, ++case_n);
check(2, 0x70000000, 1, ++case_n);
printf("%x\n", INT_MIN);
printf("%x\n", INT_MAX);
return 0;
}
test pass case:1
test pass case:2
test pass case:3
test pass case:4
test pass case:5
test pass case:6
test pass case:7
test pass case:8
test pass case:9
test pass case:10
test pass case:11
test pass case:12
test pass case:13
test pass case:14
test pass case:15
80000000
7fffffff

int copy_array(int* array,int count)
{
int *myarray = (int*)malloc(count*sizeof(int));
if(myarray==NULL)
{
return -1;
}
for(int i=0;i<count;i++)
myarray[i]=array[i];
return count;
}

第2讲 整数除法运算


int main() {
int a = 0x80000000;
int b = a/-1;
printf("%d\n",b);//-2147483648
printf("%d\n",-a);//-2147483648
int c = -1;
int d = a/c;
printf("%d",d);//这里无输出结果
return 0;
}


对于C语言程序中的一个char型变量x,若x=-15,则x/4的机器数为( 1111 1101 )。
这里不能整除,需要添加偏置量。

第3讲 浮点数运算
附录float、double类型数据精度范围问题
| 类型 | 比特数 | 有效数字(精度) | 数值范围 |
|---|---|---|---|
| float | 32 | 6~7 | -3.4*10^38~3.4*10^38 |
| double | 64 | 15~16 | -1.79*10^308~1.79*10^308 |
| long double | 128/ | 18~19 | -1.2*10^4932~1.2*10^4932 |
在计算机中,浮点数类型(如 float 和 double)的精度是由其存储格式和位数决定的。
对于 float 类型,它通常使用 IEEE 754 单精度浮点数表示法,占用 32 位(4 字节)存储空间。其中,1 位用于表示符号位,8 位用于指数,剩下的 23 位用于表示尾数。这意味着 float 类型可以提供大约 7 位有效数字的精度。
而对于 double 类型,它通常使用 IEEE 754 双精度浮点数表示法,占用 64 位(8 字节)存储空间。其中,1 位用于表示符号位,11 位用于指数,剩下的 52 位用于表示尾数。这使得 double 类型可以提供大约 15 位有效数字的精度。
需要注意的是,这些数字精度是近似值,因为浮点数的存储和计算都涉及到舍入误差。在进行浮点数计算时,可能会出现舍入误差导致精度损失。因此,在对浮点数进行比较和精确计算时,需要注意处理舍入误差可能引起的问题。
如果需要更高精度的计算,可以考虑使用其他表示方法,如使用任意精度的库(例如 BigDecimal 类型)或进行符号位、指数和尾数的自定义存储。这样可以在需要时灵活调整精度要求。但请注意,这些方法可能会牺牲计算速度和内存开销。
float 类型使用 IEEE 754 单精度浮点数表示法,其中尾数部分占据了 23 位。为了理解为什么 float 类型可以提供大约 7 位有效数字的精度,我们需要了解浮点数的表示方式。
在 IEEE 754 单精度浮点数表示法中,浮点数被分为三个部分:符号位、指数部分和尾数部分。符号位用于表示正数或负数,指数部分用于调整浮点数的大小范围,而尾数部分则表示浮点数的精度。
尾数部分占据了 23 位,其中最高位默认为 1,并且在存储时省略了这个最高位。这意味着尾数部分可以表示 24 个二进制位,即 2^24 = 16,777,216 种不同的值。然而,由于尾数部分只有 23 位,因此只能表示 2^23 = 8,388,608 个不同的值。
有效数字的位数可以通过以下公式计算:log10(2^N),其中 N 表示尾数部分的位数。对于 float 类型,N = 23,因此有效数字的位数为 log10(2^23) ≈ 7.22。所以,float 类型可以提供大约 7 位有效数字的精度。
请注意,这个数字是一个近似值,并且在进行浮点数计算时可能会存在舍入误差。因此,在进行精确计算或比较时,需要考虑舍入误差可能带来的影响。
2^52一共16位,故double类型数据的精度为15~16位。
附录定点小数和浮点小数的区别
定点小数和浮点小数是两种不同的表示和处理实数的方法。
-
定点小数:
- 定点小数使用固定的小数点位置来表示实数。小数点位置在数值中是固定的,通常是在最后一位或者是固定的位置。例如,假设小数点位置固定在整数部分和小数部分之间的某个位置,如 "123.456" 中的小数点位置。
- 定点小数的表示方式更直观和易于理解,因为小数点位置是固定的,有助于对数值的理解和操作。然而,它的范围和精度是固定的,不够灵活。
- 定点小数在计算机中通常使用固定位数的整数表示,其中一个固定的位数表示小数点的位置。这样可以通过位移和固定精度的整数运算来处理定点小数。
-
浮点小数:
- 浮点小数使用科学计数法的形式来表示实数。它由三个部分组成:符号位、尾数部分和指数部分。浮点小数的小数点位置是可变的,通过指数部分来表示。
- 浮点小数的表示方式更适合处理非常大或非常小的数值范围,因为指数部分可以调整小数点的位置,提供了更大的数值范围和灵活性。
- 浮点小数在计算机中通常使用 IEEE 754 标准(单精度或双精度)来表示,其中尾数部分和指数部分以二进制形式存储,并进行特定的规范化处理和舍入操作。
总结: 定点小数和浮点小数是不同的数值表示方式。定点小数使用固定的小数点位置,适合处理小范围和固定精度的数值。浮点小数使用科学计数法,通过指数来调整小数点位置,适合处理较大范围和可变精度的数值。浮点小数的表示方式更复杂,计算也会涉及舍入误差,但提供了更大的数值范围和灵活性。
1. 浮点加减运算(23分钟)



#include <stdio.h>
#include <conio.h>
int main()
{
int a=1,b=0;
printf("Division by zero:%d\n",a/b);
getchar();
return 0;
}
Process returned -1073741676 (0xC0000094) execution time : 0.543 s
整数除0的结果无法用01序列表示
#include <stdio.h>
#include <conio.h>
int main()
{
double x=1.0,y=-1.0,z=0.0;
printf("Division by zero:%f %f\n",x/z,y/z);
getchar();
return 0;
}
Division by zero:1.#INF00 -1.#INF00
浮点数除0可以表示为无穷大



2. 浮点运算的精度(22分钟)


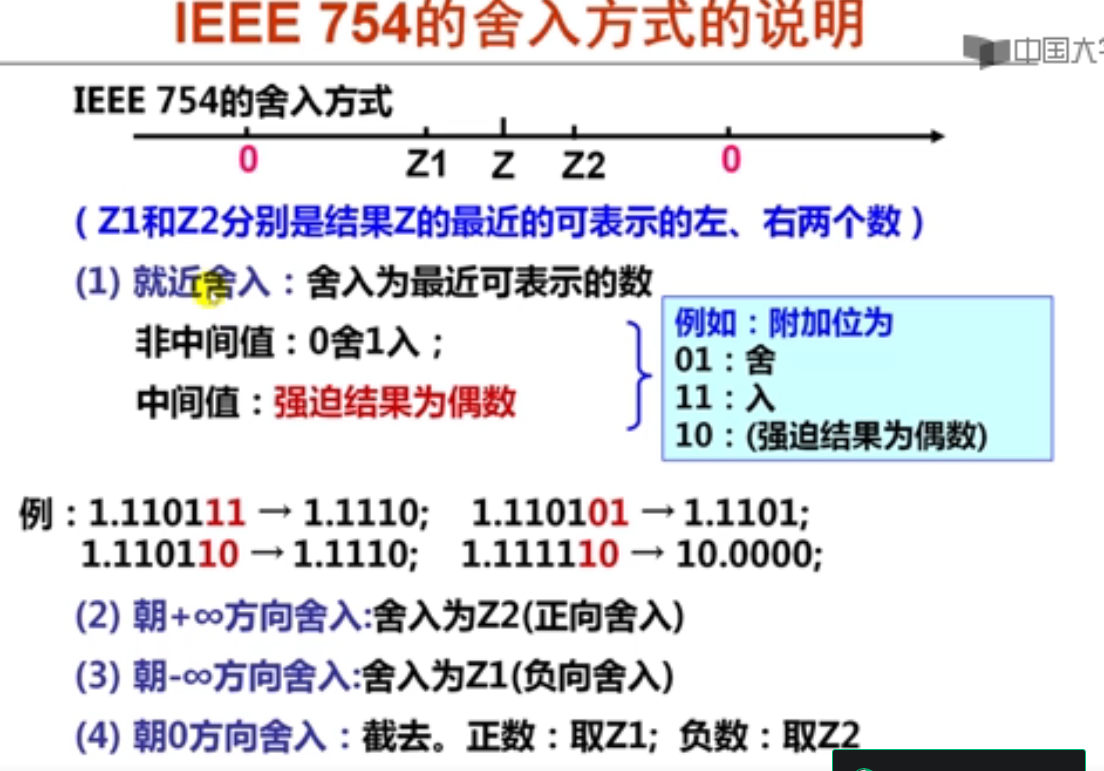
附加位为01时,要强制结果为偶数,末位需要加1




3. 浮点运算精度举例(16分钟)





第四周小测验
1单选(0.5分)
若在一个8位计算机中完成x+2y的运算,假定变量x和y的机器数用补码表示为[x]补=44H,[y]补= DCH,则x+2y的机器数及相应的溢出标志OF分别是( FCH、0)。
解析: x和y的机器数是用补码表示的,分别是0100 0100、1101 1100,因为是做x+2y,所以,先对y算术左移一位,然后和x相加,此时sub=0,即0100 0100 + 1011 1000+0 = 1111 1100(FCH),因为两个加数符号相异,所以不会发生溢出,即OF=0。
2单选(0.5分)
若在一个8位计算机中完成x–2y,假定变量x和y的机器数用补码表示为[x]补=44H,[y]补= DCH,则x–2y的机器数及相应的溢出标志OF分别是(8CH、1 )。
解析: x和y的机器数是用补码表示的,分别是0100 0100、1101 1100,因为是做x–2y,所以,先对y算术左移一位,得1011 1000,然后各位取反,再和x相加,此时sub=1,即0100 0100 + 0100 0111+1 = 1000 1100(8CH),因为两个加数符号都为0,而结果符号为1,所以发生了溢出,即OF=1。
3单选(0.5分)
若在一个8位计算机中完成x/2+2y,假定变量x和y的机器数用补码表示为[x]补=44H,[y]补= DCH,则x/2+2y的机器数及相应的溢出标志OF分别是( DAH、0 )。
解析: x和y的机器数是用补码表示的,分别是0100 0100、1101 1100,因为是做x/2+2y,所以,先对x算术右移一位,得0010 0010;再对y算术左移一位,得1011 1000,两者相加,此时sub=0,即0010 0010 + 1011 1000+0 = 1101 1010(DAH),因为两个加数符号相异,所以不会发生溢出,即OF=0。
4单选(0.5分)
假定变量r1 和r2的机器数用8位补码表示为[r1]补=F5H,[r2]补=EEH。若将运算结果存放在一个8位寄存器中,则下列运算中会发生溢出的是(B )。
A. r1/r2
B. r1× r2
C. r1+ r2
D. r1– r2
正确答案:B你选对了
C. r1(-11)+ r2(-18)结果为1 1110 0011(-29)
5单选(0.5分)
假定整数加法指令、整数减法指令和移位指令所需时钟周期(CPI)都为1,整数乘法指令所需时钟周期为10。若x为整型变量,为了使计算64*x所用时钟周期数最少,编译器应选用的最佳指令序列为(1条左移指令 )。
解析: 因为64*x可以用x左移6位来实现,左移指令比乘法指令快10倍,因此最佳指令序列为1条左移指令,只要一个时钟周期。
6单选(0.5分)
假定整数加法指令、整数减法指令和移位指令所需时钟周期(CPI)都为1,整数乘法指令所需时钟周期为10。若x为整型变量,为了使计算54*x所用时钟周期数最少,编译器应选用的最佳指令序列为(3条左移指令和两条减法指令 )。
解析:一条整数乘法指令需要10个时钟周期。 而54*x=(64-8-2)*x=64*x -8*x -2*x,可用3条左移指令和两条减法指令来实现,共需5个时钟周期。
7单选(0.5分)
假定整数加法指令、逻辑运算指令和移位指令所需时钟周期(CPI)都为1,整数除法指令所需时钟周期为32。若x为整型变量,为了使计算x/64所用时钟周期数最少,编译器应选用的最佳指令序列为(两条右移指令、1条与操作指令、1条加法指令 )。
A. 1条右移指令
B. 两条右移指令、1条与操作指令、1条加法指令
C. 1条加法指令、1条右移指令
D. 1条除法指令
正确答案:B你选对了
解析: A、若x为负数且不能被64整除,则x右移6位和x/64的结果不相等。 B、x/64 = ( x>=0 ? x : (x+63) ) >> 6,因此关键是计算偏移量b,这里,x为正时b=0,x为负时b=63。可从x的符号得到b,x>>31得到32位符号,正数为32位0,负数为32位1,然后通过“与”操作提取低6位,这就是偏移量b。也即:x/64 = ( x+ ( x>>31)&0x3F ) ) >> 6,用2条右移、1条加和1条与指令即可实现,只要4个时钟周期。 C、若x为负数,则x/64=(x+63)>>6,但该公式不适合正数x,因此无法用一条加和一条右移指令实现。 D、一条整数乘法指令需要32个时钟周期。
8单选(0.5分)
已知float型变量用IEEE 754单精度浮点格式表示,float型变量x和y的机器数分别表示为x=40E8 0000H,y=C204 0000H,则在计算x+y时,第一步对阶操作的结果[Ex-Ey]补为(1111 1101 )。
解析: 因为x=40E8 0000H=0100 0000 1110 1000 0...0,y=C204 0000H=1100 0010 0000 0100 0...0,所以x和y的阶码分别为100 0000 1、100 0010 0,对阶时计算过程为 1000 0001 + 0111 1100 = 1111 1101。
9单选(0.5分)
对于IEEE 754单精度浮点数加减运算,只要对阶时得到的两个阶之差的绝对值|ΔE|大于等于(25 ),就无需继续进行后续处理,此时,运算结果直接取阶大的那个数。
解析: 对于IEEE 754单精度浮点格式,当出现“1.bb…b + 0.00…0 01bb…b”情况时会发生“大数吃小数”现象,小数0.00…0 01bb…b中的小数点被左移了25位。
10多选(0.5分)
变量dx、dy和dz的声明和初始化如下:
double dx = (double) x;
double dy = (double) y;
double dz = (double) z;
若float和double分别采用IEEE 754单精度和双精度浮点数格式,sizeof(int)=4,则对于任意int型变量x、y和z,以下哪个关系表达式是永真的?
A. dx*dy*dz == dz*dy*dx
B. (double)(float) x == dx
C. (dx+dy)+dz == dx+(dy+dz)
D. dx*dx >= 0
正确答案:C、D你错选为B、D
解析: A、非永真。相乘的结果可能产生舍入。 B、非永真。当int型数据x的有效位数比float型可表示的最大有效位数24更多时,x强制转换为float型数据时有效位数丢失,而将x转换为double型数据时没有有效位数丢失。也即等式左边可能是近似值,而右边是精确值。 C、永真。因为dx、dy和dz是由32位int型数据转换得到的,而double类型可以精确表示int类型数据,并且对阶时尾数移位位数不会超过52位,因此尾数不会舍入,因而不会发生大数吃小数的情况。但是,如果dx、dy和dz是任意double类型数据,则非永真。 D、永真。double型数据用IEEE 754标准表示,尾数用原码小数表示,符号和数值部分分开运算。不管结果是否溢出都不会影响乘积的符号。