前言
本仓库是对《算法设计与分析》课程内容的记录,主要内容来自《算法设计与分析》第三版(屈婉玲等著)。
把《算法设计与分析》的内容加入《数据结构》仓库中会使得《数据结构》仓库异常臃肿,这里新开一个仓库详细记录《算法设计与分析》相关的内容。
思维导图来源:
最值得收藏的 算法分析与设计 全部知识点思维导图整理(北大慕课课程)
算法基础知识
算法的基本概念
算法定义:算法是指解决问题的一种方法或一个过程。
基本特性:有穷性、确定性、正确性、输入输出
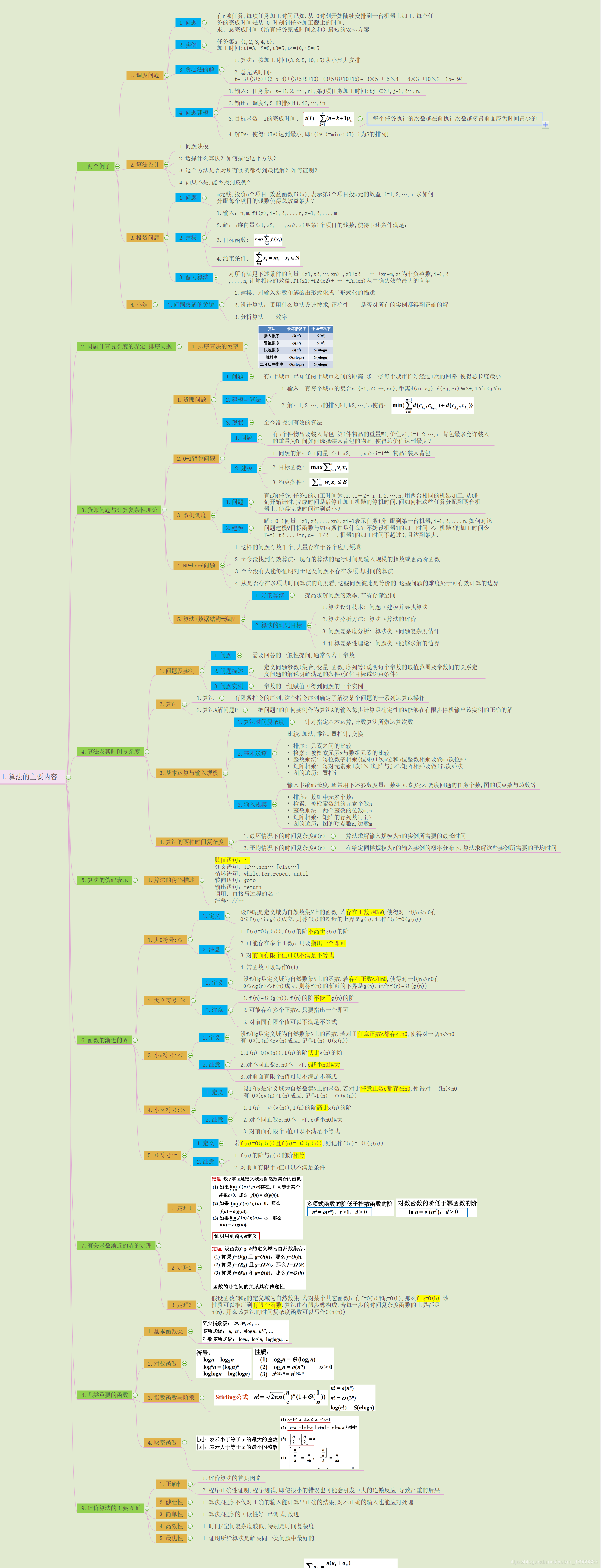
渐近分析 Asymptotics
函数的渐近的界

渐近分析 Asymptotics







这里应该是
little 符号比 big 符号更精确。
数学归纳法和斯特林公式
良序原理=>归纳法

斯特林公式
调和级数和二叉树
幂级数
主定理和等比级数
错位相减法
算法平均时间复杂度
算法的数学基础
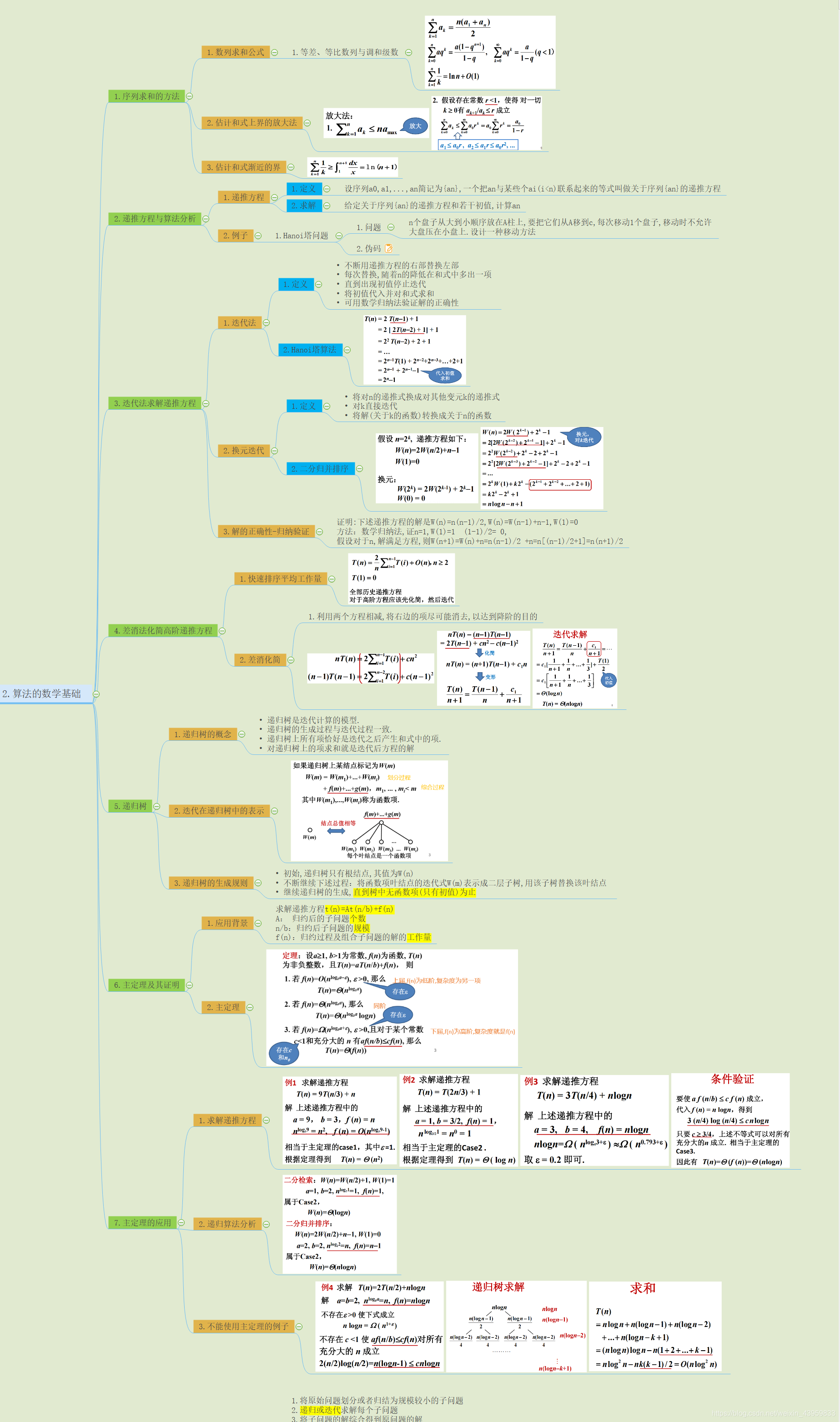
Master 定理
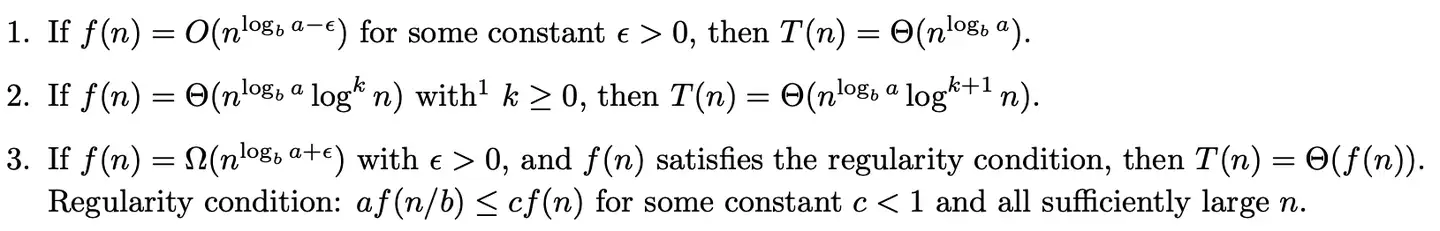
- https://blog.csdn.net/qq_41739364/article/details/101224786
- http://people.csail.mit.edu/thies/6.046-web/master.pdf
下面这篇文章介绍的比较详细。
master 定理的证明又长又臭,我也不会证,有兴趣的同学可以看这篇文章。

注释:这里的最常见的那个符号是 ,不是 ,最后一点写法可能有问题。
推荐下面的视频:
油管视频链接
2.4.1 Masters Theorem in Algorithms for Dividing Function
这位印度老师是 Udemy 的教师,评论中好评如潮。本人专门看了下屈婉玲《算法设计与分析》发现书中的这块内容也很老套,很难理解。
B站视频链接
Master Theorem in Algorithms for Dividing Functions - Abdul Bari 主定理 递推式求时间复杂度
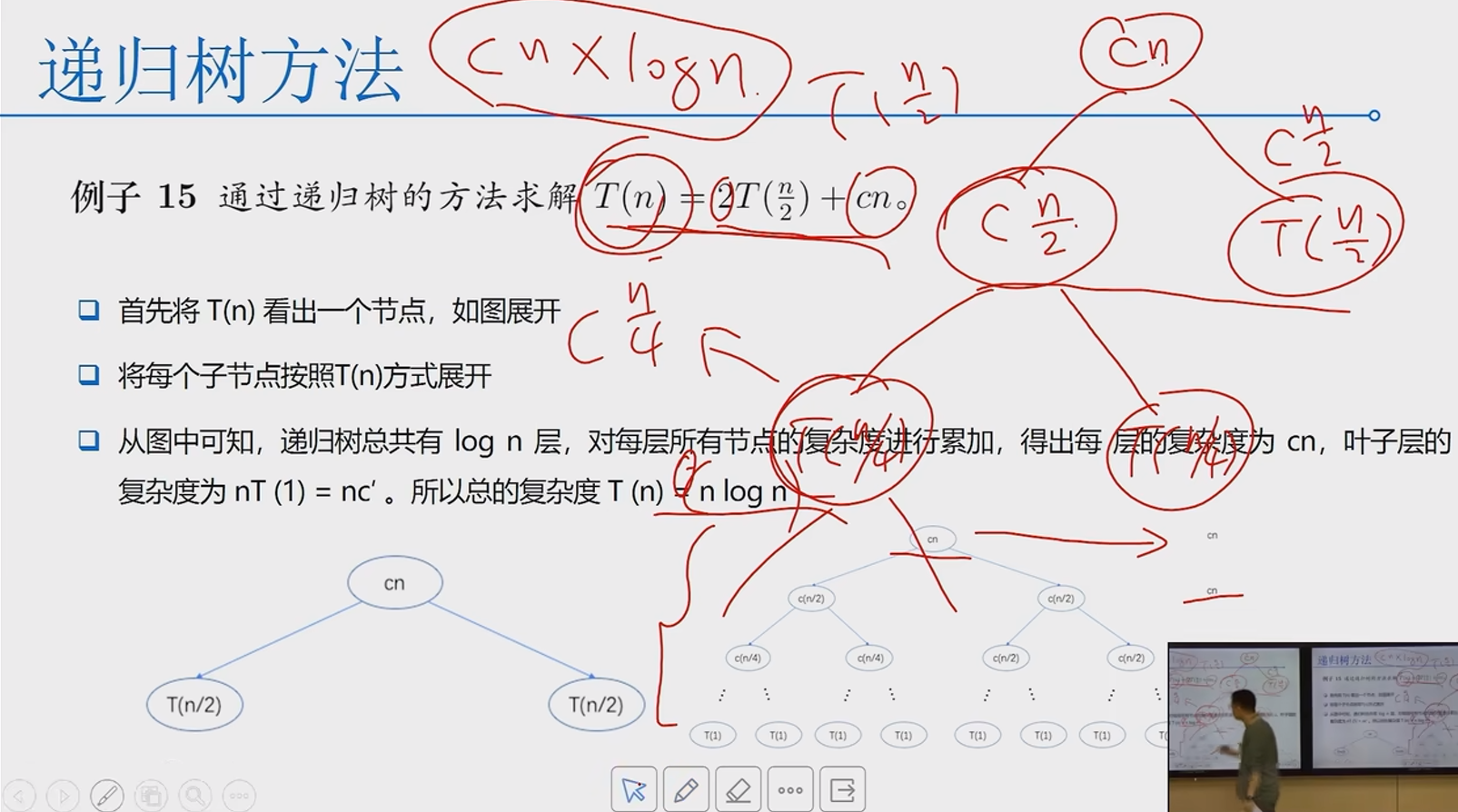
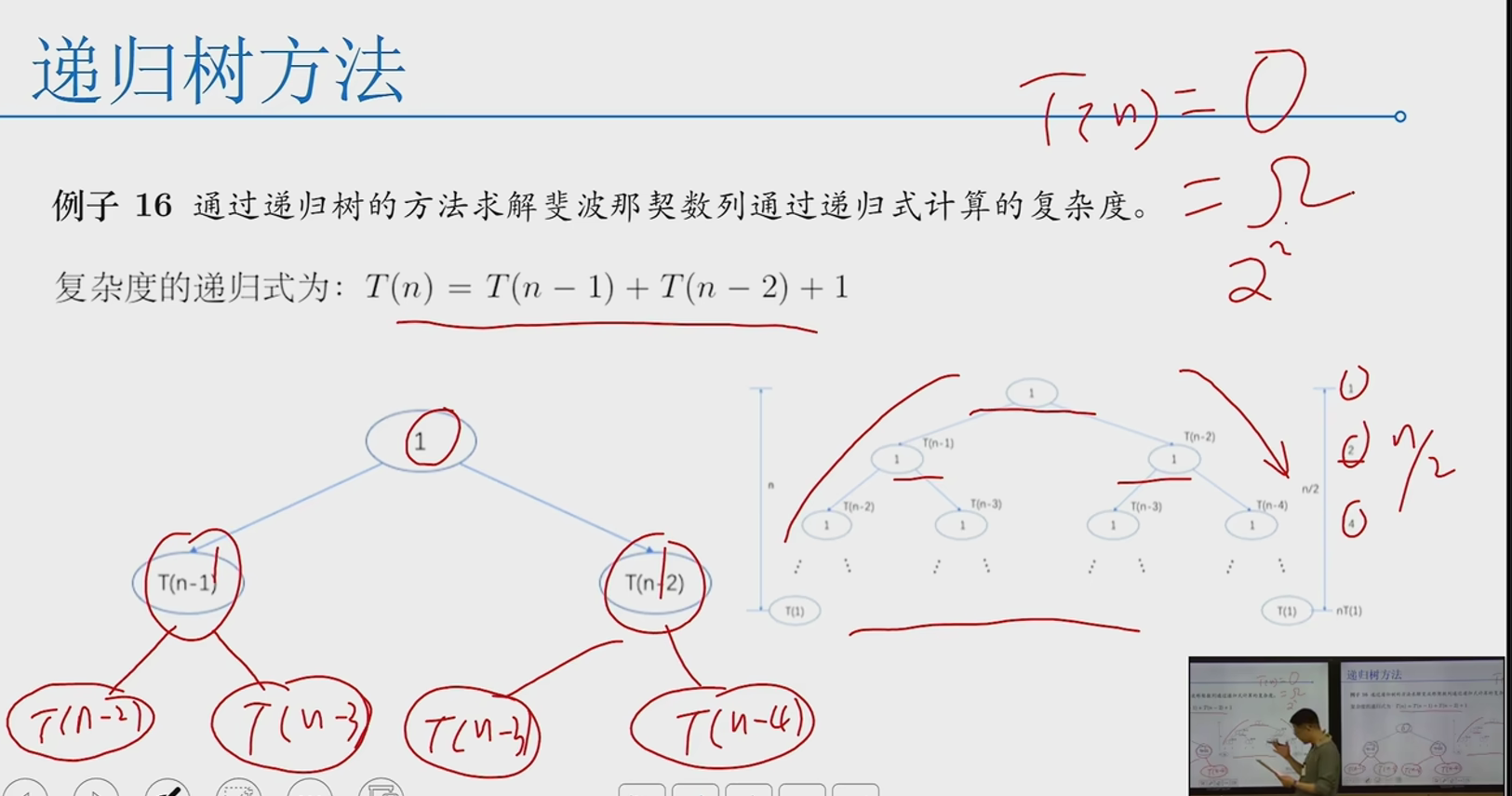
递归树
首先将复杂度的递归式展开为树的形式;之后,计算树每层的复杂度;最后,将所有层的复杂度相加,得到T(n)的复杂度。


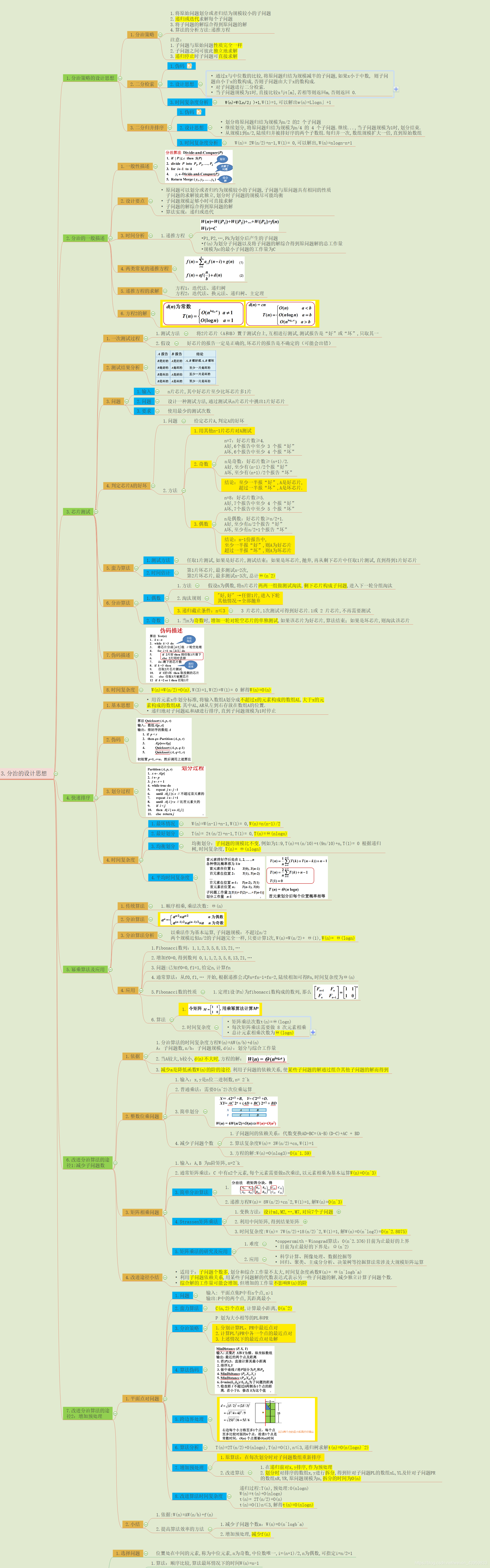
分治策略
分治的设计思想
改进分治算法的途经:
- 通过代数变换减少子问题个数
- 利用预处理减少递归内部的计算量
典型的分治算法
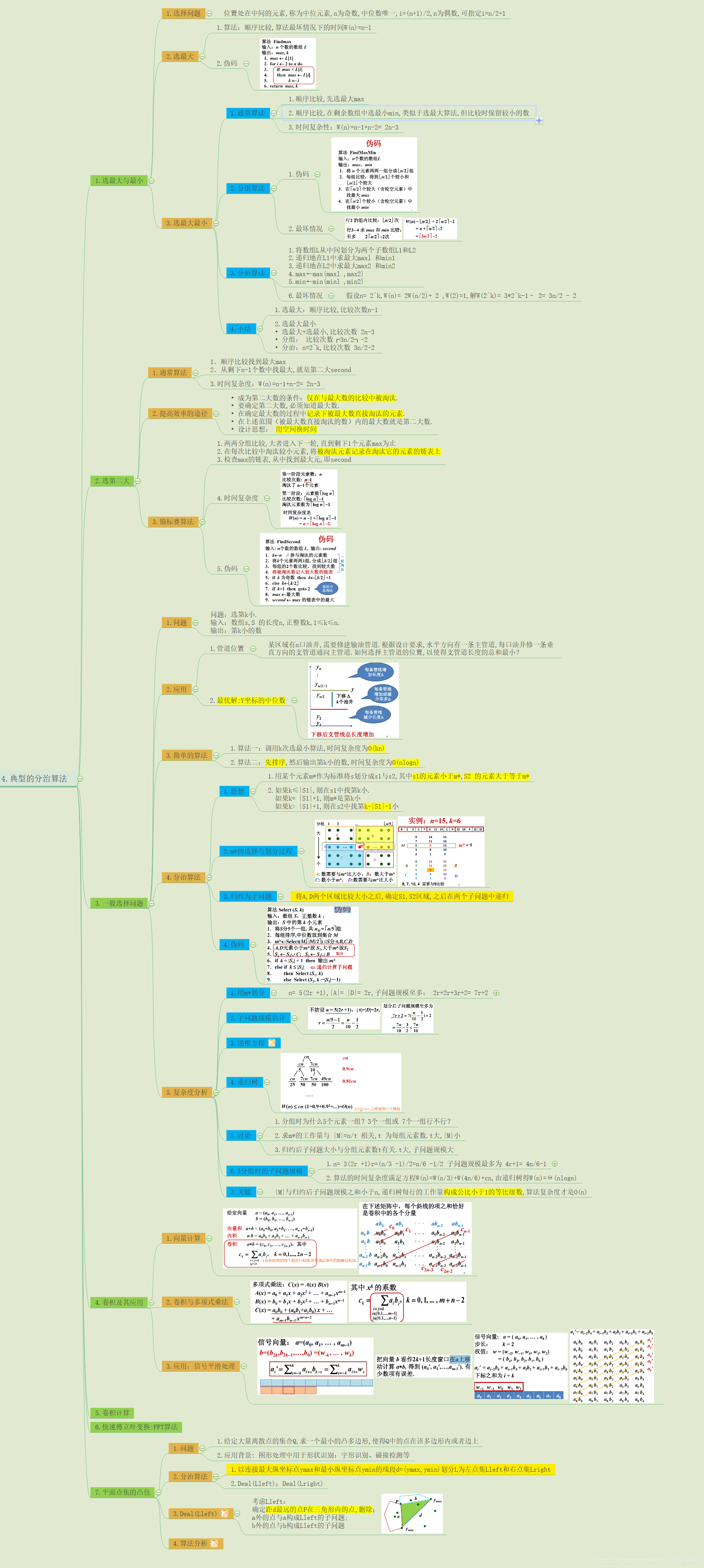
选择问题
选最大
选最小
选最大最小
选第二大
选第 k 小
求第 k 大的元素 最好:
高度之和小于等于 n - 1
证明:


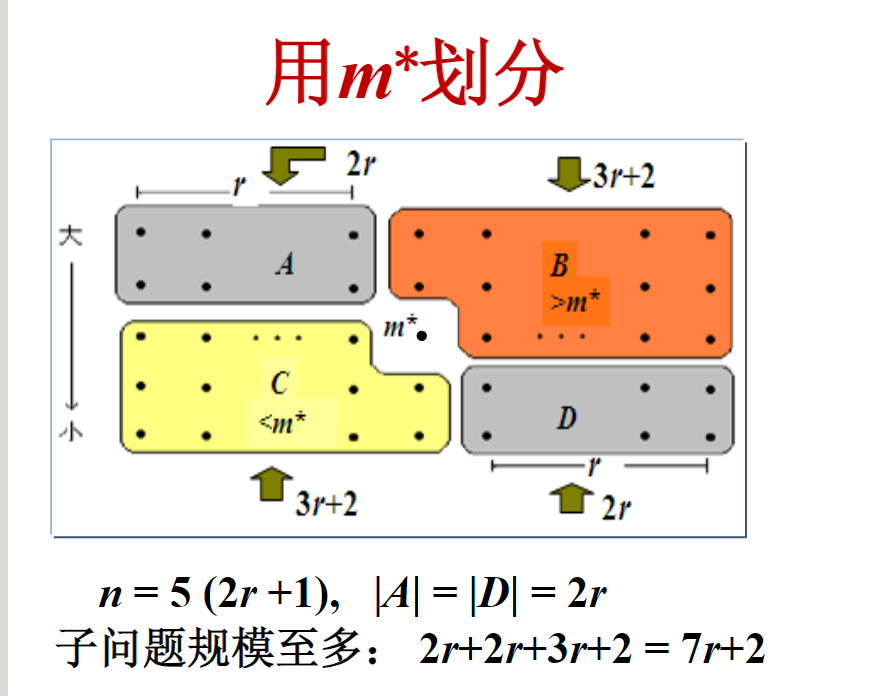

讨论分组时为什么5个元素一组,3个一组或7个一组行不行?
分析:递归调用
1.求m*的工作量与 相关,t 为每组元素数,t 大, 小
2.归约后子问题大小与分组元素数 t 有关, t 大,子问题规模大
关键:
与归约后子问题规模之和小于 n,递归树每行的工作量构成公比小于 1 的等比级数,算法复杂度才是
选第k小算法的时间分析
- 递推方程
- 分组时每组元素数的多少对时间复杂度的影响
3分组不行,5分组可以,7分组也行
卷积计算和 FFT 算法
平面点集的凸包
动态规划
概论
动态规划通常用于求解最优化问题。
基本要素:(1)最优子结构性质;(2)重叠子问题性质
动态规划五部曲:(1)明确 dp 数组的含义(2)递推公式(3)初始化(4)遍历顺序(5)打印 dp 数组
动态规划基本步骤:
- 找出最优解的性质,并自上而下刻画其最优解结构特征。
- 递归地定义最优值。
- 以自底向上的方式计算出最优值。
- 根据计算最优值时得到的信息,构造最优解。
以自底向上的方式:首先找到子问题的最优解,然后根据子问题的最优解找到原问题的最优解。
动态规划的设计
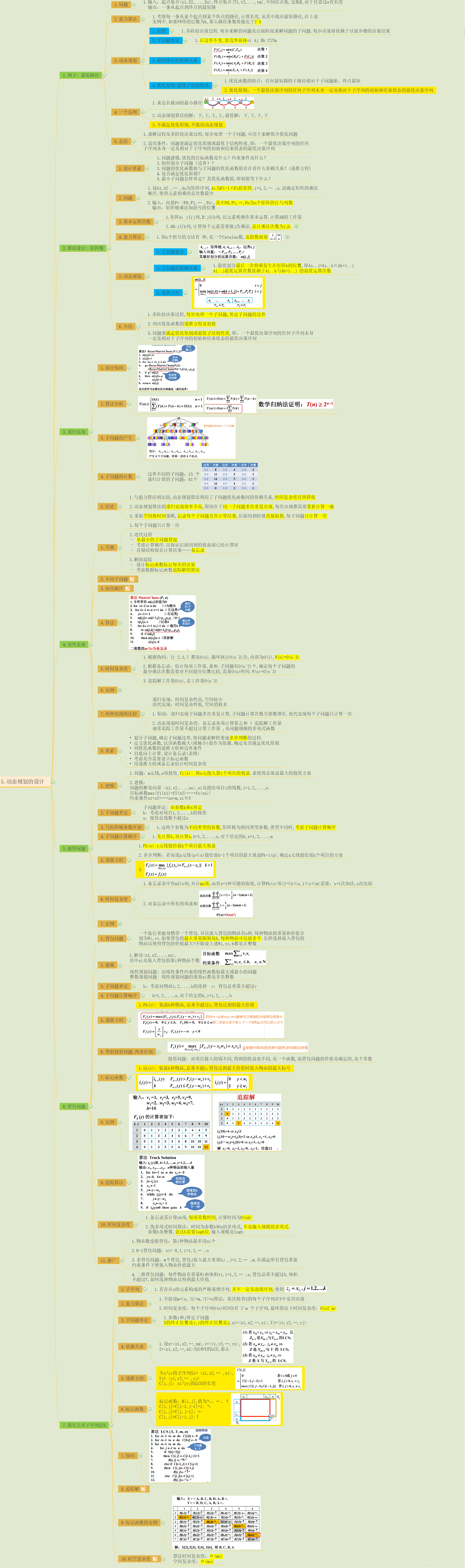
动态规划的应用

实例
流水线作业调度
矩阵链乘法问题
最长公共子序列
二维数组dp[i][j]表示nums1[0..i-1]下标(包括i-1)和nums2[0..j-1]下标(包括j-1)的最长公共子序列长度。
这样表示方便初始化。
最优二叉搜索树
图像压缩
序列对齐(Hirschberg算法)
带权区间调度
最大子段(数组)和
分段最小二乘法
RNA 二级结构
背包问题(knapsack)
备忘录算法(Memorization method)
递归实现,没有使用对角线技巧,需要更多的递归调用
贪心法
灵魂拷问
什么是贪心算法(Greedy Algorithm)?
什么是贪心选择性质?
如何证明贪心算法的正确性?
动态规划和贪心算法的区别是什么?
贪心概念
适用于最优化问题的算法往往包含一系列步骤,每一步都包含若干选择。贪心算法总是做出在当前看来是最好的选择。
贪心算法的基本要素:
(1)最优子结构性质:通过贪心选择可以将问题转移到子问题上,原始问题最优解=贪心选择+子问题的最优解
(2)贪心选择性质:全局最优解可以通过局部最优选择得到
贪心法的设计

说实话贪心算法并没有固定的套路。
所以唯一的难点就是如何通过局部最优,推出整体最优。
那么如何能看出局部最优是否能推出整体最优呢?有没有什么固定策略或者套路呢?
不好意思,也没有! 靠自己手动模拟,如果模拟可行,就可以试一试贪心策略,如果不可行,可能需要动态规划。
有同学问了如何验证可不可以用贪心算法呢?
最好用的策略就是举反例,如果想不到反例,那么就试一试贪心吧。
贪心一般解题步骤
贪心算法一般分为如下四步:
- 将问题分解为若干个子问题
- 找出适合的贪心策略
- 求解每一个子问题的最优解
- 将局部最优解堆叠成全局最优解
这个四步其实过于理论化了,我们平时在做贪心类的题目 很难去按照这四步去思考,真是有点“鸡肋”。
做题的时候,只要想清楚 局部最优 是什么,如果推导出全局最优,其实就够了。
重要的贪心算法

硬币找零问题
活动安排问题
区间划分问题
分数背包问题
哈夫曼编码
单源最短路径
最小生成树
回溯算法
概论
回溯法(Backtracking)的思想: 能进则进,不进则换,不换则退。
回溯法也可以叫做回溯搜索法,它是一种搜索的方式。
回溯是递归的副产品,只要有递归就会有回溯。
因为回溯的本质是穷举,穷举所有可能,然后选出我们想要的答案,如果想让回溯法高效一些,可以加一些剪枝的操作,但也改不了回溯法就是穷举的本质。
回溯法解决的问题都可以抽象为树形结构,因为回溯法解决的都是在集合中递归查找子集,集合的大小就构成了树的宽度,递归的深度就构成了树的深度。
递归就要有终止条件,所以必然是一棵高度有限的树(N叉树)。
回溯算法的框架:
以DFS的方式进行搜索,在搜索的过程中用剪枝条件(限界函数)避免无效搜索。约束函数,在扩展结点处剪去得不到可行解的子树;限界函数:在扩展结点处剪去得不到最优解的子树。
回溯算法求解问题的一般步骤:
1、 针对所给问题,定义问题的解空间,它至少包含问题的一个(最优)解。
2 、确定易于搜索的解空间结构,使得能用回溯法方便地搜索整个解空间 。
3 、以深度优先的方式搜索解空间,并且在搜索过程中用剪枝函数避免无效搜索。
常用剪枝函数:
用约束函数在扩展结点处剪去不满足约束的子树;
用限界函数剪去得不到最优解的子树。
回溯法,一般可以解决如下几种问题:
- 组合问题:N个数里面按一定规则找出k个数的集合
- 切割问题:一个字符串按一定规则有几种切割方式
- 子集问题:一个N个数的集合里有多少符合条件的子集
- 排列问题:N个数按一定规则全排列,有几种排列方式
- 棋盘问题:N皇后,解数独等等
回溯算法的设计

回溯算法模板
回溯算法模板框架如下:
void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;
backtracking(路径,选择列表); // 递归
回溯,撤销处理结果
}
}
Although backtracking seems very efficient. The time complexity for this algorithm is O(n2^n).
2^n is the time for searching the solution space.
n is the time to store the best solution.
解空间树
子集树、满m叉树、排列树区别:
子集树:从n个元素的集合S中找到满足某种性质的子集时,相应的解空间树就成为了子集树(典型问题:01背包问题)
满m叉树:所给问题中每一个元素均有m中选择,要求确定其中的一种选择,使得对这n个元素的选择结果组成的向量满足某种性质(经典问题:图的m着色问题)
排列树:从n个元素的排列树中找出满足某种性质的一个排列的时候,相应的解空间树称为排列树(经典问题:TSP问题,n-queens 问题)
剪枝(Pruning)操作
在回溯过程中,我们用一个约束函数C(i)(constraint function)和一个限界函数B(i)(bounding function)剪掉无效的分支,从而专注于搜索最有希望的分支。
类似dfs在叶子节点收获结果,回溯算法可以通过剪枝(prune)提前中止向下搜索的过程。
约束函数C(i)(constraint function):检查当前解的可行性
Constraint function is to check the feasibility of the current solution.
限界函数B(i)(bounding function)
Bounding function is for optimization problem.
回溯法的典型应用
集装箱问题(Container Loading Problem)
Container Loading problem is to load as many containers as is possible without sinking the ship.
子集和(Sum of Subsets)
0/1 Knapsack Problem
First, rank the item by their value per unit weight.
棋盘问题之 N-Queens Problem
棋盘问题之解数独
组合问题之切割子串
排列问题之全排列
最大团问题
旅行商问题
图的 m 着色问题
分支限界法
概念
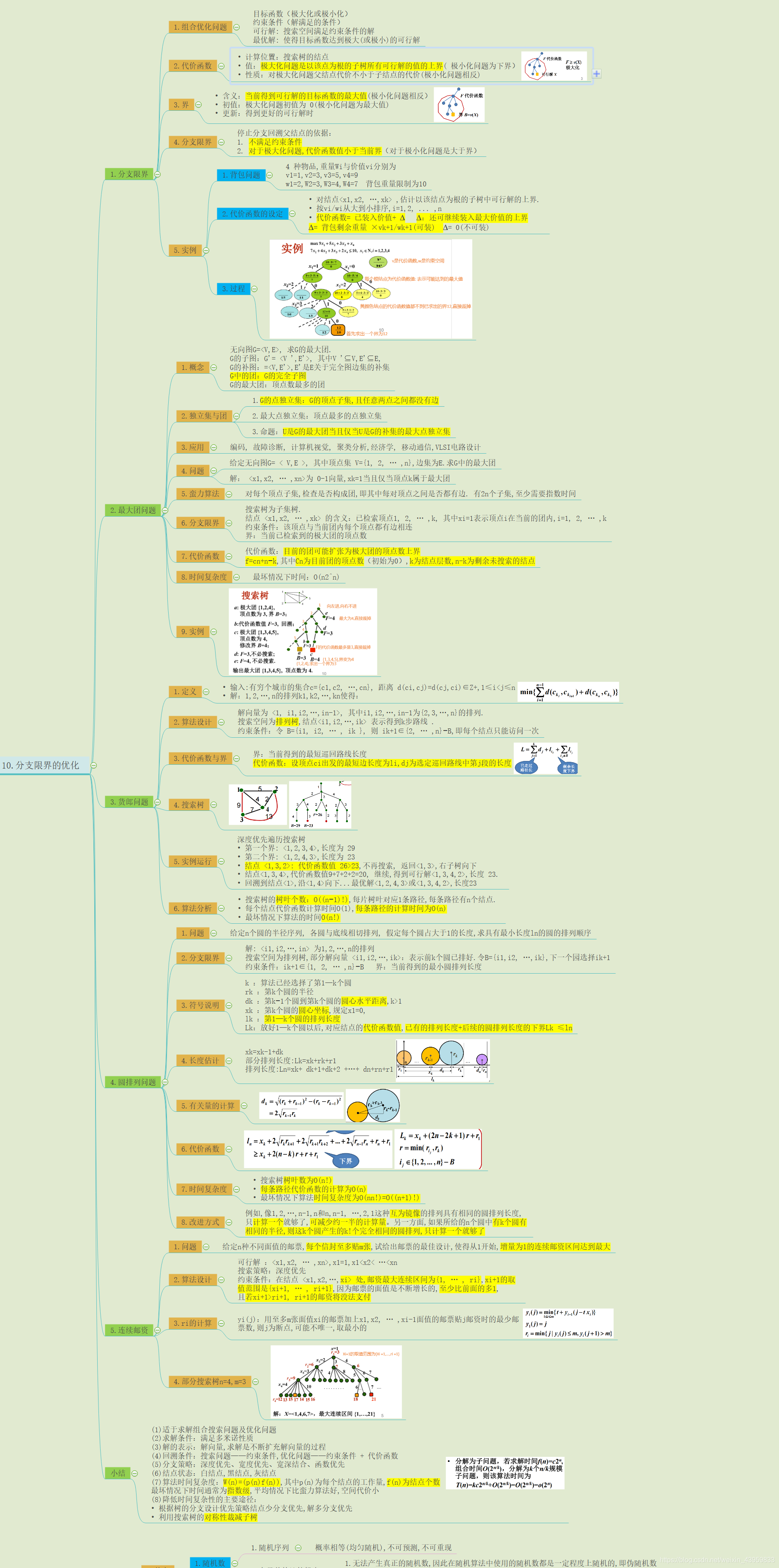
分支限界的应用
背包问题
最大团问题
货郎问题
圆排列问题
连续邮资问题
计算复杂性理论
NP 完全性思维导图

P类与NP类
易解的问题与难解的问题
判定问题
NP类
多项式时间变换与NP完全性
多项式时间变换
NP完全性及其性质
Cook-Levin定理—第—个NP完全问题
几个NP完全问题
最大可满足性与二元可满足性
顶点覆盖、团与独立集
哈密顿回路与货郎问题
恰好覆盖
子集和、背包、装箱与双机调度
整数线性规划
近似算法
近似算法思维导图
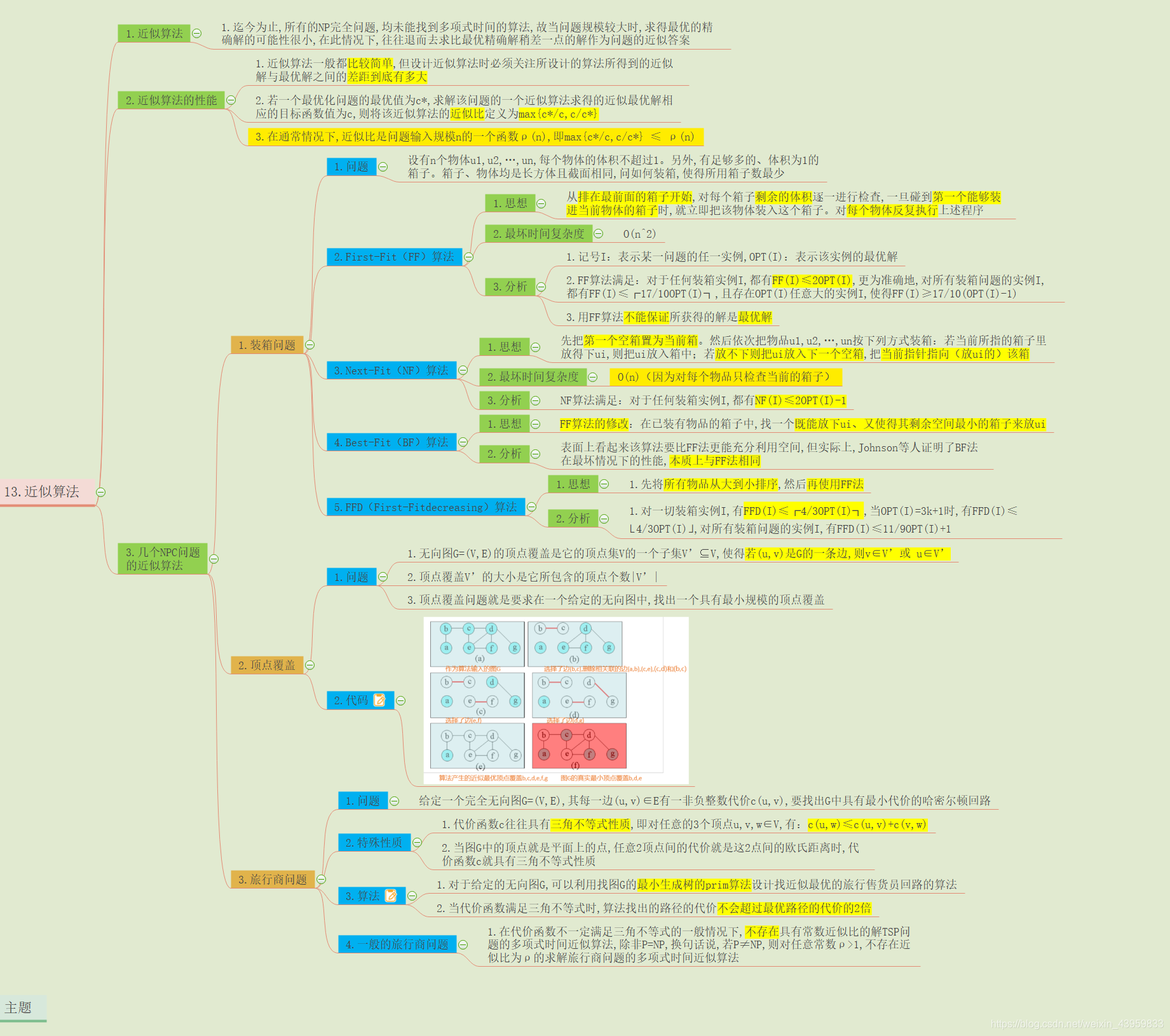
近似算法及其近似比

多机调度问题
货郎问题
最邻近法
最小生成树法
最小权匹配法
背包问题
一个简单的贪心算法
多项式时间近似方案
伪多项式时间算法与完全多项式时间近似方案
随机算法
随机算法思维导图
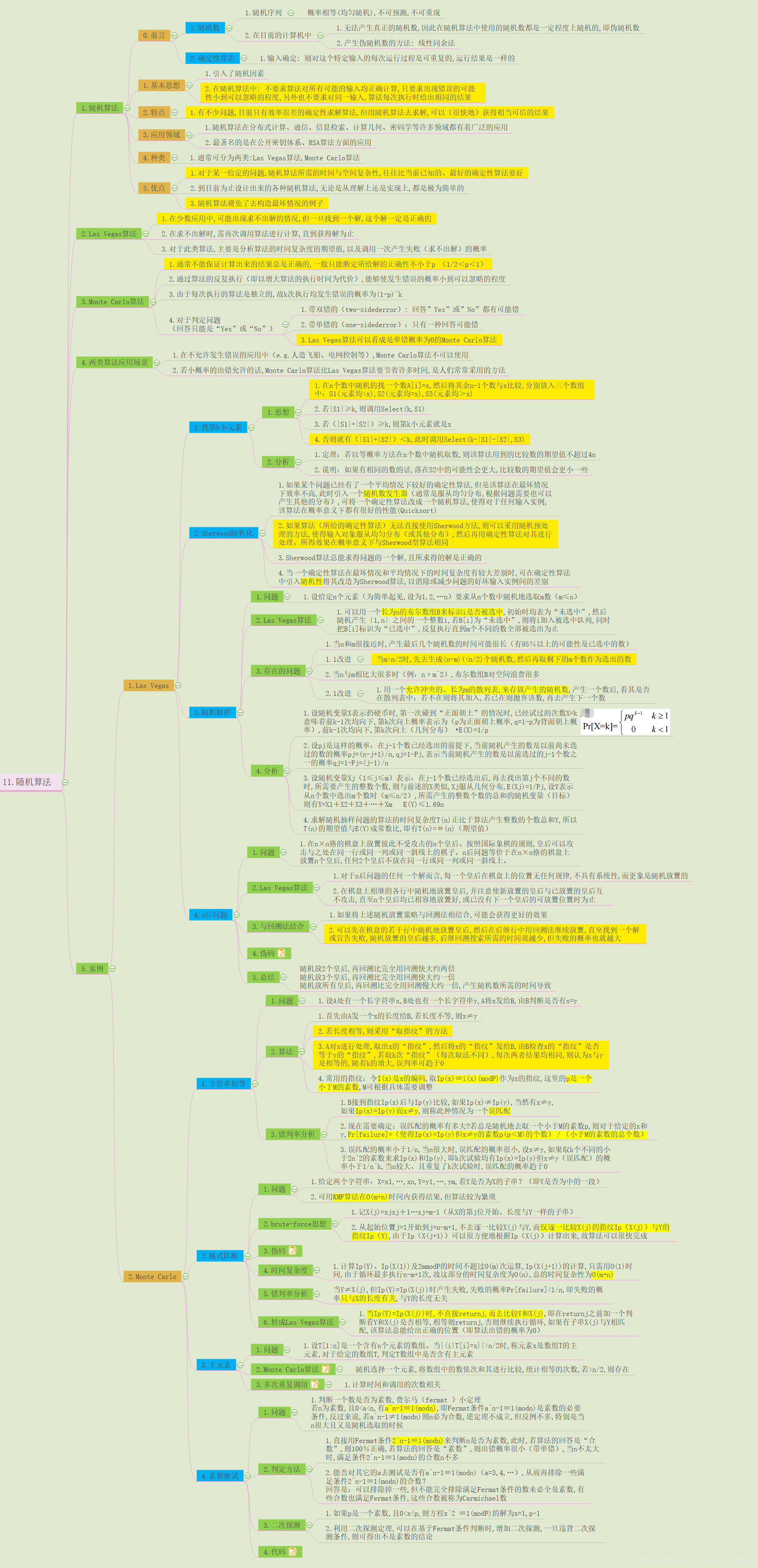
随机算法的分类及其局限性
本节介绍随机算法的分类,包括拉斯维加斯型和蒙特卡洛型这两大类,并且从计算复杂度理论的角度,介绍NP完全问题不太可能有多项式时间随机算法的结论。
Las Vegas 型随机算法
随机快速排序算法、随机选择算法都是典型的拉斯维加斯型随机算法,这种算法总是给出正确的结果,但有时运行时间长些,有时运行时间短些.对于拉斯维加斯型算法,通常需要分析算法的平均运行时间。例如,随机快速排序算法总是给出已经排序的数组,期望的运行时间则是2nlogn。拉斯维加斯型随机算法的运行时间本身是一个随机变量,把期望运行时间是输入规模的多项式且总是给出正确答案的随机算法称为有效的拉斯维加斯型算法.随机快速排序算法就是一个有效的拉斯维加斯型算法。
Monte-Carlo 型随机算法
蒙特卡洛型随机算法有时会给出错误的答案,后面两节将要介绍的素数检验、多项式恒等检验的随机算法和布尔可满足性问题的随机游动算法都是这类算法的例子。对于蒙特卡洛型算法,通常需要分析算法的出错概率,蒙特卡洛型算法不但运行时间是随机变量,而且计算的结果也是随机事件.把总是在多项式时间内运行且出错概率不超过1/3的随机算法称为有效的蒙特卡洛型算法。这里的出错概率1/3可以变得任意小,只要让算法执行足够多次,从所有单次结果中选择出现次数最多的结果作为总的结果即可。1/3这个值本身也不重要,只需要独立重复执行多次,就可以把错误概率降到1/3以下,甚至降低到输入规模的多项式倒数或者更低.。
蒙特卡洛型算法又可分为单侧错误和双侧错误两类,单侧错误又可分为弃真型和取伪型这两种.所谓弃真型错误,就是在求解一个判定问题时把本应接受的输人误判为拒绝。对于弃真型的单侧错误随机算法来说,当算法宣布接受时,结果一定是对的;而当算法宣布拒绝时,结果有可能是错的。所谓取伪型错误,就是把本应拒绝的输入误判为接受。对于取伪型的单侧错误随机算法来说,当算法宣布拒绝时,结果一定是对的;而当算法宣布接受时,结果有可能是错的。单侧错误的蒙特卡洛型算法在所有输入上,要么只犯弃真的错误,要么只犯取伪的错误,不同时出现这两种不同的错误。双侧错误的蒙特卡洛型算法在所有输入上,可以同时出现这两种不同的错误。后面将要介绍的随机游动算法就是弃真型的单侧错误的蒙特卡洛型随机算法。
MonteCarlo 算法
一些问题,不论采用确定性算法或概率算法都无法保证每次都能得到正确的解答。
蒙特卡罗算法则在一般情况下可以保证对问题的所有实例都以高概率给出正确解,但是通常无法判定一个具体解是否正确。


随机算法的局限性
在计算复杂性理论中,有效的拉斯维加斯型算法也称为ZPP类(zero-error probabilistic polynomial time)算法,即零错误概率多项式时间随机算法。有效的蒙特卡洛型算法也被为BPP类(bounded-error probabilistic polynomial time)算法,即错误概率有界的多项式时间随机算法,其中有效的弃真型单侧错误随机算法又称为RP类算法,有效的取伪型单侧错误随机算法则称为coRP类算法。把ZPP类算法可以求解的判定问题类记作ZPP类,类似地可以定义BPP、RP、coRP等判定问题类.有效的拉斯维加斯型算法是有效的蒙特卡洛型算法的特殊情况,可以证明上述复杂性类满足

随机算法及应用
随机数

数值随机化算法
计算Pi值、定积分的值、解非线性方程组
解非线性方程组可以用粒子群算法或模拟退火算法(这两种算法也属于数值随机化算法)
舍伍德算法

回忆学过的舍伍德算法:
(1)线性时间选择算法
(2)快速排序算法
当在数据基本有序情况下,partition
()算法的两个分组严重不平衡,导致这两个算法的时间复杂性都是O(n²)
改造的方法将partition()算法改为randomizedpartition()算法
当无法直接改造成舍伍德型算法时,可借助于随机预处理技术(洗牌算法)
void Shuffle(Type a[], int n)
{ //随机洗牌算法
staticRandomNumber rnd;
for (int i=0;i<n;i++) {
int j=rnd.Random(n-i)+i;
Swap(a[il, a[j]);
}
}

在动态变化中维持跳跃表中附加指针的平衡性:随机化策略
拉斯维加斯算法之结合回溯法解决 n-queen 问题
拉斯维加斯算法之整数因子分解
蒙特卡罗算法之寻找主元素
确定性算法:分治
蒙特卡罗算法之找素数
