随机算法
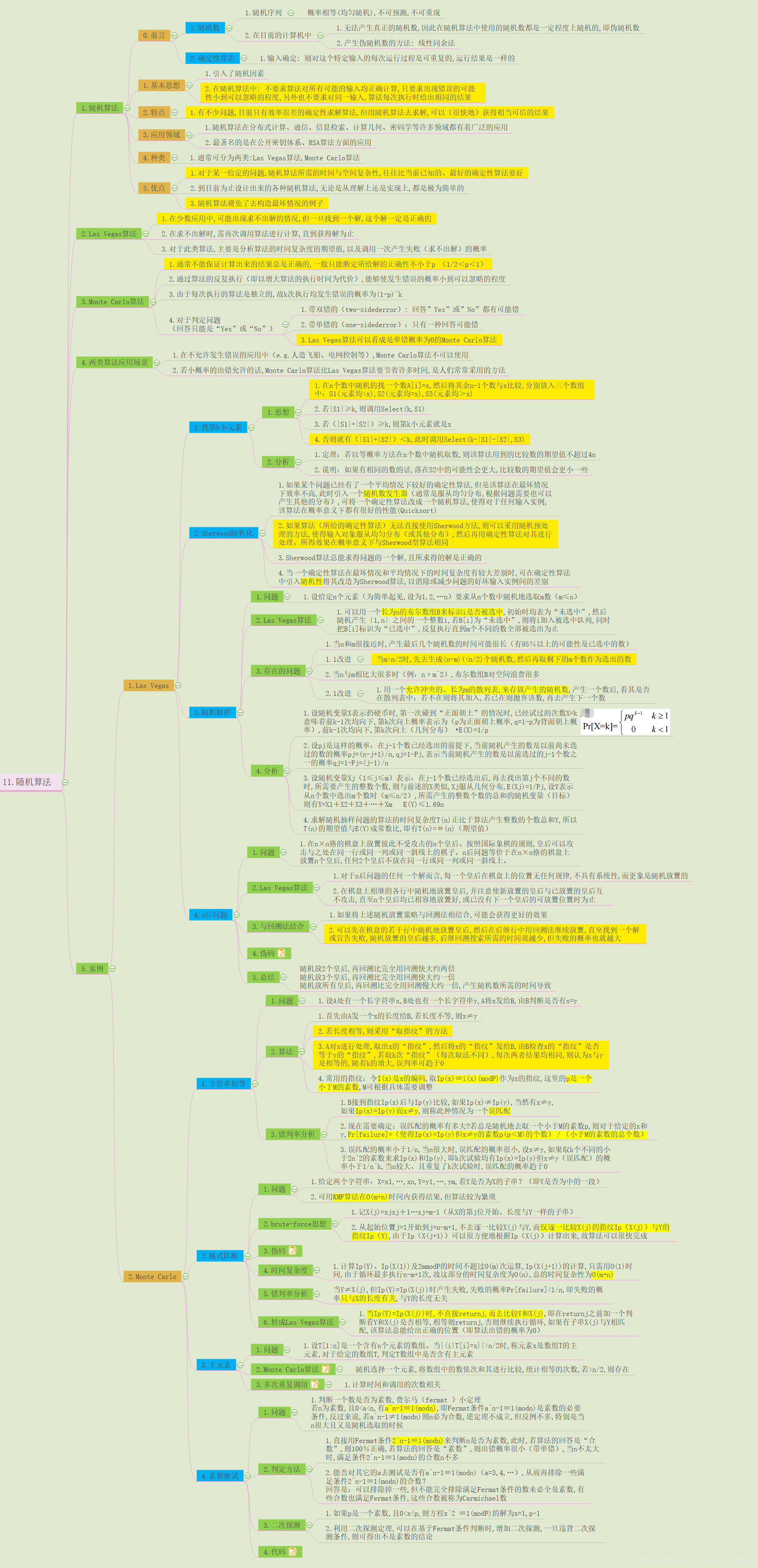
随机算法思维导图
随机算法的分类及其局限性
本节介绍随机算法的分类,包括拉斯维加斯型和蒙特卡洛型这两大类,并且从计算复杂度理论的角度,介绍NP完全问题不太可能有多项式时间随机算法的结论。
Las Vegas 型随机算法
随机快速排序算法、随机选择算法都是典型的拉斯维加斯型随机算法,这种算法总是给出正确的结果,但有时运行时间长些,有时运行时间短些.对于拉斯维加斯型算法,通常需要分析算法的平均运行时间。例如,随机快速排序算法总是给出已经排序的数组,期望的运行时间则是2nlogn。拉斯维加斯型随机算法的运行时间本身是一个随机变量,把期望运行时间是输入规模的多项式且总是给出正确答案的随机算法称为有效的拉斯维加斯型算法.随机快速排序算法就是一个有效的拉斯维加斯型算法。
Monte-Carlo 型随机算法
蒙特卡洛型随机算法有时会给出错误的答案,后面两节将要介绍的素数检验、多项式恒等检验的随机算法和布尔可满足性问题的随机游动算法都是这类算法的例子。对于蒙特卡洛型算法,通常需要分析算法的出错概率,蒙特卡洛型算法不但运行时间是随机变量,而且计算的结果也是随机事件.把总是在多项式时间内运行且出错概率不超过1/3的随机算法称为有效的蒙特卡洛型算法。这里的出错概率1/3可以变得任意小,只要让算法执行足够多次,从所有单次结果中选择出现次数最多的结果作为总的结果即可。1/3这个值本身也不重要,只需要独立重复执行多次,就可以把错误概率降到1/3以下,甚至降低到输入规模的多项式倒数或者更低.。
蒙特卡洛型算法又可分为单侧错误和双侧错误两类,单侧错误又可分为弃真型和取伪型这两种.所谓弃真型错误,就是在求解一个判定问题时把本应接受的输人误判为拒绝。对于弃真型的单侧错误随机算法来说,当算法宣布接受时,结果一定是对的;而当算法宣布拒绝时,结果有可能是错的。所谓取伪型错误,就是把本应拒绝的输入误判为接受。对于取伪型的单侧错误随机算法来说,当算法宣布拒绝时,结果一定是对的;而当算法宣布接受时,结果有可能是错的。单侧错误的蒙特卡洛型算法在所有输入上,要么只犯弃真的错误,要么只犯取伪的错误,不同时出现这两种不同的错误。双侧错误的蒙特卡洛型算法在所有输入上,可以同时出现这两种不同的错误。后面将要介绍的随机游动算法就是弃真型的单侧错误的蒙特卡洛型随机算法。
MonteCarlo 算法
一些问题,不论采用确定性算法或概率算法都无法保证每次都能得到正确的解答。
蒙特卡罗算法则在一般情况下可以保证对问题的所有实例都以高概率给出正确解,但是通常无法判定一个具体解是否正确。


随机算法的局限性
在计算复杂性理论中,有效的拉斯维加斯型算法也称为ZPP类(zero-error probabilistic polynomial time)算法,即零错误概率多项式时间随机算法。有效的蒙特卡洛型算法也被为BPP类(bounded-error probabilistic polynomial time)算法,即错误概率有界的多项式时间随机算法,其中有效的弃真型单侧错误随机算法又称为RP类算法,有效的取伪型单侧错误随机算法则称为coRP类算法。把ZPP类算法可以求解的判定问题类记作ZPP类,类似地可以定义BPP、RP、coRP等判定问题类.有效的拉斯维加斯型算法是有效的蒙特卡洛型算法的特殊情况,可以证明上述复杂性类满足

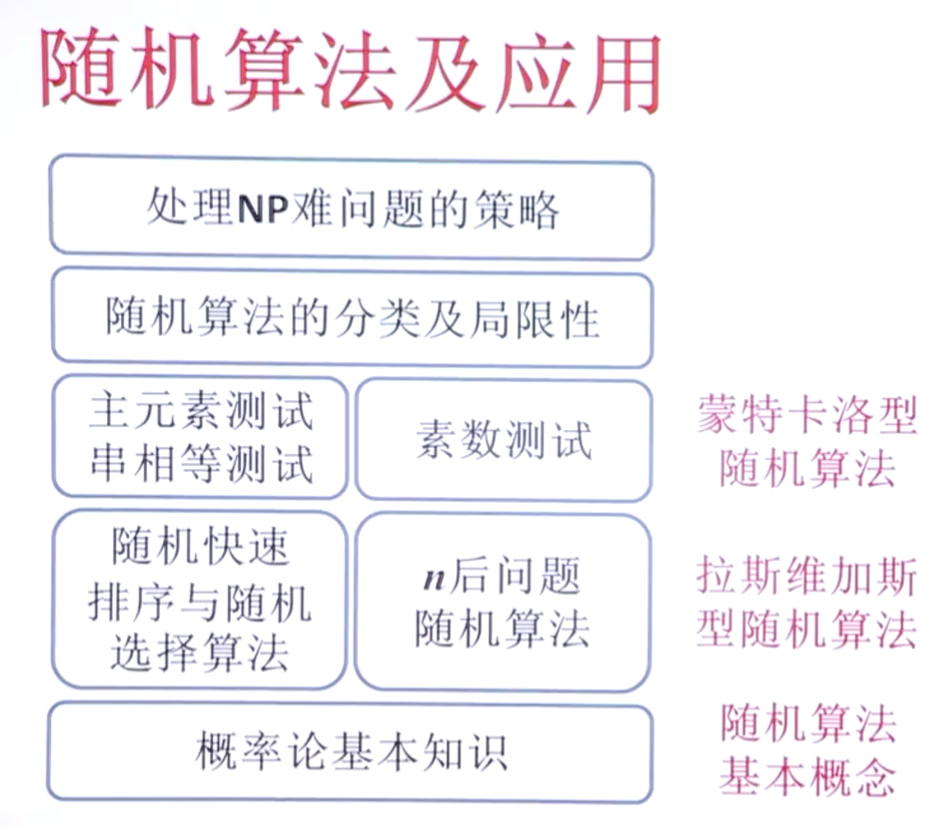
随机算法及应用
随机数

数值随机化算法
计算Pi值、定积分的值、解非线性方程组
解非线性方程组可以用粒子群算法或模拟退火算法(这两种算法也属于数值随机化算法)
舍伍德算法

回忆学过的舍伍德算法:
(1)线性时间选择算法
(2)快速排序算法
当在数据基本有序情况下,partition
()算法的两个分组严重不平衡,导致这两个算法的时间复杂性都是O(n²)
改造的方法将partition()算法改为randomizedpartition()算法
当无法直接改造成舍伍德型算法时,可借助于随机预处理技术(洗牌算法)
void Shuffle(Type a[], int n)
{ //随机洗牌算法
staticRandomNumber rnd;
for (int i=0;i<n;i++) {
int j=rnd.Random(n-i)+i;
Swap(a[il, a[j]);
}
}

在动态变化中维持跳跃表中附加指针的平衡性:随机化策略
拉斯维加斯算法之结合回溯法解决 n-queen 问题
拉斯维加斯算法之整数因子分解
蒙特卡罗算法之寻找主元素
确定性算法:分治
蒙特卡罗算法之找素数
