动态规划
概论
动态规划通常用于求解最优化问题。
基本要素:(1)最优子结构性质;(2)重叠子问题性质
动态规划五部曲:(1)明确 dp 数组的含义(2)递推公式(3)初始化(4)遍历顺序(5)打印 dp 数组
动态规划基本步骤:
- 找出最优解的性质,并自上而下刻画其最优解结构特征。
- 递归地定义最优值。
- 以自底向上的方式计算出最优值。
- 根据计算最优值时得到的信息,构造最优解。
以自底向上的方式:首先找到子问题的最优解,然后根据子问题的最优解找到原问题的最优解。
动态规划的设计
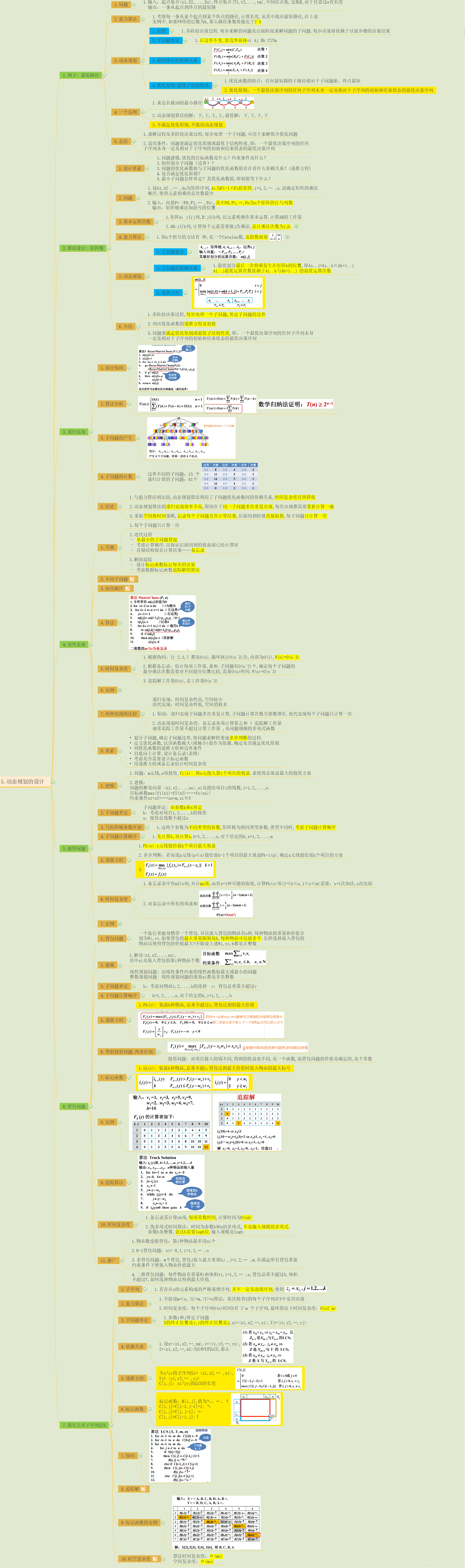
动态规划的应用

实例
流水线作业调度
矩阵链乘法问题
最长公共子序列
二维数组dp[i][j]表示nums1[0..i-1]下标(包括i-1)和nums2[0..j-1]下标(包括j-1)的最长公共子序列长度。
这样表示方便初始化。
最优二叉搜索树
图像压缩
序列对齐(Hirschberg算法)
带权区间调度
最大子段(数组)和
分段最小二乘法
RNA 二级结构
背包问题(knapsack)
备忘录算法(Memorization method)
递归实现,没有使用对角线技巧,需要更多的递归调用