分治策略
分治的设计思想
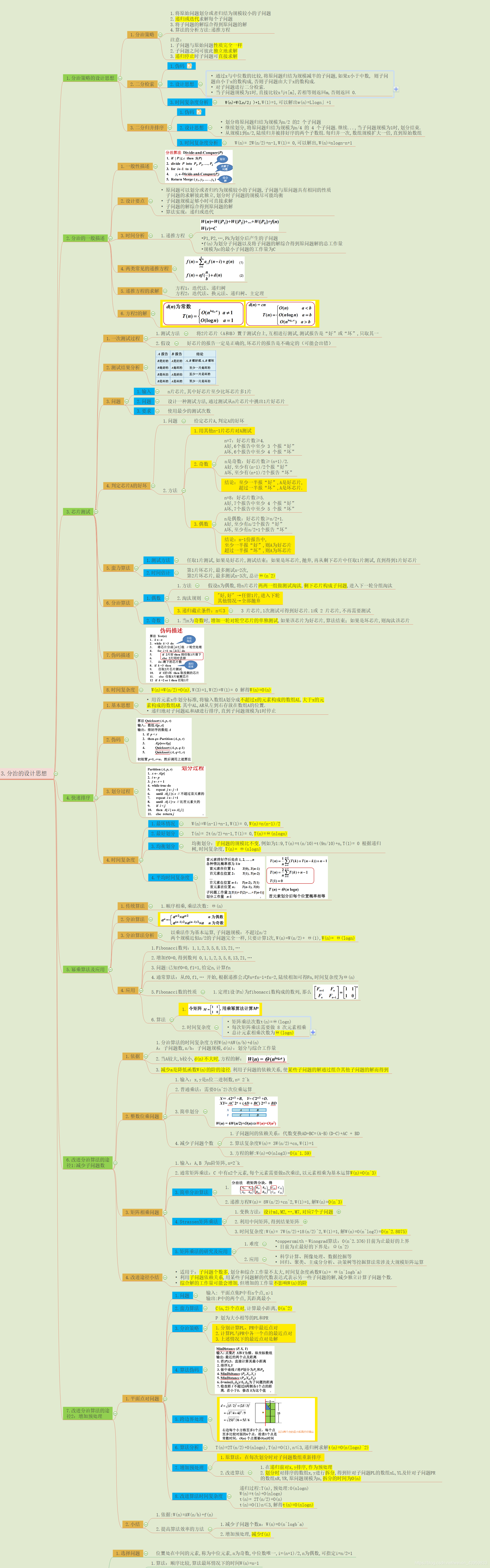
改进分治算法的途经:
- 通过代数变换减少子问题个数
- 利用预处理减少递归内部的计算量
典型的分治算法
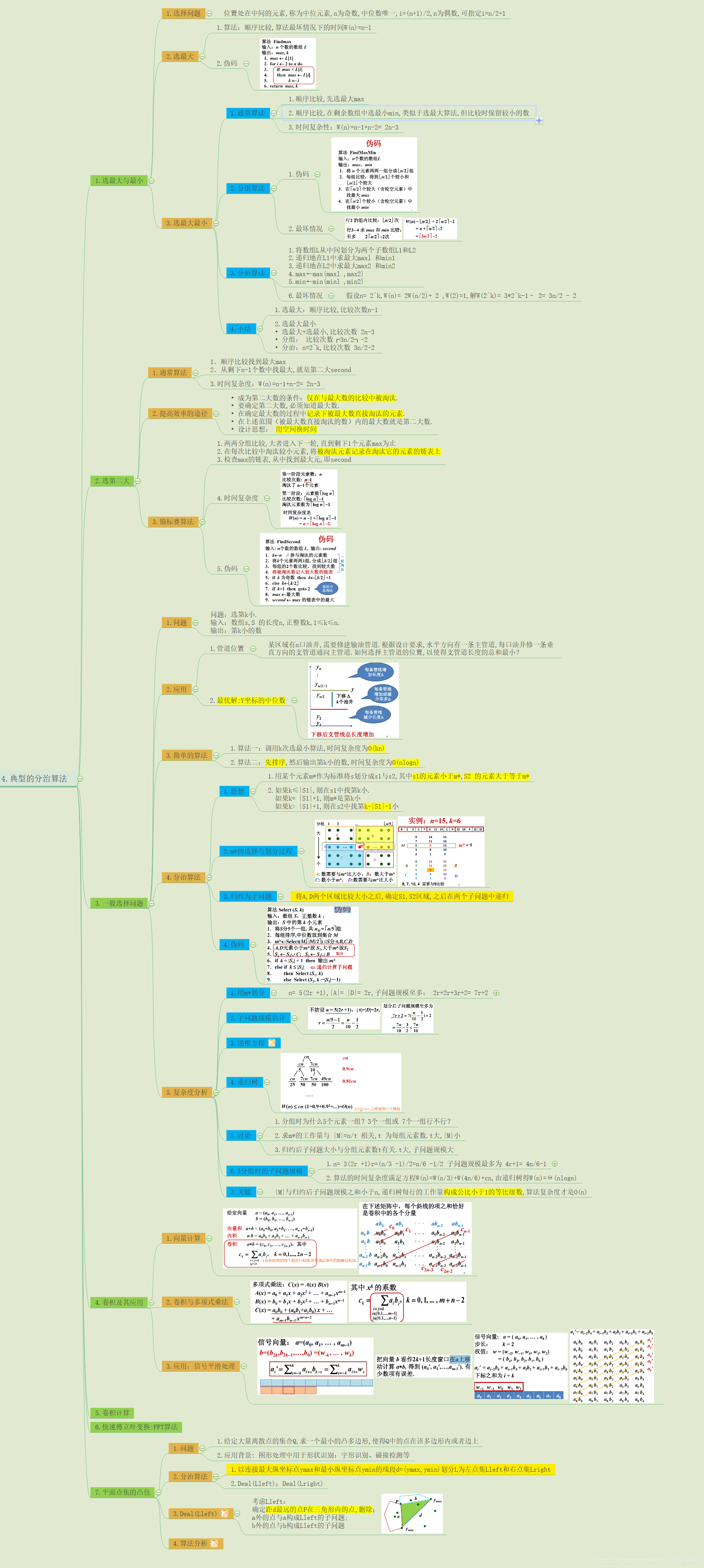
选择问题
选最大
选最小
选最大最小
选第二大
选第 k 小
求第 k 大的元素 最好:
高度之和小于等于 n - 1
证明:


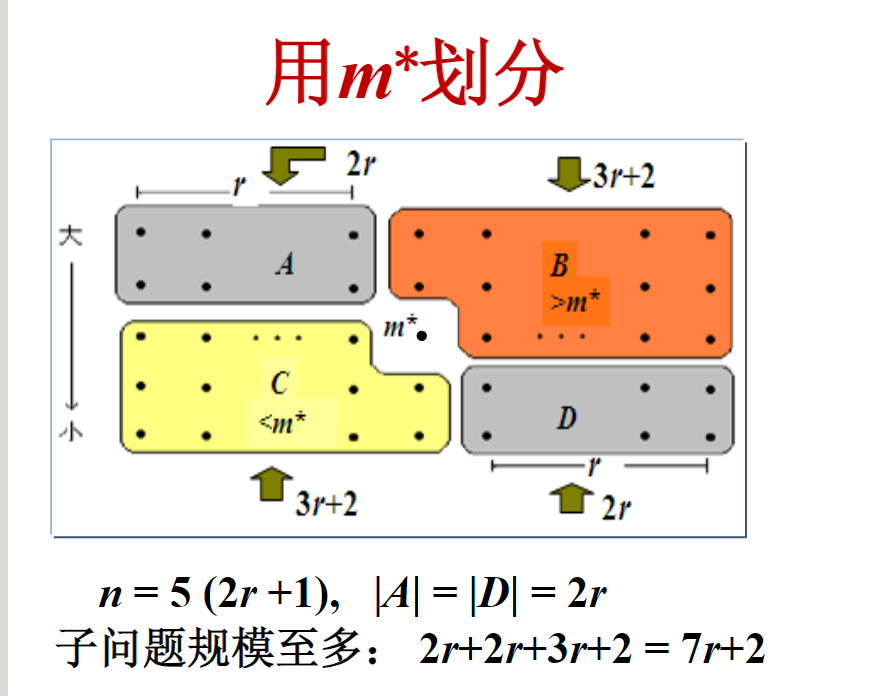

讨论分组时为什么5个元素一组,3个一组或7个一组行不行?
分析:递归调用
1.求m*的工作量与 相关,t 为每组元素数,t 大, 小
2.归约后子问题大小与分组元素数 t 有关, t 大,子问题规模大
关键:
与归约后子问题规模之和小于 n,递归树每行的工作量构成公比小于 1 的等比级数,算法复杂度才是
选第k小算法的时间分析
- 递推方程
- 分组时每组元素数的多少对时间复杂度的影响
3分组不行,5分组可以,7分组也行