子序列

300. Longest Increasing Subsequence
674. Longest Continuous Increasing Subsequence
718. Maximum Length of Repeated Subarray
1143. Longest Common Subsequence
1035. Uncrossed Lines
53. Maximum Subarray
- 思路
- C++解法

300. Longest Increasing Subsequence

Given an integer array nums, return the length of the longest strictly increasing subsequence.

Example 1:

Input: nums = [10,9,2,5,3,7,101,18]
Output: 4
Explanation: The longest increasing subsequence is [2,3,7,101], therefore the length is 4.

Example 2:

Input: nums = [0,1,0,3,2,3]
Output: 4

Example 3:

Input: nums = [7,7,7,7,7,7,7]
Output: 1

Constraints:

1 <= nums.length <= 2500
-10^4 <= nums[i] <= 10^4

Follow up: Can you come up with an algorithm that runs in O(n log(n)) time complexity?

思路

首先通过本题大家要明确什么是子序列，“子序列是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序”。

本题也是代码随想录中子序列问题的第一题，如果没接触过这种题目的话，本题还是很难的，甚至想暴力去搜索也不知道怎么搜。子序列问题是动态规划解决的经典问题，当前下标i的递增子序列长度，其实和i之前的下表j的子序列长度有关系，那又是什么样的关系呢。

接下来，我们依然用动规五部曲来详细分析一波：

dp[i]的定义

本题中，正确定义dp数组的含义十分重要。

dp[i]表示i之前包括i的以nums[i]结尾的最长递增子序列的长度

为什么一定表示 “以nums[i]结尾的最长递增子序” ，因为我们在做递增比较的时候，如果比较 nums[j] 和 nums[i] 的大小，那么两个递增子序列一定分别以nums[j]为结尾和 nums[i]为结尾，要不然这个比较就没有意义了，不是尾部元素的比较那么如何算递增呢。

状态转移方程

位置i的最长升序子序列等于j从0到i-1各个位置的最长升序子序列 + 1 的最大值。

所以：if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);

注意这里不是要dp[i] 与 dp[j] + 1进行比较，而是我们要取dp[j] + 1的最大值。

dp[i]的初始化

每一个i，对应的dp[i]（即最长递增子序列）起始大小至少都是1.

确定遍历顺序

dp[i] 是有0到i-1各个位置的最长递增子序列推导而来，那么遍历i一定是从前向后遍历。

j其实就是遍历0到i-1，那么是从前到后，还是从后到前遍历都无所谓，只要吧 0 到 i-1 的元素都遍历了就行了。所以默认习惯从前向后遍历。

遍历i的循环在外层，遍历j则在内层，代码如下：

for (int i = 1; i < nums.size(); i++) {  
    for (int j = 0; j < i; j++) {  
        if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);  
    }  
    if (dp[i] > result) result = dp[i]; // 取长的子序列  
}

举例推导dp数组

输入：[0,1,0,3,2]，dp数组的变化如下：

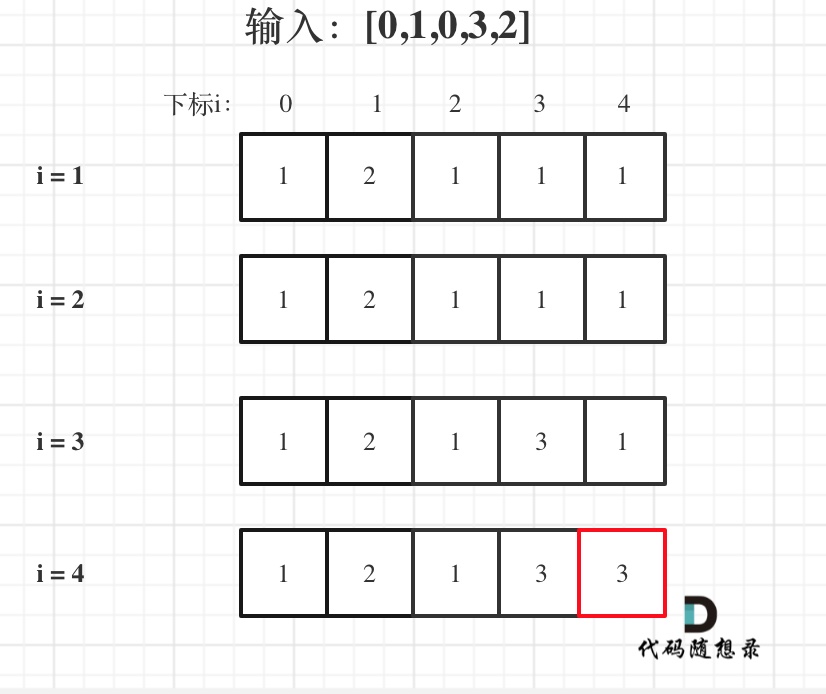
300.最长上升子序列

如果代码写出来，但一直AC不了，那么就把dp数组打印出来，看看对不对！

Java解法

class Solution {
    public int lengthOfLIS(int[] nums) {
        int[] dp = new int[nums.length];
        int res = 1;
        Arrays.fill(dp, 1);
        for (int i = 1; i < dp.length; i++) {
            for (int j = 0; j < i; j++) {
                if (nums[i] > nums[j]) {
                    dp[i] = Math.max(dp[i], dp[j] + 1);
                }
                res = Math.max(res, dp[i]);
            }
        }
        return res;
    }
}

674. Longest Continuous Increasing Subsequence

Given an unsorted array of integers nums, return the length of the longest continuous increasing subsequence (i.e. subarray). The subsequence must be strictly increasing.

A continuous increasing subsequence is defined by two indices l and r (l < r) such that it is [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] and for each l <= i < r, nums[i] < nums[i + 1].

Example 1:

Input: nums = [1,3,5,4,7]
Output: 3
Explanation: The longest continuous increasing subsequence is [1,3,5] with length 3. Even though [1,3,5,7] is an increasing subsequence, it is not continuous as elements 5 and 7 are separated by element 4.

Example 2:

Input: nums = [2,2,2,2,2]
Output: 1
Explanation: The longest continuous increasing subsequence is [2] with length 1. Note that it must be strictly increasing.

Constraints:

1 <= nums.length <= 10^4
-10^9 <= nums[i] <= 10^9

思路

本题相对于昨天的动态规划：300.最长递增子序列最大的区别在于“连续”。

本题要求的是最长连续递增序列

动规五部曲分析如下：

确定dp数组（dp table）以及下标的含义

dp[i]：以下标i为结尾的连续递增的子序列长度为dp[i]。

注意这里的定义，一定是以下标i为结尾，并不是说一定以下标0为起始位置。

确定递推公式

如果 nums[i] > nums[i - 1]，那么以 i 为结尾的连续递增的子序列长度一定等于以i - 1为结尾的连续递增的子序列长度 + 1 。

即：dp[i] = dp[i - 1] + 1;

注意这里就体现出和动态规划：300.最长递增子序列的区别！

因为本题要求连续递增子序列，所以就只要比较nums[i]与nums[i - 1]，而不用去比较nums[j]与nums[i] （j是在0到i之间遍历）。

既然不用j了，那么也不用两层for循环，本题一层for循环就行，比较nums[i] 和 nums[i - 1]。

这里大家要好好体会一下！

dp数组如何初始化

以下标i为结尾的连续递增的子序列长度最少也应该是1，即就是nums[i]这一个元素。

所以dp[i]应该初始1;

确定遍历顺序

从递推公式上可以看出， dp[i + 1]依赖dp[i]，所以一定是从前向后遍历。

本文在确定递推公式的时候也说明了为什么本题只需要一层for循环，代码如下：

for (int i = 1; i < nums.size(); i++) {  
    if (nums[i] > nums[i - 1]) { // 连续记录  
        dp[i] = dp[i - 1] + 1;  
    }  
}

举例推导dp数组

已输入nums = [1,3,5,4,7]为例，dp数组状态如下：

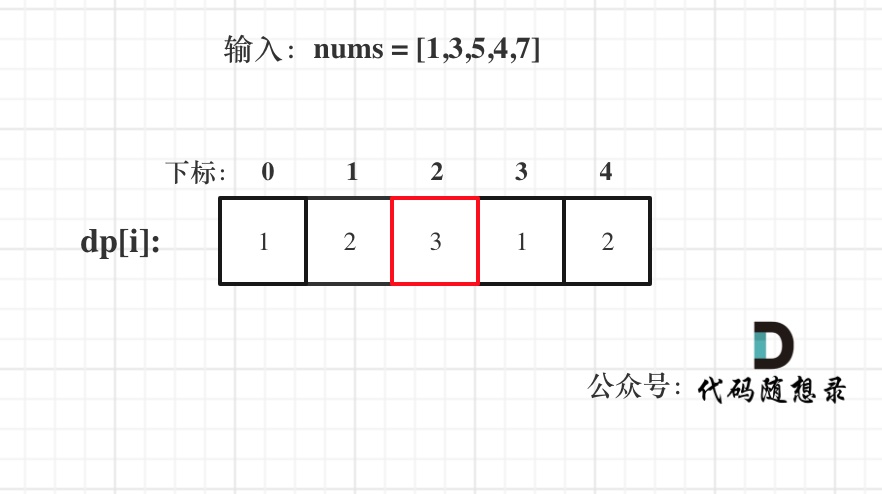
674.最长连续递增序列

注意这里要取dp[i]里的最大值，所以dp[2]才是结果！

本题也是动规里子序列问题的经典题目，但也可以用贪心来做，大家也会发现贪心好像更简单一点，而且空间复杂度仅是O(1)。

在动规分析中，关键是要理解和动态规划：300.最长递增子序列的区别。

要联动起来，才能理解递增子序列怎么求，递增连续子序列又要怎么求。

概括来说：不连续递增子序列的跟前0-i 个状态有关，连续递增的子序列只跟前一个状态有关

C++解法

以上分析完毕，C++代码如下：

class Solution {  
public:  
    int findLengthOfLCIS(vector<int>& nums) {  
        if (nums.size() == 0) return 0;  
        int result = 1;  
        vector<int> dp(nums.size() ,1);  
        for (int i = 1; i < nums.size(); i++) {  
            if (nums[i] > nums[i - 1]) { // 连续记录  
                dp[i] = dp[i - 1] + 1;  
            }  
            if (dp[i] > result) result = dp[i];  
        }  
        return result;  
    }  
};

时间复杂度：O(n)
空间复杂度：O(n)

这道题目也可以用贪心来做，也就是遇到nums[i] > nums[i - 1]的情况，count就++，否则count为1，记录count的最大值就可以了。

代码如下：

class Solution {  
public:  
    int findLengthOfLCIS(vector<int>& nums) {  
        if (nums.size() == 0) return 0;  
        int result = 1; // 连续子序列最少也是1  
        int count = 1;  
        for (int i = 1; i < nums.size(); i++) {  
            if (nums[i] > nums[i - 1]) { // 连续记录  
                count++;  
            } else { // 不连续，count从头开始  
                count = 1;  
            }  
            if (count > result) result = count;  
        }  
        return result;  
    }  
};

时间复杂度：O(n)
空间复杂度：O(1)

Java解法

动态规划：

 /**  
     * 1.dp[i] 代表当前下标最大连续值  
     * 2.递推公式 if（nums[i+1]>nums[i]） dp[i+1] = dp[i]+1  
     * 3.初始化 都为1  
     * 4.遍历方向，从其那往后  
     * 5.结果推导 。。。。  
     * @param nums  
     * @return  
     */  
    public static int findLengthOfLCIS(int[] nums) {  
        int[] dp = new int[nums.length];  
        for (int i = 0; i < dp.length; i++) {  
            dp[i] = 1;  
        }  
        int res = 1;  
    //可以注意到，這邊的 i 是從 0 開始，所以會出現和卡哥的C++ code有差異的地方，在一些地方會看到有 i + 1 的偏移。  
        for (int i = 0; i < nums.length - 1; i++) {  
            if (nums[i + 1] > nums[i]) {  
                dp[i + 1] = dp[i] + 1;  
            }  
            res = res > dp[i + 1] ? res : dp[i + 1];  
        }  
        return res;  
    }

动态规划状态压缩

class Solution {  
    public int findLengthOfLCIS(int[] nums) {  
        // 记录以 前一个元素结尾的最长连续递增序列的长度 和 以当前 结尾的......  
        int beforeOneMaxLen = 1, currentMaxLen = 0;  
        // res 赋最小值返回的最小值1  
        int res = 1;  
        for (int i = 1; i < nums.length; i ++) {  
            currentMaxLen = nums[i] > nums[i - 1] ? beforeOneMaxLen + 1 : 1;  
            beforeOneMaxLen = currentMaxLen;  
            res = Math.max(res, currentMaxLen);  
        }  
        return res;  
    }  
}

贪心法：

public static int findLengthOfLCIS(int[] nums) {  
    if (nums.length == 0) return 0;  
    int res = 1; // 连续子序列最少也是1  
    int count = 1;  
    for (int i = 0; i < nums.length - 1; i++) {  
        if (nums[i + 1] > nums[i]) { // 连续记录  
            count++;  
        } else { // 不连续，count从头开始  
            count = 1;  
        }  
        if (count > res) res = count;  
    }  
    return res;  
}

718. Maximum Length of Repeated Subarray

Given two integer arrays nums1 and nums2, return the maximum length of a subarray that appears in both arrays.

Example 1:

Input: nums1 = [1,2,3,2,1], nums2 = [3,2,1,4,7]
Output: 3
Explanation: The repeated subarray with maximum length is [3,2,1].

Example 2:

Input: nums1 = [0,0,0,0,0], nums2 = [0,0,0,0,0]
Output: 5
Explanation: The repeated subarray with maximum length is [0,0,0,0,0].

Constraints:

1 <= nums1.length, nums2.length <= 1000
0 <= nums1[i], nums2[i] <= 100

思路

注意题目中说的子数组，其实就是连续子序列。

要求两个数组中最长重复子数组，如果是暴力的解法只需要先两层for循环确定两个数组起始位置，然后再来一个循环可以是for或者while，来从两个起始位置开始比较，取得重复子数组的长度。

本题其实是动规解决的经典题目，我们只要想到用二维数组可以记录两个字符串的所有比较情况，这样就比较好推递推公式了。动规五部曲分析如下：

确定dp数组（dp table）以及下标的含义

dp[i][j] ：以下标i - 1为结尾的A，和以下标j - 1为结尾的B，最长重复子数组长度为dp[i][j]。（特别注意： “以下标i - 1为结尾的A” 标明一定是以A[i-1]为结尾的字符串）

此时细心的同学应该发现，那dp[0][j]是什么含义呢？总不能是以下标-1为结尾的A数组吧。

其实dp[i][j]的定义也就决定着，我们在遍历dp[i][j]的时候i 和 j都要从1开始。

那有同学问了，我就定义dp[i][j]为以下标i为结尾的A，和以下标j 为结尾的B，最长重复子数组长度。不行么？

行倒是行！但实现起来就麻烦一点，需要单独处理初始化部分，在本题解下面的拓展内容里，我给出了第二种 dp数组的定义方式所对应的代码和讲解，大家比较一下就了解了。

确定递推公式

根据dp[i][j]的定义，dp[i][j]的状态只能由dp[i - 1][j]推导出来。

即当A[i - 1] 和B[j - 1]相等的时候，dp[i][j] = dp[i - 1][j] + 1;

根据递推公式可以看出，遍历i 和 j 要从1开始！

dp数组如何初始化

根据dp[i][j]的定义，dp[i][0] 和dp[0][j]其实都是没有意义的！

但dp[i][0] 和dp[0][j]要初始值，因为为了方便递归公式dp[i][j] = dp[i - 1][j] + 1;

所以dp[i][0] 和dp[0][j]初始化为0。

举个例子A[0]如果和B[0]相同的话，dp[1][1] = dp[0][j] + 1，只有dp[0][j]初始为0，正好符合递推公式逐步累加起来。

确定遍历顺序

外层for循环遍历A，内层for循环遍历B。

那又有同学问了，外层for循环遍历B，内层for循环遍历A。不行么？

也行，一样的，我这里就用外层for循环遍历A，内层for循环遍历B了。

同时题目要求长度最长的子数组的长度。所以在遍历的时候顺便把dp[i][j]的最大值记录下来。

代码如下：

for (int i = 1; i <= nums1.size(); i++) {  
    for (int j = 1; j <= nums2.size(); j++) {  
        if (nums1[i - 1] == nums2[j - 1]) {  
            dp[i][j] = dp[i - 1][j - 1] + 1;  
        }  
        if (dp[i][j] > result) result = dp[i][j];  
    }  
}

举例推导dp数组

拿示例1中，A: [1,2,3,2,1]，B: [3,2,1,4,7]为例，画一个dp数组的状态变化，如下：

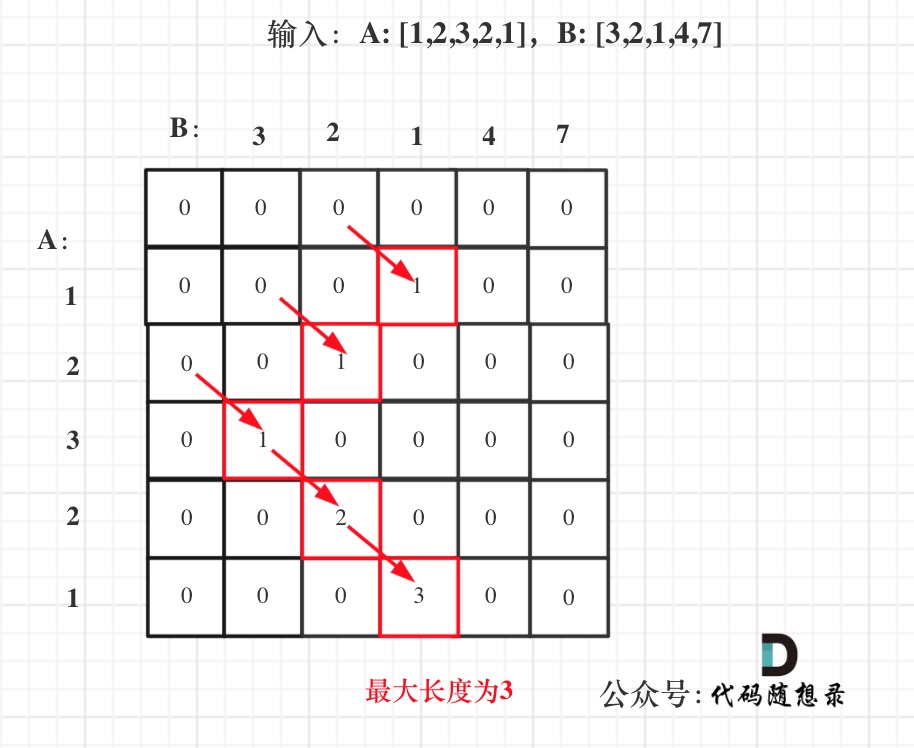
718.最长重复子数组

C++解法

以上五部曲分析完毕，C++代码如下：

// 版本一  
class Solution {  
public:  
    int findLength(vector<int>& nums1, vector<int>& nums2) {  
        vector<vector<int>> dp (nums1.size() + 1, vector<int>(nums2.size() + 1, 0));  
        int result = 0;  
        for (int i = 1; i <= nums1.size(); i++) {  
            for (int j = 1; j <= nums2.size(); j++) {  
                if (nums1[i - 1] == nums2[j - 1]) {  
                    dp[i][j] = dp[i - 1][j - 1] + 1;  
                }  
                if (dp[i][j] > result) result = dp[i][j];  
            }  
        }  
        return result;  
    }  
};

时间复杂度：O(n × m)，n 为A长度，m为B长度
空间复杂度：O(n × m)

滚动数组方法在如下图中：

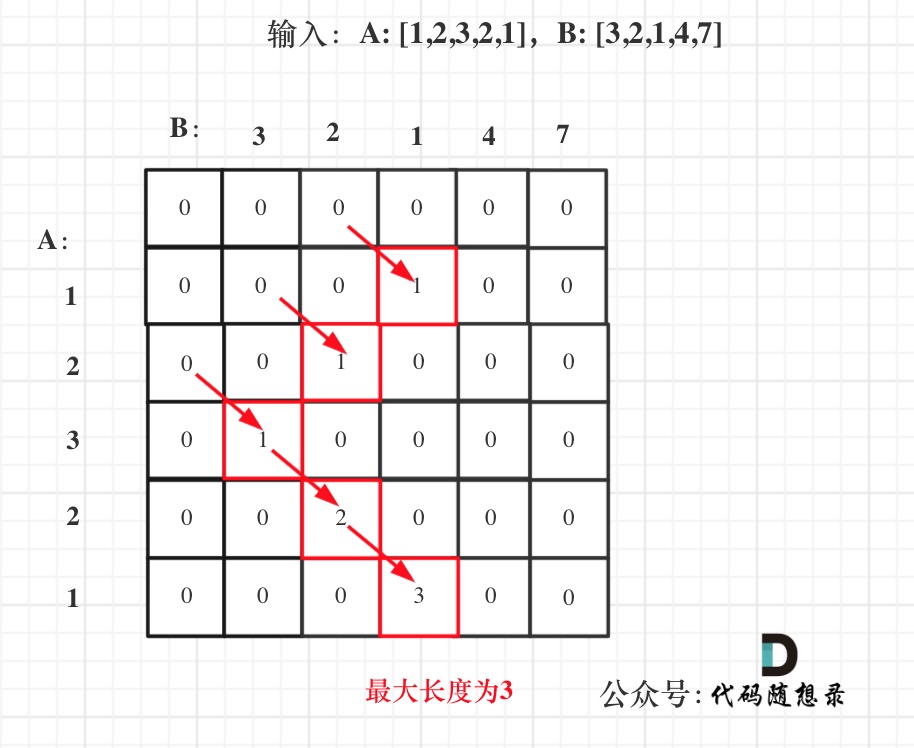
718.最长重复子数组

我们可以看出dp[i][j]都是由dp[i - 1][j]推出。那么压缩为一维数组，也就是dp[j]都是由dp[j - 1]推出。

也就是相当于可以把上一层dp[i - 1][j]拷贝到下一层dp[i][j]来继续用。

此时遍历B数组的时候，就要从后向前遍历，这样避免重复覆盖。

// 版本二  
class Solution {  
public:  
    int findLength(vector<int>& A, vector<int>& B) {  
        vector<int> dp(vector<int>(B.size() + 1, 0));  
        int result = 0;  
        for (int i = 1; i <= A.size(); i++) {  
            for (int j = B.size(); j > 0; j--) {  
                if (A[i - 1] == B[j - 1]) {  
                    dp[j] = dp[j - 1] + 1;  
                } else dp[j] = 0; // 注意这里不相等的时候要有赋0的操作  
                if (dp[j] > result) result = dp[j];  
            }  
        }  
        return result;  
    }  
};

时间复杂度： $O (n \times m)$ ，n 为A长度，m为B长度
空间复杂度： $O (m)$

Java解法

// 版本一  
class Solution {  
    public int findLength(int[] nums1, int[] nums2) {  
        int result = 0;  
        int[][] dp = new int[nums1.length + 1][nums2.length + 1];  
          
        for (int i = 1; i < nums1.length + 1; i++) {  
            for (int j = 1; j < nums2.length + 1; j++) {  
                if (nums1[i - 1] == nums2[j - 1]) {  
                    dp[i][j] = dp[i - 1][j - 1] + 1;  
                    result = Math.max(result, dp[i][j]);  
                }  
            }  
        }  
          
        return result;  
    }  
}

// 版本二: 滚动数组  
class Solution {  
    public int findLength(int[] nums1, int[] nums2) {  
        int[] dp = new int[nums2.length + 1];  
        int result = 0;  
  
        for (int i = 1; i <= nums1.length; i++) {  
            for (int j = nums2.length; j > 0; j--) {  
                if (nums1[i - 1] == nums2[j - 1]) {  
                    dp[j] = dp[j - 1] + 1;  
                } else {  
                    dp[j] = 0;  
                }  
                result = Math.max(result, dp[j]);  
            }  
        }  
        return result;  
    }  
}

1143. Longest Common Subsequence

Given two strings text1 and text2, return the length of their longest common subsequence. If there is no common subsequence, return 0.

A subsequence of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.

For example, "ace" is a subsequence of "abcde".

A common subsequence of two strings is a subsequence that is common to both strings.

Example 1:

Input: text1 = "abcde", text2 = "ace"
Output: 3
Explanation: The longest common subsequence is "ace" and its length is 3.

Example 2:

Input: text1 = "abc", text2 = "abc"
Output: 3
Explanation: The longest common subsequence is "abc" and its length is 3.

Example 3:

Input: text1 = "abc", text2 = "def"
Output: 0
Explanation: There is no such common subsequence, so the result is 0.

Constraints:

1 <= text1.length, text2.length <= 1000
text1 and text2 consist of only lowercase English characters.

思路

本题和动态规划：718. 最长重复子数组区别在于这里不要求是连续的了，但要有相对顺序，即："ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。

继续动规五部曲分析如下：

确定dp数组（dp table）以及下标的含义

dp[i][j]：长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列为dp[i][j]

有同学会问：为什么要定义长度为[0, i - 1]的字符串text1，定义为长度为[0, i]的字符串text1不香么？

这样定义是为了后面代码实现方便，如果非要定义为长度为[0, i]的字符串text1也可以，我在动态规划：718. 最长重复子数组中的「拓展」里详细讲解了区别所在，其实就是简化了dp数组第一行和第一列的初始化逻辑。

确定递推公式

主要就是两大情况： text1[i - 1] 与 text2[j - 1]相同，text1[i - 1] 与 text2[j - 1]不相同

如果text1[i - 1] 与 text2[j - 1]相同，那么找到了一个公共元素，所以dp[i][j] = dp[i - 1][j] + 1;

如果text1[i - 1] 与 text2[j - 1]不相同，那就看看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列和 text1[0, i - 1]与text2[0, j - 2]的最长公共子序列，取最大的。

即：dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);

代码如下：

if (text1[i - 1] == text2[j - 1]) {  
    dp[i][j] = dp[i - 1][j - 1] + 1;  
} else {  
    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);  
}

dp数组如何初始化

先看看dp[i][j]应该是多少呢？

test1[0, i-1]和空串的最长公共子序列自然是0，所以dp[i][0] = 0;

同理dp[0][j]也是0。

其他下标都是随着递推公式逐步覆盖，初始为多少都可以，那么就统一初始为0。

代码：

vector<vector<int>> dp(text1.size() + 1, vector<int>(text2.size() + 1, 0));

确定遍历顺序

从递推公式，可以看出，有三个方向可以推出dp[i][j]，如图：

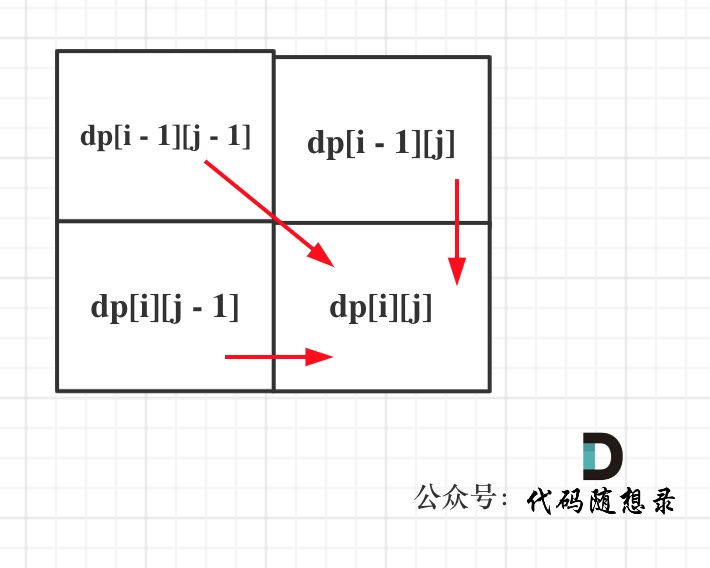
1143.最长公共子序列

那么为了在递推的过程中，这三个方向都是经过计算的数值，所以要从前向后，从上到下来遍历这个矩阵。

举例推导dp数组

以输入：text1 = "abcde", text2 = "ace" 为例，dp状态如图：

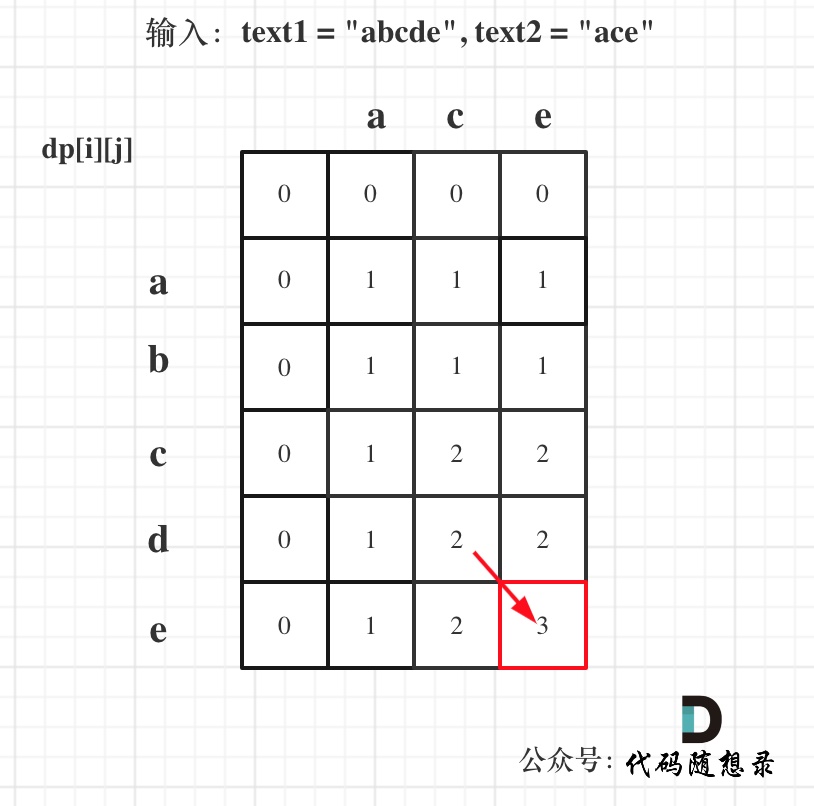
1143.最长公共子序列1

最后红框dptext1.size()为最终结果。

C++解法

以上分析完毕，C++代码如下：

class Solution {  
public:  
    int longestCommonSubsequence(string text1, string text2) {  
        vector<vector<int>> dp(text1.size() + 1, vector<int>(text2.size() + 1, 0));  
        for (int i = 1; i <= text1.size(); i++) {  
            for (int j = 1; j <= text2.size(); j++) {  
                if (text1[i - 1] == text2[j - 1]) {  
                    dp[i][j] = dp[i - 1][j - 1] + 1;  
                } else {  
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);  
                }  
            }  
        }  
        return dp[text1.size()][text2.size()];  
    }  
};

时间复杂度: O(n * m)，其中 n 和 m 分别为 text1 和 text2 的长度
空间复杂度: O(n * m)

Java解法

/*  
    二维dp数组  
*/  
class Solution {  
    public int longestCommonSubsequence(String text1, String text2) {  
        // char[] char1 = text1.toCharArray();  
        // char[] char2 = text2.toCharArray();  
    // 可以在一開始的時候就先把text1, text2 轉成char[]，之後就不需要有這麼多爲了處理字串的調整  
    // 就可以和卡哥的code更一致  
      
        int[][] dp = new int[text1.length() + 1][text2.length() + 1]; // 先对dp数组做初始化操作  
        for (int i = 1 ; i <= text1.length() ; i++) {  
            char char1 = text1.charAt(i - 1);  
            for (int j = 1; j <= text2.length(); j++) {  
                char char2 = text2.charAt(j - 1);  
                if (char1 == char2) { // 开始列出状态转移方程  
                    dp[i][j] = dp[i - 1][j - 1] + 1;  
                } else {  
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);  
                }  
            }  
        }  
        return dp[text1.length()][text2.length()];  
    }  
}  
  
  
  
/**  
    一维dp数组  
*/  
class Solution {  
    public int longestCommonSubsequence(String text1, String text2) {  
        int n1 = text1.length();  
        int n2 = text2.length();  
  
        // 多从二维dp数组过程分析    
        // 关键在于  如果记录  dp[i - 1][j - 1]  
        // 因为 dp[i - 1][j - 1]  <!=>  dp[j - 1]  <=>  dp[i][j - 1]  
        int [] dp = new int[n2 + 1];  
  
        for(int i = 1; i <= n1; i++){  
  
            // 这里pre相当于 dp[i - 1][j - 1]  
            int pre = dp[0];  
            for(int j = 1; j <= n2; j++){  
  
                //用于给pre赋值  
                int cur = dp[j];  
                if(text1.charAt(i - 1) == text2.charAt(j - 1)){  
                    //这里pre相当于dp[i - 1][j - 1]   千万不能用dp[j - 1] !!  
                    dp[j] = pre + 1;  
                } else{  
                    // dp[j]     相当于   dp[i - 1][j]  
                    // dp[j - 1] 相当于   dp[i][j - 1]  
                    dp[j] = Math.max(dp[j], dp[j - 1]);  
                }  
  
                //更新dp[i - 1][j - 1], 为下次使用做准备  
                pre = cur;  
            }  
        }  
  
        return dp[n2];  
    }  
}

1035. Uncrossed Lines

You are given two integer arrays nums1 and nums2. We write the integers of nums1 and nums2 (in the order they are given) on two separate horizontal lines.

We may draw connecting lines: a straight line connecting two numbers nums1[i] and nums2[j] such that:

nums1[i] == nums2[j], and
the line we draw does not intersect any other connecting (non-horizontal) line.

Note that a connecting line cannot intersect even at the endpoints (i.e., each number can only belong to one connecting line).

Return the maximum number of connecting lines we can draw in this way.

Example 1:

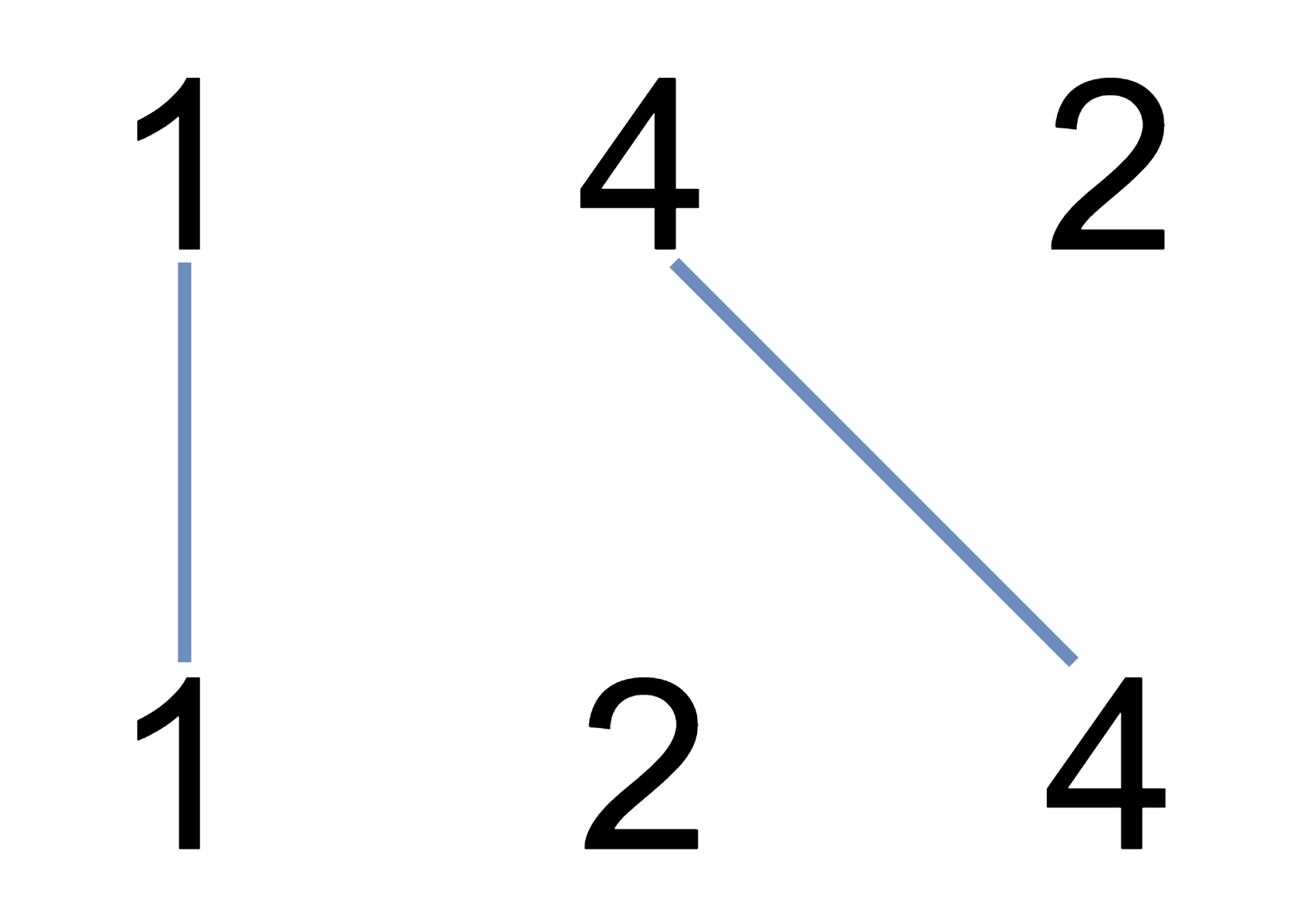
Input: nums1 = [1,4,2], nums2 = [1,2,4]
Output: 2
Explanation: We can draw 2 uncrossed lines as in the diagram. We cannot draw 3 uncrossed lines, because the line from nums1[1] = 4 to nums2[2] = 4 will intersect the line from nums1[2]=2 to nums2[1]=2.

Example 2:

Input: nums1 = [2,5,1,2,5], nums2 = [10,5,2,1,5,2]
Output: 3

Example 3:

Input: nums1 = [1,3,7,1,7,5], nums2 = [1,9,2,5,1]
Output: 2

Constraints:

1 <= nums1.length, nums2.length <= 500
1 <= nums1[i], nums2[j] <= 2000

思路

绘制一些连接两个数字 A[i] 和 B[j] 的直线，只要 A[i] == B[j]，且直线不能相交！

直线不能相交，这就是说明在字符串A中找到一个与字符串B相同的子序列，且这个子序列不能改变相对顺序，只要相对顺序不改变，链接相同数字的直线就不会相交。

拿示例一A = [1,4,2], B = [1,2,4]为例，相交情况如图：

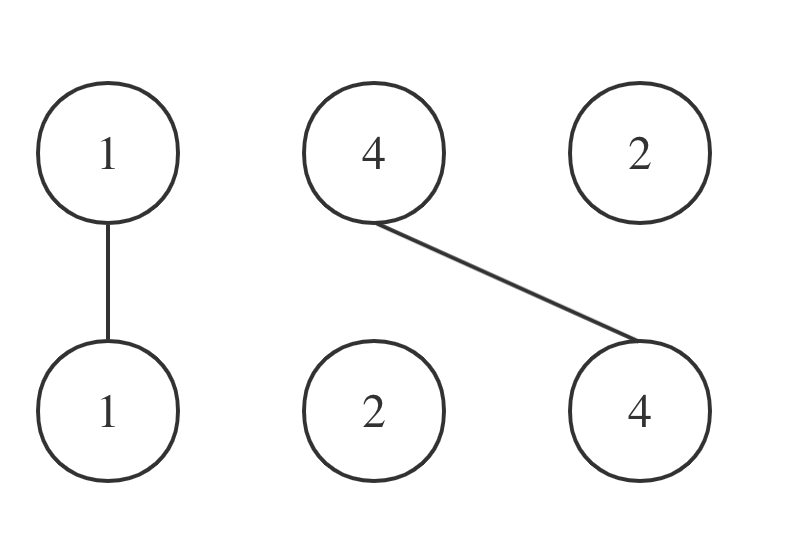
其实也就是说A和B的最长公共子序列是[1,4]，长度为2。这个公共子序列指的是相对顺序不变（即数字4在字符串A中数字1的后面，那么数字4也应该在字符串B数字1的后面）

这么分析完之后，大家可以发现：本题说是求绘制的最大连线数，其实就是求两个字符串的最长公共子序列的长度！

那么本题就和我们刚刚讲过的这道题目动态规划：1143.最长公共子序列就是一样一样的了。

一样到什么程度呢？把字符串名字改一下，其他代码都不用改，直接copy过来就行了。

其实本题就是求最长公共子序列的长度，介于我们刚刚讲过动态规划：1143.最长公共子序列，所以本题我就不再做动规五部曲分析了。

如果大家有点遗忘了最长公共子序列，就再看一下这篇：动态规划：1143.最长公共子序列

C++解法

本题代码如下：

class Solution {  
public:  
    int maxUncrossedLines(vector<int>& A, vector<int>& B) {  
        vector<vector<int>> dp(A.size() + 1, vector<int>(B.size() + 1, 0));  
        for (int i = 1; i <= A.size(); i++) {  
            for (int j = 1; j <= B.size(); j++) {  
                if (A[i - 1] == B[j - 1]) {  
                    dp[i][j] = dp[i - 1][j - 1] + 1;  
                } else {  
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);  
                }  
            }  
        }  
        return dp[A.size()][B.size()];  
    }  
};

时间复杂度: O(n * m)
空间复杂度: O(n * m)

Java解法

  class Solution {
    public int maxUncrossedLines(int[] nums1, int[] nums2) {
        int len1 = nums1.length;
        int len2 = nums2.length;
        int[][] dp = new int[len1 + 1][len2 + 1];

        for (int i = 1; i <= len1; i++) {
            for (int j = 1; j <= len2; j++) {
                if (nums1[i - 1] == nums2[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }

        return dp[len1][len2];
    }
}

53. Maximum Subarray

Given an integer array nums, find the subarray with the largest sum, and return its sum.

Example 1:

Input: nums = [-2,1,-3,4,-1,2,1,-5,4]
Output: 6
Explanation: The subarray [4,-1,2,1] has the largest sum 6.

Example 2:

Input: nums = [1]
Output: 1
Explanation: The subarray [1] has the largest sum 1.

Example 3:

Input: nums = [5,4,-1,7,8]
Output: 23
Explanation: The subarray [5,4,-1,7,8] has the largest sum 23.

Constraints:

1 <= nums.length <= 10^5
-10^4 <= nums[i] <= 10^4

Follow up: If you have figured out the O(n) solution, try coding another solution using the divide and conquer approach, which is more subtle.

思路

这道题之前我们在讲解贪心专题的时候用贪心算法解决过一次，贪心算法：最大子序和。

这次我们用动态规划的思路再来分析一次。

动规五部曲如下：

确定dp数组（dp table）以及下标的含义

dp[i]：包括下标i（以nums[i]为结尾）的最大连续子序列和为dp[i]。

确定递推公式

dp[i]只有两个方向可以推出来：

dp[i - 1] + nums[i]，即：nums[i]加入当前连续子序列和
nums[i]，即：从头开始计算当前连续子序列和

一定是取最大的，所以dp[i] = max(dp[i - 1] + nums[i], nums[i]);

dp数组如何初始化

从递推公式可以看出来dp[i]是依赖于dp[i - 1]的状态，dp[0]就是递推公式的基础。

dp[0]应该是多少呢?

根据dp[i]的定义，很明显dp[0]应为nums[0]即dp[0] = nums[0]。

确定遍历顺序

递推公式中dp[i]依赖于dp[i - 1]的状态，需要从前向后遍历。

举例推导dp数组

以示例一为例，输入：nums = [-2,1,-3,4,-1,2,1,-5,4]，对应的dp状态如下：

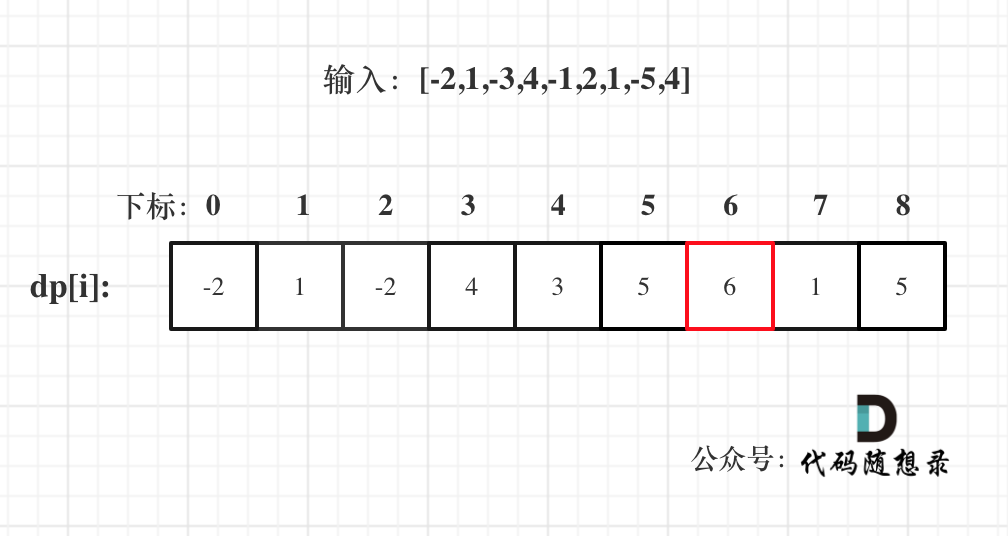
53.最大子序和（动态规划）

注意最后的结果可不是dp[nums.size() - 1]！ ，而是dp[6]。

在回顾一下dp[i]的定义：包括下标i之前的最大连续子序列和为dp[i]。

那么我们要找最大的连续子序列，就应该找每一个i为终点的连续最大子序列。

所以在递推公式的时候，可以直接选出最大的dp[i]。

C++解法

以上动规五部曲分析完毕，完整代码如下：

class Solution {  
public:  
    int maxSubArray(vector<int>& nums) {  
        if (nums.size() == 0) return 0;  
        vector<int> dp(nums.size());  
        dp[0] = nums[0];  
        int result = dp[0];  
        for (int i = 1; i < nums.size(); i++) {  
            dp[i] = max(dp[i - 1] + nums[i], nums[i]); // 状态转移公式  
            if (dp[i] > result) result = dp[i]; // result 保存dp[i]的最大值  
        }  
        return result;  
    }  
};

时间复杂度：O(n)
空间复杂度：O(n)

剑指Offer