买卖股票

121. Best Time to Buy and Sell Stock
- 思路
- C++解法
- Java解法
122. Best Time to Buy and Sell Stock II
123. Best Time to Buy and Sell Stock III
188. Best Time to Buy and Sell Stock IV
309. Best Time to Buy and Sell Stock with Cooldown
714. Best Time to Buy and Sell Stock with Transaction Fee

121. Best Time to Buy and Sell Stock

You are given an array prices where prices[i] is the price of a given stock on the ith day.

You want to maximize your profit by choosing a single day to buy one stock and choosing a different day in the future to sell that stock.

Return the maximum profit you can achieve from this transaction. If you cannot achieve any profit, return 0.

Example 1:

Input: prices = [7,1,5,3,6,4]
Output: 5
Explanation: Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5. Note that buying on day 2 and selling on day 1 is not allowed because you must buy before you sell.

Example 2:

Input: prices = [7,6,4,3,1]
Output: 0
Explanation: In this case, no transactions are done and the max profit = 0.

Constraints:

1 <= prices.length <= 10^5
0 <= prices[i] <= 10^4

思路

动规五部曲分析如下：

确定dp数组（dp table）以及下标的含义

dp[i][j] 表示第i天持有股票所得最多现金，这里可能有同学疑惑，本题中只能买卖一次，持有股票之后哪还有现金呢？

其实一开始现金是0，那么加入第i天买入股票现金就是 -prices[i]，这是一个负数。

dp[i][j] 表示第i天不持有股票所得最多现金

注意这里说的是“持有”，“持有”不代表就是当天“买入”！也有可能是昨天就买入了，今天保持持有的状态

很多同学把“持有”和“买入”没区分清楚。

在下面递推公式分析中，我会进一步讲解。

确定递推公式

如果第i天持有股票即dp[i][j]，那么可以由两个状态推出来

第i-1天就持有股票，那么就保持现状，所得现金就是昨天持有股票的所得现金即：dp[i-1][j]
第i天买入股票，所得现金就是买入今天的股票后所得现金即：-prices[i]

那么dp[i][j]应该选所得现金最大的，所以dp[i][j] = max(dp[i-1][j], -prices[i]);

如果第i天不持有股票即dp[i][j]，也可以由两个状态推出来

第i-1天就不持有股票，那么就保持现状，所得现金就是昨天不持有股票的所得现金即：dp[i-1][j]
第i天卖出股票，所得现金就是按照今天股票价格卖出后所得现金即：prices[i] + dp[i-1][j]

同样dp[i][j]取最大的，dp[i][j] = max(dp[i-1][j], prices[i] + dp[i-1][j]);

这样递推公式我们就分析完了

dp数组如何初始化

由递推公式 dp[i][j] = max(dp[i-1][j], -prices[i]); 和 dp[i][j] = max(dp[i-1][j], prices[i] + dp[i-1][j]);可以看出

其基础都是要从dp[0][0]和dp[0][1]推导出来。

那么dp[0][1]表示第0天持有股票，此时的持有股票就一定是买入股票了，因为不可能有前一天推出来，所以dp[0][1] -= prices[0];

dp[0][0]表示第0天不持有股票，不持有股票那么现金就是0，所以dp[0][0] = 0;

确定遍历顺序

从递推公式可以看出dp[i]都是由dp[i - 1]推导出来的，那么一定是从前向后遍历。

举例推导dp数组

以示例1，输入：[7,1,5,3,6,4]为例，dp数组状态如下：

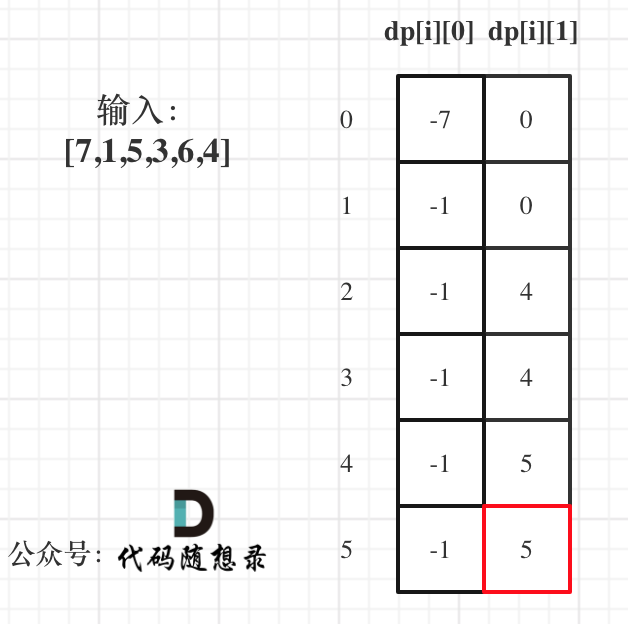
121.买卖股票的最佳时机

`dp[5][1]就是最终结果。

为什么不是dp[5][0]呢？

因为本题中不持有股票状态所得金钱一定比持有股票状态得到的多！

C++解法

动态规划

以上分析完毕，C++代码如下：

// 版本一  
class Solution {  
public:  
    int maxProfit(vector<int>& prices) {  
        int len = prices.size();  
        if (len == 0) return 0;  
        vector<vector<int>> dp(len, vector<int>(2));  
        dp[0][0] -= prices[0];  
        dp[0][1] = 0;  
        for (int i = 1; i < len; i++) {  
            dp[i][0] = max(dp[i - 1][0], -prices[i]);  
            dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);  
        }  
        return dp[len - 1][1];  
    }  
};

时间复杂度：O(n)
空间复杂度：O(n)

从递推公式可以看出，dp[i]只是依赖于dp[i - 1]的状态。

dp[i][0] = max(dp[i - 1][0], -prices[i]);  
dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);

那么我们只需要记录当前天的dp状态和前一天的dp状态就可以了，可以使用滚动数组来节省空间，代码如下：

// 版本二  
class Solution {  
public:  
    int maxProfit(vector<int>& prices) {  
        int len = prices.size();  
        vector<vector<int>> dp(2, vector<int>(2)); // 注意这里只开辟了一个2 * 2大小的二维数组  
        dp[0][0] -= prices[0];  
        dp[0][1] = 0;  
        for (int i = 1; i < len; i++) {  
            dp[i % 2][0] = max(dp[(i - 1) % 2][0], -prices[i]);  
            dp[i % 2][1] = max(dp[(i - 1) % 2][1], prices[i] + dp[(i - 1) % 2][0]);  
        }  
        return dp[(len - 1) % 2][1];  
    }  
};

时间复杂度：O(n)
空间复杂度：O(1)

这里能写出版本一就可以了，版本二虽然原理都一样，但是想直接写出版本二还是有点麻烦，容易自己给自己找bug。

所以建议是先写出版本一，然后在版本一的基础上优化成版本二，而不是直接就写出版本二。

暴力

这道题目最直观的想法，就是暴力，找最优间距了。

class Solution {  
public:  
    int maxProfit(vector<int>& prices) {  
        int result = 0;  
        for (int i = 0; i < prices.size(); i++) {  
            for (int j = i + 1; j < prices.size(); j++){  
                result = max(result, prices[j] - prices[i]);  
            }  
        }  
        return result;  
    }  
};

时间复杂度：O(n^2)
空间复杂度：O(1)

当然该方法超时了。

贪心

因为股票就买卖一次，那么贪心的想法很自然就是取最左最小值，取最右最大值，那么得到的差值就是最大利润。

C++代码如下：

class Solution {  
public:  
    int maxProfit(vector<int>& prices) {  
        int low = INT_MAX;  
        int result = 0;  
        for (int i = 0; i < prices.size(); i++) {  
            low = min(low, prices[i]);  // 取最左最小价格  
            result = max(result, prices[i] - low); // 直接取最大区间利润  
        }  
        return result;  
    }  
};

时间复杂度：O(n)
空间复杂度：O(1)

Java解法

// 优化空间
class Solution {
    public int maxProfit(int[] prices) {
        int[] dp = new int[2];
        // 0表示持有，1表示卖出
        dp[0] = -prices[0];
        dp[1] = 0;
        for(int i = 1; i <= prices.length; i++){
            // 前一天持有; 既然不限制交易次数，那么再次买股票时，要加上之前的收益
            dp[0] = Math.max(dp[0], dp[1] - prices[i-1]);
            // 前一天卖出; 或当天卖出，当天卖出，得先持有
            dp[1] = Math.max(dp[1], dp[0] + prices[i-1]);
        }
        return dp[1];
    }
}

122. Best Time to Buy and Sell Stock II

You are given an integer array prices where prices[i] is the price of a given stock on the ith day.

On each day, you may decide to buy and/or sell the stock. You can only hold at most one share of the stock at any time. However, you can buy it then immediately sell it on the same day.

Find and return the maximum profit you can achieve.

Example 1:

Input: prices = [7,1,5,3,6,4]
Output: 7
Explanation: Buy on day 2 (price = 1) and sell on day 3 (price = 5), profit = 5-1 = 4. Then buy on day 4 (price = 3) and sell on day 5 (price = 6), profit = 6-3 = 3. Total profit is 4 + 3 = 7.

Example 2:

Input: prices = [1,2,3,4,5]
Output: 4
Explanation: Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4. Total profit is 4.

Example 3:

Input: prices = [7,6,4,3,1]
Output: 0
Explanation: There is no way to make a positive profit, so we never buy the stock to achieve the maximum profit of 0.

Constraints:

1 <= prices.length <= 3 * 10^4
0 <= prices[i] <= 10^4

思路

本题我们在讲解贪心专题的时候就已经讲解过了贪心算法：买卖股票的最佳时机II，只不过没有深入讲解动态规划的解法，那么这次我们再好好分析一下动规的解法。

本题和121. 买卖股票的最佳时机的唯一区别是本题股票可以买卖多次了（注意只有一只股票，所以再次购买前要出售掉之前的股票）

在动规五部曲中，这个区别主要是体现在递推公式上，其他都和121. 买卖股票的最佳时机一样一样的。

所以我们重点讲一讲递推公式。

这里重申一下dp数组的含义：

dp[i][j] 表示第i天持有股票所得现金。
dp[i][j] 表示第i天不持有股票所得最多现金

如果第i天持有股票即dp[i][j]，那么可以由两个状态推出来

第i-1天就持有股票，那么就保持现状，所得现金就是昨天持有股票的所得现金即：dp[i-1][j]
第i天买入股票，所得现金就是昨天不持有股票的所得现金减去今天的股票价格即：dp[i-1][j] - prices[i]

注意这里和121. 买卖股票的最佳时机唯一不同的地方，就是推导dp[i][j]的时候，第i天买入股票的情况。

在121. 买卖股票的最佳时机中，因为股票全程只能买卖一次，所以如果买入股票，那么第i天持有股票即dp[i][j]一定就是 -prices[i]。

而本题，因为一只股票可以买卖多次，所以当第i天买入股票的时候，所持有的现金可能有之前买卖过的利润。

那么第i天持有股票即dp[i][j]，如果是第i天买入股票，所得现金就是昨天不持有股票的所得现金减去今天的股票价格即：dp[i-1][j] - prices[i]。

再来看看如果第i天不持有股票即dp[i][j]的情况，依然可以由两个状态推出来

第i-1天就不持有股票，那么就保持现状，所得现金就是昨天不持有股票的所得现金即：dp[i-1][j]
第i天卖出股票，所得现金就是按照今天股票价格卖出后所得现金即：prices[i] + dp[i-1][j]

注意这里和121. 买卖股票的最佳时机就是一样的逻辑，卖出股票收获利润（可能是负值）天经地义！

C++解法

代码如下：（注意代码中的注释，标记了和121.买卖股票的最佳时机唯一不同的地方）

class Solution {  
public:  
    int maxProfit(vector<int>& prices) {  
        int len = prices.size();  
        vector<vector<int>> dp(len, vector<int>(2, 0));  
        dp[0][0] -= prices[0];  
        dp[0][1] = 0;  
        for (int i = 1; i < len; i++) {  
            dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]); // 注意这里是和121. 买卖股票的最佳时机唯一不同的地方。  
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i]);  
        }  
        return dp[len - 1][1];  
    }  
};

时间复杂度：O(n)
空间复杂度：O(n)

大家可以本题和121. 买卖股票的最佳时机的代码几乎一样，唯一的区别在：

dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);

这正是因为本题的股票可以买卖多次！ 所以买入股票的时候，可能会有之前买卖的利润即：dp[i-1][j]，所以dp[i-1][j] - prices[i]。

想到到这一点，对这两道题理解的就比较深刻了。

这里我依然给出滚动数组的版本，C++代码如下：

// 版本二  
class Solution {  
public:  
    int maxProfit(vector<int>& prices) {  
        int len = prices.size();  
        vector<vector<int>> dp(2, vector<int>(2)); // 注意这里只开辟了一个2 * 2大小的二维数组  
        dp[0][0] -= prices[0];  
        dp[0][1] = 0;  
        for (int i = 1; i < len; i++) {  
            dp[i % 2][0] = max(dp[(i - 1) % 2][0], dp[(i - 1) % 2][1] - prices[i]);  
            dp[i % 2][1] = max(dp[(i - 1) % 2][1], prices[i] + dp[(i - 1) % 2][0]);  
        }  
        return dp[(len - 1) % 2][1];  
    }  
};

时间复杂度：O(n)
空间复杂度：O(1)

Java解法

// 动态规划
class Solution 
    // 实现1：二维数组存储
    // 可以将每天持有与否的情况分别用 dp[i][0] 和 dp[i][1] 来进行存储
    // 时间复杂度：O(n)，空间复杂度：O(n)
    public int maxProfit(int[] prices) {
        int n = prices.length;
        int[][] dp = new int[n][2];     // 创建二维数组存储状态
        dp[0][0] = 0;                   // 初始状态
        dp[0][1] = -prices[0];
        for (int i = 1; i < n; ++i) {
            dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);    // 第 i 天，没有股票
            dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);    // 第 i 天，持有股票
        }
        return dp[n - 1][0];    // 卖出股票收益高于持有股票收益，因此取[0]
    }
}

贪心解法：

class Solution {
    public int maxProfit(int[] prices) {
        int result = 0;
        for(int i = 1; i < prices.length; i++){
            result += Math.max(prices[i] - prices[i - 1], 0);
        }
        return result;
    }
}

123. Best Time to Buy and Sell Stock III

You are given an array prices where prices[i] is the price of a given stock on the ith day.

Find the maximum profit you can achieve. You may complete at most two transactions.

Note: You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).

Example 1:

Input: prices = [3,3,5,0,0,3,1,4]
Output: 6
Explanation: Buy on day 4 (price = 0) and sell on day 6 (price = 3), profit = 3-0 = 3. Then buy on day 7 (price = 1) and sell on day 8 (price = 4), profit = 4-1 = 3.

Example 2:

Input: prices = [1,2,3,4,5]
Output: 4
Explanation: Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4. Note that you cannot buy on day 1, buy on day 2 and sell them later, as you are engaging multiple transactions at the same time. You must sell before buying again.

Example 3:

Input: prices = [7,6,4,3,1]
Output: 0
Explanation: In this case, no transaction is done, i.e. max profit = 0.

Constraints:

1 <= prices.length <= 10^5
0 <= prices[i] <= 10^5

思路

这道题目相对 121.买卖股票的最佳时机和 122.买卖股票的最佳时机II 难了不少。

关键在于至多买卖两次，这意味着可以买卖一次，可以买卖两次，也可以不买卖。

接来下我用动态规划五部曲详细分析一下：

确定dp数组以及下标的含义

一天一共就有五个状态，

没有操作（其实我们也可以不设置这个状态）
第一次持有股票
第一次不持有股票
第二次持有股票
第二次不持有股票

dp[i][j]中 i表示第i天，j为 [0 - 4] 五个状态，dp[i][j]表示第i天状态j所剩最大现金。

需要注意：dp[i][j]，表示的是第i天，买入股票的状态，并不是说一定要第i天买入股票，这是很多同学容易陷入的误区。

例如 dp[i][j] ，并不是说第i天一定买入股票，有可能第 i-1天就买入了，那么 dp[i][j] 延续买入股票的这个状态。

确定递推公式

达到dp[i][j]状态，有两个具体操作：

操作一：第i天买入股票了，那么dp[i][j] = dp[i-1][j] - prices[i]
操作二：第i天没有操作，而是沿用前一天买入的状态，即：dp[i][j] = dp[i-1][j]

那么dp[i][j]究竟选 dp[i-1][j] - prices[i]，还是dp[i-1][j]呢？

一定是选最大的，所以 dp[i][j] = max(dp[i-1][j] - prices[i], dp[i-1][j]);

同理dp[i][j]也有两个操作：

操作一：第i天卖出股票了，那么dp[i][j] = dp[i-1][j] + prices[i]
操作二：第i天没有操作，沿用前一天卖出股票的状态，即：dp[i][j] = dp[i-1][j]

所以dp[i][j] = max(dp[i-1][j] + prices[i], dp[i-1][j])

同理可推出剩下状态部分：

dp[i][j] = max(dp[i-1][j], dp[i-1][j] - prices[i]);

dp[i][j] = max(dp[i-1][j], dp[i-1][j] + prices[i]);

dp数组如何初始化

第0天没有操作，这个最容易想到，就是0，即：dp[0][0] = 0;

第0天做第一次买入的操作，dp[0][1] = -prices[0];

第0天做第一次卖出的操作，这个初始值应该是多少呢？

此时还没有买入，怎么就卖出呢？其实大家可以理解当天买入，当天卖出，所以dp[0][2] = 0;

第0天第二次买入操作，初始值应该是多少呢？应该不少同学疑惑，第一次还没买入呢，怎么初始化第二次买入呢？

第二次买入依赖于第一次卖出的状态，其实相当于第0天第一次买入了，第一次卖出了，然后再买入一次（第二次买入），那么现在手头上没有现金，只要买入，现金就做相应的减少。

所以第二次买入操作，初始化为：dp[0][3] = -prices[0];

同理第二次卖出初始化dp[0][4] = 0;

确定遍历顺序

从递归公式其实已经可以看出，一定是从前向后遍历，因为dp[i]，依靠dp[i - 1]的数值。

举例推导dp数组

以输入[1,2,3,4,5]为例

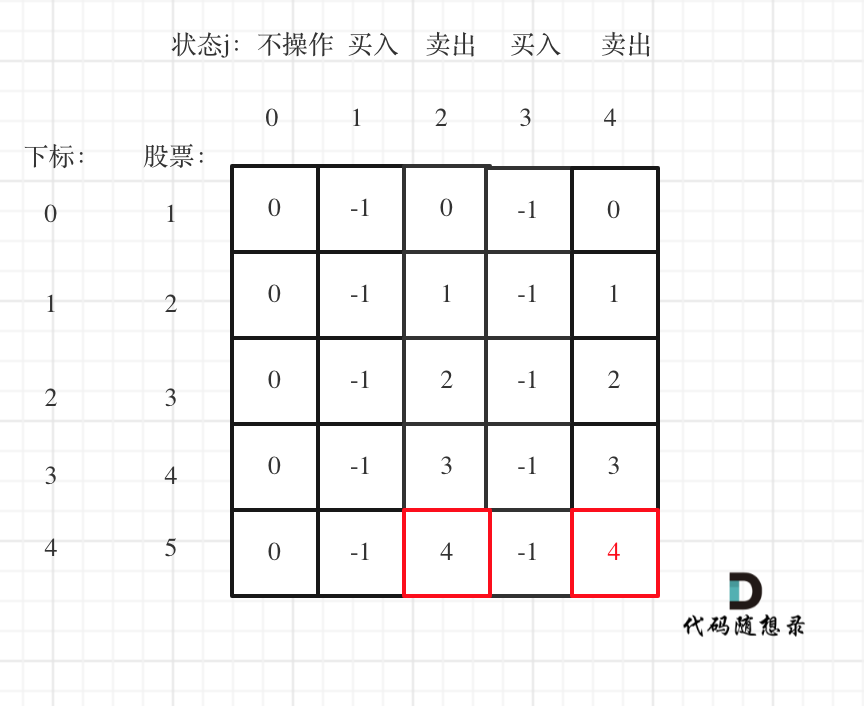
123.买卖股票的最佳时机III

大家可以看到红色框为最后两次卖出的状态。

现在最大的时候一定是卖出的状态，而两次卖出的状态现金最大一定是最后一次卖出。如果想不明白的录友也可以这么理解：如果第一次卖出已经是最大值了，那么我们可以在当天立刻买入再立刻卖出。所以dp[4][4]已经包含了dp[4][4]的情况。也就是说第二次卖出手里所剩的钱一定是最多的。

所以最终最大利润是dp[4][4]

C++解法

以上五部都分析完了，不难写出如下代码：

// 版本一  
class Solution {  
public:  
    int maxProfit(vector<int>& prices) {  
        if (prices.size() == 0) return 0;  
        vector<vector<int>> dp(prices.size(), vector<int>(5, 0));  
        dp[0][1] = -prices[0];  
        dp[0][3] = -prices[0];  
        for (int i = 1; i < prices.size(); i++) {  
            dp[i][0] = dp[i - 1][0];  
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);  
            dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i]);  
            dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);  
            dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);  
        }  
        return dp[prices.size() - 1][4];  
    }  
};

时间复杂度：O(n)
空间复杂度：O(n × 5)

当然，大家可以看到力扣官方题解里的一种优化空间写法，我这里给出对应的C++版本：

// 版本二  
class Solution {  
public:  
    int maxProfit(vector<int>& prices) {  
        if (prices.size() == 0) return 0;  
        vector<int> dp(5, 0);  
        dp[1] = -prices[0];  
        dp[3] = -prices[0];  
        for (int i = 1; i < prices.size(); i++) {  
            dp[1] = max(dp[1], dp[0] - prices[i]);  
            dp[2] = max(dp[2], dp[1] + prices[i]);  
            dp[3] = max(dp[3], dp[2] - prices[i]);  
            dp[4] = max(dp[4], dp[3] + prices[i]);  
        }  
        return dp[4];  
    }  
};

时间复杂度：O(n)
空间复杂度：O(1)

大家会发现dp[2]利用的是当天的dp[1]。但结果也是对的。

我来简单解释一下：

dp[1] = max(dp[1], dp[0] - prices[i]); 如果dp[1]取dp[1]，即保持买入股票的状态，那么 dp[2] = max(dp[2], dp[1] + prices[i]);中dp[1] + prices[i] 就是今天卖出。

如果dp[1]取dp[0] - prices[i]，今天买入股票，那么dp[2] = max(dp[2], dp[1] + prices[i]);中的dp[1] + prices[i]相当于是今天再卖出股票，一买一卖收益为0，对所得现金没有影响。相当于今天买入股票又卖出股票，等于没有操作，保持昨天卖出股票的状态了。

这种写法看上去简单，其实思路很绕，不建议大家这么写，这么思考，很容易把自己绕进去！

对于本题，把版本一的写法研究明白，足以！

Java解法

// 版本一
class Solution {
    public int maxProfit(int[] prices) {
        int len = prices.length;
        // 边界判断, 题目中 length >= 1, 所以可省去
        if (prices.length == 0) return 0;

        /*
         * 定义 5 种状态:
         * 0: 没有操作, 1: 第一次买入, 2: 第一次卖出, 3: 第二次买入, 4: 第二次卖出
         */
        int[][] dp = new int[len][5];
        dp[0][1] = -prices[0];
        // 初始化第二次买入的状态是确保 最后结果是最多两次买卖的最大利润
        dp[0][3] = -prices[0];

        for (int i = 1; i < len; i++) {
            dp[i][1] = Math.max(dp[i - 1][1], -prices[i]);
            dp[i][2] = Math.max(dp[i - 1][2], dp[i - 1][1] + prices[i]);
            dp[i][3] = Math.max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
            dp[i][4] = Math.max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
        }

        return dp[len - 1][4];
    }
}

// 版本二: 空间优化
class Solution {
    public int maxProfit(int[] prices) {
        int[] dp = new int[4]; 
        // 存储两次交易的状态就行了
        // dp[0]代表第一次交易的买入
        dp[0] = -prices[0];
        // dp[1]代表第一次交易的卖出
        dp[1] = 0;
        // dp[2]代表第二次交易的买入
        dp[2] = -prices[0];
        // dp[3]代表第二次交易的卖出
        dp[3] = 0;
        for(int i = 1; i <= prices.length; i++){
            // 要么保持不变，要么没有就买，有了就卖
            dp[0] = Math.max(dp[0], -prices[i-1]);
            dp[1] = Math.max(dp[1], dp[0]+prices[i-1]);
            // 这已经是第二次交易了，所以得加上前一次交易卖出去的收获
            dp[2] = Math.max(dp[2], dp[1]-prices[i-1]);
            dp[3] = Math.max(dp[3], dp[2]+ prices[i-1]);
        }
        return dp[3];
    }
}

188. Best Time to Buy and Sell Stock IV

You are given an integer array prices where prices[i] is the price of a given stock on the ith day, and an integer k.

Find the maximum profit you can achieve. You may complete at most k transactions: i.e. you may buy at most k times and sell at most k times.

Note: You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).

Example 1:

Input: k = 2, prices = [2,4,1]
Output: 2
Explanation: Buy on day 1 (price = 2) and sell on day 2 (price = 4), profit = 4-2 = 2.

Example 2:

Input: k = 2, prices = [3,2,6,5,0,3]
Output: 7
Explanation: Buy on day 2 (price = 2) and sell on day 3 (price = 6), profit = 6-2 = 4. Then buy on day 5 (price = 0) and sell on day 6 (price = 3), profit = 3-0 = 3.

Constraints:

1 <= k <= 100
1 <= prices.length <= 1000
0 <= prices[i] <= 1000

思路

这道题目可以说是动态规划：123.买卖股票的最佳时机III的进阶版，这里要求至多有k次交易。

动规五部曲，分析如下：

确定dp数组以及下标的含义

在动态规划：123.买卖股票的最佳时机III中，我是定义了一个二维dp数组，本题其实依然可以用一个二维dp数组。

使用二维数组 dp[i][j] ：第i天的状态为j，所剩下的最大现金是dp[i][j]

j的状态表示为：

0 表示不操作
1 第一次买入
2 第一次卖出
3 第二次买入
4 第二次卖出
.....

大家应该发现规律了吧，除了0以外，偶数就是卖出，奇数就是买入。

题目要求是至多有K笔交易，那么j的范围就定义为 2 * k + 1 就可以了。

所以二维dp数组的C++定义为：

vector<vector<int>> dp(prices.size(), vector<int>(2 * k + 1, 0));

确定递推公式

还要强调一下：dp[i][j]，表示的是第i天，买入股票的状态，并不是说一定要第i天买入股票，这是很多同学容易陷入的误区。

达到dp[i][j]状态，有两个具体操作：

操作一：第i天买入股票了，那么dp[i][j] = dp[i-1][j] - prices[i]
操作二：第i天没有操作，而是沿用前一天买入的状态，即：dp[i][j] = dp[i-1][j]

选最大的，所以 dp[i][j] = max(dp[i-1][j] - prices[i], dp[i-1][j]);

同理dp[i][j]也有两个操作：

操作一：第i天卖出股票了，那么dp[i][j] = dp[i-1][j] + prices[i]
操作二：第i天没有操作，沿用前一天卖出股票的状态，即：dp[i][j] = dp[i-1][j]

所以``dp[i][j] = max(dp[i-1][j]+ prices[i],dp[i-1][j])

同理可以类比剩下的状态，代码如下：

for (int j = 0; j < 2 * k - 1; j += 2) {  
    dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);  
    dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);  
}

本题和动态规划：123.买卖股票的最佳时机III最大的区别就是这里要类比j为奇数是买，偶数是卖的状态。

dp数组如何初始化

第0天没有操作，这个最容易想到，就是0，即：dp[0][0] = 0;

第0天做第一次买入的操作，dp[0][1] = -prices[0];

第0天做第一次卖出的操作，这个初始值应该是多少呢？

此时还没有买入，怎么就卖出呢？其实大家可以理解当天买入，当天卖出，所以dp[0][2] = 0;

第0天第二次买入操作，初始值应该是多少呢？应该不少同学疑惑，第一次还没买入呢，怎么初始化第二次买入呢？

第二次买入依赖于第一次卖出的状态，其实相当于第0天第一次买入了，第一次卖出了，然后在买入一次（第二次买入），那么现在手头上没有现金，只要买入，现金就做相应的减少。

所以第二次买入操作，初始化为：dp[0][1] = -prices[0];

第二次卖出初始化dp[0][2] = 0;

所以同理可以推出dp[0][1]当j为奇数的时候都初始化为 -prices[0]

代码如下：

for (int j = 1; j < 2 * k; j += 2) {  
    dp[0][j] = -prices[0];  
}

在初始化的地方同样要类比j为偶数是卖、奇数是买的状态。

确定遍历顺序

从递归公式其实已经可以看出，一定是从前向后遍历，因为dp[i]，依靠dp[i - 1]的数值。

举例推导dp数组

以输入[1,2,3,4,5]，k=2为例。

最后一次卖出，一定是利润最大的，dp[prices.size() - 1][2 * k]即红色部分就是最后求解。

C++解法

以上分析完毕，C++代码如下：

class Solution {  
public:  
    int maxProfit(int k, vector<int>& prices) {  
  
        if (prices.size() == 0) return 0;  
        vector<vector<int>> dp(prices.size(), vector<int>(2 * k + 1, 0));  
        for (int j = 1; j < 2 * k; j += 2) {  
            dp[0][j] = -prices[0];  
        }  
        for (int i = 1;i < prices.size(); i++) {  
            for (int j = 0; j < 2 * k - 1; j += 2) {  
                dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);  
                dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);  
            }  
        }  
        return dp[prices.size() - 1][2 * k];  
    }  
};

时间复杂度: O(n * k)，其中 n 为 prices 的长度
空间复杂度: O(n * k)

当然有的解法是定义一个三维数组dp[i][j][k]，第i天，第j次买卖，k表示买还是卖的状态，从定义上来讲是比较直观。

但感觉三维数组操作起来有些麻烦，我是直接用二维数组来模拟三维数组的情况，代码看起来也清爽一些。

Java解法

// 版本二: 二维 dp数组
class Solution {
    public int maxProfit(int k, int[] prices) {
        if (prices.length == 0) return 0;

        // [天数][股票状态]
        // 股票状态: 奇数表示第 k 次交易持有/买入, 偶数表示第 k 次交易不持有/卖出, 0 表示没有操作
        int len = prices.length;
        int[][] dp = new int[len][k*2 + 1];
        
        // dp数组的初始化, 与版本一同理
        for (int i = 1; i < k*2; i += 2) {
            dp[0][i] = -prices[0];
        }

        for (int i = 1; i < len; i++) {
            for (int j = 0; j < k*2 - 1; j += 2) {
                dp[i][j + 1] = Math.max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);
                dp[i][j + 2] = Math.max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);
            }
        }
        return dp[len - 1][k*2];
    }
}

309. Best Time to Buy and Sell Stock with Cooldown

You are given an array prices where prices[i] is the price of a given stock on the ith day.

Find the maximum profit you can achieve. You may complete as many transactions as you like (i.e., buy one and sell one share of the stock multiple times) with the following restrictions:

After you sell your stock, you cannot buy stock on the next day (i.e., cooldown one day).

Note: You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).

Example 1:

Input: prices = [1,2,3,0,2]
Output: 3
Explanation: transactions = [buy, sell, cooldown, buy, sell]

Example 2:

Input: prices = [1]
Output: 0

Constraints:

1 <= prices.length <= 5000
0 <= prices[i] <= 1000

思路

相对于动态规划：122.买卖股票的最佳时机II，本题加上了一个冷冻期

在动态规划：122.买卖股票的最佳时机II 中有两个状态，持有股票后的最多现金，和不持有股票的最多现金。

动规五部曲，分析如下：

确定dp数组以及下标的含义

dp[i][j]，第i天状态为j，所剩的最多现金为dp[i][j]。

其实本题很多同学搞的比较懵，是因为出现冷冻期之后，状态其实是比较复杂度，例如今天买入股票、今天卖出股票、今天是冷冻期，都是不能操作股票的。

具体可以区分出如下四个状态：

状态一：持有股票状态（今天买入股票，或者是之前就买入了股票然后没有操作，一直持有）
不持有股票状态，这里就有两种卖出股票状态
- 状态二：保持卖出股票的状态（两天前就卖出了股票，度过一天冷冻期。或者是前一天就是卖出股票状态，一直没操作）
- 状态三：今天卖出股票
状态四：今天为冷冻期状态，但冷冻期状态不可持续，只有一天！

j的状态为：

0：状态一
1：状态二
2：状态三
3：状态四

很多题解为什么讲的比较模糊，是因为把这四个状态合并成三个状态了，其实就是把状态二和状态四合并在一起了。

从代码上来看确实可以合并，但从逻辑上分析合并之后就很难理解了，所以我下面的讲解是按照这四个状态来的，把每一个状态分析清楚。

「今天卖出股票」我是没有单独列出一个状态的归类为「不持有股票的状态」，而本题为什么要单独列出「今天卖出股票」一个状态呢？

因为本题我们有冷冻期，而冷冻期的前一天，只能是「今天卖出股票」状态，如果是「不持有股票状态」那么就很模糊，因为不一定是卖出股票的操作。

注意这里的每一个状态，例如状态一，是持有股票股票状态并不是说今天一定就买入股票，而是说保持买入股票的状态即：可能是前几天买入的，之后一直没操作，所以保持买入股票的状态。

确定递推公式

达到买入股票状态（状态一）即：dp[i][j]，有两个具体操作：

操作一：前一天就是持有股票状态（状态一），dp[i][j] = dp[i-1][j]
操作二：今天买入了，有两种情况
- 前一天是冷冻期（状态四），dp[i-1][j] - prices[i]
- 前一天是保持卖出股票的状态（状态二），dp[i-1][j] - prices[i]

那么dp[i][j] = max(dp[i-1][j], dp[i-1][j] - prices[i], dp[i-1][j] - prices[i]);

达到保持卖出股票状态（状态二）即：dp[i][j]，有两个具体操作：

操作一：前一天就是状态二
操作二：前一天是冷冻期（状态四）

dp[i][j] = max(dp[i-1][j], dp[i-1][j]);

达到今天就卖出股票状态（状态三），即：dp[i][j] ，只有一个操作：

昨天一定是持有股票状态（状态一），今天卖出

即：dp[i][j] = dp[i-1][j] + prices[i];

达到冷冻期状态（状态四），即：dp[i][j]，只有一个操作：

昨天卖出了股票（状态三）

dp[i][j] = dp[i-1][j];

综上分析，递推代码如下：

dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][3], dp[i - 1][1]) - prices[i]);  
dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);  
dp[i][2] = dp[i - 1][0] + prices[i];  
dp[i][3] = dp[i - 1][2];

dp数组如何初始化

这里主要讨论一下第0天如何初始化。

如果是持有股票状态（状态一）那么：dp[0][0] = -prices[0]，一定是当天买入股票。

保持卖出股票状态（状态二），这里其实从「状态二」的定义来说，很难明确应该初始多少，这种情况我们就看递推公式需要我们给他初始成什么数值。

如果i为1，第1天买入股票，那么递归公式中需要计算 dp[i-1][j] - prices[i] ，即 dp[0][j] - prices[1]，那么大家感受一下dp[0][2] （即第0天的状态二）应该初始成多少，只能初始为0。想一想如果初始为其他数值，是我们第1天买入股票后手里还剩的现金数量是不是就不对了。

今天卖出了股票（状态三），同上分析，dp[0][2]初始化为0，dp[0][3]也初始为0。

确定遍历顺序

从递归公式上可以看出，dp[i] 依赖于 dp[i-1]，所以是从前向后遍历。

举例推导dp数组

以 [1,2,3,0,2] 为例，dp数组如下：

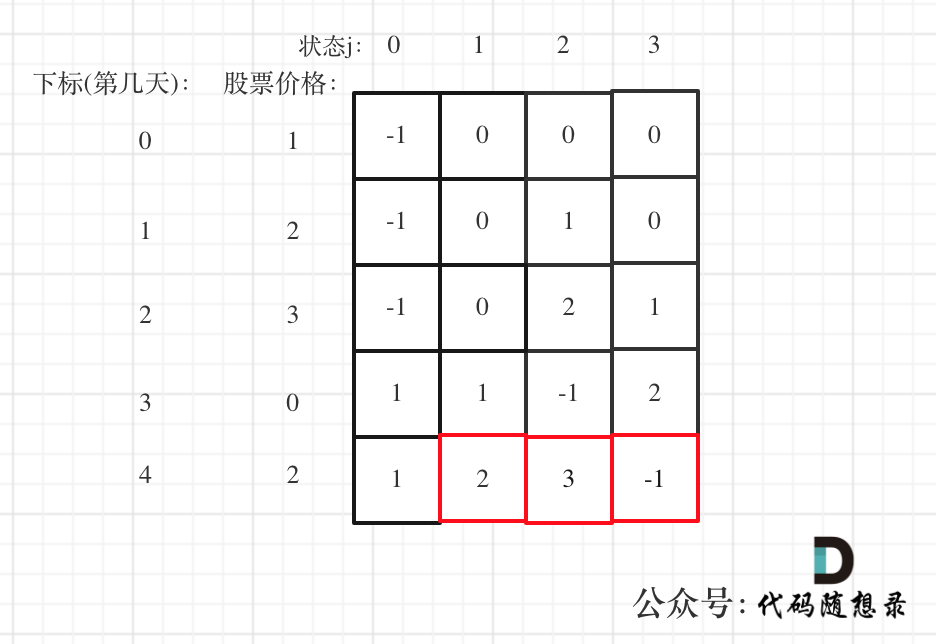
309.最佳买卖股票时机含冷冻期

最后结果是取状态二，状态三和状态四的最大值，不少同学会把状态四忘了，状态四是冷冻期，最后一天如果是冷冻期也可能是最大值。

C++解法

代码如下：

class Solution {  
public:  
    int maxProfit(vector<int>& prices) {  
        int n = prices.size();  
        if (n == 0) return 0;  
        vector<vector<int>> dp(n, vector<int>(4, 0));  
        dp[0][0] -= prices[0]; // 持股票  
        for (int i = 1; i < n; i++) {  
            dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][3] - prices[i], dp[i - 1][1] - prices[i]));  
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);  
            dp[i][2] = dp[i - 1][0] + prices[i];  
            dp[i][3] = dp[i - 1][2];  
        }  
        return max(dp[n - 1][3], max(dp[n - 1][1], dp[n - 1][2]));  
    }  
};

时间复杂度：O(n)
空间复杂度：O(n)

当然，空间复杂度可以优化，定义一个dp[2][4]大小的数组就可以了，就保存前一天的当前的状态，感兴趣的同学可以自己去写一写，思路是一样的。

Java解法

class Solution {
    public int maxProfit(int[] prices) {
        if (prices == null || prices.length < 2) {
            return 0;
        }
        int[][] dp = new int[prices.length][2];

        // bad case
        dp[0][0] = 0;
        dp[0][1] = -prices[0];
        dp[1][0] = Math.max(dp[0][0], dp[0][1] + prices[1]);
        dp[1][1] = Math.max(dp[0][1], -prices[1]);

        for (int i = 2; i < prices.length; i++) {
            // dp公式
            dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
            dp[i][1] = Math.max(dp[i - 1][1], dp[i - 2][0] - prices[i]);
        }

        return dp[prices.length - 1][0];
    }
}

714. Best Time to Buy and Sell Stock with Transaction Fee

You are given an array prices where prices[i] is the price of a given stock on the ith day, and an integer fee representing a transaction fee.

Find the maximum profit you can achieve. You may complete as many transactions as you like, but you need to pay the transaction fee for each transaction.

Note:

You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).
The transaction fee is only charged once for each stock purchase and sale.

Example 1:

Input: prices = [1,3,2,8,4,9], fee = 2
Output: 8
Explanation: The maximum profit can be achieved by:

Buying at prices[0] = 1
Selling at prices[3] = 8
Buying at prices[4] = 4
Selling at prices[5] = 9 The total profit is ((8 - 1) - 2) + ((9 - 4) - 2) = 8.

Example 2:

Input: prices = [1,3,7,5,10,3], fee = 3
Output: 6

Constraints:

1 <= prices.length <= 5 * 10^4
1 <= prices[i] < 5 * 10^4
0 <= fee < 5 * 10^4

思路

本题贪心解法：贪心算法：买卖股票的最佳时机含手续费

性能是：

时间复杂度：O(n)
空间复杂度：O(1)

本题使用贪心算法并不好理解，也很容易出错，那么我们再来看看是使用动规的方法如何解题。

相对于动态规划：122.买卖股票的最佳时机II，本题只需要在计算卖出操作的时候减去手续费就可以了，代码几乎是一样的。

唯一差别在于递推公式部分，所以本篇也就不按照动规五部曲详细讲解了，主要讲解一下递推公式部分。

这里重申一下dp数组的含义：

dp[i][j] 表示第i天持有股票所省最多现金。 dp[i][j] 表示第i天不持有股票所得最多现金

如果第i天持有股票即dp[i][j]，那么可以由两个状态推出来

第i-1天就持有股票，那么就保持现状，所得现金就是昨天持有股票的所得现金即：dp[i-1][j]
第i天买入股票，所得现金就是昨天不持有股票的所得现金减去今天的股票价格即：dp[i-1][j] - prices[i]

所以：dp[i][j] = max(dp[i-1][j], dp[i-1][j] - prices[i]);

在来看看如果第i天不持有股票即dp[i][j]的情况，依然可以由两个状态推出来

第i-1天就不持有股票，那么就保持现状，所得现金就是昨天不持有股票的所得现金即：dp[i-1][j]
第i天卖出股票，所得现金就是按照今天股票价格卖出后所得现金，注意这里需要有手续费了即：dp[i-1][j] + prices[i] - fee

所以：dp[i][j] = max(dp[i-1][j], dp[i-1][j] + prices[i] - fee);

本题和动态规划：122.买卖股票的最佳时机II的区别就是这里需要多一个减去手续费的操作。

C++解法

以上分析完毕，C++代码如下：

class Solution {  
public:  
    int maxProfit(vector<int>& prices, int fee) {  
        int n = prices.size();  
        vector<vector<int>> dp(n, vector<int>(2, 0));  
        dp[0][0] -= prices[0]; // 持股票  
        for (int i = 1; i < n; i++) {  
            dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);  
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i] - fee);  
        }  
        return max(dp[n - 1][0], dp[n - 1][1]);  
    }  
};

时间复杂度：O(n)
空间复杂度：O(n)

Java解法

/**
 * 买入时支付手续费
 * @param prices
 * @param fee
 * @return
 */
public int maxProfit(int[] prices, int fee) {
    int len = prices.length;
    // 0 : 持股（买入）
    // 1 : 不持股（售出）
    // dp 定义第i天持股/不持股 所得最多现金
    int[][] dp = new int[len][2];
    // 考虑买入的时候就支付手续费
    dp[0][0] = -prices[0] - fee;
    for (int i = 1; i < len; i++) {
        dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] - prices[i] - fee);
        dp[i][1] = Math.max(dp[i - 1][0] + prices[i], dp[i - 1][1]);
    }
    return Math.max(dp[len - 1][0], dp[len - 1][1]);
}

剑指Offer