移除链表元素

• 19. Remove Nth Node From End of List
  • 思路
  • C++解法
  • Java解法
  • Python3解法
• 203. Remove Linked List Elements
  • Description
  • 思路
  • C++解法
  • Java解法
  • Python3解法
  • Go解法
• 237. Delete Node in a Linked List
  • 思路
  • C++解法
  • Java解法
  • Python3解法
  • Go解法
• 2095. Delete the Middle Node of a Linked List
  • 思路
  • C++解法
  • Java解法
  • Python解法
• 2487. Remove Nodes From Linked List
  • 思路
    • Approach 1: Stack
    • Approach 2: Recursion
    • Approach 3: Reverse Twice
  • C++解法
  • Java解法
  • Python3解法
  • Go解法
• 3217. Delete Nodes From Linked List Present in Array
  • 思路
  • C++解法

要点：需要处理头节点时，使用虚拟头节点。如果要删除slow->next，则slow指针要慢一步。

19. Remove Nth Node From End of List

Given the head of a linked list, remove the nth node from the end of the list and return its head.

Example 1:

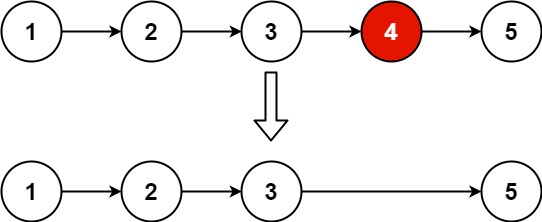
Input: head = [1,2,3,4,5], n = 2
Output: [1,2,3,5]

Example 2:

Input: head = [1], n = 1
Output: []

Example 3:

Input: head = [1,2], n = 1
Output: [1]

Constraints:

• The number of nodes in the list is sz.
• 1 <= sz <= 30
• 0 <= Node.val <= 100
• 1 <= n <= sz

Follow up: Could you do this in one pass?

思路

快慢指针求解，因为要删除slow->next，所以slow指针要慢一步。

Maintain two pointers and update one with a delay of n steps.

Complexity

• Time complexity: O(n)
• Space complexity: O(1)

C++解法

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode* dummyHead = new ListNode(0);
        dummyHead->next = head;
        ListNode* slow = dummyHead;
        ListNode* fast = head;
        for(int i = 0; i < n; i++){
            fast = fast->next;
        }
        while(fast != NULL){
            fast = fast->next;
            slow = slow->next;
        }
        slow->next = slow->next->next;
        return dummyHead->next;    
    }
};

Java解法

class Solution {
    public ListNode removeNthFromEnd(ListNode head, int n) {
        ListNode fast = head, slow = head;
        for (int i = 0; i < n; i++) fast = fast.next;
        if (fast == null) return head.next;
        while (fast.next != null) {
            fast = fast.next;
            slow = slow.next;
        }
        slow.next = slow.next.next;
        return head;
    }
}

Python3解法

class Solution:
    def removeNthFromEnd(self, head: ListNode, n: int) -> ListNode:
        fast, slow = head, head
        for _ in range(n): fast = fast.next
        if not fast: return head.next
        while fast.next: fast, slow = fast.next, slow.next
        slow.next = slow.next.next
        return head

203. Remove Linked List Elements

Description

Given the head of a linked list and an integer val, remove all the nodes of the linked list that has Node.val == val, and return the new head.

Example 1:

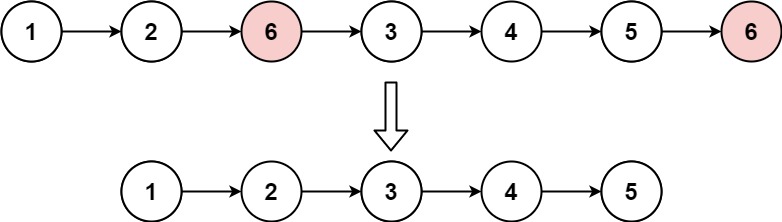
Input: head = [1,2,6,3,4,5,6], val = 6
Output: [1,2,3,4,5]

Example 2:

Input: head = [], val = 1
Output: []

Example 3:

Input: head = [7,7,7,7], val = 7
Output: []

Constraints:

• The number of nodes in the list is in the range [0, 10^4].
• 1 <= Node.val <= 50
• 0 <= val <= 50

思路

1. 单独处理头节点
2. 使用虚拟头节点

推荐使用虚拟头节点。

C++解法

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* removeElements(ListNode* head, int val) {
        ListNode* dummyHead = new ListNode(0);
        dummyHead->next = head;
        ListNode* cur = dummyHead;
        while(cur->next != NULL){
            if(cur->next->val == val){
                ListNode* temp = cur->next;
                cur->next = cur->next->next;
                delete temp;
            }else{
                cur = cur->next;
            }
        }
        return dummyHead->next;
    }
};

Java解法

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode removeElements(ListNode head, int val) {
        ListNode dummyHead = new ListNode(0);
        dummyHead.next = head;
        ListNode cur = dummyHead;
        while(cur.next != null){
            if(cur.next.val == val){
                cur.next = cur.next.next;
            }else{
                cur = cur.next;
            }
        }
        return dummyHead.next;
    }
}

Python3解法

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def removeElements(self, head: Optional[ListNode], val: int) -> Optional[ListNode]:
        temp = ListNode(0)
        temp.next = head
        prev, curr = temp, head
        while curr:
            if curr.val == val:
                prev.next = curr.next
            else:
                prev = curr
            curr = curr.next
        return temp.next

Go解法

/**
 * Definition for singly-linked list.
 * type ListNode struct {
 *     Val int
 *     Next *ListNode
 * }
 */
func removeElements(head *ListNode, val int) *ListNode {
    dummyHead := &ListNode{Val:0, Next: head}
    pre := dummyHead
    cur := pre.Next

    for cur != nil {
        if cur.Val == val{
            pre.Next = cur.Next
            cur = pre.Next
        }else{
            pre = cur
            cur = cur.Next
        }
    }
    return dummyHead.Next
}

237. Delete Node in a Linked List

There is a singly-linked list head and we want to delete a node node in it.

You are given the node to be deleted node. You will not be given access to the first node of head.

All the values of the linked list are unique, and it is guaranteed that the given node node is not the last node in the linked list.

Delete the given node. Note that by deleting the node, we do not mean removing it from memory. We mean:

• The value of the given node should not exist in the linked list.
• The number of nodes in the linked list should decrease by one.
• All the values before node should be in the same order.
• All the values after node should be in the same order.

Custom testing:

• For the input, you should provide the entire linked list head and the node to be given node. node should not be the last node of the list and should be an actual node in the list.
• We will build the linked list and pass the node to your function.
• The output will be the entire list after calling your function.

Example 1:

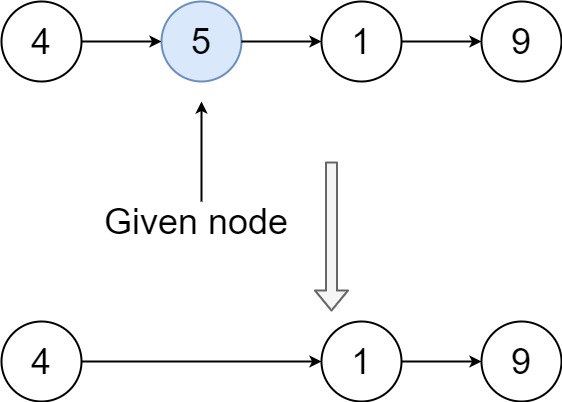
Input: head = [4,5,1,9], node = 5
Output: [4,1,9]
Explanation: You are given the second node with value 5, the linked list should become 4 -> 1 -> 9 after calling your function.

Example 2:

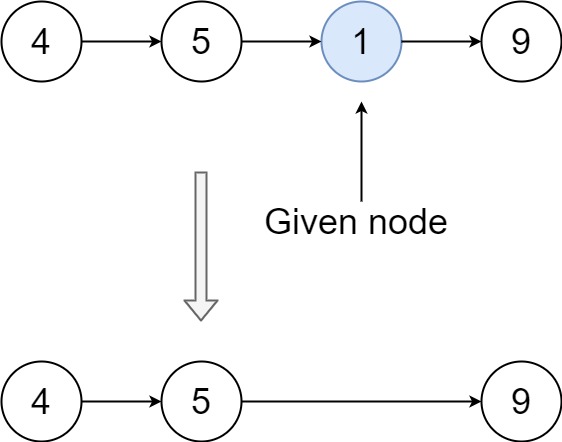
Input: head = [4,5,1,9], node = 1
Output: [4,5,9]
Explanation: You are given the third node with value 1, the linked list should become 4 -> 5 -> 9 after calling your function.

Constraints:

• The number of the nodes in the given list is in the range [2, 1000].
• -1000 <= Node.val <= 1000
• The value of each node in the list is unique.
• The node to be deleted is in the list and is not a tail node.

思路

Approach: Data Overwriting

Note: This method will not work if we need to delete the last node of the linked list since there is no immediate successor. However, the problem description explicitly states that the node to be deleted is not the tail node in the list.

Algorithm

1. Copy the data from the successor node into the current node to be deleted.
2. Update the next pointer of the current node to reference the next pointer of the successor node.

用待删除结点下一个节点覆盖待删除结点，此时删除原待删除结点下一个节点即可

Complexity Analysis

• Time Complexity: O(1)

  • The method involves a constant number of operations: updating the data of the current node and altering its next pointer. Each of these operations requires a fixed amount of time, irrespective of the size of the linked list.

• Space Complexity: O(1)

  • This deletion technique does not necessitate any extra memory allocation, as it operates directly on the existing nodes without creating additional data structures.

C++解法

/**
 * Definition for singly-linked list.  //单链表的定义
 * struct ListNode {
 *     int val;                 //当前结点的值(数据域)
 *     ListNode *next;          //指向下一个结点的指针(指针域)
 *     ListNode(int x) : val(x), next(NULL) {}     //初始化当前结点的值为x,指针为空
 * };
 */
class Solution {
public:
    void deleteNode(ListNode* node) {
        // Overwrite data of next node on current node.
        node->val = node->next->val;
        // Make current node point to next of next node.
        node->next = node->next->next;
    }
};

Java解法

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {

    public void deleteNode(ListNode node) {
        // Overwrite data of next node on current node.
        node.val = node.next.val;
        // Make current node point to next of next node.
        node.next = node.next.next;
    }
}

Python3解法

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def deleteNode(self, node):
        """
        :type node: ListNode
        :rtype: void Do not return anything, modify node in-place instead.
        """
        # Overwrite data of next node on current node.
        node.val = node.next.val
        # Make current node point to next of next node.
        node.next = node.next.next
        

Go解法

2095. Delete the Middle Node of a Linked List

You are given the head of a linked list. Delete the middle node, and return the head of the modified linked list.

The middle node of a linked list of size n is the ⌊n / 2⌋th node from the start using 0-based indexing, where ⌊x⌋ denotes the largest integer less than or equal to x.

• For n = 1, 2, 3, 4, and 5, the middle nodes are 0, 1, 1, 2, and 2, respectively.

Example 1:

Input: head = [1,3,4,7,1,2,6]
Output: [1,3,4,1,2,6]
Explanation: The above figure represents the given linked list. The indices of the nodes are written below. Since n = 7, node 3 with value 7 is the middle node, which is marked in red. We return the new list after removing this node.

Example 2:

Input: head = [1,2,3,4]
Output: [1,2,4]
Explanation: The above figure represents the given linked list. For n = 4, node 2 with value 3 is the middle node, which is marked in red.

Example 3:

Input: head = [2,1]
Output: [2]
Explanation: The above figure represents the given linked list. For n = 2, node 1 with value 1 is the middle node, which is marked in red. Node 0 with value 2 is the only node remaining after removing node 1.

Constraints:

• The number of nodes in the list is in the range [1, 10^5].
• 1 <= Node.val <= 10^5

思路

普通解法：求长度的一半然后遍历到这里并删除该节点，需要考虑只有一个节点的情况

双指针解法：快指针比慢指针的速度快一倍，快指针到头说明慢指针到达了一半的位置，跳过该节点即可。Complexity 👈

• Time complexity: O(n)
• Space complexity: O(1)

C++解法

双指针解法：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* deleteMiddle(ListNode* head) {
        if(head == NULL || head->next == NULL){
            return NULL;
        }
        ListNode* dummyHead = new ListNode(0);
        dummyHead->next = head;
        ListNode* slow = dummyHead;
        ListNode* fast = head;
        while(fast != NULL && fast->next != NULL){
            fast = fast->next->next;
            slow = slow->next;
        }
        slow->next = slow->next->next;
        return dummyHead->next;
    }
};

普通解法：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* deleteMiddle(ListNode* head) {
        int length = 0;
        ListNode* pMove = head;
        while(pMove){
            length += 1;
            pMove = pMove->next;
        }
        if(length <= 1){
            return NULL;
        }
        int index = length % 2 == 1 ? (length - 1) / 2 : length / 2;
        ListNode* pre = NULL;
        ListNode* cur = head;
        for(; index > 0; index--){
            pre = cur;
            cur = cur->next;
        }
        if(pre->next){
            pre->next = cur->next;
        }
        return head;
    }
};

Java解法

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode deleteMiddle(ListNode head) {
        if(head == null)return null;
        ListNode prev = new ListNode(0);
        prev.next = head;
        ListNode slow = prev;
        ListNode fast = head;
        while(fast != null && fast.next != null){
            slow = slow.next;
            fast = fast.next.next;
        }
        slow.next = slow.next.next;
        return prev.next;
    }
}

Python解法

# Definition for singly-linked list.
# class ListNode(object):
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution(object):
    def deleteMiddle(self, head):
        """
        :type head: Optional[ListNode]
        :rtype: Optional[ListNode]
        """
        if head == None :return None
        prev = ListNode(0)
        prev.next = head
        slow = prev
        fast = head
        while fast != None and fast.next != None:
            slow = slow.next
            fast = fast.next.next
        
        slow.next = slow.next.next
        return prev.next

2487. Remove Nodes From Linked List

You are given the head of a linked list.

Remove every node which has a node with a greater value anywhere to the right side of it.

Return the head of the modified linked list.

Example 1:

Input: head = [5,2,13,3,8]
Output: [13,8]
Explanation: The nodes that should be removed are 5, 2 and 3.

• Node 13 is to the right of node 5.
• Node 13 is to the right of node 2.
• Node 8 is to the right of node 3.

Example 2:

Input: head = [1,1,1,1]
Output: [1,1,1,1]
Explanation: Every node has value 1, so no nodes are removed.

Constraints:

• The number of the nodes in the given list is in the range [1, 10^5].
• 1 <= Node.val <= 10^5

思路

题解链接

Iterate on nodes in reversed order.

When iterating in reversed order, save the maximum value that was passed before.

Overview

Given the head of a linked list, the task is to remove every node that has a node with a greater value anywhere on its right side. This means that after processing the linked list, every node will only have nodes with smaller values to their right, or the linked list should be in decreasing order.

Key Observations

1. The nodes in the linked list have positive values.
2. There may be duplicate values.
3. We manipulate the list by deleting values, not by sorting it.

Approach 1: Stack

Intuition

A challenge associated with this problem is that, for a given node, we need to not only delete the node directly to the right if it has a larger value but also delete all other nodes to the right that have larger values. The brute force approach involves iterating through the linked list using nested loops, comparing the value of each node with the nodes that follow it, and deleting any nodes whose values are smaller than the following nodes. However, this approach is inefficient, with a quadratic time complexity.

The resultant linked list should be in decreasing order. We can leverage this fact to develop a more efficient solution.

A list in decreasing order, if reversed, is in increasing order.

If we reverse the list, the node values should be in increasing order after deleting nodes. We can delete any nodes whose values are smaller than the nodes before them. This strategy ensures efficient deletion of all nodes that have nodes with a greater value to their right (in the original order) without using nested loops.

The list we are given is a singly linked list, so we can't easily traverse it in reverse from tail to head.

Whenever a problem requires reversing a sequence, it is worth considering using a stack.

Stacks are a First-In-Last-Out (FILO) data structure, meaning that the first items added to the stack are the last ones removed. Consequently, if you push a sequence of items into a stack and then remove them, the sequence will be reversed. Learn more about stacks by reading our Stack Explore Card.

We start by adding all of the nodes to a stack.

Next, we create a new linked list to store the result. We keep track of the maximum node value encountered so far using the variable maximum.

Then, we pop each node from the stack. If the node's value is not smaller than the maximum, we create a new node with that value and add it to the resultList. Since the linked list is reversed, we build the resultList from back to front, continuously adding new nodes to the beginning.

Algorithm

1. Initialize an empty stack to be used for reversing the nodes.
2. Set a pointer current to head.
3. While current is not Null:
   • Add current to the stack.
   • Set current to current.next.
4. Pop the node from the top of the stack and set current to that node.
5. Initialize a variable maximum to current.val.
6. Create a new ListNode resultList with maximum as its value.
7. While the stack is not empty:
   • Pop the node from the top of the stack and set current to that node.
   • If current.val < maximum:
     • Continue; this node does not need to be added to the resultList.
   • Otherwise, add a new node to the front of the resultList:
     • Create a new ListNode newNode with current.val as its value.
     • Set newNode.next to resultList.
     • Set resultList to newNode.
     • Update maximum to current.val.
8. Return resultList.

Complexity Analysis

Let n be the length of the original linked list.

• Time complexity: O(n)

  Adding the nodes from the original linked list to the stack takes O(n).

  Removing nodes from the stack and adding them to the result takes O(n), as each node is popped from the stack exactly once.

  Therefore, the time complexity is O(2n), which simplifies to O(n).

• Space complexity: O(n)

  We add each of the nodes from the original linked list to the stack, making its size n.

  We only use resultList to store the result, so it does not contribute to the space complexity.

  Therefore, the space complexity is O(n).

Approach 2: Recursion

Intuition

The nodes we retain in the linked list must meet the following criteria: Each node's value is not smaller than the values of the following nodes.

Linked lists are often manipulated using recursion. This problem is an excellent candidate for recursion because it can be broken down into subproblems that collectively solve the main problem.

Consider a node B situated in the middle of the linked list, where all subsequent nodes have values less than or equal to B's value. If node B satisfies this criterion, its value is not smaller than the values of the following nodes. For the node A directly preceding B, if A is not smaller than B, then A is also not smaller than any nodes following B. This holds due to the transitive property: if a≥b and b≥c, then a≥c.

This means that if we've solved the subproblem for nodes to the right of a given node in the linked list, we can efficiently solve the problem for that node.

Let`s begin by discussing the base cases:

1. The linked list is empty:

   • An empty list meets the criteria, so we return the head.

2. The linked list has only one node:

   • A list with one node also meets the criteria, because there are no following nodes. Again, we return the head.

We can develop a strategy for handling longer lists by thinking about handling a linked list with two nodes.

For a linked list with two nodes, there are two cases for the head node:

1. The head node's value is the same size or larger than the next node's value.

   • This linked list meets the criteria. Return the list.

2. The head node's value is smaller than the next node's value.

   • We need to delete head. Return the next node.

For linked lists with more than two nodes, the main adjustment we need to make is to check the rest of the linked list.

The challenge we face is ensuring that head.next is set to the correct next node. Does the next node also need to be deleted? Are there other nodes later in the linked list that have values that are greater than head?

Instead of simply setting head to head.next to progress to the next node, we recursively call removeNodes(head.next). This recursive function removes nodes with greater values anywhere to the right. This ensures that head is set to the correct node and that the rest of the linked list also meets the criteria.

Algorithm

1. Base Case: If head or head.next is Null, return head.
2. Recursive Call: Set nextNode to removeNodes(head.next).
3. Comparison: If head.val is less than nextNode.val, we need to remove head. Return nextNode.
4. Otherwise, set head to head.next and then return head.

Complexity Analysis

Let n be the length of the original linked list.

• Time complexity: O(n)

  We call removeNodes() once for each node in the original linked list. The other operations inside the function all take constant time, so the time complexity is dominated by the recursive calls. Thus, the time complexity is O(n).

• Space complexity: O(n)

  Since we make n recursive calls to removeNodes(), the call stack can grow up to size n. Therefore, the space complexity is O(n).

Approach 3: Reverse Twice

Intuition

The first approach used a stack to reverse the linked list, resulting in linear auxiliary space. However, instead of using a stack, we can write a function to reverse the nodes in place, avoiding the need for auxiliary space. This task is explored in the problem Reverse Linked List. The basic idea is to set each node's next field to point to the previous node.

After reversing the linked list, the node values will be in increasing order, allowing us to delete any nodes whose values are smaller than the nodes preceding them.

To facilitate this process, we maintain the maximum node value found so far using the variable maximum.

We traverse each node, current, in the reversed linked list and update the maximum value accordingly. If the value of the current node is smaller than the maximum, we delete current. Deleting nodes in place requires us to track the previous node so that we can correctly link it to the next node if we delete the current node.

Once we have traversed the linked list to delete the nodes, we have a linked list that is in increasing order.

However, since the desired result should be in decreasing order, we reverse the modified linked list and then return it.

Interview Tip: In-place Algorithms

This approach modifies the input. In-place algorithms overwrite the input to save space, but sometimes this can cause problems.

Here are a couple of situations where an in-place algorithm might not be suitable.

1. The algorithm needs to run in a multi-threaded environment, without exclusive access to the array. Other threads might need to read the array too, and might not expect it to be modified.

2. Even if there is only a single thread, or the algorithm has exclusive access to the array while running, the array might need to be reused later or by another thread once the lock has been released.

In an interview, you should always check whether the interviewer minds you overwriting the input. Be ready to explain the pros and cons of doing so if asked!

Algorithm

1. Define a function reverseList that takes the head of a linked list as input and reverses it, returning the new head.
   • Initialize three pointers, prev to null, current to head, and nextTemp to null.
   • While current is not null:
     • Set nextTemp to current.next.
     • Reverse the order of the nodes by setting current.next to prev.
     • Progress both pointers by setting prev to current and current to nextTemp.
   • Return prev.
2. Reverse the original linked list using reverseList(head). Set head to the reversed linked list.
3. Initialize a variable maximum to 0.
4. Initialize two pointers, prev to null and current to head.
5. Delete the nodes that are smaller than the node before them. While current is not null:
   • Update maximum to the max between maximum and current.val.
   • If current.val is less than maximum, delete current.
     • Skip the current node by setting prev.next to current.next.
     • Set a pointer deleted to current.
     • Move current to current.next to progress to the next node.
     • Set deleted.next to null to remove any additional pointers to the new current node.
   • Otherwise, if current.val is not less than maximum, retain current and progress both pointers by setting prev to current and current to current.next.
6. Reverse and return the modified linked list using reverseList(head).

Complexity Analysis

Let n be the length of the original linked list.

• Time complexity: O(n)

  Reversing the original linked list takes O(n).

  Traversing the reversed original linked list and removing nodes takes O(n).

  Reversing the modified linked list takes an additional O(n) time.

  Therefore, the total time complexity is O(3n), which simplifies to O(n).

• Space complexity: O(1)

  We use a few variables and pointers that use constant extra space. Since we don't use any data structures that grow with input size, the space complexity remains O(1).

C++解法

Approach 3: Reverse Twice

class Solution {
private:
    ListNode* reverseList(ListNode* head) {
        ListNode* prev = nullptr;
        ListNode* current = head;
        ListNode* nextTemp = nullptr;

        // Set each node's next pointer to the previous node
        while (current != nullptr) {
            nextTemp = current->next;
            current->next = prev;
            prev = current;
            current = nextTemp;
        }
        
        return prev;
    }
public:
    ListNode* removeNodes(ListNode* head) {
        // Reverse the original linked list
        head = reverseList(head);

        int maximum = 0;
        ListNode* prev = nullptr;
        ListNode* current = head;

        // Traverse the list deleting nodes
        while (current != nullptr) {
            maximum = max(maximum, current->val);

            // Delete nodes that are smaller than maximum
            if (current->val < maximum) {
                // Delete current by skipping
                prev->next = current->next;
                ListNode* deleted = current;
                current = current->next;
                deleted->next = nullptr;
            }

            // Current does not need to be deleted
            else {
                prev = current;
                current = current->next;
            }
        }
        
        // Reverse and return the modified linked list
        return reverseList(head);
    }
};

Approach 2: Recursion

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* removeNodes(ListNode* head) {
        // Base case, reached end of the list
        if (head == nullptr || head->next == nullptr) {
            return head;
        }

        // Recursive call
        ListNode* nextNode = removeNodes(head->next);

        // If the next node has greater value than head delete the head
        // Return next node, which removes the current head and makes next the new head
        if (head->val < nextNode->val) {
            return nextNode;
        }

        // Keep the head
        head->next = nextNode;
        return head;
    }
};

Approach 1: Stack

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* removeNodes(ListNode* head) {
        stack<ListNode*> stack;
        ListNode* current = head;

        // Add nodes to the stack
        while (current != nullptr) {
            stack.push(current);
            current = current->next;
        }

        current = stack.top();
        stack.pop();
        int maximum = current->val;
        ListNode* resultList = new ListNode(maximum);

        // Remove nodes from the stack and add to result
        while (!stack.empty()) {
            current = stack.top();
            stack.pop();
            // Current should not be added to the result
            if (current->val < maximum) {
                continue;
            }
            // Add new node with current's value to front of the result
            else {
                ListNode* newNode = new ListNode(current->val);
                newNode->next = resultList;
                resultList = newNode;
                maximum = current->val;
            }
        }

        return resultList;
    }
};

Java解法

Approach 2: Recursion

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
 class Solution {   
    public ListNode removeNodes(ListNode head) {
        // Base case, reached end of the list
        if (head == null || head.next == null) {
            return head;
        }

        // Recursive call
        ListNode nextNode = removeNodes(head.next);

        // If the next node has greater value than head, delete the head
        // Return next node, which removes the current head and makes next the new head
        if (head.val < nextNode.val) {
            return nextNode;
        }

        // Keep the head
        head.next = nextNode;
        return head;
    }
}

Python3解法

Approach 1: Stack

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def removeNodes(self, head: Optional[ListNode]) -> Optional[ListNode]:
        stack = []
        current = head

        # Add nodes to the stack
        while current:
            stack.append(current)
            current = current.next

        current = stack.pop()
        maximum = current.val
        result_list = ListNode(maximum)

        # Remove nodes from the stack and add to result
        while stack:
            current = stack.pop()
            # Current should not be added to the result
            if current.val < maximum:
                continue
            # Add new node with current's value to front of the result
            else:
                new_node = ListNode(current.val)
                new_node.next = result_list
                result_list = new_node
                maximum = current.val

        return result_list
        

Go解法

3217. Delete Nodes From Linked List Present in Array

You are given an array of integers nums and the head of a linked list. Return the head of the modified linked list after removing all nodes from the linked list that have a value that exists in nums.

Example 1:

Input: nums = [1,2,3], head = [1,2,3,4,5]

Output: [4,5]

Explanation:

Remove the nodes with values 1, 2, and 3.

Example 2:

Input: nums = [1], head = [1,2,1,2,1,2]

Output: [2,2,2]

Explanation:

Remove the nodes with value 1.

Example 3:

Input: nums = [5], head = [1,2,3,4]

Output: [1,2,3,4]

Explanation:

No node has value 5.

Constraints:

• 1 <= nums.length <= 10^5
• 1 <= nums[i] <= 10^5
• All elements in nums are unique.
• The number of nodes in the given list is in the range [1, 10^5].
• 1 <= Node.val <= 10^5
• The input is generated such that there is at least one node in the linked list that has a value not present in nums.

思路

方法一：迭代处理数组中的元素，然后调用removeElements()函数，这种方法会超时。

方法二：哈希数组，遍历一遍链表

不要删除指针，否则容易出现悬挂指针问题，具体报错信息为ERROR: AddressSanitizer: heap-use-after-free on address

C++解法

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* modifiedList(vector<int>& nums, ListNode* head) {
        if (nums.size() == 0 || head == NULL) {
            return head;
        }
        bitset<100001> hasN = 0;
        for(int x : nums){
            hasN[x] = 1;
        }
        ListNode* dummyHead = new ListNode(0);
        dummyHead->next = head;
        ListNode* pre = dummyHead;
        ListNode* cur = head;
        while(cur){
            if(hasN[cur->val]){
                pre->next = cur->next;
                cur = pre->next;
            }else{
                pre = cur;
                cur = cur->next;
            }
        }
        return dummyHead->next;
    }
};