债务偿还

• 学习目标
• 思维导图
• 5.1 未偿还本金余额
• 5.2 本息分解
• 5.3 例题：本息分解
• 5.4 等额偿债基金
• 5.5 例题：等额偿债基金
• 5.6 偿债基金的价值方程
• 5.7 变额分期偿还：算术级数变化
• 5.8 变额分期偿还：几何级数变化
• 5.9 变额偿债基金
• 5.10 例题：变额偿债基金

学习目标

在分期偿还方法中，可以计算偿还本金、支付利息和未偿还本金余额；在偿债基金方法中，可以计算向偿债基金的储蓄额、支付的利息和本金余额；在出现负偿的还情况下，可以计算合理的贷款本金；可以分析偿债基金方法与分期偿还方法之间的关系。

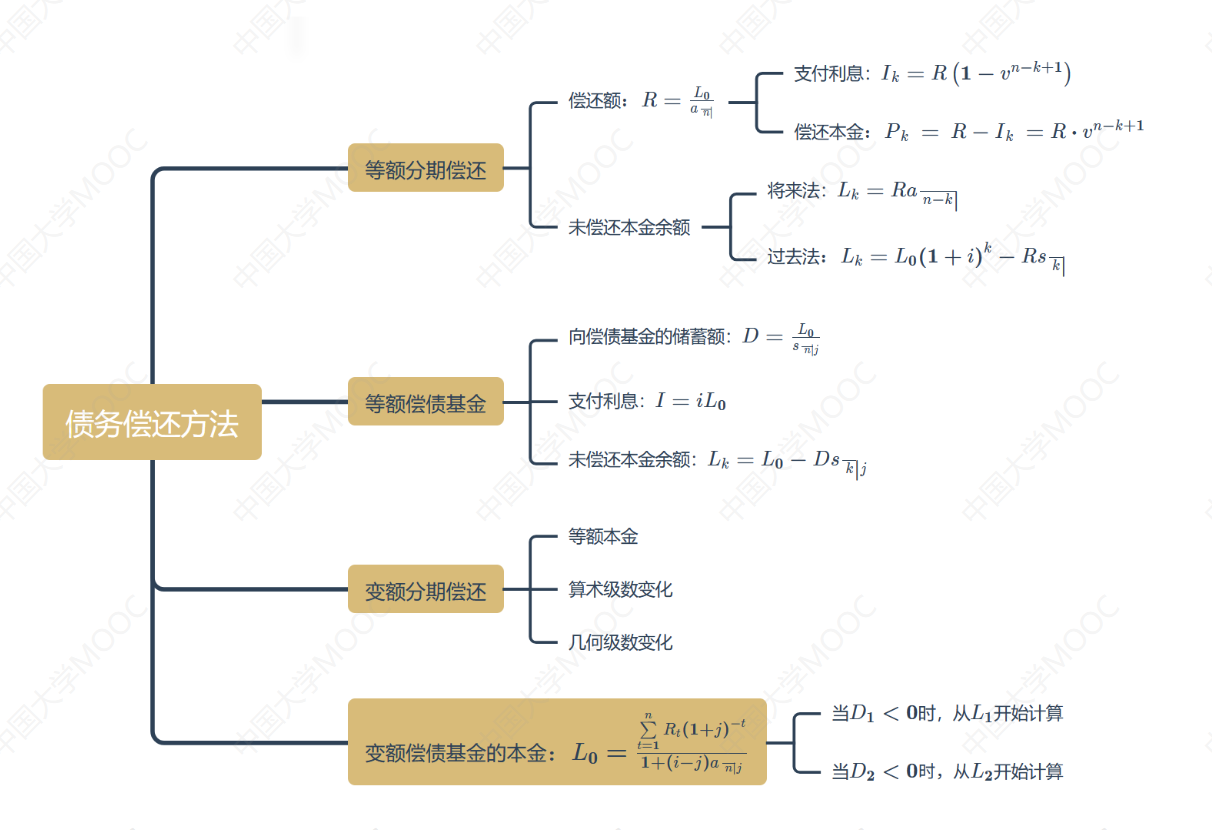
思维导图

债务偿还PPT

5.1 未偿还本金余额

本视频介绍了债务偿还的两种常用方法：分期偿还和偿债基金。在分期偿还方法中，又分为等额分期偿还和变额分期偿还。在偿债基金方法中，又分为等额偿债基金和变额偿债基金。视频重点解决了等额分期偿还方法中的三个问题：计算借款人每次偿还的金额、每一期末借款人未偿还的本金余额、每次偿还的总金额中本金和利息的分配。视频还介绍了两种计算未偿还本金余额的方法：将来法和过去法，并证明了这两种方法计算的结果是相同的。最后，视频通过一个例子演示了如何计算在特定情况下的贷款余额。

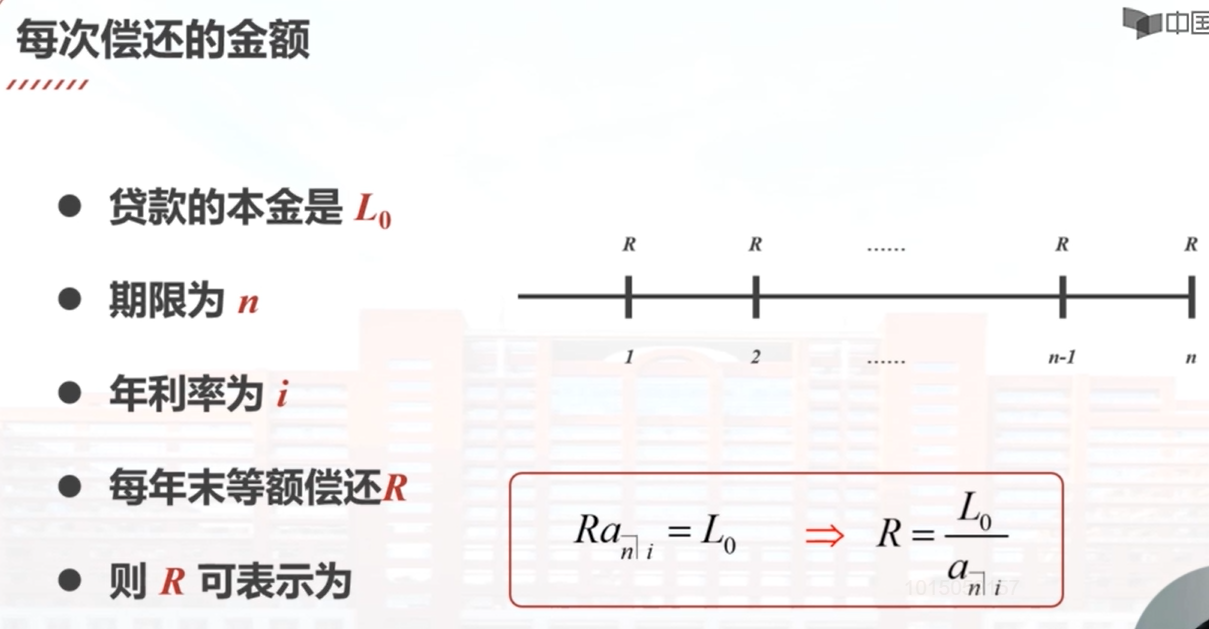
问题：每年偿还R，第k年末的未偿还本金余额?

方法：将来法、过去法

方法一：将来法

把将来需要偿还的金额折现到第k年末。将来需要偿还n-k次。

$\boxed{\begin{array}{c}{L}_k=R{a}_{\overline{n-k}|i}\end{array}}$

方法二：过去法

从贷款本金的累积值中减去已偿还金额的累积值

$\boxed{\begin{array}{c}{L}_k=L_0(1+i{)}^k-R{s}_{\overline{k}|}\end{array}}$

例：一笔贷款的年利率为9%，期限为20年，每年末偿还1000。在第5年末，借款人希望多偿还2000，然后将剩余本金在未来12年内等额偿还。计算后12年每年末等额偿还的金额。

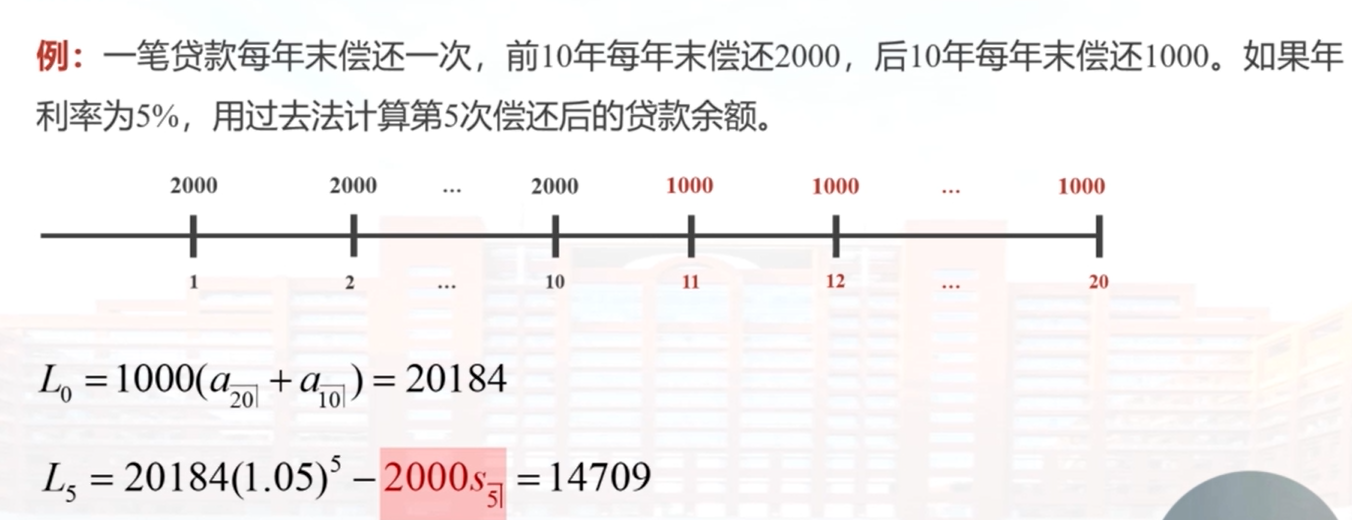
5.2 本息分解

本息分解是等额分期偿还方法中的一个重要概念。在每年末，借款人偿还的总金额R可以分解为利息Ik和本金Pk。利息的计算可以通过将年初本金余额乘以贷款利率得到。而年初本金余额可以通过将R乘以一个n-k+1年期的年金现值因子来计算。本金Pk可以通过将R减去利息来得到。等额分期偿还表可以根据每年末的还款额、未偿还本金余额和本金利息分解来构造。在等额分期偿还中，每年偿还的总金额相等，但构成不同。早期偿还主要是利息，后期偿还主要是本金。未偿还本金余额逐年减小，特别是在较长期限的情况下，未偿还本金余额几乎与原始贷款本金相等。

构成要素：

• 每年末的还款额
• 每年末未偿还的本金余额
• 本息分解：
  • 偿还本金
  • 支付利息

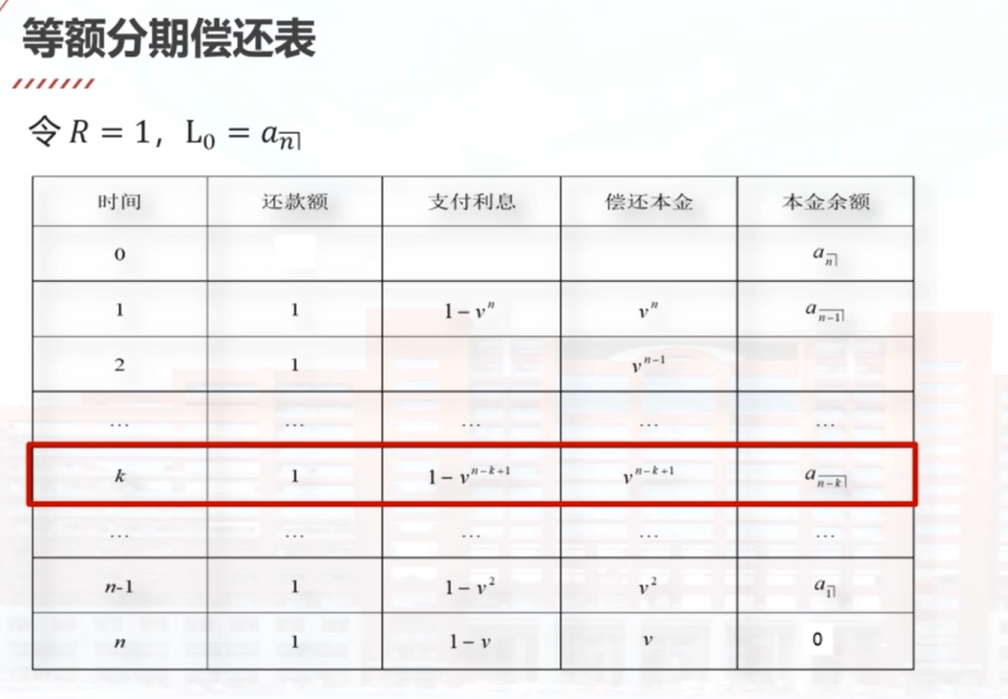
5.3 例题：本息分解

本视频介绍了一个贷款的例子，贷款期限为2年，每季度末等额偿还一次。贷款利率为6%，每个季度的利率为1.5%。第一年末偿还的本金为2000元，需要计算第二年末偿还的本金。通过公式计算得到第二年末偿还的本金为2122.73元。视频还介绍了如何使用EXCEL计算分期偿还表。

例：1000的贷款在每年末偿还100，直至偿还完所有贷款本息为止，如果最后一次偿还金额不足100时，按实际需要偿还的金额偿还。假设年利率为4%，计算第四次的还款额中包含的利息和本金分别是多少?

5.4 等额偿债基金

债务偿还的方法可以分为两大类，分期偿还和偿债基金。等额偿债基金是指借款人每年末支付的金额完全相等，包括贷款利息和向偿债基金的储蓄额。偿债基金累积到贷款到期时，价值等于贷款本金，用于偿还贷款本金。借款人每年支付的总金额是相等的，包括利息和向偿债基金的储蓄额。借款人每年末向偿债基金的储蓄额可以通过贷款本金除以n年期的累积值因子来计算。当贷款利率和偿债基金利率相等时，等额偿债基金方法等价于等额分期偿还方法。

借款人每年末支付相等金额：一部分是贷款利息，另一部分是向偿债基金的储蓄。

例：借款人从银行获得10000元的贷款，期限为5年，年利率为6%。双方约定：

（1）借款人每年末向银行支付600元利息;

（2）借款人在银行开设一个存款账户，每年末存入1791.76元，按5.5%的利率计息。到第5年末，帐户余额正好是10000元，用于偿还贷款本金。

借款人在银行开设的帐户就是偿债基金。

符号：

• 贷款利率：i
• 偿债基金利率：j
• 每年支付的利息：$I=i{L}_0$
• 每年向偿债基金的储蓄额：D

5.5 例题：等额偿债基金

这个视频讲解了等额偿债基金方法和分期偿还方法的比较。在偿债基金方法中，借款人的资金使用成本取决于偿债基金利率，而不是贷款利率。如果偿债基金利率小于贷款利率，借款人的资金使用成本会高于贷款利率。相反，如果偿债基金利率大于贷款利率，借款人的资金使用成本会低于贷款利率。通过一个例子，我们可以计算出等价的分期偿还方法的贷款利率，该利率为6.552%。这个利率要高于偿债基金方法中的名义贷款利率，因为偿债基金方法中的偿债基金利率为5%。视频还介绍了如何使用Excel构建等额偿债基金表。

例：对借款人而言，下列哪种贷款的成本较低？

分期偿还法：贷款利率为6% 偿债基金法：贷款利率为6%，偿债基金利率为5%

解释：在偿债基金方法中，贷款成本高于6%

例：对借款人而言，下列哪种贷款的成本较低？

分期偿还法：贷款利率为6%

偿债基金法：贷款利率为6%，偿债基金利率为7%

解释：在偿债基金方法中，贷款成本低于6%

例：两笔贷款的本金均为10000元，期限均为5年，但偿还方式不同：

第一笔：采用偿债基金方法偿还，贷款利率为6%，偿债基金利率为5%。

第二笔：采用等额分期方法偿还。

当第二笔贷款的利率为多少时，两笔贷款对借款人而言是等价的。

5.6 偿债基金的价值方程

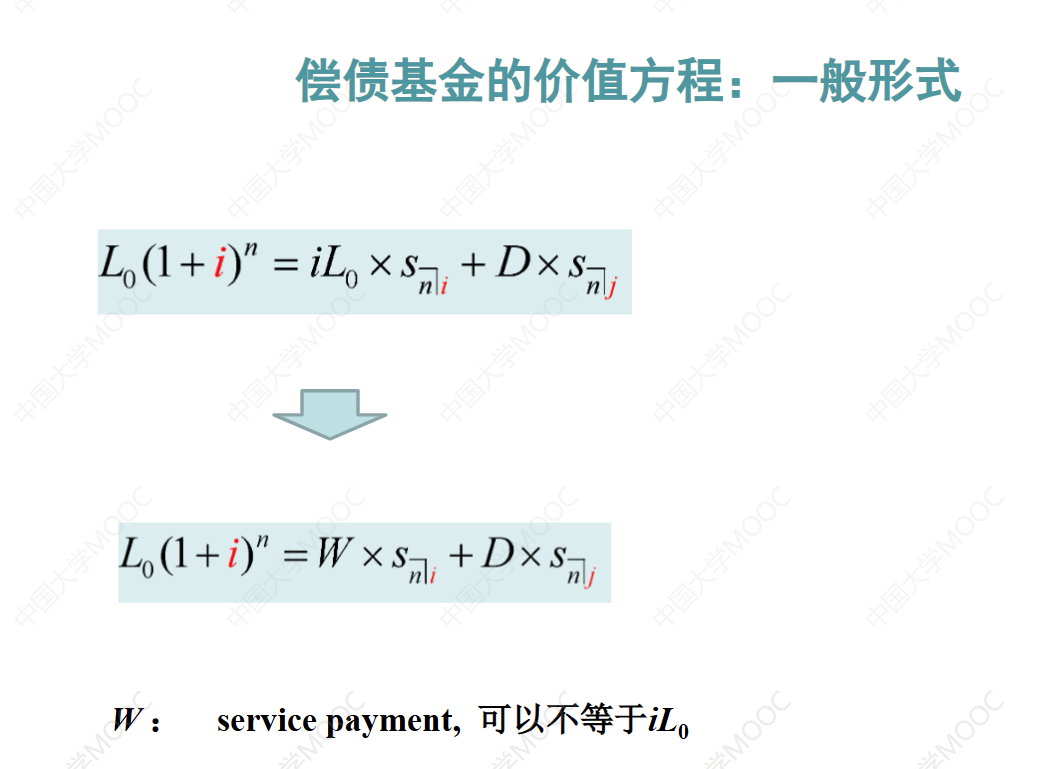
这节课讨论了偿债基金的价值方程，左边表示贷款本金在第n年末的累积值，右边表示借款人每年末的偿还金额的累积值。通过数学变换和经济学解释，证明了这个价值方程成立。在偿债基金方法中，借款人每年的还款额包括支付的利息和向偿债基金的储蓄额。通过这个价值方程，可以求解未知量。举例计算了贷款本金为1万，用偿债基金方法偿还10年，贷款利率为5%，每年支付600的服务费的情况下，借款人每年向偿债基金的储蓄额为728.15。同时计算了与等额分期偿还方法等价的贷款利率为5.52%。分期偿还方法和偿债基金方法的区别在于计算利息时使用的利率不同。

偿债基金的价值方程

$L_0(1+i{)}^n=i{L}_0\times s_{n|i}+D\times s_{n|j}$

验证

$\begin{array}{rlrl}& i{L}_0\times s_{\overline{n}|i}+D\times s_{\overline{n}|j}& & =i{L}_0\times s_{\overline{n}|i}+L_0\\ & & & =L_0\left(i\times \frac{{\left(1+i\right)}^n-1}{i}+1\right)\\ & & & =L_0(1+i{)}^n\end{array}$

5.7 变额分期偿还：算术级数变化

本视频介绍了变额分期偿还的概念和三种具体方法：等额本金偿还、算术级数变化和几何级数变化。以等额本金偿还为例，假设贷款本金为1万元，期限为5年，年利率为5%，每年末偿还2000元的本金。通过构造分期偿还表，可以计算出每年末的未偿还本金余额和支付的利息。另外，还介绍了一个例子，通过解方程可以计算出变额分期偿还的利率。最后，讲解了变额分期偿还的第二种类型，即偿还额按算术级数变化的情况。通过一个例子，计算了贷款本金和第三年末支付的利息和本金。

假设贷款金额为$L_0$，每年末偿还$R_t,t=(1,2,...,n)$则有$L_0={\sum }_t^n{v}^t{R}_t$

变额分期偿还方法：

• 等额本金
• 算术级数变化
• 几何级数变化

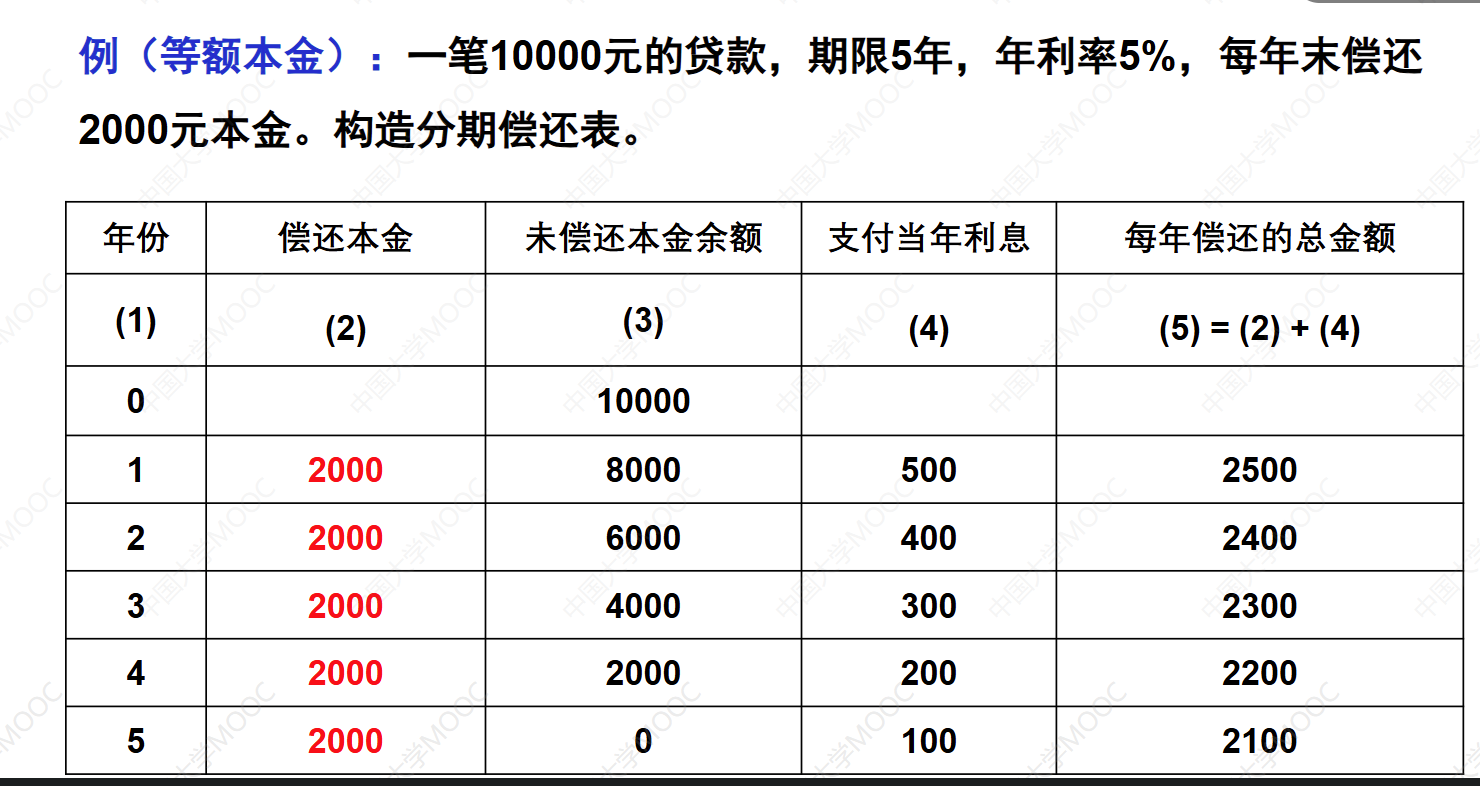
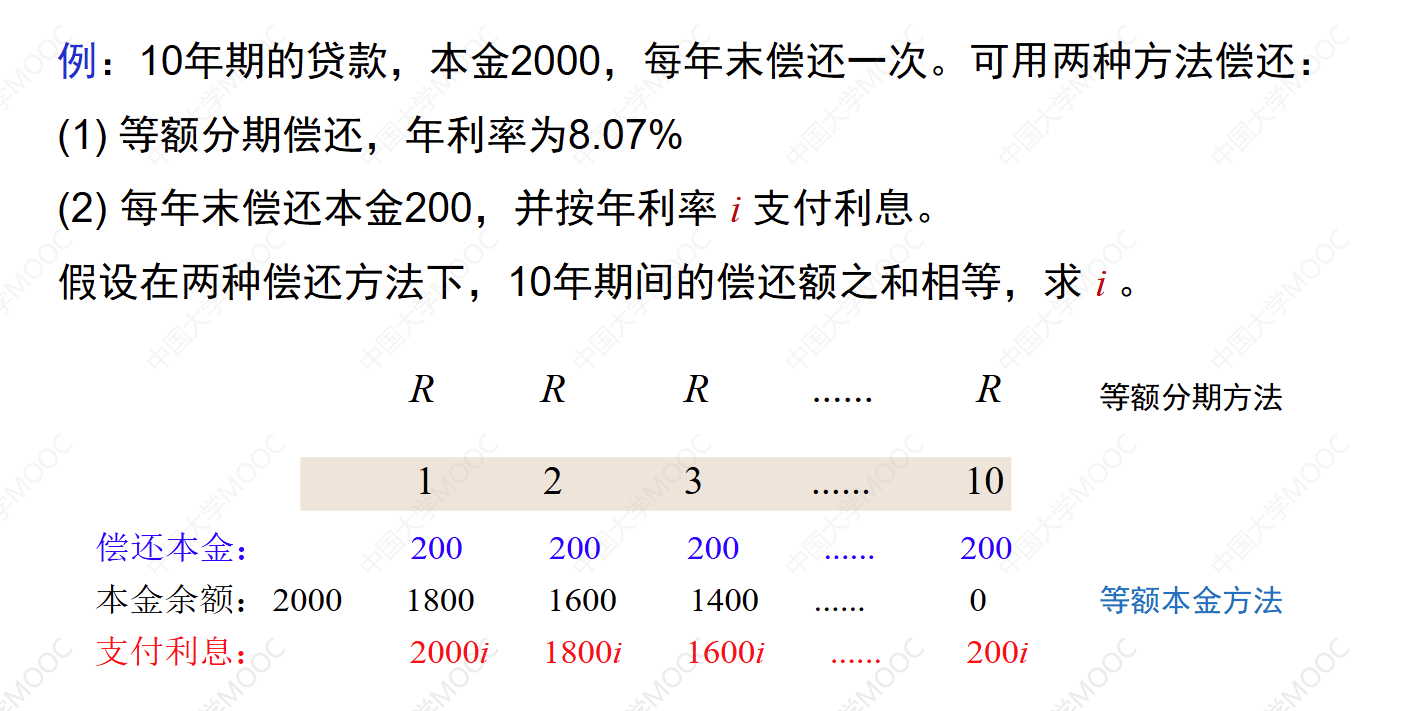
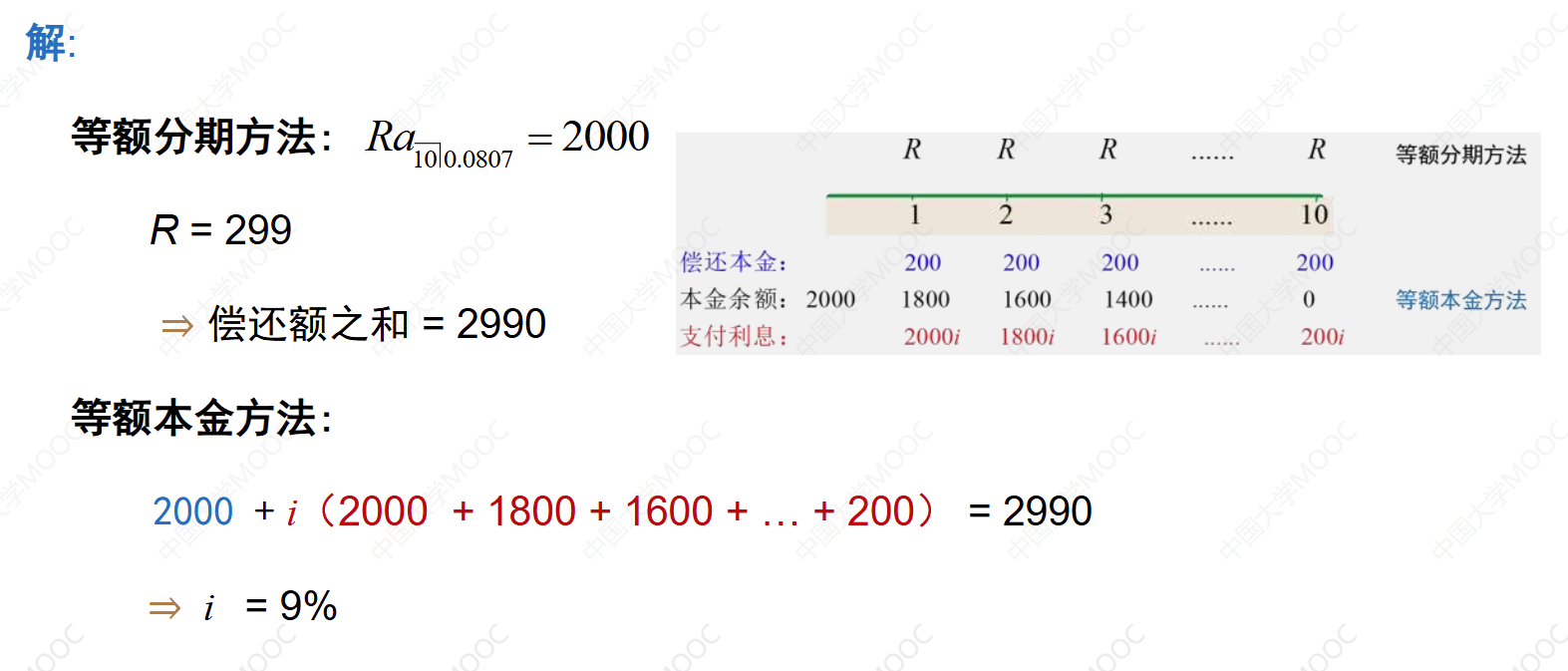
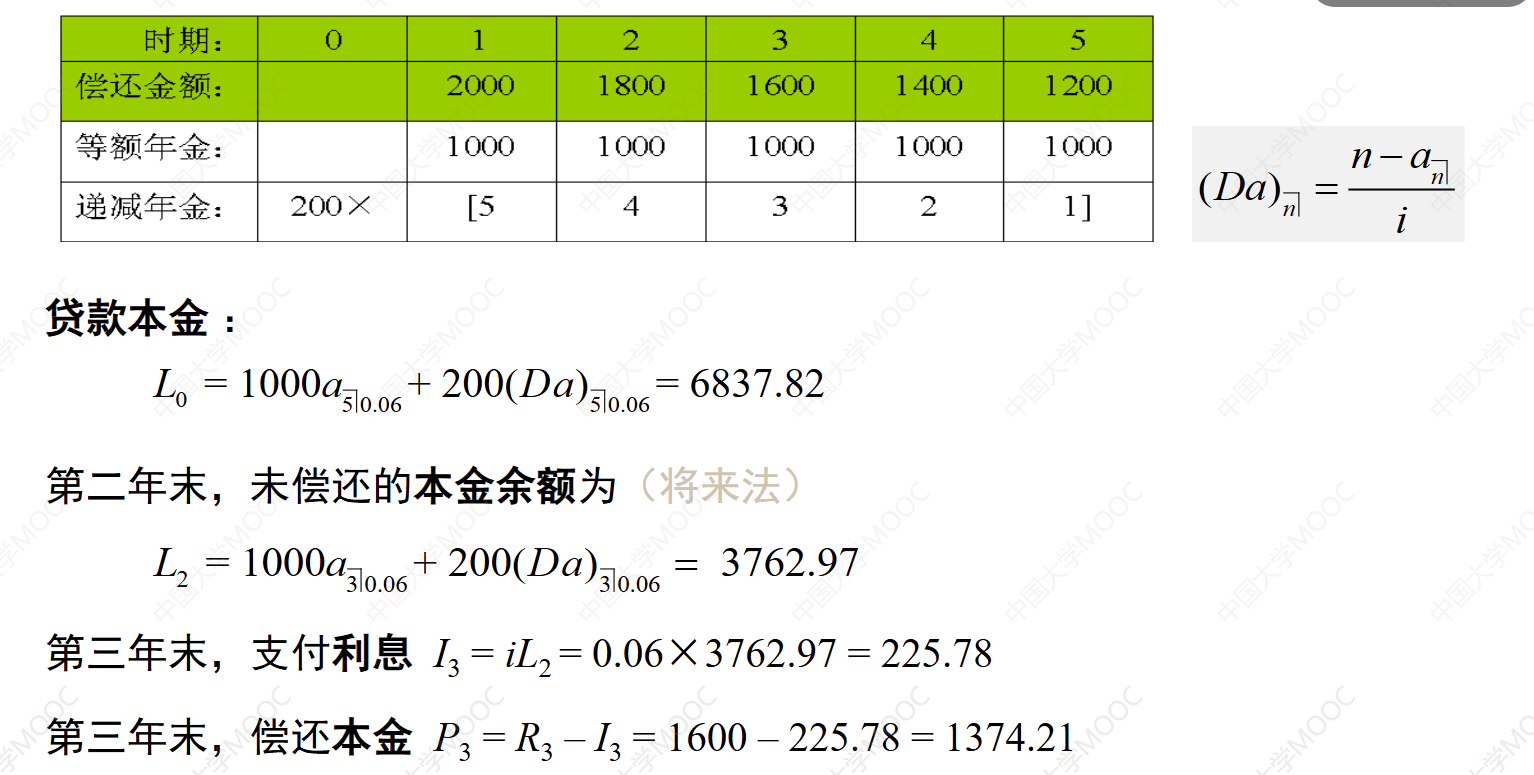
例（算术级数变化）：贷款期限为5年，年利率为6%。借款人每年末的偿还额为： 2000，1800，1600, 1400，1200。计算：

（1）贷款本金为多少？

（2）第三年末支付的利息和偿还的本金分别为多少？

5.8 变额分期偿还：几何级数变化

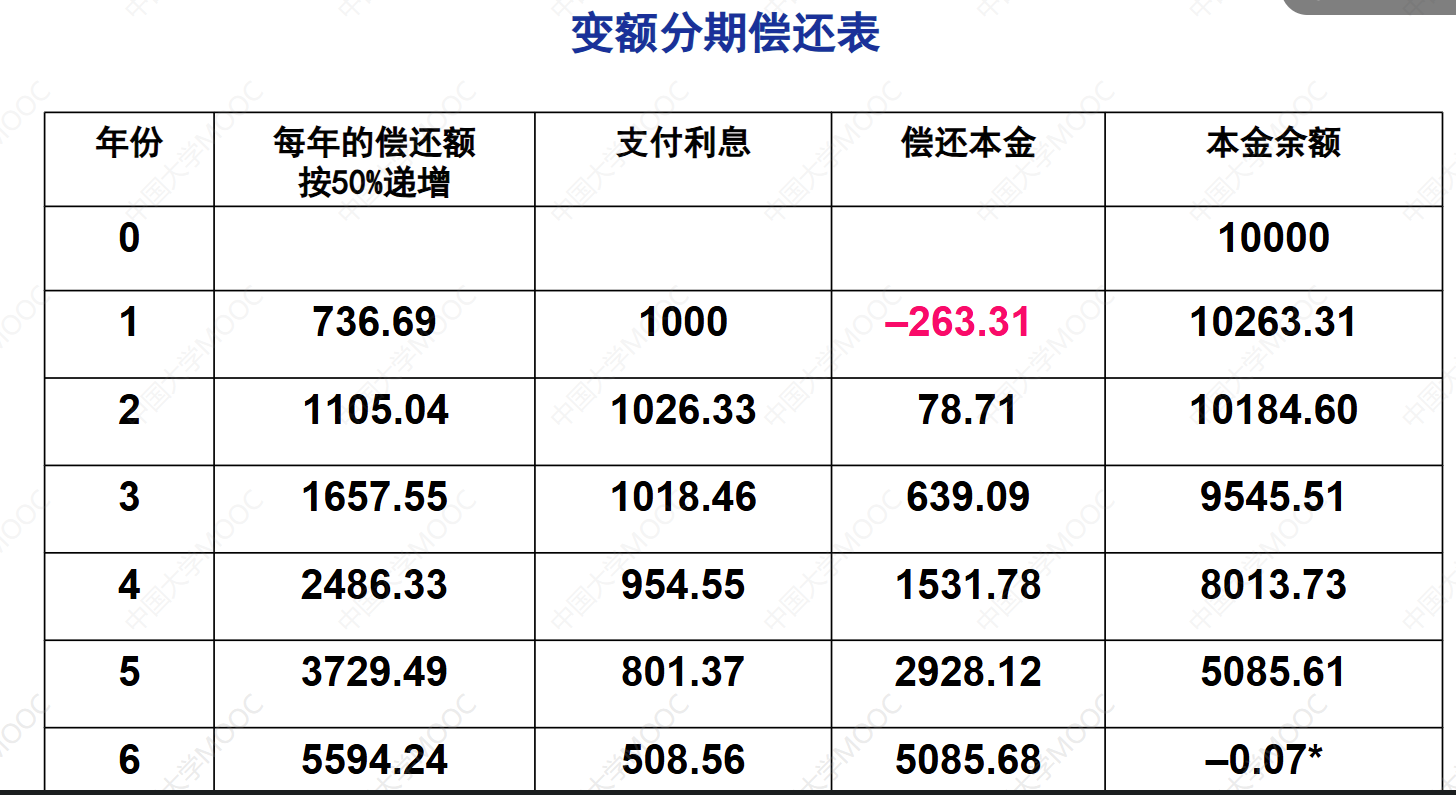
这个视频介绍了变额分期偿还的第三种类型，即还款额按几何级数变化。以一个例子来说明，假设贷款本金为1万，年利率为10%，贷款期限为6年，借款人每年末偿还一次，每次的偿还额以50%递增。根据这些条件，可以构造出分期偿还表，计算每年支付的利息和偿还的本金。通过计算，得到了每年末的还款总额和支付的利息，以及每年末的本金余额。最后，根据时间零点的贷款本金和还款总额的现值相等的条件，解出了第一年末的还款额为736.69元。

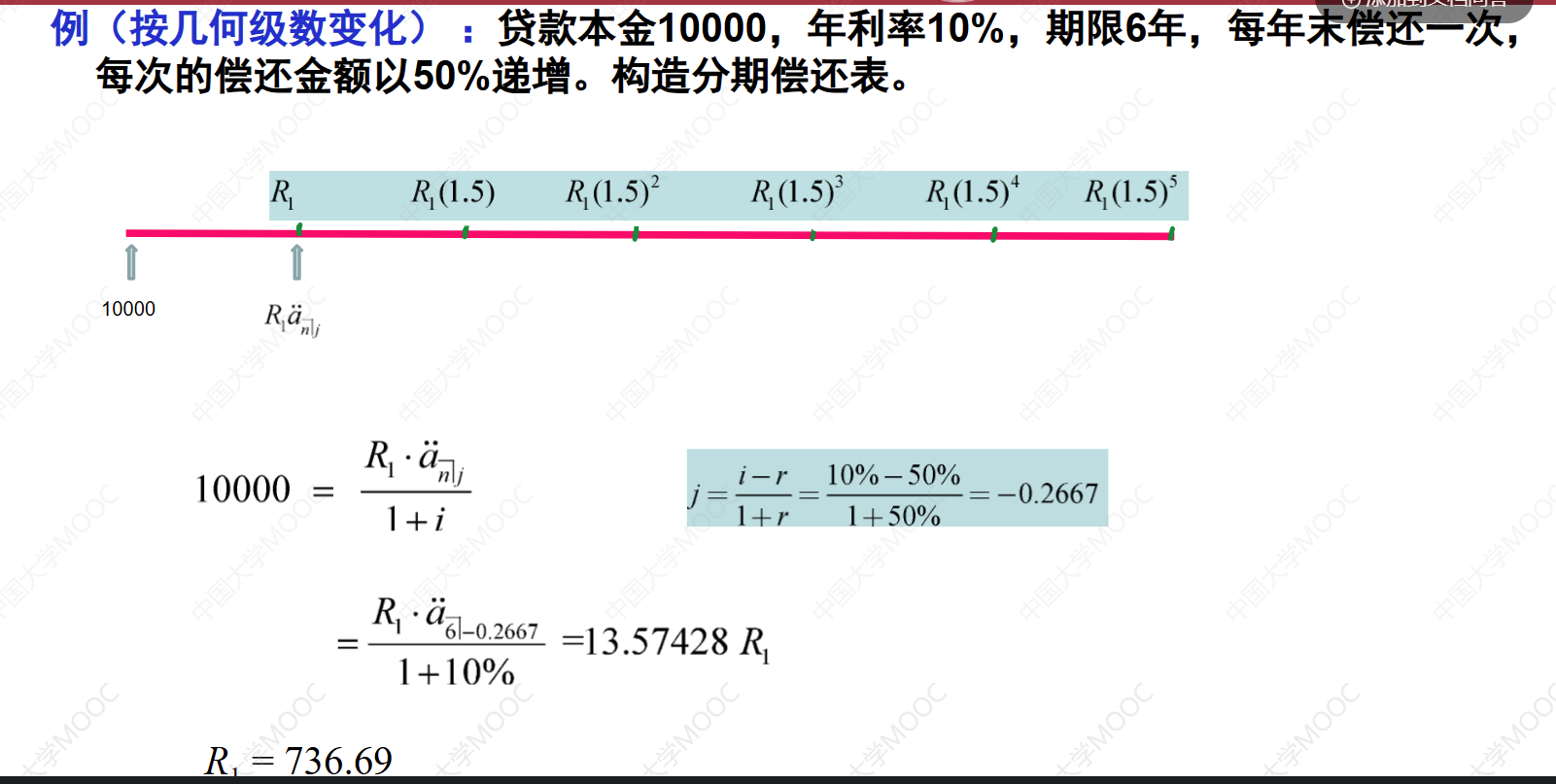
解：第一年末的偿还额R1=736.69

第一年，利息为I1=10000×0.1=1000

第一年的偿还额736.69元不足以支付利息1000，故偿还的本金为负 P1 =R1 - I1 = 736.69 - 1000 =-263.31

第一年末，本金余额L=L0-P1=10000+263.31=10263.31

第二年，利息为I2=iL1=0.1×10263.31=1026.33

第二年末，偿还额为R2=1.5R1= 736.69×1.5=1105.04

第二年末，偿还的本金为P2=R2-I2=1105.04－1026.33= 78.71

第二年末，本金余额L2=L1-P2=10263.31-78.71=10184.6

5.9 变额偿债基金

变额偿债基金是一种常用的贷款偿还方法，包括等额偿债基金和变额偿债基金。在变额偿债基金中，借款人每年偿还的总金额记为Rt，其中Rt表示借款人在第t年偿还的总金额。Rt可以分解为借款人每年支付的利息和向偿债基金的储蓄额。偿债基金的累积价值应该等于贷款本金，因为偿债基金是用于偿还贷款本金的。贷款本金可以通过借款人每年偿还的总金额Rt在第n年末的累积值来计算。在变额偿债基金方法中，贷款本金可以表示为借款人每年偿还的总金额Rt在第n年末的累积值除以Rt在第n年末的累积值。当贷款利率和偿债基金的利率相等时，偿债基金方法和分期偿还方法是等价的。

5.10 例题：变额偿债基金

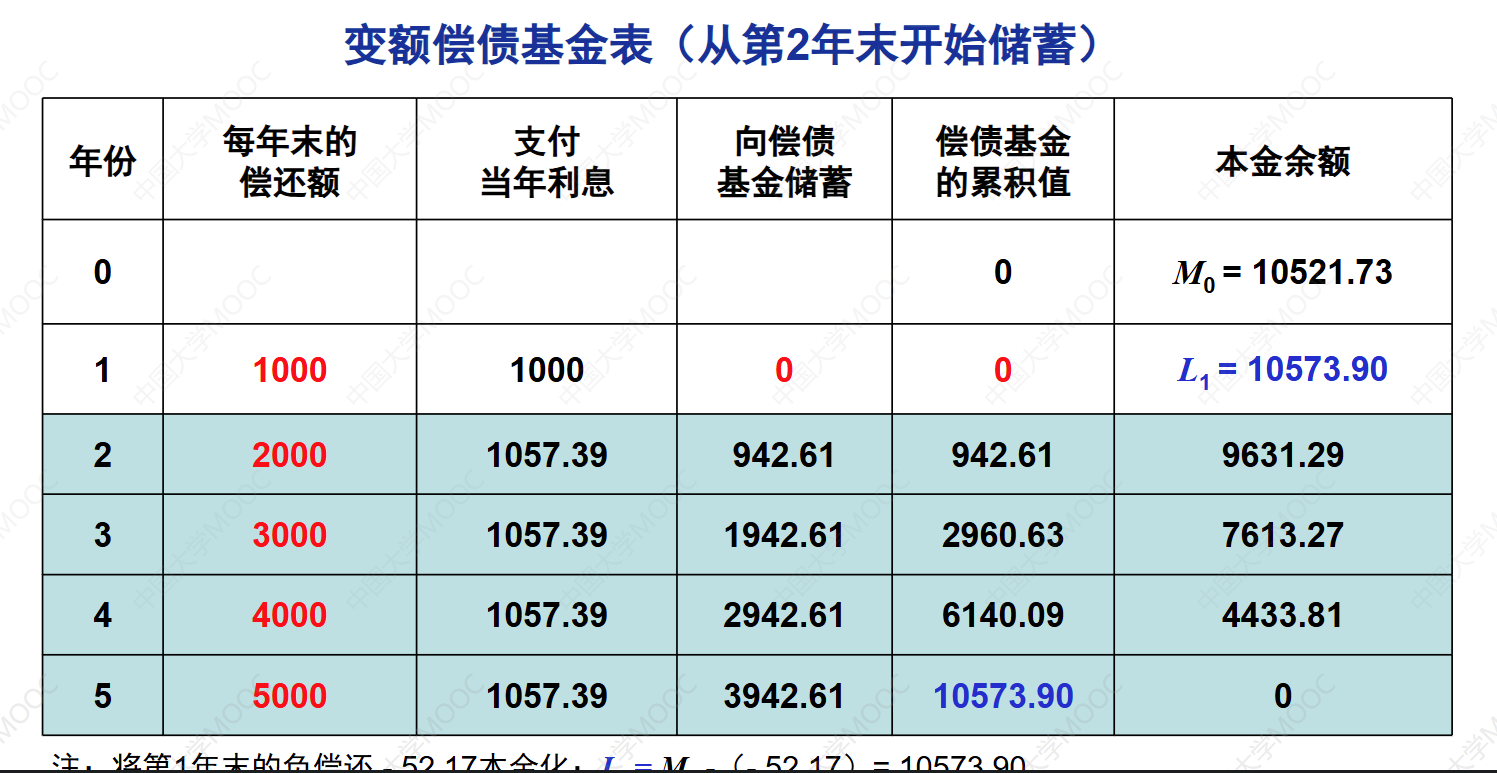
这个视频讲解了变额偿债基金方法的例子。假设贷款期限为5年，贷款利率为10%，偿债基金的利率为8%。借款人希望每年末的还款额从1000到5000递增，形成一个递增年金现金流。根据偿债基金的定义，借款人每年末向偿债基金的储蓄额累积到第五年末应该等于贷款本金。根据这个定义，建立了一个价值方程来求解贷款本金。通过计算，得出贷款本金为10524.69。然而，根据计算结果发现，借款人从偿债基金中借出了一笔贷款，而偿债基金的利率小于贷款利率，不符合要求。因此，需要调整和解决这个问题。通过反解，得出合理的贷款本金为10521.73。

例：贷款期限5年，用偿债基金方法偿还。贷款利率10%，偿债基金利率8%。借款人每年末的偿还额：1000，2000，3000，4000，5000。计算贷款本金。

$L_0=\frac{{\sum }_{t=1}^n{R}_t(1+j{)}^{-t}}{1+(i-j)a_{\overline{n}|j}}$