债券

• 学习目标
• 思维导图
• 6.1 债券的基本概念
• 6.2 债券定价的基本公式
• 6.3 债券定价的溢价公式
• 6.4 债券在付息日期的价格和账面值
• 6.5 债券在任意日期的价格和账面值
• 6.6 例题：债券在任意日期的价格和账面值
• 6.7 可赎回债券
• 6.8 分期偿还债券
• 衡量债券收益水平的指标

学习目标

可以应用债券的基本公式和溢价公式计算债券的价格，分析债券价格的影响因素；可以计算债券在任意日期的价格和账面值；可以计算债券的收益率；掌握可赎回债券和贴现债券的价格计算方法。

思维导图

债券PPT

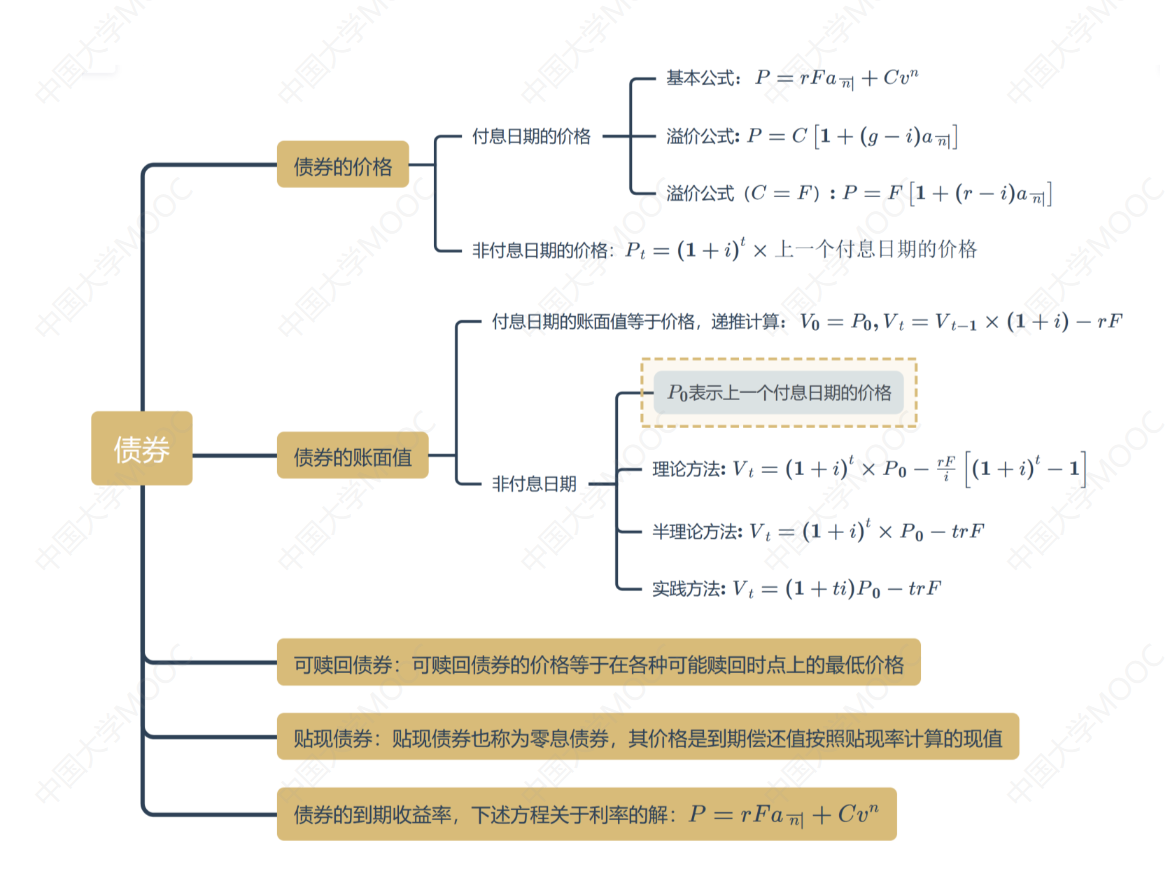
6.1 债券的基本概念

这个教学视频介绍了债券的基本概念和分类。债券是一种债权债务凭证，借款人向投资者出具的一种借款凭证。债券可以分为政府债券、金融债券和公司债券。债券的要素包括票面价值（面值）、价格、票面利率（息票率）和到期收益率。债券的价格可以是平价、溢价或折价。根据利息支付方式的不同，债券可以分为附息债券（coupon）和零息债券（zero-coupon）。附息债券每年支付利息，而零息债券在到期时一次性支付利息。债券的现金流包括每年支付的利息和到期时的偿还值。债券的定价可以使用基本公式、溢价公式、基价公式和Makeham公式进行计算。

重点掌握基本公式、溢价公式。

6.2 债券定价的基本公式

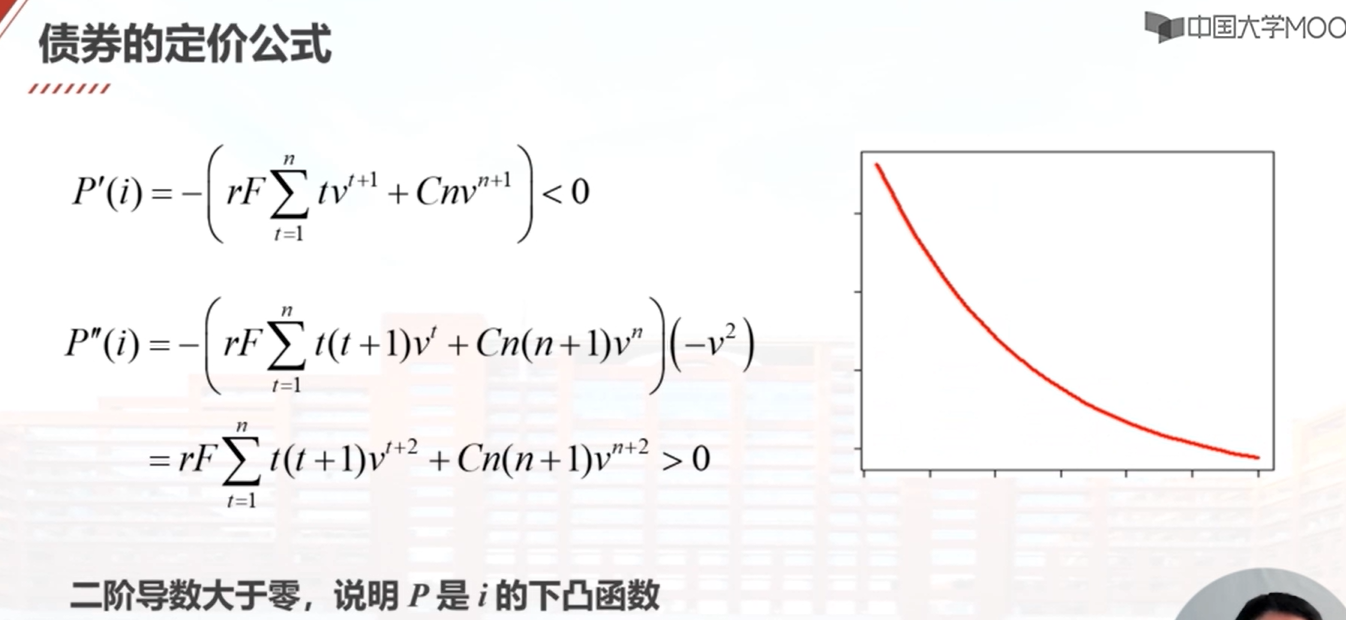
本教学视频介绍了债券定价的基本公式。首先，给定债券的面值、到期偿还值、息票率和支付次数，可以确定债券的现金流。债券在时间零点的价格可以通过将每年的利息收入折现和到期偿还值折现后相加得到。债券价格还可以写成rF乘以an加上C乘以v的n次方的形式。债券价格受到到期收益率、到期期限和息票率的影响。当到期收益率上升时，债券价格下降，而当到期收益率下降时，债券价格上升。债券的期限越长，价格越低，而债券的息票率越高，价格越高。债券价格与到期时间的关系是一个下凸函数。当债券的息票率小于到期收益率时，债券价格随着到期时间的增加而下降，而当债券的息票率大于到期收益率时，债券价格随着到期时间的增加而上升。

$P=rF{a}_{\vec{n}|}+C{v}^n=rF{\sum }_{t=1}^n{v}^t+C\cdot v^n$

例：30年期的债券面值和到期偿还值为1000，年息票率为12%，每季度支付一次利息，售价为850。计算该债券每季度复利一次的年名义收益率。

6.3 债券定价的溢价公式

本视频介绍了债券定价的溢价公式。首先，讲解了息票率的概念，即息票收入与债券面值的比率。然后引入了修正息票率的概念，即息票收入与到期偿还值的比率。接着，推导了债券定价的基本公式和溢价公式。债券定价的溢价公式可以表示为债券价格等于面值加上面值乘以修正息票率减去到期收益率再乘以一个n年期期末付等额年金的现值因子。根据溢价公式，讨论了债券价格和面值之间的关系，以及债券期限对债券价格的影响。最后，通过一个例子计算了一个5年期债券的价格。

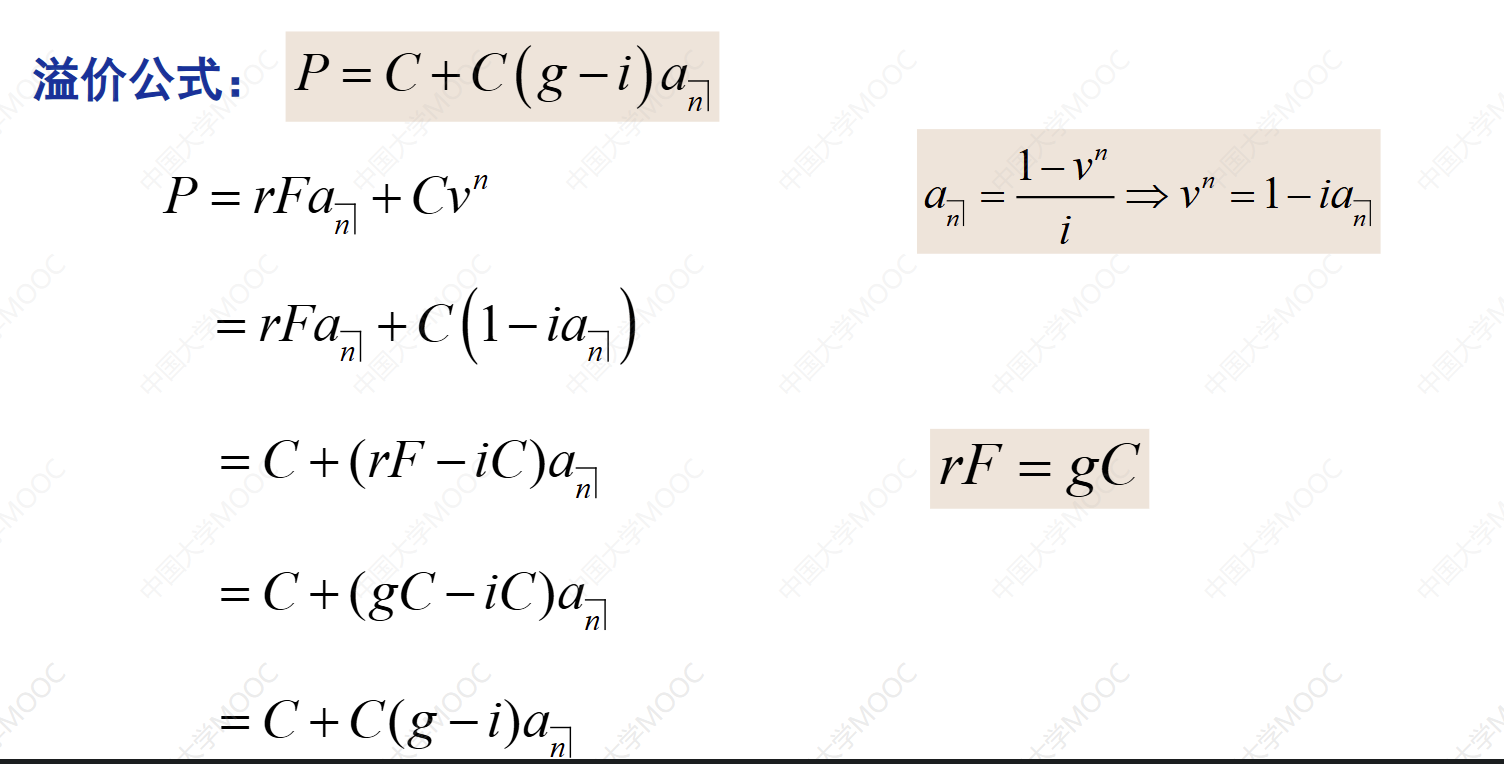
债券价格与面值的关系？

$$P=F+F(r-i)a_{n|}$$

平价发行，$r=i$

溢价发行，$r>i$

折价发行，$r<i$

例：一个5年期债券每半年支付一次利息，年息票率为5%，到期按面值100偿还。如果到期年收益率为7%，计算该债券的价格。

6.4 债券在付息日期的价格和账面值

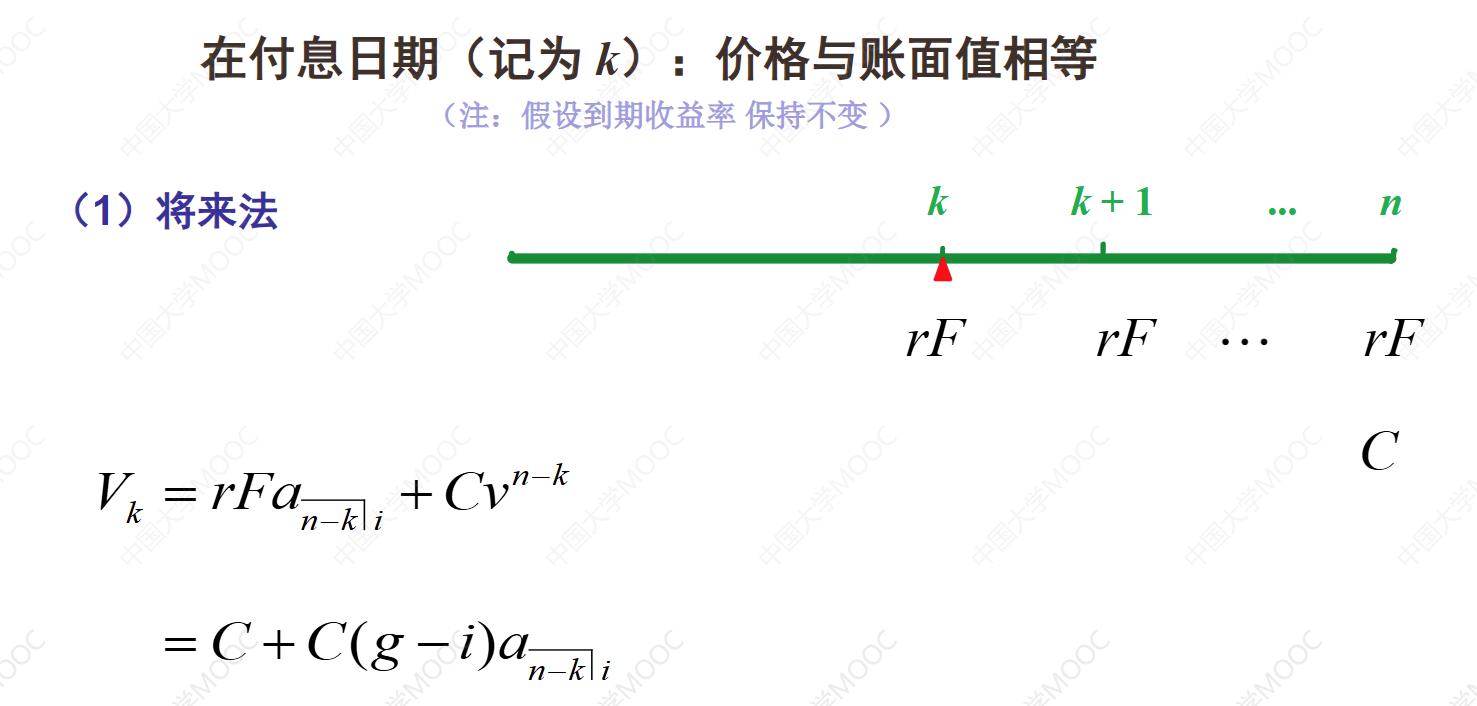
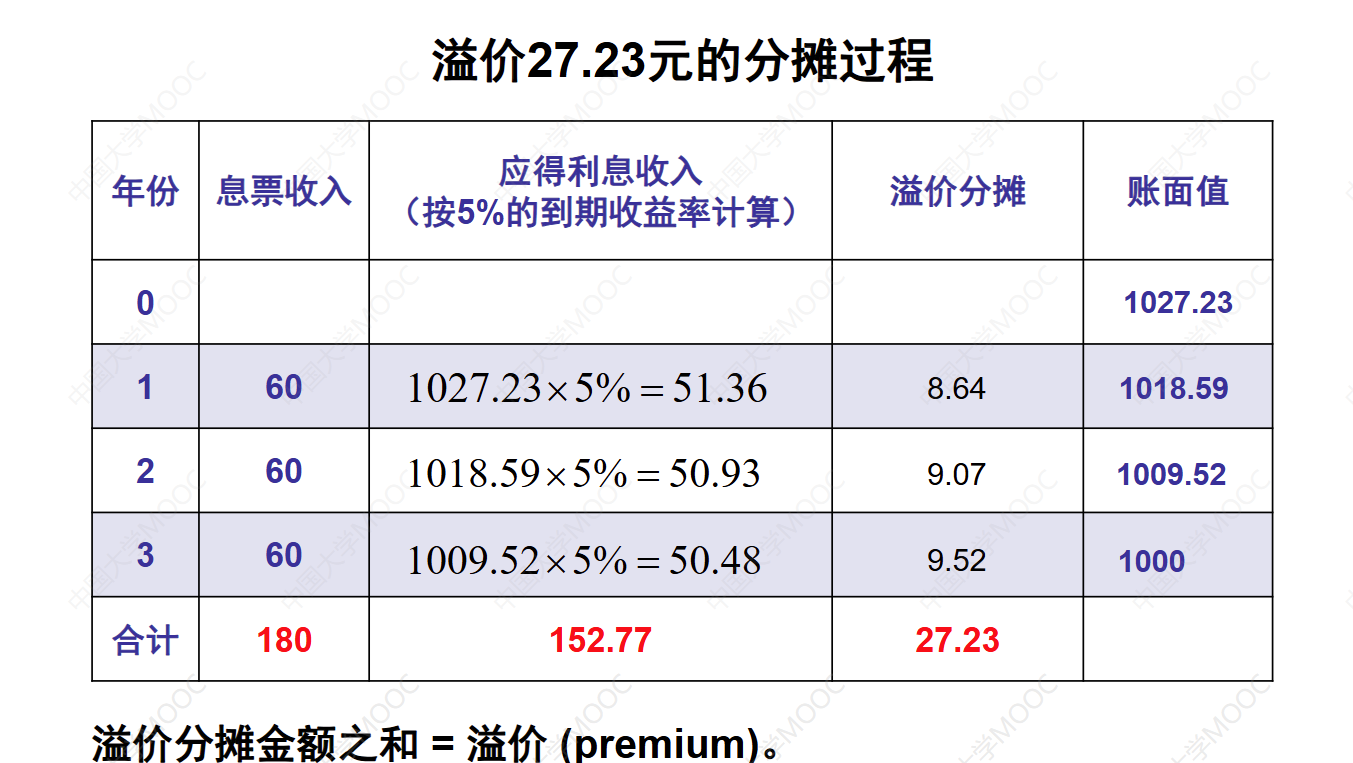
这节课主要讲解了债券在未来付息时间点上的价格和账面值。付息时间点是指利息支付的时间点，对于n年期的债券，每年末都要支付一次利息。在计算债券在未来某个时间点上的价格和账面值时，假设债券的到期收益率保持不变。债券的价格和账面值在付息时间点上是相等的，都是债券的投资余额。可以使用过去法、将来法或递推公式计算每年末的账面值。溢价发行的债券价格高于面值，投资者多支付的溢价通过每年多支付的利息进行补偿。

债券在付息时点上的价格和账面值

账面值：债券持有人的投资余额

基于购买债券时的到期收益率i计算，不是市场价格

在付息时点上，价格与账面值相等

计算债券在付息日期的价格和账面值有三种方法：过去法、将来法和递推公式。三种方法等价。

$\begin{array}{rl}& V_0=P\\ & V_k=V_{k-1}(1+i)-rF\end{array}$

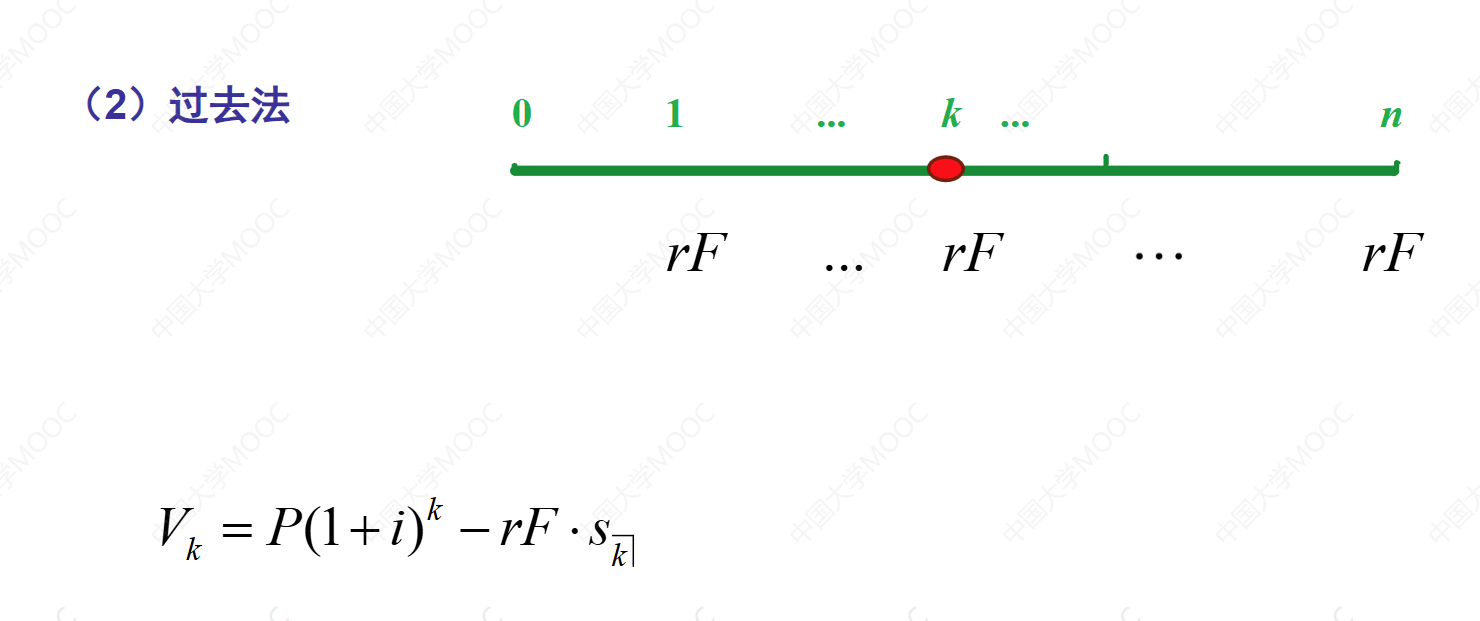
6.5 债券在任意日期的价格和账面值

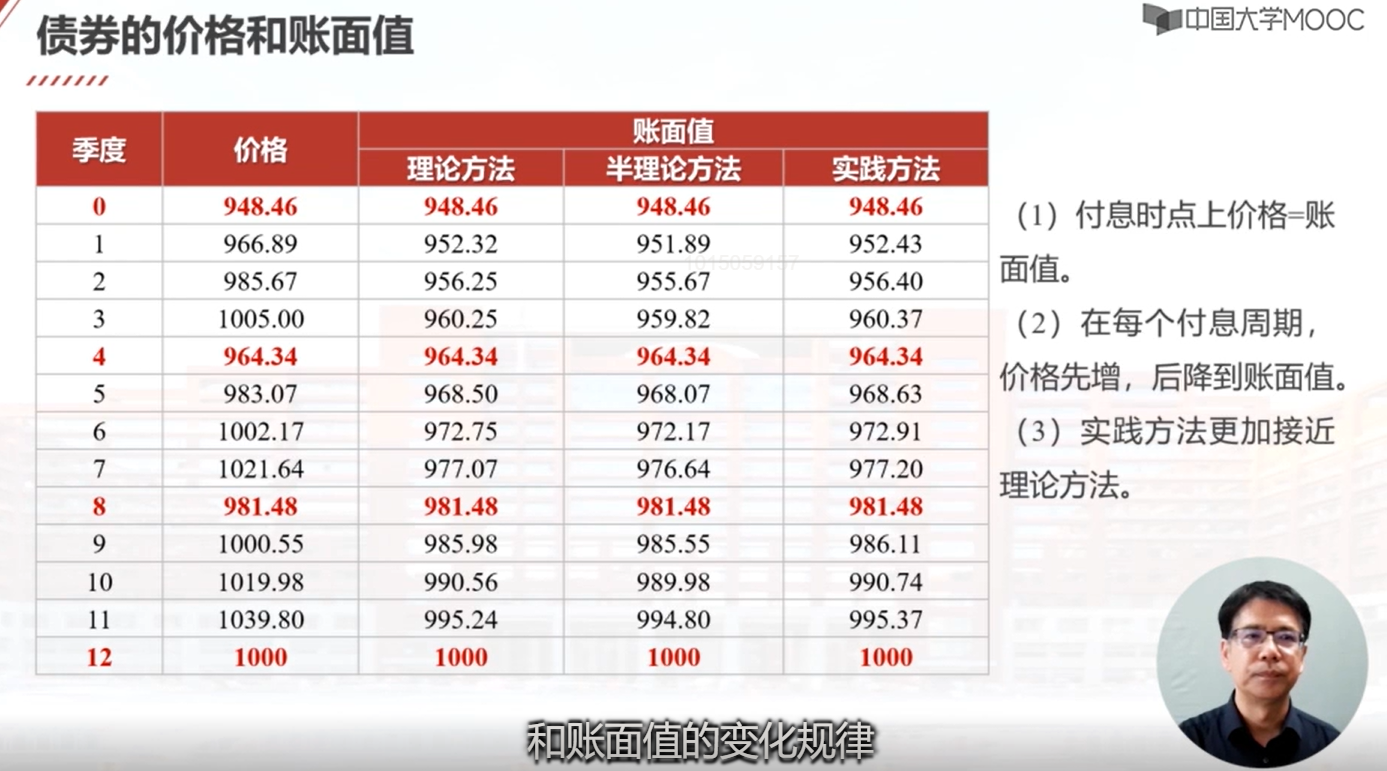
本视频介绍了债券在任意日期的价格和账面值的计算方法。在债券的付息时间点上，债券的价格和账面值相等。计算债券在任意时间点上的价格有两种方法：过去法和将来法。过去法是从过去的价格开始计算，将价格累积到目标时间点。将来法是从未来的价格开始计算，将价格往前贴现到目标时间点。这两种方法计算的结果是等价的。计算债券的账面值时，只需从价格中扣除应计的利息收入。有了价格和应计利息收入，就可以计算出债券在任意时间点的账面值。

非付息日期的价格

上一个付息日期的价格为$P_0$，下一个付息日期的价格为$P_1$

用$P_t$表示在两个付息日期之间的价格(0<t< 1)

过去法：$P_t=(1+i{)}^t{P}_0$

将来法：$P_t=(rF+P_1)(1+i{)}^{-(1-t)}$

两者等价

注：$P_1=P_0(1+i)-rF$

债券在任意时点上的账面值

账面值：从价格中扣除应计息票收入。

6.6 例题：债券在任意日期的价格和账面值

例：债券面值为1000元，年息票率为6%，每年末支付一次利息，期限为3年，到期按面值偿还。债券的到期收益率为8%。计算债券在购买6个月后的价格和账面值。

6.7 可赎回债券

可赎回债券：发行人有权赎回的债券。

为什么发行可赎回债券？降低资金成本。

可赎回债券通常有赎回保护期，有相对较高的收益率，补偿赎回风险。

赎回价格：大于到期偿还值。差额为赎回溢价。

例：8年期的可赎回债券的年息票率为12%，按面值1000元发行，到期按面值偿还。赎回保护期为5年。假设发行人从第5年末开始可以在任何一年末行使赎回权。如果投资者要求的收益率为10%，他愿意支付的价格应为多少？

如果在第5年末赎回，赎回价格为1050元

如果在第6年末赎回，赎回价格为1030元

如果在第7年末赎回，赎回价格为1010元

投资者的购买价：在各种赎回日期下，债券的最低价格。

如果在第5年末赎回，债券价格应为P =120a_5 +1050v^5 =1106.86

如果在第6年末赎回，债券价格应为1104.04

如果在第7年末赎回，债券价格应为1102.50

如果债券到期时偿还，债券价格应为1106.70

投资者的购买价格应为1102.50元。

何时赎回，债券的价格最低?

$$P=C+C(g-i)a_{\overline{n}}$$ $$P=F+F(r-i)a_{\overline{n}}$$

• $g-i>0$，偿还期 $n$ 越短，价格越低。
• $g-i<0$，偿还期 $n$ 越长，价格越低。

例：10年期可赎回债券的面值为100，年息票率为6%，每半年支付1次利息。5年以后的可赎回价格为102。如果债券每半年复利一次的年收益率为7%，计算债券的价格。

练习：投资者购买了10年期可赎回债券，面值为100，年息票率为6%，每年支付2次利息。5年以后的可赎回价格为102。如果债券每半年复利一次的收益率为5%，计算债券的价格。105.94

6.8 分期偿还债券

本视频介绍了债券定价的基价公式和Makeham公式。基价公式是按照基价计算债券价格的公式，基价是按照债券的到期收益率计算投资收入的投资额。Makeham公式是对债券定价的基本公式进行变形得到的，用于计算分期偿还债券的价格。分期偿还债券可以看作是若干个偿还期限不同的债券组成的债券，每个债券的修正息票率和到期收益率相同。通过一个例子，我们可以看到用Makeham公式计算分期偿还债券的价格相对简化。

基价公式（了解）

基价（G）。为了获得周期性收益 rF 所需的投资额

每期的利息收入等于息票收入：iG=rF

息票收入：rF = gC = iG

基价公式：$P=G+(C-G){\nu }^n$

$\begin{array}{rl}& \\ \mathrm{P}& =rF{a}_{n|}+C{\nu }^n\\ & =iG{a}_n+C{\nu }^n\\ & =G(1-{\nu }^n)+C{\nu }^n\\ & =G+(C-G){\nu }^n\end{array}$

$P_s=\frac{g}{i}(C_s-K_s)+K_s$

$P={\sum }_{s=1}^n{P}_s=\frac{g}{i}\left({\sum }_{s=1}^n{C}_s-{\sum }_{s=1}^n{K}_s\right)+{\sum }_{s=1}^n{K}_s$

Makeham公式简化分期偿还债券的价格计算过程。

分期偿还债券的价格（应用Makeham公式）

例：假设债券的面值为1000元，年息票率为5%，从第6年末开始，发行人分5 次偿还，每次偿还1/5，每年末的偿还额为205元，第10年末还清。假设到期收益率为6%，求该债券的价格。953.99

1. 计算修正息票率g：g = 200 × 5% ÷ 205 = 0.04878
2. 偿还值之和C的计算公式为：$C={\sum }_{s=1}^5{C}_s=205\times 5=1025$
3. 偿还值的现值之和K的计算公式为：$K={\sum }_{s=1}^5{K}_s=205^5\times {\alpha }_1/5!\approx 645.28$
4. 原债券的价格P的计算公式为：$P=\frac{g}{i}(C-K)+K=953.99$

衡量债券收益水平的指标

息票率(r) = $\frac{息票收入}{面值(F)}$

修正是息票率(g) = $\frac{息票收入}{偿还值(C)}$

到期收益率(i) = $\frac{息票收入}{基价(G)}$

当期收益率(current yield) = $\frac{息票收入}{债券价格}$