收益率
- 学习目标
- 思维导图
- 4.1 净现值与收益率
- 4.2 净现值与收益率的计算
- 4.3 求解收益率可能出现的三种情况
- 4.4 收益率唯一性的条件
- 4.5 再投资
- 4.6 例题:再投资
- 4.7 修正收益率
- 4.8 币值加权收益率
- 4.9 时间加权收益率
- 4.10 例题:收益率的计算
- 4.11 基金的收益分配
学习目标
理解收益率的定义、计算方法和唯一性判别准则;掌握在出现再投资的情况下收益率的计算方法;可以计算基金的时间加权收益率和币值加权收益率。
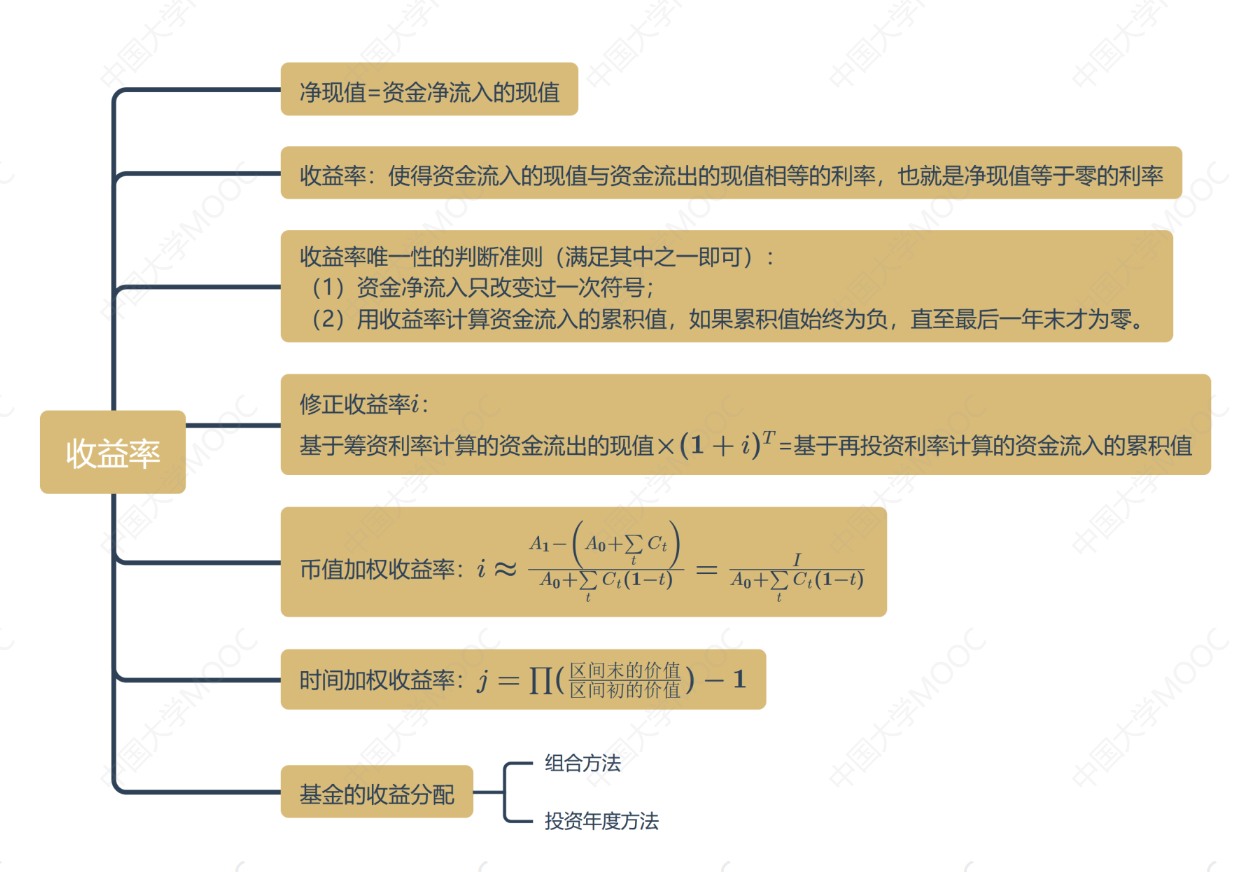
思维导图
4.1 净现值与收益率
本视频介绍了收益率的概念和计算方法。收益率是资金流入的现值与资金流出的现值相等时的利率,也可以定义为使净现值等于零的利率。净现值是将所有现金流折现到时间零点后的现值之和,表示投资项目的收益大小。收益率和净现值的定义虽然形式不同,但本质上是一致的。通过一个例子,我们可以更好地理解收益率的定义和计算方法。
净现值NPV=资金流入的现值 - 资金流出的现值
净现值越大,表示收益越高
(内部)收益率IRR:使得资金流入的现值和资金流出的现值相等时的利率。
收益率实质上是使得净现值为零的利率:
例(收益率的定义):时间零点投资100元,年末收回110元,计算收益率。
解:三种方法
(1)价值方程:100(1+i)=110,故收益率i=10%
(2)资金流入的现值=110/(1+i),资金流出的现值=100
令上述两者相等:110/(1+i)=100,也得到前述价值方程。
(3) 净现值= 110/(1+i)-100
令净现值=0,也得到前述价值方程。
4.2 净现值与收益率的计算
这个视频介绍了净现值和收益率的计算方法。以一个投资项目为例,假设期初投资20万元,每年末可以获得5万元的收入。在5%和10%的利率水平下,计算净现值和收益率。净现值是资金流入和资金流出的差值,它的大小与利率有关。如果使用5%的利率,净现值大于0,表示赚钱了;如果使用10%的利率,净现值小于0,表示亏损。收益率是使净现值等于零的利率,通过解方程可以得到。在这个例子中,收益率为7.93%。计算净现值和收益率可以使用Excel的NPV和IRR函数。
4.3 求解收益率可能出现的三种情况
在这个教学视频中,我们学习了求解收益率可能出现的三种情况。收益率是使得资金流入的现值和资金流出的现值相等时的利率。我们可以通过计算现金流的净现值来求解收益率。然而,由于净现值方程往往是关于利率的高次方程,所以可能出现三种情况:无解、多个解和唯一解。无解意味着收益率不存在,而多个解意味着存在多个收益率。我们通过净现值相等的条件来解决多个解的问题。通过一个简单的例子,我们可以看到收益率可能不存在的情况。另外,我们还讨论了多个解可能导致的问题。
4.4 收益率唯一性的条件
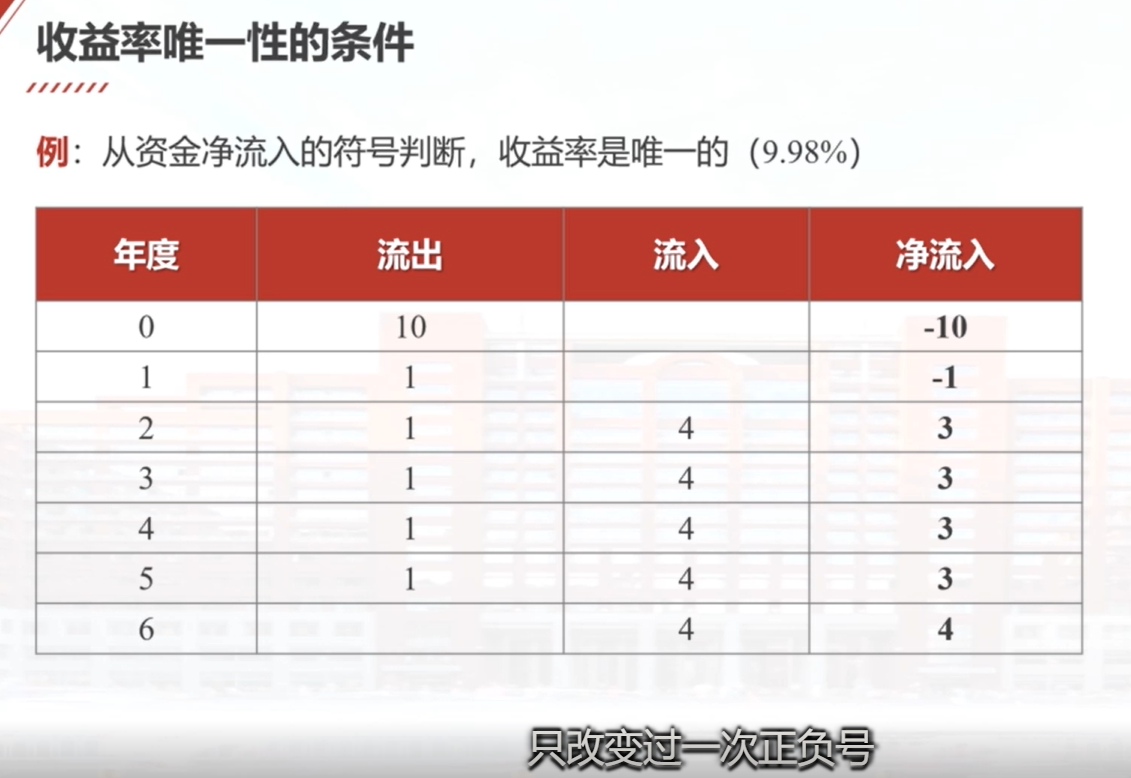
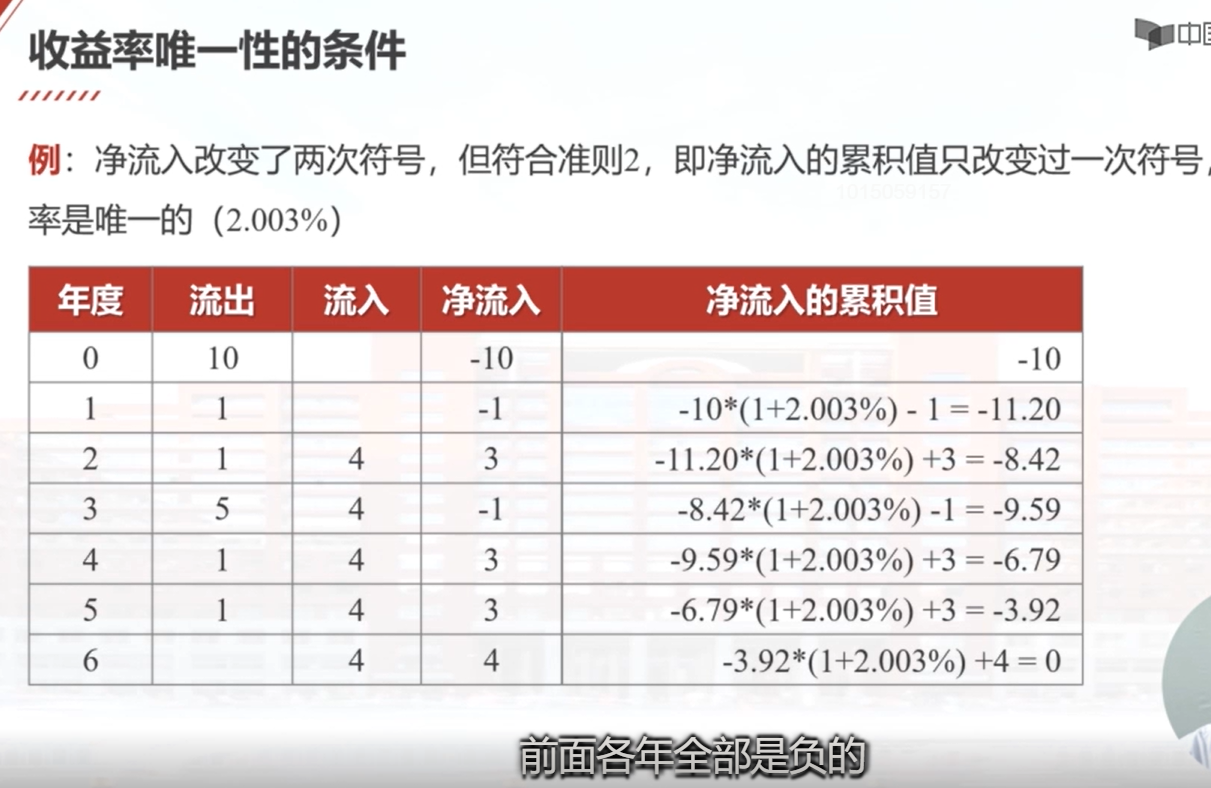
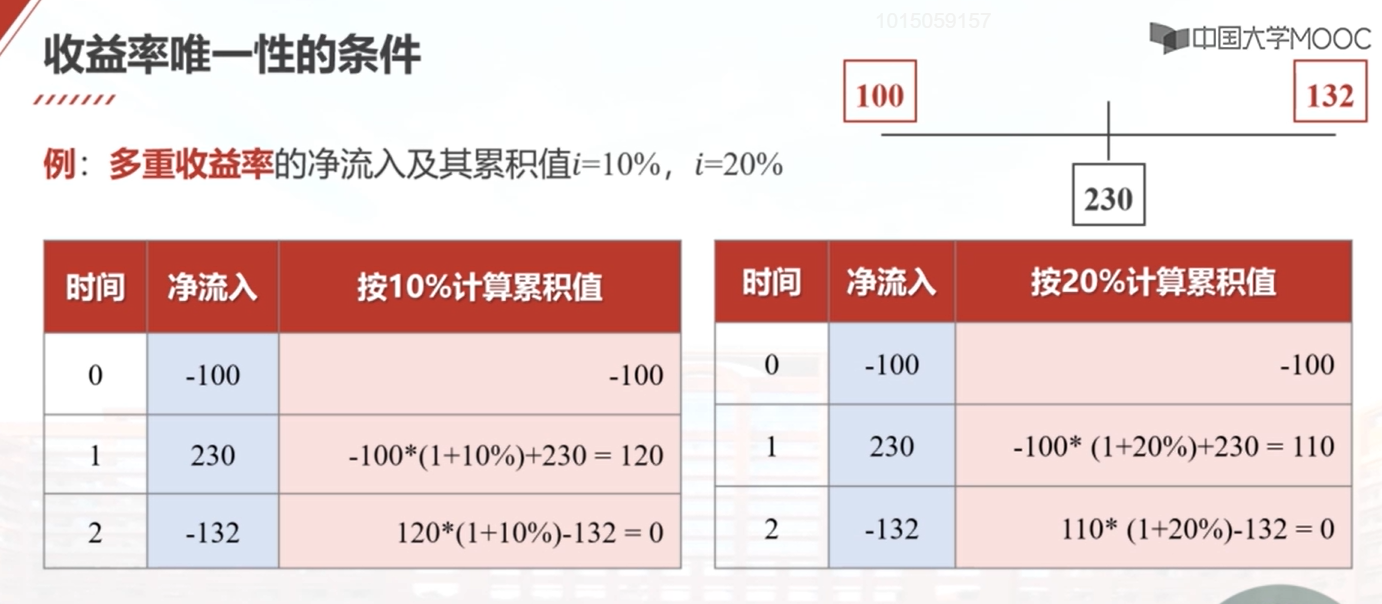
收益率可以定义为使得资金流入的现值和资金流出的现值相等时的利率,也可以定义为使得净现值等于零时的利率。计算收益率需要解关于利率的高次方程,可能存在无解、多重解和唯一解三种情况。判断收益率是否唯一有两个准则:净流入只改变过一次符号,或者净流入的累积值前面一直是负的,到最后一年才变为0。如果满足这两个准则之一,就可以得到一个唯一的收益率。如果不满足第一个准则,可以考虑是否满足第二个准则。通过计算净流入的累积值,可以判断收益率是否唯一。
收益率唯一性的条件
满足下述两个准则之一即可:
准则1:资金净流入只改变过一次符号(正负号)。
准则2:用收益率计算资金净流入的累积值,始终为负,最后一年末等于零。
4.5 再投资
再投资:前期投资的收入按新的利率再次进行投资
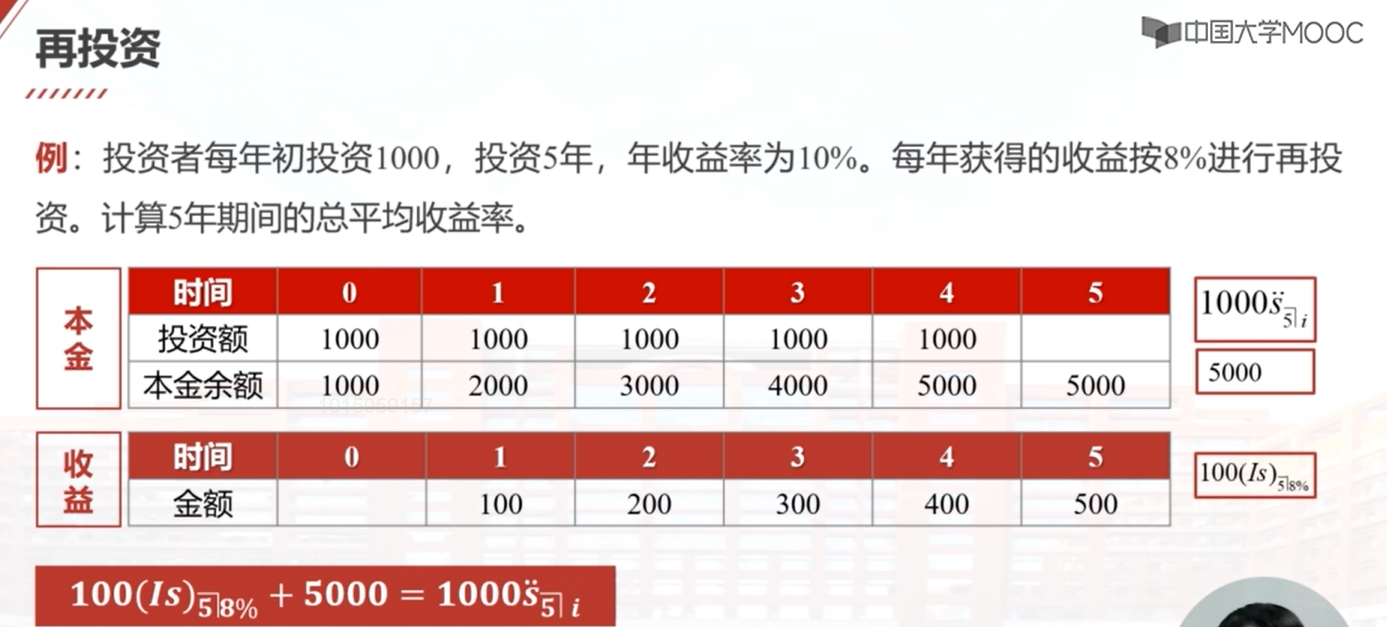
在这个教学视频中,我们学习了再投资的概念和如何计算投资收益率。通过一个简单的例子,我们看到了如果两个投资项目在10年期间产生相同的收益,那么第一个项目在后5年的投资收益率应该达到多少。我们还学习了如何计算投资者在一段时间内的总平均收益率,以及如何解决投资收益率在不同时间段变化的情况。最后,我们给出了两个练习题,供大家练习和巩固所学知识。

练习:投资者在时间零点存入12,在第10年末存入12,年利率为i。利息每年末支付一次,并按0.75i的利率再投资。在第20年末,利息再投资形成的累积值为64。计算i。

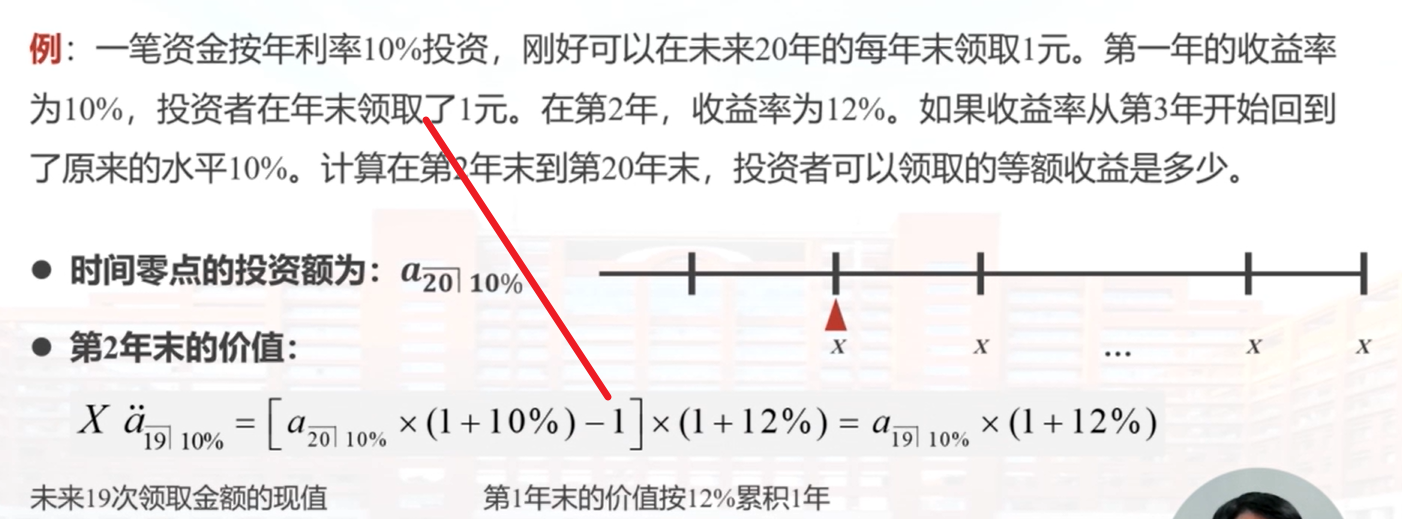
例:一笔资金按年利率10%投资,刚好可以在未来20年的每年末领取1元。第一年的收益率为10%,投资者在年末领取了1元。在第2年,收益率为12%。如果收益率从第3年开始回到了原来的水平10%。计算在第2年末到第20年末,投资者可以领取的等额收益是多少?
练习:一笔资金按年利率10%投资,刚好可以在未来20年的每年末领取1元。在第一年,收益率为10%,投资者在年末领取了1元。假设从第2年开始,收益率为12%。计算在第2年末到第20年末投资者可以领取的等额收益是多少?
第一年末的价值:
左边:将来法
中间:过去法
4.6 例题:再投资
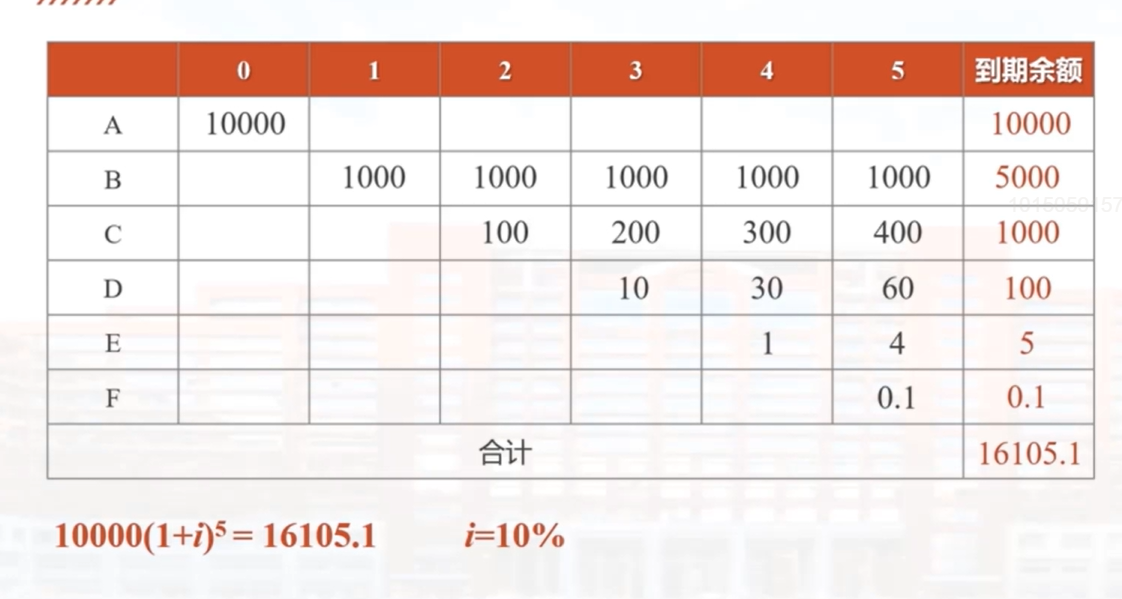
这个视频讲解了再投资的概念和计算方法。投资者在时间零点在账户A投资1万元,账户A的年收益率为10%,每年产生1000元的利息收入。这些利息收入全部投资在账户B,账户B的年收益率也是10%。账户B产生的收益又投资到账户C,账户C的年收益率还是10%。以此类推,直到账户F。在第五年末,账户A的本金余额是1万元,账户B是5000元,账户C是1000元,账户D是100元,账户E是5元,账户F是1元。这些账户的累积值加在一起是16105.1元。根据这个结果,投资者在这5年的收益率是10%。另外,视频还给出了一个例题,投资者在账户A投资2000元,账户A的收益率是5%,账户B的收益率是10%,账户C的收益率是7%。在第五年末,投资者的总价值是2500元,根据这个结果可以计算出投资者在这5年的平均收益率为5.53%。
练习:在t=0,投资者在账户A中投资10000,每年赚取10%的收益率。
账户A每年产生的利息收入投资于账户B,账户B的年收益率为10%; 帐户B每年产生的利息收入投资于账户C,账户C的年收益率为10%; 帐户C每年产生的利息收入投资于账户D,账户D的年收益率为10%; 帐户D每年产生的利息收入投资于账户E,账户E的年收益率为10%; 帐户E每年产生的利息收入投资于账户F,账户F的年收益率为10%;
计算t=5时每个账户的累积值,以及投资者在这5年期间的年收益率。
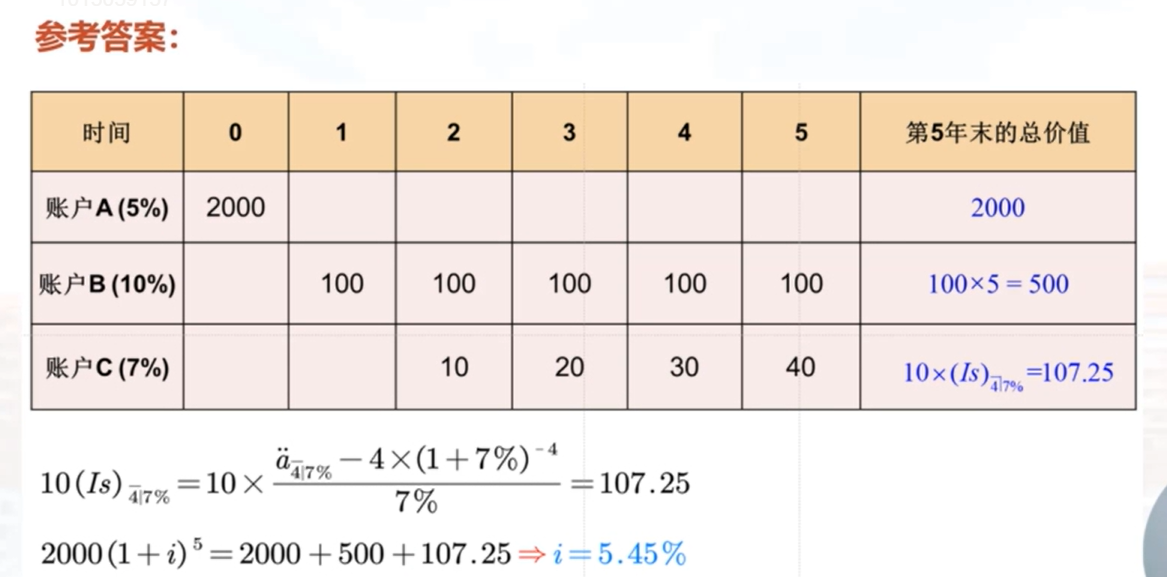
练习:在t=0,投资者在账户A中投资2000,每年赚取5%的收益率。账户A每年产生的利息收入投资于账户B,账户B的年收益率为10%。帐户B每年产生的利息收入投资于账户C,账户C的年收益率为7%。
计算t=5时,整个投资的累积值,以及这5年期间的年收益率。
4.7 修正收益率
收益率定义为使得资金流入的现值和资金流出的现值相等时的利率,也可以定义为使得净现值等于零时的利率。求解收益率的方程往往是一个高次方程,可能无解或存在多重解。如果收益率不存在或存在多个收益率,可以计算修正收益率。计算修正收益率需要筹资利率和再投资利率两个辅助信息。筹资利率用于计算资金流出的现值,再投资利率用于计算资金流入的累积值。通过解方程可以得到修正收益率。计算修正收益率可以使用Excel函数MIRR。
资金流出(成本):用筹资利率计算现值
资金流入(收益):用再投资利率计算累积值
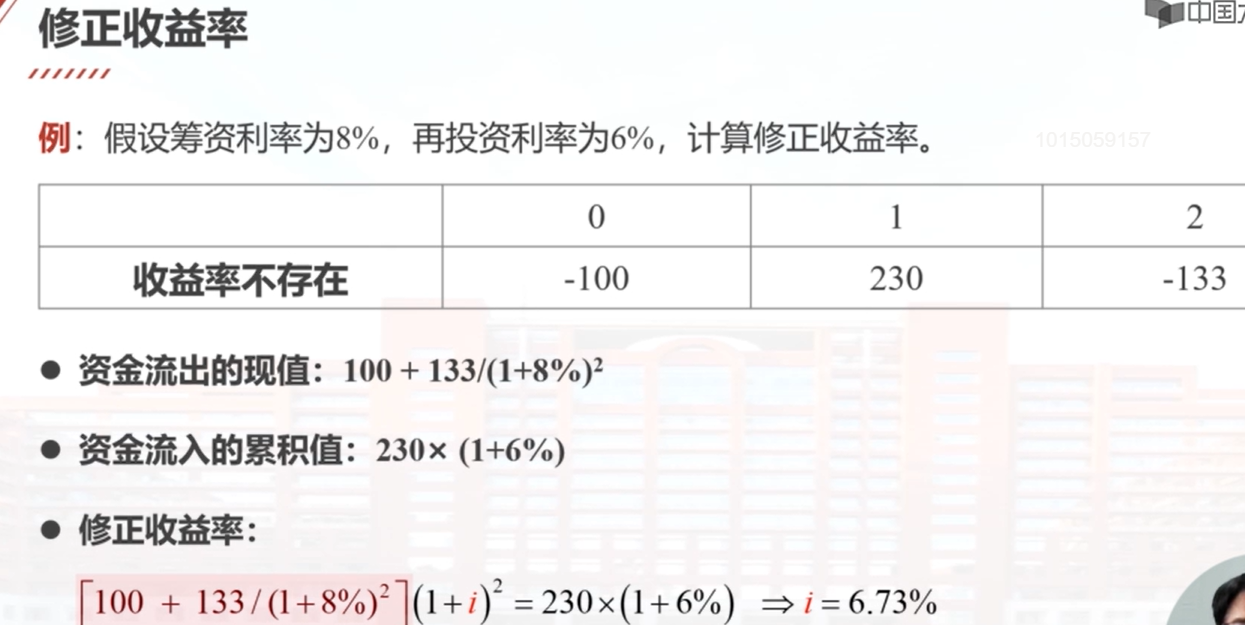
具体命令为=MIRR(A1:C1,8%,6%)

4.8 币值加权收益率
币值加权收益率是用于度量投资者个人收益水平的重要指标。币值加权收益率受到每个个人投资者本金增减变化的时间和金额的影响。而基金管理人的业绩则需要剔除本金增减变化的影响,使用时间加权收益率来度量。币值加权收益率的计算需要求解一个关于收益率的高次方程,为了简化计算,可以使用单利来近似复利。币值加权收益率的计算公式为利息收入除以平均每天的资金占用额。通过一个例子的计算,可以看到近似值和精确值非常接近,因此在实际应用中通常使用近似公式来计算币值加权收益率。
币值加权收益率(dollar-weighted yield rate):度量投资者个人的收益水平
币值加权收益率
假设:年初本金为, 在时刻 的新增投资为, 收益率为 ,在年末累积值为
注:增加投资;减少投资。
用 表示年末的累积值,则有
由此求得收益率

例:年初存入100万,t=0.5时存入20万,t=0.8时取出50万。
(1)计算日均资金占用额 (平均本金余额)
(2)如果年末账户余额为80万,账户的币值加权收益率是多少?

例:在年初存入1000,在4个月末存入1000,在6月和8月末分别取出200和500。在年末时,基金余额为1500。计算基金的币值加权收益率。
利息收入=200,日均资金占用额=1400,基金的币值加权收益率=14.29%
4.9 时间加权收益率
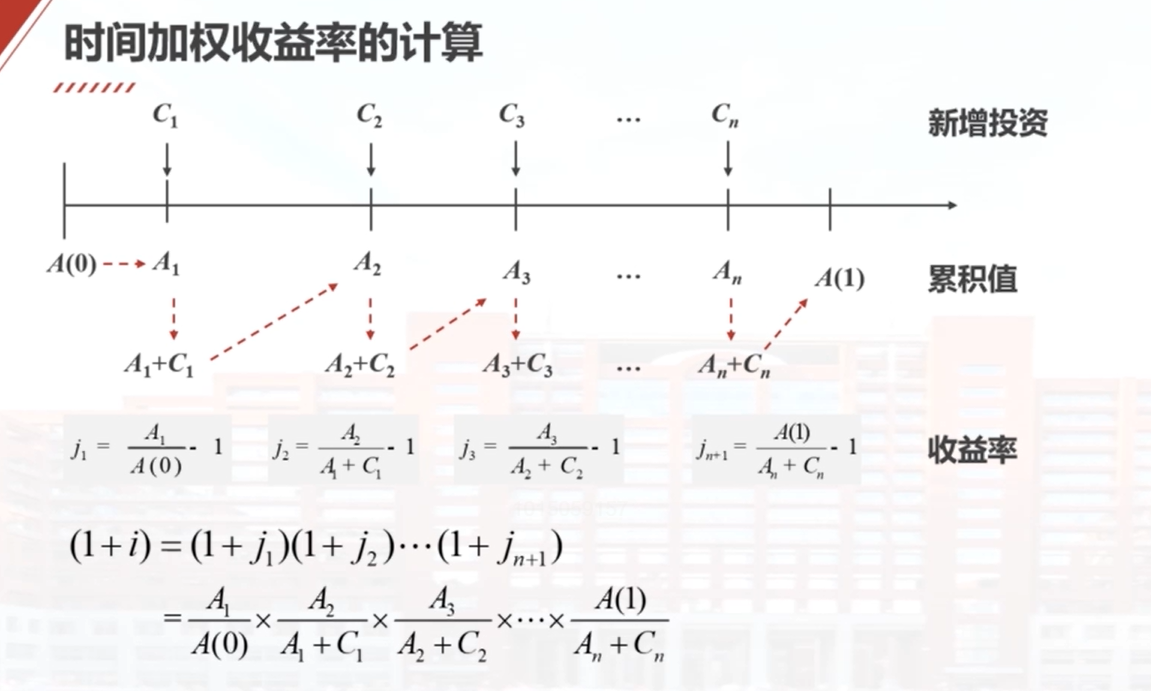
本视频介绍了基金的两种收益率计算方法:币值加权收益率和时间加权收益率。币值加权收益率用于衡量投资者个人的收益水平,受本金增减变化的影响;而时间加权收益率用于衡量基金经理人的管理业绩,剔除了本金增减变化的影响。时间加权收益率的计算方法是将一年划分成若干个时间区间,在每个时间区间内计算收益率,然后累积得到全年的收益率。通过一个例子,说明了币值加权收益率和时间加权收益率的差异。最后,还介绍了如何计算时间加权收益率和币值加权收益率的具体步骤。
时间加权收益率(time-weighted yield rate):度量基金经理人的业绩
例:1月1日,账户余额为112000,同时增加投资125000,同时减少本金100000。计算币值加权收益率和时间加权收益率。

例:2019年1月1日在基金中存入1000,在7月1日存入资金C。在2020年1月1 日,基金余额为2000。基金的时间加权收益率和币值加权收益率分别为10% 和9%。计算基金在前6个月的年有效利率。

4.10 例题:收益率的计算
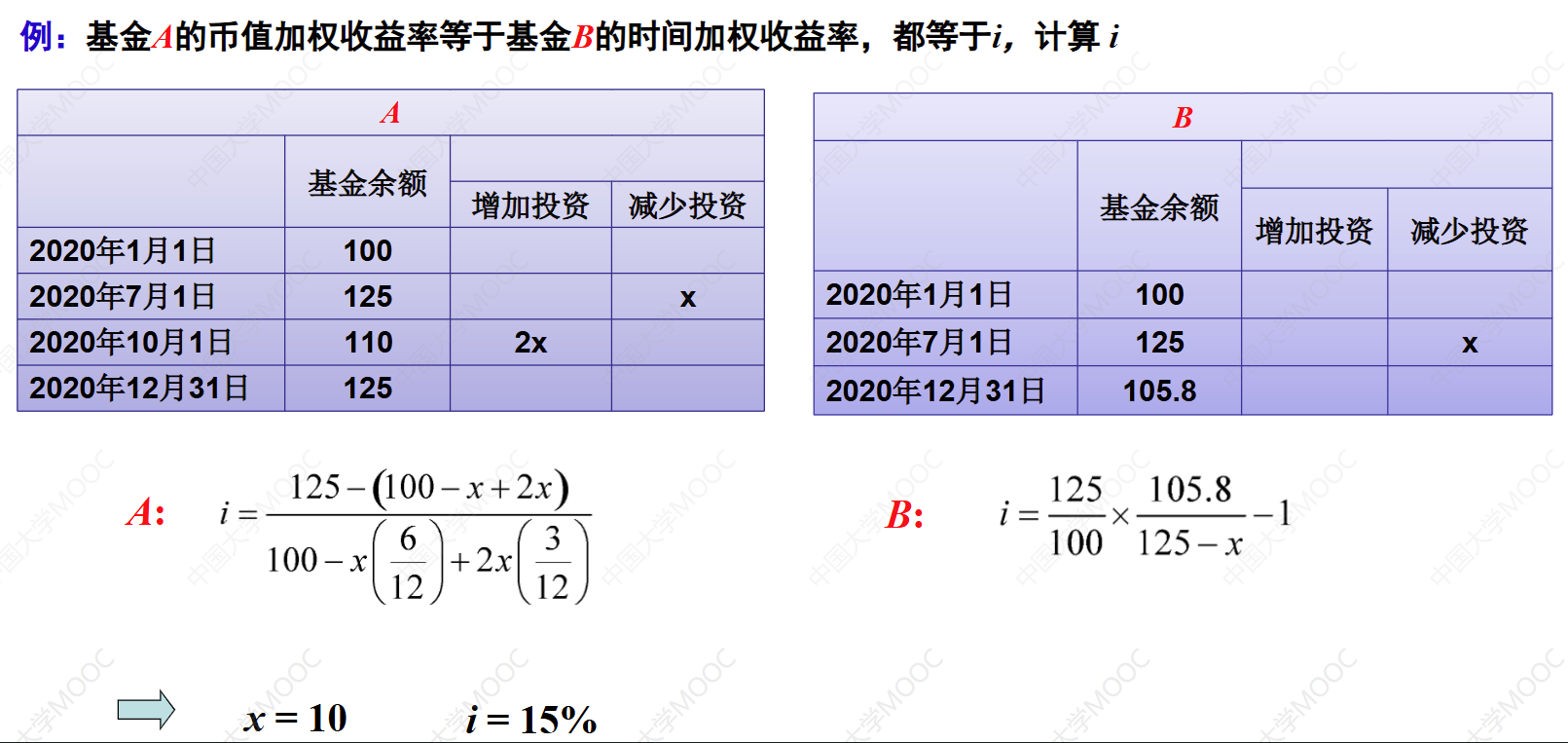
这个例子介绍了如何计算年收益率。通过给出的利息力函数,可以得到累积函数a(t),表示在任意时间t的累积价值。根据现金流,可以计算出第二年末和2.5年末的累积价值,进而得到年收益率i。另外,通过一个基金A和基金B的例子,展示了币值加权收益率和时间加权收益率的计算方法,并通过方程求解得到i的值。最终得出基金A的币值加权收益率为15%。

4.11 基金的收益分配
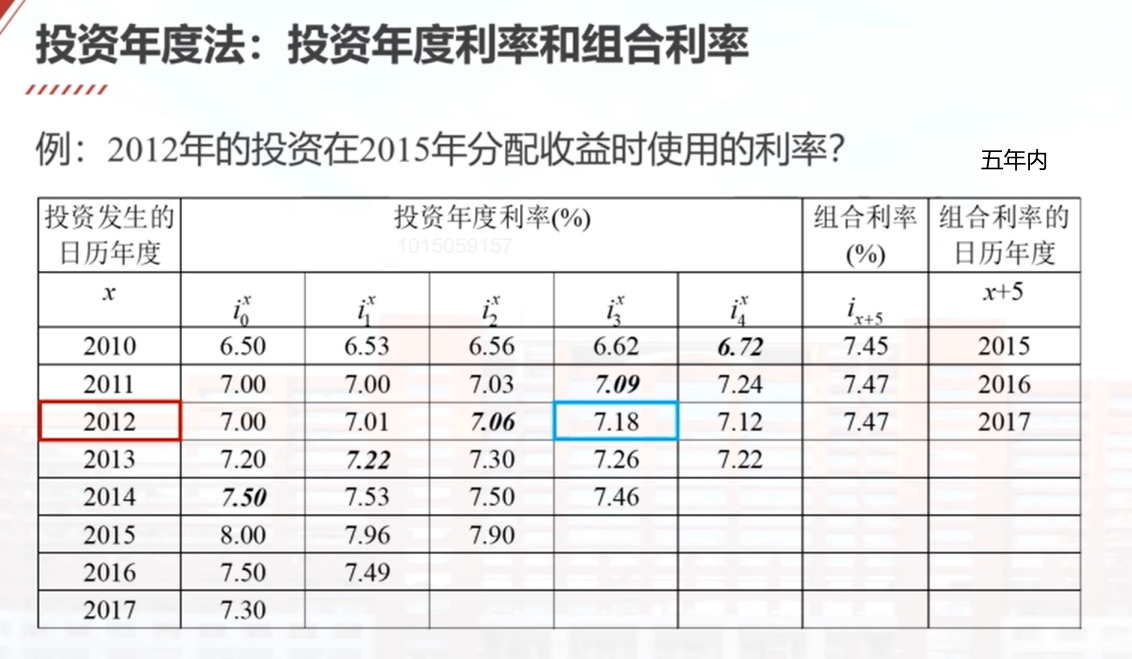
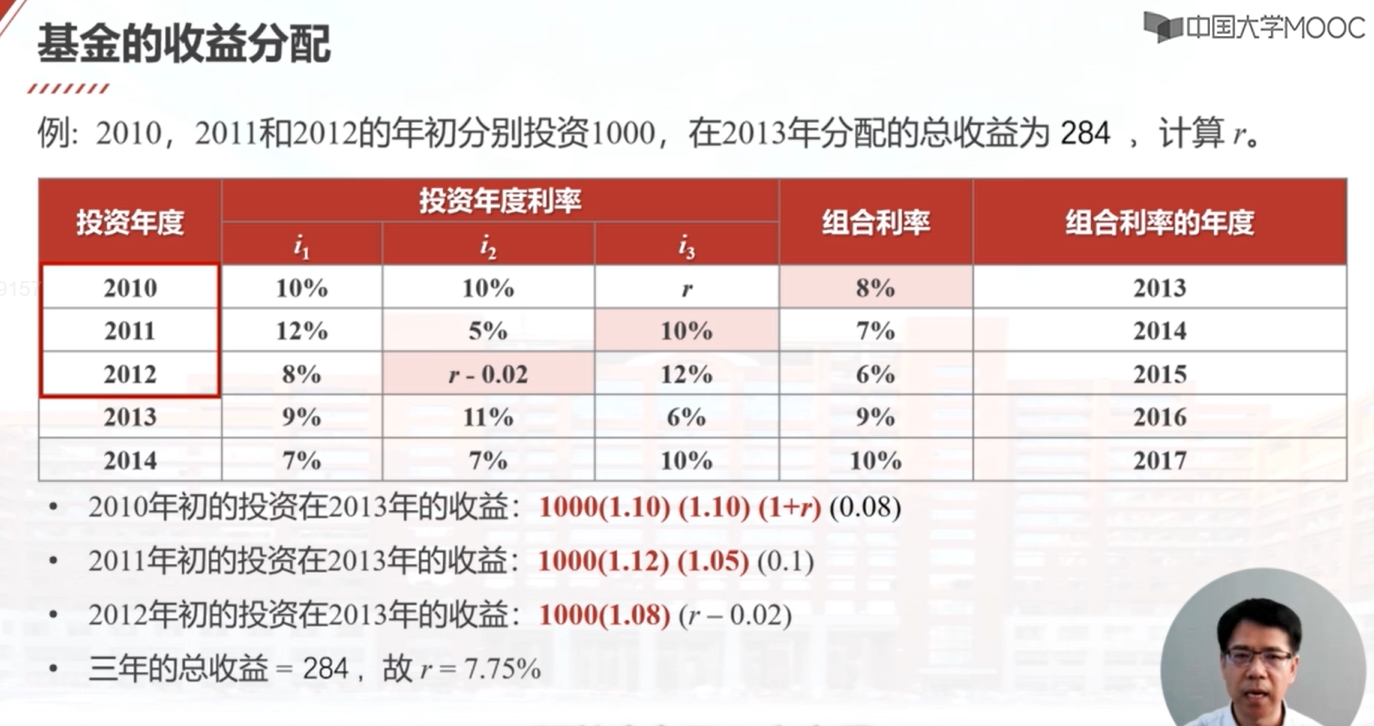
基金的收益分配有两种方法:投资组合方法和投资年度方法。投资组合方法是对所有投资采用一个平均的收益率进行分配,适用于基金收益率相对稳定的情况。投资年度方法则根据投资发生的具体时间进行分配,对于新的投资采用较高的利率,对于老的投资采用较低的利率,更公平且有利于吸引新的投资者。在投资年度方法中,涉及投资年度利率和组合利率,根据投资时间的不同使用不同的利率进行分配。通过一个例子计算,可以得到投资年度利率为7.75%。
基金包括不同时期的投资。如何把基金的收益分配给不同时期的投资?
分配方法:
- 投资组合法
- 投资年度法
投资组合法
方法:对所有投资都按照平均收益率进行分配。适用情况:收益率水平保持稳定。

投资组合法的问题:当各个年度的收益率不同时,组合法可能不公平。
2019年发生的投资,收益率8%;2020年发生的投资,收益率10%;平均9%。
如果对2020年的新投资按9%分配收益,不利于吸引新投资。如何解决?投资年度法。
投资年度法
发生在最近几年(如近三年)的投资:考虑投资发生的年度,即按投资年度利率分配收益。
发生在以前年度(如三年以前)的投资:不考虑投资发生的年度,都按组合利率(平均利率)分配收益