棋盘
51. N-Queens
The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.
Given an integer n, return all distinct solutions to the n-queens puzzle. You may return the answer in any order.
Each solution contains a distinct board configuration of the n-queens' placement, where 'Q' and '.' both indicate a queen and an empty space, respectively.
Example 1:

Input: n = 4
Output: [[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
Explanation: There exist two distinct solutions to the 4-queens puzzle as shown above
Example 2:
Input: n = 1
Output: [["Q"]]
Constraints:
1 <= n <= 9
思路
都知道n皇后问题是回溯算法解决的经典问题,但是用回溯解决多了组合、切割、子集、排列问题之后,遇到这种二维矩阵还会有点不知所措。
首先来看一下皇后们的约束条件:
- 不能同行
- 不能同列
- 不能同斜线
确定完约束条件,来看看究竟要怎么去搜索皇后们的位置,其实搜索皇后的位置,可以抽象为一棵树。
下面我用一个 3 * 3 的棋盘,将搜索过程抽象为一棵树,如图:
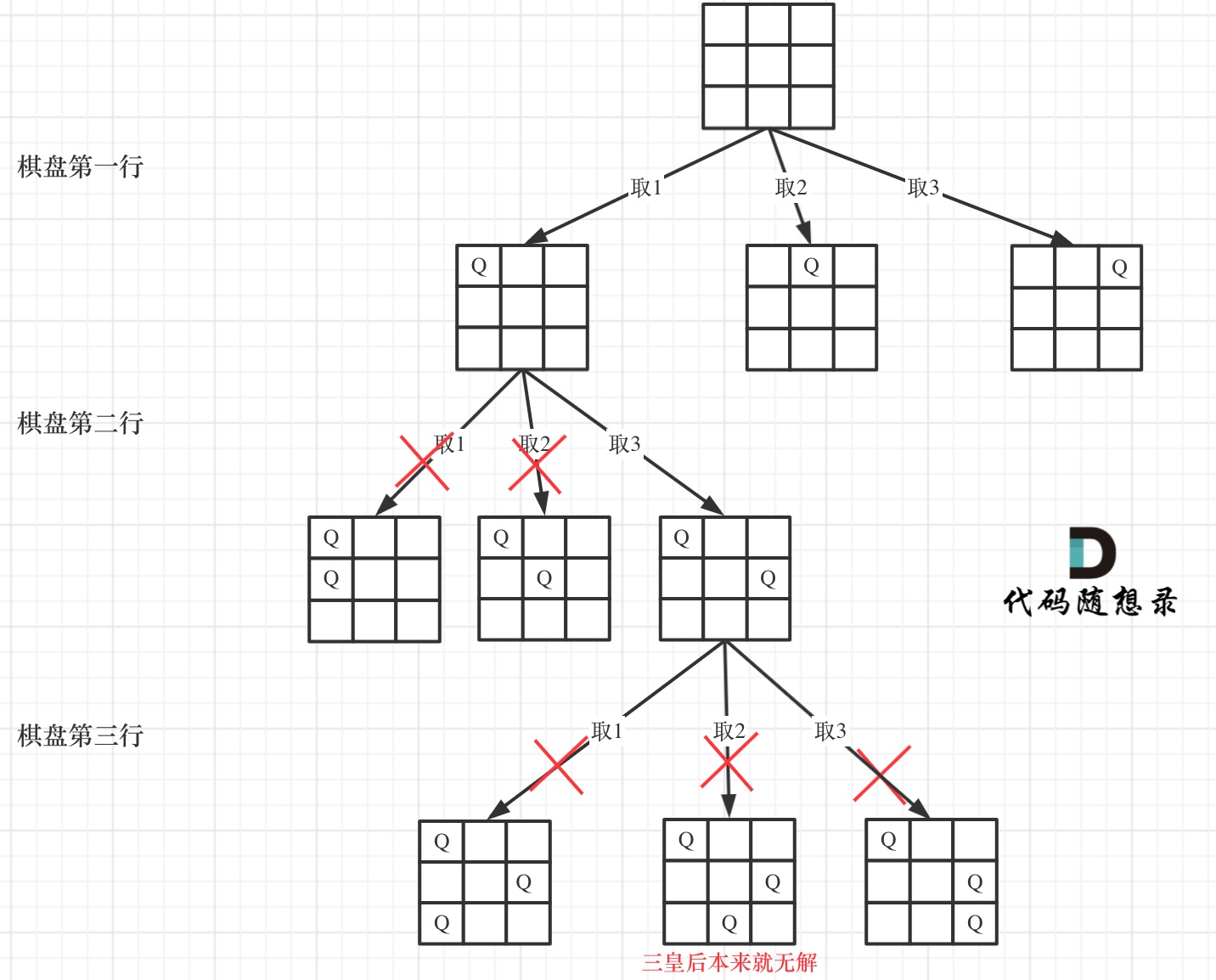
从图中,可以看出,二维矩阵中矩阵的高就是这棵树的高度,矩阵的宽就是树形结构中每一个节点的宽度。
那么我们用皇后们的约束条件,来回溯搜索这棵树,只要搜索到了树的叶子节点,说明就找到了皇后们的合理位置了。
按照我总结的如下回溯模板,我们来依次分析:
void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;
backtracking(路径,选择列表); // 递归
回溯,撤销处理结果
}
}
- 递归函数参数
我依然是定义全局变量二维数组result来记录最终结果。
参数n是棋盘的大小,然后用row来记录当前遍历到棋盘的第几层了。
代码如下:
vector<vector<string>> result;
void backtracking(int n, int row, vector<string>& chessboard) {}
- 递归终止条件
在如下树形结构中:
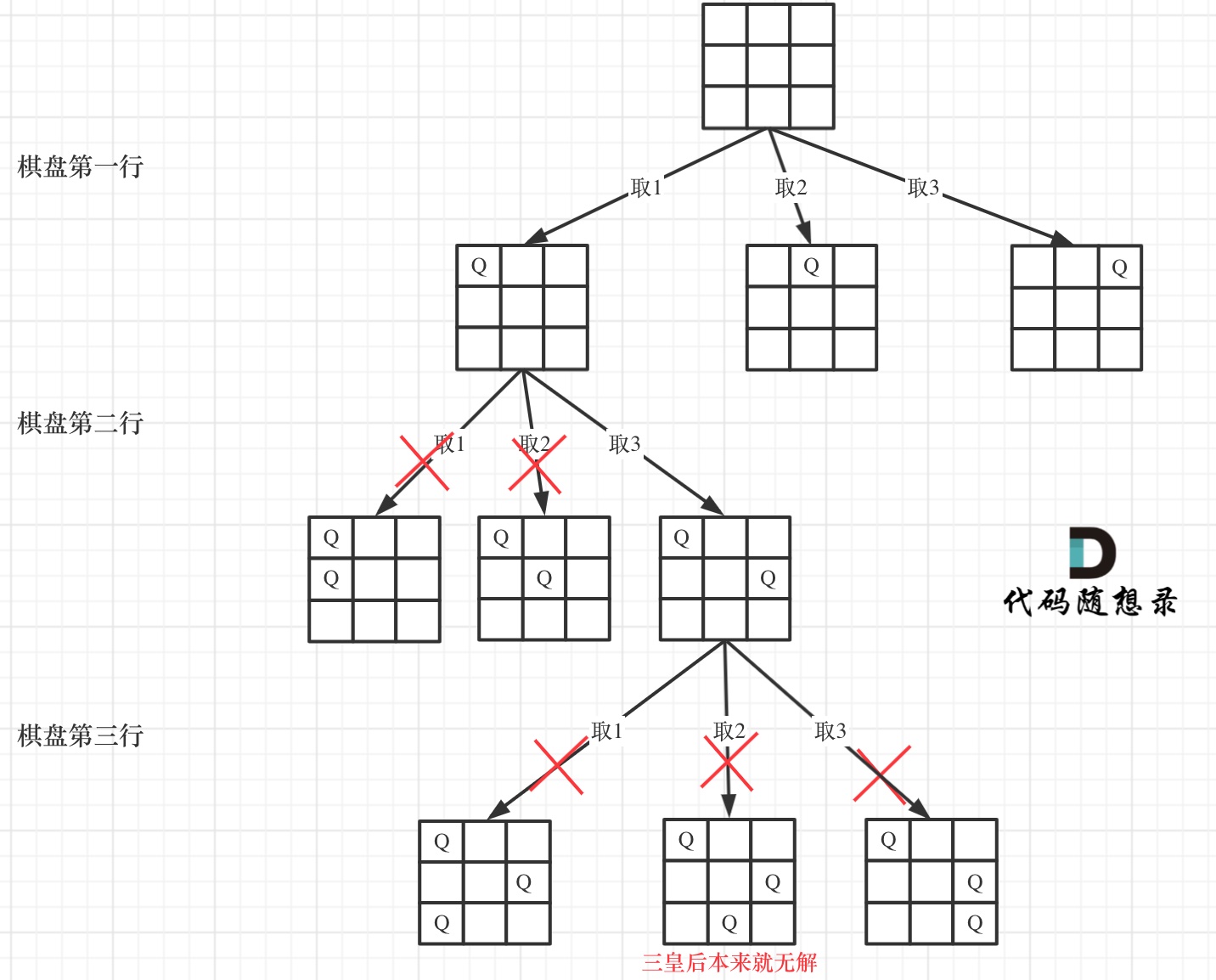
可以看出,当递归到棋盘最底层(也就是叶子节点)的时候,就可以收集结果并返回了。
代码如下:
if (row == n) {
result.push_back(chessboard);
return;
}
- 单层搜索的逻辑
递归深度就是row控制棋盘的行,每一层里for循环的col控制棋盘的列,一行一列,确定了放置皇后的位置。
每次都是要从新的一行的起始位置开始搜,所以都是从0开始。
代码如下:
for (int col = 0; col < n; col++) {
if (isValid(row, col, chessboard, n)) { // 验证合法就可以放
chessboard[row][col] = 'Q'; // 放置皇后
backtracking(n, row + 1, chessboard);
chessboard[row][col] = '.'; // 回溯,撤销皇后
}
}
- 验证棋盘是否合法
按照如下标准去重:
- 不能同行
- 不能同列
- 不能同斜线 (45度和135度角)
代码如下:
bool isValid(int row, int col, vector<string>& chessboard, int n) {
// 检查列
for (int i = 0; i < row; i++) { // 这是一个剪枝
if (chessboard[i][col] == 'Q') {
return false;
}
}
// 检查 135 度角是否有皇后
for (int i = row - 1, j = col - 1; i >=0 && j >= 0; i--, j--) {
if (chessboard[i][j] == 'Q') {
return false;
}
}
// 检查 45 度角是否有皇后
for(int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
if (chessboard[i][j] == 'Q') {
return false;
}
}
return true;
}
在这份代码中,细心的同学可以发现为什么没有在同行进行检查呢?
因为在单层搜索的过程中,每一层递归,只会选for循环(也就是同一行)里的一个元素,所以不用去重了。
如果从来没有接触过N皇后问题的同学看着这样的题会感觉无从下手,可能知道要用回溯法,但也不知道该怎么去搜。
这里我明确给出了棋盘的宽度就是for循环的长度,递归的深度就是棋盘的高度,这样就可以套进回溯法的模板里了。
C++解法
class Solution {
private:
vector<vector<string>> result;
// n 为输入的棋盘大小
// row 是当前递归到棋盘的第几行了
void backtracking(int n, int row, vector<string>& chessboard) {
if (row == n) {
result.push_back(chessboard);
return;
}
for (int col = 0; col < n; col++) {
if (isValid(row, col, chessboard, n)) { // 验证合法就可以放
chessboard[row][col] = 'Q'; // 放置皇后
backtracking(n, row + 1, chessboard);
chessboard[row][col] = '.'; // 回溯,撤销皇后
}
}
}
bool isValid(int row, int col, vector<string>& chessboard, int n) {
// 检查列
for (int i = 0; i < row; i++) { // 这是一个剪枝
if (chessboard[i][col] == 'Q') {
return false;
}
}
// 检查135度角是否有皇后
for (int i = row - 1, j = col - 1; i >=0 && j >= 0; i--, j--) {
if (chessboard[i][j] == 'Q') {
return false;
}
}
// 检查45度角是否有皇后
for(int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
if (chessboard[i][j] == 'Q') {
return false;
}
}
return true;
}
public:
vector<vector<string>> solveNQueens(int n) {
result.clear();
std::vector<std::string> chessboard(n, std::string(n, '.'));
backtracking(n, 0, chessboard);
return result;
}
};
- 时间复杂度: O(n!)
- 空间复杂度: O(n)
52. N-Queens II
The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.
Given an integer n, return the number of distinct solutions to the n-queens puzzle.
Example 1:

Input: n = 4
Output: 2
Explanation: There are two distinct solutions to the 4-queens puzzle as shown.
Example 2:
Input: n = 1
Output: 1
Constraints:
1 <= n <= 9
思路
和上面一样,计算result中的元素个数作为最终结果即可。
C++解法
class Solution {
public:
vector<vector<string>> result;
void backtracking(vector<string>& chessBoard, int n, int row){
if(row == n){
result.push_back(chessBoard);
return;
}
for(int i = 0; i < chessBoard[row].size(); i++){
if(isValid(chessBoard, n, row, i) && chessBoard[row][i] == '.'){
chessBoard[row][i] = 'Q';
backtracking(chessBoard, n, row + 1);
chessBoard[row][i] = '.';
}
}
}
bool isValid(vector<string>& chessBoard, int n, int row, int col){
// 检查列
for (int i = 0; i < row; i++) { // 这是一个剪枝
if (chessBoard[i][col] == 'Q') {
return false;
}
}
// 检查135度角是否有皇后
for (int i = row - 1, j = col - 1; i >=0 && j >= 0; i--, j--) {
if (chessBoard[i][j] == 'Q') {
return false;
}
}
// 检查45度角是否有皇后
for(int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
if (chessBoard[i][j] == 'Q') {
return false;
}
}
return true;
}
int totalNQueens(int n) {
vector<string> chessBoard(n, string(n, '.'));
backtracking(chessBoard, n, 0);
return result.size();
}
};
37. Sudoku Solver
Write a program to solve a Sudoku puzzle by filling the empty cells.
A sudoku solution must satisfy all of the following rules:
- Each of the digits
1-9must occur exactly once in each row. - Each of the digits
1-9must occur exactly once in each column. - Each of the digits
1-9must occur exactly once in each of the 93x3sub-boxes of the grid.
The '.' character indicates empty cells.
Example 1:

Input: board = [["5","3",".",".","7",".",".",".","."],["6",".",".","1","9","5",".",".","."],[".","9","8",".",".",".",".","6","."],["8",".",".",".","6",".",".",".","3"],["4",".",".","8",".","3",".",".","1"],["7",".",".",".","2",".",".",".","6"],[".","6",".",".",".",".","2","8","."],[".",".",".","4","1","9",".",".","5"],[".",".",".",".","8",".",".","7","9"]]
Output: [["5","3","4","6","7","8","9","1","2"],["6","7","2","1","9","5","3","4","8"],["1","9","8","3","4","2","5","6","7"],["8","5","9","7","6","1","4","2","3"],["4","2","6","8","5","3","7","9","1"],["7","1","3","9","2","4","8","5","6"],["9","6","1","5","3","7","2","8","4"],["2","8","7","4","1","9","6","3","5"],["3","4","5","2","8","6","1","7","9"]]
Explanation: The input board is shown above and the only valid solution is shown below:

Constraints:
board.length == 9board[i].length == 9board[i][j]is a digit or'.'.- It is guaranteed that the input board has only one solution.
思路
棋盘搜索问题可以使用回溯法暴力搜索,只不过这次我们要做的是二维递归。
怎么做二维递归呢?
N皇后问题是因为每一行每一列只放一个皇后,只需要一层for循环遍历一行,递归来遍历列,然后一行一列确定皇后的唯一位置。
本题就不一样了,本题中棋盘的每一个位置都要放一个数字(而N皇后是一行只放一个皇后),并检查数字是否合法,解数独的树形结构要比N皇后更宽更深。
因为这个树形结构太大了,我抽取一部分,如图所示:
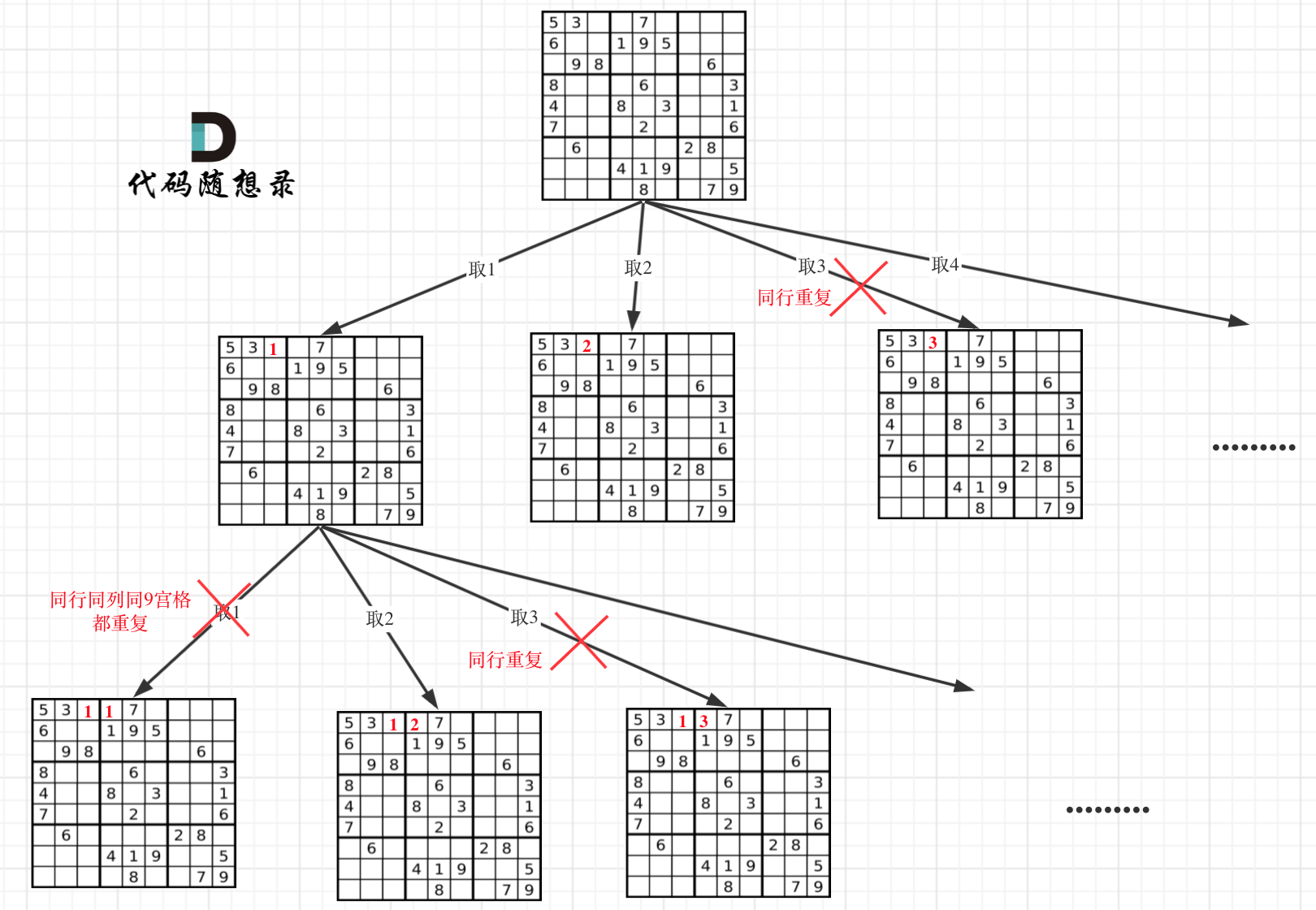
- 递归函数以及参数
递归函数的返回值需要是bool类型,为什么呢?
因为解数独找到一个符合的条件(就在树的叶子节点上)立刻就返回,相当于找从根节点到叶子节点一条唯一路径,所以需要使用bool返回值。
代码如下:
bool backtracking(vector<vector<char>>& board)
- 递归终止条件
本题递归不用终止条件,解数独是要遍历整个树形结构寻找可能的叶子节点就立刻返回。
不用终止条件会不会死循环?
递归的下一层的棋盘一定比上一层的棋盘多一个数,等数填满了棋盘自然就终止(填满当然好了,说明找到结果了),所以不需要终止条件!
那么有没有永远填不满的情况呢?
这个问题我在递归单层搜索逻辑里再来讲!
- 递归单层搜索逻辑
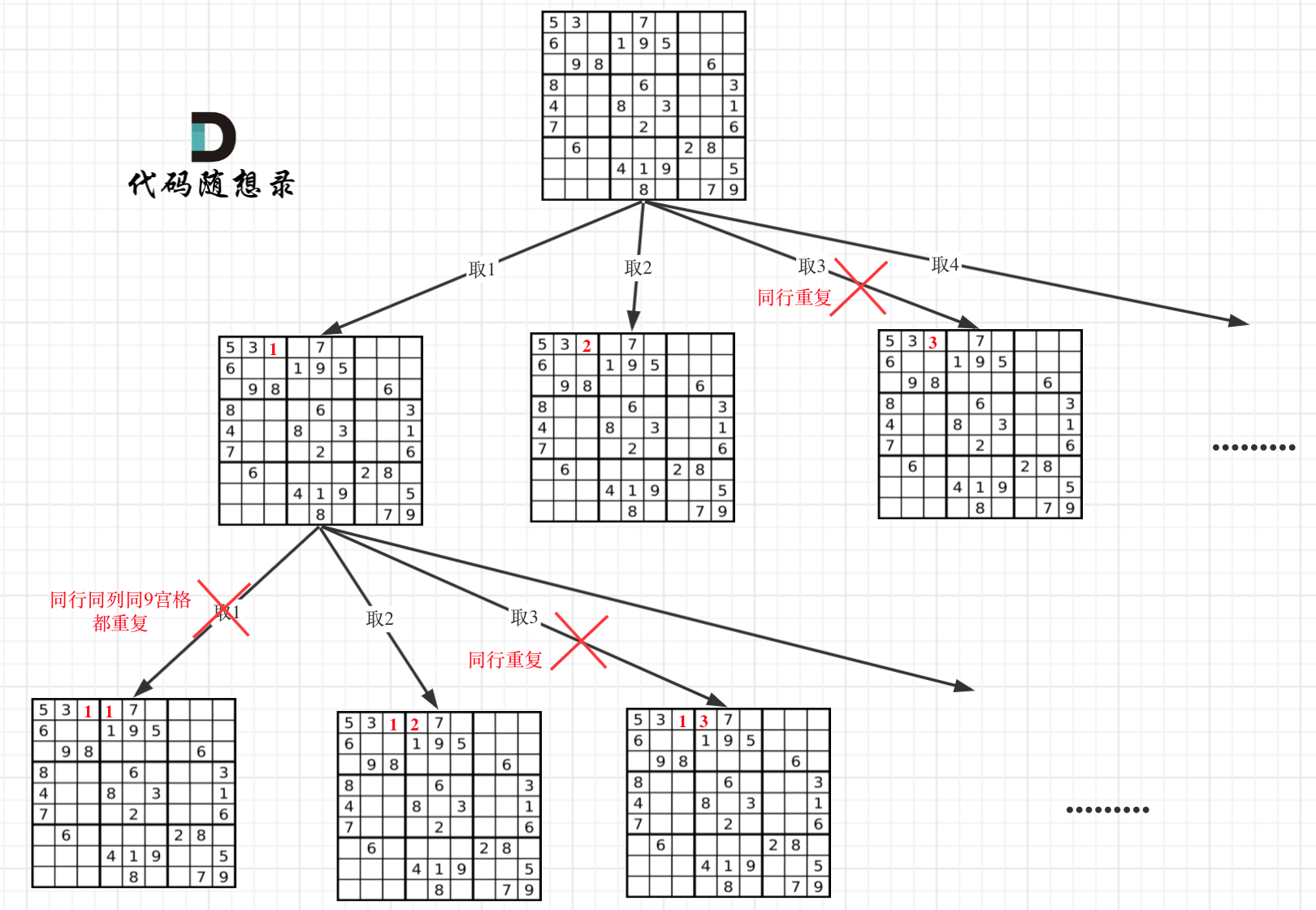
在树形图中可以看出我们需要的是一个二维的递归 (一行一列)
一个for循环遍历棋盘的行,一个for循环遍历棋盘的列,一行一列确定下来之后,递归遍历这个位置放9个数字的可能性!
代码如下:(详细看注释)
bool backtracking(vector<vector<char>>& board) {
for (int i = 0; i < board.size(); i++) { // 遍历行
for (int j = 0; j < board[0].size(); j++) { // 遍历列
if (board[i][j] != '.') continue;
for (char k = '1'; k <= '9'; k++) { // (i, j) 这个位置放k是否合适
if (isValid(i, j, k, board)) {
board[i][j] = k; // 放置k
if (backtracking(board)) return true; // 如果找到合适一组立刻返回
board[i][j] = '.'; // 回溯,撤销k
}
}
return false; // 9个数都试完了,都不行,那么就返回false
}
}
return true; // 遍历完没有返回false,说明找到了合适棋盘位置了
}
注意这里return false的地方,这里放return false 是有讲究的。
因为如果一行一列确定下来了,这里尝试了9个数都不行,说明这个棋盘找不到解决数独问题的解!
那么会直接返回, 这也就是为什么没有终止条件也不会永远填不满棋盘而无限递归下去!
判断棋盘是否合法有如下三个维度:
- 同行是否重复
- 同列是否重复
- 9宫格里是否重复
代码如下:
bool isValid(int row, int col, char val, vector<vector<char>>& board) {
for (int i = 0; i < 9; i++) { // 判断行里是否重复
if (board[row][i] == val) {
return false;
}
}
for (int j = 0; j < 9; j++) { // 判断列里是否重复
if (board[j][col] == val) {
return false;
}
}
int startRow = (row / 3) * 3;
int startCol = (col / 3) * 3;
for (int i = startRow; i < startRow + 3; i++) { // 判断9方格里是否重复
for (int j = startCol; j < startCol + 3; j++) {
if (board[i][j] == val ) {
return false;
}
}
}
return true;
}
C++解法
class Solution {
private:
bool backtracking(vector<vector<char>>& board) {
for (int i = 0; i < board.size(); i++) { // 遍历行
for (int j = 0; j < board[0].size(); j++) { // 遍历列
if (board[i][j] == '.') {
for (char k = '1'; k <= '9'; k++) { // (i, j) 这个位置放k是否合适
if (isValid(i, j, k, board)) {
board[i][j] = k; // 放置k
if (backtracking(board)) return true; // 如果找到合适一组立刻返回
board[i][j] = '.'; // 回溯,撤销k
}
}
return false; // 9个数都试完了,都不行,那么就返回false
}
}
}
return true; // 遍历完没有返回false,说明找到了合适棋盘位置了
}
bool isValid(int row, int col, char val, vector<vector<char>>& board) {
for (int i = 0; i < 9; i++) { // 判断行里是否重复
if (board[row][i] == val) {
return false;
}
}
for (int j = 0; j < 9; j++) { // 判断列里是否重复
if (board[j][col] == val) {
return false;
}
}
int startRow = (row / 3) * 3;
int startCol = (col / 3) * 3;
for (int i = startRow; i < startRow + 3; i++) { // 判断9方格里是否重复
for (int j = startCol; j < startCol + 3; j++) {
if (board[i][j] == val ) {
return false;
}
}
}
return true;
}
public:
void solveSudoku(vector<vector<char>>& board) {
backtracking(board);
}
};
36. Valid Sudoku
Determine if a 9 x 9 Sudoku board is valid. Only the filled cells need to be validated according to the following rules:
- Each row must contain the digits
1-9without repetition. - Each column must contain the digits
1-9without repetition. - Each of the nine
3 x 3sub-boxes of the grid must contain the digits1-9without repetition.
Note:
- A Sudoku board (partially filled) could be valid but is not necessarily solvable.
- Only the filled cells need to be validated according to the mentioned rules.
Example 1:

**Input:** board =
[["5","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
Output: true
Example 2:
**Input:** board =
[["8","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
Output: false
Explanation: Same as Example 1, except with the 5 in the top left corner being modified to 8. Since there are two 8's in the top left 3x3 sub-box, it is invalid.
Constraints:
board.length == 9board[i].length == 9board[i][j]is a digit1-9or'.'.
思路
遍历棋盘,分别处理每个不是.的位置,先保存,然后切换成.,最后尝试重新插入。如果不能重新插入,说明原来的棋盘不是合法的。
C++解法
class Solution {
public:
bool backtracking(vector<vector<char>>& board){
for(int i = 0; i < board.size(); i++){
for(int j = 0; j < board[i].size(); j++){
if (board[i][j] != '.'){
char val = board[i][j];
board[i][j] = '.';
if(!isValid(board, i, j, val)){
return false;
}
board[i][j] = val;
}
}
}
return true;
}
bool isValid(vector<vector<char>>& board, int row, int col, char val){
for (int i = 0; i < 9; i++) { // 判断行里是否重复
if (board[row][i] == val) {
return false;
}
}
for (int j = 0; j < 9; j++) { // 判断列里是否重复
if (board[j][col] == val) {
return false;
}
}
int startRow = (row / 3) * 3;
int startCol = (col / 3) * 3;
for (int i = startRow; i < startRow + 3; i++) { // 判断9方格里是否重复
for (int j = startCol; j < startCol + 3; j++) {
if (board[i][j] == val ) {
return false;
}
}
}
return true;
}
bool isValidSudoku(vector<vector<char>>& board) {
return backtracking(board);
}
};