排列
46. Permutations
Given an array nums of distinct integers, return all the possible permutations. You can return the answer in any order.
Example 1:
Input: nums = [1,2,3]
Output: [[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
Example 2:
Input: nums = [0,1]
Output: [[0,1],[1,0]]
Example 3:
Input: nums = [1]
Output: [[1]]
Constraints:
1 <= nums.length <= 6-10 <= nums[i] <= 10- All the integers of
numsare unique.
思路
新增一个used数组记录数字是否被使用过,如果被使用过就重新进入循环。
C++解法
class Solution {
public:
vector<vector<int>> result;
vector<int> path;
void backtracking (vector<int>& nums, vector<bool>& used) {
// 此时说明找到了一组
if (path.size() == nums.size()) {
result.push_back(path);
return;
}
for (int i = 0; i < nums.size(); i++) {
if (used[i] == true) continue; // path里已经收录的元素,直接跳过
used[i] = true;
path.push_back(nums[i]);
backtracking(nums, used);
path.pop_back();
used[i] = false;
}
}
vector<vector<int>> permute(vector<int>& nums) {
result.clear();
path.clear();
vector<bool> used(nums.size(), false);
backtracking(nums, used);
return result;
}
};
- 时间复杂度: O(n! * n)
- 空间复杂度: O(n)
47. Permutations II
Given a collection of numbers, nums, that might contain duplicates, return all possible unique permutations in any order.
Example 1:
Input: nums = [1,1,2]
Output:
[[1,1,2],
[1,2,1],
[2,1,1]]
Example 2:
Input: nums = [1,2,3]
Output: [[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
Constraints:
1 <= nums.length <= 8-10 <= nums[i] <= 10
思路
注意去重
C++解法
class Solution {
private:
vector<vector<int>> result;
vector<int> path;
void backtracking (vector<int>& nums, vector<bool>& used) {
// 此时说明找到了一组
if (path.size() == nums.size()) {
result.push_back(path);
return;
}
for (int i = 0; i < nums.size(); i++) {
// used[i - 1] == true,说明同一树枝nums[i - 1]使用过
// used[i - 1] == false,说明同一树层nums[i - 1]使用过
// 如果同一树层nums[i - 1]使用过则直接跳过
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
continue;
}
if (used[i] == false) {
used[i] = true;
path.push_back(nums[i]);
backtracking(nums, used);
path.pop_back();
used[i] = false;
}
}
}
public:
vector<vector<int>> permuteUnique(vector<int>& nums) {
result.clear();
path.clear();
sort(nums.begin(), nums.end()); // 排序
vector<bool> used(nums.size(), false);
backtracking(nums, used);
return result;
}
};
时间复杂度: 最差情况所有元素都是唯一的。复杂度和全排列1都是 O(n! * n)
对于 n 个元素一共有 n! 中排列方案。而对于每一个答案,我们需要 O(n) 去复制最终放到 result 数组
空间复杂度: O(n)
回溯树的深度取决于我们有多少个元素
784. Letter Case Permutation
Given a string s, you can transform every letter individually to be lowercase or uppercase to create another string.
Return a list of all possible strings we could create. Return the output in any order.
Example 1:
Input: s = "a1b2"
Output: ["a1b2","a1B2","A1b2","A1B2"]
Example 2:
Input: s = "3z4"
Output: ["3z4","3Z4"]
Constraints:
1 <= s.length <= 12sconsists of lowercase English letters, uppercase English letters, and digits.
思路
Consider the below recursion tree for input string S="a1b2"
Initially OUTPUT = "".
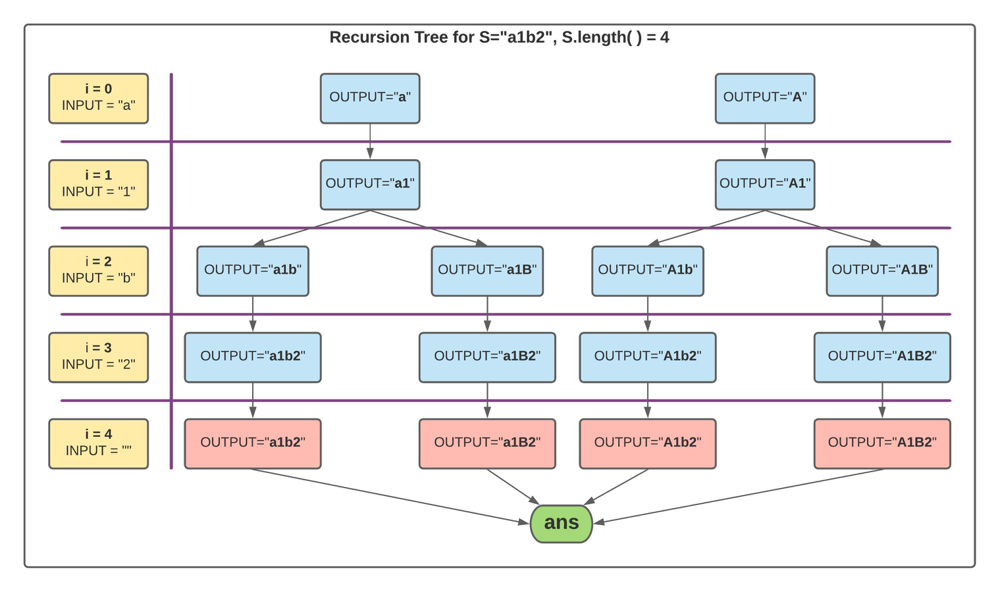
By observing the above recursion tree, we come to the below conclusion.
There are two main cases which needs to be solved recursively:
-
The element at the given index is a digit
- Append the digit to the end of
currand go to next index(i+1).curr.push_back(s[i]); solve(curr,s,i+1);
- Append the digit to the end of
-
The element at the given index is an alphabet, this case has two sub cases:
-
Append
tolower(s[i])tocurrand go to next index (i+1).//sub case 1, considering lower case string c1=curr; c1.push_back(tolower(s[i])); solve(c1,s,i+1); -
Append
toupper(s[i])tocurrand go to next index (i+1).//sub case 2, considering upper case string c2=curr; c2.push_back(toupper(s[i])); solve(c2,s,i+1);
-
If at any function call, the index = S.length(), then curr string has one of our output, so save it in ans vector,
// if end of the string is reached
if(i==s.length()){
ans.push_back(curr); // push the current "curr" string to ans
return;
}
At the end of the recursion return ans.
C++解法
class Solution {
private:
vector<string> result;
void backtracking(string s, string path, int index){
if(index == s.size()){
result.push_back(path);
return;
}
if(isdigit(s[index])){
path.push_back(s[index]);
backtracking(s, path, index + 1);
}else{
string lowerpath = path;
lowerpath.push_back(tolower(s[index]));
backtracking(s, lowerpath, index + 1);
string upperpath = path;
upperpath.push_back(toupper(s[index]));
backtracking(s, upperpath, index + 1);
}
}
public:
vector<string> letterCasePermutation(string s) {
backtracking(s, "", 0);
return result;
}
};
31. Next Permutation
A permutation of an array of integers is an arrangement of its members into a sequence or linear order.
For example, for arr = [1,2,3], the following are all the permutations of arr: [1,2,3], [1,3,2], [2, 1, 3], [2, 3, 1], [3,1,2], [3,2,1].
The next permutation of an array of integers is the next lexicographically greater permutation of its integer. More formally, if all the permutations of the array are sorted in one container according to their lexicographical order, then the next permutation of that array is the permutation that follows it in the sorted container. If such arrangement is not possible, the array must be rearranged as the lowest possible order (i.e., sorted in ascending order).
- For example, the next permutation of
arr = [1,2,3]is[1,3,2]. - Similarly, the next permutation of
arr = [2,3,1]is[3,1,2]. - While the next permutation of
arr = [3,2,1]is[1,2,3]because[3,2,1]does not have a lexicographical larger rearrangement.
Given an array of integers nums, find the next permutation of nums.
The replacement must be in place and use only constant extra memory.
Example 1:
Input: nums = [1,2,3]
Output: [1,3,2]
Example 2:
Input: nums = [3,2,1]
Output: [1,2,3]
Example 3:
Input: nums = [1,1,5]
Output: [1,5,1]
Constraints:
1 <= nums.length <= 1000 <= nums[i] <= 100
思路
先找breakpoint(从右向左第一个小于右边相邻元素的数字),
C++解法
class Solution {
public:
void nextPermutation(vector<int>& nums) {
int n = nums.size(), i = n - 2;
// Step 1: Find the breakpoint
while (i >= 0 && nums[i] >= nums[i + 1]) {
i--;
}
if (i >= 0) {
// Step 2: Find the smallest element larger than nums[i]
int j = n - 1;
while (nums[j] <= nums[i]) {
j--;
}
swap(nums[i], nums[j]);
}
// Step 3: Reverse the subarray to the right of i
reverse(nums.begin() + i + 1, nums.end());
}
};
Java解法
class Solution {
public void reverse(int[] nums, int i, int j) {
while (i < j) {
int temp = nums[j];
nums[j] = nums[i];
nums[i] = temp;
i++; // 更新 i
j--; // 更新 j
}
}
public void nextPermutation(int[] nums) {
int length = nums.length;
int i = length - 2;
// 找到第一个下降的元素
while (i >= 0 && nums[i] >= nums[i + 1]) i--;
if (i >= 0) {
int j = length - 1;
// 找到比 nums[i] 大的最右边元素
while (j >= 0 && nums[j] <= nums[i]) j--;
// 交换元素
int temp = nums[j];
nums[j] = nums[i];
nums[i] = temp;
}
// 反转后面的元素
reverse(nums, i + 1, length - 1);
}
}