回文串
647. Palindromic Substrings
Given a string s, return the number of palindromic substrings in it.
A string is a palindrome when it reads the same backward as forward.
A substring is a contiguous sequence of characters within the string.
Example 1:
Input: s = "abc"
Output: 3
Explanation: Three palindromic strings: "a", "b", "c".
Example 2:
Input: s = "aaa"
Output: 6
Explanation: Six palindromic strings: "a", "a", "a", "aa", "aa", "aaa".
Constraints:
1 <= s.length <= 1000sconsists of lowercase English letters.
思路
暴力解法
两层for循环,遍历区间起始位置和终止位置,然后还需要一层遍历判断这个区间是不是回文。所以时间复杂度:O(n^3)
动态规划
动规五部曲:
- 确定dp数组(dp table)以及下标的含义
如果大家做了很多这种子序列相关的题目,在定义dp数组的时候 很自然就会想题目求什么,我们就如何定义dp数组。
绝大多数题目确实是这样,不过本题如果我们定义,dp[i] 为 下标i结尾的字符串有 dp[i]个回文串的话,我们会发现很难找到递归关系。
dp[i] 和 dp[i-1] ,dp[i + 1] 看上去都没啥关系。
所以我们要看回文串的性质。 如图:
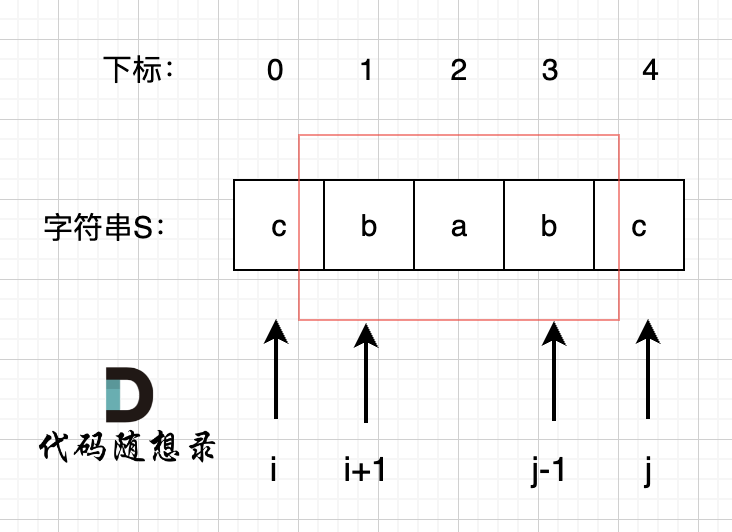
我们在判断字符串S是否是回文,那么如果我们知道 s[1],s[2],s[3] 这个子串是回文的,那么只需要比较 s[0]和s[4]这两个元素是否相同,如果相同的话,这个字符串s 就是回文串。
那么此时我们是不是能找到一种递归关系,也就是判断一个子字符串(字符串的下表范围[i,j])是否回文,依赖于,子字符串(下表范围[i + 1, j - 1])) 是否是回文。
所以为了明确这种递归关系,我们的dp数组是要定义成一位二维dp数组。
布尔类型的dp[i][j]:表示区间范围[i,j] (注意是左闭右闭)的子串是否是回文子串,如果是dp[i][j]为true,否则为false。
- 确定递推公式
在确定递推公式时,就要分析如下几种情况。
整体上是两种,就是s[i]与s[j]相等,s[i]与s[j]不相等这两种。
当s[i]与s[j]不相等,那没啥好说的了,dp[i][j]一定是false。
当s[i]与s[j]相等时,这就复杂一些了,有如下三种情况
- 情况一:下标i 与 j相同,同一个字符例如a,当然是回文子串
- 情况二:下标i 与 j相差为1,例如aa,也是回文子串
- 情况三:下标:i 与 j相差大于1的时候,例如cabac,此时s[i]与s[j]已经相同了,我们看i到j区间是不是回文子串就看aba是不是回文就可以了,那么aba的区间就是 i+1 与 j-1区间,这个区间是不是回文就看
dp[i + 1][j - 1]是否为true。
以上三种情况分析完了,那么递归公式如下:
if (s[i] == s[j]) {
if (j - i <= 1) { // 情况一 和 情况二
result++;
dp[i][j] = true;
} else if (dp[i + 1][j - 1]) { // 情况三
result++;
dp[i][j] = true;
}
}
result就是统计回文子串的数量。
注意这里我没有列出当s[i]与s[j]不相等的时候,因为在下面dp[i][j]初始化的时候,就初始为false。
- dp数组如何初始化
dp[i][j]可以初始化为true么? 当然不行,怎能刚开始就全都匹配上了。
所以dp[i][j]初始化为false。
- 确定遍历顺序
遍历顺序可有有点讲究了。
首先从递推公式中可以看出,情况三是根据dp[i + 1][j - 1]是否为true,在对dp[i][j]进行赋值true的。
dp[i + 1][j - 1]在 dp[i][j]的左下角,如图:
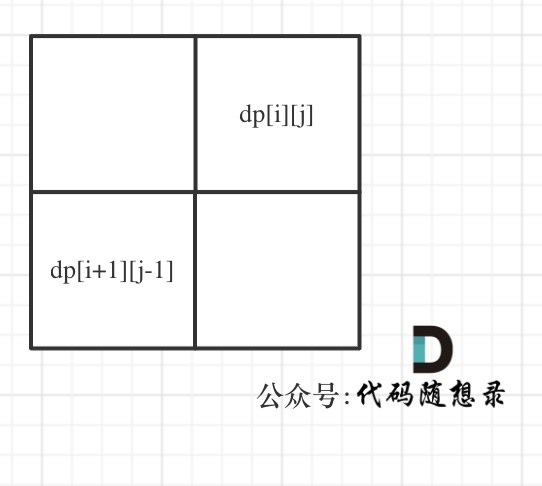
如果这矩阵是从上到下,从左到右遍历,那么会用到没有计算过的dp[i + 1][j - 1],也就是根据不确定是不是回文的区间[i+1,j-1],来判断了[i,j]是不是回文,那结果一定是不对的。
所以一定要从下到上,从左到右遍历,这样保证dp[i + 1][j - 1]都是经过计算的。
有的代码实现是优先遍历列,然后遍历行,其实也是一个道理,都是为了保证dp[i + 1][j - 1]都是经过计算的。
代码如下:
for (int i = s.size() - 1; i >= 0; i--) { // 注意遍历顺序
for (int j = i; j < s.size(); j++) {
if (s[i] == s[j]) {
if (j - i <= 1) { // 情况一 和 情况二
result++;
dp[i][j] = true;
} else if (dp[i + 1][j - 1]) { // 情况三
result++;
dp[i][j] = true;
}
}
}
}
- 举例推导dp数组
举例,输入:"aaa",dp[i][j]状态如下:
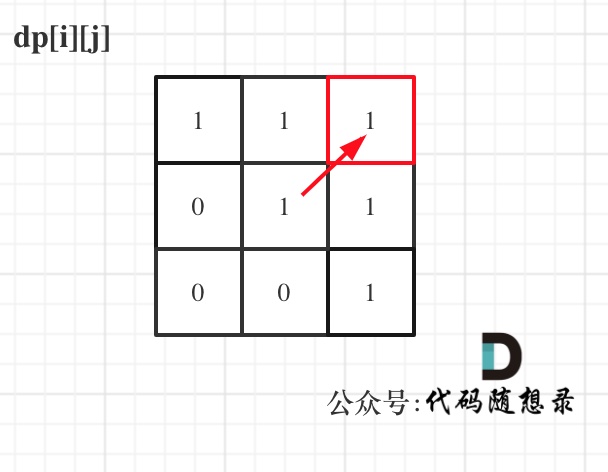
图中有6个true,所以就是有6个回文子串。
注意因为dp[i][j]的定义,所以j一定是大于等于i的,那么在填充dp[i][j]的时候一定是只填充右上半部分。
C++解法
以上分析完毕,C++代码如下:
class Solution {
public:
int countSubstrings(string s) {
vector<vector<bool>> dp(s.size(), vector<bool>(s.size(), false));
int result = 0;
for (int i = s.size() - 1; i >= 0; i--) { // 注意遍历顺序
for (int j = i; j < s.size(); j++) {
if (s[i] == s[j]) {
if (j - i <= 1) { // 情况一 和 情况二
result++;
dp[i][j] = true;
} else if (dp[i + 1][j - 1]) { // 情况三
result++;
dp[i][j] = true;
}
}
}
}
return result;
}
};
以上代码是为了凸显情况一二三,当然是可以简洁一下的,如下:
class Solution {
public:
int countSubstrings(string s) {
vector<vector<bool>> dp(s.size(), vector<bool>(s.size(), false));
int result = 0;
for (int i = s.size() - 1; i >= 0; i--) {
for (int j = i; j < s.size(); j++) {
if (s[i] == s[j] && (j - i <= 1 || dp[i + 1][j - 1])) {
result++;
dp[i][j] = true;
}
}
}
return result;
}
};
- 时间复杂度:O(n^2)
- 空间复杂度:O(n^2)
双指针法
动态规划的空间复杂度是偏高的,我们再看一下双指针法。
首先确定回文串,就是找中心然后向两边扩散看是不是对称的就可以了。
在遍历中心点的时候,要注意中心点有两种情况。
一个元素可以作为中心点,两个元素也可以作为中心点。
那么有人同学问了,三个元素还可以做中心点呢。其实三个元素就可以由一个元素左右添加元素得到,四个元素则可以由两个元素左右添加元素得到。
所以我们在计算的时候,要注意一个元素为中心点和两个元素为中心点的情况。
这两种情况可以放在一起计算,但分别计算思路更清晰,我倾向于分别计算,代码如下:
class Solution {
public:
int countSubstrings(string s) {
int result = 0;
for (int i = 0; i < s.size(); i++) {
result += extend(s, i, i, s.size()); // 以i为中心
result += extend(s, i, i + 1, s.size()); // 以i和i+1为中心
}
return result;
}
int extend(const string& s, int i, int j, int n) {
int res = 0;
while (i >= 0 && j < n && s[i] == s[j]) {
i--;
j++;
res++;
}
return res;
}
};
- 时间复杂度:O(n^2)
- 空间复杂度:O(1)
Java解法
动态规划:
class Solution {
public int countSubstrings(String s) {
char[] chars = s.toCharArray();
int len = chars.length;
boolean[][] dp = new boolean[len][len];
int result = 0;
for (int i = len - 1; i >= 0; i--) {
for (int j = i; j < len; j++) {
if (chars[i] == chars[j]) {
if (j - i <= 1) { // 情况一 和 情况二
result++;
dp[i][j] = true;
} else if (dp[i + 1][j - 1]) { //情况三
result++;
dp[i][j] = true;
}
}
}
}
return result;
}
}
动态规划:简洁版
class Solution {
public int countSubstrings(String s) {
boolean[][] dp = new boolean[s.length()][s.length()];
int res = 0;
for (int i = s.length() - 1; i >= 0; i--) {
for (int j = i; j < s.length(); j++) {
if (s.charAt(i) == s.charAt(j) && (j - i <= 1 || dp[i + 1][j - 1])) {
res++;
dp[i][j] = true;
}
}
}
return res;
}
}
中心扩散法:
class Solution {
public int countSubstrings(String s) {
int len, ans = 0;
if (s == null || (len = s.length()) < 1) return 0;
//总共有2 * len - 1个中心点
for (int i = 0; i < 2 * len - 1; i++) {
//通过遍历每个回文中心,向两边扩散,并判断是否回文字串
//有两种情况,left == right,right = left + 1,这两种回文中心是不一样的
int left = i / 2, right = left + i % 2;
while (left >= 0 && right < len && s.charAt(left) == s.charAt(right)) {
//如果当前是一个回文串,则记录数量
ans++;
left--;
right++;
}
}
return ans;
}
}
5. Longest Palindromic Substring
Given a string s, return the longest palindromic substring in s.
Example 1:
Input: s = "babad"
Output: "bab"
Explanation: "aba" is also a valid answer.
Example 2:
Input: s = "cbbd"
Output: "bb"
Constraints:
1 <= s.length <= 1000sconsist of only digits and English letters.
思路
Approach 1: Check All Substrings
Approach 2: Dynamic Programming
Approach 3: Expand From Centers
Approach 4: Manacher's Algorithm
C++解法
Approach 4: Manacher's Algorithm
Believe it or not, this problem can be solved in linear time.
Manacher's algorithm finds the longest palindromic substring in O(n) time and space.
Note: this algorithm is completely out of scope for coding interviews. Because of this, we will not be talking about the algorithm in detail. This approach has been included for the sake of completeness and for those who are curious about algorithms beyond the scope of interviews.
class Solution {
public:
string longestPalindrome(string s) {
string s_prime = "#";
for (char c : s) {
s_prime += c;
s_prime += "#";
}
int n = s_prime.length();
vector<int> palindrome_radii(n, 0);
int center = 0;
int radius = 0;
for (int i = 0; i < n; i++) {
int mirror = 2 * center - i;
if (i < radius) {
palindrome_radii[i] = min(radius - i, palindrome_radii[mirror]);
}
while (i + 1 + palindrome_radii[i] < n &&
i - 1 - palindrome_radii[i] >= 0 &&
s_prime[i + 1 + palindrome_radii[i]] ==
s_prime[i - 1 - palindrome_radii[i]]) {
palindrome_radii[i]++;
}
if (i + palindrome_radii[i] > radius) {
center = i;
radius = i + palindrome_radii[i];
}
}
int max_length = 0;
int center_index = 0;
for (int i = 0; i < n; i++) {
if (palindrome_radii[i] > max_length) {
max_length = palindrome_radii[i];
center_index = i;
}
}
int start_index = (center_index - max_length) / 2;
string longest_palindrome = s.substr(start_index, max_length);
return longest_palindrome;
}
};
Java解法
你的Java代码有一些小错误,导致在构建最长回文子串时无法正确返回结果。主要问题在于以下几点:
StringBuilder result需要初始化为一个空对象,或者可以使用String直接保存最长回文子串。- 在更新
result时,你应该使用str.substring(i, j + 1),而不是str.substring(i, j - i + 1)。 - 在更新
result时,应该在循环外声明并保存最长的回文子串,而不是每次都更新。
以下是修正后的代码:
class Solution {
public String longestPalindrome(String s) {
if (s == null || s.length() < 1) return "";
int start = 0, end = 0;
boolean[][] dp = new boolean[s.length()][s.length()];
for (int j = 0; j < s.length(); j++) {
for (int i = 0; i <= j; i++) {
if (s.charAt(i) == s.charAt(j) && (j - i <= 2 || dp[i + 1][j - 1])) {
dp[i][j] = true;
if (j - i > end - start) {
start = i;
end = j;
}
}
}
}
return s.substring(start, end + 1);
}
}
主要改动:
- 使用
start和end变量来追踪最长回文子串的起始和结束索引。 - 使用
dp[i + 1][j - 1]来判断当前的子串是否是回文,并在条件成立时更新start和end。 - 最后返回
s.substring(start, end + 1)获取正确的回文子串。
这段代码在性能上也是优化了,因为现在它只在必要时更新 start 和 end,使得代码更简洁高效。
516. Longest Palindromic Subsequence
Given a string s, find the longest palindromic subsequence's length in s.
A subsequence is a sequence that can be derived from another sequence by deleting some or no elements without changing the order of the remaining elements.
Example 1:
Input: s = "bbbab"
Output: 4
Explanation: One possible longest palindromic subsequence is "bbbb".
Example 2:
Input: s = "cbbd"
Output: 2
Explanation: One possible longest palindromic subsequence is "bb".
Constraints:
1 <= s.length <= 1000sconsists only of lowercase English letters.
思路
我们刚刚做过了 动态规划:回文子串,求的是回文子串,而本题要求的是回文子序列, 要搞清楚这两者之间的区别。
回文子串是要连续的,回文子序列可不是连续的! 回文子串,回文子序列都是动态规划经典题目。
回文子串,可以做这两题:
- 647.回文子串
- 5.最长回文子串
思路其实是差不多的,但本题要比求回文子串简单一点,因为情况少了一点。
动规五部曲分析如下:
- 确定dp数组(dp table)以及下标的含义
dp[i][j]:字符串s在[i, j]范围内最长的回文子序列的长度为dp[i][j]。
- 确定递推公式
在判断回文子串的题目中,关键逻辑就是看s[i]与s[j]是否相同。
如果s[i]与s[j]相同,那么``dp[i][j] = dp[i + 1][j - 1] + 2;
如图: 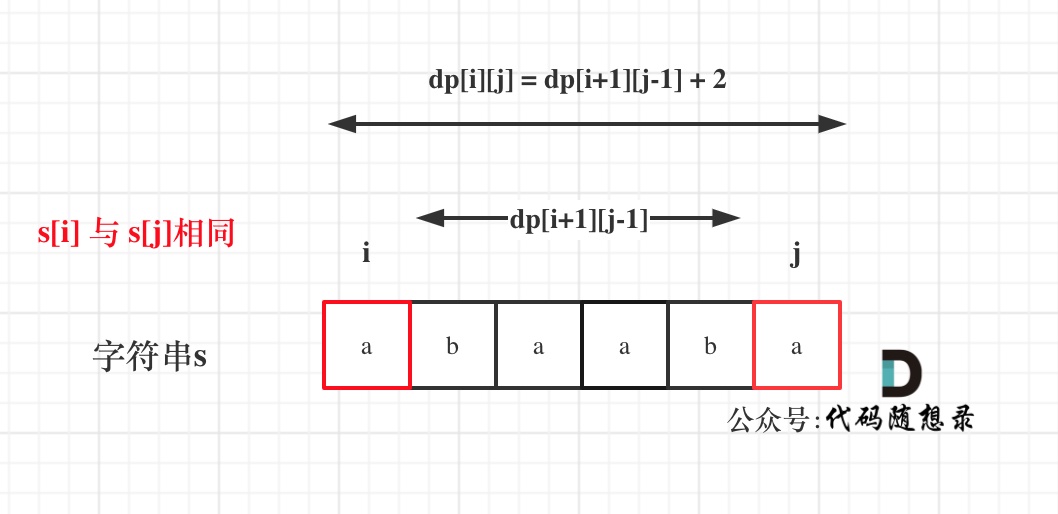
(如果这里看不懂,回忆一下dpi的定义)
如果s[i]与s[j]不相同,说明s[i]和s[j]的同时加入 并不能增加[i,j]区间回文子序列的长度,那么分别加入s[i]、s[j]看看哪一个可以组成最长的回文子序列。
加入s[j]的回文子序列长度为dp[i + 1][j]。
加入s[i]的回文子序列长度为`dp[i][j - 1]。
那么dpi一定是取最大的,即:dp[i][j] = max(dp[i + 1][j], dp[i][j - 1];
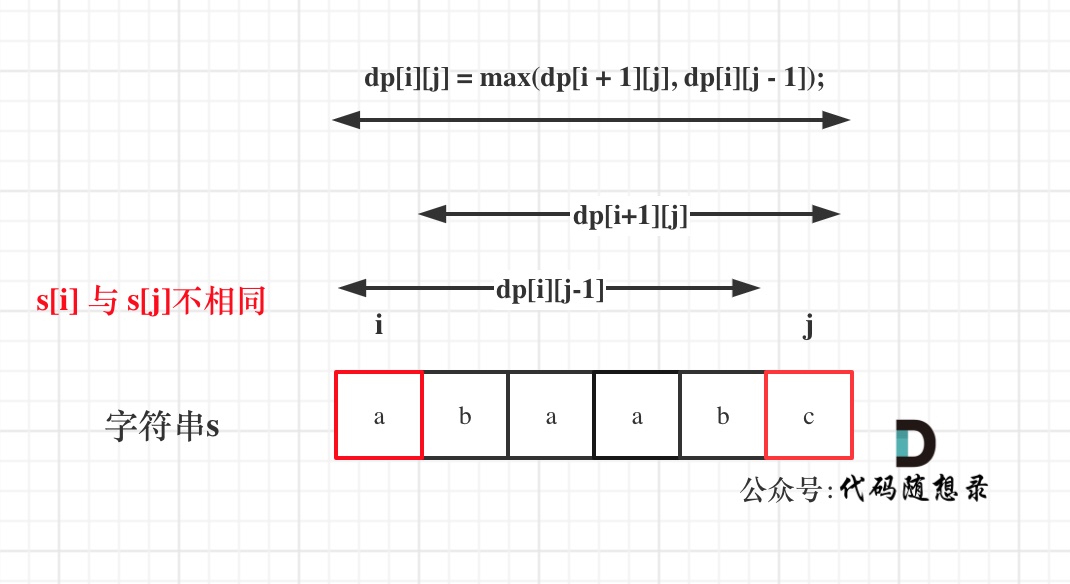
代码如下:
if (s[i] == s[j]) {
dp[i][j] = dp[i + 1][j - 1] + 2;
} else {
dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
}
- dp数组如何初始化
首先要考虑当i 和j 相同的情况,从递推公式:dp[i][j] =dp[i + 1][j - 1] + 2; 可以看出 递推公式是计算不到 i 和j相同时候的情况。
所以需要手动初始化一下,当i与j相同,那么dp[i][j]一定是等于1的,即:一个字符的回文子序列长度就是1。
其他情况dp[i][j]初始为0就行,这样递推公式:dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]); 中dp[i][j]才不会被初始值覆盖。
vector<vector<int>> dp(s.size(), vector<int>(s.size(), 0));
for (int i = 0; i < s.size(); i++) dp[i][i] = 1;
- 确定遍历顺序
从递归公式中,可以看出,dp[i][j]依赖于 dp[i][j - 1],dp[i + 1][j]和 dp[i + 1][j - 1],如图:
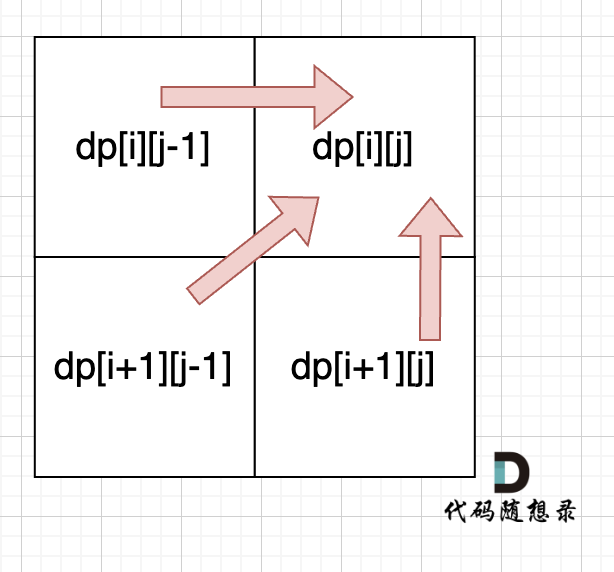
所以遍历i的时候一定要从下到上遍历,这样才能保证下一行的数据是经过计算的。
j的话,可以正常从左向右遍历。
代码如下:
for (int i = s.size() - 1; i >= 0; i--) {
for (int j = i + 1; j < s.size(); j++) {
if (s[i] == s[j]) {
dp[i][j] = dp[i + 1][j - 1] + 2;
} else {
dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
}
}
}
- 举例推导dp数组
输入s:"cbbd" 为例,dp数组状态如图:
红色框即:dp[0][s.size() - 1]; 为最终结果。
C++解法
以上分析完毕,C++代码如下:
class Solution {
public:
int longestPalindromeSubseq(string s) {
vector<vector<int>> dp(s.size(), vector<int>(s.size(), 0));
for (int i = 0; i < s.size(); i++) dp[i][i] = 1;
for (int i = s.size() - 1; i >= 0; i--) {
for (int j = i + 1; j < s.size(); j++) {
if (s[i] == s[j]) {
dp[i][j] = dp[i + 1][j - 1] + 2;
} else {
dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
}
}
}
return dp[0][s.size() - 1];
}
};
- 时间复杂度: O(n^2)
- 空间复杂度: O(n^2)
Java解法
public class Solution {
public int longestPalindromeSubseq(String s) {
int len = s.length();
int[][] dp = new int[len + 1][len + 1];
for (int i = len - 1; i >= 0; i--) { // 从后往前遍历 保证情况不漏
dp[i][i] = 1; // 初始化
for (int j = i + 1; j < len; j++) {
if (s.charAt(i) == s.charAt(j)) {
dp[i][j] = dp[i + 1][j - 1] + 2;
} else {
dp[i][j] = Math.max(dp[i + 1][j], Math.max(dp[i][j], dp[i][j - 1]));
}
}
}
return dp[0][len - 1];
}
}