不同路径

62. Unique Paths
- 思路
- C++解法
- Java解法
63. Unique Paths II
980. Unique Paths III（回溯）

62. Unique Paths

There is a robot on an m x n grid. The robot is initially located at the top-left corner (i.e., grid[0][0]). The robot tries to move to the bottom-right corner (i.e., grid[m - 1][n - 1]). The robot can only move either down or right at any point in time.

Given the two integers m and n, return the number of possible unique paths that the robot can take to reach the bottom-right corner.

The test cases are generated so that the answer will be less than or equal to 2 * 10^9.

Example 1:

Input: m = 3, n = 7
Output: 28

Example 2:

Input: m = 3, n = 2
Output: 3 Explanation: From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:

Right -> Down -> Down
Down -> Down -> Right
Down -> Right -> Down

Constraints:

1 <= m, n <= 100

思路

深搜

这道题目，刚一看最直观的想法就是用图论里的深搜，来枚举出来有多少种路径。

注意题目中说机器人每次只能向下或者向右移动一步，那么其实机器人走过的路径可以抽象为一棵二叉树，而叶子节点就是终点！

如图举例：

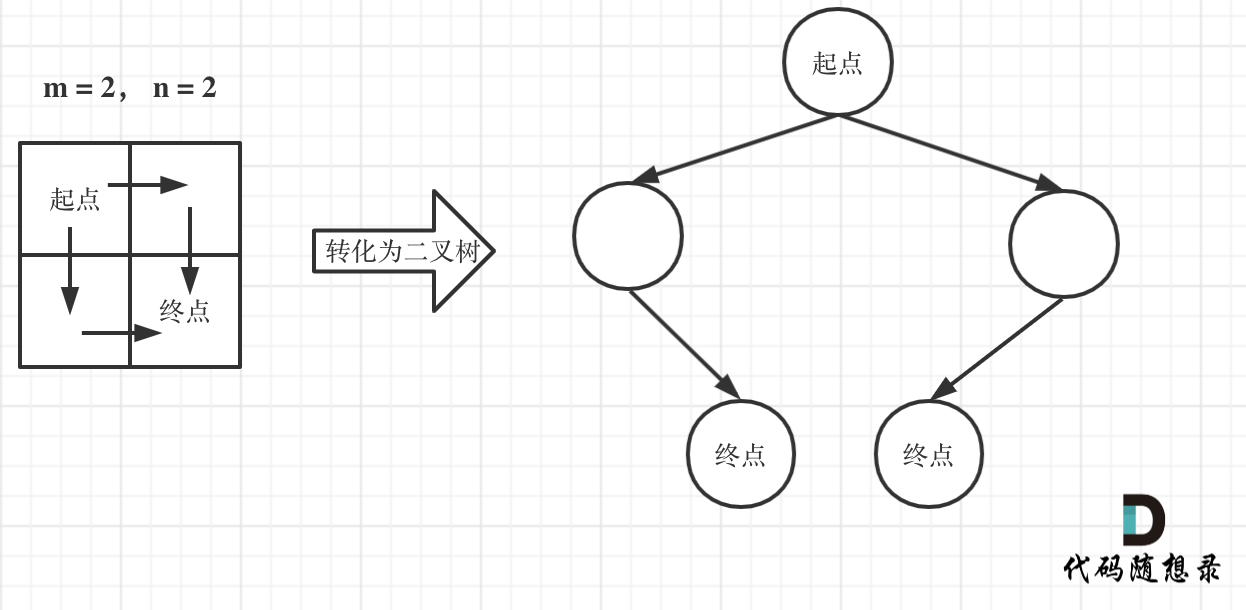
62.不同路径

此时问题就可以转化为求二叉树叶子节点的个数，代码如下：

class Solution {  
private:  
    int dfs(int i, int j, int m, int n) {  
        if (i > m || j > n) return 0; // 越界了  
        if (i == m && j == n) return 1; // 找到一种方法，相当于找到了叶子节点  
        return dfs(i + 1, j, m, n) + dfs(i, j + 1, m, n);  
    }  
public:  
    int uniquePaths(int m, int n) {  
        return dfs(1, 1, m, n);  
    }  
};

大家如果提交了代码就会发现超时了！

来分析一下时间复杂度，这个深搜的算法，其实就是要遍历整个二叉树。

这棵树的深度其实就是m+n-1（深度按从1开始计算）。

那二叉树的节点个数就是 $2^{(m + n - 1)} - 1$ 。可以理解深搜的算法就是遍历了整个满二叉树（其实没有遍历整个满二叉树，只是近似而已）

所以上面深搜代码的时间复杂度为 $O (2^{(m + n - 1)} - 1)$ ，可以看出，这是指数级别的时间复杂度，是非常大的。

动态规划

机器人从(0 , 0) 位置出发，到(m - 1, n - 1)终点。

按照动规五部曲来分析：

确定dp数组（dp table）以及下标的含义

dp[i][j]：表示从（0 ，0）出发，到(i, j) 有dp[i][j]条不同的路径。

确定递推公式

想要求dp[i][j]，只能有两个方向来推导出来，即dp[i - 1][j] 和 dp[i][j - 1]。

此时在回顾一下 dp[i - 1][j] 表示啥，是从(0, 0)的位置到(i - 1, j)有几条路径，dp[i][j]同理。

那么很自然，dp[i][j] = dp[i - 1][j] + dp[i][j - 1]，因为dp[i][j]只有这两个方向过来。

dp数组的初始化

如何初始化呢，首先dp[i][j]一定都是1，因为从(0, 0)的位置到(i, 0)的路径只有一条，那么dp0也同理。

所以初始化代码为：

for (int i = 0; i < m; i++) dp[i][0] = 1;  
for (int j = 0; j < n; j++) dp[0][j] = 1;

确定遍历顺序

这里要看一下递推公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1]，dp[i][j]都是从其上方和左方推导而来，那么从左到右一层一层遍历就可以了。

举例推导dp数组

如图所示：

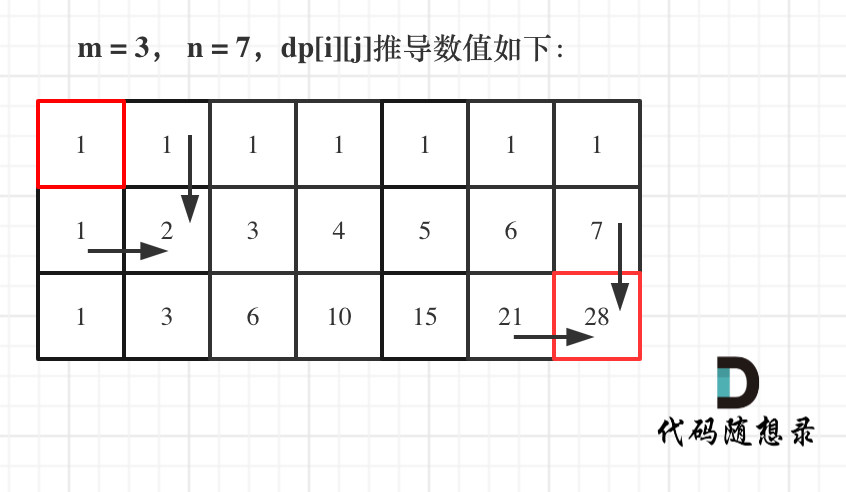
62.不同路径1

数论方法

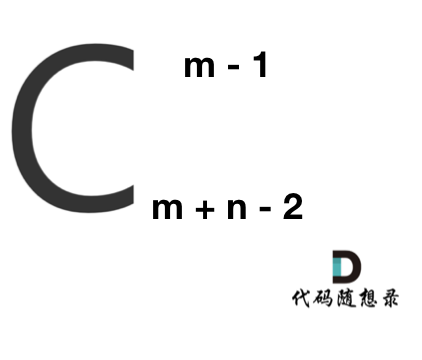
在这个图中，可以看出一共m，n的话，无论怎么走，走到终点都需要 m + n - 2 步。

62.不同路径

在这m + n - 2 步中，一定有 m - 1 步是要向下走的，不用管什么时候向下走。

那么有几种走法呢？可以转化为，给你m + n - 2个不同的数，随便取m - 1个数，有几种取法。

那么这就是一个组合问题了。

那么答案，如图所示：

62.不同路径2

求组合的时候，要防止两个int相乘溢出！ 所以不能把算式的分子都算出来，分母都算出来再做除法。

例如如下代码是不行的。

class Solution {  
public:  
    int uniquePaths(int m, int n) {  
        int numerator = 1, denominator = 1;  
        int count = m - 1;  
        int t = m + n - 2;  
        while (count--) numerator *= (t--); // 计算分子，此时分子就会溢出  
        for (int i = 1; i <= m - 1; i++) denominator *= i; // 计算分母  
        return numerator / denominator;  
    }  
};

需要在计算分子的时候，不断除以分母，代码如下：

class Solution {  
public:  
    int uniquePaths(int m, int n) {  
        long long numerator = 1; // 分子  
        int denominator = m - 1; // 分母  
        int count = m - 1;  
        int t = m + n - 2;  
        while (count--) {  
            numerator *= (t--);  
            while (denominator != 0 && numerator % denominator == 0) {  
                numerator /= denominator;  
                denominator--;  
            }  
        }  
        return numerator;  
    }  
};

时间复杂度：O(m)
空间复杂度：O(1)

计算组合问题的代码还是有难度的，特别是处理溢出的情况！

C++解法

以上动规五部曲分析完毕，C++代码如下：

class Solution {  
public:  
    int uniquePaths(int m, int n) {  
        vector<vector<int>> dp(m, vector<int>(n, 0));  
        for (int i = 0; i < m; i++) dp[i][0] = 1;  
        for (int j = 0; j < n; j++) dp[0][j] = 1;  
        for (int i = 1; i < m; i++) {  
            for (int j = 1; j < n; j++) {  
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];  
            }  
        }  
        return dp[m - 1][n - 1];  
    }  
};

时间复杂度：O(m × n)
空间复杂度：O(m × n)

其实用一个一维数组（也可以理解是滚动数组）就可以了，但是不利于理解，可以优化点空间，建议先理解了二维，在理解一维，C++代码如下：

class Solution {  
public:  
    int uniquePaths(int m, int n) {  
        vector<int> dp(n);  
        for (int i = 0; i < n; i++) dp[i] = 1;  
        for (int j = 1; j < m; j++) {  
            for (int i = 1; i < n; i++) {  
                dp[i] += dp[i - 1];  
            }  
        }  
        return dp[n - 1];  
    }  
};

时间复杂度：O(m × n)
空间复杂度：O(n)

Java解法

  /**
     * 1. 确定dp数组下标含义 dp[i][j] 到每一个坐标可能的路径种类
     * 2. 递推公式 dp[i][j] = dp[i-1][j] dp[i][j-1]
     * 3. 初始化 dp[i][0]=1 dp[0][i]=1 初始化横竖就可
     * 4. 遍历顺序 一行一行遍历
     * 5. 推导结果 。。。。。。。。
     *
     * @param m
     * @param n
     * @return
     */
    public static int uniquePaths(int m, int n) {
        int[][] dp = new int[m][n];
        //初始化
        for (int i = 0; i < m; i++) {
            dp[i][0] = 1;
        }
        for (int i = 0; i < n; i++) {
            dp[0][i] = 1;
        }

        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i][j] = dp[i-1][j]+dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }

63. Unique Paths II

You are given an m x n integer array grid. There is a robot initially located at the top-left corner (i.e., grid[0][0]). The robot tries to move to the bottom-right corner (i.e., grid[m - 1][n - 1]). The robot can only move either down or right at any point in time.

An obstacle and space are marked as 1 or 0 respectively in grid. A path that the robot takes cannot include any square that is an obstacle.

Return the number of possible unique paths that the robot can take to reach the bottom-right corner.

The testcases are generated so that the answer will be less than or equal to 2 * 10^9.

Example 1:

Input: obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
Output: 2
Explanation: There is one obstacle in the middle of the 3x3 grid above. There are two ways to reach the bottom-right corner:

Right -> Right -> Down -> Down
Down -> Down -> Right -> Right

Example 2:

Input: obstacleGrid = [[0,1],[0,0]]
Output: 1

Constraints:

m == obstacleGrid.length
n == obstacleGrid[i].length
1 <= m, n <= 100
obstacleGrid[i][j] is 0 or 1.

思路

62.不同路径中我们已经详细分析了没有障碍的情况，有障碍的话，其实就是标记对应的dp table（dp数组）保持初始值(0)就可以了。

动规五部曲：

确定dp数组（dp table）以及下标的含义

dp[i][j] ：表示从（0 ，0）出发，到(i, j) 有dp[i][j]条不同的路径。

确定递推公式

递推公式和62.不同路径一样，dp[i][j] = dp[i - 1][j] + dp[i][j - 1]

但这里需要注意一点，因为有了障碍，(i, j)如果就是障碍的话应该就保持初始状态（初始状态为0）。

所以代码为：

if (obstacleGrid[i][j] == 0) { // 当(i, j)没有障碍的时候，再推导dp[i][j]  
    dp[i][j] = dp[i - 1][j] + dp[i][j - 1];  
}

dp数组如何初始化

在62.不同路径不同路径中我们给出如下的初始化：

vector<vector<int>> dp(m, vector<int>(n, 0)); // 初始值为0  
for (int i = 0; i < m; i++) dp[i][0] = 1;  
for (int j = 0; j < n; j++) dp[0][j] = 1;

因为从(0, 0)的位置到(i, 0)的路径只有一条，所以dp[i][j]一定为1，dp0也同理。

但如果(i, 0) 这条边有了障碍之后，障碍之后（包括障碍）都是走不到的位置了，所以障碍之后的dp[i][j]应该还是初始值0。

如图：

下标(0, j)的初始化情况同理。

所以本题初始化代码为：

vector<vector<int>> dp(m, vector<int>(n, 0));  
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;  
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;

注意代码里for循环的终止条件，一旦遇到obstacleGrid[i][0] == 1的情况就停止dp[i][j]的赋值1的操作，dp[0][j]同理

确定遍历顺序

从递归公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1]中可以看出，一定是从左到右一层一层遍历，这样保证推导dp[i][j]的时候，dp[i - 1][j]和 dp[i][j - 1]一定是有数值。

代码如下：

for (int i = 1; i < m; i++) {  
    for (int j = 1; j < n; j++) {  
        if (obstacleGrid[i][j] == 1) continue;  
        dp[i][j] = dp[i - 1][j] + dp[i][j - 1];  
    }  
}

举例推导dp数组

拿示例1来举例如题：

对应的dp table 如图：

如果这个图看不懂，建议再理解一下递归公式，然后照着文章中说的遍历顺序，自己推导一下！

C++解法

动规五部分分析完毕，对应C++代码如下：

class Solution {  
public:  
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {  
        int m = obstacleGrid.size();  
        int n = obstacleGrid[0].size();  
    if (obstacleGrid[m - 1][n - 1] == 1 || obstacleGrid[0][0] == 1) //如果在起点或终点出现了障碍，直接返回0  
            return 0;  
        vector<vector<int>> dp(m, vector<int>(n, 0));  
        for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;  
        for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;  
        for (int i = 1; i < m; i++) {  
            for (int j = 1; j < n; j++) {  
                if (obstacleGrid[i][j] == 1) continue;  
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];  
            }  
        }  
        return dp[m - 1][n - 1];  
    }  
};

时间复杂度：O(n × m)，n、m 分别为obstacleGrid 长度和宽度
空间复杂度：O(n × m)

同样我们给出空间优化版本：

class Solution {  
public:  
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {  
        if (obstacleGrid[0][0] == 1)  
            return 0;  
        vector<int> dp(obstacleGrid[0].size());  
        for (int j = 0; j < dp.size(); ++j)  
            if (obstacleGrid[0][j] == 1)  
                dp[j] = 0;  
            else if (j == 0)  
                dp[j] = 1;  
            else  
                dp[j] = dp[j-1];  
  
        for (int i = 1; i < obstacleGrid.size(); ++i)  
            for (int j = 0; j < dp.size(); ++j){  
                if (obstacleGrid[i][j] == 1)  
                    dp[j] = 0;  
                else if (j != 0)  
                    dp[j] = dp[j] + dp[j-1];  
            }  
        return dp.back();  
    }  
};

时间复杂度：O(n × m)，n、m 分别为obstacleGrid 长度和宽度
空间复杂度：O(m)

Java解法

// 空间优化版本
class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int m = obstacleGrid.length;
        int n = obstacleGrid[0].length;
        int[] dp = new int[n];

        for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) {
            dp[j] = 1;
        }

        for (int i = 1; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (obstacleGrid[i][j] == 1) {
                    dp[j] = 0;
                } else if (j != 0) {
                    dp[j] += dp[j - 1];
                }
            }
        }
        return dp[n - 1];
    }
}

980. Unique Paths III（回溯）

You are given an m x n integer array grid where grid[i][j] could be:

1 representing the starting square. There is exactly one starting square.
2 representing the ending square. There is exactly one ending square.
0 representing empty squares we can walk over.
-1 representing obstacles that we cannot walk over.

Return the number of 4-directional walks from the starting square to the ending square, that walk over every non-obstacle square exactly once.

Example 1:

Input: grid = [[1,0,0,0],[0,0,0,0],[0,0,2,-1]]
Output: 2
Explanation: We have the following two paths:

(0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2)
(0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2)

Example 2:

Input: grid = [[1,0,0,0],[0,0,0,0],[0,0,0,2]]
Output: 4
Explanation: We have the following four paths:

(0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2),(2,3)
(0,0),(0,1),(1,1),(1,0),(2,0),(2,1),(2,2),(1,2),(0,2),(0,3),(1,3),(2,3)
(0,0),(1,0),(2,0),(2,1),(2,2),(1,2),(1,1),(0,1),(0,2),(0,3),(1,3),(2,3)
(0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2),(2,3)

Example 3:

Input: grid = [[0,1],[2,0]]
Output: 0
Explanation: There is no path that walks over every empty square exactly once. Note that the starting and ending square can be anywhere in the grid.

Constraints:

m == grid.length
n == grid[i].length
1 <= m, n <= 20
1 <= m * n <= 20
-1 <= grid[i][j] <= 2
There is exactly one starting cell and one ending cell.

思路

Brute Force Backtracking

First, find out where the start and end points are.

We also need to know the number of empty cells.

When we try to explore a cell, it will change 0 to -2 and perform a DFS in 4 directions.

If we hit the target and have passed all the empty cells, we increment the result.

The time complexity is comparable to dynamic programming, but it takes up less space and is easier to implement.

In the first step, we need to identify the starting point. We also want to know the number of empty cells.

Next, we iterate through the grid to count the empty cells and save the starting point as start_x and start_y.

Now, we perform a classic DFS, marking the visited cells with -1 and counting the cells we have traversed. If we reach the ending point and have passed the specified number of empty cells, it means we have visited every non-obstacle cell.

暴力回溯法

首先，找出起点和终点的位置。

我们还需要知道空单元格的数量。

当我们尝试探索一个单元格时，它将把0变为-2，并在四个方向上执行深度优先搜索（DFS）。

如果我们到达目标并经过了所有空单元格，我们就会增加结果计数。

时间复杂度与动态规划相当，但所需空间更少，且实现较为简单。

第一步，我们需要确定起点的位置。我们还想知道空单元格的数量。

接下来，我们遍历网格，计算空单元格的数量，并保存起点 start_x 和 start_y。

现在，我们执行经典的DFS，标记访问过的单元格为-1，并计算我们经过的单元格数。如果我们到达终点并经过了指定数量的空单元格，这意味着我们访问了每个非障碍物单元格。

C++解法

class Solution {
public:
    int res = 0, empty = 1;
    void dfs(vector<vector<int>>& grid, int x, int y, int count) {
        if (x < 0 || x >= grid.size() || y < 0 || y >= grid[0].size() || grid[x][y] == -1) return;
        
        if (grid[x][y] == 2) {
            if(empty == count) res++; 
            return;
        }
        
        grid[x][y] = -1;
        
        dfs(grid, x+1, y, count+1);
        dfs(grid, x-1, y, count+1);
        dfs(grid, x, y+1, count+1);
        dfs(grid, x, y-1, count+1);
        
        grid[x][y] = 0;
        
    }
    
    int uniquePathsIII(vector<vector<int>>& grid) {
        int start_x, start_y;
        for (int i = 0; i < grid.size(); i++) {
            for (int j = 0; j < grid[0].size(); j++) {
                if (grid[i][j] == 1) start_x = i, start_y = j;
                else if (grid[i][j] == 0) empty++;
            }
        }
        
        dfs(grid, start_x, start_y, 0);
        return res;
    }
};

Java解法

    int res = 0, empty = 1, sx, sy, ex, ey;
    public int uniquePathsIII(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] == 0) empty++;
                else if (grid[i][j] == 1) {
                    sx = i;
                    sy = j;
                }
            }
        }
        dfs(grid, sx, sy);
        return res;
    }

    public void dfs(int[][] grid, int x, int y) {
        if (x < 0 || x >= grid.length || y < 0 || y >= grid[0].length || grid[x][y] < 0)
            return;
        if (grid[x][y] == 2) {
            if (empty == 0) res++;
            return;
        }
        grid[x][y] = -2;
        empty--;
        dfs(grid, x + 1, y);
        dfs(grid, x - 1, y);
        dfs(grid, x, y + 1);
        dfs(grid, x, y - 1);
        grid[x][y] = 0;
        empty++;
    }

剑指Offer

980. Unique Paths III（回溯）