区间和贪心算法

• 452. Minimum Number of Arrows to Burst Balloons
  • 思路
  • C++解法
  • Java解法
• 435. Non-overlapping Intervals
  • 思路
  • C++解法
  • Java解法
• 56. Merge Intervals
  • 思路
  • C++解法
  • Java解法

452. Minimum Number of Arrows to Burst Balloons

There are some spherical balloons taped onto a flat wall that represents the XY-plane. The balloons are represented as a 2D integer array points where points[i] = [xstart, xend] denotes a balloon whose horizontal diameter stretches between xstart and xend. You do not know the exact y-coordinates of the balloons.

Arrows can be shot up directly vertically (in the positive y-direction) from different points along the x-axis. A balloon with xstart and xend is burst by an arrow shot at x if xstart <= x <= xend. There is no limit to the number of arrows that can be shot. A shot arrow keeps traveling up infinitely, bursting any balloons in its path.

Given the array points, return the minimum number of arrows that must be shot to burst all balloons.

Example 1:

Input: points = [[10,16],[2,8],[1,6],[7,12]]
Output: 2
Explanation: The balloons can be burst by 2 arrows:

• Shoot an arrow at x = 6, bursting the balloons [2,8] and [1,6].
• Shoot an arrow at x = 11, bursting the balloons [10,16] and [7,12].

Example 2:

Input: points = [[1,2],[3,4],[5,6],[7,8]]
Output: 4
Explanation: One arrow needs to be shot for each balloon for a total of 4 arrows.

Example 3:

Input: points = [[1,2],[2,3],[3,4],[4,5]]
Output: 2 Explanation: The balloons can be burst by 2 arrows:

• Shoot an arrow at x = 2, bursting the balloons [1,2] and [2,3].
• Shoot an arrow at x = 4, bursting the balloons [3,4] and [4,5].

Constraints:

• 1 <= points.length <= 10^5
• points[i].length == 2
• -2^31 <= xstart < xend <= 2^31 - 1

思路

如何使用最少的弓箭呢？

直觉上来看，貌似只射重叠最多的气球，用的弓箭一定最少，那么有没有当前重叠了三个气球，我射两个，留下一个和后面的一起射这样弓箭用的更少的情况呢？

尝试一下举反例，发现没有这种情况。

那么就试一试贪心吧！局部最优：当气球出现重叠，一起射，所用弓箭最少。全局最优：把所有气球射爆所用弓箭最少。

算法确定下来了，那么如何模拟气球射爆的过程呢？是在数组中移除元素还是做标记呢？

如果真实的模拟射气球的过程，应该射一个，气球数组就remove一个元素，这样最直观，毕竟气球被射了。

但仔细思考一下就发现：如果把气球排序之后，从前到后遍历气球，被射过的气球仅仅跳过就行了，没有必要让气球数组remove气球，只要记录一下箭的数量就可以了。

以上为思考过程，已经确定下来使用贪心了，那么开始解题。

为了让气球尽可能的重叠，需要对数组进行排序。

那么按照气球起始位置排序，还是按照气球终止位置排序呢？

其实都可以！只不过对应的遍历顺序不同，我就按照气球的起始位置排序了。

既然按照起始位置排序，那么就从前向后遍历气球数组，靠左尽可能让气球重复。

从前向后遍历遇到重叠的气球了怎么办？

如果气球重叠了，重叠气球中右边边界的最小值 之前的区间一定需要一个弓箭。

以题目示例： [[10,16],[2,8],[1,6],[7,12]]为例，如图：（方便起见，已经排序）

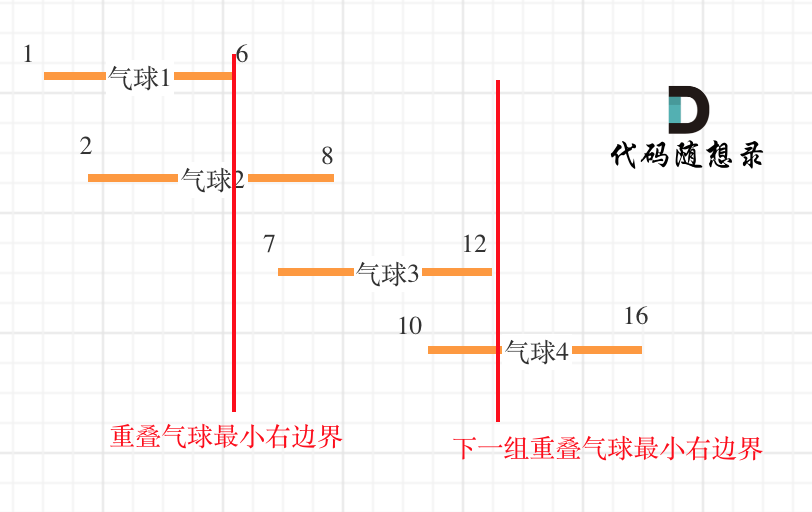
可以看出首先第一组重叠气球，一定是需要一个箭，气球3的左边界大于了第一组重叠气球的最小右边界，所以再需要一支箭来射气球3了。

注意事项

注意题目中说的是：满足 xstart ≤ x ≤ xend，则该气球会被引爆。那么说明两个气球挨在一起不重叠也可以一起射爆，

所以代码中 if (points[i][0] > points[i - 1][1]) 不能是>=

总结

这道题目贪心的思路很简单也很直接，就是重复的一起射了，但本题我认为是有难度的。

就算思路都想好了，模拟射气球的过程，很多同学真的要去模拟了，实时把气球从数组中移走，这么写的话就复杂了。

而且寻找重复的气球，寻找重叠气球最小右边界，其实都有代码技巧。

贪心题目有时候就是这样，看起来很简单，思路很直接，但是一写代码就感觉贼复杂无从下手。

这里其实是需要代码功底的，那代码功底怎么练？

多看多写多总结！

C++解法

C++代码如下：

class Solution {  
private:  
    static bool cmp(const vector<int>& a, const vector<int>& b) {  
        return a[0] < b[0];  
    }  
public:  
    int findMinArrowShots(vector<vector<int>>& points) {  
        if (points.size() == 0) return 0;  
        sort(points.begin(), points.end(), cmp);  
​  
        int result = 1; // points 不为空至少需要一支箭  
        for (int i = 1; i < points.size(); i++) {  
            if (points[i][0] > points[i - 1][1]) {  // 气球i和气球i-1不挨着，注意这里不是>=  
                result++; // 需要一支箭  
            }  
            else {  // 气球i和气球i-1挨着  
                points[i][1] = min(points[i - 1][1], points[i][1]); // 更新重叠气球最小右边界  
            }  
        }  
        return result;  
    }  
};

• 时间复杂度：$O(nlogn)$，因为有一个快排
• 空间复杂度：$O(1)$，有一个快排，最差情况(倒序)时，需要n次递归调用。因此确实需要O(n)的栈空间

Java解法

import java.util.Arrays;
import java.util.Comparator;

class Solution {
    public int findMinArrowShots(int[][] points) {
        if (points == null || points.length == 0) {
            return 0;
        }

        // 使用Comparator接口实现自定义排序，按照气球的右边界升序排列
        Arrays.sort(points, Comparator.comparingInt(a -> a[1]));

        int num = 1; // 至少需要一支箭
        int end = points[0][1]; // 第一支箭射击的位置，初始化为第一个气球的右边界

        for (int i = 1; i < points.length; i++) {
            // 如果当前气球的左边界大于之前的最小右边界，则需要一支新的箭
            if (points[i][0] > end) {
                num++; // 增加箭的数量
                end = points[i][1]; // 更新箭的射击位置为当前气球的右边界
            }
        }
        return num;
    }
}

代码逻辑：

1. 对气球按照右边界进行升序排序。
2. 初始化箭的数量为1，第一支箭射击的位置为第一个气球的右边界。
3. 遍历剩余的气球，如果当前气球的左边界大于当前箭可以射爆的最远右边界，则需要一支新的箭，并更新箭的射击位置为当前气球的右边界。
4. 返回箭的数量。

435. Non-overlapping Intervals

Given an array of intervals intervals where intervals[i] = [starti, endi], return the minimum number of intervals you need to remove to make the rest of the intervals non-overlapping.

Note that intervals which only touch at a point are non-overlapping. For example, [1, 2] and [2, 3] are non-overlapping.

Example 1:

Input: intervals = [[1,2],[2,3],[3,4],[1,3]]
Output: 1
Explanation: [1,3] can be removed and the rest of the intervals are non-overlapping.

Example 2:

Input: intervals = [[1,2],[1,2],[1,2]]
Output: 2
Explanation: You need to remove two [1,2] to make the rest of the intervals non-overlapping.

Example 3:

Input: intervals = [[1,2],[2,3]]
Output: 0
Explanation: You don't need to remove any of the intervals since they're already non-overlapping.

Constraints:

• 1 <= intervals.length <= 10^5
• intervals[i].length == 2
• -5 * 10^4 <= starti < endi <= 5 * 10^4

思路

相信很多同学看到这道题目都冥冥之中感觉要排序，但是究竟是按照右边界排序，还是按照左边界排序呢？

其实都可以。主要就是为了让区间尽可能的重叠。

我来按照右边界排序，从左向右记录非交叉区间的个数。最后用区间总数减去非交叉区间的个数就是需要移除的区间个数了。

此时问题就是要求非交叉区间的最大个数。

这里记录非交叉区间的个数还是有技巧的，如图：

区间，1，2，3，4，5，6都按照右边界排好序。

当确定区间 1 和 区间2 重叠后，如何确定是否与 区间3 也重贴呢？

就是取 区间1 和 区间2 右边界的最小值，因为这个最小值之前的部分一定是 区间1 和区间2 的重合部分，如果这个最小值也触达到区间3，那么说明 区间 1，2，3都是重合的。

接下来就是找大于区间1结束位置的区间，是从区间4开始。那有同学问了为什么不从区间5开始？别忘了已经是按照右边界排序的了。

区间4结束之后，再找到区间6，所以一共记录非交叉区间的个数是三个。

总共区间个数为6，减去非交叉区间的个数3。移除区间的最小数量就是3。

C++解法

C++代码如下：

class Solution {  
public:  
    // 按照区间右边界排序  
    static bool cmp (const vector<int>& a, const vector<int>& b) {  
        return a[1] < b[1];  
    }  
    int eraseOverlapIntervals(vector<vector<int>>& intervals) {  
        if (intervals.size() == 0) return 0;  
        sort(intervals.begin(), intervals.end(), cmp);  
        int count = 1; // 记录非交叉区间的个数  
        int end = intervals[0][1]; // 记录区间分割点  
        for (int i = 1; i < intervals.size(); i++) {  
            if (end <= intervals[i][0]) {  
                end = intervals[i][1];  
                count++;  
            }  
        }  
        return intervals.size() - count;  
    }  
};

• 时间复杂度：$O(nlogn)$ ，有一个快排
• 空间复杂度：$O(n)$，有一个快排，最差情况(倒序)时，需要n次递归调用。因此确实需要$O(n)的栈空间

Java解法

修改后的代码：

import java.util.Arrays;
import java.util.Comparator;

class Solution {
    public int eraseOverlapIntervals(int[][] intervals) {
        if (intervals == null || intervals.length == 0) {
            return 0;
        }

        // 按照区间的结束时间升序排序
        Arrays.sort(intervals, Comparator.comparingInt(a -> a[1]));

        int num = 0; // 需要移除的区间数量
        int end = intervals[0][1]; // 初始化为第一个区间的结束时间

        for (int i = 1; i < intervals.length; i++) {
            if (intervals[i][0] < end) {
                // 发现重叠区间，需要移除一个
                num++;
            } else {
                // 没有重叠，更新 end 为当前区间的结束时间
                end = intervals[i][1];
            }
        }

        return num;
    }
}

代码解释：

1. 排序： 首先，我们按照每个区间的结束时间对所有区间进行排序。这样做是为了确保我们总是优先选择结束时间最早的区间，这样可以尽可能多地保留不重叠的区间。

2. 贪心选择：

   • 我们初始化 num 为0，表示需要移除的区间数量。
   • end 变量用来记录当前已选择的、不重叠的区间的结束时间。初始值设置为第一个区间的结束时间。
   • 然后，我们遍历排序后的区间。对于每个区间，我们检查它是否与当前已选择的区间重叠（即，当前区间的开始时间是否小于 end）。
   • 如果重叠，则 num 加1，表示需要移除当前区间。
   • 如果不重叠，则更新 end 为当前区间的结束时间。

3. 返回结果： 最后，返回需要移除的区间数量 num。

56. Merge Intervals

Given an array of intervals where intervals[i] = [starti, endi], merge all overlapping intervals, and return an array of the non-overlapping intervals that cover all the intervals in the input.

Example 1:

Input: intervals = [[1,3],[2,6],[8,10],[15,18]]
Output: [[1,6],[8,10],[15,18]]
Explanation: Since intervals [1,3] and [2,6] overlap, merge them into [1,6].

Example 2:

Input: intervals = [[1,4],[4,5]]
Output: [[1,5]] Explanation: Intervals [1,4] and [4,5] are considered overlapping.

Constraints:

• 1 <= intervals.length <= 10^4
• intervals[i].length == 2
• 0 <= starti <= endi <= 10^4

思路

本题的本质其实还是判断重叠区间问题。

大家如果认真做题的话，话发现和我们刚刚讲过的452. 用最少数量的箭引爆气球 和 435. 无重叠区间 都是一个套路。

这几道题都是判断区间重叠，区别就是判断区间重叠后的逻辑，本题是判断区间重贴后要进行区间合并。

所以一样的套路，先排序，让所有的相邻区间尽可能的重叠在一起，按左边界，或者右边界排序都可以，处理逻辑稍有不同。

按照左边界从小到大排序之后，如果 intervals[i][0] <= intervals[i - 1][1] 即intervals[i]的左边界 <= intervals[i - 1]的右边界，则一定有重叠。（本题相邻区间也算重贴，所以是<=）

这么说有点抽象，看图：（注意图中区间都是按照左边界排序之后了）

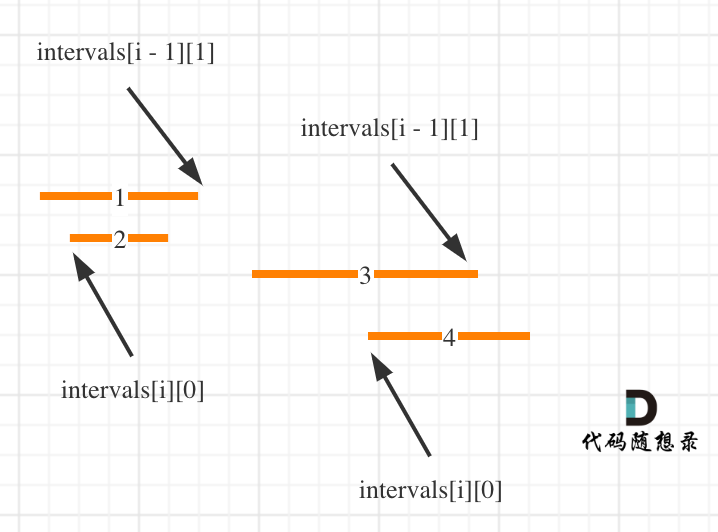
知道如何判断重复之后，剩下的就是合并了，如何去模拟合并区间呢？

其实就是用合并区间后左边界和右边界，作为一个新的区间，加入到result数组里就可以了。如果没有合并就把原区间加入到result数组。

C++解法

C++代码如下：

class Solution {  
public:  
    vector<vector<int>> merge(vector<vector<int>>& intervals) {  
        vector<vector<int>> result;  
        if (intervals.size() == 0) return result; // 区间集合为空直接返回  
        // 排序的参数使用了lambda表达式  
        sort(intervals.begin(), intervals.end(), [](const vector<int>& a, const vector<int>& b){return a[0] < b[0];});  
​  
        // 第一个区间就可以放进结果集里，后面如果重叠，在result上直接合并  
        result.push_back(intervals[0]);   
​  
        for (int i = 1; i < intervals.size(); i++) {  
            if (result.back()[1] >= intervals[i][0]) { // 发现重叠区间  
                // 合并区间，只更新右边界就好，因为result.back()的左边界一定是最小值，因为我们按照左边界排序的  
                result.back()[1] = max(result.back()[1], intervals[i][1]);   
            } else {  
                result.push_back(intervals[i]); // 区间不重叠   
            }  
        }  
        return result;  
    }  
};

• 时间复杂度: O(nlogn)
• 空间复杂度: O(logn)，排序需要的空间开销

Java解法

下面是修改后的代码：

import java.util.ArrayList;
import java.util.Arrays;
import java.util.Comparator;
import java.util.List;

class Solution {
    public int[][] merge(int[][] intervals) {
        if (intervals == null || intervals.length <= 1) {
            return intervals; // 如果为空或只有一个区间，则直接返回
        }

        // 按照区间的起始位置排序
        Arrays.sort(intervals, Comparator.comparingInt(a -> a[0]));

        List<int[]> result = new ArrayList<>();
        int start = intervals[0][0];
        int end = intervals[0][1];

        for (int i = 1; i < intervals.length; i++) {
            if (intervals[i][0] <= end) {
                // 如果当前区间的起始位置小于等于end，则合并区间
                end = Math.max(end, intervals[i][1]); //end取最大值，考虑[1,5][2,3]这种情况
            } else {
                // 否则，将当前区间添加到结果列表中
                result.add(new int[]{start, end});
                start = intervals[i][0];
                end = intervals[i][1];
            }
        }

        // 添加最后一个区间
        result.add(new int[]{start, end});

        // 将List<int[]>转换为int[][]
        return result.toArray(new int[result.size()][]);
    }
}

代码解释和改进:

1. 空值和单区间检查: 添加了对 intervals 为空或只有一个区间的检查，直接返回原数组，避免了后续的空指针异常和不必要的处理。
2. 使用 ArrayList: 使用 ArrayList<int[]> 来动态存储合并后的区间。
3. 正确的添加方式: 使用 result.add(new int[]{start, end}) 来添加新的区间到 ArrayList 中。
4. 处理最后一个区间: 在循环结束后，将最后一个合并的区间添加到 result 中。
5. 转换为 int[][]: 使用 result.toArray(new int[result.size()][]) 将 ArrayList<int[]> 转换为 int[][] 并返回。
6. 合并区间时的 end 更新: 使用 end = Math.max(end, intervals[i][1]); 确保 end 总是包含到目前为止的最远位置。 考虑类似 [1,5] 和 [2,3] 这样的例子，合并后应该是 [1,5]。
7. 注释: 添加了更详细的注释，方便理解代码的逻辑。