字符串和贪心算法
- 763. Partition Labels
- 316. Remove Duplicate Letters
- 1081. Smallest Subsequence of Distinct Characters(同上)
- 738. Monotone Increasing Digits
763. Partition Labels
You are given a string s. We want to partition the string into as many parts as possible so that each letter appears in at most one part. For example, the string "ababcc" can be partitioned into ["abab", "cc"], but partitions such as ["aba", "bcc"] or ["ab", "ab", "cc"] are invalid.
Note that the partition is done so that after concatenating all the parts in order, the resultant string should be s.
Return a list of integers representing the size of these parts.
Example 1:
Input: s = "ababcbacadefegdehijhklij"
Output: [9,7,8]
Explanation:
The partition is "ababcbaca", "defegde", "hijhklij".
This is a partition so that each letter appears in at most one part.
A partition like "ababcbacadefegde", "hijhklij" is incorrect, because it splits s into less parts.
Example 2:
Input: s = "eccbbbbdec"
Output: [10]
Constraints:
1 <= s.length <= 500sconsists of lowercase English letters.
思路
Try to greedily choose the smallest partition that includes the first letter. If you have something like "abaccbdeffed", then you might need to add b. You can use an map like "last['b'] = 5" to help you expand the width of your partition.
一想到分割字符串就想到了回溯,但本题其实不用回溯去暴力搜索。
题目要求同一字母最多出现在一个片段中,那么如何把同一个字母的都圈在同一个区间里呢?
如果没有接触过这种题目的话,还挺有难度的。
在遍历的过程中相当于是要找每一个字母的边界,如果找到之前遍历过的所有字母的最远边界,说明这个边界就是分割点了。此时前面出现过所有字母,最远也就到这个边界了。
可以分为如下两步:
- 统计每一个字符最后出现的位置
- 从头遍历字符,并更新字符的最远出现下标,如果找到字符最远出现位置下标和当前下标相等了,则找到了分割点
如图:
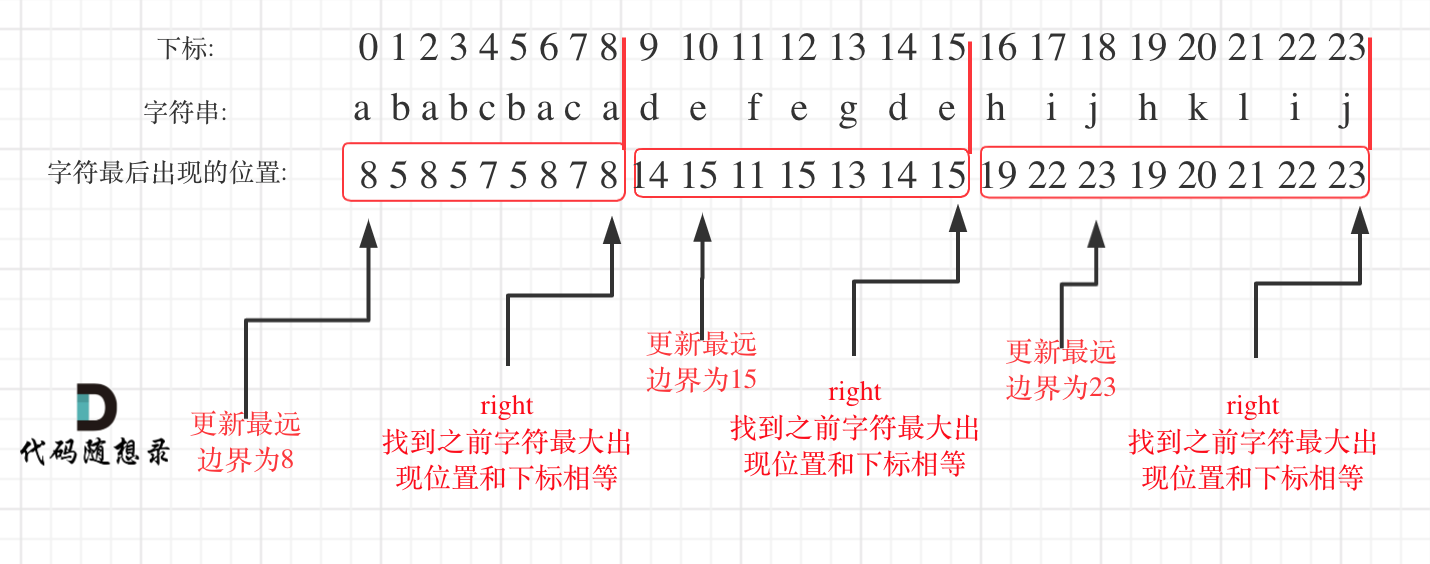
C++解法
明白原理之后,代码并不复杂,如下:
class Solution {
public:
vector<int> partitionLabels(string S) {
int hash[27] = {0}; // i为字符,hash[i]为字符出现的最后位置
for (int i = 0; i < S.size(); i++) { // 统计每一个字符最后出现的位置
hash[S[i] - 'a'] = i;
}
vector<int> result;
int left = 0;
int right = 0;
for (int i = 0; i < S.size(); i++) {
right = max(right, hash[S[i] - 'a']); // 找到字符出现的最远边界
if (i == right) {
result.push_back(right - left + 1);
left = i + 1;
}
}
return result;
}
};
- 时间复杂度:O(n)
- 空间复杂度:O(1),使用的hash数组是固定大小
Java解法
class Solution {
public List<Integer> partitionLabels(String S) {
List<Integer> list = new LinkedList<>();
int[] edge = new int[26];
char[] chars = S.toCharArray();
for (int i = 0; i < chars.length; i++) {
edge[chars[i] - 'a'] = i;
}
int idx = 0;
int last = -1;
for (int i = 0; i < chars.length; i++) {
idx = Math.max(idx,edge[chars[i] - 'a']);
if (i == idx) {
list.add(i - last);
last = i;
}
}
return list;
}
}
316. Remove Duplicate Letters
Given a string s, remove duplicate letters so that every letter appears once and only once. You must make sure your result is the smallest in lexicographical order among all possible results.
Example 1:
Input: s = "bcabc"
Output: "abc"
Example 2:
Input: s = "cbacdcbc"
Output: "acdb"
Constraints:
1 <= s.length <= 10^4sconsists of lowercase English letters.
Note: This question is the same as 1081: https://leetcode.com/problems/smallest-subsequence-of-distinct-characters/
思路
Greedily try to add one missing character. How to check if adding some character will not cause problems ? Use bit-masks to check whether you will be able to complete the sub-sequence if you add the character at some index i.
Approach: Stack and Greedy
To address the "Remove Duplicate Letters" problem using a stack and greedy algorithm, we lean on the properties of the stack to maintain lexicographical order:
Key Data Structures:
- stack: A dynamic data structure to hold characters in the desired order.
- seen: A set to track characters already in the stack.
- last_occurrence: A dictionary to track the last occurrence of each character in the string.
Enhanced Breakdown:
- Initialization: Initialize the stack, seen set, and last_occurrence dictionary.
- Iterate through the string:
- For each character, if it's in the seen set, skip it.
- If it's not in the seen set, add it to the stack. While adding, compare it with the top character of the stack. If the current character is smaller and the top character appears later in the string, pop the top character.
- Output: Convert the stack to a string and return.
Time Complexity:
- The solution iterates over each character in the string once, leading to a time complexity of O(n), where
nis the length of the strings.
Space Complexity:
- The space complexity is O(n) due to the stack, seen set, and last_occurrence dictionary.
C++解法
class Solution {
public:
string removeDuplicateLetters(string s) {
vector<int> lastIndex(26, 0);
for (int i = 0; i < s.length(); i++){
lastIndex[s[i] - 'a'] = i; // track the lastIndex of character presence
}
vector<bool> seen(26, false); // keep track seen
stack<char> st;
for (int i = 0; i < s.size(); i++) {
int curr = s[i] - 'a';
if (seen[curr]) continue; // if seen continue as we need to pick one char only
while(st.size() > 0 && st.top() > s[i] && i < lastIndex[st.top() - 'a']){
seen[st.top() - 'a'] = false; // pop out and mark unseen
st.pop();
}
st.push(s[i]); // add into stack
seen[curr] = true; // mark seen
}
string ans = "";
while (st.size() > 0){
ans += st.top();
st.pop();
}
reverse(ans.begin(), ans.end());
return ans;
}
};
Java解法
class Solution {
public String removeDuplicateLetters(String s) {
int[] lastIndex = new int[26];
for (int i = 0; i < s.length(); i++){
lastIndex[s.charAt(i) - 'a'] = i; // track the lastIndex of character presence
}
boolean[] seen = new boolean[26]; // keep track seen
Stack<Integer> st = new Stack();
for (int i = 0; i < s.length(); i++) {
int curr = s.charAt(i) - 'a';
if (seen[curr]) continue; // if seen continue as we need to pick one char only
while (!st.isEmpty() && st.peek() > curr && i < lastIndex[st.peek()]){
seen[st.pop()] = false; // pop out and mark unseen
}
st.push(curr); // add into stack
seen[curr] = true; // mark seen
}
StringBuilder sb = new StringBuilder();
while (!st.isEmpty())
sb.append((char) (st.pop() + 'a'));
return sb.reverse().toString();
}
}
1081. Smallest Subsequence of Distinct Characters(同上)
738. Monotone Increasing Digits
An integer has monotone increasing digits if and only if each pair of adjacent digits x and y satisfy x <= y.
Given an integer n, return the largest number that is less than or equal to n with monotone increasing digits.
Example 1:
Input: n = 10
Output: 9
Example 2:
Input: n = 1234
Output: 1234
Example 3:
Input: n = 332
Output: 299
Constraints:
0 <= n <= 10^9
思考
Build the answer digit by digit, adding the largest possible one that would make the number still less than or equal to N.
暴力解法
题意很简单,那么首先想的就是暴力解法了,来我替大家暴力一波,结果自然是超时!
代码如下:
class Solution {
private:
// 判断一个数字的各位上是否是递增
bool checkNum(int num) {
int max = 10;
while (num) {
int t = num % 10;
if (max >= t) max = t;
else return false;
num = num / 10;
}
return true;
}
public:
int monotoneIncreasingDigits(int N) {
for (int i = N; i > 0; i--) { // 从大到小遍历
if (checkNum(i)) return i;
}
return 0;
}
};
- 时间复杂度:O(n × m) m为n的数字长度
- 空间复杂度:O(1)
贪心算法
题目要求小于等于N的最大单调递增的整数,那么拿一个两位的数字来举例。
例如:98,一旦出现strNum[i - 1] > strNum[i]的情况(非单调递增),首先想让strNum[i - 1]--,然后strNum[i]变为9,这样这个整数就是89,即小于98的最大的单调递增整数。
这一点如果想清楚了,这道题就好办了。
此时是从前向后遍历还是从后向前遍历呢?
从前向后遍历的话,遇到strNum[i - 1] > strNum[i]的情况,让strNum[i - 1]减一,但此时如果strNum[i - 1]减一了,可能又小于strNum[i - 2]。
这么说有点抽象,举个例子,数字:332,从前向后遍历的话,那么就把变成了329,此时2又小于了第一位的3了,真正的结果应该是299。
那么从后向前遍历,就可以重复利用上次比较得出的结果了,从后向前遍历332的数值变化为:332 -> 329 -> 299
确定了遍历顺序之后,那么此时局部最优就可以推出全局,找不出反例,试试贪心。
C++解法
本题只要想清楚个例,例如98,一旦出现strNum[i - 1] > strNum[i]的情况(非单调递增),首先想让strNum[i - 1]减一,strNum[i]赋值9,这样这个整数就是89。就可以很自然想到对应的贪心解法了。
想到了贪心,还要考虑遍历顺序,只有从后向前遍历才能重复利用上次比较的结果。
最后代码实现的时候,也需要一些技巧,例如用一个flag来标记从哪里开始赋值9。
C++代码如下:
class Solution {
public:
int monotoneIncreasingDigits(int N) {
string strNum = to_string(N);
// flag用来标记赋值9从哪里开始
// 设置为这个默认值,为了防止第二个for循环在flag没有被赋值的情况下执行
int flag = strNum.size();
for (int i = strNum.size() - 1; i > 0; i--) {
if (strNum[i - 1] > strNum[i] ) {
flag = i;
strNum[i - 1]--;
}
}
for (int i = flag; i < strNum.size(); i++) {
strNum[i] = '9';
}
return stoi(strNum);
}
};
- 时间复杂度:O(n),n 为数字长度
- 空间复杂度:O(n),需要一个字符串,转化为字符串操作更方便
Java解法
class Solution {
public int monotoneIncreasingDigits(int n) {
String s = Integer.toString(n); // 将整数转换为字符串
char[] arr = s.toCharArray(); // 将字符串转换为字符数组,方便修改
int flag = arr.length;
for(int i = arr.length - 1; i > 0; i--){
if(arr[i] < arr[i - 1]){
arr[i - 1]--; // 字符自减
flag = i;
}
}
for(int i = flag; i < arr.length; i++){
arr[i] = '9'; // 将后面的所有字符设置为 '9'
}
return Integer.parseInt(new String(arr)); // 将字符数组转换回字符串,再转换为整数
}
}
主要修改说明:
- 类型转换:
Integer.toString(n): 将整数n转换为字符串,因为 Java 中没有直接名为toString的全局函数来转换整数。s.toCharArray(): 将字符串s转换为字符数组。这样可以方便地修改字符串中的字符。Integer.parseInt(new String(arr)): 将修改后的字符数组转换回字符串,然后再将字符串解析为整数,作为结果返回。
- 字符自减:
arr[i - 1]--: 字符数组中的元素是char类型,可以直接进行自减操作。
- 使用字符数组:
- 使用
char[] arr代替string s,因为 Java 的 String 类型是不可变的。为了能够修改字符串中的字符,我们需要将其转换为字符数组。
- 使用
- valueOf() 方法:
String类没有valueOf()实例方法。应该使用new String(arr)从字符数组创建一个新的字符串。
这段代码的思路是找到从右到左第一个降序的位置,将该位置的数字减 1,然后将该位置之后的所有数字都置为 9,以保证结果是单调递增的。