等额年金

• 学习目标
• 思维导图
• 2.1 年金的类型
• 2.2 期末付等额年金
• 2.3 期初付等额年金
• 2.4 例题：等额年金的计算
• 2.5 例题：应用EXCEL计算等额年金
• 2.6 延期年金
• 2.7 永续年金
• 2.8 例题：延期年金和永续年金
• 2.9 每年支付m次的期末付年金
• 2.10 每年支付m次的期初付年金
• 2.11 连续支付的等额年金
• 2.12 价值方程
• 课后练习

学习目标

基于不同的利息度量工具，可以计算等额年金的现值、终值以及在任意日期的价值。掌握不同支付周期的年金在价值上的相互关系。

思维导图

等额年金PPT

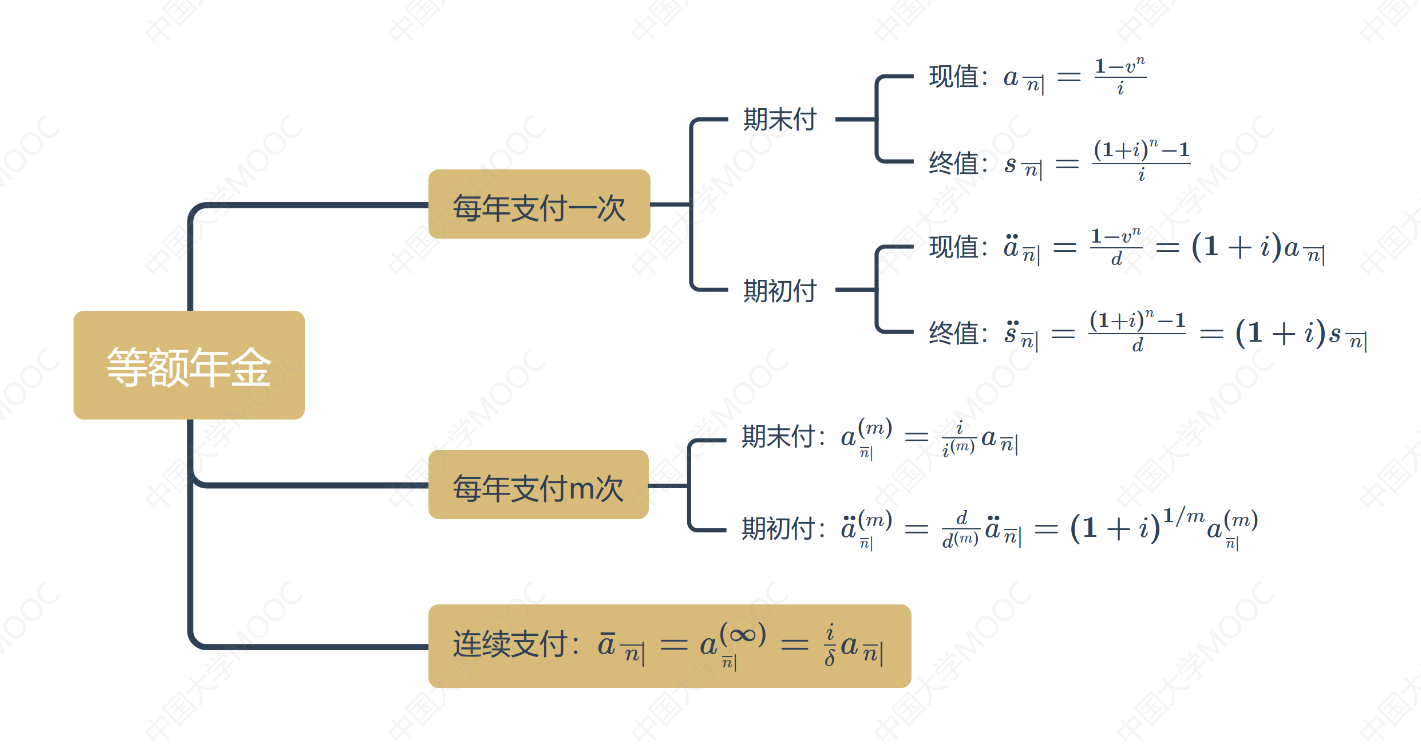
2.1 年金的类型

本视频介绍了年金的价值计算，包括等额年金和变额年金两大部分。等额年金是由一系列的收款或者付款所形成的现金流，具有一定的规律性。年金可以根据支付时间和支付金额的确定性划分为确定年金和风险年金，根据支付期限划分为定期年金和永续年金，根据支付时点划分为期初付年金和期末付年金，根据开始支付的时间划分为即期年金和延期年金。年金现金流还可以划分为等额年金和变额年金，其中变额年金的金额变化具有一定规律性。为了方便计算等额年金的价值，等额年金进一步划分为每年支付一次、每年支付m次和连续支付（每年支付无穷次）的三种类型，并讨论它们的价值计算方法以及相互转化关系。

2.2 期末付等额年金

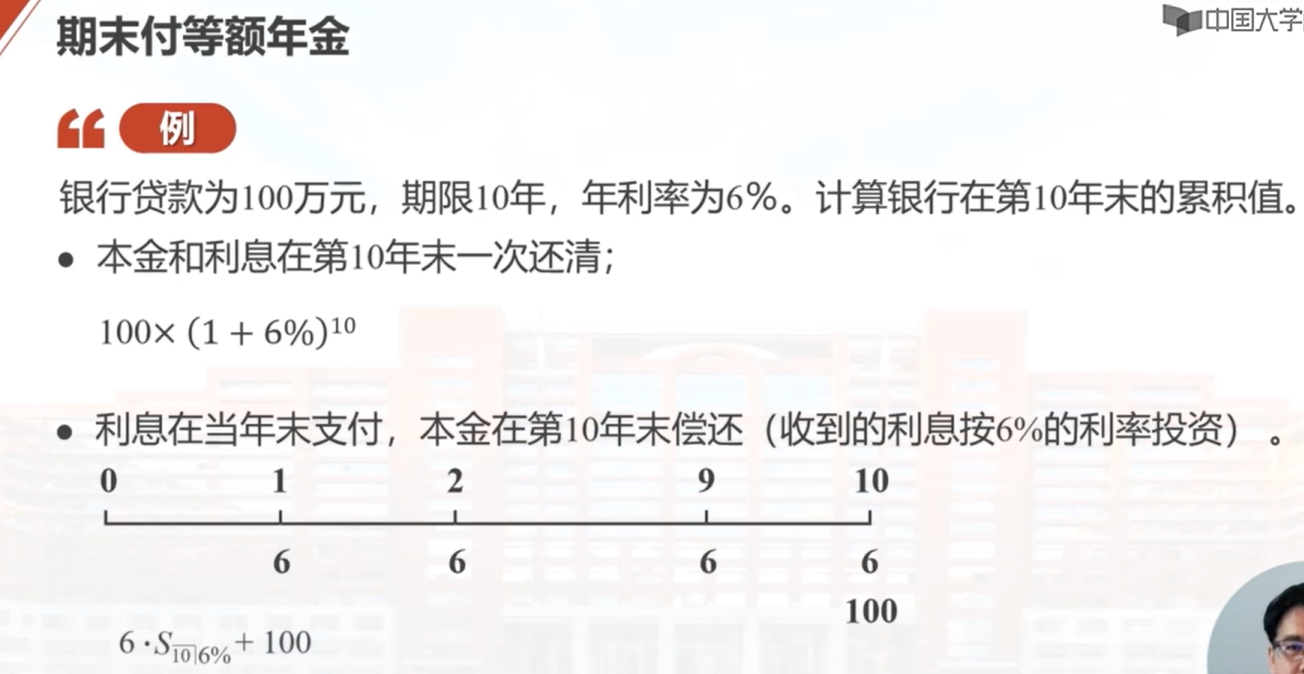
本教学视频介绍了每年末支付一次的等额年金的概念和计算方法。等额年金是指每年末支付相同金额的现金流，我们将其表示为每次支付1元的现金流。为了计算等额年金的价值，我们需要找到一个固定的时间点进行研究，通常选择时间零点和现金流的到期时间。等额年金在时间零点的价值称为年金的现值，而在第n年末的价值称为年金的终值或累积值。计算等额年金在时间零点的现值的公式是1减去v的n次方除以i，其中v是贴现函数，i是利率。而等额年金在第n年末的价值的公式是1加i的n次方减1除以i。这两个价值之间有一个简单的换算关系，即a角n的倒数等于s角n的倒数加上i。

终值$s_{n|}=a_{n|}(1+i{)}^n=\frac{1-v^n}{i}(1+i{)}^n=\frac{(1+i{)}^n-1}{i}$

$\begin{array}{rl}& (1)100\times (1+0.06{)}^{10}=179.08\\ & (2)6s_{\overline{10}|}+100=6\times \frac{1.06^{10}-1}{0.06}+100=179.08\end{array}$

2.3 期初付等额年金

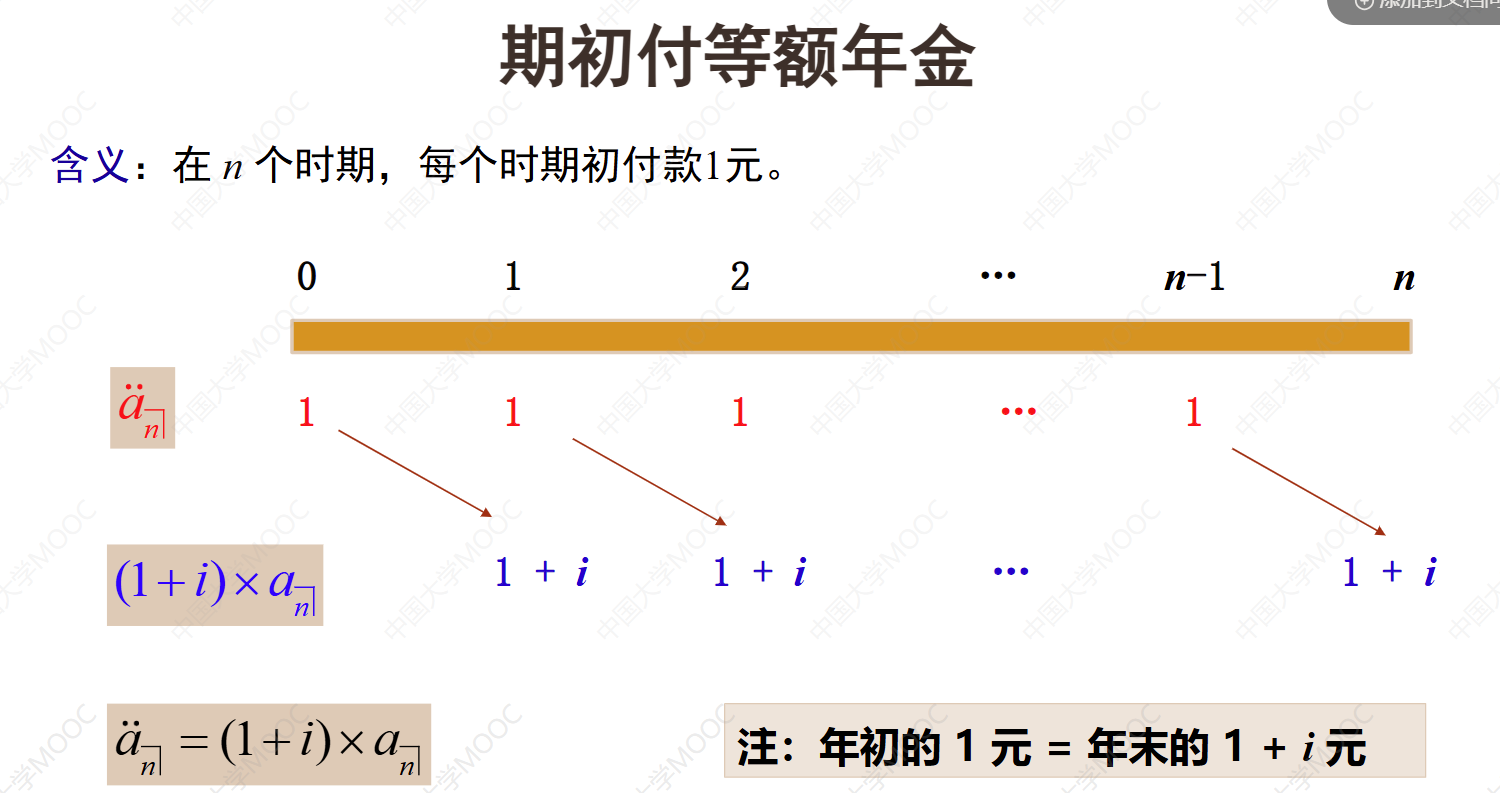
本视频介绍了期初付等额年金的价值计算方法。期初付等额年金是指每个时期期初支付1元，一共支付n个时期所形成的等额年金现金流。为了计算这个现金流的价值，可以将期初付的年金现金流转化为期末付的年金现金流。每年初支付1元的现金流在时间零点的现值用a两点角n表示。每年末支付1加i元的第一个期末付等额年金现金流在时间零点的价值可以直接计算出来，写成1加i乘以a角n。期初付年金的价值等于期末付年金的价值乘以1加i，这是一个重要的年金计算公式。对于n年期的每年初支付1元的等额年金，它在时间零点的价值可以用期末付年金的价值计算，即1减v的n次方除以d。对于期初付等额年金，现值用a两点角n表示，终值用s两点角n表示，它们之间有一个简单的转化关系，即a两点角n累积n年等于s两点角n。a两点角n的倒数等于s两点角n的倒数再加上d。

2.4 例题：等额年金的计算

这个教学视频介绍了等额年金的计算方法。首先，视频给出了一个例题，其中一个年金有12次付款，每年初支付1万元。然后，视频讲解了如何将这个年金替换为一个25年期的期末付年金，每年末支付X。通过建立等值的方程，可以求解出X的值。接下来，视频给出了另一个例子，讲解了如何计算一个账户在40年末的累积值。通过建立方程并解出每4年的有效利率，可以计算出40年末的累积值。最后，视频给出了具体的计算结果。

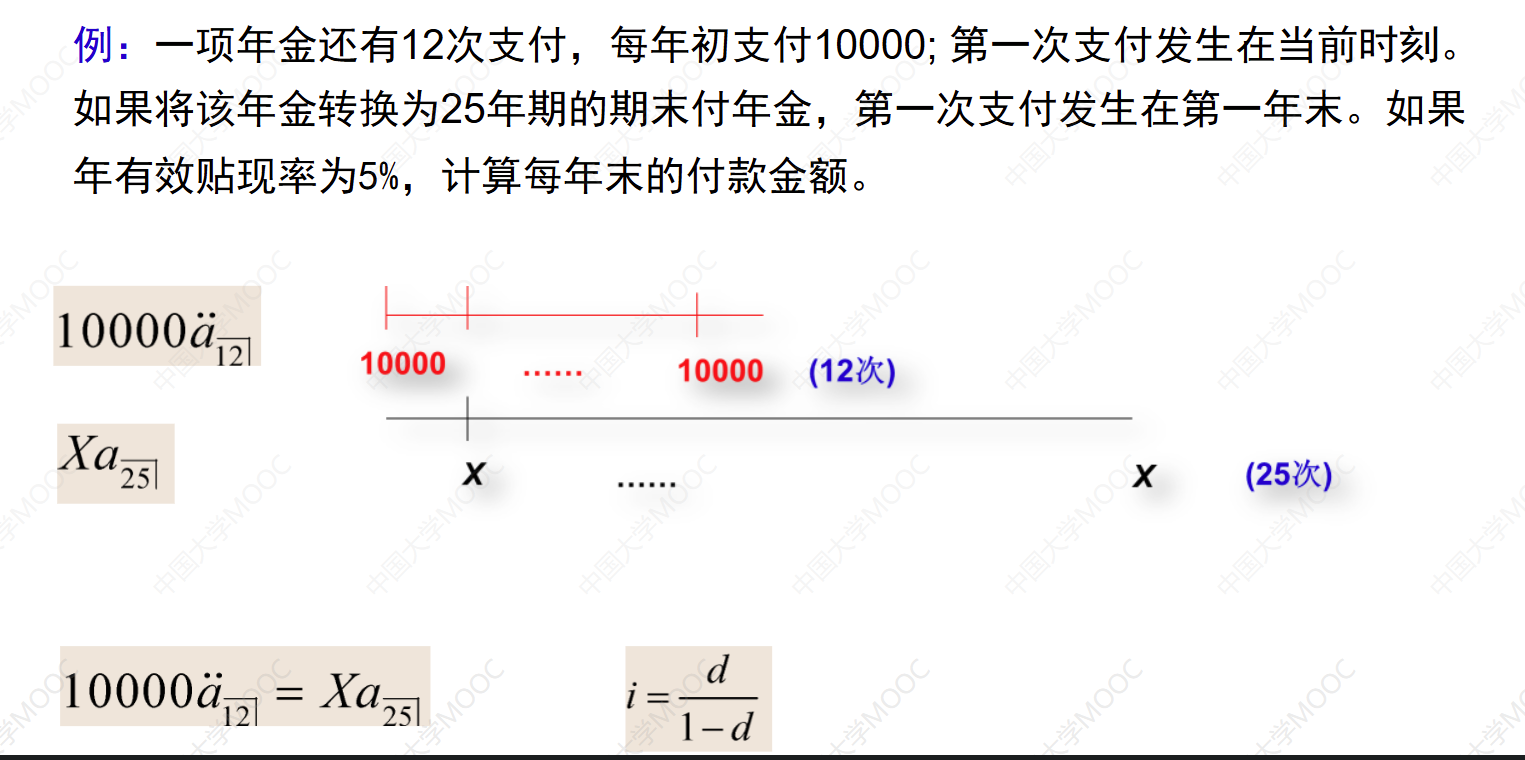
X=6695.61

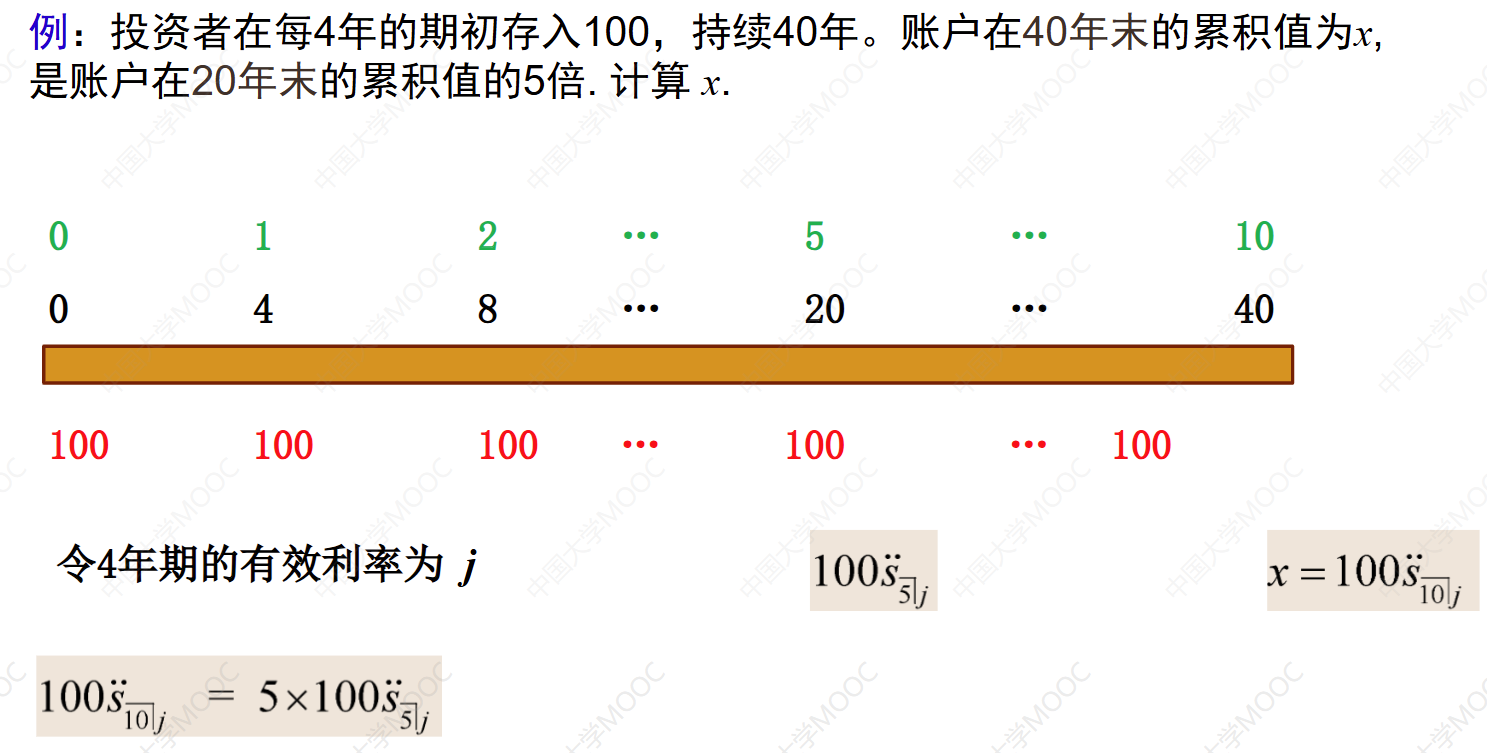
j=31.9508%, X=6194.72

2.5 例题：应用EXCEL计算等额年金

2.6 延期年金

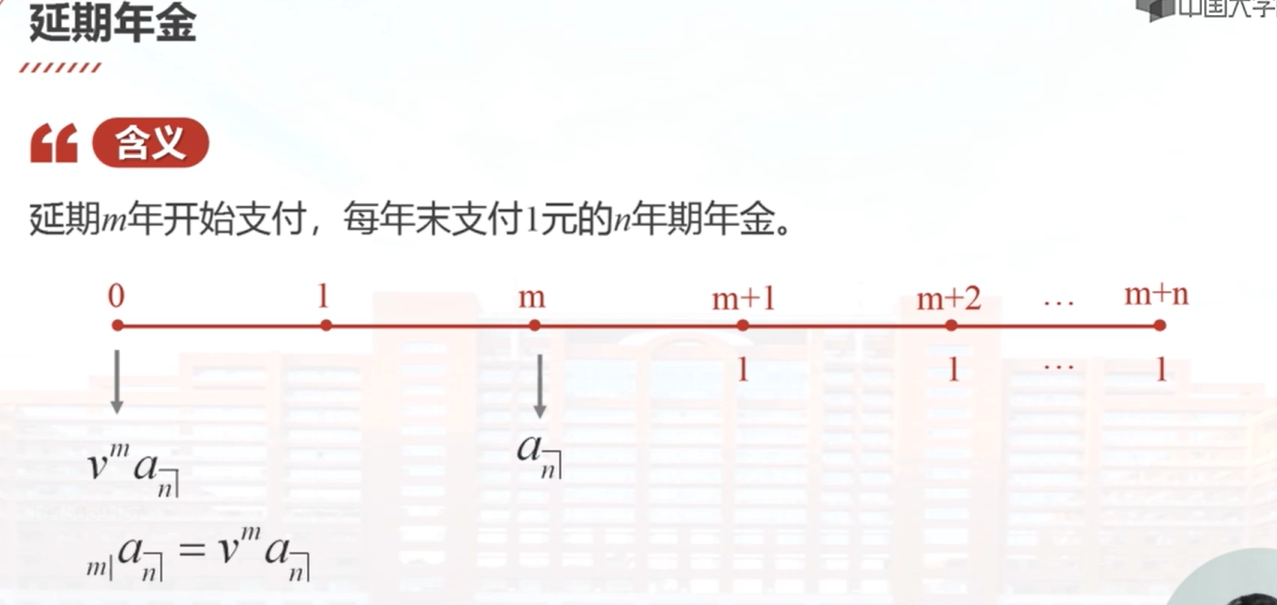
本节课学习了延期年金的概念和计算方法。延期年金是指延期m年后开始支付的n年期年金，每年末支付1元。延期m年的n年期年金在时间零点的现值可以表示为vm乘以a角n。另一种计算方法是将延期年金看作是一个延期m年的n年期等额年金，其现值可以表示为a(m+n)减去前m年每年末的付款am。通过一个例子，我们计算了一个延期7年的年金在时间零点的现值和第12年末的累积值。

2.7 永续年金

本视频介绍了永续年金的概念和价值计算方法。永续年金是指年金的支付次数无穷大，也就是无限期支付下去的年金。在期末付的永续年金中，其现值等于1/i，其中i是有效利率。对于期初付的永续年金，其现值可以简单地写为1/d，其中d是年有效贴现率。视频还解释了n年期定期年金可以看作是两个永续年金相减的结果，其中一个是从时间零点开始的永续年金，另一个是延期了n年的永续年金。最后，视频给出了一个例题，通过求解有效贴现率和年有效贴现率，计算出了每2年初支付R的永续年金的现值。

n年期年金=两个永续年金之差 $a_{n|}=\frac{1}{i}-\frac{v^n}{i}$

例：每年初支付1元的永续年金的现值是20，如果将该年金转换为一个每2年初支付R的永续年金，且两个永续年金的现值相等。计算R。

法一：

R=1+(1-d)=2-d

1/ d = 20

参考答案2 $\frac{1}{d}=20$

两年期的实际贴现率D为

$$1-D=(1-d{)}^2\Rightarrow D=1-(1-1/20{)}^2$$

故新的永续年金的现值为

$$\frac{R}{D}=20⟶R=\frac{39}{20}$$

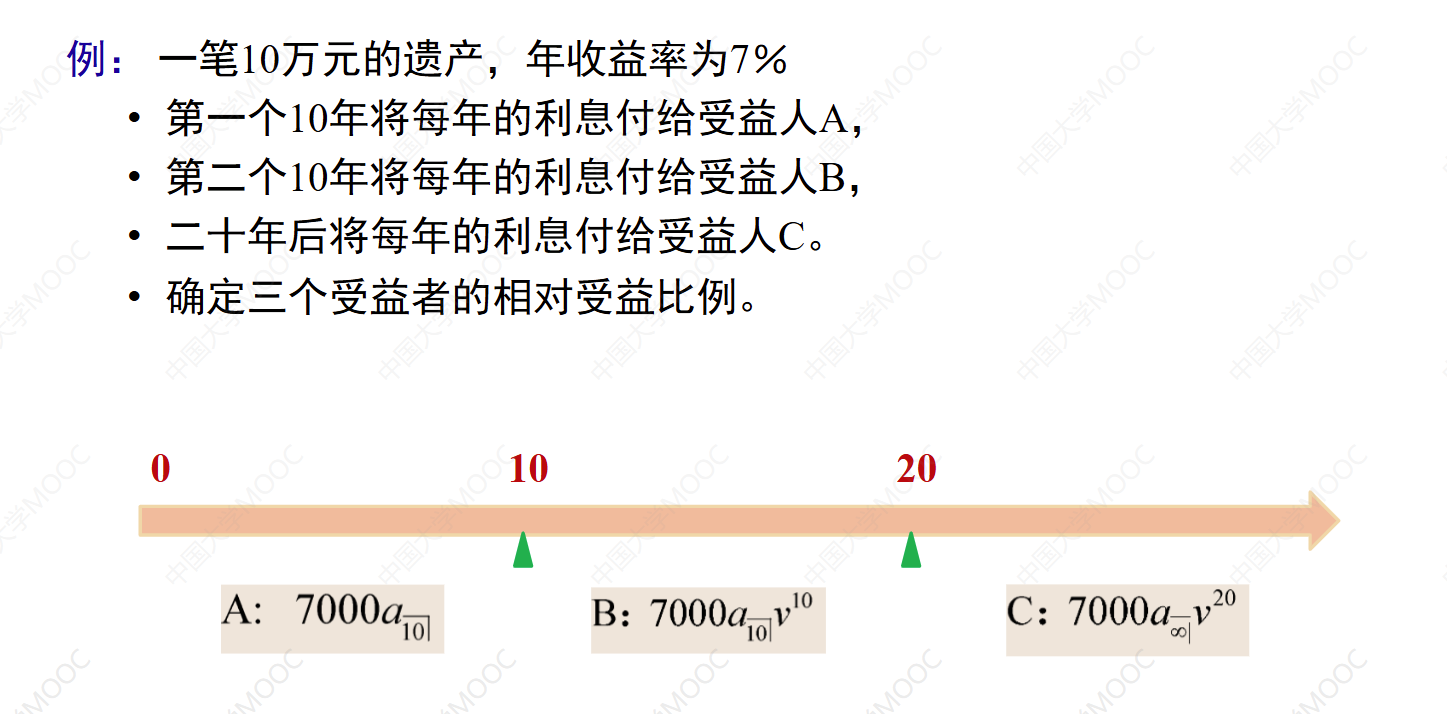
2.8 例题：延期年金和永续年金

2.9 每年支付m次的期末付年金

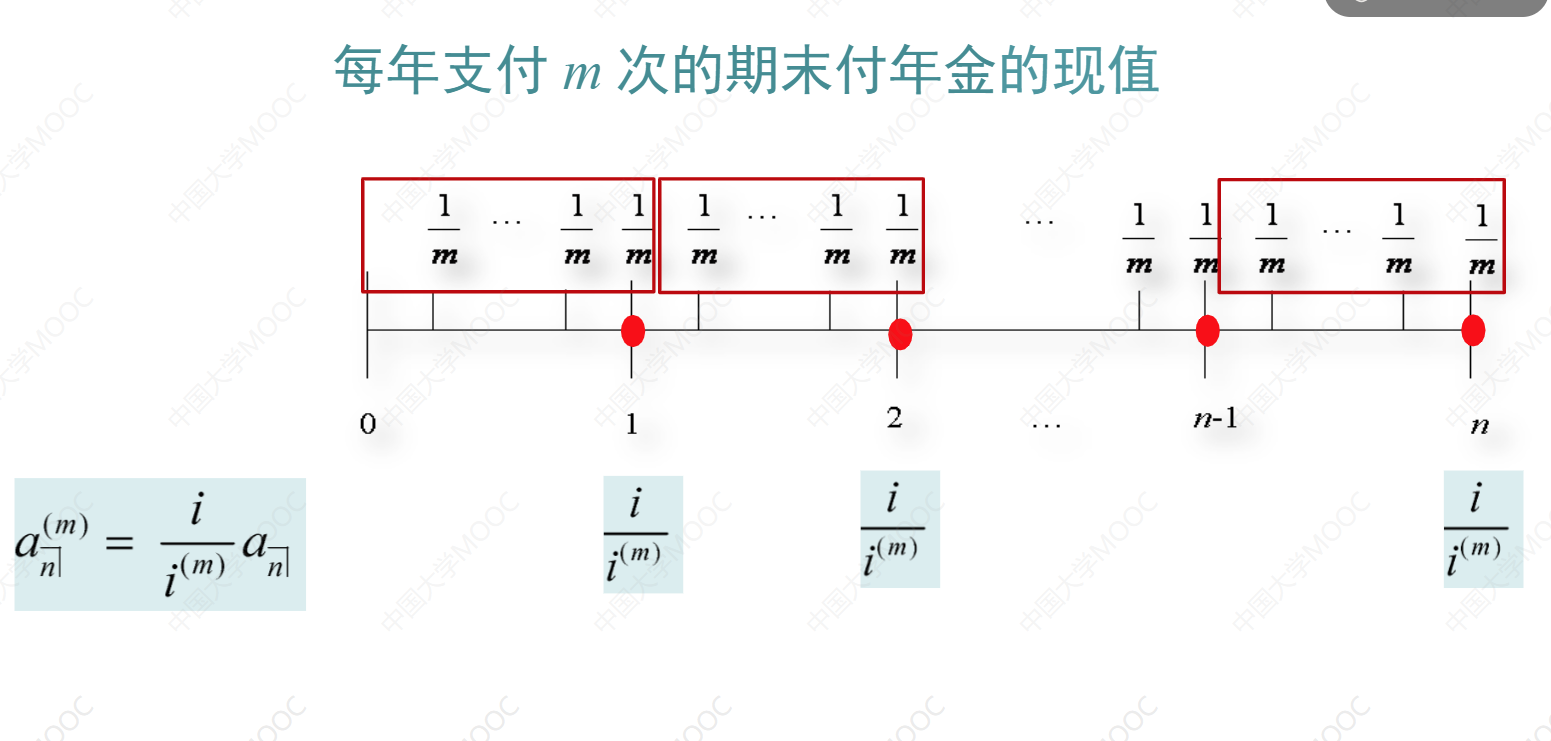
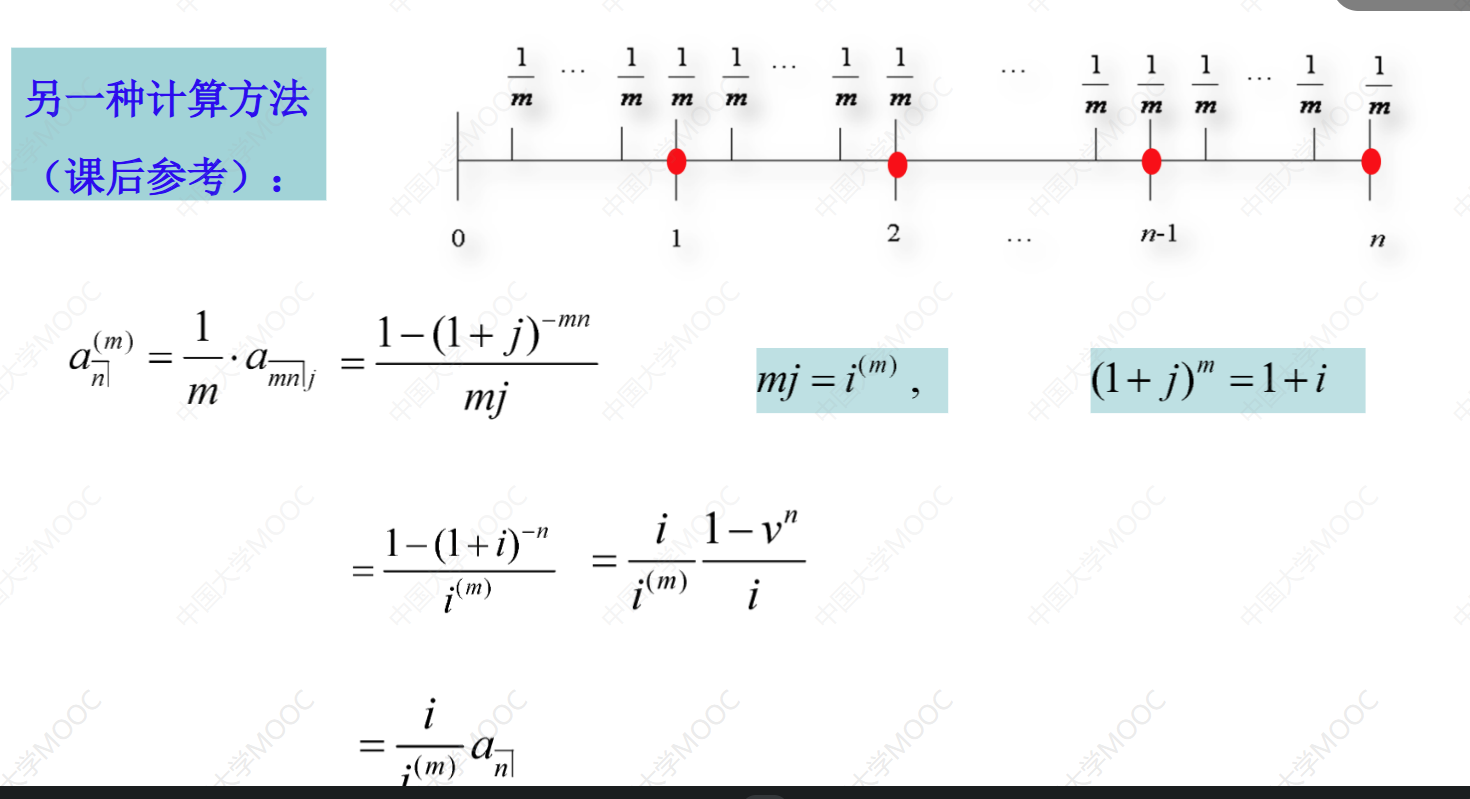
这节课介绍了每年支付m次的期末付年金。这种年金在现实生活中很常见，比如住房贷款每月支付一次，每月还款额形成了每年支付12次的年金。首先学习了每年支付m次的标准期末付年金，假设每年付款总额为1元，分成m次支付。然后介绍了计算这种年金的现值和终值的方法，分别是现值等于每年支付一次的等额年金的现值乘以i除以i(m)，终值等于每年支付一次的等额年金的终值乘以i除以i(m)。最后，给出了计算每年支付m次的期末付年金现值的另一种方法，即每年支付一次的等额年金的现值乘以i除以i(m)。

2.10 每年支付m次的期初付年金

x=566.92

2.11 连续支付的等额年金

本视频介绍了连续支付的等额年金。连续支付的等额年金是指付款连续不断地进行，但每年的付款总量保持为1元。现值可以通过每年支付m次的等额年金的现值公式，让m趋于无穷大得到。连续支付年金的现值可以写成1减去v的n次方除以δ，或者用i除以δ乘以n年期期末付等额年金的现值。累积值或终值可以通过将现值乘以一个n年期的累积函数得到。另外，连续支付年金的终值也可以通过积分的方式计算，积分结果为1加i的n次方减1除以δ。

2.12 价值方程

在这个教学视频中，我们学习了价值方程的概念。要计算年金的价值，我们需要知道付款次数n和利率i。对于n年期期末付年金，在时间零点的现值可以表示为1减去v的n次方除以i。如果我们已知年金的现值和付款次数n，可以求解出利率i；或者已知年金的现值和利率i，可以求解出付款次数n。我们以一个例子来说明，假设投资者每年初向基金存入1万元，求当年利率等于多少时，基金在第20年末的累积值等于30万元。通过解方程，我们可以得到利率j等于0.0372。

课后练习

在等额年金的支付次数n给定的条件下，利率越高，年金的终值（累积值）越大。✔

对于n年期的年金，在利率不变的条件下，年金的现值越大，终值也越大。✔

已知年利率为10%，则期初付年金的终值是期末付年金终值的1.1倍。✔

对于每年支付一次的年金，如果已知期初付年金的现值PV，年金的支付次数 n和年利率 i，则期末付年金的终值为$FV=PV\ast (1+i{)}^{(n-1)}$✔

对于延期m年的年金，利率越高，年金的现值越小。✔

一项20年期的年金，如果每年末等额支付一次，年金的现值为PV。如果将该年金改为每月末支付一次，每年的付款总额保持不变，则新年金的现值会大于PV。✔

将每年末等额支付一次的年金转化为每年支付m次，每年的付款总额保持不变，则m越大，新年金的价值越大。✔

将每年初等额支付一次的年金转化为每年支付m次，每年的付款总额保持不变，则m越大，新年金的价值越大。❌

一项20年期的年金，如果每年初等额支付一次，年金的终值为FV。如果将该年金改为每月初支付一次，每年的付款总额保持不变，则新年金的终值会大于FV。❌

一项20年期的期初付等额年金，其现值大于一项20年期的期末付等额年金。如果将这两项年金全部转化为连续支付的等额年金，每年的付款总额保持不变，则这两个新年金的价值相等。✔