利息度量

• 学习目标
• 思维导图
• 1.1 累积函数
• 1.2 贴现函数
• 1.3 有效利率（实际利率）
• 1.4 计息时间
• 1.5 单利和复利的比较
• 1.6 有效贴现率（实际贴现率）
• 1.7 例题：有效利率和有效贴现率
• 1.8 名义利率
• 1.9 例题：名义利率
• 1.10 名义贴现率
• 1.11 名义利率与名义贴现率的关系
• 1.12 利息力的定义
• 1.13 利息力的应用
• 1.14 例题：利息力
• 1.15 利率概念辨析
• 课后自测

学习目标

理解累积函数和贴现函数的含义，可以熟练应用单利和复利的累积函数；掌握有效利率、年名义利率、有效贴现率、年名义贴现率和利息力之间的相互转化关系。

思维导图

利息度量PPT

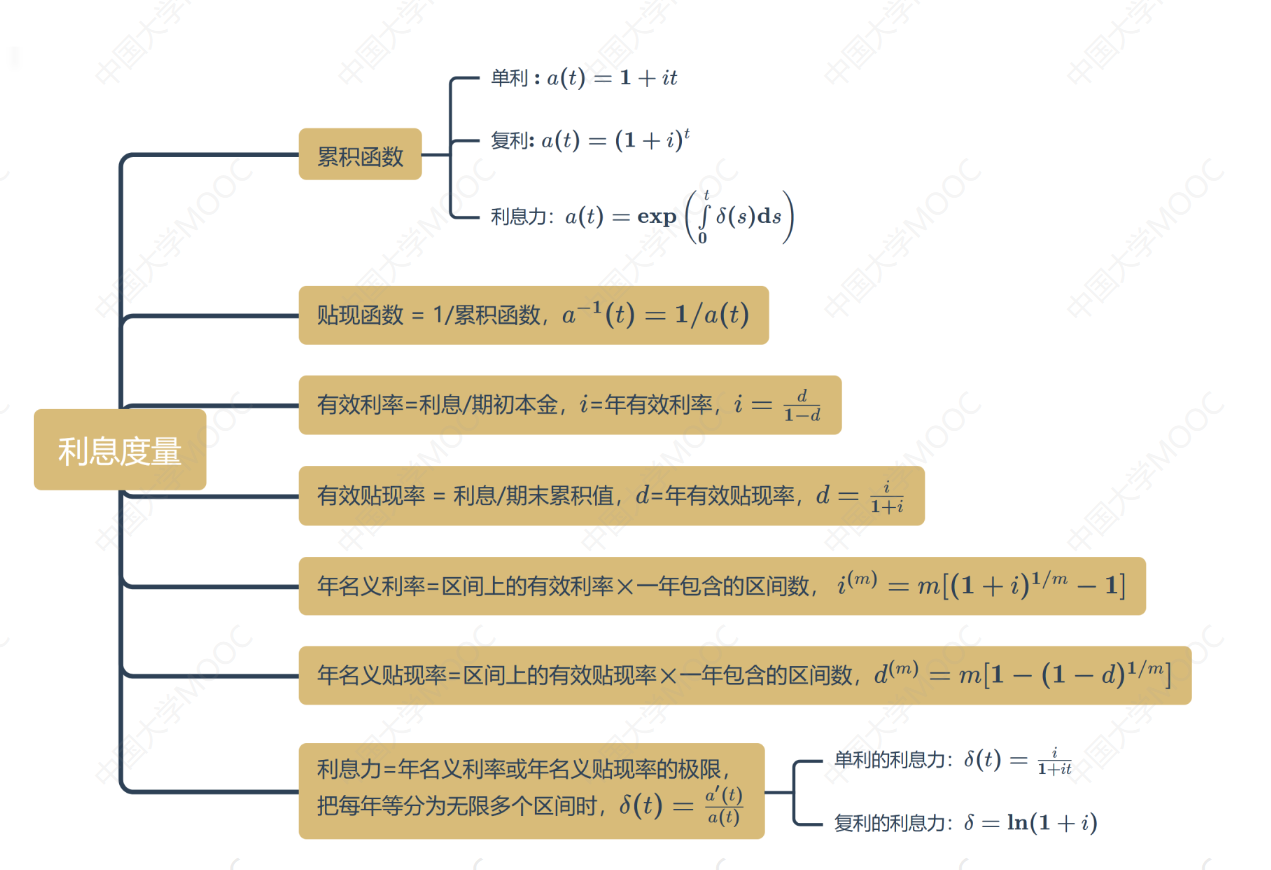
1.1 累积函数

利息度量是金融数据中非常重要的基础概念，我们需要不断使用各种工具和方法来进行利息度量。利息度量指的是利息的计算方法，对于不同的投资产品，有不同的计息方法和利率。本章重点讨论了累积函数和贴现函数的原理和定义，以及不同利息度量之间的相互转化关系。累积函数定义了资金增长变化的全部过程，是时间t的一个函数。累积函数具有几个重要性质，包括在时间零点的价值等于1，通常是时间的增函数，以及通常假设为时间的连续函数。累积函数可以用来计算任意时间区间上的资金的增长率，从而定义利息度量。通过一个具体的例子，我们可以看到累积函数的应用。

累积函数定义：时间零点的1元在时间t的累积值，记为 a(t)

性质:

• a(0)=1;
• a(t)通常是时间的增函数;
• 当利息是连续产生时，为了方便数学处理，a(t)可以看作时间的连续函数

假设累积函数为$a(t)=1+t^2$

计算t=0时的500元，在t=2的累积值为2500

1.2 贴现函数

累积函数定义了时间零点1元的在时间t的累积价值，而贴现函数定义了时间t的1元在时间零点的现值。累积函数是将时间零点的价值累积到时间t，而贴现函数是将时间t的价值贴现到时间零点。在具体应用中，单利的累积函数是线性增加的，而复利的累积函数是指数基数递增的。有了累积函数，我们可以定义对应的贴现函数。在后面的具体应用中，主要使用复利的累积函数和贴现函数。

贴现函数定义：时间t的1元在时间零点的现值,记为$a^{-1}(t)$

性质：与累积函数互为倒数

假设累积函数为$a(t)=1+t^2$

计算t=3时的500元，在 t=0 的现值为50

现实中两大常用的累计函数：

• 单利累积函数：$a(t)=1+it$
• 复利累积函数：$a(t)=(1+i{)}^t$

现实中两大常用的贴现函数：

• 单利贴现函数：$a^{-1}(t)=(1+it{)}^{-1}$
• 复利贴现函数：$a^{-1}(t)=(1+i{)}^{-t}$

1.3 有效利率（实际利率）

有效利率是指期末的利息与期初本金之比，可以定义在任意的一个时期上。

$i=\frac{期末利息}{期初本金}=\frac{期末累积值-期初本金}{期初本金}$

在实际应用中，最常用的是年有效利率。有效利率通常用百分比表示，利息是在期末支付的，时间单位通常是年。如果没有特别说明，利率通常指的是年利率。

视频还介绍了单利和复利条件下的有效利率计算方法。在单利条件下，有效利率是时间的减函数，随着时间的增加逐渐递减。而在复利条件下，有效利率是一个常数，与时间无关。

1.4 计息时间

本视频介绍了计算利息所需的计息时间的概念。利率通常以年利率的形式表示，即指本金经过一年后所产生的利息金额。在实际投资中，投资时间可能不是以年为单位表示，因此需要将投资时间转化为年数。视频介绍了三种常用的计算方法：实际比365规则、实际比360规则和30比360规则。通过这些规则，可以将投资天数转化为投资年数，并计算出相应的利息金额。

通过一个例子，视频演示了如何使用这三种规则计算投资者在不同投资期间可以获得的利息金额。最后，视频指出由于不同规则在将天数转化为年数时使用的方法不同，因此得到的利息金额也会有所不同。

以下是一个简单的示例代码，展示如何计算2019年6月14日和2020年2月7日之间的天数差：

from datetime import datetime  

# 定义日期格式  
date_format = "%Y-%m-%d"  

# 创建日期对象  
date1 = datetime.strptime("2019-06-14", date_format)  
date2 = datetime.strptime("2020-02-07", date_format)  

# 计算日期差  
delta = date2 - date1  

# 输出相差的天数  
print(f"两个日期之间相差 {delta.days} 天")

1.5 单利和复利的比较

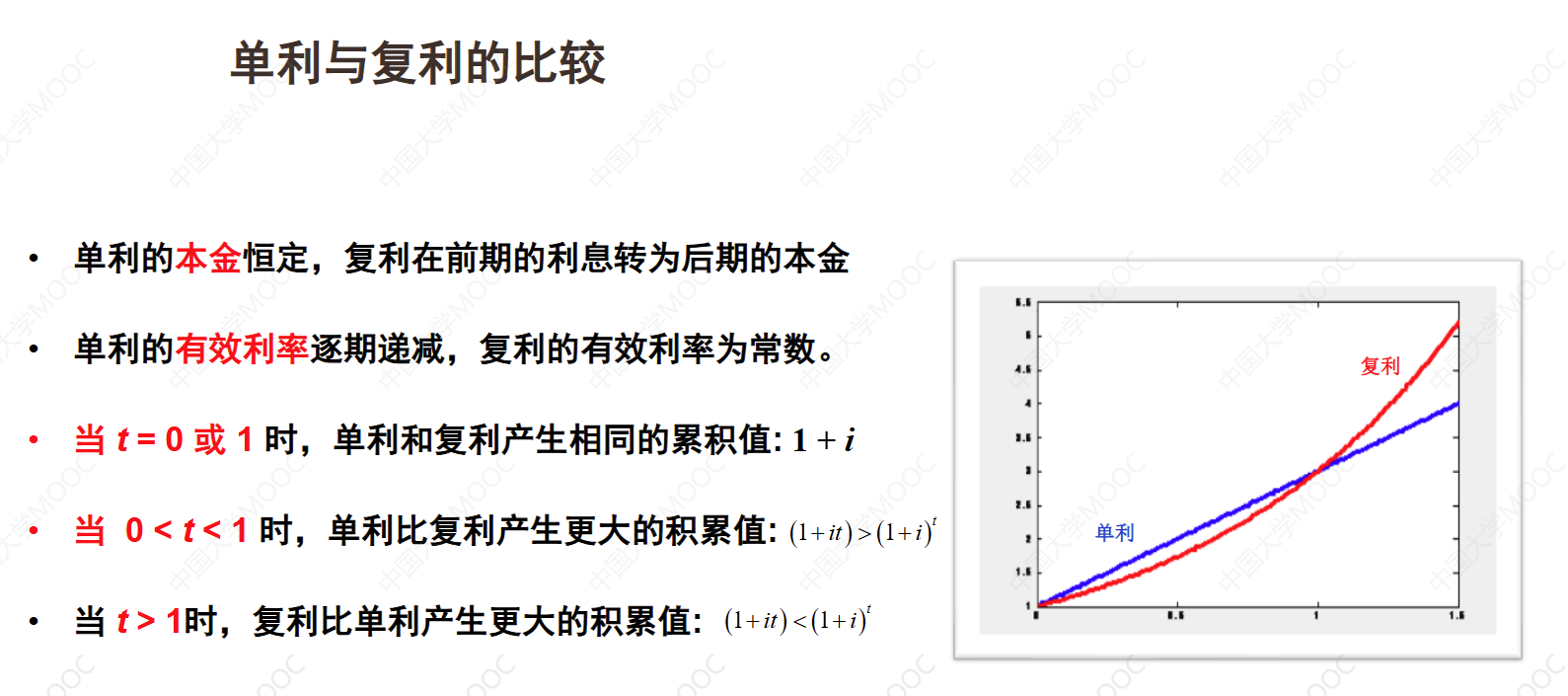
单利和复利是最常用的两种计息方式。单利的本金是恒定的，而复利在前期产生的利息会转化为后期的本金。单利的有效利率逐期递减，而复利的有效利率保持为常数。在t等于0和t等于1的时间点上，单利和复利的累积值相同。在t大于0和小于1的区间，单利产生的累积值大于复利的累积值。到t大于1的时候，复利比单利产生更大的累积值。复利的累积函数可以用单利的累积函数来近似表示，这样可以简化计算。复利的神奇之处在于即使每天增长或亏损1%，经过一年的复利，效果也会非常惊人。

单利不满足一致性（分段投资能产生更大的累积值）：若$t=t_1+t_2$，则$a(t_1)+a(t_2)>a(t)$

复利满足一致性：若$t=t_1+t_2$，则$a(t_1)+a(t_2)=a(t)$

1.6 有效贴现率（实际贴现率）

有效贴现率是对利息相对大小的度量，是期末利息和期末的累积值相比较。有效利率是期末利息和期初本金相比较。有效贴现率可以定义在任意的时间区间，最常使用的是年有效贴现率。年末的1元在时间零点的现值可以表示为1减d，其中d是年有效贴现率。有效利率和有效贴现率之间存在着各种变换关系，如年末的1元在时间零点的现值可以表示为1加i的负1次方，其中i是年有效利率。有效利率和有效贴现率之间还有其他关系，如d可以写成i乘以v，其中v是贴现因子。有效利率和有效贴现率之间还有对称关系，即i减去d等于i乘以d。如果有效利率可以表示为1/n，那么有效贴现率可以表示为$1/(n+1)$。有效利率和有效贴现率的极限关系是当有效利率趋于无穷大时，有效贴现率取于1。

$有效利率(i)=\frac{期末利息}{期初本金}$

$有效贴现率(d)=\frac{期末利息}{期末累积值}$

$利息=期末累积值-期初本金$

有效利率i和有效贴现率d有6种关系和一种极限关系

年末的1元在年初的现值为1-d

$i=\frac{d}{1-d}$

$d=\frac{i}{1+i}$

$d=\frac{i}{1+i}=1-\frac{1}{1+i}=1-v$

$d=iv=i\times \frac{1}{1+i}=iv$

$d=\frac{i}{1+i}=i\cdot \nu =i\cdot (1-d)=i-id$

$i=\frac{1}{n}\iff d=\frac{1}{n+1}$ 证明：$d=\frac{i}{1+i}=\frac{1/n}{1+1/n}=\frac{1}{n+1}$

累积函数与贴现函数的不同表示方式

$$a(t)=(1+i{)}^t=(1-d{)}^{-t}$$

$$a^{-1}(t)=(1+i{)}^{-t}={\nu }^t=(1-d{)}^t$$

1.7 例题：有效利率和有效贴现率

这个视频讲解了有效利率和有效贴现率的概念和计算方法。首先通过一个例子，介绍了如何根据已知条件计算出利率i。然后，利用已知的利率i，计算了账户在第10年末的累积值。接着，通过另一个例子，演示了如何根据已知条件计算出利率i，并计算了三笔投资在时间零点的现值。最后，比较了债券和储蓄存款的贴现率和利率，得出了应该投资债券的结论。视频还介绍了如何计算利息和提前预收利息，以及有效贴现率的计算方法。

1.8 名义利率

名义利率是现实应用中最常使用的一种利息度量，反映了资金在一个时间区间上的增长率。有效利率可以定义在任意的时间区间上，但最常使用的是年有效利率。对于定义在小于一年或大于一年的时间区间上的有效利率，通常会将其转化为年名义利率进行表示。年名义利率可以表示为每个区间上的有效利率乘以一年包含的区间数。年名义利率也可以叫做年化的收益率。年名义利率和任意区间上的有效利率之间存在一种比例关系，相差一个m倍，其中m表示一年包含的区间个数。年名义利率$i^{(m)}$可以解释为在$1/m$年这个区间上和复利利率等价的那个单利利率。

例：每个季度的有效利率为1.5%，通常表述为年名义利率为6%

例：月有效利率为1%，通常表述为年名义利率为12%

例：3年期的有效利率为15%，通常表述为年名义利率为5%

例考虑下述两笔贷款

（1）贷款100万，年利率为12%，年末支付利息12万。

12%是年有效利率

（2）贷款100万，年利率为12%，每月末支付一次利息，每次支付1万元。

12%是年名义利率

例：理财产品的期限是一个月，到期可获得0.5%的收益率（月有效利率）

表述：理财产品的期限是一个月，年化收益率是6%。

含义：6%是年名义利率

年名义利率=区间的有效利率×一年包含的区间数

6% = 0.5% x 12

季度的有效利率为3%，通常表述为年名义利率：

• 年利率为12%，每年结转4次利息
• 年利率为12%，每年复利4次
• 年利率为12%，每季度结转一次利息
• 年利率为12%，每季度复利一次

符号表示：

• $i^{(m)}$表示年名义利率
• m表示每年包含的区间数，每年复利的次数，或每1/m年支付一次利息

$i^{(m)}$ <=> 每$\frac{1}{m}$年的有效利率=$\frac{i^{(m)}}{m}$

例：$i^{(4)}=8\%$ 表示每年复利4次，每季度的有效利率为2%。

例：$i^{(1/5)}=10\%$表示每5年复利1次，5年期的有效利率为50%。

年名义利率与年有效利率的关系：$年名义利率i^{(m)}=\frac{1}{m}年区间上的有效利率\times m$

考虑时间零点的1元在年末的累积值：$1+i=(1+\frac{i^{(m)}}{m}{)}^m$

年名义利率：在1/m年的时间区间上，与复利利率等价的单利利率。

1.9 例题：名义利率

这个教学视频介绍了名义利率的概念和计算方法。视频中给出了两个例子来说明不同条件下的累积值计算。

当复利次数增加时，年有效利率会逐渐增加。

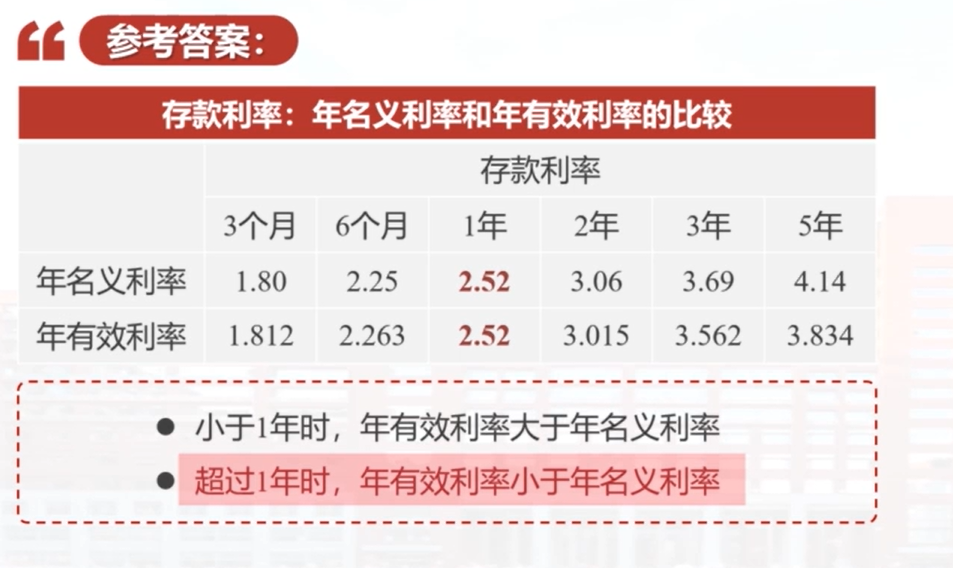
最后，视频给出了一些银行存款的年名义利率，并通过转化为等价的年有效利率进行比较。对于存款期限小于1年的，等价的年有效利率大于年名义利率；对于存款期限大于1年的，等价的年有效利率小于年名义利率。

例：投资100万元，年利率为12%。在下述条件下计算1个月末的累积值：

（1）假设上述利率是年有效利率

（2）假设上述利率是年名义利率，每年复利12次

$\begin{array}{rl}& (1)100\times {\left(1+0.12\right)}^{\frac{1}{12}}=100.95\\ & (2)100\times \left(1+\frac{0.12}{12}\right)=101\end{array}$

例：下述哪个利率对投资者更加有利？

年利率为5%，每半年复利一次，$i^{(2)}=5\%$

年利率为4.95%，每天复利一次（每年按365天计算）$i^{(365)}=4.95\%$

$1+i={\left(1+\frac{0.05}{2}\right)}^2=1.0506\Rightarrow i=5.06\%$

$1+i={\left(1+\frac{0.0495}{365}\right)}^{365}=1.0507\Rightarrow i=5.07\%$

在长度为 t 天的时间区间上定义的有效利率为x, 则对应的年名义利率为多少？（一年按365天计算）答案是365x/t

1.10 名义贴现率

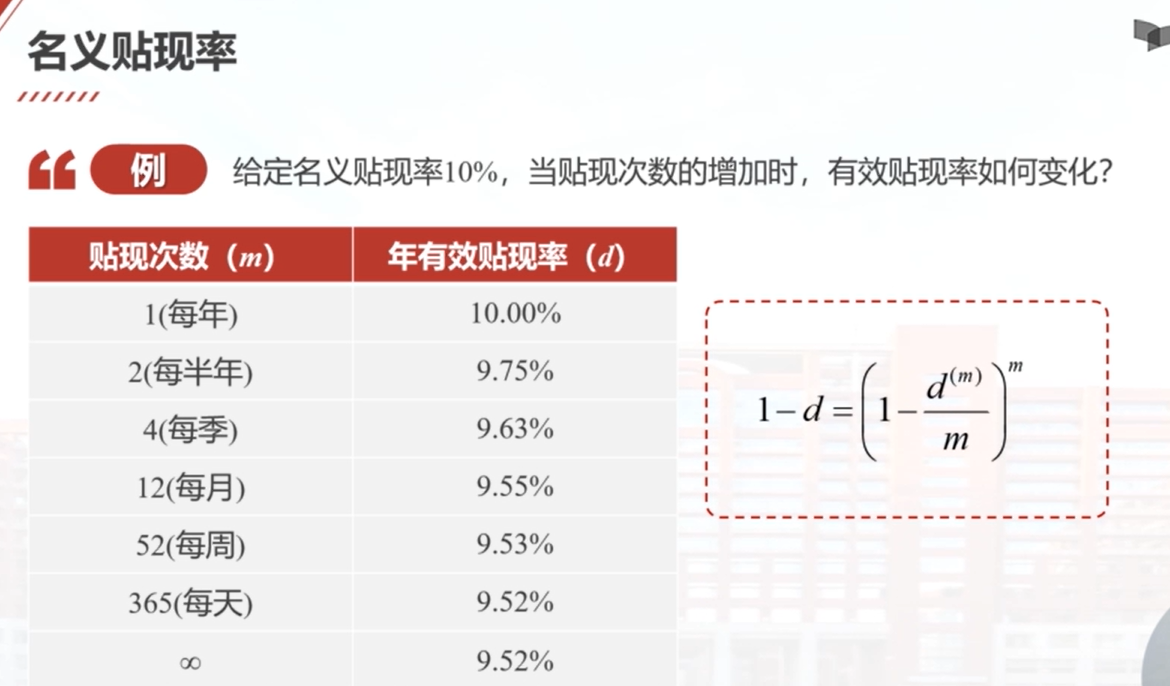
本视频介绍了名义贴现率的概念和计算方法。首先回顾了有效贴现率的定义，即一个时期所产生的利息与期末的累积值相比。有效贴现率可以定义在任意的时间区间上，常用的是年有效贴现率。年名义贴现率是定义在一年时间区间上的有效贴现率。对于定义在任意长度时间区间上的有效贴现率，通常会将其转化为年名义贴现率进行表述。年名义贴现率可以用d(m)符号表示，其中m表示每年贴现m次。在计算现值时，年名义贴现率可以转化为年有效贴现率。通过例子和计算，展示了年名义贴现率和年有效贴现率之间的相互转化关系。最后，通过计算不同贴现次数m下的年有效贴现率，发现当m趋于无穷大时，年有效贴现率接近每天贴现一次的年有效贴现率。

有效贴现率：期末的利息与期末累积值之比

年有效贴现率：年末的利息与年末累积值之比

年名义贴现率：用于表述任意区间上的有效贴现率

年名义贴现率=任意区间上的有效贴现率×一年包含的区间数

例：

月有效贴现率为1%=年名义贴现率为12%，每年贴现12次

2年期的有效贴现率为8%=年名义贴现率为4%，每2年贴现1次

名义贴现率的符号表示

$d^{(m)}:$每 1/m 年的有效贴现率为 $\frac{d^{(m)}}{m}$

名义贴现率与有效贴现率的关系：

$1-d={\left(1-\frac{d^{(m)}}{m}\right)}^m$

${\left(1-d\right)}^{\frac{1}{m}}=1-\frac{1}{m}{d}^{(m)}$

年名义贴现率：在1/m年的时间区间内，与年有效贴现率d等价的单贴现率。

1.11 名义利率与名义贴现率的关系

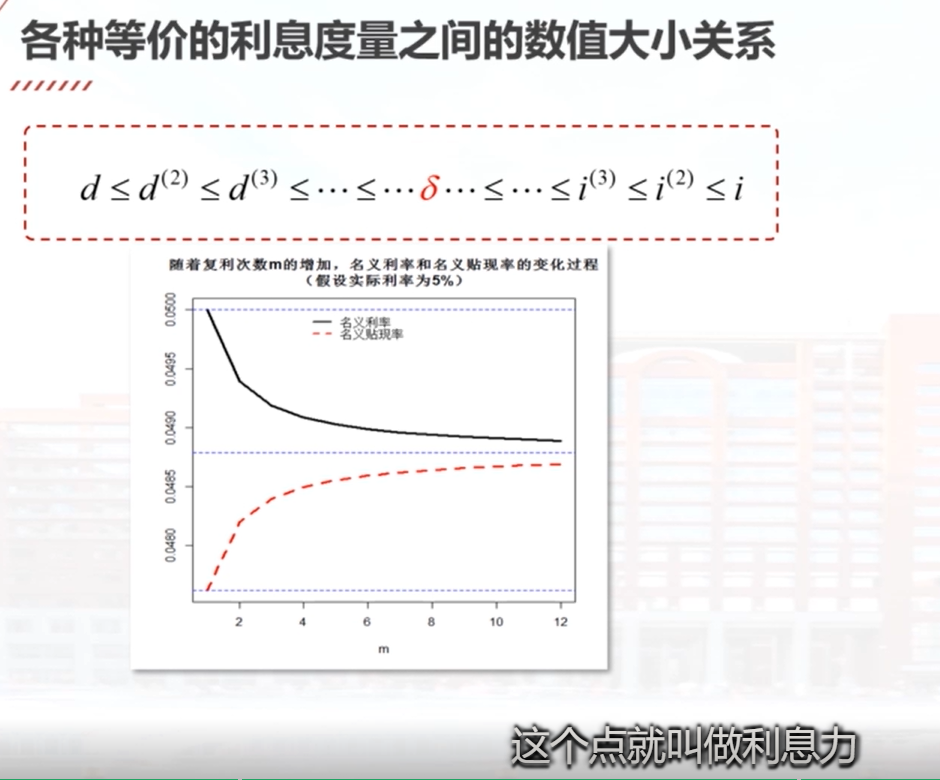
本视频介绍了名义利率与名义贴现率之间的相互转化关系。在时间区间0到1/m年内，名义利率i(m)除以m得到该区间的有效利率，名义贴现率d(m)除以m得到1到1/m区间的有效贴现率。有效贴现率可以定义为该区间产生的利息i(m)除以m再除以期末的累积值。名义贴现率d(m)可以表示为名义利率i(m)除以1加i(m)除以m。在时间区间0到1/m年内，期末的现值可以表示为1减去该区间的有效贴现率。根据这些关系，可以用名义利率计算名义贴现率，或者用名义贴现率计算名义利率。此外，视频还介绍了有效利率、有效贴现率、名义利率和名义贴现率之间的大小关系，以及利息力的概念。

$d^{(m)}/m=\frac{i^{(m)}/m}{1+i^{(m)}/m}\iff d^{(m)}=\frac{i^{(m)}}{1+i^{(m)}/m}$

$i^{(m)}/m=\frac{d^{(m)}/m}{1-d^{(m)}/m}\iff \{\begin{array}{ll}{i}^{(m)}=\frac{d^{(m)}}{1-d^{(m)}/m}& \\ & \\ d^{(m)}=i^{(m)}\left(1-\frac{d^{(m)}}{m}\right)& \end{array}$

$\begin{array}{rl}& i-d=i\times d\\ & \frac{i^{(m)}}{m}-\frac{d^{(m)}}{m}=\frac{i^{(m)}}{m}\times \frac{d^{(m)}}{m}\end{array}$

用名义利率和名义贴现率表示的累积函数和贴现函数

中间桥梁——累积函数

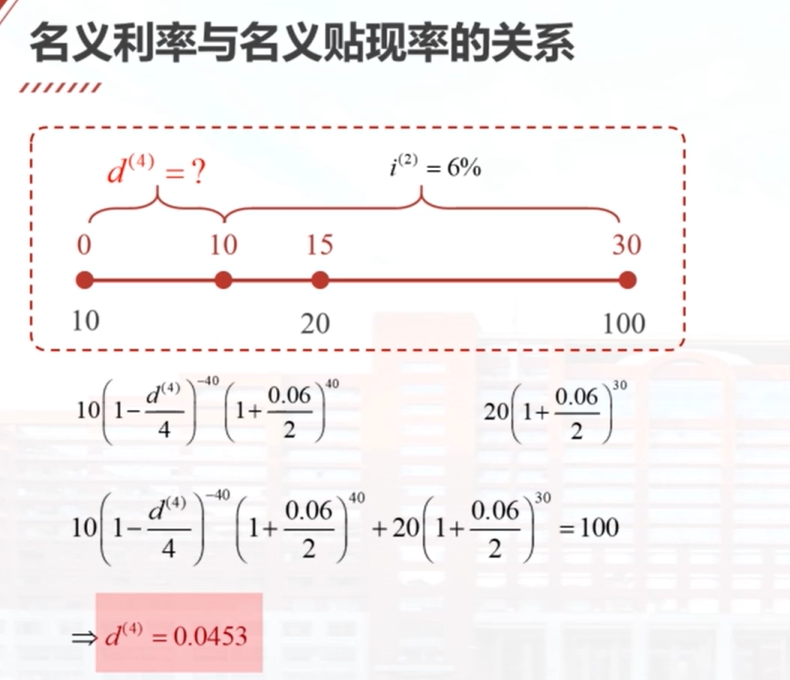
已知在三个月的时间区间上，有效利率与有效贴现率之差为1%，则这个区间上有效利率与有效贴现率的乘积是多少？1%

每年复利m次的年名义利率越大，则与其等价的每年贴现m次的年名义贴现率越大。

1.12 利息力的定义

本节课介绍了利息力的定义。年有效利率是指一年期间所产生的利息与期初本金相比的比率，度量了资金在一个年度的增长率。年名义利率主要用于度量资金在任意时间区间上的增长率，可以表示为区间上的有效利率乘以一年包含的区间个数。利息力是对年名义利率求极限，度量了资金在一个无穷小的时间区间上的增长率。利息力的定义公式为a(t)的一阶导数除以a(t)，表示单位资金在单位时间上的增长率。单利的利息力随着时间的增加越来越小，而复利的利息力是一个常数，与时间无关。复利的利息力可以用$ln(1+i)$或者$e^{\delta }$表示。

年有效利率：度量资金在一个年度的增长率

年名义利率：度量资金在任意区间上的增长率

年名义利率=区间上的有效利率×一年包含的区间数

例：如果月有效利率为0.5%，则年名义利率为6%

利息力：度量资金在无穷小时间区间上的增长率

单利的利息力

单利的累积函数$a(t)=1+it$

单利的利息力为$\delta (t)=\frac{a^{\prime }(t)}{a(t)}=\frac{i}{1+it}$

复利的利息力

$\begin{array}{c}a(t)=(1+i{)}^t{a}^{\prime }(t)=(1+i{)}^t\ln (1+i)\\ \delta (t)=\frac{a^{\prime }(t)}{a(t)}=\frac{(1+i{)}^t\ln (1+i)}{(1+i{)}^t}=\ln (1+i)\end{array}$

复利的利息力是常数：$\delta =\ln (1+i)\nLeftrightarrow 1+i={\mathrm{e}}^{\delta }$

复利的累积函数：$a(t)=(1+i{)}^t={\mathrm{e}}^{\delta t}$****

1.13 利息力的应用

在这个教学视频中，我们学习了利息力的应用。利息力是根据累积函数定义的，用来表示在时间点s的利息力。利息力可以通过累积函数的一阶导数除以累积函数来定义。我们还可以将其写成$lna(s)$的一阶导数。根据这个等式，我们可以对左边和右边分别进行积分，得到两个不同的结果。利息力也可以用来表示累积函数，通过对利息力在0到t之间求积分再做指数变换得到累积函数。在复利条件下，名义利率的极限就是利息力。我们还证明了在复利条件下，名义贴现率也趋于连续复利。利息力也叫做连续复利或连续收益率，因为它可以表示为$ln(1+i)$，其中i是有效利率。利息力具有可加性，可以简化计算。根据累积函数和贴现函数的一阶导数，我们可以定义利息力和贴现力，但由于它们等价，我们在应用中只使用利息力的概念。

用利息力表示累积函数

$\delta (s)=\frac{a^{\prime }(s)}{a(s)}={\left[\begin{array}{c}\ln a(s)\end{array}\right]}^{\prime }$

$\ln a(t)={\int }_0^t\delta (s)\mathrm{d}s$

$a(t)={\mathrm{e}}^{{\int }_0^t\delta (s)\mathrm{d}s}$

连续复利的另一种解释：

复利条件下，当$m\to \infty$的名义利率是利息力（连续复利）: ${\lim }_m\to \infty i^{(m)}=\delta$

${\lim }_{m\to \infty }{i}^{(m)}={\lim }_{m\to \infty }m\lceil {\left(1+i\right)}^{\frac{1}{m}}-1\rceil$

$={\lim }_{x\to 0}\frac{(1+i{)}^x-1}{x}$ (令$x=\frac{1}{m}$)

$={\lim }_{x\to 0}\left[{\left(1+i\right)}^x\ln (1+i\right)$

$=\ln (1+i)$

$\begin{array}{rl}& \text{当 }m\text{ 趋于无穷时,名义贴现率 }{d}^{(m)}\text{ 与连续复利的关系?}\underset{m\to \infty }{\lim }{d}^{(m)}=\delta \\ & d^{(m)}=m\left[1-(1-d{)}^{\frac{1}{m}}\right]\\ & \underset{m\to \infty }{\lim }{d}^{(m)}=\underset{m\to \infty }{\lim }m\left[1-(1-d{)}^{\frac{1}{m}}\right]\stackrel{令x=1/m}{\to }\underset{x\to 0}{\lim }\frac{1-(1-d{)}^x}{x}\\ & =-\ln (1-d)=-\ln {\mathrm{e}}^{-\delta }=\delta \end{array}$

复利的累积函数可以用连续收益率或对数收益率表示。

$\delta =ln(1+i)$

对数收益率具有可加性，方便计算。

连续两天的对数收益率等于第一天对数收益率加上第二天对数收益率。

贴现力=利息力

$\begin{array}{rl}& \bullet \text{ 在 }t\text{ 时刻的贴现力为}{\delta }^{\prime }(t)=-\frac{{\left[a^{-1}(t)\right]}^{\prime }}{a^{-1}(t)}\\ & {\delta }^{\ast }(t)=-\frac{{\left[a^{-1}(t)\right]}^{\prime }}{a^{-1}(t)}=\frac{a^{-2}(t)}{a^{-1}(t)}\cdot {\left[a(t)\right]}^{\prime }=\frac{{\left[a(t)\right]}^{\prime }}{a(t)}=\delta (t)\end{array}$

加负号是为了保证贴现率为正。

1.14 例题：利息力

这个视频介绍了如何计算前4年的年有效利率。根据给定的利息力条件，利息力在0-3年为0.02t，在3年后为0.05。为了计算年平均有效利率i，可以将时间零点的1元按照给定的利息力累积到第4年末，然后与按照年有效利率i累积4年的累积值相等。通过解方程，可以得到i等于3.56%。视频还介绍了另一个例子，比较了按照每年复利两次的年名义利率计息和按照单利利率计息的两个账户在第5年末的利息力相等的情况下，求解单利利率i的方法。根据已知条件，解方程可以得到i等于0.1905。

结果：$i=3.56\%$

这里的公式实际上应该是$\frac{i}{i+5i}=2\times ln(1+5\%)$

结果：$i=0.1905$

1.15 利率概念辨析

本视频介绍了利息度量的两个重要概念：有效利率和名义利率。在金融数学中，实际利率和名义利率的定义与经济学中的定义完全不同。经济学中的名义利率包含通货膨胀率，而实际利率是扣除了通货膨胀率的利率。实际利率等于名义利率减去通胀率。通过一个例子，解释了为什么实际利率和名义利率之间存在这样的关系。此外，还介绍了利率和贴现率的概念，以及在计算现值时使用不同的比率。在使用这些概念时，需要准确区分利率、贴现率和利息率。

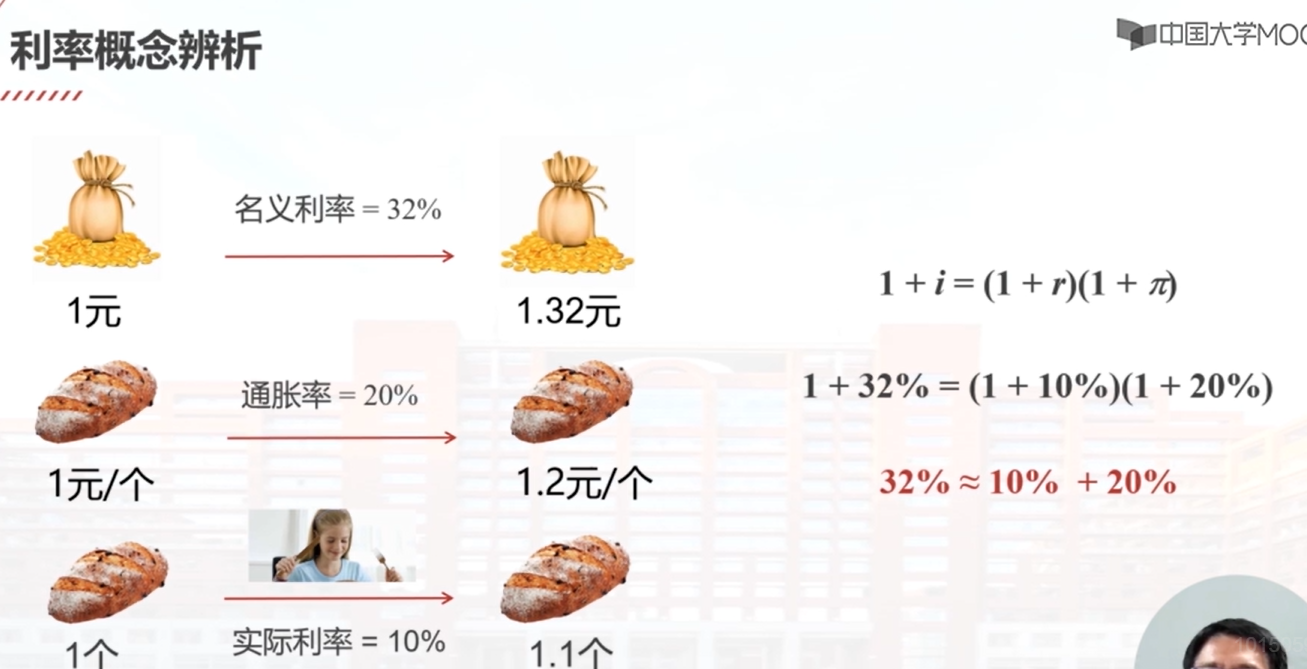
利率和贴现率：在计算现值时，利率有时被误称为贴现率。计算现值可以用利率、贴现率、利息力

$a^{-1}(t)=(1+i{)}^{-t}=(1-d{)}^t=e^{-\delta t}$

课后自测

已知累积函数为  $a(t)=1+0.1\ast t$，计算 t = 0时投资100万元，在 t = 2时赚取的利息是多少万元？20

已知累积函数为$a(t)=1+0.1\ast t$，计算 t = 2时100万元在t = 1时的价值是多少？91.67

已知累积函数为a(t) = 1.1^t，则年有效利率是多少？10%

投资者2021年3月2日在基金账户中存入10000元，2021年8月25日取出。该基金按年单利利率2%计息。按照“实际/365”规则计息，投资者可以获得多少利息？大于90

投资者2021年3月2日在基金账户中存入10000元，2021年8月25日取出。该基金按年单利利率2%计息。按照“30/360”规则计息，投资者可以获得多少利息？小于97约为96

已知单利和复利的年利率均为40%，在（0，1）的时间区间上，当 t  等于多少时，单利与复利的累积值差异最大？ 0.514

$\Delta =1+0.4t-(1+0.4{)}^t$求导得到极值点即可

已知有效利率为10%，则有效贴现率为多少？1/11

3年期银行存款的挂牌年利率为6%，则意味着存款100万元满3年可以获得的利息是多少万元？ 18

三个月期限的银行存款年利率为3%，则存款100万元满三个月的利息是多少万元？0.75

在长度为 t 天的时间区间上定义的有效利率为x, 则对应的年名义利率为多少？（一年按365天计算）$365x/t$

年名义贴现率为12%，每年贴现4次，则年末的100万元在年初的现值是多少？ 大于85大约为89

已知在三个月的时间区间上，有效利率与有效贴现率之差为1%，则这个区间上有效利率与有效贴现率的乘积是多少？1%

已知累积函数为$a(t)=1+0.1\ast t$，则在t = 2时的利息力是多少？0.08

已知累积函数为a(t) = 1.08^t，则在t = 20时的利息力是多少？$ln(1.08)=0.076961041136=8\%$