远期、期货和互换
- 学习目标
- 思维导图
- 8.1 远期、期货与互换的基本概念
- 8.2 远期利率协议
- 8.3 期货
- 8.4 远期定价原理
- 8.5 远期价格:到期前不产生收益的资产
- 8.6 远期价格:产生已知收益的资产
- 8.7 远期价格:产生连续收益的资产
- 8.8 远期利率协议的定价
- 8.9 合成远期
- 8.10 互换
- 8.11 利率互换及其定价
- 8.12 例题:利率互换
学习目标
掌握远期、期货和互换的基本概念,理解无套利定价原理,可以计算不同金融资产的远期价格;可以计算远期合约和互换合约的价值;掌握利率互换合约的定价方法。
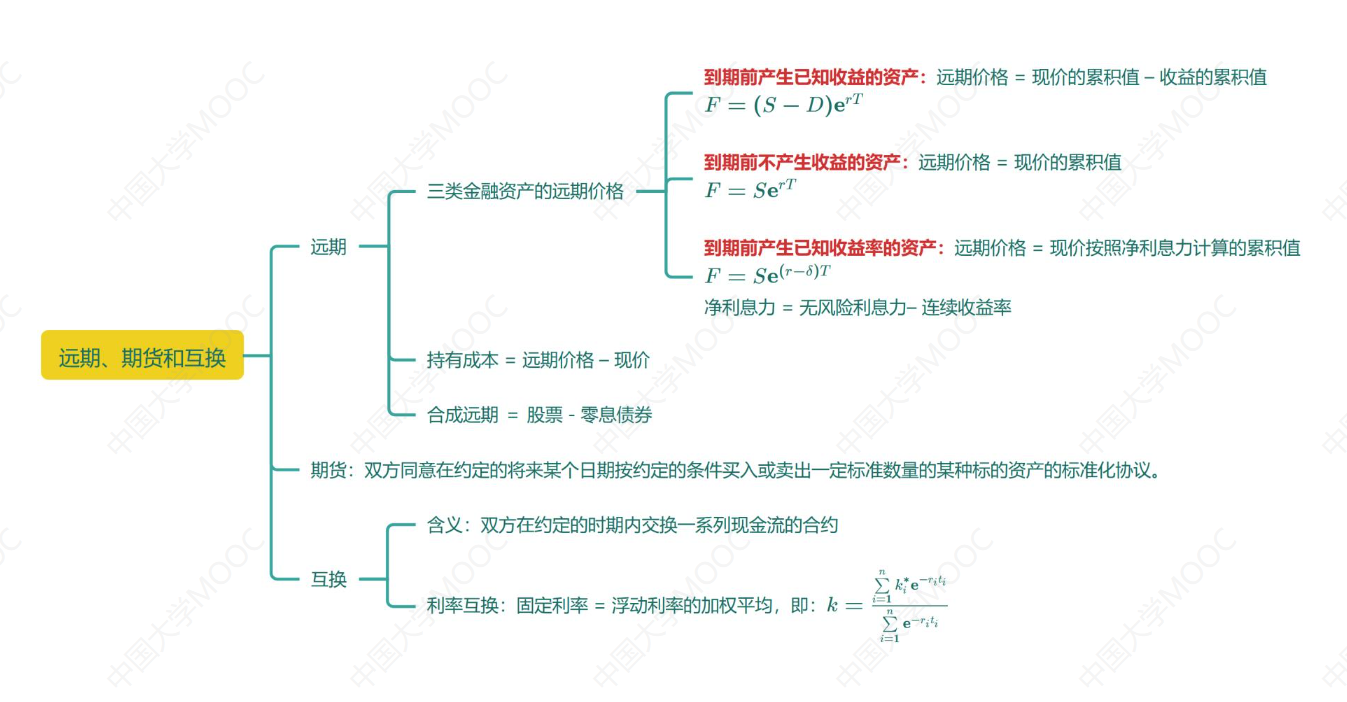
思维导图
8.1 远期、期货与互换的基本概念
本视频介绍了金融衍生工具的基本概念,包括远期合约、期货合约和互换合约。金融衍生工具是基于基础资产(如股票、债券、商品或利率等)派生出来的金融产品,其价值依赖于基础资产的价格变动或其他相关变量。这类工具在风险管理、投机和增加流动性等方面具有重要作用。
1. 金融衍生工具概述
常见的金融衍生工具包括:
- 远期合约(Forward Contracts)
- 期货合约(Futures Contracts)
- 互换合约(Swaps)
- 期权合约(Options)
这些工具为投资者提供了多种交易策略,允许他们对市场波动进行预测和规避风险。
2. 远期合约
远期合约是指交易双方约定在未来某一特定时间,以事先确定的价格买卖一定数量的基础资产的协议。
常用术语:
- 标的资产(基础资产):双方约定买卖的资产。
- 交割价格:约定的成交价格。
- 空头:卖出标的资产的一方。
- 多头:买入标的资产的一方。
远期合约具有以下特点:
- 非标准化:远期合约是根据交易双方的需求量身定制的,因此条款通常没有统一标准。
- 场外交易:这类合约通常在场外市场交易,不通过交易所。
- 信用风险:由于缺乏交易所的清算机制,远期合约面临较高的违约风险。
进一步了解远期合约时,需要关注以下概念:
- 合约回收:合约到期时,持有人能够实现的现金价值。回收价值取决于合约标的资产的市场价格与合约约定价格之间的差异。
- 盈亏计算:盈亏是指合约到期时的回收价值减去初始费用的终值。初始费用包括签署合约时的任何交易费用或保证金。

在远期合约中,双方约定交易的资产称作标的资产。
双方约定,A在一年以后以30元的价格从B购买1只股票,如果到期时股票的价格为25元,则远期合约多头的回收是(-5)元。
双方约定,A在一年以后以30元的价格从B购买1只股票,如果到期时股票的价格为25元,则远期合约多头的盈亏是(-5)元。
例:投资者通过远期合约购买股票,约定一年后的交割价格为105元。如果一年后股票价格上升为115元,没有分红,计算远期合约多头的回收和盈亏。
解:回收=115—105=10,盈亏=10-0=10
3. 远期合约的类型
远期合约可以分为几种类型:
- 商品远期合约:用于交易商品,如石油、黄金或农产品。
- 金融远期合约:用于金融工具,如股票、外汇和利率。具体例子包括:
- 远期利率协议(Forward Rate Agreements, FRA):一种金融合约,允许交易双方就未来某一时期的利率达成协议。
- 远期外汇合约:使交易双方能够以事先约定的汇率在未来某一时间买卖外币。
- 远期股票合约:涵盖特定股票的期权,允许持有者在合约到期时以约定价格购买或出售股票。
4. 总结
金融衍生工具不仅为投资者提供了多样的投资策略,也在风险管理方面发挥了至关重要的作用。通过使用远期、期货和互换等工具,市场参与者可以有效地对冲风险,捕捉潜在的市场机会,从而优化投资组合的表现。
8.2 远期利率协议
本视频介绍了远期利率协议(Forward Rate Agreement, FRA)的定义和计算方法。远期利率是指从将来某个时间点开始,并持续一定期限的利率。这种利率通常是由一系列即期利率(即当前市场利率)决定的,以反映预期的未来利率变化。

1. 远期利率协议的定义
远期利率协议是交易双方同意在未来某一时间点开始,在一个特定时期内按照约定的协议利率借贷一笔名义本金的协议。
双方订立远期利率协议的目的:
- 借入方一规避利率上升的风险
- 借出方规避利率下降的风险
尽管协议中提到了名义本金,但在实际操作中,交易双方并不交换本金,只需支付结算金(利息差额的现值),这一过程称为结算。例:若参照利率(市场利率)下降,借出方获得结算金。
参照利率如何选择?参照利率:不易操纵,定义明确,如曾经的LIBOR和现在的SHIBOR。伦敦银行间同业拆借利率(LIBOR)是商业贷款、抵押贷款的基准利率,即将退出历史舞台。原因:被操纵、不利于金融稳定。上海银行间同业拆借利率(Shanghai Interbank Offered Rate)于2007年1月4日正式运行,是单利利率,包括隔夜、1周、2周、1个月、3个月、6个月、9个月及1年。
如果1年期的即期利率为5%,2年期的即期利率为6%,则从第一年末到第2年末的远期利率为7%
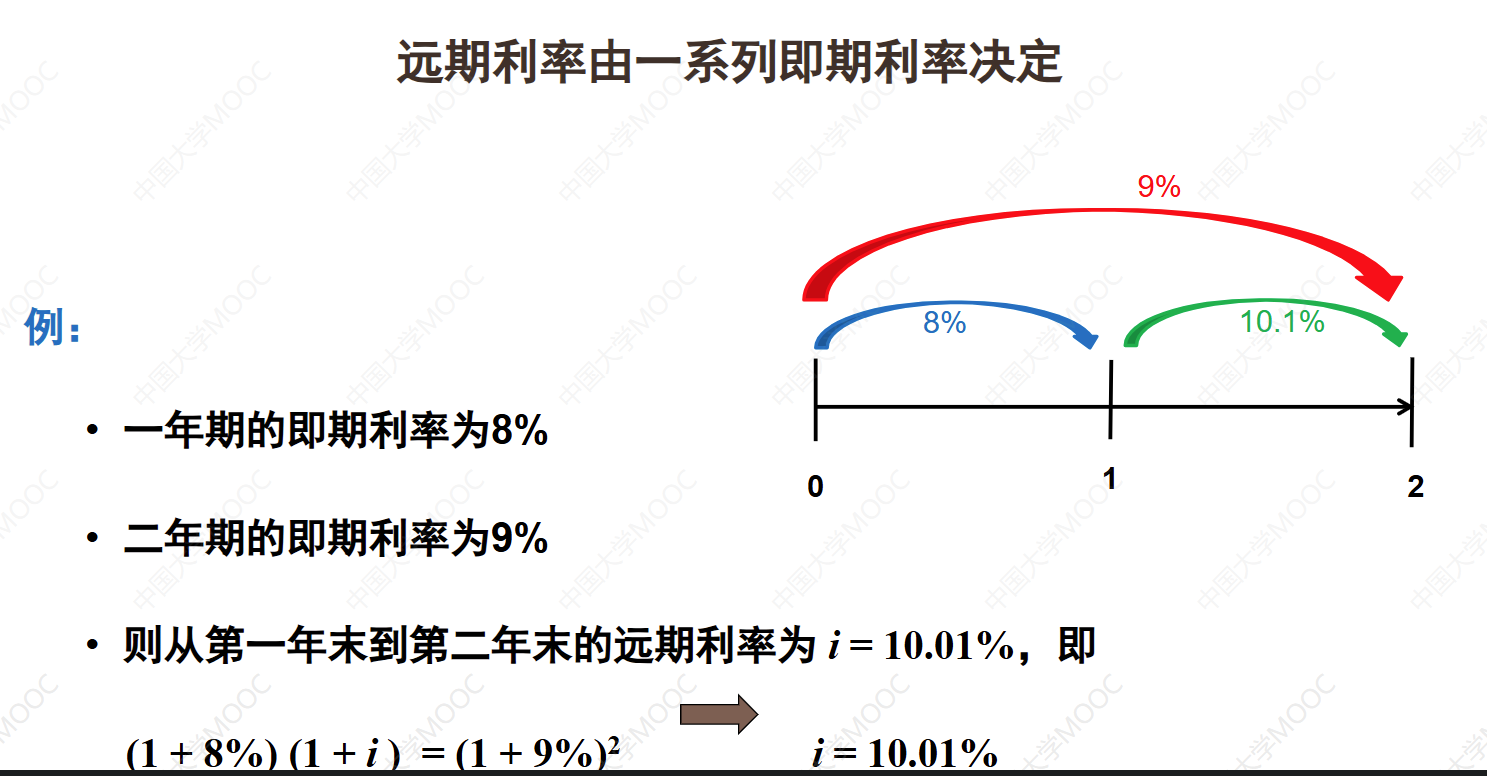
如果用利息力(连续复利)表示的1年期即期利率为5%,2年期即期利率为6%,则从第一年末到第2年末用利息力表示的远期利率为7%。
2. 利息的结算
在FRA的执行过程中,结算金(或叫利息差额的现金流)是双方根据协议利率与市场利率之间的差异来计算的。结算金的大小取决于以下两者的关系:
-
参照利率:通常是市场上流通的利率,例如:
- LIBOR(London Interbank Offered Rate):伦敦银行间拆借利率,是国际金融市场上广泛使用的参照利率。
- SHIBOR(Shanghai Interbank Offered Rate):上海银行间同业拆借利率,是中国市场常用的参照利率。
-
协议利率:双方在签订FRA时约定的利率。
如果市场利率(如LIBOR或SHIBOR)高于协定利率,借款方将支付结算金;如果市场利率低于协定利率,贷款方将支付结算金。
在计算结算金时,通常需要将利息差额折现到贷款的起始时间点。这是因为未来的现金流在折现时具有不同的时间价值,折现公式如下:
这意味着结算金是在贷款开始的时刻进行计算的,有助于准确反映预期的现金流。

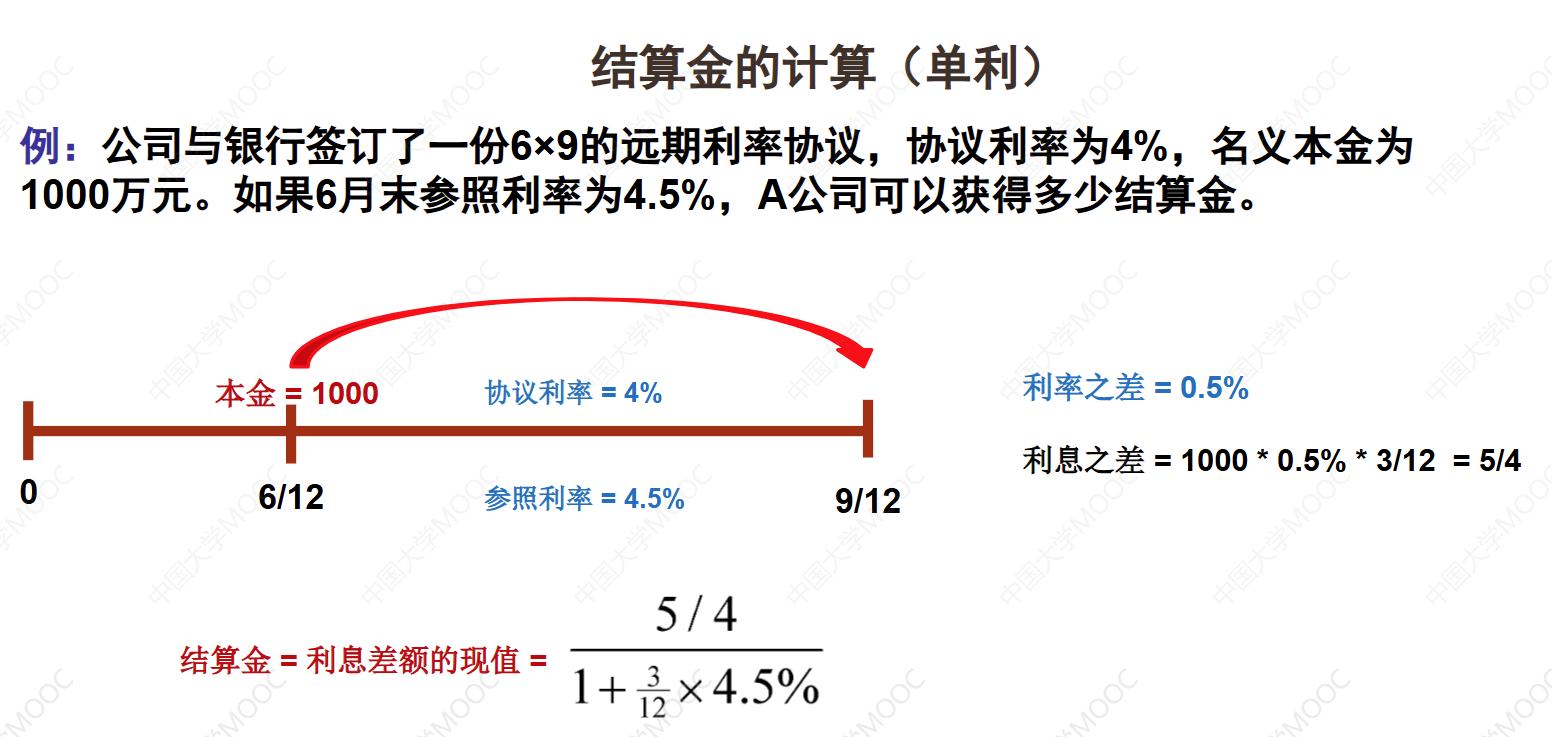
结算金可以用以下公式计算:
其中,期限是从协议开始日到结束日的时间长度,以年为单位表示。
3. 总结
远期利率协议是金融市场中一种重要的衍生工具,为企业和金融机构提供了一种管理利率风险的有效手段。通过锁定未来的借贷利率,市场参与者能够减少由于利率波动带来的财务不确定性。此外,FRA的灵活性使得它在许多不同的金融交易中得到广泛应用,为合约双方提供了更多的策略选择。
8.3 期货
本视频介绍了期货合约(Futures Contract)的概念和特点。期货合约是指交易双方按照约定条件,在未来某个特定日期(到期日)买卖一定数量的标的资产的标准化协议。这种合约通常在期货交易所进行交易,以增强透明度和流动性。
1. 期货合约的基本特征
1.1 标准化
期货合约与远期合约的主要区别在于其标准化特征。远期合约是根据双方需求定制的,缺乏统一的条款,而期货合约对交易的资产、数量、价格及交易方式都进行了规范和标准化。这意味着,所有交易者在同样的合约中使用相同的条款,便于买卖。
1.2 交易单位
每种期货合约都有明确的交易单位,即每份合约所涉及的基本资产数量。例如,标准的黄金期货合约通常为100盎司,而原油的期货合约则为1000桶。
1.3 报价单位
期货合约的报价单位也有统一标准,比如在股指期货中,通常以指数点(如标准普尔500指数)进行报价,而在商品期货(如黄金)中,则以每盎司美元报价。
1.4 价格波动限制
为了防范市场的极端波动,期货合约设置了价格波动限制,即允许的最大涨跌幅度,通常以百分比表示。例如,某些合约可能规定价格在一个交易日内最高上涨不得超过5%。
2. 期货合约的分类
期货合约可以根据交易的标的物不同分为两类:
- 商品期货(Commodity Futures):这种期货合约的标的物通常为实物商品,如铜、铝、大豆、棉花等。商品期货用于对冲实际商品价格波动带来的风险,广泛应用于生产和贸易行业。
- 金融期货(Financial Futures):这种合约的标的物通常为金融工具或金融指标,包括股票指数、国债等。金融期货通常被用作投资组合的风险管理工具,以防范市场波动对资产价值的影响。
3. 主要期货交易所
在中国,主要的四个期货交易所分别是:
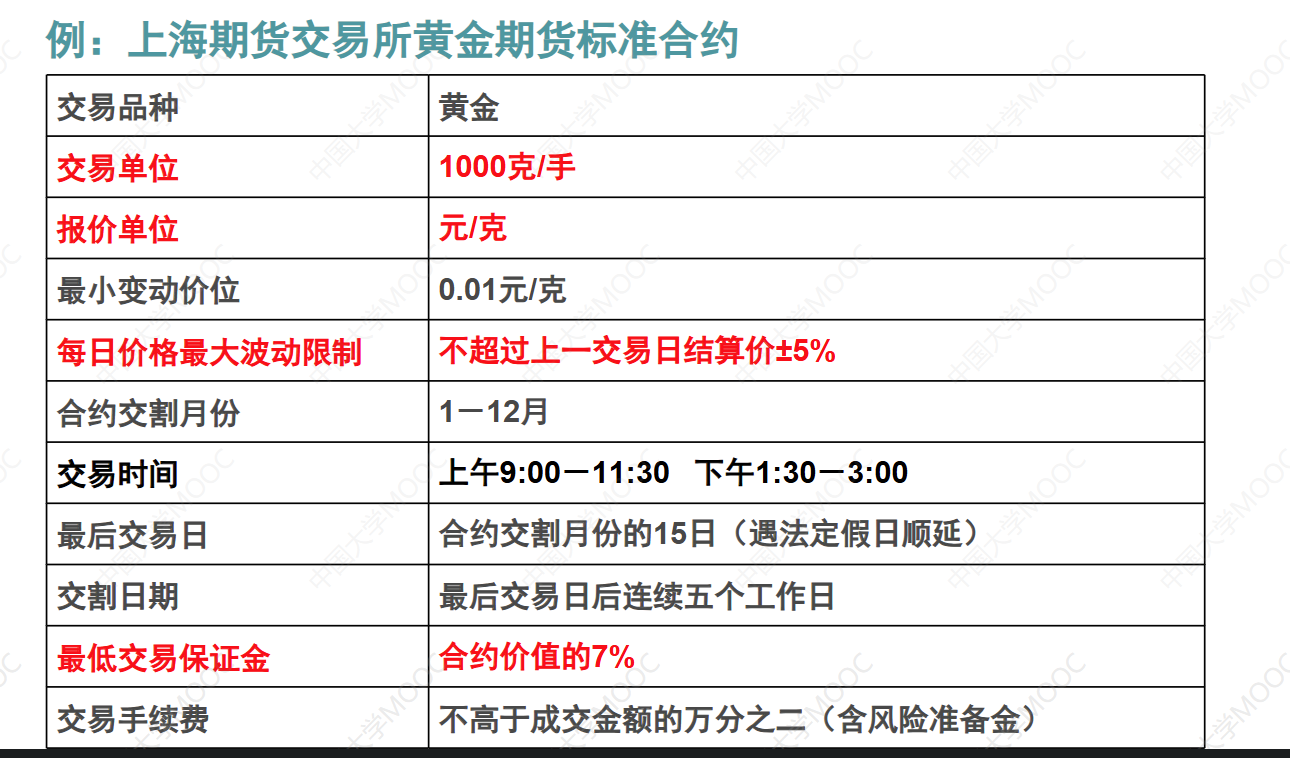
- 上海期货交易所:主要交易金属、能源及化工品。
- 大连商品交易所:主要交易农产品与商品期货。
- 郑州商品交易所:以农产品和其他大宗商品交易为主。
- 中国金融期货交易所:专注于金融期货及相关衍生品的交易。
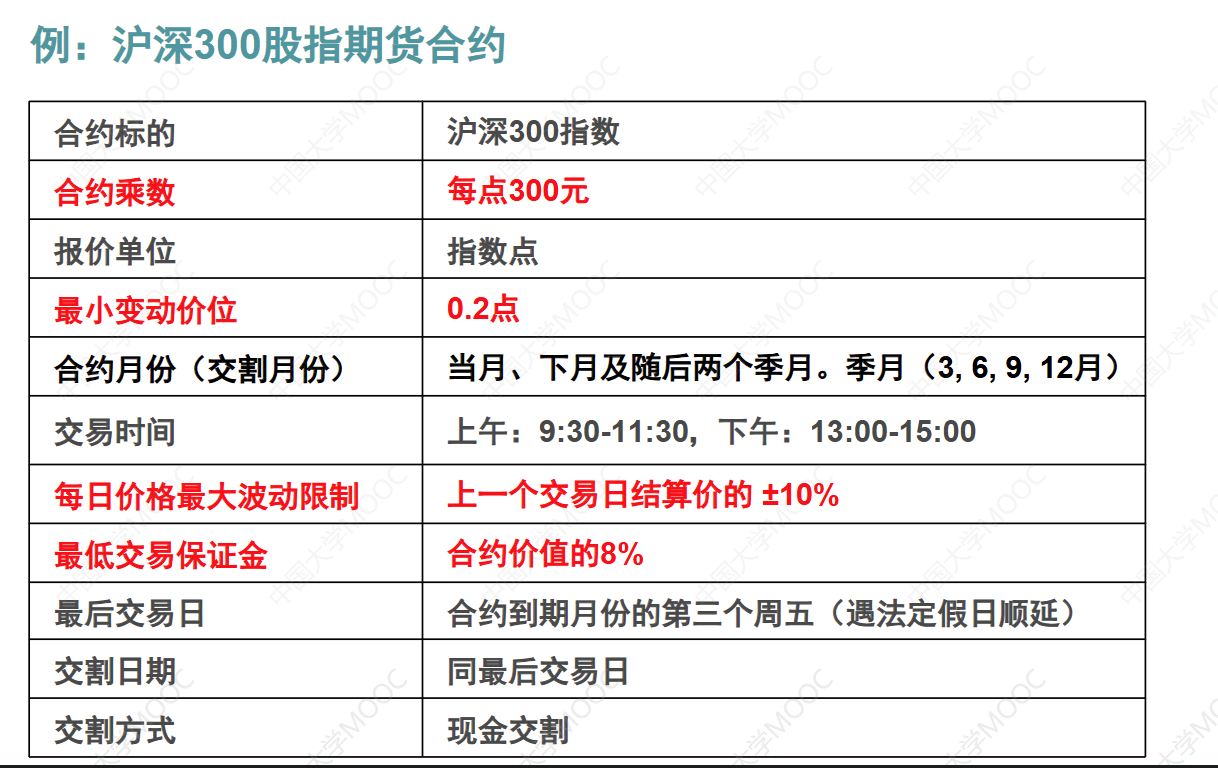
4. 风险管理机制
期货合约具有一些标准化的约定,包括:
- 最低保证金:期货交易需要投资者按照合约总价值的一定比例(通常为5%-10%)缴纳保证金,以确保有足够的资金覆盖潜在损失。保证金的数额会根据标的资产的波动性调整。
- 盯市制度:为防范信用风险和市场风险,期货合约实施盯市制度,即实时计算日内的盈亏,并根据市场价格波动调整投资者的保证金账户。这意味着,如果市场过于波动,投资者可能会被要求追加保证金,确保账户内的资金能够覆盖所有潜在损失。
期货交易的初始保证金:(5% - 20%)
盯市:每天根据期货价格的涨跌计算盈亏,调整保证金账户。例:当日购买价格100万,次日跌至99万,浮动亏损1万,保证金账户核减1万。
保证金低于维持保证金水平时,要追加保证金。维持保证金:通常是初始保证金的75%。
5. 盈亏计算
在期货交易中,盈亏通常通过计算合约的市场价值与平仓时的市场价值之间的差额来确定。
假设合约的开盘价格为 ,平仓价格为 ,合约的交易单位为 ,那么:
- 盈亏计算公式为:

6. 总结
期货合约在全球金融市场扮演着重要角色,不仅为生产者和消费者提供了规避价格波动的工具,也为投机者提供了投资机会。由于其高度的标准化和透明度,期货合约成为资金流动和风险管理的重要场所。
8.4 远期定价原理
本视频介绍了远期合约(Forward Contracts)和期货合约(Futures Contracts)的定价原理,重点关注远期合约的定价方法。
1. 远期价格概念
远期价格是指标的资产在未来某一时间点上交易的理论价格。该价格是通过各种市场因素和成本计算得出的,旨在提供一个无套利的交易机会。计算远期价格时,我们需要考虑基础资产的当前市场价格、融资成本、存储成本及可能的收益等因素。
远期的定价:使用无套利定价法计算资产的远期价格
远期价格:标的资产在未来某个时点上的理论价格
例:
- A公司:年末需一批材料,价格是1000万元。公司目前没钱,也无处存放。
- B公司:我替你买好,先存着,年末再卖给你。
- 年末的价格应该是多少?
远期合约中标的资产的类型
- 到期前不产生收益的资产:零息债券
- 到期前产生已知收益的资产:附息债券
- 到期前连续产生收益的资产:股票指数
2. 无套利定价法
远期定价采用无套利定价法(Arbitrage Pricing),意味着如果市场存在价格差异,交易者可以通过买入现值较低的资产和卖出现值较高的资产来获得无风险利润。在理论上,市场的竞争会使得这一机会迅速消失,从而实现价格的趋同。
套利:低价买入,高价卖出。
套利类型:
- 跨期套利、跨市套利
- 正向套利,反向套利(先高价卖出,后低价买入)
无套利定价法:终值相等,现值也相等,否则就存在套利机会:买入现值较低的资产·卖出现值较高的资产。
具体来说,如果我们假设当前时刻的资产价格为 ,远期合约的到期日为 ,且无风险利率为 ,那么远期价格可以使用以下公式计算:
在这个公式中:
- 是合约到期日的远期价格。
- 是当前时刻的现货价格。
- 是无风险利率(连续复利)。
- 是合约的到期时间(以年为单位)。

3. 交割价格与远期价格的关系
在远期合约中,交割价格与远期价格是两个不同的概念。交割价格是指合约到期时实际交割时所支付的价格,而远期价格是在合约签订时预计的未来价格。在合约签订的时间点上,由于所有因素都已考虑在内,交割价格等于远期价格。也就是说,在无套利条件下:
其中, 表示交割价格。
4. 远期合约的标的资产类型
远期合约可以针对不同类型的标的资产,计算远期价格的方法有所区别。主要分为三类资产:
-
到期前不产生收益的资产:
- 例如黄金、原油等。
- 其远期价格计算方式如上述所示,考虑现货价格和无风险利率的关系。
-
到期前产生已知收益的资产:
- 这种资产可能如债券,其所产生的利息在到期前是已知的。
- 远期价格的计算要减去收益的现值,公式为:
其中, 是在合约到期前产生的收益的现值。
-
到期前连续产生收益的资产:
- 例如房地产或股票,这类资产在到期前会产生持续的现金流。
- 在计算期间,必须考虑现金流的折现,远期价格的计算公式为:
这里, 表示资产在时间 时产生的现金流。
5. 总结
了解远期合约的定价原理,有助于投资者在市场中做出更明智的决策。通过无套利定价法,投资者可以确定合约的理论价值,从而在交易中有效管理风险,并捕捉潜在的利润机会。同时,不同类型标的资产的远期价格计算方法的差异性进一步丰富了交易策略。
下面的视频介绍了远期价格的计算方法,针对三类不同的资产进行深入讨论:到期前不产生收益的资产、到期前产生已知收益的资产和到期前连续产生收益的资产。每种资产的远期价格计算方法不同,其基本原理均基于无套利定价理论。

远期价格=现价+持有成本
持有成本:
- 对于普通商品,包括资金占用成本、储存成本、保险成本等。
- 对于金融资产,仅包括资金占用成本
8.5 远期价格:到期前不产生收益的资产
对于到期前不产生任何收益的资产(例如黄金或原油等),可以用两个不同的资产组合来计算其远期价格。这种方法基于无套利原则,确保没有机会获利而不承担风险。


1.1 组合A
组合A由以下两部分组成:
- 一份远期合约的多头:这意味着投资者同意在未来某一日期以价格 购买一单位的标的资产。
- 一笔现金,表示交割价格 在当前时刻的现值。假设现行的无风险利率为 ,则现金的现值可表示为 ,其中 是合约到期时间(以年为单位)。
在合约到期时,组合A变为现金 ,同时获得单位资产。
1.2 组合B
组合B只由单位标的资产构成。在合约到期时,组合B的价值仍然是单位资产的市场价值。因此,假设到期时的市场价格为 ,组合B的现值为 。
1.3 远期价格的计算
根据无套利定价原理,组合A的现值与现金现值的和应等于组合B的现值。用公式表示为:
即:
通过这些等式,我们可以得到远期价格的计算公式:
其中, 是当前时刻的现货价格。
应用举例
例:股票不支付红利,当前价格为50美元。无风险年利率为5%。计算该股票一年期的远期价格。
解:

8.6 远期价格:产生已知收益的资产


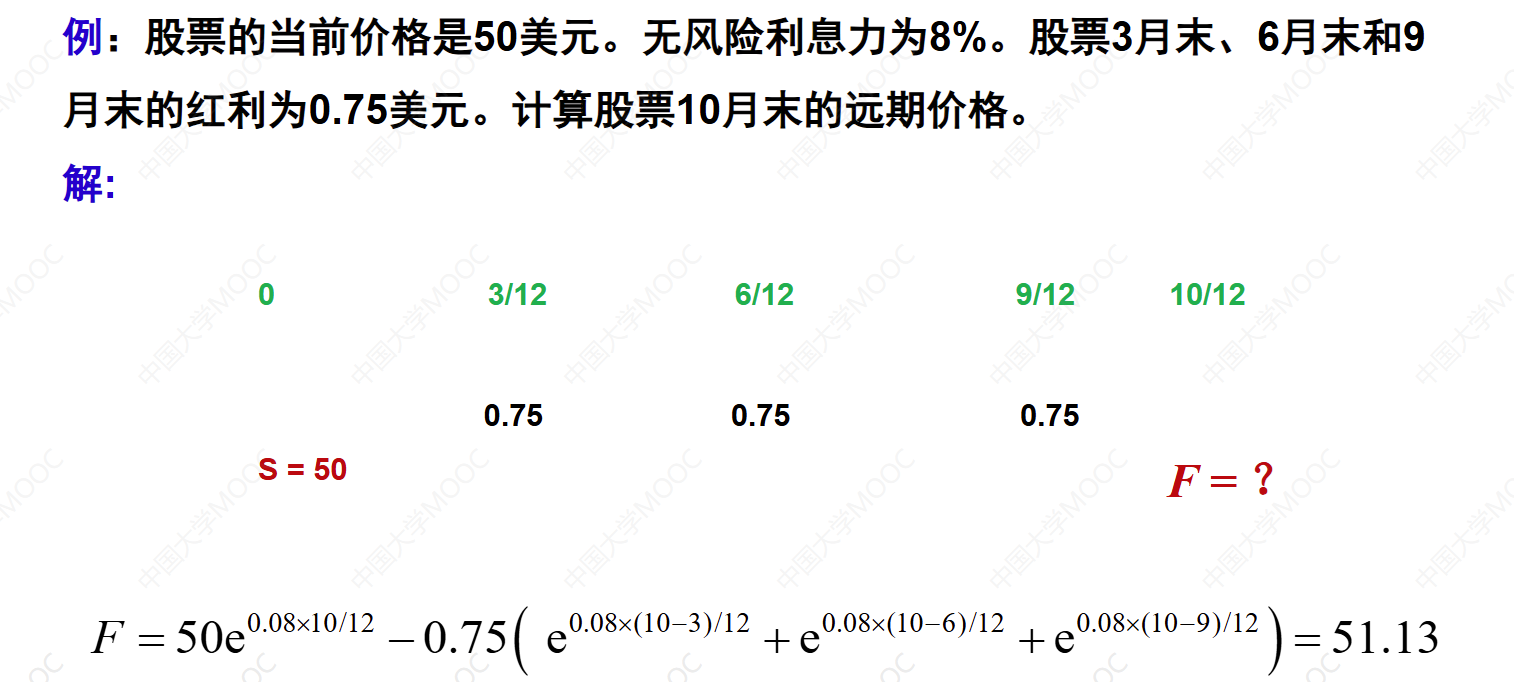
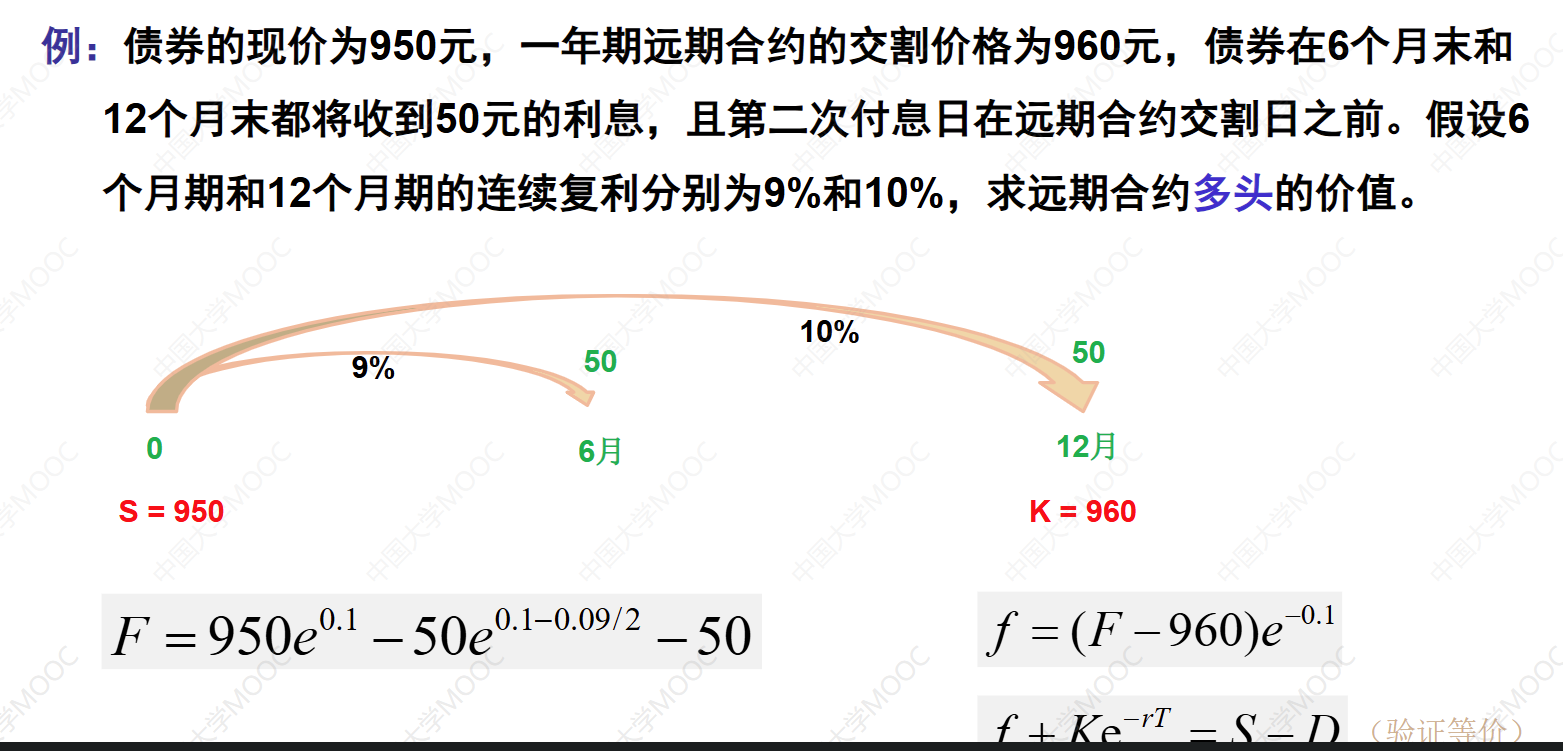
对于到期前产生已知收益的资产(如债券),其远期价格计算需要考虑未来收益的现值。假设资产在到期前产生的已知收益为 ,其远期价格计算如下:
这里, 是在远期合约到期前产生的收益的现值。
8.7 远期价格:产生连续收益的资产


对于到期前持续产生收益的资产(如股票或房地产),远期价格的计算考虑了在整个合同期间的现金流影响。假设在合同中 是在时间 产生的现金流,则远期价格的计算公式为:
在这里, 表示在到期日前所有现金流的现值总和。

8.8 远期利率协议的定价
本视频介绍了 远期利率协议(Forward Rate Agreement, FRA)的定价过程。远期利率协议是一种金融衍生工具,允许双方在未来的某个时间点以事先约定的利率进行资金借贷。这种工具常用于管理利率风险。
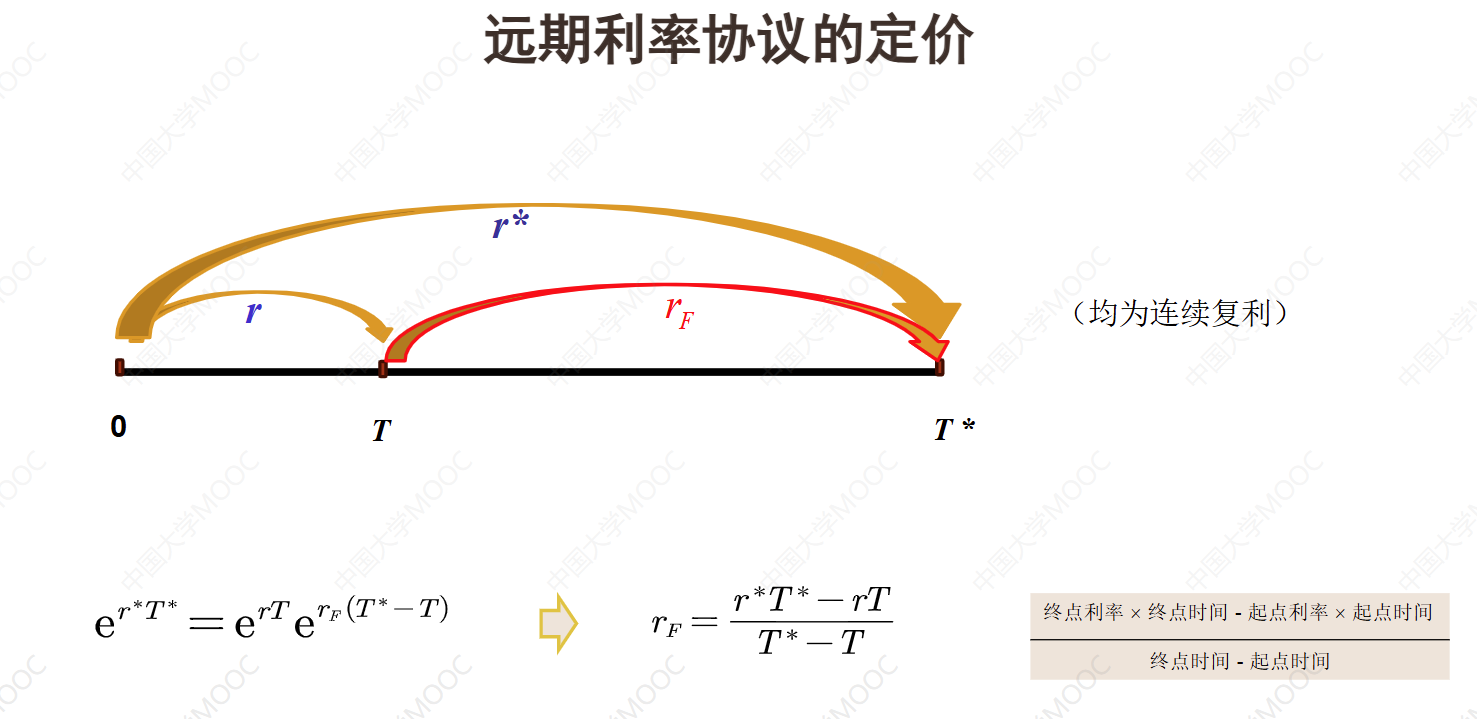
在计算远期利率时,通常会依据即期利率(Spot Rate)。即期利率是指在某个特定时间点的瞬时利率,它反映了市场对未来利率的预期。在根据即期利率计算远期利率时,有两种主要方法:
- 一次性累积到 T*:这种方法涉及将即期利率从当前时点累积到约定的未来时点 ,即在这一段时间内的收益率完全根据即期利率来计算。
- 先累积到 T,再按远期利率累积到 T*:这种方法首先将资金从当前时点累积到 ,然后再根据未来的远期利率累积到 。
这两种方法的累积值应该是相等的,即: 其中 是到时间 的即期利率, 是从 到 的远期利率, 是当前时点到远期开始的时间长度。
通过建立方程并求解,我们可以得到计算远期利率的表达式。该表达式的计算公式如下: 在这个公式中,分子是较长期限的即期利率 的累积值,减去较短期限的即期利率 的累积值,而分母是远期利率所属区间的长度 。
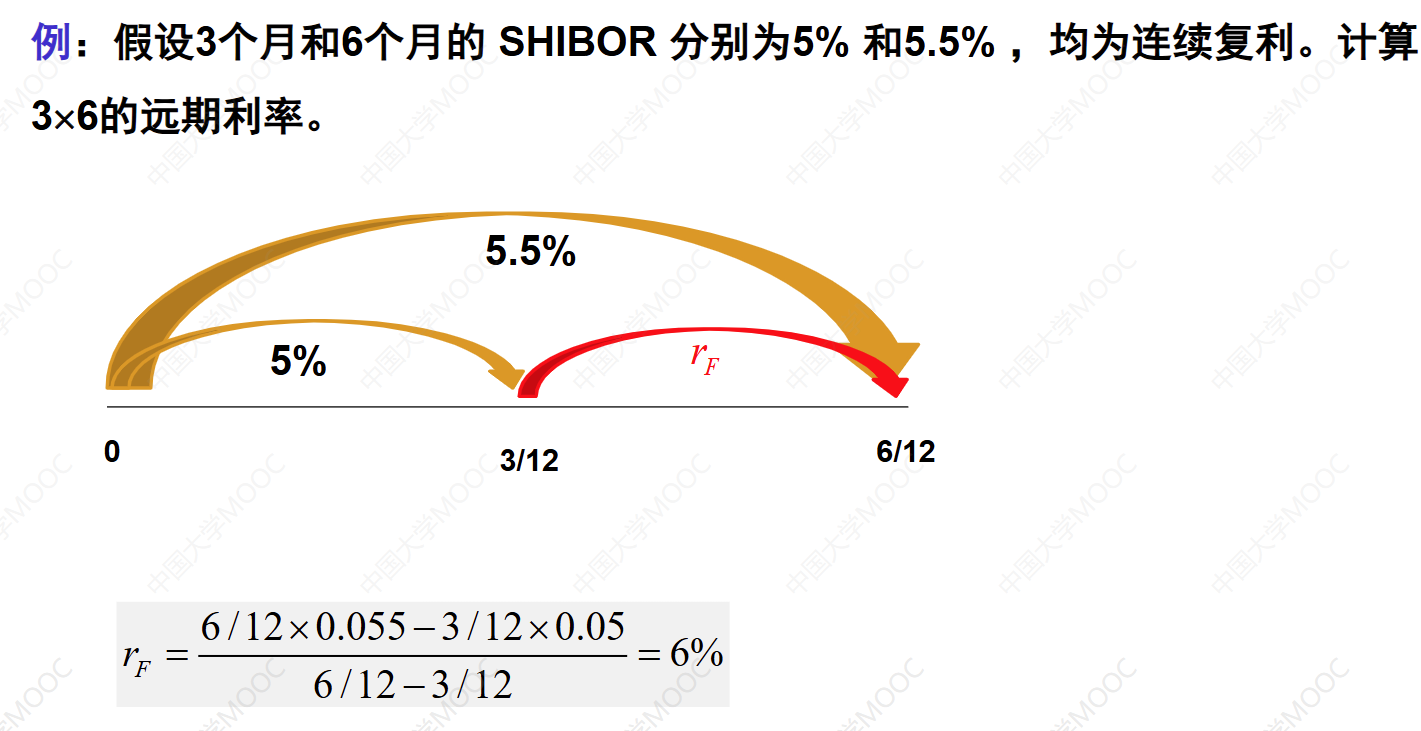
为了更好地理解,可以通过一个简单的例子来演示如何使用上述表达式计算远期利率。例如,假设即期利率为5%()和8%(),且时间长度分别为1年和2年,我们带入的运算过程会得出远期利率 的值。
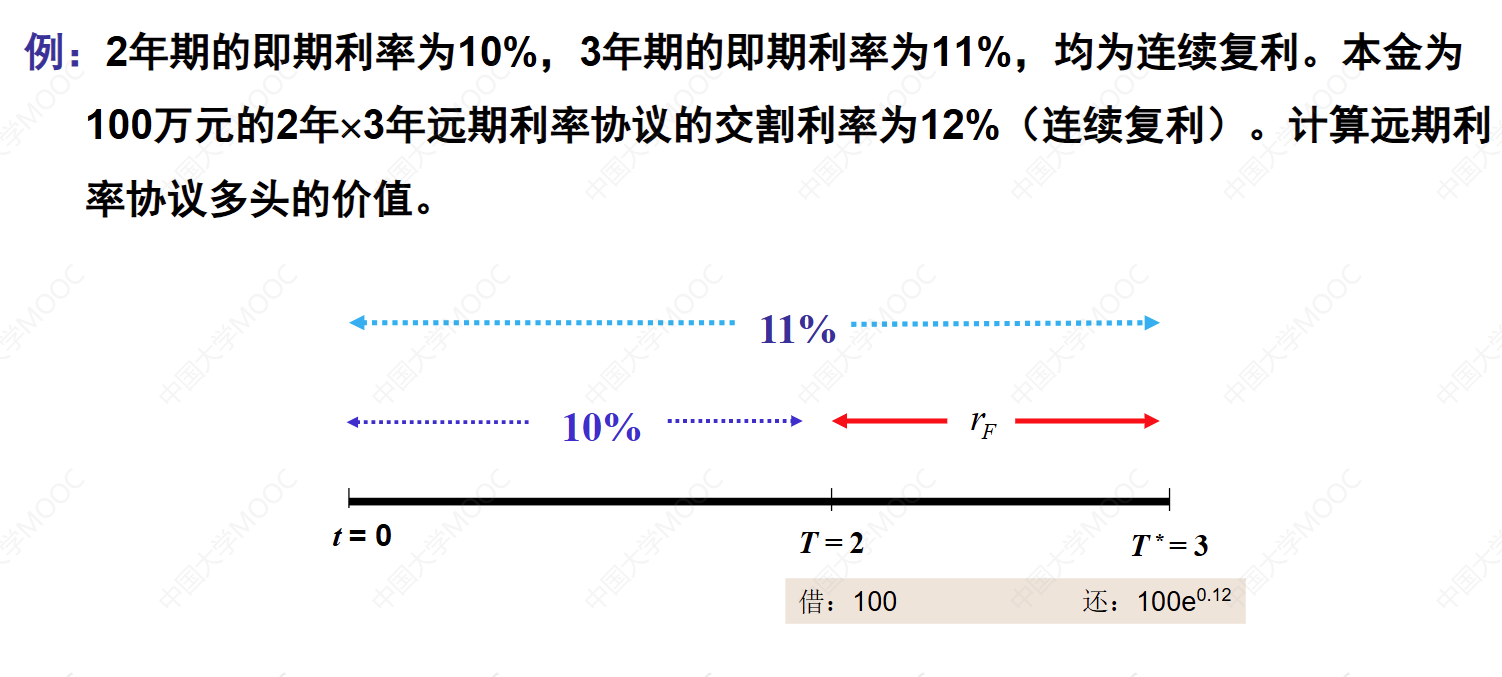
此外,视频中还介绍了远期利率协议多头的价值计算方法。具体包括:
- 借入资金的现值(PV):根据借入的名义本金和即期利率来计算未来现金流的现值。
- 偿还值的现值:即按照约定的远期利率将未来的现金流折现回现在的价值。
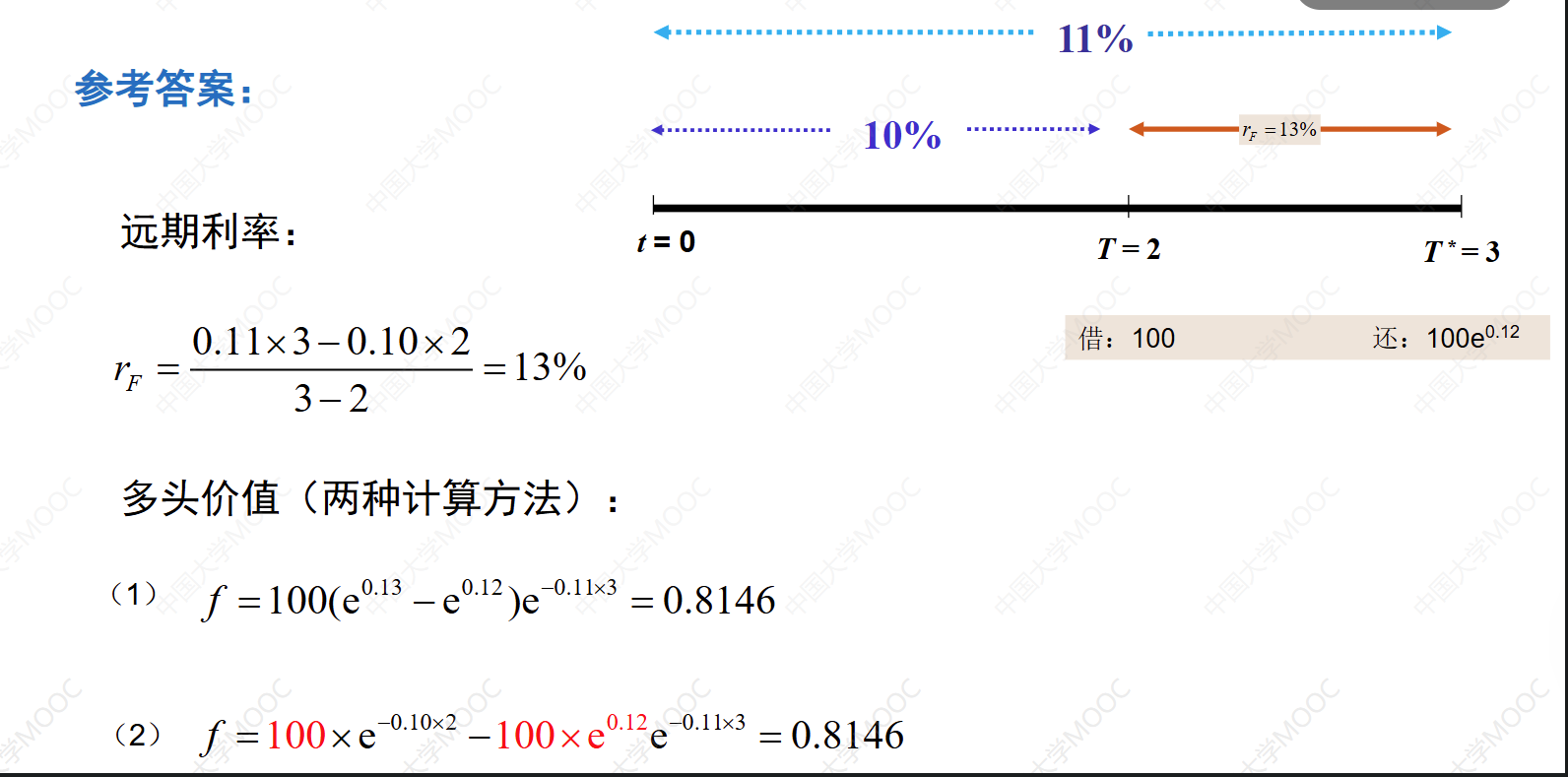
最后,视频给出了远期利率的计算结果为 13%(),合约多头的价值为 8146.51 元(PV)。这个价值是基于当前的市场条件和即期利率计算出来的,意味着在合约到期时,多头将从远期利率的变动中获益。
3个月和6个月的Shibor分别为2%和2.1%,均为连续复利(即用利息力表示)。计算3月末到6月末的远期利率为2.2%。
8.9 合成远期
合成远期(Synthetic Forward)是一种资产组合,其功能和投资效果与传统的远期合约相同。通过特定的金融工具组合,投资者可以在没有直接交易远期合约的情况下,实现类似的投资收益与风险管理。
1. 合成远期的构造
合成远期多头可以通过以下方法构造:
- 出售零息债券:零息债券是指定期支付本金而不支付利息的债务工具。通过出售这些债券,投资者能够获得当前的现金流。
- 购买股票:以现货价格购买股票,投资者就能够在未来获得股票的增值收益。
因此,合成远期多头的构造可以表示为:

通过这种方式,投资者不仅能够参与股价的上涨,还有效地锁定未来的收益。
| 远期多头 | 远期空头 |
|---|---|
| 出售零息债券,购买股票 | 出售股票,购买零息债券 |
| 远期=股票-零息债券 | 远期=-股票+零息债券 |
2. 合成远期的应用
合成远期多头策略可用于套利和套保:
套利:正向套利(先买后卖)、反向套利(先卖后买)
套保:正向套保(先买后卖)、反向套保(先卖后买)
2.1 套利
套利是利用市场之间的价格差异来获取无风险利润的策略。主要有两种形式:
-
正向套利(Forward Arbitrage):这种套利策略的基本思路是先在现货市场以低价格买入资产,然后在远期市场以高价格卖出该资产。具体步骤为:
- 在现货市场上以价格 买入一单位资产。
- 在远期市场以价格 卖出该单位资产,合约到期时获得 。
利润为:
-
反向套利(Reverse Arbitrage):这种套利策略先在现货市场卖空资产,然后在远期市场买入资产。具体步骤为:
- 在现货市场上卖空一单位资产,获得 的现金流。
- 在合约到期时,以远期价格 买回该单位资产。
利润为:

套利机会:价格价格>远期价格
套利方法:买入现货,卖出远期

交割价格大于远期价格,意味着资产的现价偏低,可以进行正向套利。
如果远期价格大于交割价格,意味着可以进行反向套利。
2.2 套保
套保(Hedging)是指投资者通过构建合成远期多头或空头来规避市场风险。
- 正向套保(Long Hedge):投资者在预期未来价格上涨时,使用合成远期多头来规避风险。具体操作为先购买资产并出售零息债券,以确保在合约到期时以未来的远期价格获得该资产。例如,如果预期未来价格将会超过当前价格,则通过运用合成远期多头来锁定当前价格,从而避免价格波动带来的风险。
- 反向套保(Short Hedge):投资者在持有现货资产的情况下,可能担心未来价格下跌。因此,可以通过合成远期空头来锁定价格,具体操作为先卖空现货并购买远期合约。这样可以在市场价格下跌的情况下获得保障。


3. 总结
合成远期作为一种有效的金融工具,使得投资者可以灵活地管理投资风险,无论是通过套利还是套保策略。理解合成远期的构造和应用,有助于投资者制定更为完善的市场策略,采取果断的行动来应对市场波动。
8.10 互换
本视频介绍了互换合约(Swap Contracts)的概念及其作用。互换合约是一种金融衍生工具,允许两个投资者之间交换现金流,通常是基于不同的基础资产或利率结构,从而实现风险管理或提高资金使用效率。
互换合约中隐含着一个远期利率协议。✔
如果将若干个远期合约合并成一个合约,可以形成一个互换合约。
1. 互换合约的基本概念
与远期合约不同,远期合约通常只能对一笔单一现金流的风险进行管理,而互换合约能够针对一系列现金流进行更为复杂的风险管理。这使得互换合约在金融市场中占据了重要的位置,特别在利率、外汇和商品交易等领域。
远期合约:只交换一次现金流。
现实:许多交易是重复发生的,如:农场主每年出售小麦
互换合约:交换一系列现金流。由多个远期合约组合而成。
互换的作用:对一系列具有不确定性的现金流进行风险管理。
2. 互换合约的主要类型
互换合约的类型主要包括:
- 利率互换(Interest Rate Swap):投资者交换各自支付的一系列利息现金流,通常是一方支付固定利息,另一方支付浮动利息(如与LIBOR挂钩的利率)。
- 货币互换(Currency Swap):两方在约定的时间内交换不同货币的本金和利息支付,以便管理外汇风险。
- 商品互换(Commodity Swap):涉及商品价格的现金流交换,常用于对冲商品价格波动的风险,如石油或金属。
3. 互换合约的示例
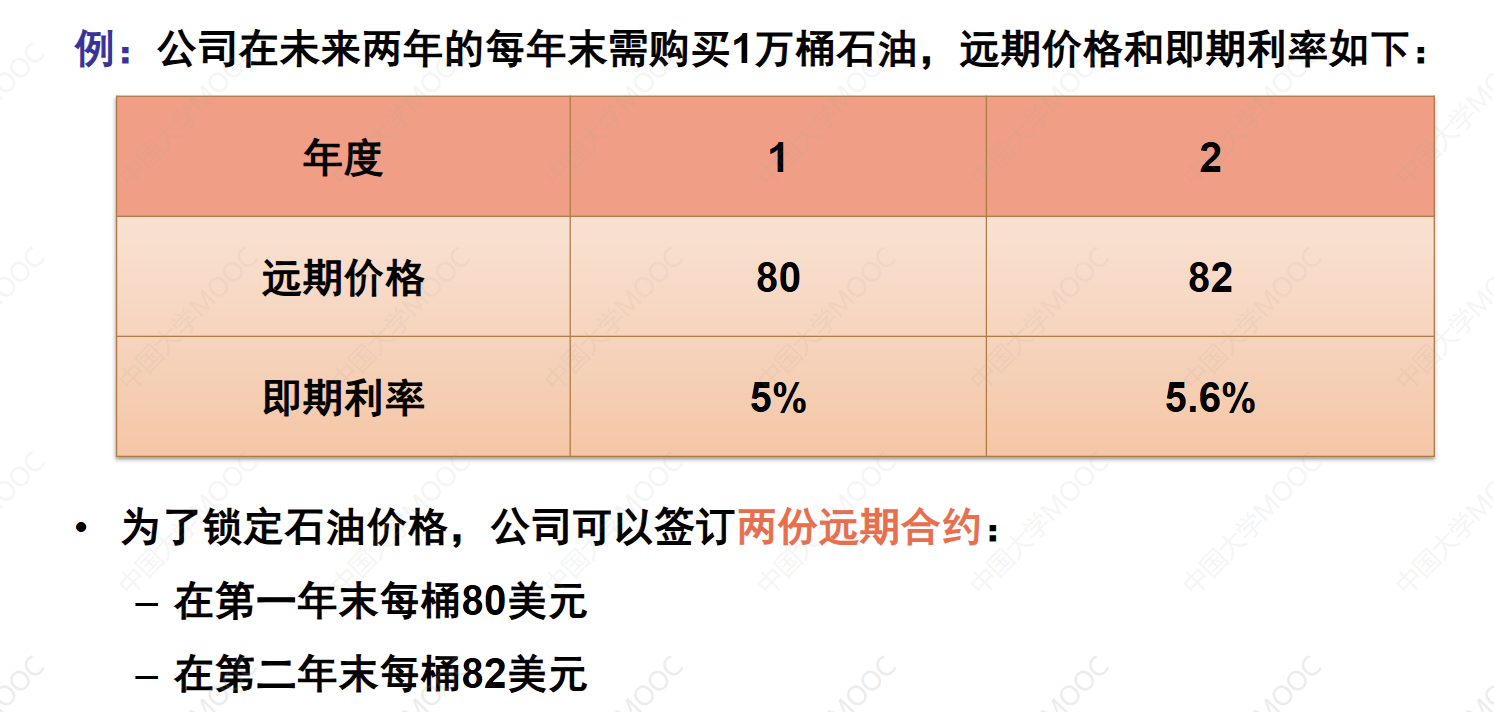
通过一个实例来说明互换合约如何帮助规避石油价格上升的风险。例如,一家航空公司可能预期未来石油价格会大幅上升,从而增加其运营成本。为了规避这种风险,航空公司可以与另一方进行商品互换,约定在未来一段时间内以固定价格购买石油。
在这种情况下,航空公司每月支付固定的价格,而另一方则按照市场浮动价格相应支付。如果市场价格超过固定价格,航空公司将从中受益;如果市场价格低于固定价格,航空公司则需支付更高的成本,但至少可以保证其成本不会过高。
4. 互换合约的定价
互换合约的定价通常涉及到未来现金流的现值计算。互换合约的价格是基于市场的远期价格进行计算的,具体过程如下:
-
确定远期利率:远期合约的价格可以通过观察市场利率及其他相关指标来得出。
-
计算现值:使用无风险利率对未来的现金流进行折现,公式为:
其中, 是未来现金流的现值, 是第 期的现金流, 是无风险利率, 是总的现金流期数。
-
隐含协议关系:进一步地,互换合约可以被视为由一系列远期合约的组合构成,其中某些远期合约是远期利率协议(FRA)。这种关联使得互换合约在进行现金流管理时具有更大灵活性。
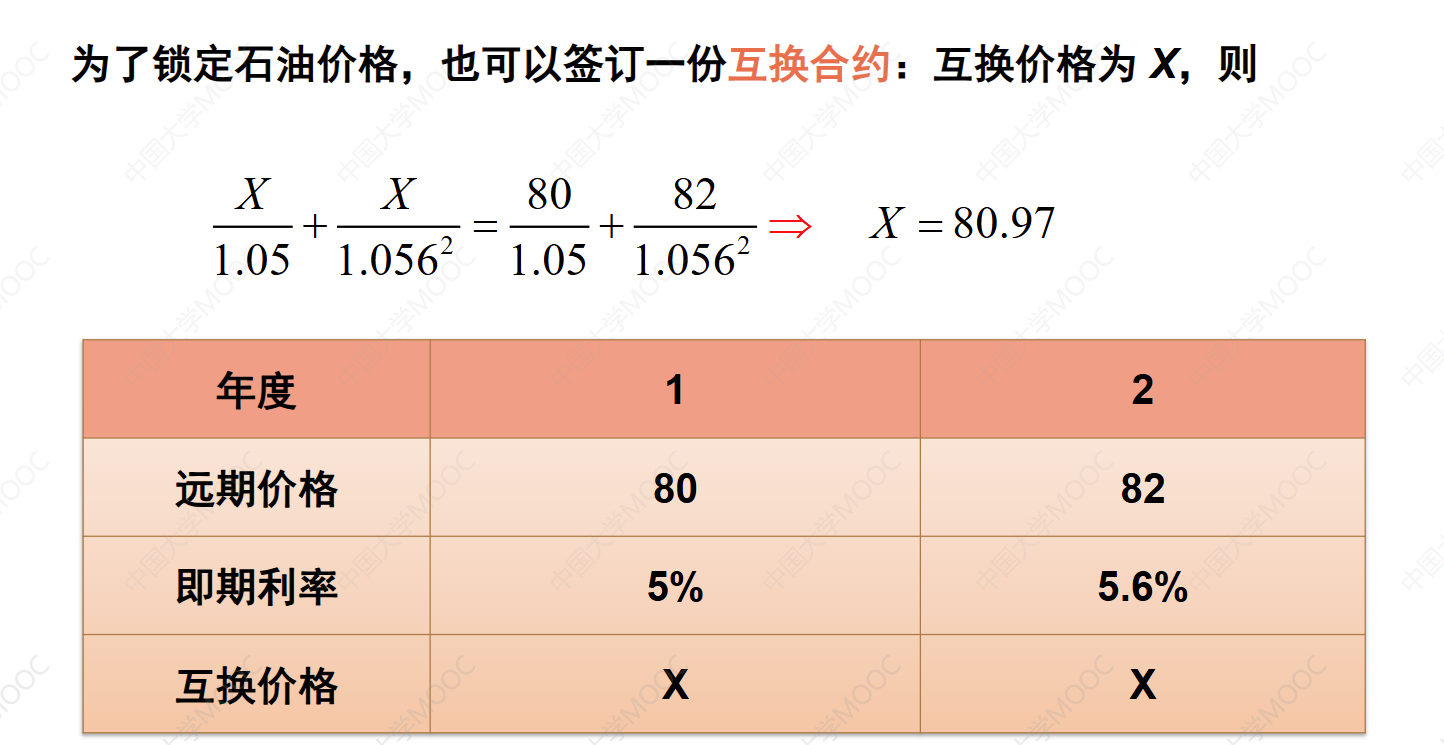
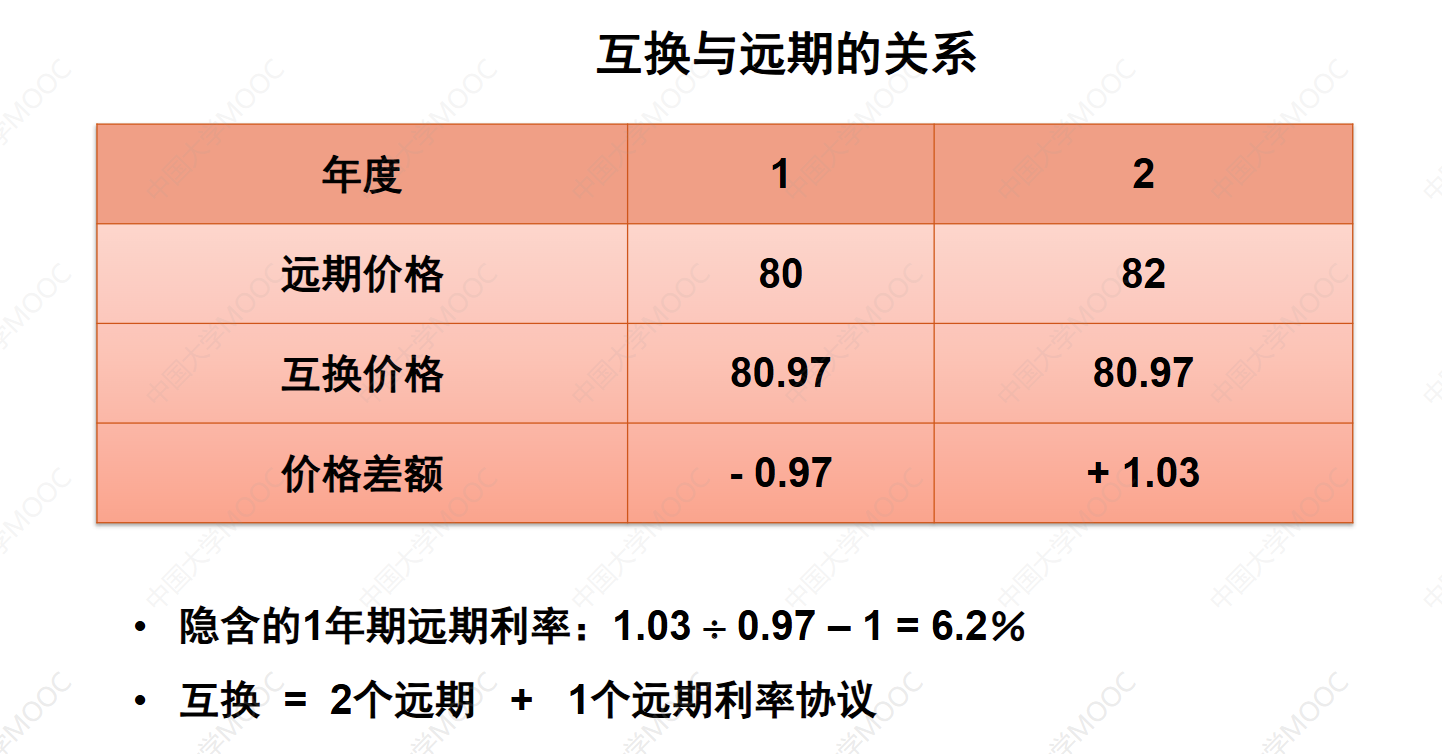
理解:第一年末投资0.97,第二年末获得1.03
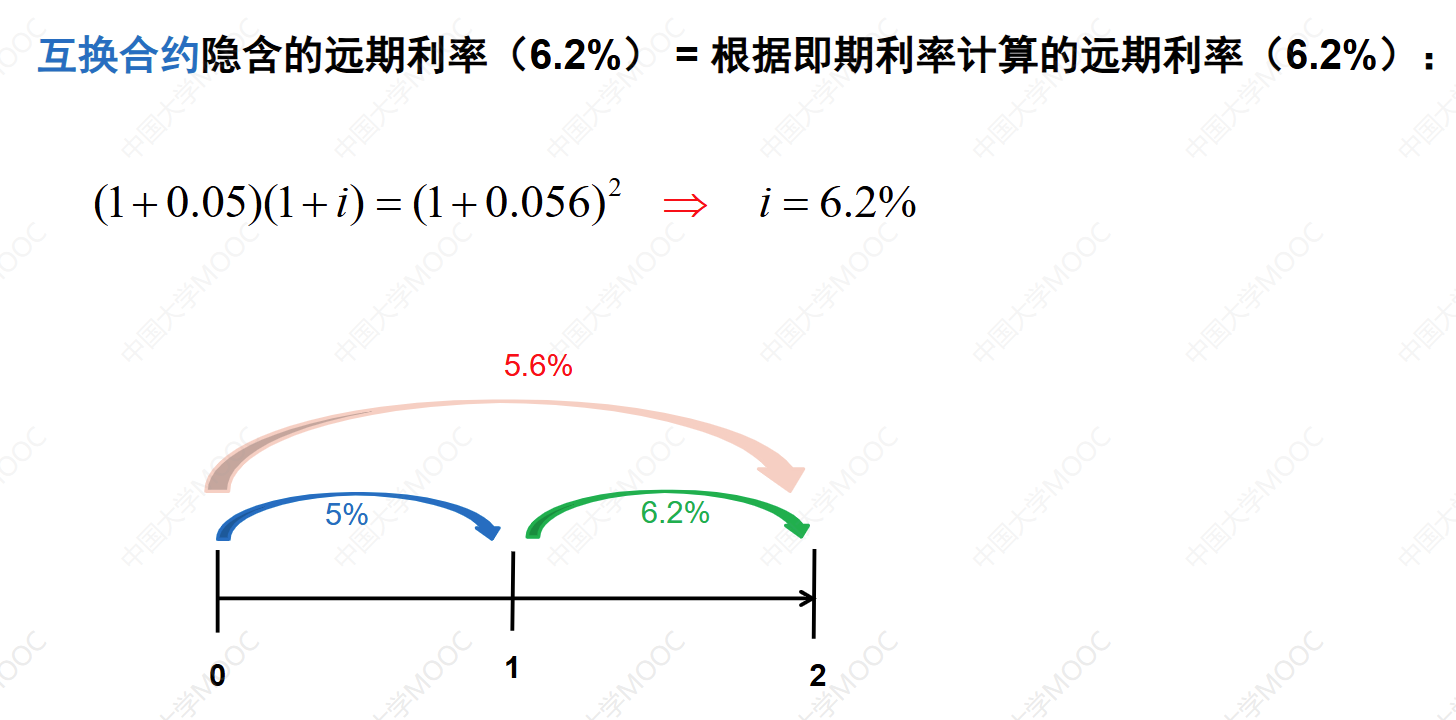
互换与远期的关系:
- 互换等价于若干个远期,其中一个是远期利率协议。
- 远期的初始价值为零,故互换的初始价值也为零。
- 合约签订以后,当市场条件发生变化,互换的价值将不再等于零。
5. 互换合约的动态价值
互换合约的价值在合约签订后会随着市场条件的变化而变化。这种变化主要受以下因素的影响:
- 市场利率的波动;
- 基础资产价格的波动(对于商品互换而言);
- 信用风险和流动性风险等市场条件。
在合约有效期内,投资者可能需要重新评估互换合约的价值,以确保其风险管理策略的有效性。互换合约的市场价值通常计算为:
其中, 是互换的净现值, 是固定现金流的现值, 是浮动现金流的现值。
6. 总结
互换合约是管理多重现金流风险的有效工具,通过合成不同的现金流组合,投资者能够灵活地应对市场波动,提高自身的资金使用效率。此外,理解互换合约相关市场利率和价格的动态变化,
8.11 利率互换及其定价
利率互换(Interest Rate Swap)是一种金融衍生工具,主要用于交易双方在未来一定期限内交换现金流的合约。该合约涉及相同的货币和名义本金,其中一方的现金流根据浮动利率计算,另一方的现金流则根据固定利率计算。利率互换的主要目的是帮助参与方管理利率风险,并优化财务结构。
1. 利率互换的基本结构
在利率互换中,交互的现金流基于以下两个要素:
-
固定利率现金流:一方同意支付基于预设的固定利率(例如 4%)计算出的现金流,现金流的计算公式为:
-
浮动利率现金流:另一方则根据市场浮动利率(通常与LIBOR或其他基准利率挂钩)计算其现金流,浮动现金流的计算公式为:
2. 利率互换的目的
通过利率互换,参与方能够有效地管理利率风险。具体来说:
- 对冲风险:例如,一家拥有浮动利率贷款的企业可能希望对冲未来利率上涨的风险,因此可以与另一家拥有固定利率贷款的机构进行互换。
- 优化财务结构:通过利率互换,企业可以根据市场状况和自身财务状况,选择最合适的利率结构,使得其整体财务成本更低或风险更小。
3. 利率互换的示例
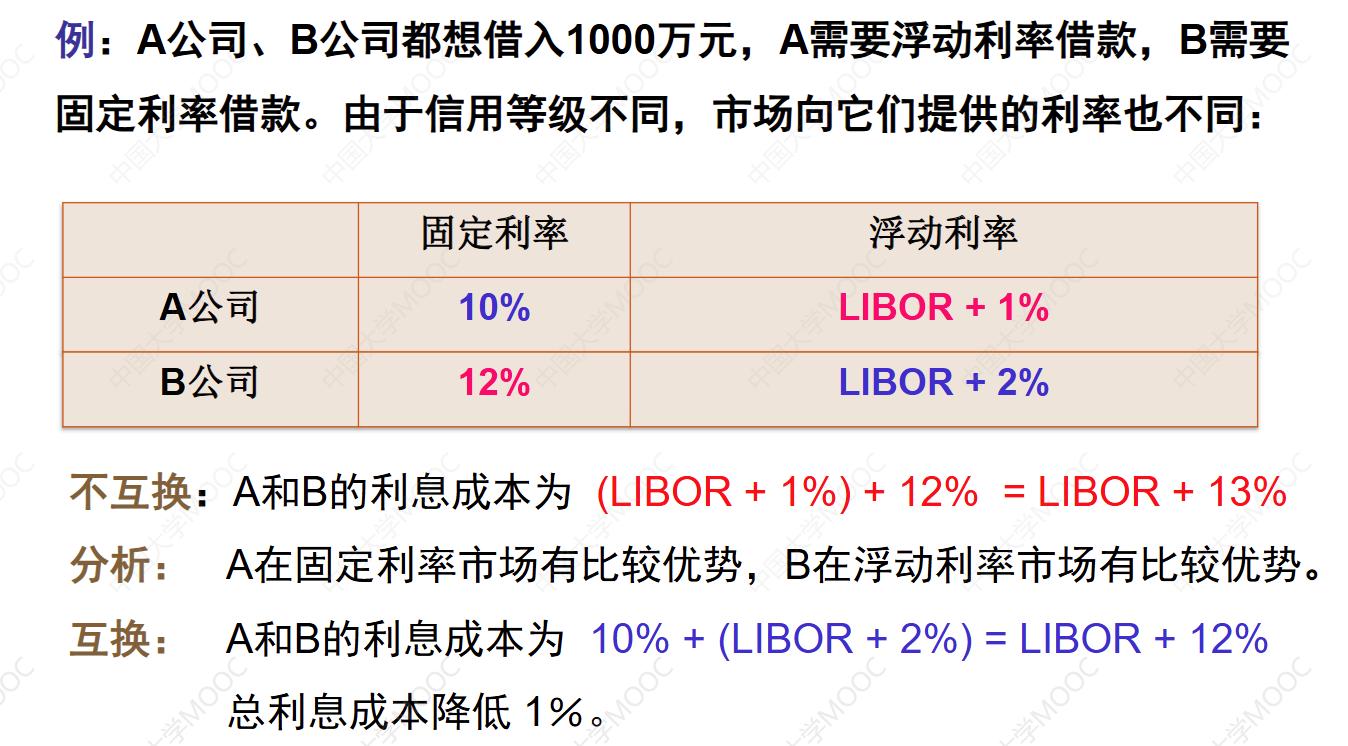
假设银行A和银行B进行利率互换:
- 银行A持有一个名义本金为的浮动利率贷款,利率基于3个月LIBOR。
- 银行B持有一个同样名义本金的固定利率贷款,固定利率为4%。
在利率互换中,银行A支付浮动利率现金流,而银行B支付固定利率现金流。通过互换,银行A能够获得稳定的支付,而银行B则能够享受浮动利率带来的潜在利率降低的好处。
4. 利率互换的定价

利率互换的定价过程核心是确定固定利率,这个固定利率需使得互换的现值相等,从而使得双方在合同签订时的现金流现值相等。
假设互换的现金流由未来个周期组成,固定利率需要通过浮动利率的加权平均来计算。
可使用以下公式进行计算:
其中, 为第个周期的浮动利率,为折现因子,折现因子的计算公式为:
这里的是每个期间的利率。
5. 计算示例
例:1年期、2年期和3年期的即期利率(年有效利率)分别为5%、5.5%、6%。在一个3年期的利率互换合约中,每年互换一次利息,计算互换利率是多少。
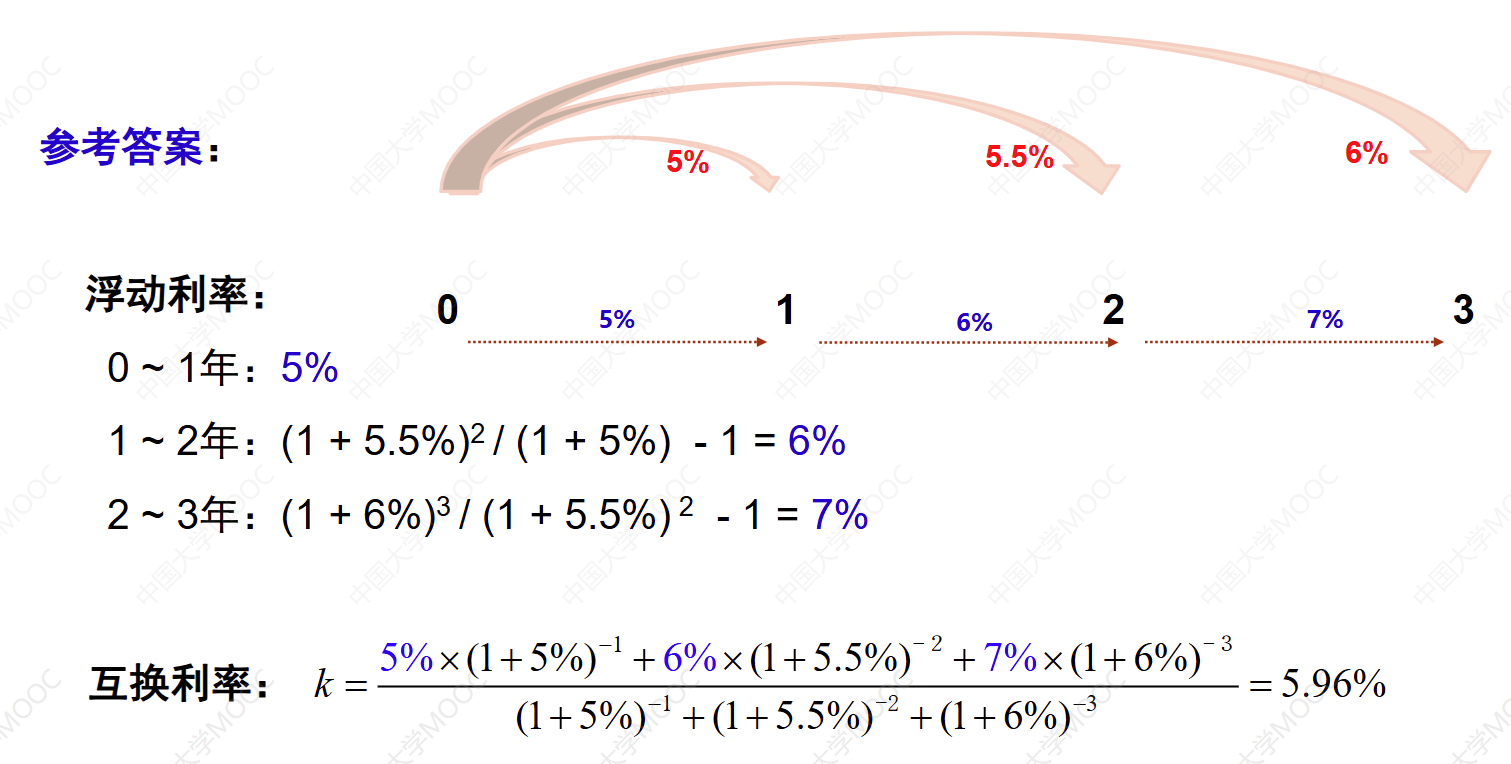
假设3月、6月、9月、12月的Shibor分别为1.1%,1.2%,1.3%,1.4%,均为连续复利(即用利息力表示)。交易双方约定,每3个月交换一次利息,名义本金为100万元。计算互换利率为1.4%。
6. 总结
利率互换为金融市场参与者提供了一种管理利率风险的重要工具,通过固定和浮动利率现金流的交换,允许双方在面对利率波动时进行有效的风险对冲。通过上述示例及计算过程,我们可以更清楚地理解利率互换的构造、定价及其在实际操作中的应用。
7. 利率互换的优缺点
如同任何金融工具,利率互换也有其优缺点:
优点:
- 风险管理:参与各方能够有效管理未来利率波动带来的风险,从而稳定其财务成本。
- 成本效益:企业可以通过互换降低融资成本,尤其是在强烈不确定的利率环境下。
- 灵活性:利率互换可以根据不同的需求和状况定制,允许企业实现更复杂的财务战略。
缺点:
- 信用风险:如果一方无法履行其现金流支付义务,另一方将面临信用风险。
- 流动性风险:由于利率互换通常是场外交易(OTC),因此在某些情况下可能面临流动性约束。
- 市场风险:市场利率的波动会直接影响到互换合约的市场价值,参与者需时刻监控市场情况。
8. 结论
综上所述,利率互换是一种强大的金融工具,其具有有效管理利率风险的能力,同时也存在如信用风险和流动性风险等潜在挑战。投资者和企业在使用利率互换时,需全面评估自身的风险承受能力和市场环境,充分利用这一工具以优化财务表现与风险控制。
对于金融学的学生和从业者,深入理解利率互换的操作原理、定价机制及其在金融市场中的作用,将为未来在金融行业的发展奠定坚实的基础。
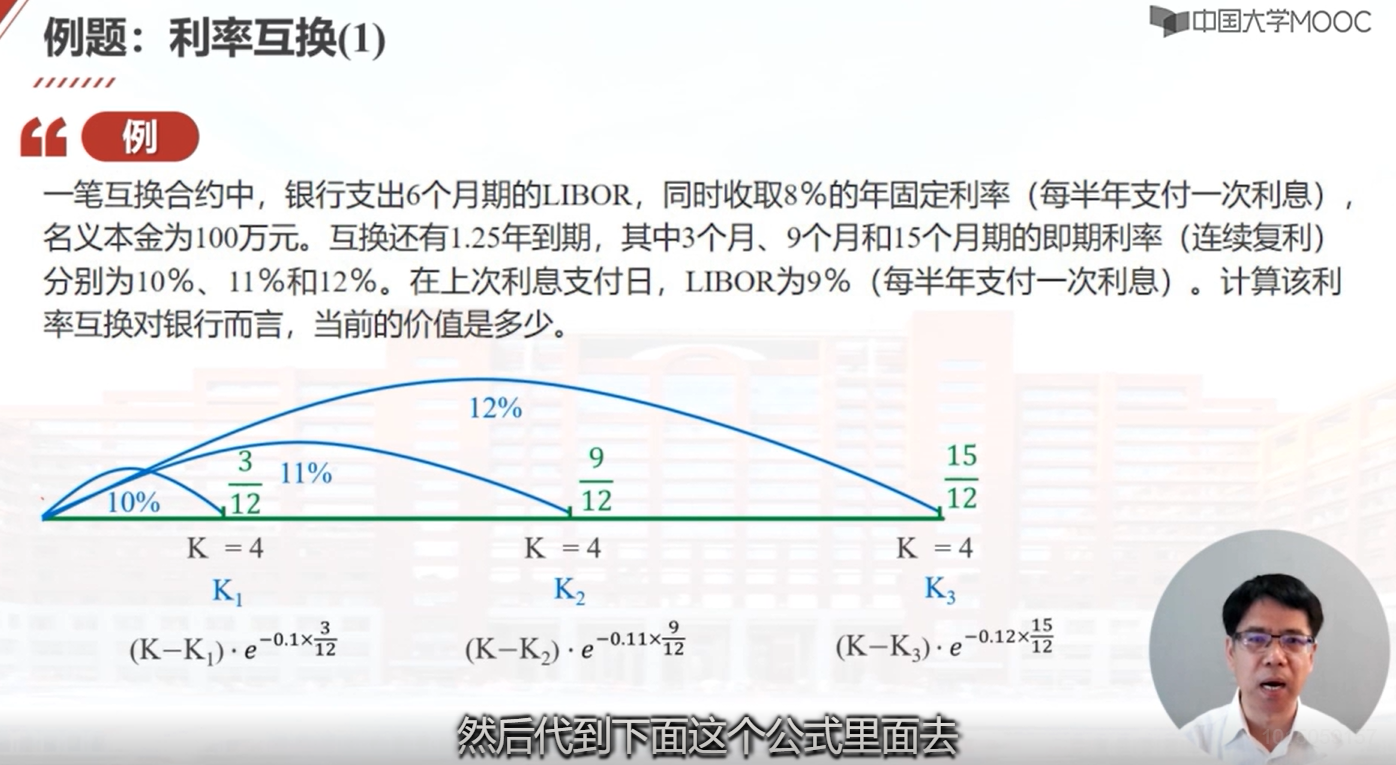
8.12 例题:利率互换
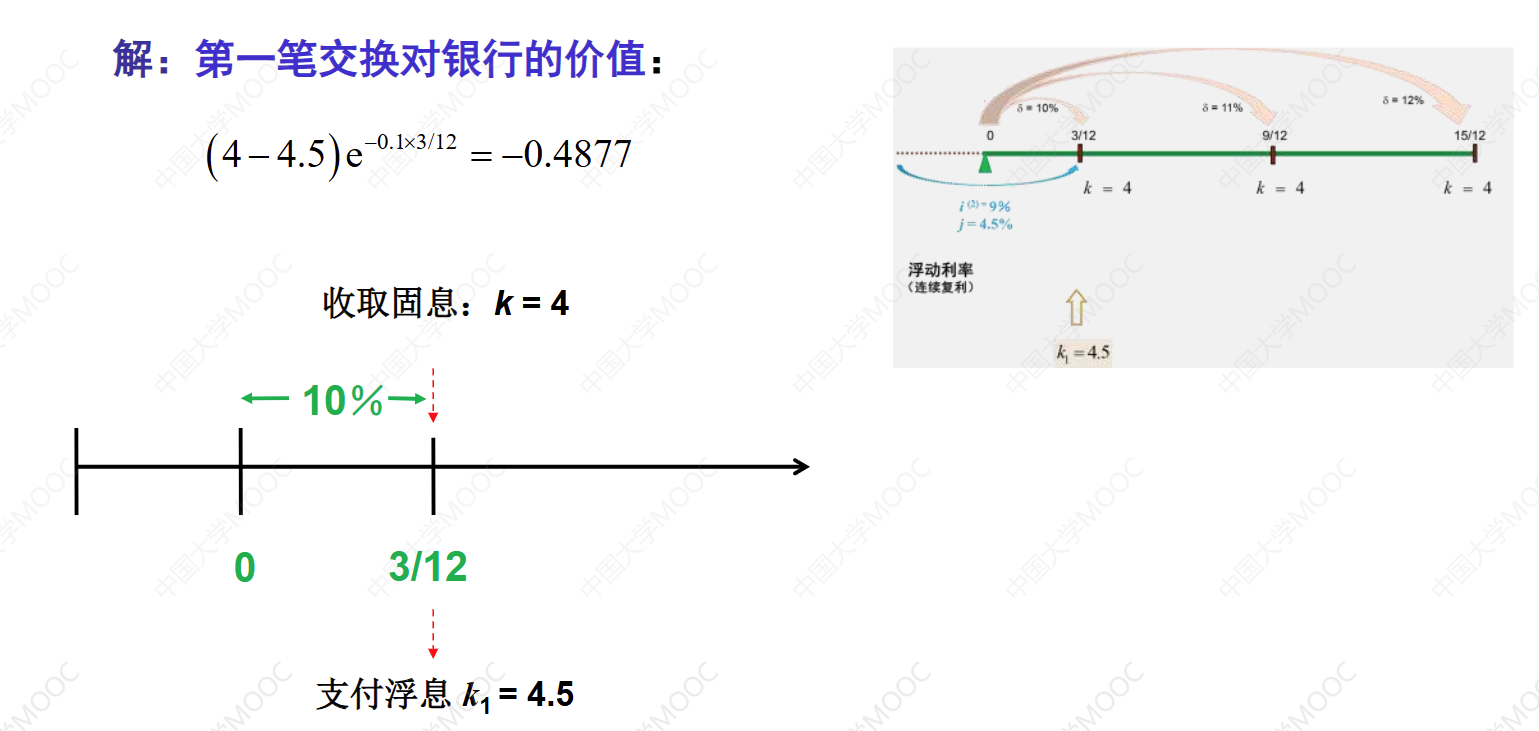
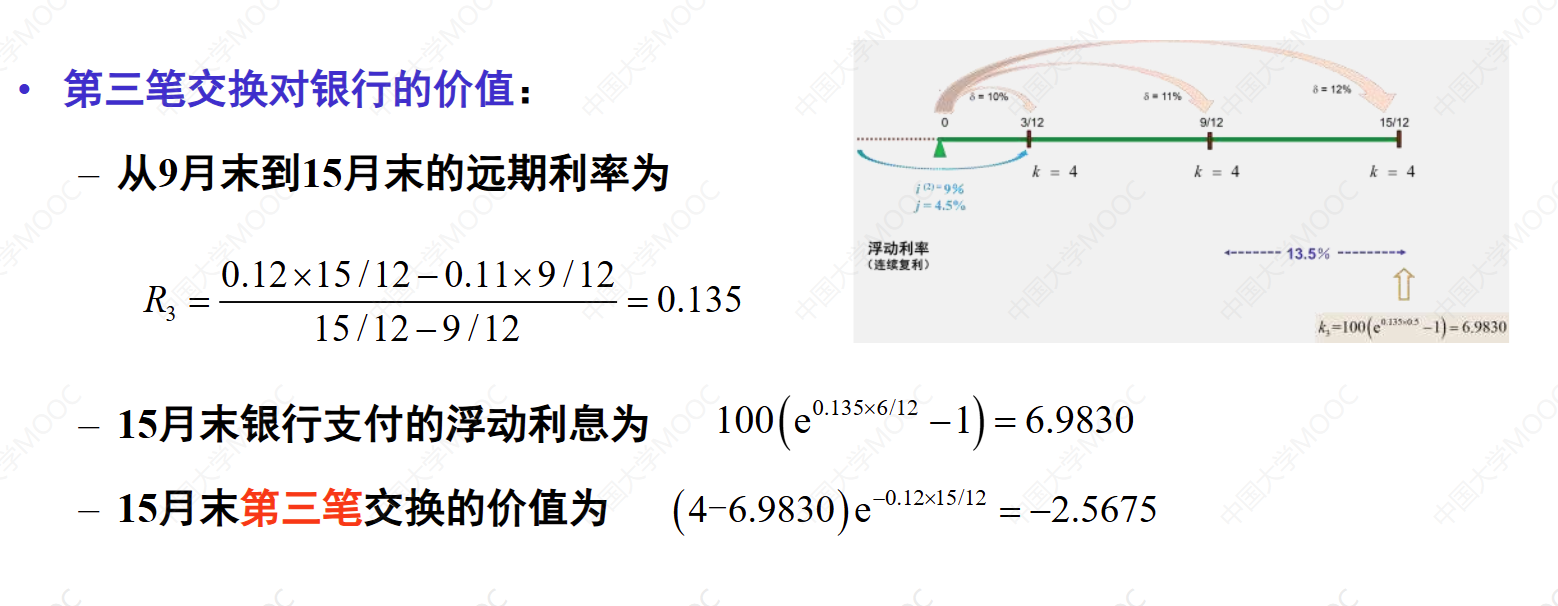
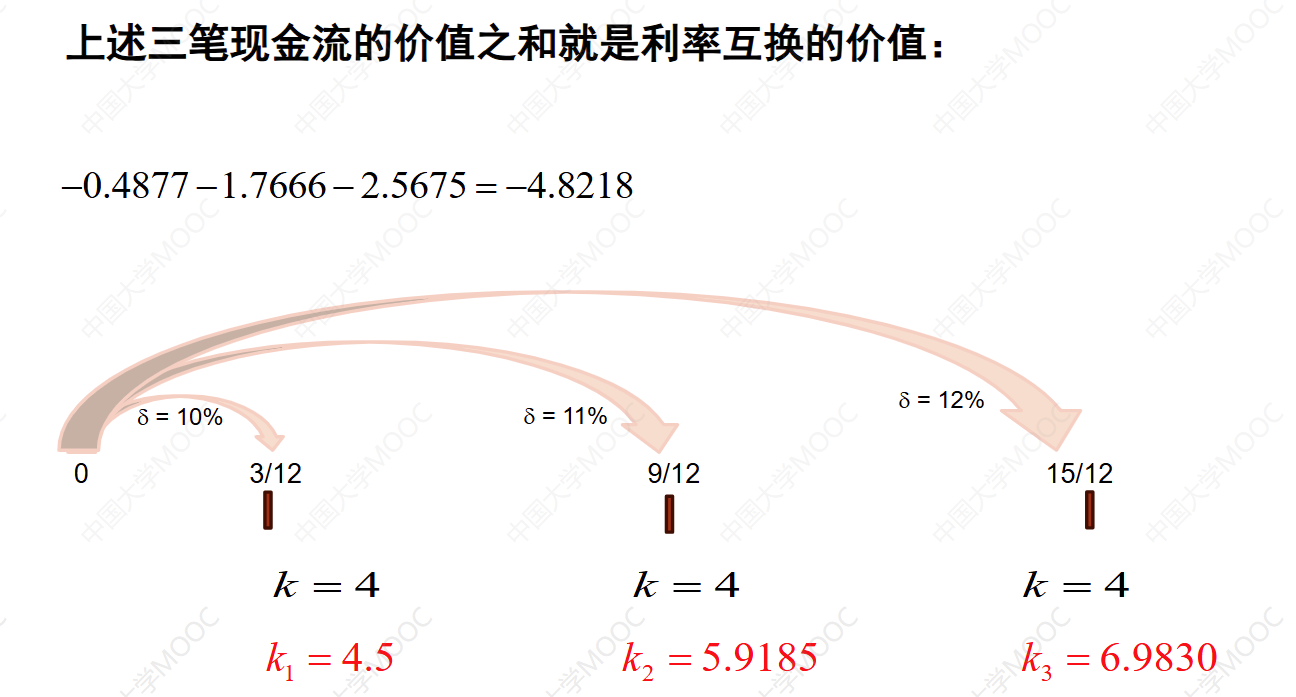
这个教学视频介绍了利率互换的例子。银行支出6个月的LIBOR,收到8%的年固定利率。每半年支付一次利息,固定利率为4%。名义本金为100万,每半年收到4万元的固定利息。互换还有1.25年到期,其中3个月、9个月和15个月的即期利率分别为10%、11%和12%。根据已知条件,计算了互换对银行的价值。银行收到的固定利息为4万元,支出的浮动利息为4.5万元、5.9185万元和6.983万元。将这些价值折现到时间零点,计算出互换对银行的价值为负4.8218万元。另一种解法是将银行收到的固定利息理解为购买了一种固定利率债券,价值为97.09812万元。银行支付的浮动利息理解为出售了一种浮动利率债券,价值为101.91989万元。两种债券相减得到互换对银行的价值为负4.8218万元。

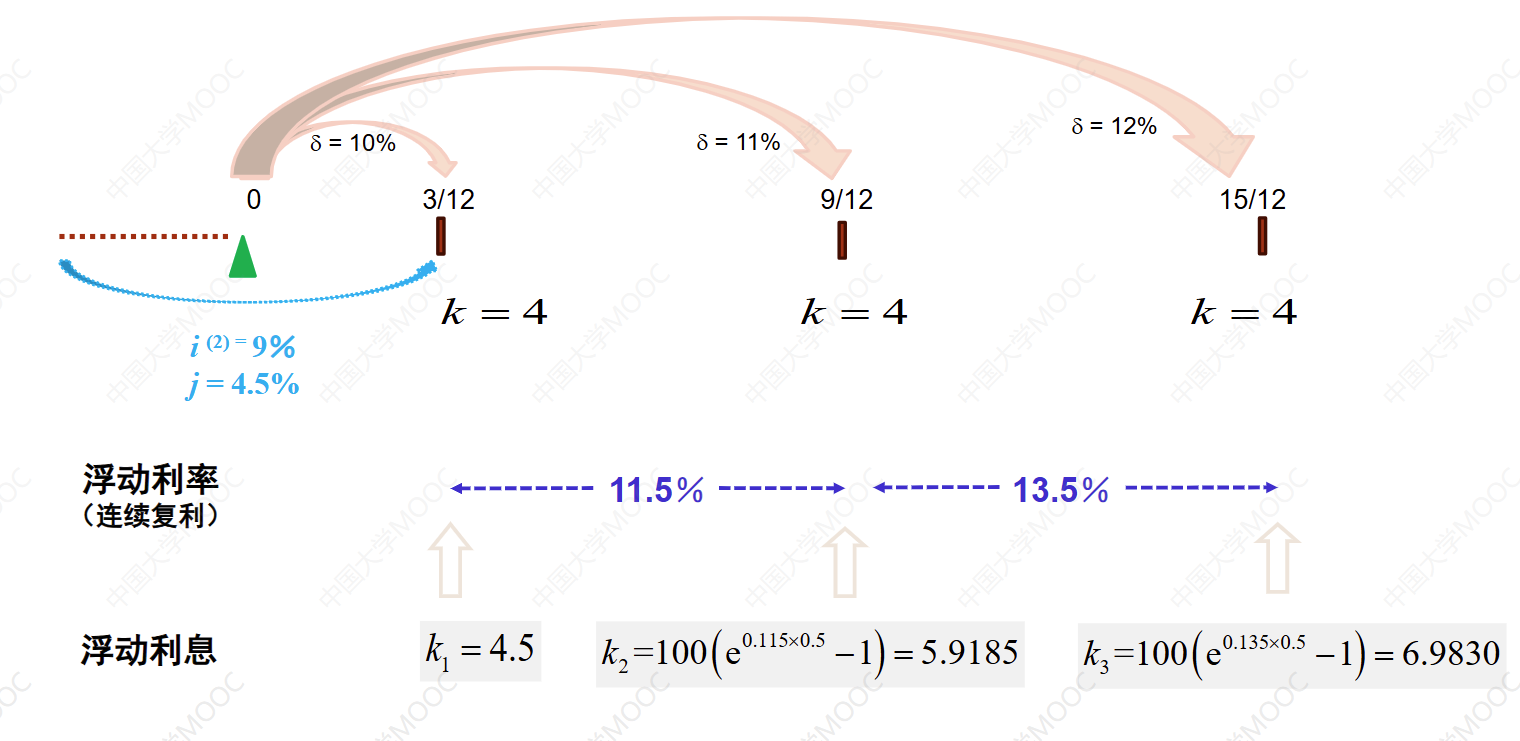


【7】银行在一个2年期的利率互换合约中,支付浮动利率,收取固定利率,每半年支付一次利息,名义本金为1000万元。已知6个月、12个月和18个月和24个月期的即期利率(连续复利)分别为6%、6.5%和7%和7.5%。计算银行在该互换合约中收到的固定利率(连续复利)是多少?
【7】 固定利率7.45%
【8】假设3个月和6个月的 LIBOR 分别为4% 和4.1% ,均为连续复利。远期合约的名义本金为100万美元,从3个月末到6个月末的交割利率为4.2%(连续复利)。计算该远期合约多头的价值。
【8】 远期合约多头的价值为0