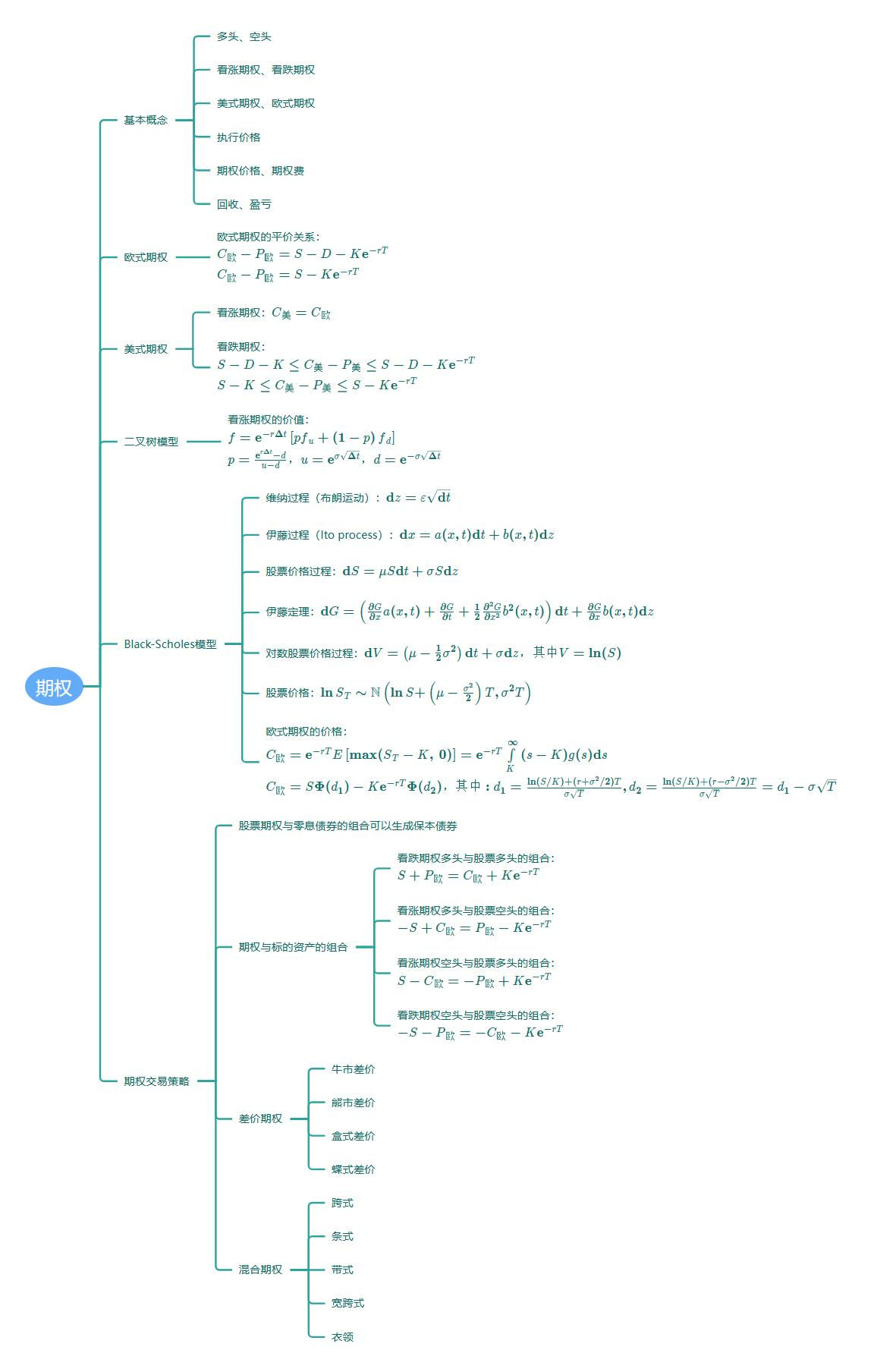
期权

• 学习目标
• 思维导图
• 9.1 期权的基本概念
  • 1. 期权定义
  • 2. 期权的参与者
  • 3. 重要术语
  • 4. 期权的类型
  • 5. 期权的行权方式
  • 6. 期权的内在价值与时间价值
  • 图示说明
• 9.2 期权的回收和盈亏
  • 1. 回收与盈亏的基本概念
  • 2. 看涨期权的回收和盈亏
  • 3. 看跌期权的回收和盈亏
  • 4. 盈亏图的分析
  • 图示说明
• 9.3 欧式期权的平价关系
  • 1. 欧式期权的平价关系
  • 2. 平价关系的证明
  • 3. 远期价格与期权价值关系
• 9.4 美式期权的价格关系
  • 1. 美式期权的定义与特点
  • 2. 美式期权与欧式期权的价格关系
  • 3. 美式看涨期权的提前执行
  • 4. 美式看跌期权的提前执行
  • 5. 美式期权的价格关系
  • 6. 小结
• 9.5 期权定价基本原理
  • 1. 无套利定价原理
  • 2. 复制技术实例
  • 3. 风险中性定价法
  • 4. 小结与实例
• 9.6 单步二叉树模型
• 9.7 单步二叉树模型
• 9.8 多步二叉树模型
• 9.9 例题：欧式看涨期权的多步二叉树模型
  • 使用二叉树模型计算欧式看涨期权的价格Python代码实现
  • 使用二叉树模型计算欧式看跌期权的价格Python代码实现
• 9.10 例题：美式看跌期权的多步二叉树模型
• 9.11 Black-Scholes模型简介
  • B-S定价模型计算期权价值的Python实现

学习目标

掌握期权的基本概念，期权定价的无套利定价原理和风险中性原理；理解欧式期权的平价公式；可以应用二叉树模型计算期权的价值。

思维导图

期权PPT

9.1 期权的基本概念

期权是一种金融衍生工具，赋予期权持有人在特定日期或之前以约定价格买入或卖出标的资产的权利，但不承担必须执行的义务。它通常用于对冲风险或进行投机活动。以下是期权的一些基本概念：

1. 期权定义

• 期权：期权是买卖资产的权利，具有规定的期限、约定的价格以及一定的数量。按照约定，期权持有人可以选择在到期日或之前行使其权利。

2. 期权的参与者

• 期权多头：期权的买方或持有人，他们支付期权费以获得权利。如果选择行使该权利，期权多头可能会获得利润。
• 期权空头：期权的卖方，他们收取期权费，并根据买方的要求履行义务。期权空头在某些情况下可能面临潜在的损失，尤其是在市场价格显著变动时。

3. 重要术语

• 执行价格（Strike Price）：期权合约中规定的买卖资产的价格，即在行权时所使用的价格。
• 期权费（Option Premium）：期权持为了获得该权利向期权卖方支付的费用。这是期权合约的实际价格，通常由多个因素决定，包括标的资产的价格、到期时间、市场波动率等。

4. 期权的类型

• 看涨期权（Call Option）：赋予持有人以执行价格买入标的资产的权利。例如，假设在12月20日，投资者购买了一份看涨期权，可以以每股20元的价格购买1万股某公司的股票。如果资产价格上涨，则该看涨期权的价值可能随着标的资产价格的大幅提升而增大。
• 看跌期权（Put Option）：赋予持有人以执行价格卖出标的资产的权利。例如，在同样的日期，投资者也可以购买一份看跌期权，允许他以每股30元的价格出售1万股某公司的股票。如果资产价格下跌得越多，看跌期权的价值也将随之增加。

5. 期权的行权方式

• 欧式期权：只能在到期日行使权利。这意味着期权持有人必须在到期日当天决定是否行使权利。
• 美式期权：允许在到期前的任何日期行使期权。这种灵活性通常使得美式期权的价值高于或至少等于相应的欧式期权。

注意：美式期权的价值通常不低于相应欧式期权的价值，这是因为美式期权在时间上提供了更多的灵活性。

6. 期权的内在价值与时间价值

根据市场价格和执行价格的关系，期权可以划分为以下几种类型：

• 实值期权（In-the-Money, ITM）：当市场价格大于执行价格时，看涨期权为实值，看跌期权为实值。如看涨期权的执行价格为20元，而当前市场价格为25元，则该看涨期权为实值。
• 虚值期权（Out-of-the-Money, OTM）：当市场价格小于执行价格时，看涨期权为虚值，看跌期权为虚值。例如，如果看涨期权的执行价格为20元而市场价格为15元，则该看涨期权为虚值。
• 平价期权（At-the-Money, ATM）：当市场价格等于执行价格时，无论是看涨期权还是看跌期权都被视为平价。例如，看涨期权和市场价格均为20元。

以看跌期权为例，状态与看涨期权的定义相反：

• 看跌期权为实值：当市场价格低于执行价格时（如执行价格为30元，市场价格为25元）。
• 看跌期权为虚值：当市场价格高于执行价格时（如执行价格为30元，市场价格为35元）。
• 看跌期权为平价：当市场价格等于执行价格时（如执行价格和市场价格均为30元）。

图示说明

这张图示很好地描绘了期权的三种状态，帮助我们理解不同情况下的价值变化。

9.2 期权的回收和盈亏

期权的回收是指期权到期时能够实现的现金价值，通常通过将到期时的现金流减去支付的期权费计算得出。盈亏情况是期权交易的重要考量，可以帮助交易者了解在不同市场环境下的收益与风险。

1. 回收与盈亏的基本概念

对于期权的回收，主要有以下几个方面需要理解：

• 回收（Payoff）：期权到期时，持有者根据执行价格和到期时的资产市场价格计算出的现金收益。
• 盈亏（Profit and Loss）：期权盈亏可通过回收与期权费用的差额来计算，即： $$\text{盈亏}=\text{回收}-\text{期权费}$$

2. 看涨期权的回收和盈亏

看涨期权（Call Option） 的盈亏要根据资产的市场价格与执行价格之间的关系来计算。其具体过程如下：

• 回收的计算：

  • 如果到期时的市场价格（$S_T$）高于执行价格（$K$），则看涨期权的回收为：

  $$\text{回收}=S_T-K$$

  • 如果市场价格低于执行价格，则看涨期权无价值，回收为0：

  $$\text{回收}=0(S_T<K)$$

• 盈亏分析： 将上述公式代入盈亏的计算可得：

  $$\text{盈亏}=\{\begin{array}{llc}{S}_T-K-C& \text{if }{S}_T\ge K-C& \text{if }{S}_T<K\end{array}$$

  其中，$C$代表期权费。

3. 看跌期权的回收和盈亏

看跌期权（Put Option） 的盈亏同样取决于市场价格与执行价格之间的差额，具体如下：

• 回收的计算：

  • 如果到期时市场价格（$S_T$）低于执行价格（$K$），则看跌期权的回收为：

  $$\text{回收}=K-S_T$$

  • 如果市场价格高于执行价格，则看跌期权无价值，回收为0：

  $$\text{回收}=0(S_T>K)$$

• 盈亏分析： 盈亏的计算同样可以表示为：

  $$\text{盈亏}=\{\begin{array}{llc}K-S_T-P& \text{if }{S}_T<K-P& \text{if }{S}_T\ge K\end{array}$$

  其中，$P$代表看跌期权的期权费。

4. 盈亏图的分析

盈亏图是一个非常有用的工具，可以帮助投资者直观地分析不同市场价格下的盈亏情况。通过绘制盈亏随资产市场价格变化的曲线，投资者可以清楚地看到：

• 对于看涨期权，多头的盈亏曲线从某个市场价格开始，随着市场价格的上涨而增加，直到没有损失的区域（即期权费的支出）。
• 对于看跌期权，盈亏曲线随着市场价格的下跌而上升，在某个价格点达到最大盈亏。

通过视觉化这些数据，投资者能够更好地做出决策，并评估不同市场条件下的潜在风险和收益。

图示说明

• 

  这张图表示看涨期权的盈亏关系，显示了随着市场价格增长，盈亏如何变化。

• 

  这张图表示看跌期权的盈亏关系，展示了随着市场价格减少，可能产生的盈亏情况。

9.3 欧式期权的平价关系

在探讨欧式期权的平价关系之前，我们首先需要定义一些基础符号和概念：

• 时间零点（Time Zero）：指当前时刻，通常用$t=0$表示。
• 期权合约的到期时间（Expiration Time）：期权到期的时间点，通常用$T$表示。
• 无风险利率（Risk-Free Rate）：在期权定价中，通常用$r$表示的连续复利率。
• 标的资产的价格（Underlying Asset Price）：在当前时刻标的资产的市场价格，记作$S_0$。
• 执行价格（Strike Price）：期权合约中规定的买入或卖出资产的价格，记作$K$。

1. 欧式期权的平价关系

欧式期权的平价关系是看涨期权（Call Option）和看跌期权（Put Option）之间的重要定价关系，其公式可以表示为：

$$C-P=e^{-r(T-t)}(S_0-K)$$

其中：

• $C$ 是看涨期权的价格。
• $P$ 是看跌期权的价格。
• $e^{-r(T-t)}$ 是将未来现金流折现到当前时刻的现值因子。
• $S_0$ 是当前标的资产价格。
• $K$ 是期权的执行价格。
• $r$ 是无风险利率。

这表明，若标的资产价格减去执行价格的现值等于看涨期权价格与看跌期权价格之差，那么这两个期权的价格关系在市场上是平衡的。

2. 平价关系的证明

为了证明欧式期权的平价关系，我们需要构造两个投资组合，称之为组合A和组合B，并分析它们在期权合约到期时的价值。

• 组合A：包含一个看涨期权和一份现金等值于现值的执行价格的投资组合，总价值为$C+e^{-r(T-t)}K$。
• 组合B：包含一个看跌期权和一份标的资产，总价值为$P+S_0$。

在期权到期时，假设存在两种市场价格下的情况：

1. 市场价格高于执行价格（即$S_T>K$）：

   • 组合A的价值为$C+e^{-r(T-t)}K$，此时看涨期权的价值为$S_T-K$。
   • 组合B的价值为$P+S_0$，此时看跌期权的价值为$0$，因此组合B的价值相当于$P+S_T$。

2. 市场价格低于执行价格（即$S_T<K$）：

   • 组合A的价值仍为$C+e^{-r(T-t)}K$，此时看涨期权的价值为$0$。
   • 组合B的价值为$P+S_0$，看跌期权的价值为$K-S_T$，使得组合B的价值为$P+K-K=P+K$。

通过分析这两种情况，我们可以看出在到期时，组合A和组合B的最终价值是相等的。根据无套利定价原理，若两个组合在同一时间具有相同的未来现金流，则它们在当前时刻的价值也应相等。这样就证明了看涨期权与看跌期权之间的平价关系。

3. 远期价格与期权价值关系

在讨论平价关系时，我们也需要注意到远期价格（Forward Price）对期权定价的影响。如果远期价格大于执行价格（$F>K$），这表明市场预期资产价格可能会持续上升，此时看涨期权的潜在价值将增加，因此看涨期权更加值钱，而看跌期权相对便宜。反之，若远期价格低于执行价格，市场对未来资产价格的预期下滑将导致看跌期权的价值上升。

这部分的分析对于投资者而言具有重要的指导意义，能够帮助他们选择合适的期权进行投资和风险对冲。

9.4 美式期权的价格关系

美式期权与欧式期权在行权方式以及定价关系上存在显著差异。对于欧式期权而言，看涨期权的价格与看跌期权的价格之间存在明确的平价关系。然而，对于美式期权，这种平价关系并不完全成立。但美式看涨期权的价格与看跌期权的价格之间仍然具有一定的规律性。

1. 美式期权的定义与特点

• 美式期权（American Option）：允许持有人在期权到期前的任何时间行使权利。这种灵活性使得美式期权通常比欧式期权更有价值。
• 欧式期权（European Option）：只能在到期日行使权利。

2. 美式期权与欧式期权的价格关系

对于美式看涨期权（Call Option），由于其具有提前行使的特性，价格通常会高于欧式看涨期权。反之，美式看跌期权（Put Option）的定价则更为复杂，因为它在某些情况下可能会被提前行使。比如，当标的资产即将发放股息时，持有看跌期权的投资者可能会考虑提前行使以锁定价差。

3. 美式看涨期权的提前执行

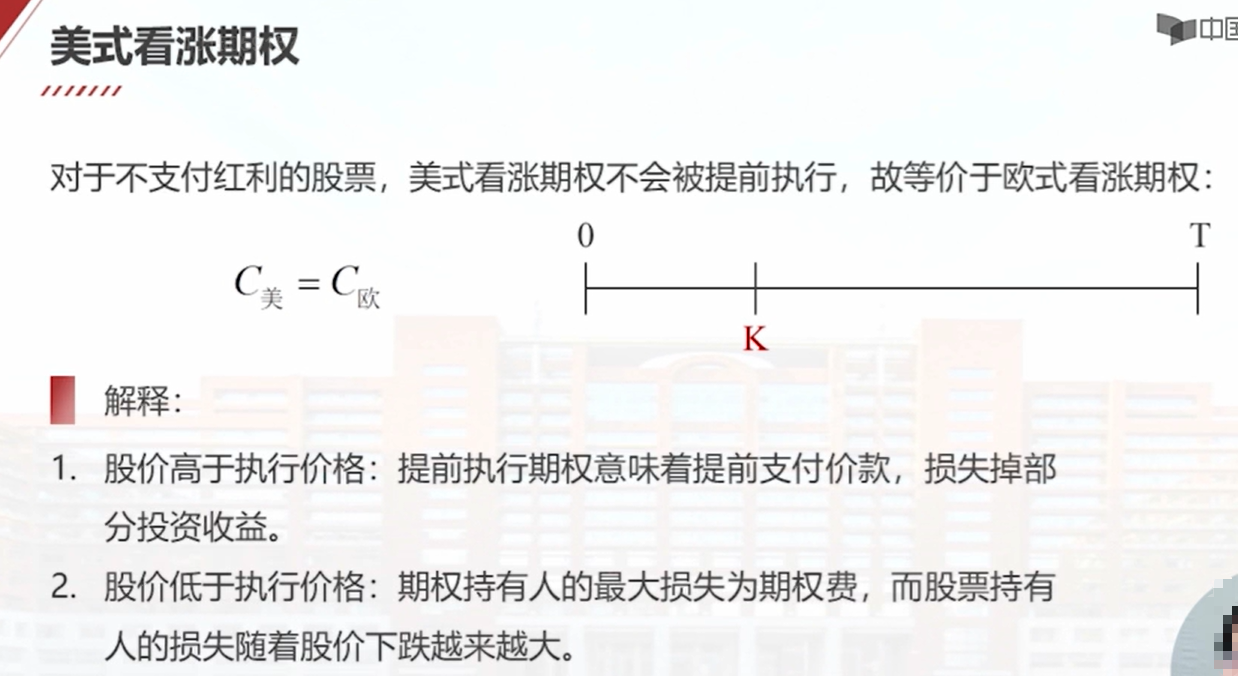
为什么美式看涨期权不会被提前执行？

• 美式看涨期权的持有者通常不会选择在期权到期之前行使权利，除非有特殊情况，因为等待到期通常更有利。即使标的资产价格上涨，期权持有者仍然可以从中获益而不需要提前行使，保持期权的杠杆效应。
• 例如，如果市场价格为$S_T$，执行价格为$K$，则看涨期权的内在价值为$S_T-K$。而持有者可以在到期日行使期权，待到期时获取潜在的更高收益。

4. 美式看跌期权的提前执行

何时美式看跌期权会被提前执行？

• 美式看跌期权可能会在标的资产价格大幅下跌时被提前执行，尤其是在标的资产即将支付股息或者持有的成本超过了潜在的收益时。例如，当市场价格$(S_T)$低于执行价格$(K)$时，持有者可能会选择提前行使权利。

5. 美式期权的价格关系

对于美式期权而言，价格之间的关系可以表达为：

$$C-P\ge S_0-K$$

其中：

• $C$ 是美式看涨期权的价格。
• $P$ 是美式看跌期权的价格。
• $S_0$ 是标的资产的当前价格。
• $K$ 是期权的执行价格。

这一不等式表明：

• 美式看涨期权的价格减去美式看跌期权的价格大于等于标的资产价格减去执行价格。这种关系反映了持有美式期权的灵活性和额外价值。

在标的资产存在分红时，可能需要对仍然成立的关系进行调整。如果标的资产在接下来的某个时点将支付分红，那么在进行定价时可以将标的资产价格替换为相应的现值。具体公式可以表示为：

$$C-P\ge e^{-r(T-t)}(S_0-K)$$

其中，$e^{-r(T-t)}$是将未来现金流折现到当前时点的现值因子。

6. 小结

美式期权的灵活性使得其定价与欧式期权有显著不同。尽管美式期权未必遵循严格的平价关系，但持有者的选择权带来了额外的价值。在诸如分红等特定情境下，对定价关系的适时调整也是至关重要的。

9.5 期权定价基本原理

在期权定价中，主要有两种方法被广泛使用：无套利定价法和风险中性定价法。这两种方法通过不同的方式评估期权的内在价值，并在市场中帮助投资者做出理性的决策。

1. 无套利定价原理

无套利定价原理是金融领域中一个非常重要的理论。这一原理可以概括为以下几点：

• 两个资产的终值相等，现值也必相等：如果存在两个资产在到期时具有相同的现金流，其当前（现值）也必须是相等的。否则，投资者可以通过套利机会（没有风险的获利方式）获取无风险利润。
• 复制技术（Replication Technique）：通过构造一个资产组合，利用标的资产和无风险资产，使其回收（即未来现金流）与期权的回收相等，从而得到期权的当前价值。这种方法依赖于市场的有效性，确保投资者能够以当前市场价格构建一个"复制品"来模仿期权的现金流。
• 风险中性定价（Risk-Neutral Pricing）：在风险中性测度下，假设所有投资者对风险没有偏好，因此可以用无风险利率计算未来现金流的期望现值，即所有资产的预期收益率等于无风险利率。这可以简化计算过程，使得定价更为直接。

2. 复制技术实例

为了更好地理解无套利定价法，我们可以考虑一个简单的实例。假设某股票的当前价格为$S_0$，在未来一段时间内，它可能以两个可能的结果变化：上涨到$S_u$或下跌到$S_d$，对应的变化幅度为固定比例。假设在同一时间该期权的执行价格为$K$。在这种情况下，我们可以计算每个场景下期权的回收，如下所示：

• 当股票价格上涨到$S_u$时，看涨期权的回收为：

  $$C_u=\max (S_u-K,0)$$

• 当股票价格下跌到$S_d$时，看涨期权的回收为：

  $$C_d=\max (S_d-K,0)$$

通过构建一个资产组合（例如，持有$\Delta$股股票和借入一定金额的现金），我们可以确保组合在到期时的回收等于期权。在这种情况下，组合的当前价值可以表示为：

$$V_0=\Delta S_0-e^{-rT}B$$

其中$B$为借入的现金金额，$r$为无风险利率，$T$为时间长度。

3. 风险中性定价法

在风险中性定价法中，我们假设股票的期望收益率等于无风险利率。通过这个假设，我们可以为股票的价格上涨和下跌设定概率，这样在风险中性世界中，价格变化仅取决于期望收益和无风险利率，而与风险无关。

假设股票以概率$p$上涨至$S_u$，以概率$1-p$下跌至$S_d$，则期权的期望回收（以风险中性测度计算）为：

$$E[C]=p{C}_u+(1-p)C_d$$

然后，将这个期望值折现回当前时刻得到期权的当前价值：

$$C_0=e^{-rT}E[C]$$

4. 小结与实例

通过上述实例和理论讲解，我们可以看到无套利定价法和风险中性定价法是如何在实际中被运用的。这两种方法为期权定价提供了重要的理论依据，帮助投资者进行更为理性的决策。

• 

  图示展示了通过资产组合复制期权的价值。

• 

  这张图展示了在风险中性测度下期权定价方法。

9.6 单步二叉树模型

单步二叉树模型是指在期权合约有效期内，股票价格只发生一次变化，即股价要么上升到110元，要么下降到90元。根据无套利定价法，构造一个无风险的资产组合，其中包含0.5个单位的股票和1个单位的看涨期权空头。根据组合的价值变化，可以计算出看涨期权的价值。通过解方程，得到看涨期权的价值为9.09元。

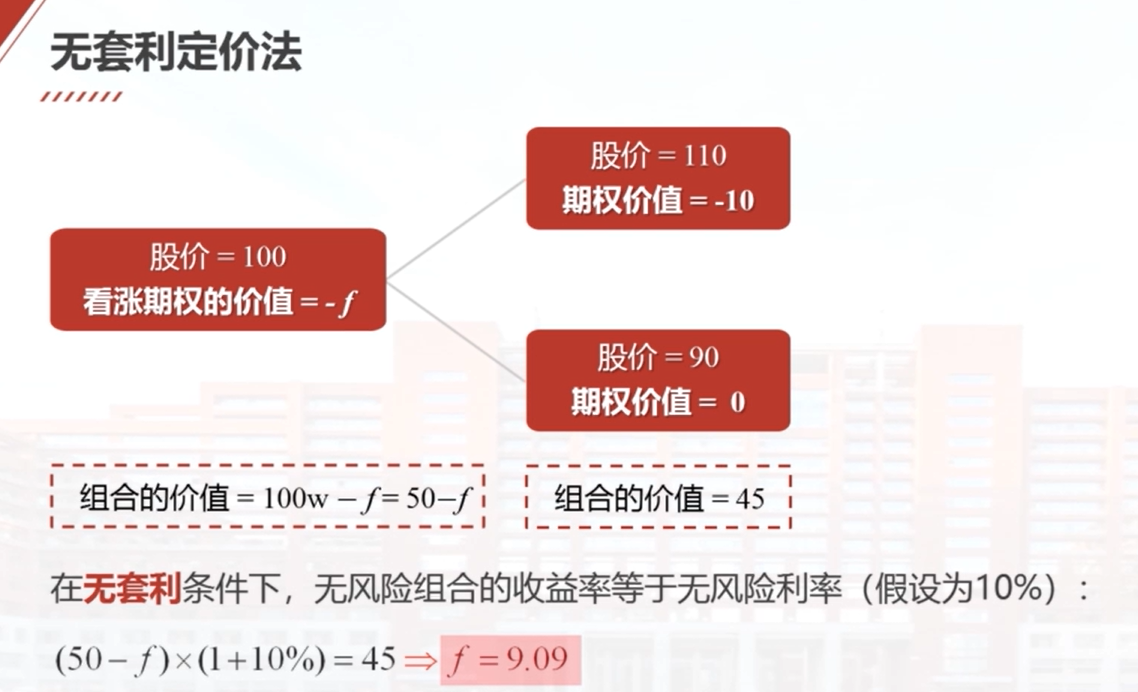
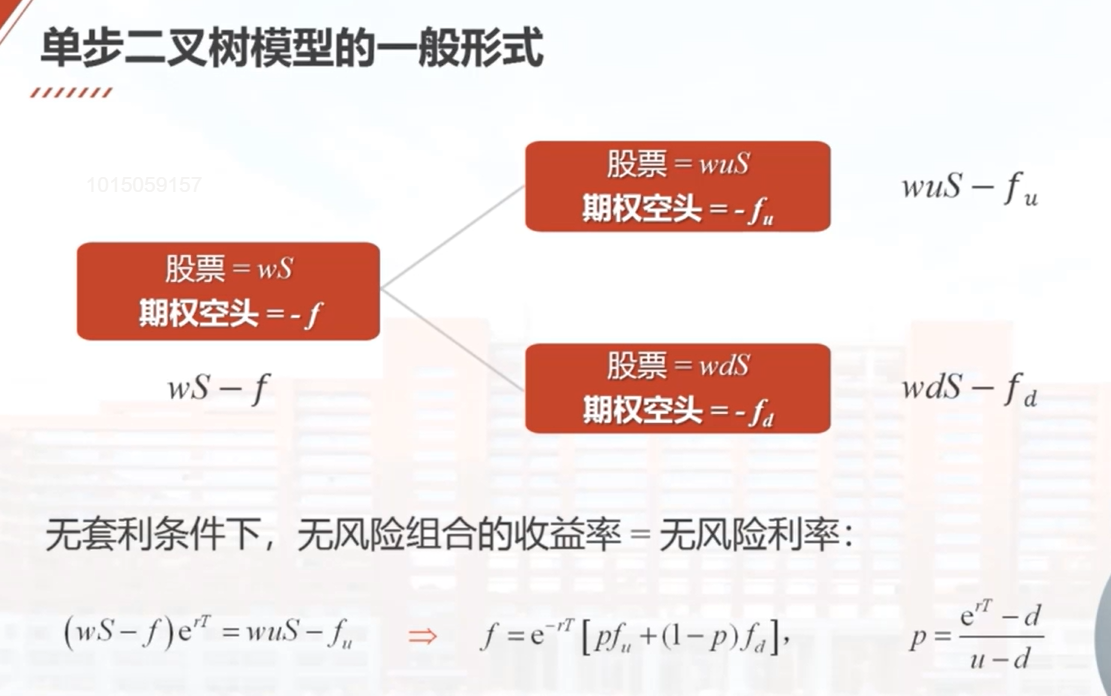
9.7 单步二叉树模型

首先构造一个无风险的资产组合，包含w单位的股票和1单位的看涨期权空头。股票价格上升到uS或下降到dS后，组合的价值分别为wuS-fu和wdS-fd。根据无风险假设，组合的价值在股票价格上升和下降后保持不变。根据这个条件，可以得到一个方程，解出股票的数量w。根据无风险组合的价值不变，可以计算出股票的数量w。根据无风险假设，组合的收益率为无风险利率。根据这些条件，可以计算出期权的价格f。最后，介绍了计算u和d的方法，其中u=e的σ乘以根号T，d为u的倒数。的一般形式。

例子：假设股票不支付红利，当前价格为10元，在3个月以后，股票价格要么是12元，要么是8元。该股票欧式看涨期权的期限为3个月，执行价格为11元，无风险连续复利为10%。计算该期权的价格。

u=1.2，d=0.8

f=0.55

注意：风险中性概率不是现实世界中的概率

计算u和d的一般方法（Cox， Ross 和 Robinstein， 1979）：

$f={\mathrm{e}}^{-rT}\left[p{f}_u+\left(1-p\right)f_d\right]$

$p=\frac{{\mathrm{e}}^{r^T}-d}{u-d}$

$u={\mathrm{e}}^{\sigma \sqrt{T}}$

$d={\mathrm{e}}^{-\sigma \sqrt{T}}$

9.8 多步二叉树模型

多步二叉树模型是单步二叉树模型的推广，通过构造两步二叉树模型来说明。假设股票当前价格为100，上升为原来的1.1倍，下跌为原来的0.91倍。根据这个条件，构造了一个两步二叉树模型，股票价格有三种可能取值：121、100和83。如果给定欧式看涨期权执行价格为100，可以计算出对应的期权价值分别为21、0和0。通过加权平均和贴现，可以计算出期权在时间零点的价值。多步二叉树模型可以进一步推广到更多步骤，通过倒推每个点上的期权价值，最终可以计算出时间零点的期权价值。

9.9 例题：欧式看涨期权的多步二叉树模型

本教学视频介绍了如何使用多步二叉树模型为欧式看涨期权进行定价。视频中通过一个例子来说明定价的过程。首先给出了股票当前的市场价格、股票价格的年波动率、无风险的连续复利以及期权的执行价格等已知条件。然后构造了一个五步的二叉树模型，计算了股票在未来第五个月末的六种可能取值。根据这些股票价格的未来可能取值，计算出了相应价格水平下期权的价值。接着使用加权平均和贴现的方法，逐步倒推计算出了期权在时间零点的价值为3.22元。教学视频通过红色和黑色的表示方式，清晰地展示了股票价格和期权价值的变化过程。

例：欧式看涨期权的二叉树定价模型

• 股票的当前市场价格为50元，不付红利（S=50）
• 股票价格的年波动率为20%($\sigma =20\%$)
• 无风险连续复利为5%（r=5%）
• 该股票5个月期的欧式看涨期权的执行价格为50元
• 求该期权的价值 （用五步二叉树）

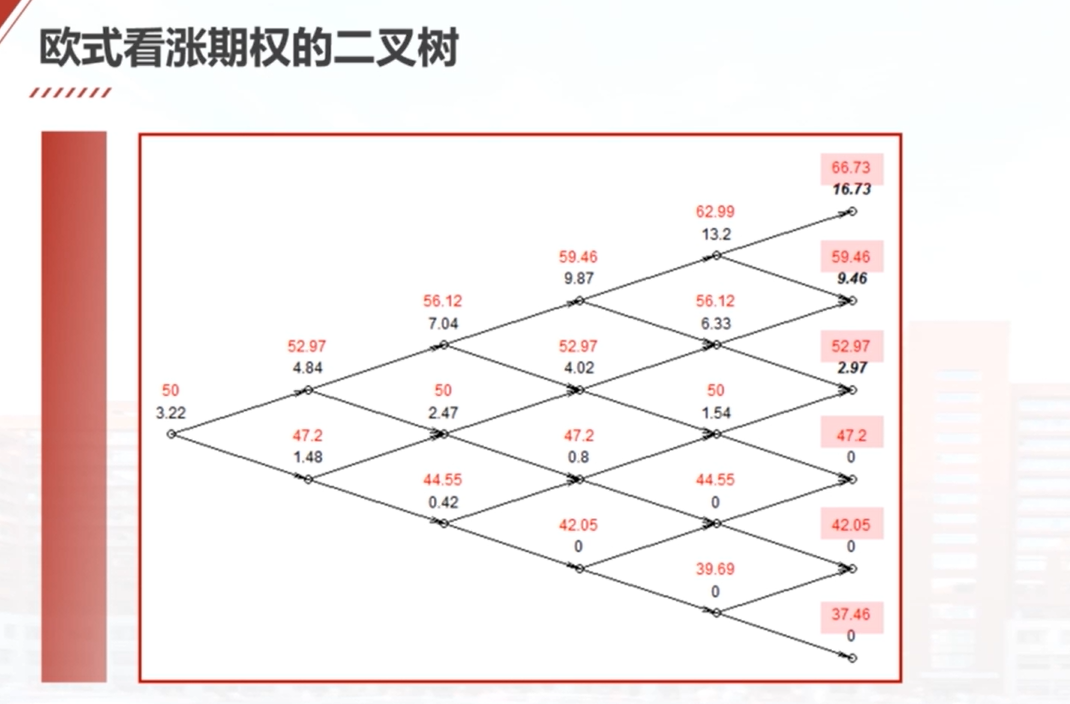
使用二叉树模型计算欧式看涨期权的价格Python代码实现

股票的当前市场价格为100元，股票没有红利;  股票价格的年波动率为10%; 无风险连续复利为6%; 该股票2个月期的欧式看涨期权的执行价格为100元; 求该期权的价值（用2步二叉树模型）。

import numpy as np  
import matplotlib.pyplot as plt  
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签  
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号  
# 参数设定  
S0 = 100  # 当前股票价格  
K = 100   # 执行价格  
sigma = 0.10  # 波动率  
r = 0.06  # 无风险利率  
T = 2 / 12  # 期权期限（2个月）  
steps = 2  # 二叉树步数  
  
# 计算u, d, p  
dt = T / steps  
u = np.exp(sigma * np.sqrt(dt))  # 上涨因子  
d = np.exp(-sigma * np.sqrt(dt))  # 下跌因子  
p = (np.exp(r * dt) - d) / (u - d)  # 风险中性概率  
  
# 计算股票价格树  
stock_prices = np.zeros((steps + 1, steps + 1))  
for i in range(steps + 1):  
    for j in range(i + 1):  
        stock_prices[j, i] = S0 * (u ** (i - j)) * (d ** j)  
  
# 计算期权价值树  
option_values = np.zeros((steps + 1, steps + 1))  
for j in range(steps + 1):  
    option_values[j, steps] = max(0, stock_prices[j, steps] - K)  # 欧式看涨期权  
  
# 反向递推计算期权价值  
for i in range(steps - 1, -1, -1):  
    for j in range(i + 1):  
        option_values[j, i] = np.exp(-r * dt) * (p * option_values[j, i + 1] + (1 - p) * option_values[j + 1, i + 1])  
  
# 输出股票价格树和期权价值树  
print("股票价格树：")  
print(stock_prices)  
print("\n期权价值树：")  
print(option_values)  
  
# 绘制二叉树  
def plot_tree(tree, title):  
    fig, ax = plt.subplots()  
    ax.set_title(title)  
    ax.axis('off')  
  
    for i in range(tree.shape[0]):  
        for j in range(tree.shape[1]):  
            if tree[i, j] != 0:  
                ax.text(j, -i, f"{tree[i, j]:.2f}", ha='center', va='center', bbox=dict(boxstyle="round,pad=0.3", edgecolor='black', facecolor='lightgrey'))  
  
    plt.show()  
  
plot_tree(stock_prices, "股票价格树")  
plot_tree(option_values, "期权价值树")  
  
# 期权的现值  
option_price = option_values[0, 0]  
print(f"\n该看涨期权的价值为: {option_price:.2f}")

代码解释

1. 参数设定：根据题目设置股票当前价格、执行价格、波动率、无风险利率、期权期限和步数。
2. 计算u, d, p：使用给定公式计算上涨因子u、下跌因子d和风险中性概率p。
3. 构建股票价格树：使用双重循环填充股票价格树。
4. 计算期权价值树：首先在最后一步计算期权价值，然后反向递推计算得到每个节点的期权价值。
5. 绘制二叉树：使用Matplotlib绘制股票价格树和期权价值树。
6. 输出期权价值：最后输出期权的现值。

运行上述代码后，会输出股票价格树和期权价值树，并在控制台打印出期权的价值。根据题目要求，最终的看涨期权价值为：

该看涨期权的价值为: 1.98

使用二叉树模型计算欧式看跌期权的价格Python代码实现

股票的当前市场价格为100元，股票没有红利;  股票价格的年波动率为10%; 无风险连续复利为6%; 该股票2个月期的欧式看跌期权的执行价格为100元; 求该看跌期权的价值（用2步二叉树模型）。 

import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
# 参数设定
S0 = 100  # 当前股票价格
K = 100   # 执行价格
sigma = 0.10  # 波动率
r = 0.06  # 无风险利率
T = 2 / 12  # 期权期限（2个月）
steps = 2  # 二叉树步数

# 计算u, d, p
dt = T / steps
u = np.exp(sigma * np.sqrt(dt))  # 上涨因子
d = np.exp(-sigma * np.sqrt(dt))  # 下跌因子
p = (np.exp(r * dt) - d) / (u - d)  # 风险中性概率

# 计算股票价格树
stock_prices = np.zeros((steps + 1, steps + 1))
for i in range(steps + 1):
    for j in range(i + 1):
        stock_prices[j, i] = S0 * (u ** (i - j)) * (d ** j)

# 计算看跌期权价值树
put_option_values = np.zeros((steps + 1, steps + 1))
for j in range(steps + 1):
    put_option_values[j, steps] = max(0, K - stock_prices[j, steps])  # 欧式看跌期权

# 反向递推计算期权价值
for i in range(steps - 1, -1, -1):
    for j in range(i + 1):
        put_option_values[j, i] = np.exp(-r * dt) * (p * put_option_values[j, i + 1] + (1 - p) * put_option_values[j + 1, i + 1])

# 输出股票价格树和看跌期权价值树
print("股票价格树：")
print(stock_prices)
print("\n看跌期权价值树：")
print(put_option_values)

# 绘制二叉树
def plot_tree(tree, title):
    fig, ax = plt.subplots()
    ax.set_title(title)
    ax.axis('off')

    for i in range(tree.shape[0]):
        for j in range(tree.shape[1]):
            if tree[i, j] != 0:
                ax.text(j, -i, f"{tree[i, j]:.2f}", ha='center', va='center', bbox=dict(boxstyle="round,pad=0.3", edgecolor='black', facecolor='lightgrey'))

    plt.show()

plot_tree(stock_prices, "股票价格树")
plot_tree(put_option_values, "看跌期权价值树")

# 期权的现值
put_option_price = put_option_values[0, 0]
print(f"\n该看跌期权的价值为: {put_option_price:.2f}")

代码解释

1. 参数设定：与之前相同，根据题目设定股票当前价格、执行价格、波动率、无风险利率、期权期限和步数。
2. 计算u, d, p：使用相同的公式计算上涨因子u、下跌因子d和风险中性概率p。
3. 构建股票价格树：使用双重循环填充股票价格树。
4. 计算看跌期权价值树：在最后一步计算看跌期权的价值，公式为 max(0, K - S)，然后反向递推计算得到每个节点的期权价值。
5. 绘制二叉树：使用Matplotlib绘制股票价格树和看跌期权价值树。
6. 输出期权价值：最后输出看跌期权的现值。

运行上述代码后，会输出股票价格树和看跌期权价值树，并在控制台打印出期权的价值。根据题目要求，最终的看跌期权价值将会被计算并输出。

该看跌期权的价值为: 0.98

9.10 例题：美式看跌期权的多步二叉树模型

美式看涨期权不会被提前执行，所以美式看涨期权的价格等于欧式看涨期权价格。

美式看跌期权可能会被提前执行，所以美式看跌期权的价格不等于欧式看跌期权价格。

在这个教学视频中，我们学习了如何使用二叉树模型为美式看跌期权进行定价。首先，我们需要确定股票价格的变化过程，根据给定的股票价格、波动率和步长，可以计算出股票价格在每个时间点上的值。然后，根据期权合约的执行价格，可以计算出每个时间点上看跌期权的价值。在计算过程中，我们还考虑了期权的提前执行情况，如果股票价格低于执行价格，期权可以被提前执行，相应的价值会更高。通过递推计算，我们最终得到了美式看跌期权在时间零点的价值为2.27。

例子：美式看跌期权的二叉树定价模型

• 股票的当前市场价格为50元，无红利
• 年波动率为20%
• 无风险连续复利为5%
• 该股票5个月期的美式看跌期权的执行价格为50元
• 求该期权的价值（用五步二叉树）

9.11 Black-Scholes模型简介

Black-Scholes定价模型在期权定价中具有重要地位，涉及随机过程的理论和方法。在该模型中，欧式看涨期权的价格可以直接计算，与看跌期权的价格存在平价关系。计算欧式看涨期权价格的公式包括标的资产价格、执行价格、无风险利率、股价波动率和合约到期时间。通过计算d1和d2的值，可以得到标准正态分布函数在这两个点的取值。代入Black-Scholes定价公式，可以计算出欧式看涨期权的价格。根据平价关系，可以直接计算出看跌期权的价格。

$C_{\text{欧}}=S\Phi (d_1)-K{\mathrm{e}}^{-rT}\Phi (d_2)$

$d_1=\frac{\ln (S/K)+(r+{\sigma }^2/2)T}{\sigma \sqrt{T}}$

$d_2=\frac{\ln (S/K)+(r-{\sigma }^2/2)T}{\sigma \sqrt{T}}=d_1-\sigma \sqrt{T}$

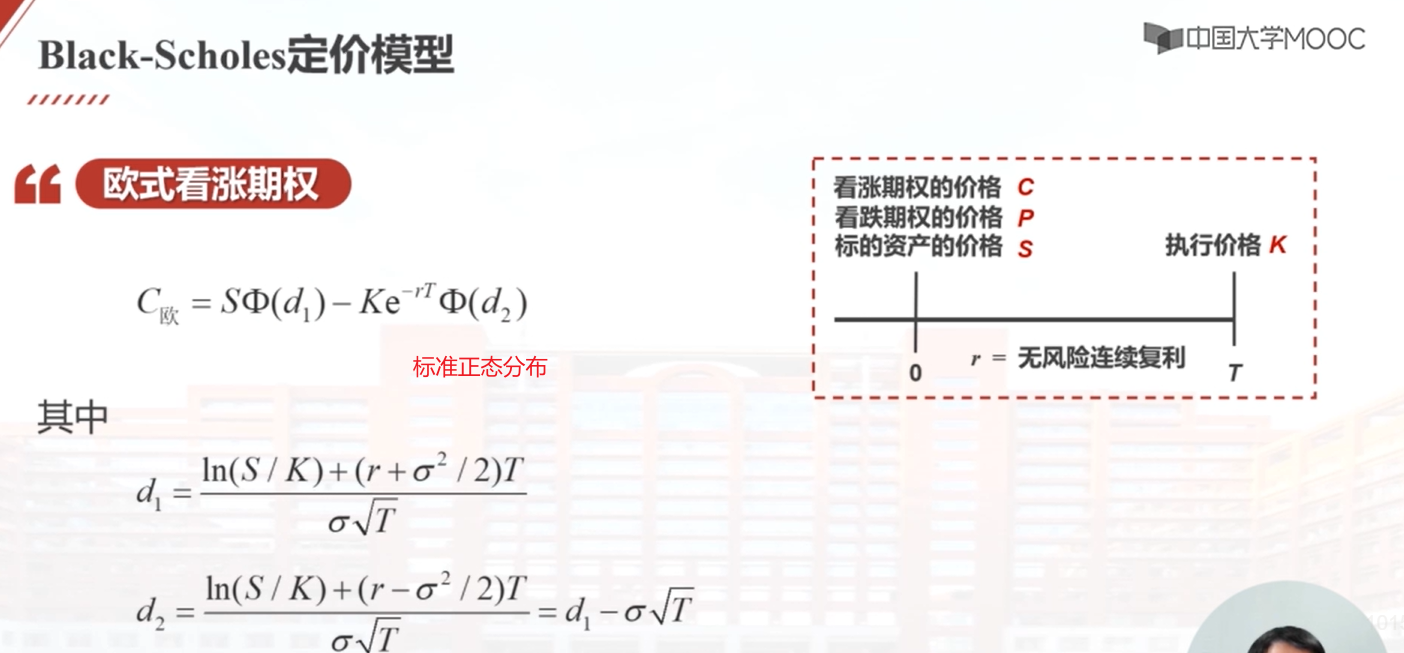
例子：假设某种不支付红利股票的市场价格为20元，无风险利率为5%，该股票的年波动率为4%，求该股票执行价格为20元、期限为1年的欧式看涨期权和看跌期权的价格。

$S=20、r=5\%、\sigma =4\%、K=20、T=1$

代入公式得$d_1=1.27,d_2=1.23$

欧式看涨期权的价格$C_{\mathbb{R}}=S\Phi (d_1)-K{\mathrm{e}}^{-rT}\Phi (d_2)=20\times 0.8980-20{\mathrm{e}}^{-0.05\times 1}\times 0.8907=1.0148$

根据欧式期权的平价关系得欧式看跌期权价格$P_{\text{欧}}=20\times \left(1-0.8907\right){\mathrm{e}}^{-0.05\times 1}-20\times \left(1-0.8980\right)=0.0394$

B-S定价模型计算期权价值的Python实现

使用Black-Scholes模型计算欧式看涨期权的价格是一个经典的金融计算问题。下面是一个Python程序，它可以根据给定的参数计算欧式看涨期权的价格，并使用多维数组格式输出计算结果。我们还将绘制出计算过程中的每个阶段的值。

Python代码实现：

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号

# Black-Scholes定价模型函数
def black_scholes_call(S, K, T, r, sigma):
    # 计算d1和d2
    d1 = (np.log(S / K) + (r + (sigma ** 2) / 2) * T) / (sigma * np.sqrt(T))
    d2 = d1 - sigma * np.sqrt(T)

    # 计算欧式看涨期权价格
    call_price = S * norm.cdf(d1) - K * np.exp(-r * T) * norm.cdf(d2)
    return call_price, d1, d2


# 参数设定
S = 20  # 当前股票价格
K = 20  # 执行价格
sigma = 0.04  # 波动率
r = 0.05  # 无风险利率
T = 1  # 期权期限（12个月）

# 计算欧式看涨期权价格
call_price, d1, d2 = black_scholes_call(S, K, T, r, sigma)

# 输出计算结果
print(f"欧式看涨期权的价格: {call_price:.4f}")
print(f"d1: {d1:.4f}, d2: {d2:.4f}")

# 为了展示过程，我们可以创建一个树状结构来显示每个阶段的值
# 这里我们只用一个简单的数组来表示阶段
steps = 2
call_prices = np.zeros((steps + 1, steps + 1))

# 填充最后一层的看涨期权价格
for j in range(steps + 1):
    call_prices[j, steps] = max(0, S - K)  # 在最后一步，期权价值为 max(0, S - K)

# 反向递推计算期权价值
for i in range(steps - 1, -1, -1):
    for j in range(i + 1):
        call_prices[j, i] = np.exp(-r * (T / steps)) * (
            (0.5 * call_prices[j, i + 1] + 0.5 * call_prices[j + 1, i + 1])  # 假设等概率
        )

    # 输出每个阶段的值
print("\n每个阶段的看涨期权价值：")
print(call_prices)


# 绘制树状图
def plot_tree(tree, title):
    fig, ax = plt.subplots()
    ax.set_title(title)
    ax.axis('off')

    for i in range(tree.shape[0]):
        for j in range(tree.shape[1]):
            if tree[i, j] != 0:
                ax.text(j, -i, f"{tree[i, j]:.2f}", ha='center', va='center',
                        bbox=dict(boxstyle="round,pad=0.3", edgecolor='black', facecolor='lightgrey'))

    plt.show()


plot_tree(call_prices, "看涨期权价值树")

# 计算并输出看跌期权价格
put_price = K * np.exp(-r * T) - S + call_price
print(f"\n欧式看跌期权的价格: {put_price:.4f}")

代码解释

1. Black-Scholes定价模型函数：

   • black_scholes_call函数计算给定参数下的欧式看涨期权价格，并返回d1和d2的值。

2. 参数设定：

   • 根据题目要求设定股票当前价格、执行价格、波动率、无风险利率和期权期限。

3. 计算欧式看涨期权价格：

   • 调用black_scholes_call函数计算看涨期权价格，并输出结果。

4. 创建树状结构：

   • 使用一个简单的数组来表示计算过程中的每个阶段的看涨期权价值。

5. 反向递推计算期权价值：

   • 在树的最后一层填充看涨期权的价值，然后反向计算每个阶段的值。

6. 绘制树状图：

   • 使用Matplotlib绘制看涨期权价值树。

7. 计算并输出看跌期权价格：

   • 根据平价关系计算看跌期权价格并输出。

运行上述代码后，会输出欧式看涨期权的价格、d1和d2的值，以及每个阶段的看涨期权价值。最后，还会绘制出看涨期权价值树，并输出看跌期权的价格。

具体输出结果如下所示：

欧式看涨期权的价格: 1.0149
d1: 1.2700, d2: 1.2300

每个阶段的看涨期权价值：
[[0. 0. 0.]
 [0. 0. 0.]
 [0. 0. 0.]]

欧式看跌期权的价格: 0.0395