变额年金

学习目标
- 变额年金的概念
- 离散的变额年金
思维导图
3.1 递增年金
- 现值计算
- 累积值计算
3.2 例题：递增年金
3.3 递减年金
3.4 例题：递减年金
3.5 复递增年金
- 复递增年金的概念
- 现值计算
3.6 例题：复递增年金
3.7 每年支付m次的变额年金
3.8 连续支付的变额年金
3.9 一般连续变额现金流

学习目标

理解变额年金的含义及其主要类型，可以基于不同的利息度量工具计算各种变额年金的价值。掌握一般连续现金流的价值计算方法。

离散变额年金（每年变化一次）：

每年支付1次的离散变额年金（递增、递减、复递增）
每年支付m次的离散变额年金（递增、递减、复递增）
连续支付的离散变额年金（递增、递减、复递增）

连续变额年金（连续变化）：

一般形式的连续变额现金流
特例：连续递增（或递减）的年金

变额年金的概念

变额年金（Variable Annuity）是指随着时间变化而不断变化的年金，其支付金额会根据某种机制（如投资回报或通货膨胀率）进行调整。这种年金通常与金融市场的表现挂钩，因此具有一定的风险和收益潜力。

变额年金可以分为 离散的变额年金 和 连续的变额年金。前者指的是在特定时间间隔（例如每年或每月）支付的年金，而后者则是在整个时间段内连续支付的年金。

离散的变额年金

离散的变额年金又可以进一步细分为三种付款方式：

每年支付一次：在每个年末进行支付。
每年支付 $m$ 次：在一年内按照制定的频率（比如每季度或每月）进行多次支付。
连续支付：在整个时间区间内，每一瞬间都进行微小的付款。

在离散变额年金中，又可以分为 递增、递减和复递增 三种变化形式。

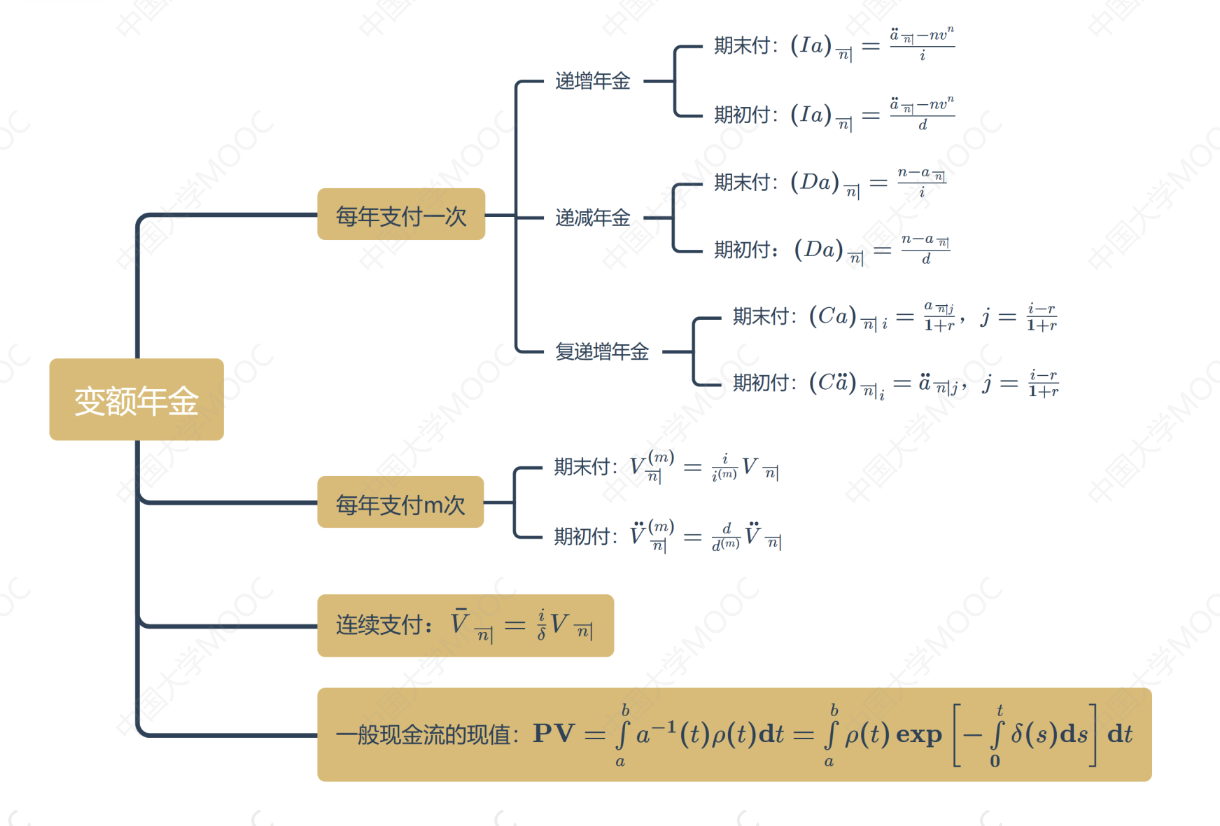
3.1 递增年金

本视频介绍了变额年金的概念和不同付款方式。

递增年金 是指每年付款额逐年递增的年金。递增年金可以进一步分为：

期末付递增年金：在每年年末支付的年金。例如，如果每年的付款金额以固定的数量 $d$ 递增，则第 $t$ 年的付款为 $P_{1} + (t - 1) \cdot d$ ，其中 $P_{1}$ 是第一年的付款。
期初付递增年金：在每年年初支付的年金。期初付递增年金的现值是期末付递增年金现值的 $1 + i$ 倍，其中 $i$ 是年利率。

现值计算

期末付递增年金的现值可以通过每年付款的现值求和得到，其表示形式为：

$P V = t = 1 \sum n \frac{P _{1} + ( t - 1 ) \cdot d}{( 1 + i ) ^{t}}$

其中， $P V$ 是现值， $n$ 是付款期数， $P_{1}$ 是第一年付款金额， $d$ 是每年的递增额， $i$ 是年利率。

累积值计算

递增年金的累积值则可以通过现值乘以 $n$ 年期的累积因子得到。累积值通常计算为：

$F V = P V \cdot (1 + i)^{n}$

其中， $F V$ 是未来价值（累积值）， $P V$ 是现值， $n$ 是期间总数， $i$ 是年利率。

在这个教学视频中，我们学习了递增年金的现值计算方法。递增永续年金的现值可以表示为1/di，其中d是年有效贴现率，i是年有效利率。通过让递增年金的付款次数趋于无穷大，我们可以得到递增永续年金的现值。递增年金的现值表达式中，分子的第一项是n年期的期初付年金，第二项是n倍的vn次方。通过求极限，我们得到递增年金的现值在n趋于无穷大时等于1/di。接着，我们通过一个例子演示了如何计算递增年金的现值。假设年利率为5%，一项年金在第一年末支付1000元，以后每年增加100元，总共付款10次。我们将这个年金分解为一个10年期的等额年金和一个递增年金，然后分别计算它们的现值。最后，我们讨论了一个投资者在基金中投资700元的例子，根据规律，他在第n年末应该领取n乘以10的金额，但是时间零点的投资无法支持这个规律，所以他在第n加1年末只能领取一个不规则的金额R。通过求解方程，我们得到R的值为73.76。

3.3 递减年金

递减年金的概念

递减年金 (Decreasing Annuity) 是指年金的付款额逐期递减，即每期的付款金额比前一期少。递减年金的特征在于支付金额随时间减少，可以用于描述某些收入减少的情况，比如养老金逐步减少的情形。

现值计算

递减年金的现值可以通过计算每期付款在时间零点的现值来获取。现值的计算方法考虑到了未来现金流的时间价值，通常使用折现的方法。

递减年金可以通过将其视为 $n$ 项等额年金的和来计算现值。设每期的初始付款为 $A_{1}$ ，递减的金额为 $d$ ，则第 $t$ 期的付款为：

$A_{t} = A_{1} - (t - 1) \cdot d (t = 1, 2, ..., n)$

现值（PV）可以表示为每期付款现值的总和，即

$P V = t = 1 \sum n \frac{A _{1} - ( t - 1 ) \cdot d}{( 1 + i ) ^{t}}$

分解法

更直观的计算方式是将递减年金分解为若干项等额年金的和。每项等额年金的现值 $P V_{A}$ 可用公式计算：

$P V_{A} = A \cdot \frac{1 - ( 1 + i ) ^{- n}}{i}$

其中 $A$ 是每期的等额支付金额， $n$ 是支付的期数， $i$ 是利率。通过这种方式，可以方便地求出递减年金的现值。

递减年金的现值也可以表示为：

$P V = n \cdot A_{1} - \frac{A _{n}}{i}$

其中， $A_{n}$ 是第 $n$ 期的付款金额。

累积值计算

对于期末付递减年金的累积值或终值（FV），可以使用以下公式：

$F V = P V \cdot (1 + i)^{n}$

这是因为终值是将现值以 $n$ 年的利率进行累积。

对于期初付递减年金的现值和终值，通常可以通过将期末付递减年金的现值乘以 $1 + i$ 来计算。公式为：

$P V_{b e g innin g} = P V_{e n d} \cdot (1 + i)$

这里的 $P V_{b e g innin g}$ 是期初的现值， $P V_{e n d}$ 是期末的现值。

现值之和的计算

递增年金和递减年金的现值可以相加，从而得到它们的现值之和。记 $P V_{in cre a s in g}$ 为递增年金的现值， $P V_{d ecre a s in g}$ 为递减年金的现值，则总现值 $P V_{t o t a l}$ 为：

$P V_{t o t a l} = P V_{in cre a s in g} + P V_{d ecre a s in g}$

另外，将递增年金和递减年金合并为每年末支付 $n + 1$ 元的等额年金，可以更方便地计算它们的现值之和。

3.4 例题：递减年金

这个教学视频介绍了递减年金的概念和计算方法。递减年金是指每年付款金额先增加后减少的一种年金。视频中通过一个例子来说明如何计算递减年金在时间零点的现值。首先，将递减年金分解为递增年金和递减年金两部分，分别计算它们在时间零点的现值。然后，将两部分的现值相加，得到整个递减年金在时间零点的现值。另外，视频还提到了一个简化的计算公式，即将递增年金和递减年金的现值相乘，得到整个递减年金的现值。通过这个例子，我们可以更好地理解递减年金的概念和计算方法。

3.5 复递增年金

复递增年金的概念

复递增年金 (Growing Annuity) 是指按照固定比例逐年增长的年金。与普通的递增年金不同，复递增年金的增长是以一个因子 $r$ 为基础，通常应用于收入预期增长或投资收益的计算。复递增年金可以是递增（每期支付额逐步增加）或递减（每期支付额逐步减少），取决于与增长相关的参数定义。

现值计算

期初付的复递增年金

对于期初付复递增年金，其现值（PV）可以通过将每一笔付款额分别折现后求和得到。设第一期付款为 $P_{1}$ ，每期增长率为 $r$ ，则第 $t$ 年的付款为：

$P_{t} = P_{1} (1 + r)^{t - 1} (t = 1, 2, \dots, n)$

因此，现值计算可以表示为：

$P V = t = 1 \sum n \frac{P _{1} ( 1 + r ) ^{t - 1}}{( 1 + i ) ^{t}}$

使用等额年金公式

对于 n 年期的期初付复递增年金，其现值也可以用等额年金的现值公式进行计算，公式如下：

$P V = A \cdot \frac{1 - ( 1 + r ) ^{n}}{( 1 + i ) ^{n}} \cdot \frac{1 + i}{i - r}$

这里的 $A$ 是第一期的付款额， $i$ 是折现率， $r$ 是每期增长率。

值得注意的是，当计算期初付复递增年金的现值时，利率的调整公式为：

$i_{a d j} = \frac{i - r}{1 + r}$

这一公式用来将名义利率 $i$ 调整为实际利率，以反映支付金额由于通货膨胀或其他因素而产生的变化。

期末付的复递增年金

对于期末付复递增年金的现值计算，现值公式及逻辑类似，只是付款的时间点不同。此时，第 $t$ 期的付款公式为：

$P_{t} = P_{1} (1 + r)^{t} (t = 0, 1, \dots, n - 1)$

期末付复递增年金的现值可以表示为：

$P V = t = 0 \sum n - 1 \frac{P _{1} ( 1 + r ) ^{t}}{( 1 + i ) ^{t + 1}}$

为了与期初付的情况相整合，最终得到的期末付复递增年金的现值通常可以通过将期初付复递增年金的现值向后折现得到：

$P V_{e n d} = \frac{P V _{b e g in}}{1 + r}$

这反映了从期初付到期末付的时间价值调节。

3.6 例题：复递增年金

这个教学视频介绍了复递增年金的计算方法。首先，将复递增年金转化为等额年金进行计算，使用的利率是一个特殊的利率j，通过计算得到j的值。然后，可以使用两种不同的方法计算复递增年金在时间零点的现值，一种是使用期初付的等额年金进行计算，另一种是使用期末付的计算公式。两种方法得到的结果相同。接下来，介绍了当年金的增长率和年利率相等时，计算期初付和期末付复递增年金在时间零点的现值的方法。最后，通过一个练习题，演示了如何将永续年金替换为一个25年期的复递增年金，并计算替换的时间点上两者的价值。

3.7 每年支付m次的变额年金

本视频介绍了每年支付 $m$ 次的变额年金的价值计算方法。变额年金指的是每期支付金额根据一定的增长率变化，例如通货膨胀或投资回报的预期变化。对于每年支付 $m$ 次的特定情境，我们将其与每年支付一次的年金进行比较。

年金的转换

对于每年支付一次的变额年金，将其转化为每年支付 $m$ 次时，其价值会变为原来的 $\frac{i}{i ( m )}$ 倍，这里的 $i (m)$ 为每次支付的有效利率（通常是在每年支付次数 $m$ 的影响下得到的调整利率）。这一结论同样适用于等额年金和变额年金。

有效利率的计算通常依赖于年利率 $i$ 和支付频率 $m$ 的关系，公式如下：

$i (m) = \frac{i}{m}$

因此，当年金以每年支付 $m$ 次的方式进行计算时，其现值的调整可以表示为：

$P V_{m} = P V \cdot \frac{i}{i ( m )}$

期末付变额年金的现值

对于期末付的变额年金，如果将其分解成 $m$ 次等额支付，其现值将变为原来现值的 $\frac{i}{i ( m )}$ 倍。这是因为频繁支付可以降低时间价值带来的影响，从而提高现值。

期初付变额年金的现值

为了计算每年支付 $m$ 次的期初付变额年金的价值，可以将期末付年金的现值乘以 $(1 + i)^{1/ m}$ 倍，以进行时间上的调整。具体公式为：

$P V_{b e g in} = P V_{e n d} \cdot (1 + i)^{1/ m}$

这样，我们能有效地将期末付的现值转化为期初付的现值。

实例计算

最后，通过一个例题来计算一项 $10$ 年期的年金。假设该年金每月末支付一次，并且付款额每年增长 $5%$ （即 $r = 0.05$ ）。首先，我们需要将该年金转化为每年末支付一次的年金。相关的计算步骤如下：

计算有效利率：根据每年支付 $m$ 次的情况，每月支付一次，我们有 $m = 12$ 。
转换年金类型：可以通过计算相应的现值公式，将每月支付的年金转换为年末支付的形式。
计算现值：用转换后的现值乘以 $\frac{i}{i ( m )}$ ，得到在时间零点的现值。

现值公式

对于每年支付 $m$ 次的年金，其现值可以表示为：

$P V = t = 1 \sum n \frac{P _{t}}{( 1 + i ) ^{t}}$

其中， $P_{t}$ 是每期付款， $n$ 是总的支付期数。

3.8 连续支付的变额年金

本视频介绍了连续支付的变额年金的计算方法。连续支付的变额年金是指每一时刻（即付款是连续发生的）所支付的金额不固定，可能会随着一定的规则而变化。与传统的年金不同，连续支付形式能够更精确地反映在某些金融产品中，特别是在现金流和收益逐渐变化的情境下。

常见的变额年金

在金融数学中，变额年金分为三类主要形式：

递增年金 (Increasing Annuity)：每年的支付额随着时间逐年增加。例如，如果每年增加固定的金额 $d$ ，那么第 $t$ 年的付款 $P_{t}$ 可以表示为 $P_{1} + (t - 1) \cdot d$ 。
递减年金 (Decreasing Annuity)：每年的支付额逐年减少。即每年的付款按某个固定的减少幅度递减。
复递增年金 (Growing Annuity)：支付的金额按固定比例逐年增加。公式一般为 $P_{t} = P_{1} (1 + r)^{t - 1}$ ，其中 $r$ 为增长率。

价值计算方法

对于这三种变额年金，在连续支付条件下的现值计算方法如下：

现值转换

在连续支付的情况下，每年末支付一次的变额年金的现值计算结果会通过以下公式进行调整：

$P V_{co n t in u o u s} = P V_{d i scre t e} \cdot \frac{i}{δ}$

其中：

$P V_{co n t in u o u s}$ 表示连续支付的年金现值。
$P V_{d i scre t e}$ 表示每年支付一次的年金现值。
$i$ 是年利率。
$δ$ 是持续支付的贴现率，通常表示为 $δ = ln (1 + i)$ 。

这个公式说明，连续支付的年金将得到更高的现值，因为多频支付减少了时间价值的影响。

各类变额年金的现值

对于连续支付的递增年金、递减年金和复递增年金，它们的现值分别等于每年末支付一次的对应年金现值乘以 $\frac{i}{δ}$ 。因此，公式为：

连续递增年金：

$P V_{increasing} = P V_{discrete, increasing} \cdot \frac{i}{δ}$
连续递减年金：

$P V_{decreasing} = P V_{discrete, decreasing} \cdot \frac{i}{δ}$
连续复递增年金：

$P V_{growing} = P V_{discrete, growing} \cdot \frac{i}{δ}$

永续年金的价值计算

此外，连续支付的递增年金的现值还可以通过极限的方式计算其对应的永续年金的价值，其结果为：

$P V_{perpetuity} = \frac{1}{d \cdot δ}$

这里的 $d$ 是每年增长的绝对值，而 $δ$ 是相应的贴现率。这一公式表明，若支付是无限期的，现值的计算将依据增长幅度与时间贴现之间的关系进行。

3.9 一般连续变额现金流

本视频介绍了连续变额现金流的计算方法。连续变额现金流指的是付款额随着时间的推移而连续不断变化的现金流。这种现金流常见于投资和金融产品的分析中，尤其是在贷款、租赁和某些类型的年金中。

现值的计算方法

在计算连续变额现金流在时间零点的现值时，可以使用积分的方法。具体步骤如下：

付款率的定义：设连续变额现金流的付款率为 $R (t)$ ，即在时间 $t$ 的付款额。
贴现因子的定义：使用贴现函数 $e^{- r t}$ ，其中 $r$ 是连续的贴现率。这一函数用于将未来某时点的现金流折现到当前时点。
现值的计算：将付款率与贴现函数相乘，并在付款期间 $[0, T]$ 进行积分，得到的公式为：

$P V = \int_{0}^{T} R (t) e^{- r t}, d t$

这个结果即为连续变额现金流在时间零点的现值。

连续递增年金和连续递减年金

对于连续递增年金和连续递减年金，可以使用类似的方法进行计算。假设每年的付款率以固定比例递增或递减，现值计算公式稍作调整。例如，对于连续递增年金，付款率可表述为：

$R (t) = R_{0} (1 + g)^{t}$

其中 $R_{0}$ 是初始付款额， $g$ 是增长率。相应的现值计算将为：

$P V = \int_{0}^{T} R_{0} (1 + g)^{t} e^{- r t}, d t$

类似的，对于递减年金，付款率将相应调整为递减形式，并进行相同的积分计算。

期末付变额年金和分期支付

对于期末付的变额年金，若将每年末的付款转化为每年分 $m$ 次支付，则年金的现值将会变为原来的 $\frac{i}{i ( m )}$ 倍，其中 $i (m)$ 是调整后的有效利率。调整有效利率的方式如下：

$i (m) = \frac{i}{m}$

这里的 $i$ 是年利率。这样的分期支付可以帮助在计算上更好地反映出时间价值的效应。

连续支付的变额年金

对于连续支付的变额年金，其价值将变为原年金价值的 $\frac{i}{δ}$ 倍，这里 $δ$ 是连续支付过程中使用的贴现率，通常为 $δ = ln (1 + i)$ ：

$P V_{co n t in u o u s} = P V \cdot \frac{i}{δ}$

这样的方法可以更好地运用于连续现金流的分析，确保其时间价值的准确折现。

结论

最后，连续变额现金流的现值可以通过将付款率 $R (t)$ 乘以贴现函数 $e^{- r t}$ ，然后在付款区间 $[0, T]$ 进行积分的方法进行计算。综合以上计算方法，可以有效地对不同形式的现金流进行评估和分析。

財務金融