子数组与贪心算法
53. Maximum Subarray
Given an integer array nums, find the subarray with the largest sum, and return its sum.
Example 1:
Input: nums = [-2,1,-3,4,-1,2,1,-5,4]
Output: 6
Explanation: The subarray [4,-1,2,1] has the largest sum 6.
Example 2:
Input: nums = [1]
Output: 1
Explanation: The subarray [1] has the largest sum 1.
Example 3:
Input: nums = [5,4,-1,7,8]
Output: 23
Explanation: The subarray [5,4,-1,7,8] has the largest sum 23.
Constraints:
1 <= nums.length <= 10^5-10^4 <= nums[i] <= 10^4
Follow up: If you have figured out the O(n) solution, try coding another solution using the divide and conquer approach, which is more subtle.
思路
贪心
贪心贪的是哪里呢?
如果 -2 1 在一起,计算起点的时候,一定是从 1 开始计算,因为负数只会拉低总和,这就是贪心贪的地方!
局部最优:当前“连续和”为负数的时候立刻放弃,从下一个元素重新计算“连续和”,因为负数加上下一个元素 “连续和”只会越来越小。
全局最优:选取最大“连续和”
局部最优的情况下,并记录最大的“连续和”,可以推出全局最优。
从代码角度上来讲:遍历 nums,从头开始用 count 累积,如果 count 一旦加上 nums[i]变为负数,那么就应该从 nums[i+1]开始从 0 累积 count 了,因为已经变为负数的 count,只会拖累总和。
这相当于是暴力解法中的不断调整最大子序和区间的起始位置。
那有同学问了,区间终止位置不用调整么? 如何才能得到最大“连续和”呢?
区间的终止位置,其实就是如果 count 取到最大值了,及时记录下来了。例如如下代码:
if (count > result) result = count;
这样相当于是用 result 记录最大子序和区间和(变相的算是调整了终止位置)。
如动画所示:

红色的起始位置就是贪心每次取 count 为正数的时候,开始一个区间的统计。
当然题目没有说如果数组为空,应该返回什么,所以数组为空的话返回啥都可以了。
常见误区一:
不少同学认为 如果输入用例都是-1,或者都是负数,这个贪心算法跑出来的结果是 0, 这是又一次证明脑洞模拟不靠谱的经典案例,建议大家把代码运行一下试一试,就知道了,也会理解为什么 result 要初始化为最小负数了。
常见误区二:
大家在使用贪心算法求解本题,经常陷入的误区,就是分不清,是遇到 负数就选择起始位置,还是连续和为负选择起始位置。
在动画演示用,大家可以发现, 4,遇到 -1 的时候,我们依然累加了,为什么呢?
因为和为 3,只要连续和还是正数就会 对后面的元素 起到增大总和的作用。 所以只要连续和为正数我们就保留。
这里也会有录友疑惑,那 4 + -1 之后 不就变小了吗? 会不会错过 4 成为最大连续和的可能性?
其实并不会,因为还有一个变量 result 一直在更新最大的连续和,只要有更大的连续和出现,result 就更新了,那么 result 已经把 4 更新了,后面连续和变成 3,也不会对最后结果有影响。
动态规划
这次我们用动态规划的思路再来分析一次。
动规五部曲如下:
- 确定dp数组(dp table)以及下标的含义
dp[i]:包括下标i(以nums[i]为结尾)的最大连续子序列和为dp[i]。
- 确定递推公式
dp[i]只有两个方向可以推出来:
- dp[i - 1] + nums[i],即:nums[i]加入当前连续子序列和
- nums[i],即:从头开始计算当前连续子序列和
一定是取最大的,所以dp[i] = max(dp[i - 1] + nums[i], nums[i]);
- dp数组如何初始化
从递推公式可以看出来dp[i]是依赖于dp[i - 1]的状态,dp[0]就是递推公式的基础。
dp[0]应该是多少呢?
根据dp[i]的定义,很明显dp[0]应为nums[0]即dp[0] = nums[0]。
- 确定遍历顺序
递推公式中dp[i]依赖于dp[i - 1]的状态,需要从前向后遍历。
- 举例推导dp数组
以示例一为例,输入:nums = [-2,1,-3,4,-1,2,1,-5,4],对应的dp状态如下:
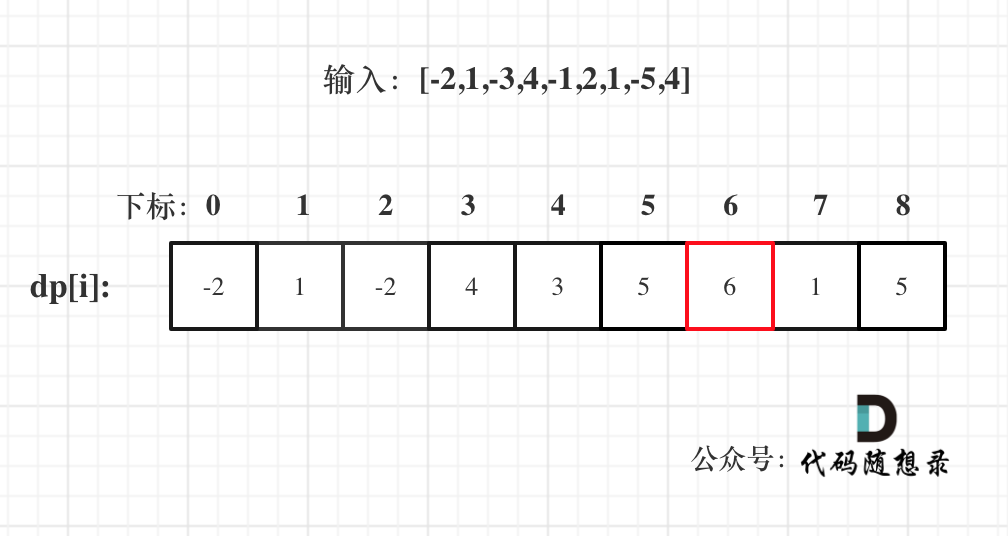
注意最后的结果可不是dp[nums.size() - 1]! ,而是dp[6]。
在回顾一下dp[i]的定义:包括下标i之前的最大连续子序列和为dp[i]。
那么我们要找最大的连续子序列,就应该找每一个i为终点的连续最大子序列。
所以在递推公式的时候,可以直接选出最大的dp[i]。
C++解法
贪心解法:
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int result = INT32_MIN;
int count = 0;
for (int i = 0; i < nums.size(); i++) {
count += nums[i];
if (count > result) { // 取区间累计的最大值(相当于不断确定最大子序终止位置)
result = count;
}
if (count <= 0) count = 0; // 相当于重置最大子序起始位置,因为遇到负数一定是拉低总和
}
return result;
}
};
- 时间复杂度:O(n)
- 空间复杂度:O(1)
动态规划解法:
class Solution {
public:
int maxSubArray(vector<int>& nums) {
if (nums.size() == 0) return 0;
vector<int> dp(nums.size());
dp[0] = nums[0];
int result = dp[0];
for (int i = 1; i < nums.size(); i++) {
dp[i] = max(dp[i - 1] + nums[i], nums[i]); // 状态转移公式
if (dp[i] > result) result = dp[i]; // result 保存dp[i]的最大值
}
return result;
}
};
- 时间复杂度:O(n)
- 空间复杂度:O(n)
Java解法
贪心算法:
class Solution {
public int maxSubArray(int[] nums) {
int currSum = 0;
int maxSum = Integer.MIN_VALUE; // 修正这里的MIN_VALUE
for (int i = 0; i < nums.length; i++) {
currSum += nums[i];
if (currSum > maxSum) {
maxSum = currSum;
}
if (currSum < 0) {
currSum = 0;
}
}
return maxSum;
}
}