N叉树基本操作

• 589. N-ary Tree Preorder Traversal
  • 思路
  • C++解法
• 590. N-ary Tree Postorder Traversal
  • 思路
  • C++解法
• 429. N-ary Tree Level Order Traversal
  • 思路
  • C++解法
• 310. Minimum Height Trees
  • 思路
  • C++解法
  • Java解法
  • Python3解法

589. N-ary Tree Preorder Traversal

Given the root of an n-ary tree, return the preorder traversal of its nodes' values.

Nary-Tree input serialization is represented in their level order traversal. Each group of children is separated by the null value (See examples)

Example 1:

Input: root = [1,null,3,2,4,null,5,6]
Output: [1,3,5,6,2,4]

Example 2:

Input: root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
Output: [1,2,3,6,7,11,14,4,8,12,5,9,13,10]

Constraints:

• The number of nodes in the tree is in the range [0, 10^4].
• 0 <= Node.val <= 10^4
• The height of the n-ary tree is less than or equal to 1000.

Follow up: Recursive solution is trivial, could you do it iteratively?

思路

递归或迭代求解

C++解法

递归法完整代码如下所示：

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val) {
        val = _val;
    }

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
public:
    void traversal(Node* root, vector<int>& result){
        if(root == NULL){
            return;
        }
        result.push_back(root->val);
        for(Node* child : root->children){
            traversal(child, result);
        }
    }
    vector<int> preorder(Node* root) {
        vector<int> result;
        traversal(root, result);
        return result;
    }
};

迭代法完整代码如下所示：

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val) {
        val = _val;
    }

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
public:
    vector<int> preorder(Node* root) {
        vector<int> result;
        if(root == NULL) return result;
        stack<Node*> st;
        st.push(root);
        while(!st.empty()){
            Node* node = st.top();
            st.pop();
            result.push_back(node->val);
            int size = node->children.size();
            for(int i = size - 1; i >= 0; i--){
                st.push(node->children[i]);
            }
        }
        return result;
    }
};

590. N-ary Tree Postorder Traversal

Given the root of an n-ary tree, return the postorder traversal of its nodes' values.

Nary-Tree input serialization is represented in their level order traversal. Each group of children is separated by the null value (See examples)

Example 1:

Input: root = [1,null,3,2,4,null,5,6]
Output: [5,6,3,2,4,1]

Example 2:

Input: root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
Output: [2,6,14,11,7,3,12,8,4,13,9,10,5,1]

Constraints:

• The number of nodes in the tree is in the range [0, 10^4].
• 0 <= Node.val <= 10^4
• The height of the n-ary tree is less than or equal to 1000.

Follow up: Recursive solution is trivial, could you do it iteratively?

思路

递归或迭代

C++解法

递归法完整代码如下所示：

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val) {
        val = _val;
    }

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
public:
    void traversal(Node* root, vector<int>& result){
        if(root == NULL){
            return;
        }
        for(Node* child : root->children){
            traversal(child, result);
        }
        result.push_back(root->val);
    }
    vector<int> postorder(Node* root) {
        vector<int> result;
        traversal(root, result);
        return result;
    }
};

迭代法完整代码如下所示：

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val) {
        val = _val;
    }

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
public:
    vector<int> postorder(Node* root) {
        vector<int> result;
        if(root == NULL) return result;
        stack<Node*> st;
        st.push(root);
        while(!st.empty()){
            Node* node = st.top();
            st.pop();
            int size = node->children.size();
            for(int i = 0; i < size; i++){
                st.push(node->children[i]);
            }
            result.push_back(node->val);
        }
        reverse(result.begin(), result.end());
        return result;
    }
};

429. N-ary Tree Level Order Traversal

Given an n-ary tree, return the level order traversal of its nodes' values.

Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value (See examples).

Example 1:

Input: root = [1,null,3,2,4,null,5,6]
Output: [[1],[3,2,4],[5,6]]

Example 2:

Input: root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
Output: [[1],[2,3,4,5],[6,7,8,9,10],[11,12,13],[14]]

Constraints:

• The height of the n-ary tree is less than or equal to 1000
• The total number of nodes is between [0, 10^4]

思路

改写层序遍历代码即可

C++解法

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val) {
        val = _val;
    }

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
public:
    vector<vector<int>> levelOrder(Node* root) {
        vector<vector<int>> result;
        queue<Node*> que;
        if(root == NULL) return result;
        que.push(root);
        while(!que.empty()){
            vector<int> nums;
            int size = que.size();
            for(int i = 0; i < size; i++){
                Node* cur = que.front();
                que.pop();
                nums.push_back(cur->val);
                for(Node* node : cur->children){
                    que.push(node);
                }
            }
            result.push_back(nums);
        }
        return result;
    }
};

310. Minimum Height Trees

A tree is an undirected graph in which any two vertices are connected by exactly one path. In other words, any connected graph without simple cycles is a tree.

Given a tree of n nodes labelled from 0 to n - 1, and an array of n - 1 edges where edges[i] = [ai, bi] indicates that there is an undirected edge between the two nodes ai and bi in the tree, you can choose any node of the tree as the root. When you select a node x as the root, the result tree has height h. Among all possible rooted trees, those with minimum height (i.e. min(h))  are called minimum height trees (MHTs).

Return a list of all MHTs' root labels. You can return the answer in any order.

The height of a rooted tree is the number of edges on the longest downward path between the root and a leaf.

Example 1:

Input: n = 4, edges = [[1,0],[1,2],[1,3]]
Output: [1]
Explanation: As shown, the height of the tree is 1 when the root is the node with label 1 which is the only MHT.

Example 2:

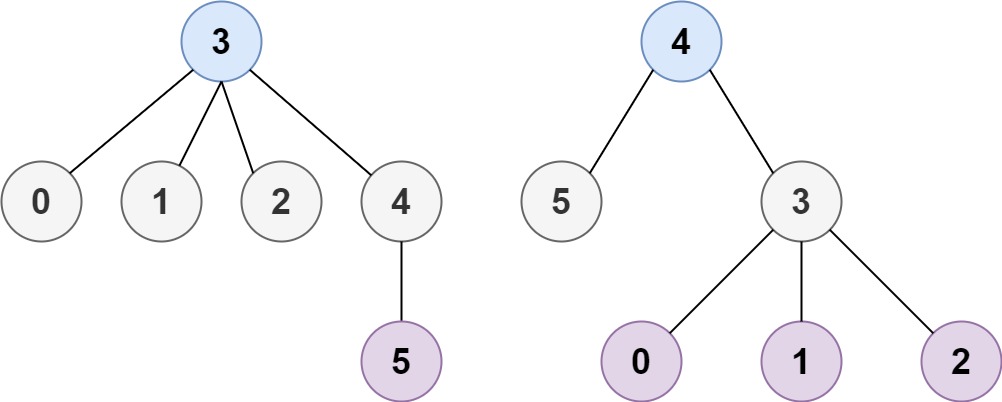
Input: n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]]
Output: [3,4]

Constraints:

• 1 <= n <= 2 * 10^4
• edges.length == n - 1
• 0 <= ai, bi < n
• ai != bi
• All the pairs (ai, bi) are distinct.
• The given input is guaranteed to be a tree and there will be no repeated edges.

思路

C++解法

class Solution {
public:
    vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) {
        if (n == 1) return {0};
    
        std::vector<std::list<int>> adjacency_list(n);
        std::vector<int> degree(n, 0);
        for (auto& edge : edges) {
            int u = edge[0], v = edge[1];
            adjacency_list[u].push_back(v);
            adjacency_list[v].push_back(u);
            degree[u]++;
            degree[v]++;
        }
        
        std::queue<int> leaves;
        for (int i = 0; i < n; ++i) {
            if (degree[i] == 1) leaves.push(i);
        }
        
        int remainingNodes = n;
        while (remainingNodes > 2) {
            int leavesCount = leaves.size();
            remainingNodes -= leavesCount;
            for (int i = 0; i < leavesCount; ++i) {
                int leaf = leaves.front();
                leaves.pop();
                for (int neighbor : adjacency_list[leaf]) {
                    if (--degree[neighbor] == 1) {
                        leaves.push(neighbor);
                    }
                }
            }
        }
        
        std::vector<int> result;
        while (!leaves.empty()) {
            result.push_back(leaves.front());
            leaves.pop();
        }
        
        return result;
    }
};

Java解法

class Solution {
    public List<Integer> findMinHeightTrees(int n, int[][] edges) {
        if (n == 1) return Collections.singletonList(0);
        
        int[] degree = new int[n];
        Map<Integer, List<Integer>> adjacencyList = new HashMap<>();
        for (int[] edge : edges) {
            degree[edge[0]]++;
            degree[edge[1]]++;
            adjacencyList.computeIfAbsent(edge[0], x -> new ArrayList<>()).add(edge[1]);
            adjacencyList.computeIfAbsent(edge[1], x -> new ArrayList<>()).add(edge[0]);
        }

        Queue<Integer> leaves = new LinkedList<>();
        for (int i = 0; i < degree.length; i++) {
            if (degree[i] == 1) {
                leaves.add(i);
            }
        }

        int remainingNodes = n;
        while (remainingNodes > 2) {
            int size = leaves.size();
            remainingNodes -= size;
            for (int i = 0; i < size; i++) {
                int leaf = leaves.poll();
                for (int neighbor : adjacencyList.get(leaf)) {
                    if (--degree[neighbor] == 1) {
                        leaves.add(neighbor);
                    }
                }
            }
        }

        return new ArrayList<>(leaves);
    }
}

Python3解法

class Solution:
    def findMinHeightTrees(self, n: int, edges: List[List[int]]) -> List[int]:
        if n == 1:
            return [0]
        
        # Initialize the adjacency list and degree of each node
        adjacency_list = defaultdict(list)
        degree = [0] * n
        for u, v in edges:
            adjacency_list[u].append(v)
            adjacency_list[v].append(u)
            degree[u] += 1
            degree[v] += 1
        
        # Initialize leaves queue
        leaves = deque([i for i in range(n) if degree[i] == 1])
        
        # Trim leaves until 2 or fewer nodes remain
        remaining_nodes = n
        while remaining_nodes > 2:
            leaves_count = len(leaves)
            remaining_nodes -= leaves_count
            for _ in range(leaves_count):
                leaf = leaves.popleft()
                for neighbor in adjacency_list[leaf]:
                    degree[neighbor] -= 1
                    if degree[neighbor] == 1:
                        leaves.append(neighbor)
        
        return list(leaves)