二叉树物理性质
- # 958. Check Completeness of a Binary Tree
- 543. Diameter of Binary Tree
- 199. Binary Tree Right Side View
- 226. Invert Binary Tree
- 655. Print Binary Tree
# 958. Check Completeness of a Binary Tree
Given the root of a binary tree, determine if it is a complete binary tree.
In a complete binary tree, every level, except possibly the last, is completely filled, and all nodes in the last level are as far left as possible. It can have between 1 and 2h nodes inclusive at the last level h.
Example 1:

Input: root = [1,2,3,4,5,6]
Output: true
Explanation: Every level before the last is full (ie. levels with node-values {1} and {2, 3}), and all nodes in the last level ({4, 5, 6}) are as far left as possible.
Example 2:

Input: root = [1,2,3,4,5,null,7]
Output: false
Explanation: The node with value 7 isn't as far left as possible.
Constraints:
- The number of nodes in the tree is in the range
[1, 100]. 1 <= Node.val <= 1000
思路
Intuition :
Given the root of a binary tree, determine if it is a complete binary tree.
Approach : Breadth First Search
Traverse the tree in level-order using a queue. At each level, we add the left and right child nodes of each node to the queue.
If we encounter a null node, we still add it to the queue so that we can check if there are any more nodes left in the next step.
Once we have traversed the entire tree, we check if there are any remaining nodes in the queue. If there are, it means the tree is not complete, and we return false.
Otherwise, the tree is complete, and we return true.
Complexity :
Time complexity : O(n)
Space complexity: O(n)
C++解法
// Define the Solution class
class Solution {
public:
// Define the isCompleteTree function that takes a TreeNode pointer as input and returns a boolean
bool isCompleteTree(TreeNode* root) {
// Check if the root node is null, if so, return true (an empty tree is complete)
if (root == nullptr)
return true;
// Create a queue to store the nodes of the tree in level order
queue<TreeNode*> q{{root}};
// Traverse the tree in level order
while (q.front() != nullptr) {
// Remove the first node from the queue
TreeNode* node = q.front();
q.pop();
// Add the left and right child nodes of the current node to the queue
q.push(node->left);
q.push(node->right);
}
// Remove any remaining null nodes from the front of the queue
while (!q.empty() && q.front() == nullptr)
q.pop();
// Check if there are any remaining nodes in the queue
// If so, the tree is not complete, so return false
// Otherwise, the tree is complete, so return true
return q.empty();
}
};
Java解法
// Define the Solution class
class Solution {
// Define the isCompleteTree function that takes a TreeNode as input and returns a boolean
public boolean isCompleteTree(TreeNode root) {
// Check if the root node is null, if so, return true (an empty tree is complete)
if (root == null)
return true;
// Create a queue to store the nodes of the tree in level order
Queue<TreeNode> q = new LinkedList<>(Arrays.asList(root));
// Traverse the tree in level order
while (q.peek() != null) {
// Remove the first node from the queue
TreeNode node = q.poll();
// Add the left and right child nodes of the current node to the queue
q.offer(node.left);
q.offer(node.right);
}
// Remove any remaining null nodes from the end of the queue
while (!q.isEmpty() && q.peek() == null)
q.poll();
// Check if there are any remaining nodes in the queue
// If so, the tree is not complete, so return false
// Otherwise, the tree is complete, so return true
return q.isEmpty();
}
}
Python3解法
from collections import deque
class Solution:
def isCompleteTree(self, root: TreeNode) -> bool:
# Check if the root node is None, if so, return True (an empty tree is complete)
if not root:
return True
# Create a deque to store the nodes of the tree in level order
q = deque([root])
# Traverse the tree in level order
while q[0] is not None:
# Remove the first node from the deque
node = q.popleft()
# Add the left and right child nodes of the current node to the deque
q.append(node.left)
q.append(node.right)
# Remove any remaining None nodes from the beginning of the deque
while q and q[0] is None:
q.popleft()
# Check if there are any remaining nodes in the deque
# If so, the tree is not complete, so return False
# Otherwise, the tree is complete, so return True
return not bool(q)
Go解法
543. Diameter of Binary Tree
Description
Given the root of a binary tree, return the length of the diameter of the tree.
The diameter of a binary tree is the length of the longest path between any two nodes in a tree. This path may or may not pass through the root.
The length of a path between two nodes is represented by the number of edges between them.
Example 1:

Input: root = [1,2,3,4,5]
Output: 3
Explanation: 3 is the length of the path [4,2,1,3] or [5,2,1,3].
Example 2:
Input: root = [1,2]
Output: 1
Constraints:
- The number of nodes in the tree is in the range
[1, 10^4]. -100 <= Node.val <= 100
思路
方法一:深度优先搜索
首先我们知道一条路径的长度为该路径经过的节点数减一,所以求直径(即求路径长度的最大值)等效于求路径经过节点数的最大值减一。
而任意一条路径均可以被看作由某个节点为起点,从其左儿子和右儿子向下遍历的路径拼接得到。
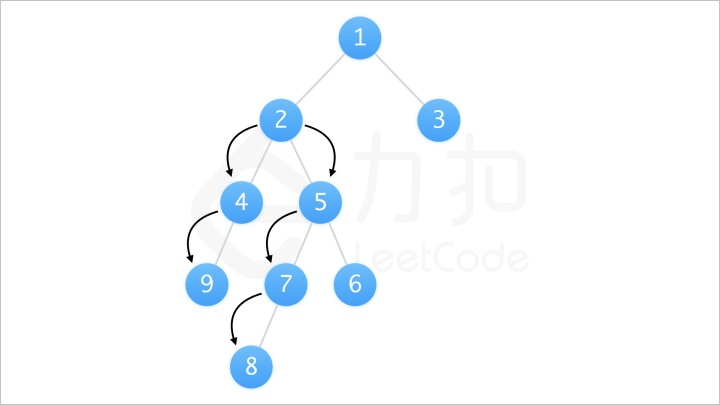
如图我们可以知道路径 [9, 4, 2, 5, 7, 8] 可以被看作以 2 为起点,从其左儿子向下遍历的路径 [2, 4, 9] 和从其右儿子向下遍历的路径 [2, 5, 7, 8] 拼接得到。
假设我们知道对于该节点的左儿子向下遍历经过最多的节点数 L (即以左儿子为根的子树的深度) 和其右儿子向下遍历经过最多的节点数 R (即以右儿子为根的子树的深度),那么以该节点为起点的路径经过节点数的最大值即为 L+R+1 。
我们记节点 node 为起点的路径经过节点数的最大值为 dnode,那么二叉树的直径就是所有节点 dnode的最大值减一。
最后的算法流程为:我们定义一个递归函数 depth(node) 计算 dnode ,函数返回该节点为根的子树的深度。先递归调用左儿子和右儿子求得它们为根的子树的深度 L 和 R ,则该节点为根的子树的深度即为max(L,R)+1
该节点的 dnode值为L+R+1
递归搜索每个节点并设一个全局变量 ans 记录 dnode的最大值,最后返回 ans-1 即为树的直径。
作者:力扣官方题解 链接: https://leetcode.cn/problems/diameter-of-binary-tree/solutions/139683/er-cha-shu-de-zhi-jing-by-leetcode-solution/ 来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
C++ 解法
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int diameterOfBinaryTree(TreeNode* root) {
int result = INT_MIN;
getMaxHeight(root, result);
return result;
}
int getMaxHeight(TreeNode* root, int& result){
if(root == NULL){
return 0;
}
int left = getMaxHeight(root->left, result);
int right = getMaxHeight(root->right, result);
result = max(result, left + right);
return max(left, right) + 1;
}
};
优化版本:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int diameterOfBinaryTree(TreeNode* root) {
int result = INT_MIN;
getMaxHeight(root, result);
return result;
}
int getMaxHeight(TreeNode* root, int& result){
if(root == NULL){
return 0;
}
if (map.count(root)) return map[root];
int left = getMaxHeight(root->left, result);
int right = getMaxHeight(root->right, result);
result = max(result, left + right);
return map[root] = max(left, right) + 1;
}
private:
unordered_map<TreeNode*, int> map;
};
Java 解法
Python 解法
199. Binary Tree Right Side View
Description
Given the root of a binary tree, imagine yourself standing on the right side of it, return the values of the nodes you can see ordered from top to bottom.
Example 1:

Input: root = [1,2,3,null,5,null,4]
Output: [1,3,4]
Example 2:
Input: root = [1,null,3]
Output: [1,3]
Example 3:
Input: root = []
Output: []
Constraints:
- The number of nodes in the tree is in the range
[0, 100]. -100 <= Node.val <= 100
思路
层次遍历,每层最后一个节点
由于树的形状无法提前知晓,不可能设计出优于 O(n) 的算法。因此,我们应该试着寻找线性时间解。带着这个想法,我们来考虑一些同等有效的方案。
方法一:深度优先搜索
思路
我们对树进行深度优先搜索,在搜索过程中,我们总是先访问右子树。那么对于每一层来说,我们在这层见到的第一个结点一定是最右边的结点。
算法
这样一来,我们可以存储在每个深度访问的第一个结点,一旦我们知道了树的层数,就可以得到最终的结果数组。
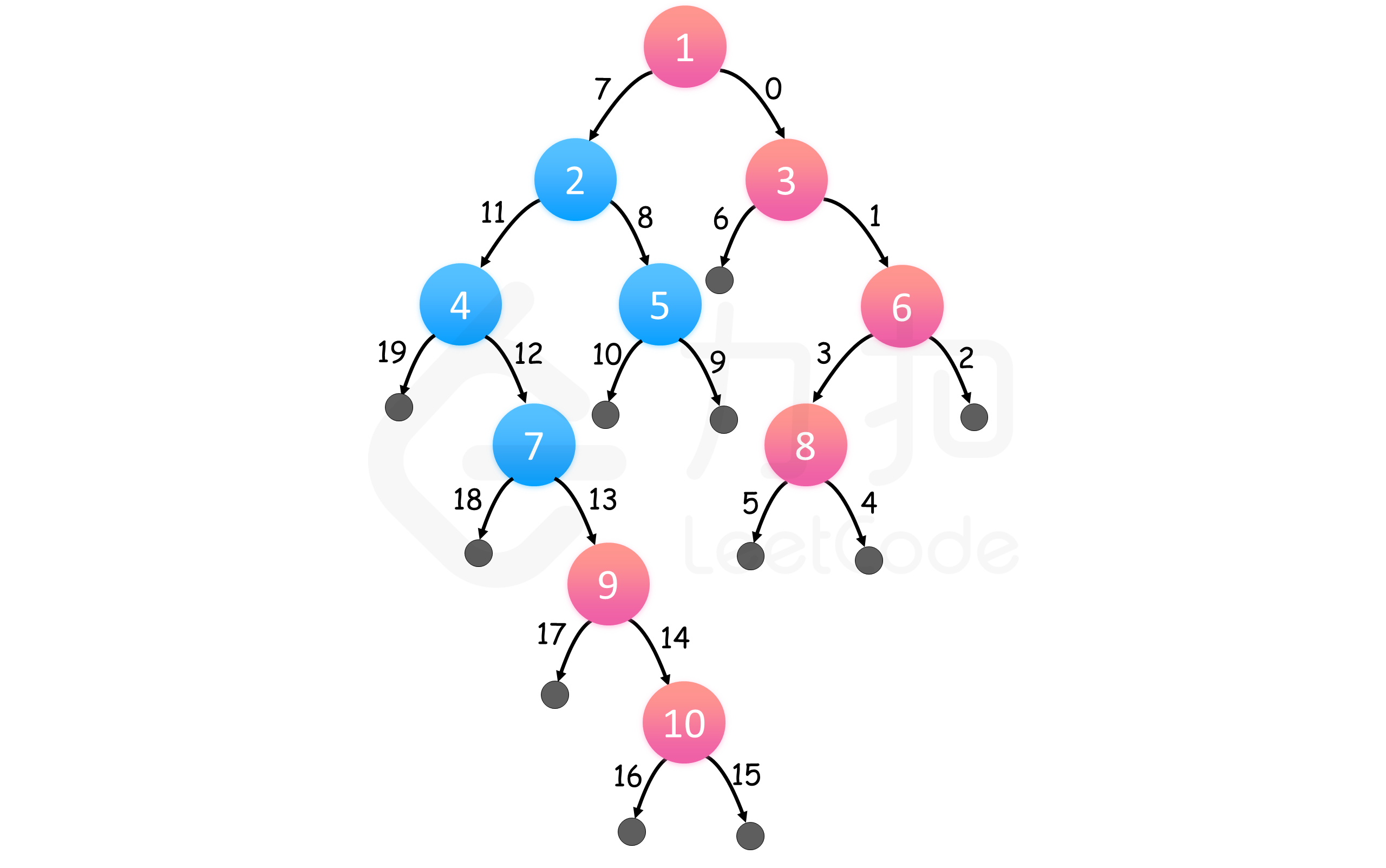
上图表示了问题的一个实例。红色结点自上而下组成答案,边缘以访问顺序标号。
复杂度分析
时间复杂度 : O(n)。深度优先搜索最多访问每个结点一次,因此是线性复杂度。
空间复杂度 : O(n)。最坏情况下,栈内会包含接近树高度的结点数量,占用 O(n) 的空间。
方法二:广度优先搜索
思路
我们可以对二叉树进行层次遍历,那么对于每层来说,最右边的结点一定是最后被遍历到的。二叉树的层次遍历可以用广度优先搜索实现。
算法
执行广度优先搜索,左结点排在右结点之前,这样,我们对每一层都从左到右访问。因此,只保留每个深度最后访问的结点,我们就可以在遍历完整棵树后得到每个深度最右的结点。除了将栈改成队列,并去除了 rightmost_value_at_depth 之前的检查外,算法没有别的改动。
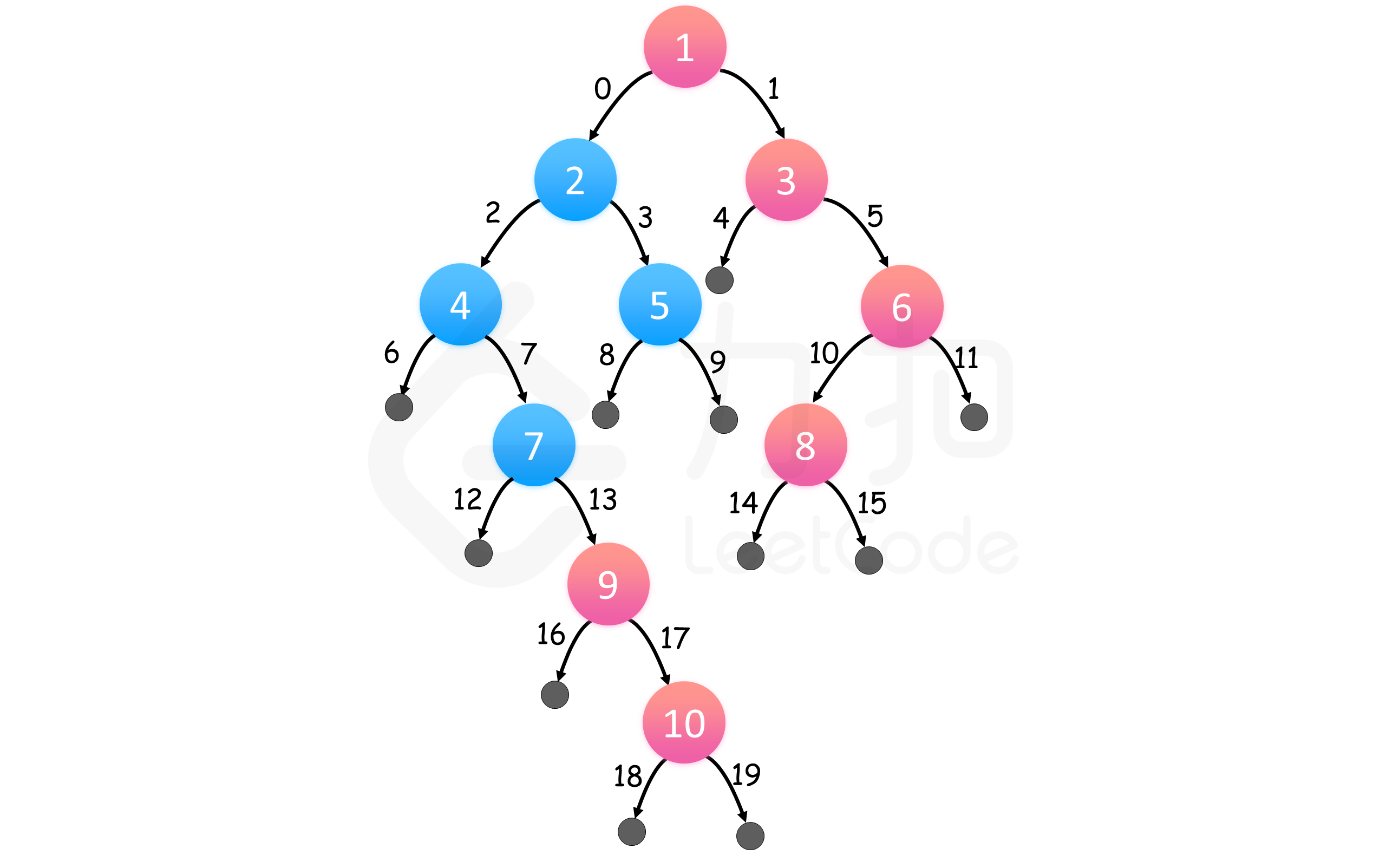
上图表示了同一个示例,红色结点自上而下组成答案,边缘以访问顺序标号。
复杂度分析
时间复杂度 : O(n)。 每个节点最多进队列一次,出队列一次,因此广度优先搜索的复杂度为线性。
空间复杂度 : O(n)。每个节点最多进队列一次,所以队列长度最大不不超过 n,所以这里的空间代价为 O(n)。
作者:力扣官方题解
链接: https://leetcode.cn/problems/binary-tree-right-side-view/solutions/213494/er-cha-shu-de-you-shi-tu-by-leetcode-solution/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
C++ 解法
dfs
class Solution {
public:
vector<int> rightSideView(TreeNode* root) {
unordered_map<int, int> rightmostValueAtDepth;
int max_depth = -1;
stack<TreeNode*> nodeStack;
stack<int> depthStack;
nodeStack.push(root);
depthStack.push(0);
while (!nodeStack.empty()) {
TreeNode* node = nodeStack.top();nodeStack.pop();
int depth = depthStack.top();depthStack.pop();
if (node != NULL) {
// 维护二叉树的最大深度
max_depth = max(max_depth, depth);
// 如果不存在对应深度的节点我们才插入
if (rightmostValueAtDepth.find(depth) == rightmostValueAtDepth.end()) {
rightmostValueAtDepth[depth] = node -> val;
}
nodeStack.push(node -> left);
nodeStack.push(node -> right);
depthStack.push(depth + 1);
depthStack.push(depth + 1);
}
}
vector<int> rightView;
for (int depth = 0; depth <= max_depth; ++depth) {
rightView.push_back(rightmostValueAtDepth[depth]);
}
return rightView;
}
};
bfs
class Solution {
public:
vector<int> rightSideView(TreeNode* root) {
unordered_map<int, int> rightmostValueAtDepth;
int max_depth = -1;
queue<TreeNode*> nodeQueue;
queue<int> depthQueue;
nodeQueue.push(root);
depthQueue.push(0);
while (!nodeQueue.empty()) {
TreeNode* node = nodeQueue.front();nodeQueue.pop();
int depth = depthQueue.front();depthQueue.pop();
if (node != NULL) {
// 维护二叉树的最大深度
max_depth = max(max_depth, depth);
// 由于每一层最后一个访问到的节点才是我们要的答案,因此不断更新对应深度的信息即可
rightmostValueAtDepth[depth] = node -> val;
nodeQueue.push(node -> left);
nodeQueue.push(node -> right);
depthQueue.push(depth + 1);
depthQueue.push(depth + 1);
}
}
vector<int> rightView;
for (int depth = 0; depth <= max_depth; ++depth) {
rightView.push_back(rightmostValueAtDepth[depth]);
}
return rightView;
}
};
Java 解法
dfs
class Solution {
public List<Integer> rightSideView(TreeNode root) {
Map<Integer, Integer> rightmostValueAtDepth = new HashMap<Integer, Integer>();
int max_depth = -1;
Deque<TreeNode> nodeStack = new LinkedList<TreeNode>();
Deque<Integer> depthStack = new LinkedList<Integer>();
nodeStack.push(root);
depthStack.push(0);
while (!nodeStack.isEmpty()) {
TreeNode node = nodeStack.pop();
int depth = depthStack.pop();
if (node != null) {
// 维护二叉树的最大深度
max_depth = Math.max(max_depth, depth);
// 如果不存在对应深度的节点我们才插入
if (!rightmostValueAtDepth.containsKey(depth)) {
rightmostValueAtDepth.put(depth, node.val);
}
nodeStack.push(node.left);
nodeStack.push(node.right);
depthStack.push(depth + 1);
depthStack.push(depth + 1);
}
}
List<Integer> rightView = new ArrayList<Integer>();
for (int depth = 0; depth <= max_depth; depth++) {
rightView.add(rightmostValueAtDepth.get(depth));
}
return rightView;
}
}
bfs
class Solution {
public List<Integer> rightSideView(TreeNode root) {
Map<Integer, Integer> rightmostValueAtDepth = new HashMap<Integer, Integer>();
int max_depth = -1;
Queue<TreeNode> nodeQueue = new LinkedList<TreeNode>();
Queue<Integer> depthQueue = new LinkedList<Integer>();
nodeQueue.add(root);
depthQueue.add(0);
while (!nodeQueue.isEmpty()) {
TreeNode node = nodeQueue.remove();
int depth = depthQueue.remove();
if (node != null) {
// 维护二叉树的最大深度
max_depth = Math.max(max_depth, depth);
// 由于每一层最后一个访问到的节点才是我们要的答案,因此不断更新对应深度的信息即可
rightmostValueAtDepth.put(depth, node.val);
nodeQueue.add(node.left);
nodeQueue.add(node.right);
depthQueue.add(depth + 1);
depthQueue.add(depth + 1);
}
}
List<Integer> rightView = new ArrayList<Integer>();
for (int depth = 0; depth <= max_depth; depth++) {
rightView.add(rightmostValueAtDepth.get(depth));
}
return rightView;
}
}
Python 解法
dfs
class Solution:
def rightSideView(self, root: TreeNode) -> List[int]:
rightmost_value_at_depth = dict() # 深度为索引,存放节点的值
max_depth = -1
stack = [(root, 0)]
while stack:
node, depth = stack.pop()
if node is not None:
# 维护二叉树的最大深度
max_depth = max(max_depth, depth)
# 如果不存在对应深度的节点我们才插入
rightmost_value_at_depth.setdefault(depth, node.val)
stack.append((node.left, depth + 1))
stack.append((node.right, depth + 1))
return [rightmost_value_at_depth[depth] for depth in range(max_depth + 1)]
bfs
class Solution:
def rightSideView(self, root: TreeNode) -> List[int]:
rightmost_value_at_depth = dict() # 深度为索引,存放节点的值
max_depth = -1
queue = deque([(root, 0)])
while queue:
node, depth = queue.popleft()
if node is not None:
# 维护二叉树的最大深度
max_depth = max(max_depth, depth)
# 由于每一层最后一个访问到的节点才是我们要的答案,因此不断更新对应深度的信息即可
rightmost_value_at_depth[depth] = node.val
queue.append((node.left, depth + 1))
queue.append((node.right, depth + 1))
return [rightmost_value_at_depth[depth] for depth in range(max_depth + 1)]
226. Invert Binary Tree
Given the root of a binary tree, invert the tree, and return its root.
Example 1:

Input: root = [4,2,7,1,3,6,9]
Output: [4,7,2,9,6,3,1]
Example 2:

Input: root = [2,1,3]
Output: [2,3,1]
Example 3:
Input: root = []
Output: []
Constraints:
- The number of nodes in the tree is in the range
[0, 100]. -100 <= Node.val <= 100
思路
-
先序遍历,左右交换
-
左右交换,后序遍历
C++ 解法
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
if(root == nullptr){
return root;
}
invertTree(root->left);
invertTree(root->right);
swap(root->left, root->right);
return root;
}
};
Java 解法
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode invertTree(TreeNode root) {
if(root == null){
return null;
}
if(root.left == null && root.right == null){
return root;
}
TreeNode temp = root.left;
root.left = root.right;
root.right = temp;
root.left = invertTree(root.left);
root.right = invertTree(root.right);
return root;
}
}
Python 解法
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
if not root:
return
temp = root.left
root.left = root.right
root.right = temp
self.invertTree(root.left)
self.invertTree(root.right)
return root
655. Print Binary Tree
Given the root of a binary tree, construct a 0-indexed m x n string matrix res that represents a formatted layout of the tree. The formatted layout matrix should be constructed using the following rules:
- The height of the tree is
heightand the number of rowsmshould be equal toheight + 1. - The number of columns
nshould be equal to2^{height+1} - 1. - Place the root node in the middle of the top row (more formally, at location
res[0][(n-1)/2]). - For each node that has been placed in the matrix at position
res[r][c], place its left child atres[r+1][c-2height-r-1]and its right child atres[r+1][c+2^{height-r-1}]. - Continue this process until all the nodes in the tree have been placed.
- Any empty cells should contain the empty string
"".
Return the constructed matrix res.
Example 1:
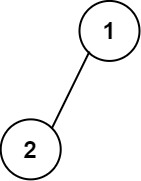
Input: root = [1,2]
Output:
[["","1",""],
["2","",""]]
Example 2:
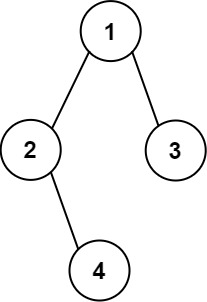
Input: root = [1,2,3,null,4]
Output:
[["","","","1","","",""],
["","2","","","","3",""],
["","","4","","","",""]]
Constraints:
- The number of nodes in the tree is in the range
[1, 210]. -99 <= Node.val <= 99- The depth of the tree will be in the range
[1, 10].
思路
C++解法
Java解法
public List<List<String>> printTree(TreeNode root) {
List<List<String>> res = new LinkedList<>();
int height = root == null ? 1 : getHeight(root);
int rows = height, columns = (int) (Math.pow(2, height) - 1);
List<String> row = new ArrayList<>();
for(int i = 0; i < columns; i++) row.add("");
for(int i = 0; i < rows; i++) res.add(new ArrayList<>(row));
populateRes(root, res, 0, rows, 0, columns - 1);
return res;
}
public void populateRes(TreeNode root, List<List<String>> res, int row, int totalRows, int i, int j) {
if (row == totalRows || root == null) return;
res.get(row).set((i+j)/2, Integer.toString(root.val));
populateRes(root.left, res, row+1, totalRows, i, (i+j)/2 - 1);
populateRes(root.right, res, row+1, totalRows, (i+j)/2+1, j);
}
public int getHeight(TreeNode root) {
if (root == null) return 0;
return 1 + Math.max(getHeight(root.left), getHeight(root.right));
}
这段代码定义了一个树的打印逻辑,用于将二叉树的结构输出为一个二维字符串列表。下面我们将详细讲解该代码,包括类TreeNode及Solution类中的各个方法,特别是populateRes函数的具体实现逻辑。
getHeight 方法
public int getHeight(TreeNode root) {
if (root == null) return 0;
else return 1 + Math.max(getHeight(root.left), getHeight(root.right));
}
- 该方法用于计算二叉树的高度。树的高度从0开始计数。
- 如果节点为空,返回0;否则,返回1加上左子树和右子树的最大高度。
- 这有助于确定打印树结构时所需的行数。
populateRes 方法
public void populateRes(TreeNode root, List<List<String>> res, int row, int totalRows, int i, int j) {
if (row == totalRows || root == null) return;
res.get(row).set((i + j) / 2, Integer.toString(root.val));
populateRes(root.left, res, row + 1, totalRows, i, (i + j) / 2 - 1);
populateRes(root.right, res, row + 1, totalRows, (i + j) / 2 + 1, j);
}
-
目的: 该方法递归地在结果列表中填充节点值。它基于树的结构定位每个节点的位置。
-
参数:
TreeNode root:当前处理的节点。List<List<String>> res:存储结果的二维列表。int row:当前的树层级。int totalRows:树的总层数。int i和int j:表示节点在当前行的索引范围。
-
逻辑:
- 基础条件:
- 如果当前层数已经达到总层数,或者当前节点为空,则返回。
- 填写当前节点值:
- 使用
res.get(row).set((i + j) / 2, Integer.toString(root.val));将当前节点的值存储在对应的二维列表中的正确位置。这里的(i + j) / 2计算出当前层节点的中间列索引,确保二叉树的节点以正确的对称方式排列。
- 使用
- 递归调用:
- 递归填充左子树和右子树:
- 左子树的调用范围是当前行的左半部分:
populateRes(root.left, res, row + 1, totalRows, i, (i + j) / 2 - 1); - 右子树的调用范围是当前行的右半部分:
populateRes(root.right, res, row + 1, totalRows, (i + j) / 2 + 1, j);
- 左子树的调用范围是当前行的左半部分:
- 递归填充左子树和右子树:
- 基础条件:
printTree 方法
public List<List<String>> printTree(TreeNode root) {
List<List<String>> result = new LinkedList<>();
int row = getHeight(root);
int col = (int) (Math.pow(2, row) - 1);
List<String> rowRes = new ArrayList<>();
for (int i = 0; i < col; i++) rowRes.add("");
for (int i = 0; i < row; i++) result.add(new ArrayList<>(rowRes));
populateRes(root, result, 0, row, 0, col);
return result;
}
- 目的: 该方法用于生成表示二叉树的二维列表。
- 逻辑:
- 计算树的高度
row和列数col。列数是基于树的高度计算得来的,最大列数是2^height - 1。 - 创建一行的初始结果,即包含所有列的空字符串(
rowRes)。 - 用内层循环初始化结果列表
result,使其中每一行的结构一致。 - 调用
populateRes来填充结果列表。 - 返回填充后的
result。
- 计算树的高度