二叉树层序遍历
- 102. Binary Tree Level Order Traversal
- 107. Binary Tree Level Order Traversal II
- 637. Average of Levels in Binary Tree
- 103. Binary Tree Zigzag Level Order Traversal
- 199. Binary Tree Right Side View
- 515. Find Largest Value in Each Tree Row
- 116. Populating Next Right Pointers in Each Node
- 117. Populating Next Right Pointers in Each Node II(同上)
- 104. Maximum Depth of Binary Tree
- 111. Minimum Depth of Binary Tree
102. Binary Tree Level Order Traversal
Given the root of a binary tree, return the level order traversal of its nodes' values. (i.e., from left to right, level by level).
Example 1:

Input: root = [3,9,20,null,null,15,7]
Output: [[3],[9,20],[15,7]]
Example 2:
Input: root = [1]
Output: [[1]]
Example 3:
Input: root = []
Output: []
Constraints:
- The number of nodes in the tree is in the range
[0, 2000]. -1000 <= Node.val <= 1000
思路
层序遍历一个二叉树。就是从左到右一层一层的去遍历二叉树。这种遍历的方式和我们之前讲过的都不太一样。
需要借用一个辅助数据结构即队列来实现,队列先进先出,符合一层一层遍历的逻辑,而用栈先进后出适合模拟深度优先遍历也就是递归的逻辑。
而这种层序遍历方式就是图论中的广度优先遍历,只不过我们应用在二叉树上。
使用队列实现二叉树广度优先遍历,动画如下:

这样就实现了层序从左到右遍历二叉树。
代码如下:这份代码也可以作为二叉树层序遍历的模板,打十个就靠它了。
C++解法
使用队列实现二叉树广度优先遍历
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
queue<TreeNode*> que;
if (root != NULL) que.push(root);
vector<vector<int>> result;
while (!que.empty()) {
int size = que.size();
vector<int> vec;
// 这里一定要使用固定大小size,不要使用que.size(),因为que.size是不断变化的
for (int i = 0; i < size; i++) {
TreeNode* node = que.front();
que.pop();
vec.push_back(node->val);
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
result.push_back(vec);
}
return result;
}
};
递归法:
# 递归法
class Solution {
public:
void order(TreeNode* cur, vector<vector<int>>& result, int depth)
{
if (cur == nullptr) return;
if (result.size() == depth) result.push_back(vector<int>());
result[depth].push_back(cur->val);
order(cur->left, result, depth + 1);
order(cur->right, result, depth + 1);
}
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> result;
int depth = 0;
order(root, result, depth);
return result;
}
};
Java解法
// 102.二叉树的层序遍历
class Solution {
public List<List<Integer>> resList = new ArrayList<List<Integer>>();
public List<List<Integer>> levelOrder(TreeNode root) {
//checkFun01(root,0);
checkFun02(root);
return resList;
}
//BFS--递归方式
public void checkFun01(TreeNode node, Integer deep) {
if (node == null) return;
deep++;
if (resList.size() < deep) {
//当层级增加时,list的Item也增加,利用list的索引值进行层级界定
List<Integer> item = new ArrayList<Integer>();
resList.add(item);
}
resList.get(deep - 1).add(node.val);
checkFun01(node.left, deep);
checkFun01(node.right, deep);
}
//BFS--迭代方式--借助队列
public void checkFun02(TreeNode node) {
if (node == null) return;
Queue<TreeNode> que = new LinkedList<TreeNode>();
que.offer(node);
while (!que.isEmpty()) {
List<Integer> itemList = new ArrayList<Integer>();
int len = que.size();
while (len > 0) {
TreeNode tmpNode = que.poll();
itemList.add(tmpNode.val);
if (tmpNode.left != null) que.offer(tmpNode.left);
if (tmpNode.right != null) que.offer(tmpNode.right);
len--;
}
resList.add(itemList);
}
}
}
Python3解法
# 利用长度法
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
if not root:
return []
queue = collections.deque([root])
result = []
while queue:
level = []
for _ in range(len(queue)):
cur = queue.popleft()
level.append(cur.val)
if cur.left:
queue.append(cur.left)
if cur.right:
queue.append(cur.right)
result.append(level)
return result
Go解法
/**
1. 二叉树的递归遍历
*/
func levelOrder(root *TreeNode) [][]int {
arr := [][]int{}
depth := 0
var order func(root *TreeNode, depth int)
order = func(root *TreeNode, depth int) {
if root == nil {
return
}
if len(arr) == depth {
arr = append(arr, []int{})
}
arr[depth] = append(arr[depth], root.Val)
order(root.Left, depth+1)
order(root.Right, depth+1)
}
order(root, depth)
return arr
}
107. Binary Tree Level Order Traversal II
Given the root of a binary tree, return the bottom-up level order traversal of its nodes' values. (i.e., from left to right, level by level from leaf to root).
Example 1:

Input: root = [3,9,20,null,null,15,7]
Output: [[15,7],[9,20],[3]]
Example 2:
Input: root = [1]
Output: [[1]]
Example 3:
Input: root = []
Output: []
Constraints:
- The number of nodes in the tree is in the range
[0, 2000]. -1000 <= Node.val <= 1000
思路
在上面基础上反转下即可
C++解法
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrderBottom(TreeNode* root) {
queue<TreeNode*> que;
vector<vector<int>> result;
if(root == NULL) return result;
que.push(root);
while(!que.empty()){
vector<int> level;
int size = que.size();
for(int i = 0; i < size; i++){
TreeNode* cur = que.front();
level.push_back(cur->val);
que.pop();
if(cur->left) que.push(cur->left);
if(cur->right) que.push(cur->right);
}
result.push_back(level);
}
reverse(result.begin(), result.end());
return result;
}
};
637. Average of Levels in Binary Tree
Given the root of a binary tree, return the average value of the nodes on each level in the form of an array. Answers within 10-5 of the actual answer will be accepted.
Example 1:
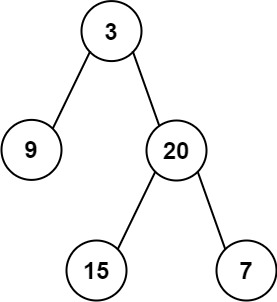
Input: root = [3,9,20,null,null,15,7]
Output: [3.00000,14.50000,11.00000]
Explanation: The average value of nodes on level 0 is 3, on level 1 is 14.5, and on level 2 is 11.
Hence return [3, 14.5, 11].
Example 2:
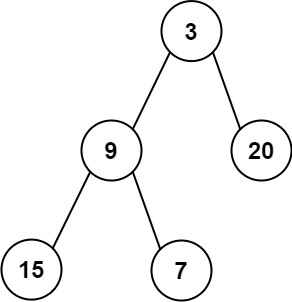
Input: root = [3,9,20,15,7]
Output: [3.00000,14.50000,11.00000]
Constraints:
- The number of nodes in the tree is in the range
[1, 10^4]. -2^31 <= Node.val <= 2^31 - 1
思路
每层遍历时就计算下结果
C++解法
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<double> averageOfLevels(TreeNode* root) {
vector<double> result;
queue<TreeNode*> que;
if(root == NULL) return result;
que.push(root);
while(!que.empty()){
double sum = 0.0;
int size = que.size();
for(int i = 0; i < size; i++){
TreeNode* cur = que.front();
que.pop();
sum += cur->val;
if(cur->left) que.push(cur->left);
if(cur->right) que.push(cur->right);
}
result.push_back(sum / size);
}
return result;
}
};
103. Binary Tree Zigzag Level Order Traversal
Given the root of a binary tree, return the zigzag level order traversal of its nodes' values. (i.e., from left to right, then right to left for the next level and alternate between).
Example 1:

Input: root = [3,9,20,null,null,15,7]
Output: [[3],[20,9],[15,7]]
Example 2:
Input: root = [1]
Output: [[1]]
Example 3:
Input: root = []
Output: []
Constraints:
- The number of nodes in the tree is in the range
[0, 2000]. -100 <= Node.val <= 100
思路
添加状态变量level判断是否需要反转,然后把每层遍历结果加入result
C++代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
queue<TreeNode*> que;
vector<vector<int>> result;
if(root == NULL) return result;
que.push(root);
int level = 0;
while(!que.empty()){
vector<int> nums;
int size = que.size();
for(int i = 0; i < size; i++){
TreeNode* cur = que.front();
nums.push_back(cur->val);
que.pop();
if(cur->left) que.push(cur->left);
if(cur->right) que.push(cur->right);
}
if(level % 2 == 1)
reverse(nums.begin(), nums.end());
level++;
result.push_back(nums);
}
return result;
}
};
199. Binary Tree Right Side View
Description
Given the root of a binary tree, imagine yourself standing on the right side of it, return the values of the nodes you can see ordered from top to bottom.
Example 1:

Input: root = [1,2,3,null,5,null,4]
Output: [1,3,4]
Example 2:
Input: root = [1,null,3]
Output: [1,3]
Example 3:
Input: root = []
Output: []
Constraints:
- The number of nodes in the tree is in the range
[0, 100]. -100 <= Node.val <= 100
思路
层次遍历,每层最后一个节点
由于树的形状无法提前知晓,不可能设计出优于 O(n) 的算法。因此,我们应该试着寻找线性时间解。带着这个想法,我们来考虑一些同等有效的方案。
方法一:深度优先搜索
思路
我们对树进行深度优先搜索,在搜索过程中,我们总是先访问右子树。那么对于每一层来说,我们在这层见到的第一个结点一定是最右边的结点。
算法
这样一来,我们可以存储在每个深度访问的第一个结点,一旦我们知道了树的层数,就可以得到最终的结果数组。
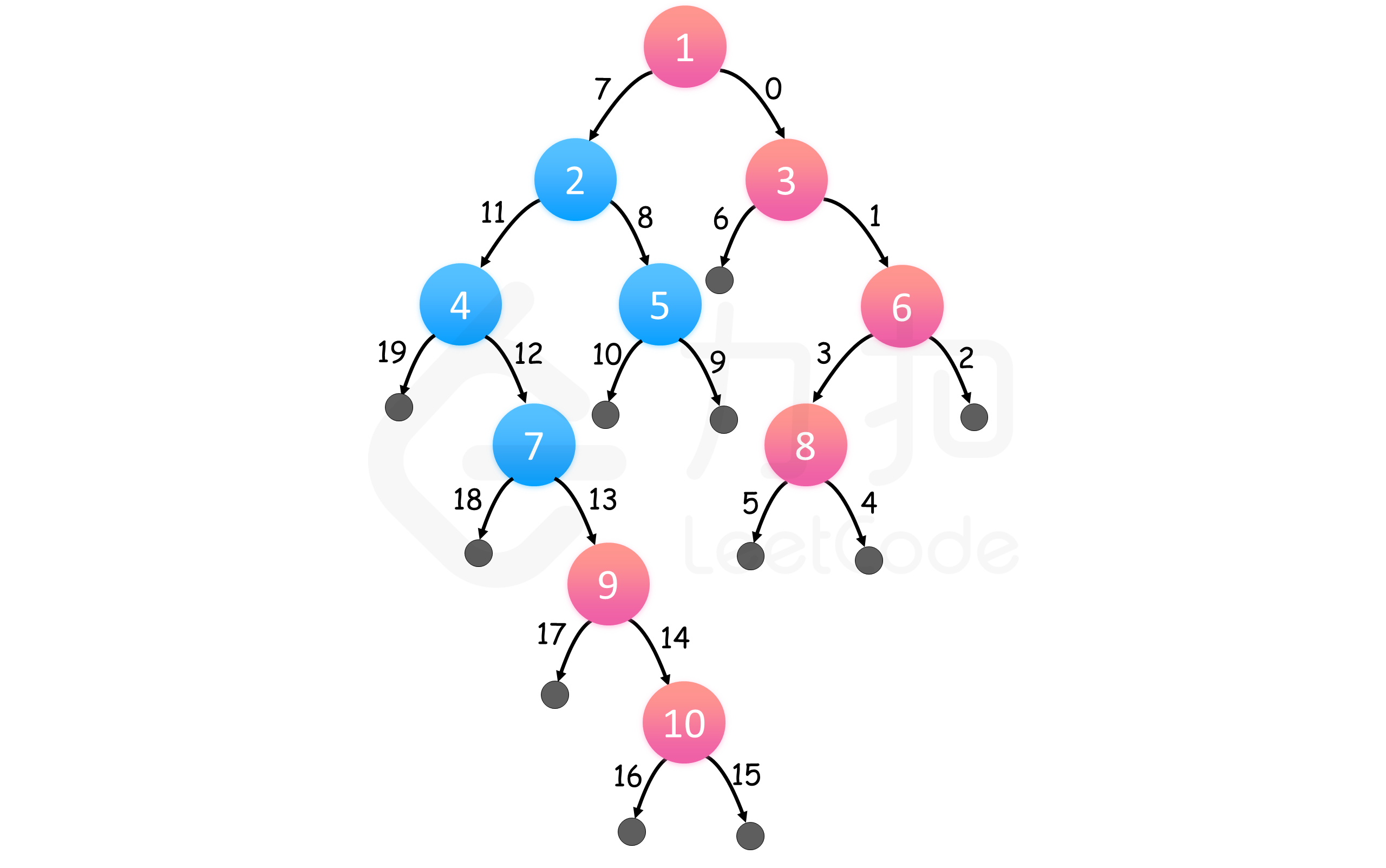
上图表示了问题的一个实例。红色结点自上而下组成答案,边缘以访问顺序标号。
复杂度分析
时间复杂度 : O(n)。深度优先搜索最多访问每个结点一次,因此是线性复杂度。
空间复杂度 : O(n)。最坏情况下,栈内会包含接近树高度的结点数量,占用 O(n) 的空间。
方法二:广度优先搜索
思路
我们可以对二叉树进行层次遍历,那么对于每层来说,最右边的结点一定是最后被遍历到的。二叉树的层次遍历可以用广度优先搜索实现。
算法
执行广度优先搜索,左结点排在右结点之前,这样,我们对每一层都从左到右访问。因此,只保留每个深度最后访问的结点,我们就可以在遍历完整棵树后得到每个深度最右的结点。除了将栈改成队列,并去除了 rightmost_value_at_depth 之前的检查外,算法没有别的改动。
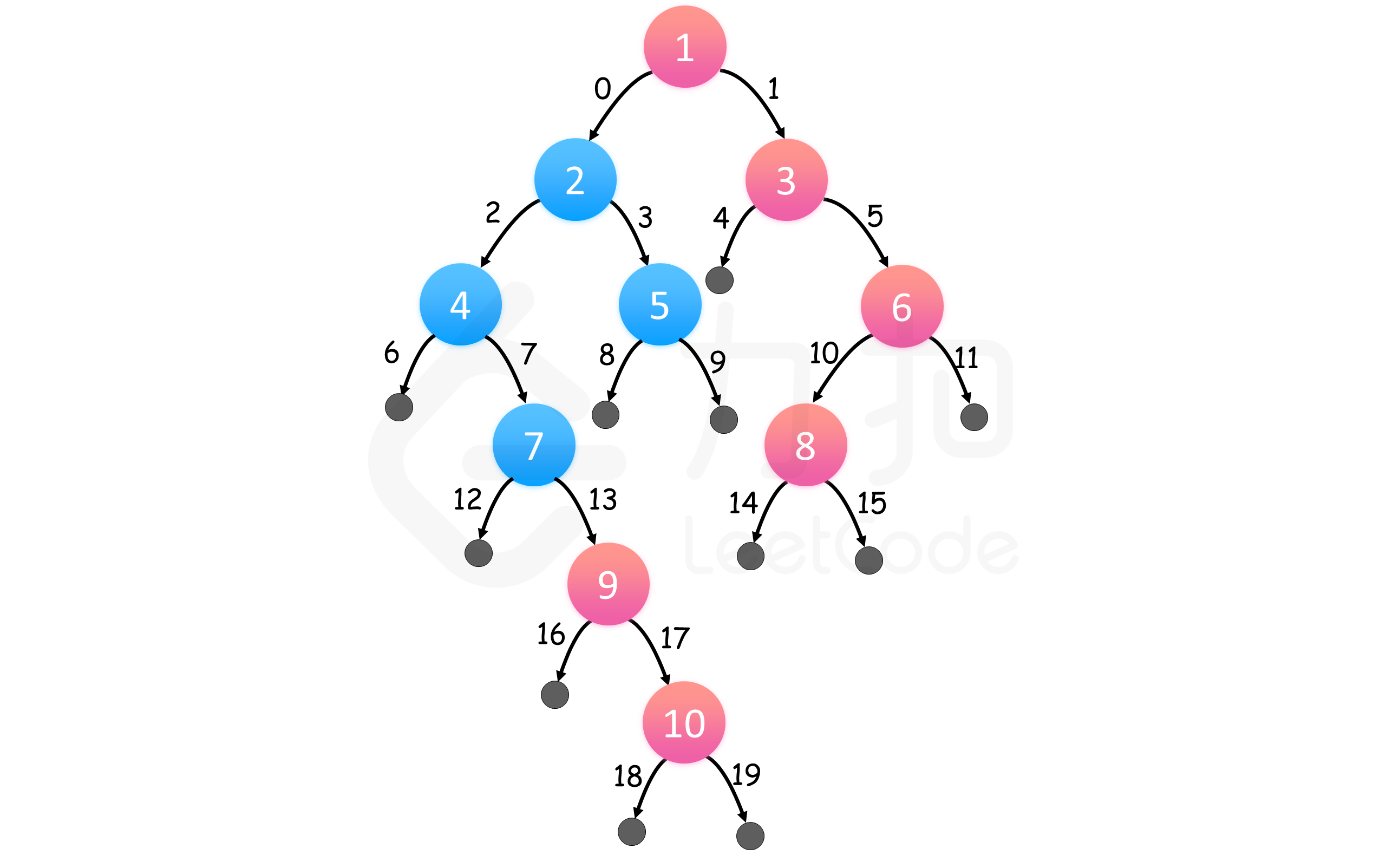
上图表示了同一个示例,红色结点自上而下组成答案,边缘以访问顺序标号。
复杂度分析
时间复杂度 : O(n)。 每个节点最多进队列一次,出队列一次,因此广度优先搜索的复杂度为线性。
空间复杂度 : O(n)。每个节点最多进队列一次,所以队列长度最大不不超过 n,所以这里的空间代价为 O(n)。
作者:力扣官方题解
链接: https://leetcode.cn/problems/binary-tree-right-side-view/solutions/213494/er-cha-shu-de-you-shi-tu-by-leetcode-solution/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
C++ 解法
dfs
class Solution {
public:
vector<int> rightSideView(TreeNode* root) {
unordered_map<int, int> rightmostValueAtDepth;
int max_depth = -1;
stack<TreeNode*> nodeStack;
stack<int> depthStack;
nodeStack.push(root);
depthStack.push(0);
while (!nodeStack.empty()) {
TreeNode* node = nodeStack.top();nodeStack.pop();
int depth = depthStack.top();depthStack.pop();
if (node != NULL) {
// 维护二叉树的最大深度
max_depth = max(max_depth, depth);
// 如果不存在对应深度的节点我们才插入
if (rightmostValueAtDepth.find(depth) == rightmostValueAtDepth.end()) {
rightmostValueAtDepth[depth] = node -> val;
}
nodeStack.push(node -> left);
nodeStack.push(node -> right);
depthStack.push(depth + 1);
depthStack.push(depth + 1);
}
}
vector<int> rightView;
for (int depth = 0; depth <= max_depth; ++depth) {
rightView.push_back(rightmostValueAtDepth[depth]);
}
return rightView;
}
};
bfs
class Solution {
public:
vector<int> rightSideView(TreeNode* root) {
unordered_map<int, int> rightmostValueAtDepth;
int max_depth = -1;
queue<TreeNode*> nodeQueue;
queue<int> depthQueue;
nodeQueue.push(root);
depthQueue.push(0);
while (!nodeQueue.empty()) {
TreeNode* node = nodeQueue.front();nodeQueue.pop();
int depth = depthQueue.front();depthQueue.pop();
if (node != NULL) {
// 维护二叉树的最大深度
max_depth = max(max_depth, depth);
// 由于每一层最后一个访问到的节点才是我们要的答案,因此不断更新对应深度的信息即可
rightmostValueAtDepth[depth] = node -> val;
nodeQueue.push(node -> left);
nodeQueue.push(node -> right);
depthQueue.push(depth + 1);
depthQueue.push(depth + 1);
}
}
vector<int> rightView;
for (int depth = 0; depth <= max_depth; ++depth) {
rightView.push_back(rightmostValueAtDepth[depth]);
}
return rightView;
}
};
Java 解法
dfs
class Solution {
public List<Integer> rightSideView(TreeNode root) {
Map<Integer, Integer> rightmostValueAtDepth = new HashMap<Integer, Integer>();
int max_depth = -1;
Deque<TreeNode> nodeStack = new LinkedList<TreeNode>();
Deque<Integer> depthStack = new LinkedList<Integer>();
nodeStack.push(root);
depthStack.push(0);
while (!nodeStack.isEmpty()) {
TreeNode node = nodeStack.pop();
int depth = depthStack.pop();
if (node != null) {
// 维护二叉树的最大深度
max_depth = Math.max(max_depth, depth);
// 如果不存在对应深度的节点我们才插入
if (!rightmostValueAtDepth.containsKey(depth)) {
rightmostValueAtDepth.put(depth, node.val);
}
nodeStack.push(node.left);
nodeStack.push(node.right);
depthStack.push(depth + 1);
depthStack.push(depth + 1);
}
}
List<Integer> rightView = new ArrayList<Integer>();
for (int depth = 0; depth <= max_depth; depth++) {
rightView.add(rightmostValueAtDepth.get(depth));
}
return rightView;
}
}
bfs
class Solution {
public List<Integer> rightSideView(TreeNode root) {
Map<Integer, Integer> rightmostValueAtDepth = new HashMap<Integer, Integer>();
int max_depth = -1;
Queue<TreeNode> nodeQueue = new LinkedList<TreeNode>();
Queue<Integer> depthQueue = new LinkedList<Integer>();
nodeQueue.add(root);
depthQueue.add(0);
while (!nodeQueue.isEmpty()) {
TreeNode node = nodeQueue.remove();
int depth = depthQueue.remove();
if (node != null) {
// 维护二叉树的最大深度
max_depth = Math.max(max_depth, depth);
// 由于每一层最后一个访问到的节点才是我们要的答案,因此不断更新对应深度的信息即可
rightmostValueAtDepth.put(depth, node.val);
nodeQueue.add(node.left);
nodeQueue.add(node.right);
depthQueue.add(depth + 1);
depthQueue.add(depth + 1);
}
}
List<Integer> rightView = new ArrayList<Integer>();
for (int depth = 0; depth <= max_depth; depth++) {
rightView.add(rightmostValueAtDepth.get(depth));
}
return rightView;
}
}
Python 解法
dfs
class Solution:
def rightSideView(self, root: TreeNode) -> List[int]:
rightmost_value_at_depth = dict() # 深度为索引,存放节点的值
max_depth = -1
stack = [(root, 0)]
while stack:
node, depth = stack.pop()
if node is not None:
# 维护二叉树的最大深度
max_depth = max(max_depth, depth)
# 如果不存在对应深度的节点我们才插入
rightmost_value_at_depth.setdefault(depth, node.val)
stack.append((node.left, depth + 1))
stack.append((node.right, depth + 1))
return [rightmost_value_at_depth[depth] for depth in range(max_depth + 1)]
bfs
class Solution:
def rightSideView(self, root: TreeNode) -> List[int]:
rightmost_value_at_depth = dict() # 深度为索引,存放节点的值
max_depth = -1
queue = deque([(root, 0)])
while queue:
node, depth = queue.popleft()
if node is not None:
# 维护二叉树的最大深度
max_depth = max(max_depth, depth)
# 由于每一层最后一个访问到的节点才是我们要的答案,因此不断更新对应深度的信息即可
rightmost_value_at_depth[depth] = node.val
queue.append((node.left, depth + 1))
queue.append((node.right, depth + 1))
return [rightmost_value_at_depth[depth] for depth in range(max_depth + 1)]
515. Find Largest Value in Each Tree Row
Given the root of a binary tree, return an array of the largest value in each row of the tree (0-indexed).
Example 1:
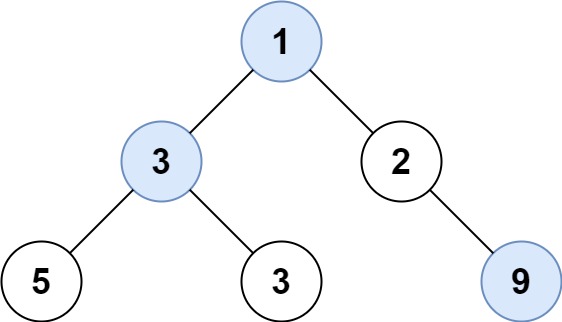
Input: root = [1,3,2,5,3,null,9]
Output: [1,3,9]
Example 2:
Input: root = [1,2,3]
Output: [1,3]
Constraints:
- The number of nodes in the tree will be in the range
[0, 10^4]. -2^31 <= Node.val <= 2^31 - 1
思路
每层计算一次最大值即可
C++解法
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int getMax(vector<int> nums){
int maxVal = nums[0];
for(int num : nums){
if(num > maxVal){
maxVal = num;
}
}
return maxVal;
}
vector<int> largestValues(TreeNode* root) {
queue<TreeNode*> que;
vector<int> result;
if(root == NULL) return result;
que.push(root);
while(!que.empty()){
vector<int> nums;
int size = que.size();
for(int i = 0; i < size; i++){
TreeNode* cur = que.front();
nums.push_back(cur->val);
que.pop();
if(cur->left) que.push(cur->left);
if(cur->right) que.push(cur->right);
}
int maxVal = getMax(nums);
result.push_back(maxVal);
}
return result;
}
};
116. Populating Next Right Pointers in Each Node
You are given a perfect binary tree where all leaves are on the same level, and every parent has two children. The binary tree has the following definition:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL.
Initially, all next pointers are set to NULL.
Example 1:

Input: root = [1,2,3,4,5,6,7]
Output: [1,#,2,3,#,4,5,6,7,#]
Explanation: Given the above perfect binary tree (Figure A), your function should populate each next pointer to point to its next right node, just like in Figure B. The serialized output is in level order as connected by the next pointers, with '#' signifying the end of each level.
Example 2:
Input: root = []
Output: []
Constraints:
- The number of nodes in the tree is in the range
[0, 2^{12} - 1]. -1000 <= Node.val <= 1000
Follow-up:
- You may only use constant extra space.
- The recursive approach is fine. You may assume implicit stack space does not count as extra space for this problem.
思路
本题依然是层序遍历,只不过在单层遍历的时候记录一下本层的头部节点,然后在遍历的时候让前一个节点指向本节点就可以了
C++代码
class Solution {
public:
Node* connect(Node* root) {
queue<Node*> que;
if (root != NULL) que.push(root);
while (!que.empty()) {
int size = que.size();
// vector<int> vec;
Node* nodePre;
Node* node;
for (int i = 0; i < size; i++) {
if (i == 0) {
nodePre = que.front(); // 取出一层的头结点
que.pop();
node = nodePre;
} else {
node = que.front();
que.pop();
nodePre->next = node; // 本层前一个节点next指向本节点
nodePre = nodePre->next;
}
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
nodePre->next = NULL; // 本层最后一个节点指向NULL
}
return root;
}
};
Java解法
class Solution {
public Node connect(Node root) {
Queue<Node> tmpQueue = new LinkedList<Node>();
if (root != null) tmpQueue.add(root);
while (tmpQueue.size() != 0){
int size = tmpQueue.size();
Node cur = tmpQueue.poll();
if (cur.left != null) tmpQueue.add(cur.left);
if (cur.right != null) tmpQueue.add(cur.right);
for (int index = 1; index < size; index++){
Node next = tmpQueue.poll();
if (next.left != null) tmpQueue.add(next.left);
if (next.right != null) tmpQueue.add(next.right);
cur.next = next;
cur = next;
}
}
return root;
}
}
Python3解法
"""
# Definition for a Node.
class Node:
def __init__(self, val: int = 0, left: 'Node' = None, right: 'Node' = None, next: 'Node' = None):
self.val = val
self.left = left
self.right = right
self.next = next
"""
class Solution:
def connect(self, root: 'Node') -> 'Node':
if not root:
return root
queue = collections.deque([root])
while queue:
level_size = len(queue)
prev = None
for i in range(level_size):
node = queue.popleft()
if prev:
prev.next = node
prev = node
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
return root
Go解法
/**
1. 填充每个节点的下一个右侧节点指针
2. 填充每个节点的下一个右侧节点指针 II
*/
func connect(root *Node) *Node {
if root == nil { //防止为空
return root
}
queue := list.New()
queue.PushBack(root)
tmpArr := make([]*Node, 0)
for queue.Len() > 0 {
length := queue.Len() //保存当前层的长度,然后处理当前层(十分重要,防止添加下层元素影响判断层中元素的个数)
for i := 0; i < length; i++ {
node := queue.Remove(queue.Front()).(*Node) //出队列
if node.Left != nil {
queue.PushBack(node.Left)
}
if node.Right != nil {
queue.PushBack(node.Right)
}
tmpArr = append(tmpArr, node) //将值加入本层切片中
}
if len(tmpArr) > 1 {
// 遍历每层元素,指定next
for i := 0; i < len(tmpArr)-1; i++ {
tmpArr[i].Next = tmpArr[i+1]
}
}
tmpArr = []*Node{} //清空层的数据
}
return root
}
117. Populating Next Right Pointers in Each Node II(同上)
Given a binary tree
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL.
Initially, all next pointers are set to NULL.
Example 1:

Input: root = [1,2,3,4,5,null,7]
Output: [1,#,2,3,#,4,5,7,#]
Explanation: Given the above binary tree (Figure A), your function should populate each next pointer to point to its next right node, just like in Figure B. The serialized output is in level order as connected by the next pointers, with '#' signifying the end of each level.
Example 2:
Input: root = []
Output: []
Constraints:
- The number of nodes in the tree is in the range
[0, 6000]. -100 <= Node.val <= 100
Follow-up:
- You may only use constant extra space.
- The recursive approach is fine. You may assume implicit stack space does not count as extra space for this problem.
思路
这道题目说是二叉树,但116题目说是完整二叉树,其实没有任何差别,一样的代码一样的逻辑一样的味道
C++解法
class Solution {
public:
Node* connect(Node* root) {
queue<Node*> que;
if (root != NULL) que.push(root);
while (!que.empty()) {
int size = que.size();
vector<int> vec;
Node* nodePre;
Node* node;
for (int i = 0; i < size; i++) {
if (i == 0) {
nodePre = que.front(); // 取出一层的头结点
que.pop();
node = nodePre;
} else {
node = que.front();
que.pop();
nodePre->next = node; // 本层前一个节点next指向本节点
nodePre = nodePre->next;
}
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
nodePre->next = NULL; // 本层最后一个节点指向NULL
}
return root;
}
};
104. Maximum Depth of Binary Tree
Given the root of a binary tree, return its maximum depth.
A binary tree's maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.
Example 1:

Input: root = [3,9,20,null,null,15,7]
Output: 3
Example 2:
Input: root = [1,null,2]
Output: 2
Constraints:
- The number of nodes in the tree is in the range
[0, 10^4]. -100 <= Node.val <= 100
思路
递归
C++解法
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int maxDepth(TreeNode* root) {
if(root == NULL){
return 0;
}
return max(maxDepth(root->left), maxDepth(root->right)) + 1;
}
};
Java解法
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int maxDepth(TreeNode root) {
if(root == null) return 0;
if(root.left == null && root.right == null) return 1;
return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
}
}
Python3解法
Go解法
111. Minimum Depth of Binary Tree
Given a binary tree, find its minimum depth.
The minimum depth is the number of nodes along the shortest path from the root node down to the nearest leaf node.
Note: A leaf is a node with no children.
Example 1:

Input: root = [3,9,20,null,null,15,7]
Output: 2
Example 2:
Input: root = [2,null,3,null,4,null,5,null,6]
Output: 5
Constraints:
- The number of nodes in the tree is in the range
[0, 10^5]. -1000 <= Node.val <= 1000
思路
递归
C++解法
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int minDepth(TreeNode* root) {
if(root == NULL){
return 0;
}
if(root->left == NULL && root->right != NULL){
return minDepth(root->right) + 1;
}
if(root->right == NULL && root->left != NULL){
return minDepth(root->left) + 1;
}
return 1 + min(minDepth(root->left), minDepth(root->right));
}
};