Python数学建模算法与应用第3章线性代数模型解答

这块习题主要是差分方程和马尔科夫链应用。

差分方程

差分方程是在离散的时间点上描述对象动态变化规律的数学表达式。有的实际问题本身就是以离散形式出现的，也有的是将现实世界中随时间连续变化的过程离散化。差分方程和微分方程都是描述状态变化问题的机理建模方法，是同一建模问题的两种思维（离散或连续）方式。

利用差分方程建模，通常是把问题看作一个系统，考察系统状态变量的变化。即首先考察任意两个相邻位置（时间或空间），通常称之为一个微元，考察状态值在这个微元内的变化，即输入、输出变化情况，分析变化的原因，进而利用一些相应规律，如质量守恒、能量守恒等定律建立起微元两端状态变量之间的关联方程。其遵循的一个基本准则就是：未来值=现在值+变化值。

若记$x_k$为第k个时刻或位置的状态变量值，则把各个状态变量的状态值次序排列，就形成了一个有序序列${x_k}^a_{k=0}$。若序列中的$x_k$和其前一个状态或前几个状态状态值$x_i(0 \leq i \lt k)$存在某种关联，则把它们的关联关系用代数方程的形式表达出去，即建立起状态之间的关联方程，称之为差分方程。差分方程也叫递推关系。

典型例子有贷款问题、人口增长问题等。

贷款问题

问题提出：假定某消费者购房需贷款240万元，还款期限为30年，贷款年利率为5.1%，采用固定额度还款方式，问每月应还款额是多少？

问题分析：当月欠款=上月欠款的当月本息-当月还款

基本假设：假定在还款期限内，利率保持不变

建立模型：记$y_n$为第n个月的欠款总额（单位：元），r为月利率，r=0.051/12x100%=0.425%，x为当月还款额度（单位：元），N为还款期限，N=30x12=360（月），Q为贷款总额（单位：元）

则数学模型为

模型求解 通过递推方法求得$y_n=(1+r)^ny_0-x\frac{(1+r)^n-1}{r}$

每月应还款额的确定：令$y_n=y_{360}=0$即可。解得$x=\frac{Qr(1+r)^N}{(1+r)^N-1}$

1
2

x=round((1+0.051/12)**360*2400000*(0.051/12)/((1+0.051/12)**360-1),2)
print(x)#13030.79

美国人口增长模型

导弹发射轨迹问题

3.1人口迁移模型

在某国家，每年有比例为p的农村居民移居城镇，有比例为q的城镇居民移居农村。假设该国总人数不变，且上述人口迁移的规律也不变。把n年后农村人口和城镇人口占总人口的比例依次记为$x_n$和$y_n$($x_n$+$y_n$=1)。

(1)求关系式 $\begin{bmatrix}x_{n+1} \\y_{n+1}\end{bmatrix}=A\begin{bmatrix}x_{n} \\y_{n}\end{bmatrix}$ 中的矩阵A。

(2)设目前农村人口和城镇人口相等，即

求$\begin{bmatrix}x_{n} \\y_{n}\end{bmatrix}$。

为了求$A^n$需要把矩阵相似对角化。先求A的特征值和特征向量，易求得A的特征值$\lambda_1$=1，$\lambda_2=1-p-q$

存在可逆阵P使得$A=P\begin{bmatrix}1&0 \\0&r\end{bmatrix}P^{-1}$，其中r=1-p-q。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

import sympy as sp

sp.var('n',positive=True,integer=True)
sp.var('p,q',positive=True)
a = sp.Matrix([[1-p,q],[p,1-q]])

print("特征值为：",a.eigenvals())
print("特征向量为：\n",a.eigenvects())

P,D = a.diagonalize()#把a相似对角化
An = P@(D**n)@(P.inv())
xyn = An@sp.Matrix([[1],[1]])/2
xyn2 = sp.simplify(xyn)

print(xyn2)

输出结果：

1
2
3

特征值为： {1: 1, -p - q + 1: 1} 
特征向量为： [(1, 1, [Matrix([ [q/p], [ 1]])]), (-p - q + 1, 1, [Matrix([ [-1], [ 1]])])] 
Matrix([[(q + (p - q)*(-p - q + 1)**n/2)/(p + q)], [(p + (-p + q)*(-p - q + 1)**n/2)/(p + q)]])

3.2求下列差分方程的解

$x_{n+2}-x_{n+1}-2x_n=0,x_0=x_1=-2$

特征方程$r^2-r-2=0$解得$r_1=2,r_2=-1$ 然后设$x_n=C_1(-1)^n+C_22^n$代入初值条件得到差分方程的解$x_n=\frac{-2}{3}(-1)^n-\frac{4}{3}2^n$

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

import sympy as sp

sp.var('n')

x = sp.Function('x')

f = x(n+2)-x(n+1)-2*x(n)

s = sp.rsolve(f,x(n),{x(0):-2,x(1):-2})

print(s)

输出结果：

1

-2*(-1)**n/3 - 4*2**n/3

马尔科夫链

马尔科夫链（Markov Chain）是一种随机过程，它具有马尔科夫性质。马尔科夫性质是指在一个随机过程中，下一时刻的状态只依赖于当前时刻的状态，而不依赖于过去的状态。因此，马尔科夫链是一种无记忆的随机过程。

在马尔可夫链的每一步，系统根据概率分布，可以从一个状态变到另一个状态，也可以保持当前状态。状态的改变叫做转移，与不同的状态改变相关的概率叫做转移概率。随机漫步就是马尔可夫链的例子。随机漫步中每一步的状态是在图形中的点，每一步可以移动到任何一个相邻的点，在这里移动到每一个点的概率都是相同的（无论之前漫步路径是如何的）。

在马尔科夫链中，状态空间是一组离散的状态，每个状态都有一个概率转移矩阵，描述了从一个状态转移到另一个状态的概率。这个矩阵中的每个元素表示从一个状态转移到另一个状态的概率。矩阵中的每一行都是一个概率分布，表示从当前状态转移到下一个状态的概率。

马尔可夫链是随机过程 这门课程中的一部分。随机过程就是使用统计模型一些事物的过程进行预测和处理。马尔科夫链可以用来建模许多实际问题，例如天气预测、股票价格、语音识别等。在这些问题中，状态空间表示了可能的状态，例如天气可能是晴天、多云、雨天等，股票价格可能是上涨、下跌、不变等。概率转移矩阵描述了从一个状态转移到另一个状态的概率，例如在晴天的情况下，第二天可能是晴天、多云或者雨天。马尔科夫链也是许多机器学习算法的基础，例如隐马尔科夫模型（HMM）、马尔科夫决策过程（MDP）等。

时齐马尔可夫链（或静态马尔可夫链）：转移概率与n无关。

核心三要素：状态空间States Space、无记忆性Memorylessness、转移矩阵Transition Matrix

稳态分布Steady State Distribution：最终的稳态是不受初始状态影响的。稳态分布数不一定为1。

举个栗子——假设小明每天的早餐选择遵循下面的规律：

当小明某日早餐选择A，下一日他有40%的概率继续选择A，60%的可能性转而选择B； 当小明某日早餐选择B，下一日他有50%的概率继续选择B，50%的可能性转而选择A。

为了满足概率的限制，概率要大于等于0，每一行中的元素之和必须等于 1。因此，转移矩阵必须满足以下条件：

状态空间只有A、B两种，并且当日的选择只受前一日的结果和对应的转移概率影响。

状态概率分布推演：假设小明第一天选择A，那么当天的概率分布为$\begin{pmatrix} 1 \ 0 \end{pmatrix}$，将其与转移矩阵相乘得到第二天的概率分布$\begin{pmatrix} 0.4&0.5\ 0.6&0.5 \end{pmatrix} \times \begin{pmatrix} 1\ 0 \end{pmatrix}=\begin{pmatrix} 0.4\ 0.6 \end{pmatrix}$重复下去最终得到稳态分布$\begin{pmatrix} 0.454545\ 0.545455 \end{pmatrix}$

假设小明第一天选择A，那么当天的概率分布为$\begin{pmatrix} 0\ 1 \end{pmatrix}$，将其与转移矩阵相乘得到第二天的概率分布$\begin{pmatrix} 0.4&0.5\ 0.6&0.5 \end{pmatrix} \times \begin{pmatrix} 0\ 1 \end{pmatrix}=\begin{pmatrix} 0.5\ 0.5 \end{pmatrix}$重复下去最终得到相同的稳态分布$\begin{pmatrix} 0.454545\ 0.545455 \end{pmatrix}$

2x2交叉列联表

3.3文章影响力评价问题

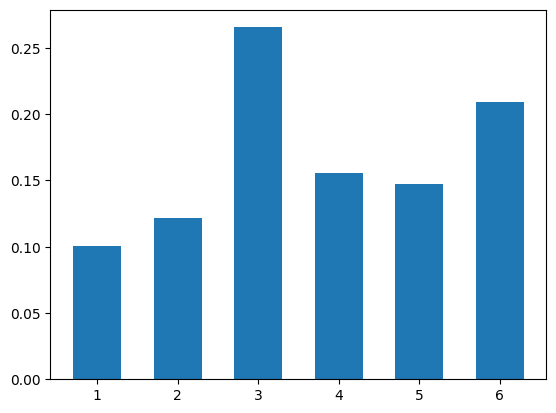
图3.1给出了6篇文章之间的引用关系，即文章1分别引用了文章2、4、5、6；文章2分别引用了文章4、5、6；文章3分别引用了1、2、4；文章4分别引用了文章5、6；文章5分别引用了文章3、6；文章6引用了文章3；试给出6篇文章影响力大小的排序。

据说用tikz可以画出文章之间的引用关系图，但我画不出来，直接用矩阵表示文章之间的引用关系。

构造有向图D=(V,A,W)，其中顶点集合$V={v_1,v_2,…,v_6}$，这里$v_1,v_2,…,v_6$分别表示文章1,2,3,4,5,6等等，A为弧的集合，$W=(w_{ij})_{6\times6}$为邻接矩阵，这里$W_{ij}=\begin{cases}1,文章i引用了文章j\\0,否则\end{cases}$即文章i引用了文章j，相当于给文章i给文章j投一票。这里

记矩阵W的行和为$r_i=\sum_{j=1}^{6} w_{i,j}$，它表示文章i投给其他文章的票数。 定义矩阵$P=(P_{ij}){6\times6}$如下：$p{ij}=\frac{1-d}{6}+d\frac{w_{ij}}{r_i},i,j=1,2,…,6$其中d为模型参数，通常去d=0.85，P为马尔科夫链的转移概率矩阵，$p_{ij}$表示文章i投票给文章j的概率。根据马尔科夫链的基本性质，对于正则马尔可夫链，存在平稳分布$x=[x_1,…,x_6]^T$，满足$P^Tx=x,\sum_{i=1}^{6} x_i=1$ x表示在极限状态（转移次数趋于无线）下各篇文章被投票的概率分布，Google将它定义为各顶点的PageRank值。假设x已经得到，则它按分量满足方程$x_k=\sum_{i=1}^{6}p_{ik}x_i=\frac{1-d}{6}+d\sum_{i:w_{ik}=1}\frac{x_{i}}{r_i}$ 顶点$v_i$的PageRank值是$x_i$，它发出的弧有$r_i$条，于是顶点$v_i$将它的PageRank值分成$r_i$份，分别”投票“给它链出的顶点。$x_k$为顶点$v_k$的PageRank值，即网络上所有顶点”投票“给顶点$v_k$的最终值。

根据马尔科夫链的基本性质还可以得到，平稳分布（PageRank值）是转移概率矩阵P的转置矩阵$P^T$的最大特征值（=1）所对应的归一化特征向量。

# Project 1: PageRank in Python

# PageRank: Link Analysis Explanation and Python Implementation from Scratch

计算得到该马尔科夫链的平稳分布为$x=[0.1003 \quad 0.1216 \quad0.2656\quad 0.1560\quad 0.1470 \quad 0.2095]^T$这就是6个顶点的PageRank值，即文章1到文章6的影响力排名序次3>6>4>5>2>1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

import numpy as np

from scipy.sparse.linalg import eigs

import pylab as plt

  

w = np.array([[0, 1, 0, 1, 1, 1],

                   [0, 0, 0, 1, 1, 1],

                   [1, 1, 0, 1, 0, 0],

                   [0, 0, 0, 0, 1, 1],

                   [0, 0, 1, 0, 0, 1],

                   [0, 0, 1, 0, 0, 0]])

r = np.sum(w,axis=1,keepdims=True)

n = w.shape[0]

d = 0.85

P = (1-d)/n+d*w/r #利用矩阵广播

w,v = eigs(P.T,1) #求最大特征值及对应的特征向量

v = v/sum(v)

v = v.real

print("最大特征值为：",w.real)

print("归一化特征向量为：\n",np.round(v,4))

plt.bar(range(1,n+1),v.flatten(),width=0.6)

plt.show()

输出结果：

1
2

最大特征值为： [1.] 
归一化特征向量为： [[0.1003] [0.1216] [0.2656] [0.156 ] [0.147 ] [0.2095]]

3.4草场放牧羊群

有一块一定面积的草场放牧羊群，管理者要估计草场能放牧多少羊，每年保留多少母羔羊，夏季要储藏多少草供冬季之用。为了解决这些问题调查了如下的背景资料：

（1）本地环境下这一品种草的日生长率如表3.1所列。

表3.1 各季节草的生长率

（2）羊的繁殖率。通常母羊每年产1~3只羊羔，5岁后被卖掉。为保持羊群的规模可以买进羊羔，或者保留一定数量的母羊。每只母羊的平均繁殖率如表3.2所列。

表3.2 母羊的平均繁殖率

（3）羊的存活率。不同年龄的母羊的自然存活率（指存活一年）如表3.3所列。

表3.3 母羊的平均自然存活率

（4）草的需求量。母羊和羊羔在各个季节每天需要草的数量（kg）如表3.4所列。

表3.4 母羊和羊羔每天草的需求量

注：只关心羊的数量，而不管它们的重量。一般在春季产羊羔，秋季将全部公羊和一部分母羊卖掉，保持羊群数量不变。

解：用$x=[x_1,x_2,x_3,x_4,x_5]^T$表示母羊按年龄01，12，23，34，4~5的概率分布向量，这里$x_i\geq0,\sum_{i=1}^{5}x_i=1$，由母羊的繁殖率和存活率可得种群数量的转移矩阵为

q是0~1岁羊羔的存活率，可以控制。为保持羊群数量N不变，需满足X=PX，由此可$q=0.1360,x=[0.6680 \quad 0.0908 \quad0.0890 \quad 0.0846\quad 0.0676 ]^T$可知当N不变时每年产羊羔数量为0.668N，秋冬季存活的母羊数量为0.3320N。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

import sympy as sp

sp.var('q')

X = sp.Matrix(sp.var('x1:6'))

A = sp.Matrix([[0,1.8,2.4,2.0,1.8],[q,0,0,0,0],[0,0.98,0,0,0],[0,0,0.95,0,0],[0,0,0,0.80,0]])

s = sp.solve([A@X-X,sum(X)-1])

print(s)

输出结果：

1

[{q: 0.135968585817933, x1: 0.667969672419994, x2: 0.0908228917282143, x3: 0.0890064338936500, x4: 0.0845561121989675, x5: 0.0676448897591740}]

注：上述非线性方程组的解不是唯一的，Python求解结果和其他软件求解结果略有差异。

设草场面积为$S(m^2)$，根据各个季节草的需求量(kg)和生长率，应有：

冬季草的需求量：$2.1\times0.3320N=0.6972N$

春季草的需求量：$0.668N+2.4\times0.3320N=1.4648N<0.003S$

冬季草的需求量：$1.65\times0.6680N+1.15\times0.3320N=1.4840N<0.007S$

冬季草的需求量：$1.35\times0.3320N=0.4482N<0.004S$

只要春季满足N/S<0.002（每平方米草地羊的数量），夏季和秋季都不成问题。若夏季储藏草$ykg/m^2$，保存到冬季用，则需有1.4840N/S<0.007-y，其中N/S以春季须满足的数值代入，可得$y<0.004kg/m^2$，而冬季的需求量是$0.6972\times0.002=0.0014kg/m^2$，故夏季的储藏足够冬季之用。