2.1画出双曲函数和指数函数图形#
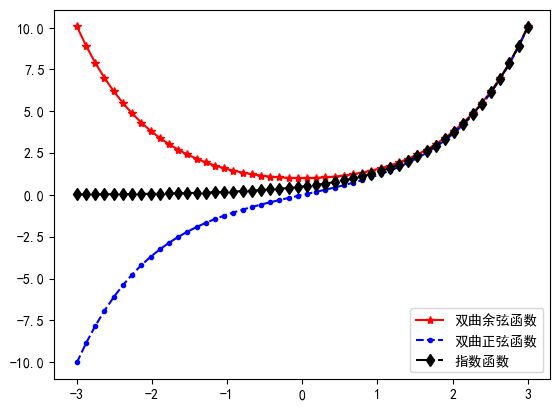
在同一个图形界面上画出如下三个函数的图形并进行标注。
$$y=chx,y=shx,y=\frac{1}{2} e^{x}$$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| import pylab as plt
import numpy as np
plt.rc('font',family='SimHei')#用来正常显示中文标签
plt.rc('axes',unicode_minus=False)#用来正常显示负号
x = np.linspace(-3,3,50)#通过定义均匀间隔创建数值序列
y1 = np.cosh(x)
y2 = np.sinh(x)
y3 = np.exp(x)/2
plt.plot(x,y1,'r-*',label="双曲余弦函数")
plt.plot(x,y2,'--.b',label="双曲正弦函数")
plt.plot(x,y3,'-.dk',label="指数函数")
plt.legend()
plt.show()
|
matplotlib的中文支持很差,如下代码可以查询其可用字体:
1
2
3
| import matplotlib as mpl
for font in mpl.font_manager.FontManager().ttflist:
print(font.name, '-', font.fname)
|
下载字体:!wget https://github.com/StellarCN/scp_zh/raw/master/fonts/SimHei.ttf
如下代码也能实现上面那种效果。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| import matplotlib.pyplot as plt
import numpy as np
from matplotlib import font_manager
font_manager.fontManager.addfont('./SimHei.ttf')
plt.rcParams['font.sans-serif']=['SimHei']#用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False#用来正常显示负号
x = np.linspace(-3,3,50)#通过定义均匀间隔创建数值序列
y1 = np.cosh(x)
y2 = np.sinh(x)
y3 = np.exp(x)/2
plt.plot(x,y1,'r-*',label="双曲余弦函数")
plt.plot(x,y2,'--.b',label="双曲正弦函数")
plt.plot(x,y3,'-.dk',label="指数函数")
plt.legend()
plt.show()
|
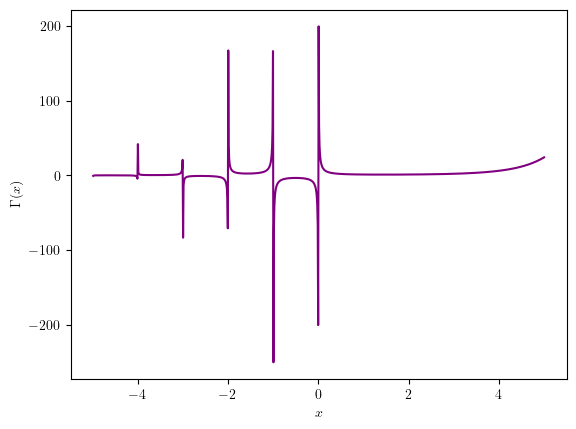
2.2画出伽马函数的图形#
$$\Gamma(z) = \int_0^\infty t^{z-1} e^{-t} dt$$
1
2
3
4
5
6
7
8
9
10
11
12
13
| from scipy.special import gamma
import pylab as plt
import numpy as np
#plt.rc('text',usetex=True)
#这一句应该可以删去,matplotlib现在默认开启latex功能,可以用print(matplotlib.rcParams['text.usetex'])检验,输出True说明已启用相应功能
x = np.linspace(-5,5,1000)
plt.plot(x,gamma(x),c='purple')
plt.xlabel('$x$')
plt.ylabel('$\Gamma(x)$')
plt.show()
|
本地画图应该好画,用GoogleColab画图需要自己安装latex插件,否则一直报错。执行下面代码安装latex插件:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| ! sudo apt-get install texlive-latex-recommended
! sudo apt-get install dvipng texlive-latex-extra texlive-fonts-recommended
! wget http://mirrors.ctan.org/macros/latex/contrib/type1cm.zip
! unzip type1cm.zip -d /tmp/type1cm
! cd /tmp/type1cm/type1cm/ && sudo latex type1cm.ins
! sudo mkdir /usr/share/texmf/tex/latex/type1cm
! sudo cp /tmp/type1cm/type1cm/type1cm.sty /usr/share/texmf/tex/latex/type1cm
! sudo texhash
! apt install cm-super
|
问题解决来源:# Latex + matplotlib + google colab
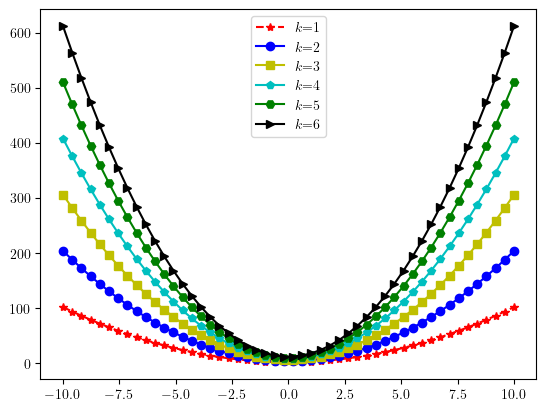
2.3曲线同图绘制#
在同一个图形界面中分别画出6条曲线$$y=kx^2+2k,k=1,2,…,6$$
1
2
3
4
5
6
7
8
9
10
11
| import pylab as plt
import numpy as np
x = np.linspace(-10,10,50)
s = ['*r--','ob-','sy-','pc-','Hg-','>k-']
fx = lambda x,k: k*x**2+2*k
for i in range(6):
plt.plot(x,fx(x,i+1),s[i],label='$k$='+str(i+1))
plt.legend()
plt.show()
|
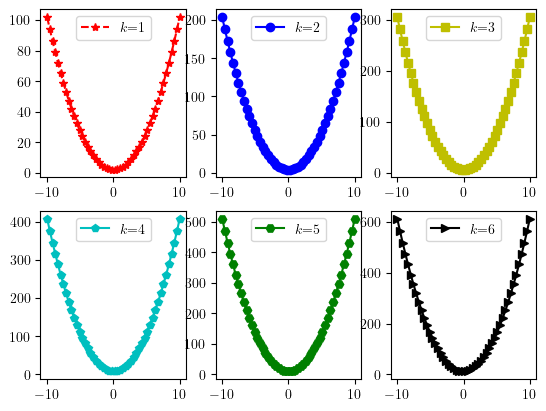
2.4曲线分块绘制#
把屏幕开成2行3列6个子窗口,每个子窗口画一条曲线,画出曲线$$y=kx^2+2k,k=1,2,…,6$$
1
2
3
4
5
6
7
8
9
10
11
12
13
| import pylab as plt
import numpy as np
x = np.linspace(-10,10,50)
s = ['*r--','ob-','sy-','pc-','Hg-','>k-']
fx = lambda x,k: k*x**2+2*k
for i in range(6):
plt.subplot(2,3,i+1)
plt.plot(x,fx(x,i+1),s[i],label='$k$='+str(i+1))
plt.legend()
plt.show()
|
2.5画二次曲面如单叶双曲面、椭圆抛物面#
分别画出下列二次曲面。
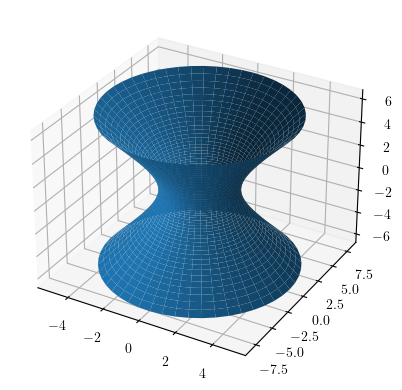
(1)单叶双曲面$\frac{x^2}{4} + \frac{y^2}{10} - \frac{z^2}{8} = 1$
先用双曲函数和三角函数把该方程化成参数方程。一般单叶双曲面参数方程为
$$F(x,y,z)=\begin{cases}
x = 2\cosh(v)cos(u)\\
y = \sqrt(10)\cosh(v) sin(u)\\
z = 2\sqrt(2)sinh(v)
\end{cases}$$
这里介绍下三元一次方程组的写法。
$$\begin{cases}
x+y+z=0\\
x+2y+3z=0\\
x+4y+5z=0
\end{cases}$$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| import pylab as plt
import numpy as np
u = np.linspace(0,2*np.pi,50)
v = np.linspace(-np.pi/2,np.pi/2,50)
u,v = np.meshgrid(u,v)
x = 2*np.cosh(v)*np.cos(u)
y = np.sqrt(10)*np.cosh(v)*np.sin(u)
z = 2*np.sqrt(2)*np.sinh(v)
ax = plt.axes(projection='3d')
ax.plot_surface(x,y,z)
plt.show()
|
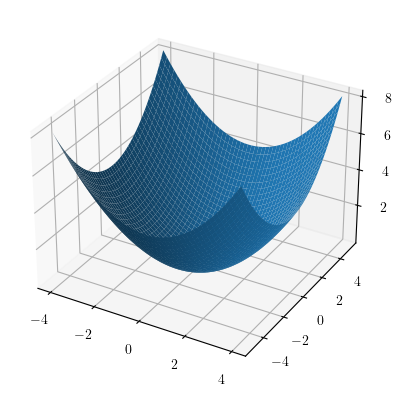
 (2)椭圆抛物面$$\frac{x^2}{4} + \frac{y^2}{6} = \frac{z}{1}$$
(2)椭圆抛物面$$\frac{x^2}{4} + \frac{y^2}{6} = \frac{z}{1}$$
1
2
3
4
5
6
7
8
9
10
11
12
| import pylab as plt
import numpy as np
x = np.linspace(-4,4,50)
y = np.linspace(-5,5,50)
x,y = np.meshgrid(x,y)
z = x**2/4+y**2/6
ax = plt.axes(projection='3d')
ax.plot_surface(x,y,z)
plt.show()
|
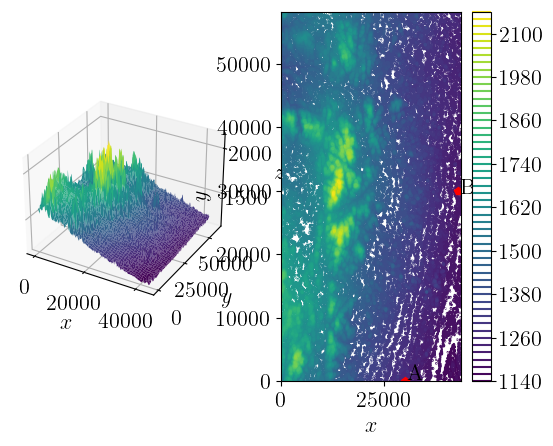
2.6区域高程数据分析#
附件1:区域高程数据.xslx给出了某区域43.65kmx58.2km的高程数据,画出该区域的三维表面图和等高线图,在A(30,0)和B(43,30)(单位:km)点处建立了两个基地,在等高线图上标注出这两个点,并求该区域地表面积的近似值。
区域高程数据是指描述地球表面或地球表面上某一区域高度信息的数据。这些数据可以在三维空间中表示出地形的形状和高度。在地理信息系统(GIS)和遥感技术中,区域高程数据通常用数字高程模型(DEM)表示,DEM是一种数字化的地形模型,它使用一系列高度值来表示二维表面的三维形状。DEM可以通过测量地球表面高度的方法来获取,例如使用雷达、激光扫描或卫星遥感技术。这些数据广泛应用于地形分析、水文学、土地利用规划、城市规划、环境评估、自然灾害预测等领域,是地理信息科学中重要的数据类型之一。
注意:附件1提供了所指区域内部分点处的高程值(单位米),区域用等距50米网格进行划分,数据共有874行,1165列。本表中,第1行第1列表示坐标(0,0)点处的高程,第m行第n列的数据代表坐标((50(m-1),50(n-1))处的高程值,坐标单位均为米。(0,0)点位于附件2示意图的左下角,(50X873,50X1164)点位于示意图右上角。请用excel2007以上版本打开此文件,2003版本打开会不完整。
利用分点xi=50i(i=0,1,…,873)把0<=x<=50x873剖分成873个小区间,利用分点yj=50j(j=0,1,2,…,1164)把0<=y<=50x1164剖分成1164个小区间,对应地把平面区域剖分成873x1164个小矩形,把所计算的三维曲面剖分成873x1164个小曲面进行计算,每个小曲面的面积用对应的三维空间中4个点所构成的两个小三角形面积的和作为近似值。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
| import numpy as np
import pylab as plt
import pandas as pd
a = pd.read_excel('/content/附件1:区域高程数据.xlsx',header=None,nrows=874)
b = a.values
[m,n] = b.shape
x0 = np.arange(m)*50
#print(x0)
#[ 0 50 100 150 200 250 300……]
y0 = np.arange(n)*50
s = 0
for i in range(m-1):
for j in range(n-1):
p1 = np.array([x0[i],y0[j],b[i,j]])
p2 = np.array([x0[i+1],y0[j],b[i+1,j]])
p3 = np.array([x0[i+1],y0[j+1],b[i+1,j+1]])
p4 = np.array([x0[i],y0[j+1],b[i,j+1]])
p12 = np.linalg.norm(p1-p2)
p23 = np.linalg.norm(p3-p2)
p13 = np.linalg.norm(p3-p1)
p14 = np.linalg.norm(p4-p1)
p34 = np.linalg.norm(p4-p3)
#求半周长L
L1 = (p12+p23+p13)/2
s1 = np.sqrt(L1*(L1-p12)*(L1-p23)*(L1-p13))
L2 = (p13+p14+p34)/2
s2 = np.sqrt(L1*(L2-p13)*(L2-p14)*(L2-p34))
s = s+s1+s2
print("区域的面积为:",s)
plt.rc('font',size=16)
ax = plt.subplot(121,projection='3d')
X,Y = np.meshgrid(x0,y0)
ax.plot_surface(X,Y,b.T,cmap='viridis')
ax.set_xlabel('$x$')
ax.set_ylabel('$y$')
ax.set_zlabel('$z$')
plt.subplot(122)
plt.contour(x0,y0,b.T,50)
plt.colorbar()
plt.plot(30000,0,'pr')#画出A点位置
plt.text(30500,200,'A')#标注A点位置
plt.plot(43000,30000,'pr')#画出B点位置
plt.text(43500,29500,'B')#标注B点位置
plt.xlabel('$x$')
plt.ylabel('$y$',rotation=90)
plt.savefig('figure2_6.png',dpi=500)
plt.show()
|
区域的面积为: 2575216164.3932223m2
2.7求解线性方程组的最小二乘解或最小范数解#
先判断下列线性方程组解的情况,然后求对应的唯一解、最小二乘解或最小范数解。
前提:A满秩,否则矩阵的逆要改成广义逆
- 当线性方程组Ax=b未知量个数不大于方程个数时,存在最小二乘解:$$x^{*}=(A^{\top}A)^{-1} {A}^{\top}b $$
- 当线性方程组Ax=b未知量个数不小于方程个数时,存在最小范数解:$$x^{*}= {A}^{\top}(AA^{\top})^{-1}b$$
具体求解过程可参考知乎文章 # 线性方程组的最小二乘解和最小范数解
在线性代数中,给定一个线性方程组,可能存在无数个解,但是在实际问题中,我们通常希望找到一个最优解,使得该解最符合我们的需求,最小范数解和最小二乘解就是其中两种常见的最优解。
最小范数解是指在所有满足线性方程组的解中,范数最小的解。其中,范数是一个向量或矩阵的长度或大小的度量,通常使用欧几里得范数(向量长度的平方和的平方根)或者Frobenius范数(矩阵元素平方和的平方根)等作为度量。最小范数解的特点是具有最小的平均误差,但不一定是线性方程组的唯一解。
最小二乘解是指通过最小化误差平方和来求解线性方程组的解。即,将线性方程组中的各个方程的误差的平方加和最小化,从而得到最小二乘解。最小二乘解具有最小的总误差,通常在数据拟合等问题中应用广泛。
需要注意的是,最小范数解和最小二乘解不一定相同,但它们都是求解线性方程组的一种常见方法,根据实际问题需要选择合适的方法。
最小范数解和最小二乘解在很多领域中都有重要的应用。以下是其中一些常见的应用场景:
数据拟合:最小二乘解经常被用于拟合实验数据或观测数据,例如在曲线拟合、图像处理、信号处理等领域中,最小二乘法常被用于拟合数据。
信号处理:最小范数解可以被用于去除信号中的噪声,例如在图像去噪、语音去噪等领域中,最小范数解可以被用于恢复原始信号。
机器学习:最小范数解和最小二乘解在机器学习中也有广泛的应用,例如在线性回归、岭回归、Lasso回归、弹性网等模型中,最小范数解和最小二乘解可以被用于求解模型参数。
优化问题:最小范数解和最小二乘解可以被用于优化问题求解,例如在线性规划、非线性规划、整数规划等问题中,最小范数解和最小二乘解可以被用于求出最优解。
图像处理:最小范数解和最小二乘解可以被用于图像处理中,例如在图像去模糊、图像超分辨率、图像重建等领域,最小范数解和最小二乘解可以被用于恢复清晰图像。
总之,最小范数解和最小二乘解在数学、物理、工程、计算机科学等许多领域中都有着广泛的应用。
最小范数解和最小二乘解都是求解线性方程组的一种方法,它们各有优缺点,下面是它们的主要优缺点:
最小范数解的优点:
最小范数解通常是具有最小平均误差的解,能够提供较好的平均拟合效果。
最小范数解具有较好的稳定性和鲁棒性,能够有效地应对数据中的噪声和异常值。
最小范数解的缺点:
最小范数解不一定是唯一的解,存在多个解的情况。
最小范数解可能会导致某些参数的值比实际情况大或小得多,这可能与具体问题的物理背景不符。
最小二乘解的优点:
最小二乘解是具有最小总误差的解,能够提供较好的全局拟合效果。
最小二乘解通常是唯一的,不存在多解情况。
最小二乘解的缺点:
最小二乘解对数据中的噪声和异常值比较敏感,可能会产生过拟合现象。
最小二乘解的计算复杂度较高,需要使用矩阵求逆等计算方法,对于大规模问题可能会面临计算困难。
综上所述,最小范数解和最小二乘解各有优缺点,具体使用哪种方法需要根据具体问题的实际情况来选择。在应用中需要根据数据的特点和拟合效果的要求来选择最合适的方法。
(1)
$$\begin{cases}
4x_1+2x_2-x_3=2\\
3x_1-x_2+2x_3=10\\
11x_1+3x_2=8
\end{cases}$$
1
2
3
4
5
6
7
8
9
10
11
12
| import numpy as np
a = np.array([[4,2,-1],[3,-1,2],[11,3,0]])
b = np.array([[2],[10],[8]])
r1 = np.linalg.matrix_rank(a)#系数矩阵的秩
ab = np.hstack([a,b])
#NumPy中的hstack函数用于将多个数组沿水平方向(列方向)拼接成一个数组。具体来说,hstack函数将多个一维或二维的数组水平拼接起来,生成一个新的数组。
r2 = np.linalg.matrix_rank(ab)#增广矩阵的秩
print("r1=",r1,"r2=",r2)
x = np.linalg.pinv(a)@b#求最小二乘解
print("最小二乘解为:\n",np.round(x,4))
#`np.round` 是 NumPy 中的一个函数,用于对数组进行四舍五入操作。 它的作用是将数组中的元素按照指定的精度进行四舍五入,返回一个新的数组。
|
输出结果:
1
2
3
4
5
| r1= 2 r2= 1
最小二乘解为:
[[ 1.213 ]
[-1.4478]
[ 1.9565]]
|
(2)
$$\begin{cases}
2x+3y+z=4\\
x-2y+4z=-5\\
3x+8y-2z=13\\
4x-y+9z=-6
\end{cases}$$
1
2
3
4
5
6
7
8
9
10
| import numpy as np
a = np.array([[2,3,1],[1,-2,4],[3,8,-2],[4,-1,9]])
b = np.array([[4],[-5],[13],[-6]])
r1 = np.linalg.matrix_rank(a)#系数矩阵的秩
ab = np.hstack([a,b])
#NumPy中的hstack函数用于将多个数组沿水平方向(列方向)拼接成一个数组。具体来说,hstack函数将多个一维或二维的数组水平拼接起来,生成一个新的数组。
r2 = np.linalg.matrix_rank(ab)#增广矩阵的秩
print("r1=",r1,"r2=",r2)
x = np.linalg.pinv(a)@b#求最小范数解
print("最小范数解为:\n",np.round(x,4))
|
输出结果:
1
2
3
4
5
| r1= 2 r2= 2
最小范数解为:
[[ 0.3333]
[ 1.3333]
[-0.6667]]
|
2.8求解线性方程组#
$$\begin{cases}
4x_1+x_x=1\\
x_1+4x_2+x_3=2\\
x_2+4x_3+x_4=3\\
...\\
x_{998}+4x_{999}+x_{1000}=999\\
x_{999}+4x_{1000}=1000\\
\end{cases}$$
1
2
3
4
5
6
7
| import numpy as np
from numpy.linalg import inv
a = 4*np.eye(1000)+np.eye(1000,k=-1)+np.eye(1000,k=1)
b = np.arange(1,1001).reshape(1000,1)
x = inv(a)@b
print(x)
|
输出结果:
1
| [[1.66666667e-01] [3.33333333e-01] [5.00000000e-01] [6.66666667e-01] [8.33333333e-01]……[1.65306678e+02] [1.69542854e+02] [1.54521906e+02] [2.11369524e+02]]
|
2.9求下列方程组的符号解和数值解#
$$\begin{cases}
x^2-y-x=3\\
x+3y=2\\
\end{cases}$$
符号解:
1
2
3
4
| import sympy as sp
sp.var('x,y')
s = sp.solve([x**2-y-x-3,x+3*y-2])
print(s)
|
输出结果:
1
| [{x: 1/3 - sqrt(34)/3, y: 5/9 + sqrt(34)/9}, {x: 1/3 + sqrt(34)/3, y: 5/9 - sqrt(34)/9}]
|
下面是将该段话转换成LaTeX代码的结果:
$${x_1= \frac{1}{3} - \frac{\sqrt{34}}{3}, y_1= \frac{5}{9} + \frac{\sqrt{34}}{9}}, {x_2= \frac{1}{3} + \frac{\sqrt{34}}{3}, y_2= \frac{5}{9} - \frac{\sqrt{34}}{9}}$$
数值解:
1
2
3
4
5
6
| from scipy.optimize import fsolve
import numpy as np
fxy = lambda x:[x[0]**2-x[1]-x[0]-3,x[0]+3*x[1]-2]
s = fsolve(fxy,np.random.randn(2))#`np.random.randn(2)`会返回一个长度为2的一维数组,其中的元素是从标准正态分布中随机生成的,这意味着数组中的元素的值是随机的,并且平均值大约为0,标准差大约为1。
print("求得的一组数值解:",np.round(s,4))#总共有两组解,不过求数值解时只能求得一组数值解
|
输出结果:
1
| 求得的一组数值解: [-1.6103 1.2034]
|
2.10求容器体积和抽水做功#
某容器内侧是由曲线$x^2+y^2=4y(1\leq y\leq 3)和x^2+y^2=4(y\leq1)$绕y轴旋转一周而形成的曲面。(1)求容器的体积。(2)若将容器内盛满的水从容器顶部全部抽出,至少需要做多少功?(长度单位为m,重力加速度g=9.8m/s^2,水的密度$\rho=10^3kg/m^3$)
要求用Visio软件画出容器内侧曲线的示意图,写出建模过程并手工求解,最后给出求符号解的Python程序。
1
2
3
4
5
6
7
8
| import sympy as sp
sp.var('y')
f1 = sp.pi*(4-y**2)
f2 = sp.pi*(4*y-y**2)
V = sp.integrate(f1,(y,-2,1))+sp.integrate(f2,(y,1,3))
W = 1000*sp.Rational(98,10)*(sp.integrate(f1*(3-y),(y,-2,1))+sp.integrate(f2*(3-y),(y,1,3)))
print(V)
print(W)
|
输出结果:
2.11求方程组的数值解#
已知$f(x)=(\lvert x+1 \rvert - \lvert x-1 \rvert)/2+sinx,g(x)=(\lvert x+3 \rvert - \lvert x-3 \rvert)/2+cosx$
求下列方程组的数值解。
$$\begin{cases}
2x_1=3f(y_1)+4g(y_2)-1,\\
3x_2=2f(y_1)+6g(y_2)-2,\\
y_1=f(x_1)+3g(x_2)-3,\\
5y_2=4f(x1)+6g(x2)-1
\end{cases}$$
1
2
3
4
5
6
7
8
9
10
11
12
| from scipy.optimize import fsolve
import numpy as np
f = lambda x:(abs(x+1)-abs(x-1))/2+np.sin(x)
g = lambda x:(abs(x+3)-abs(x-3))/2+np.cos(x)
eqs = lambda z:[3*f(z[2])+4*g(z[3])-1-2*z[0],
2*f(z[2])+6*g(z[3])-2-3*z[1],
f(z[0])+3*g(z[1])-3-z[2],
4*f(z[0])+6*g(z[1])-1-5*z[3]]
s = fsolve(eqs,np.random.randn(4))
print("求得的一组数值解:",np.round(s,4))
|
输出结果:
1
| 求得的一组数值解: [-0.8588 0.3022 -0.8451 0.0156]
|
2.12求矩阵的特征值和特征向量的数值解和符号解#
矩阵latex代码通用表达:
$$A=\begin{bmatrix}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{bmatrix}$$
$$A=\begin{bmatrix}
-1 & 1 & 0 \\
-4 & 3 & 0 \\
1 & 0 & 2
\end{bmatrix}$$
求数值解:
1
2
3
4
5
6
7
8
9
10
| import numpy as np
A = np.array([[-1,1,0],[-4,3,0],[1,0,2]])
p = np.poly(A)#计算特征多项式
w1 = np.roots(p)#计算特征值
w2,v = np.linalg.eig(A)#直接求特征值和特征向量
w3 = np.linalg.eigvals(A)#计算特征值
print("特征值为:",w2)
print("特征向量为:\n",v)
#print(w1)#输出结果为[2.+0.00000000e+00j 1.+2.83263462e-08j 1.-2.83263462e-08j]
#print(w3)#输出结果为[2. 1. 1.]
|
输出结果:
1
2
3
4
5
| 特征值为: [2. 1. 1.]
特征向量为:
[[ 0. 0.40824829 0.40824829]
[ 0. 0.81649658 0.81649658]
[ 1. -0.40824829 -0.40824829]]
|
求符号解:
1
2
3
4
5
6
7
8
9
10
11
| import sympy as sp
A = sp.Matrix([[-1,1,0],[-4,3,0],[1,0,2]])
sp.var('lamda')
p = A.charpoly(lamda)#计算特征多项式
w1 = sp.roots(p)
w2 = A.eigenvals()
v = A.eigenvects()
print(w1)
print("特征值为:",w2)
print("特征向量为:\n",v)
|
输出结果:
1
| {2: 1, 1: 2} 特征值为: {1: 2, 2: 1} 特征向量为: [(1, 2, [Matrix([ [-1], [-2], [ 1]])]), (2, 1, [Matrix([ [0], [0], [1]])])]
|
eigenvals函数用于计算矩阵的特征值及其重数,Matrix是SymPy中表示矩阵的类,需要导入后才能使用。该函数返回一个字典,字典的键是特征值,值是该特征值对应的重数。
eigenvects函数用于计算矩阵的特征向量及其重数,该函数返回一个列表,列表的每个元素是一个三元组,分别表示特征值、该特征值对应的重数以及该特征值对应的特征向量。特征向量以列表形式返回,列表中的每个元素是一个SymPy符号或数值,表示向量中的一个分量。
需要注意的是,这两个函数的参数是矩阵本身,而不是矩阵元素的值。因此,在使用这两个函数时,需要先构造一个SymPy矩阵对象,再传递给函数进行计算。
2.13求超定(矛盾)方程组的最小二乘解#
注:当初始值变化范围较大时,所求的最小二乘解是不稳定的。
已知$f(x)=(\lvert x+1 \rvert - \lvert x-1 \rvert)/2+sinx,g(x)=(\lvert x+3 \rvert - \lvert x-3 \rvert)/2+cosx$
求下列超定方程组的最小二乘解。
$$\begin{cases}
2x_1=3f(y_1)+4g(y_2)-1,\\
3x_2=2f(y_1)+6g(y_2)-2,\\
y_1=f(x_1)+3g(x_2)-3,\\
5y_2=4f(x1)+6g(x2)-1,\\
x_1+y_1 = f(y_2)+g(x_2)-2,\\
x_2-3y_2=2f(x_1)-10g(y_1)-5.
\end{cases}$$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| from scipy.optimize import least_squares
import numpy as np
f = lambda x:(abs(x+1)-abs(x-1))/2+np.sin(x)
g = lambda x:(abs(x+3)-abs(x-3))/2+np.cos(x)
eqs = lambda z:[3*f(z[2])+4*g(z[3])-1-2*z[0],
2*f(z[2])+6*g(z[3])-2-3*z[1],
f(z[0])+3*g(z[1])-3-z[2],
4*f(z[0])+6*g(z[1])-1-5*z[3],
f(z[3])+g(z[1])-2-z[0]-z[2],
2*f(z[0])-10*g(z[2])-5-z[1]-3*z[3]]
s = least_squares(eqs,np.random.randn(4))
print(s.x)
|
输出结果:
1
| [-0.70146587 0.0926214 -1.17167778 0.05542954]
|




 (2)椭圆抛物面$$\frac{x^2}{4} + \frac{y^2}{6} = \frac{z}{1}$$
(2)椭圆抛物面$$\frac{x^2}{4} + \frac{y^2}{6} = \frac{z}{1}$$
