基于OpenCV的自动对焦：多种图像清晰度评价算子的比较研究

概述

作者：Moukthika

发布日期：2025年3月11日

分类：计算机视觉、OpenCV

标签：自动对焦，Brenner梯度，熵测量，拉普拉斯算子，局部方差法，Sobel+方差，Tenengrad

Autofocus using OpenCV: A Comparative Study of Focus Measures for Sharpness Assessment

引言

自动对焦是成像系统中至关重要的环节，能够保证拍摄的图像和视频帧清晰锐利。在医学成像、安防监控、摄影等众多领域，通过从视频帧序列中选取最清晰的画面，极大提升图像的分析效果和呈现质量。

本文利用开源计算机视觉库OpenCV，对多种常用的图像焦点测量算子进行计算与比较。基于不同算子提取的图像清晰度指标，我们评估并选取视频中最清晰的帧，分析各算子在自动对焦任务中的性能优缺点及适用范围，为实际自动成像系统的设计提供参考。

环境及依赖

为了顺利复现本教程，您的系统需安装Python 3.x版本。

  • Jupyter Notebook用户
    在代码单元内执行以下命令安装依赖库：

    1

    !pip install opencv-python numpy scikit-image

    或者

    1

    %pip install opencv-python numpy scikit-image

  • Visual Studio Code及命令行用户
    直接在终端输入：

    1

    pip install opencv-python numpy scikit-image

  • Google Colab用户
    Google Colab环境已预装相关库，可直接运行代码。

数据集说明

实验所用视频包含多个含有不同清晰度的连续帧，既包括模糊帧，也有清晰帧。视频经过精心选择，确保焦点状态变化明显，便于对比各种清晰度评价算子的有效性。我们的核心目标是在此视频序列中，利用计算得分选出最锐利的画面。

常见焦点测量算子及计算原理

图像焦点测量算子通过分析图像的亮度变化、梯度强度及边缘细节，评估图像的清晰度。选择合适的算子直接关系到自动对焦系统和图像处理的准确性。本文实验以下六种典型算子：

  • 局部方差法（Local Variance）
  • 熵基法（Entropy-Based）
  • Tenengrad（基于Sobel梯度）
  • Brenner梯度法
  • Sobel算子与方差结合法（Sobel + Variance）
  • 拉普拉斯算子法（Laplacian-Based）

下面详细介绍各方法的原理、优缺点及适用场景。

1. 局部方差法

原理：
测量图像局部区域内的像素强度方差，假设清晰图像在区域内存在更大强度变化，从而更具对比度。

优点：

  • 计算简单、速度快
  • 对高对比度图像敏感，易检测焦点
  • 对部分随机噪声较不敏感

缺点：

  • 对低对比度图像表现不佳，可能误判
  • 光照不均匀时评估不准
  • 鲜有应用于复杂自动对焦场景

2. 熵基法

原理：
利用图像灰度级分布的熵值来衡量信息量，清晰图像由于细节丰富，通常熵值更高。

优点：

  • 适合纹理丰富的图像
  • 对少量噪声具有一定抵抗力
  • 在低对比度情况下优于方差法

缺点：

  • 计算量较大，速度较慢
  • 高频噪声可能导致误判为清晰
  • 对边缘主导的图像清晰度识别不够准确

3. Tenengrad焦点测量（基于Sobel梯度）

原理：
通过Sobel算子计算图像水平方向和垂直方向的梯度强度，边缘强度越大，图像越清晰。

优点：

  • 效果稳定，尤其擅长强边缘图像
  • 对光照变化具有一定鲁棒性
  • 被广泛用于自动对焦系统中

缺点：

  • 对噪声敏感，噪声可能导致误判
  • 纹理丰富而边缘弱的图像效果欠佳
  • 方向敏感性可能影响测量准确性

4. Brenner梯度法

原理：
计算相邻像素的强度差值，差异越大说明图像越清晰。

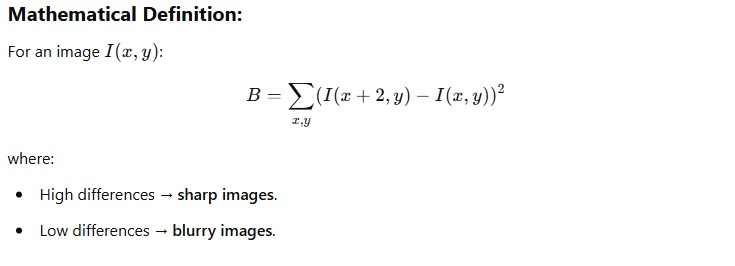
优点：

  • 简单且计算速度极快
  • 对边缘清晰度检测较有效
  • 在模糊图像识别上表现优于方差法

缺点：

  • 鲁棒性较差，低对比度图像表现欠佳
  • 对噪声敏感，误判概率较高
  • 适用范围有限，仅部分自动对焦场景有效

5. Sobel + 方差结合法

原理：
结合Sobel梯度和局部方差两种度量，同时考虑图像边缘强度和强度变化幅度，提高焦点测量的稳健性。

优点：

  • 综合边缘和强度信息，效果更可靠
  • 适应多种图像类型，包括纹理和边缘主导图像
  • 减少噪声对结果的干扰

缺点：

  • 计算复杂度较高，速度较慢
  • 仍对极端噪声敏感
  • 需要合理调整参数（如Sobel卷积核大小）以获得最佳效果

6. 拉普拉斯算子法

原理：
使用拉普拉斯二阶导数算子检测图像的高频细节，计算其响应方差，方差越大表示图像越清晰。

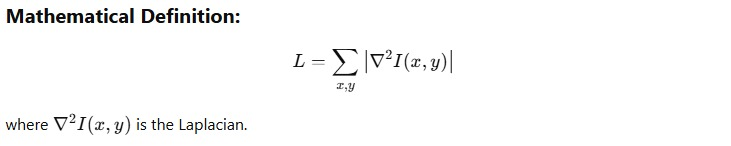
优点：

  • 对细节和微弱边缘表现敏感
  • 适合多种自动对焦和显微成像场景
  • 光照变化对测量影响较小

缺点：

  • 对噪声高度敏感，容易放大噪点
  • 计算开销较大
  • 边缘过度强调可能造成误判

常用聚焦度量函数实现

为了评估不同的聚焦度量方法，我们将每种方法应用于视频的每一帧，计算其聚焦得分，然后选择得分最高的最清晰帧。各方法的代码框架相同，仅替换聚焦度量函数。

主要流程包括：

  1. 逐帧读取视频。
  2. 用选定的聚焦度量函数计算聚焦得分。
  3. 记录帧和对应的得分，便于后续比较。
  4. 选择聚焦得分最高的帧作为“最清晰帧”。
  5. 打印最优帧编号及其得分。
  6. 显示最优帧，直观验证聚焦效果。

Python 示例代码（通用框架）

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

import cv2
import numpy as np

videoPath = "C:/Users/ssabb/Desktop/opencv_courses/articles/data/autofocus1.mp4"
cap = cv2.VideoCapture(videoPath)
focus_scores = []
frames = []

# 请在此处定义聚焦度量函数，例如 compute_focus_measure(image)

if cap.isOpened():
    print("视频文件成功打开")
else:
    print("无法打开视频文件")

while True:
    ret, frame = cap.read()
    if not ret:
        print("无法读取帧，退出循环")
        break
    score = compute_focus_measure(frame)  # 替换为实际聚焦函数
    focus_scores.append(score)
    frames.append(frame)

cap.release()

best_score_index = np.argmax(focus_scores)
best_frame = frames[best_score_index]
print(f"最佳帧索引: {best_score_index}，得分: {focus_scores[best_score_index]}")

# 按比例缩放宽度到600像素，调整高度保持纵横比
orig_h, orig_w = best_frame.shape[:2]
new_w = 600
new_h = int(orig_h * (new_w / orig_w))
resized = cv2.resize(best_frame, (new_w, new_h))

cv2.imshow("最佳帧", resized)
cv2.waitKey(0)
cv2.destroyAllWindows()

1. 局部方差法（Local Variance）

1
2
3
4
5
6

def compute_local_variance(image, ksize=5):
    gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
    mean = cv2.blur(gray, (ksize, ksize))
    squared_mean = cv2.blur(gray**2, (ksize, ksize))
    variance = squared_mean - mean**2
    return np.mean(variance)

2. 基于熵的度量（Entropy）

1
2
3
4
5

from skimage.measure import shannon_entropy

def compute_entropy(image):
    gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
    return shannon_entropy(gray)

3. Tenengrad法（基于Sobel梯度）

1
2
3
4
5
6

def compute_tenengrad(image):
    gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
    sobel_x = cv2.Sobel(gray, cv2.CV_64F, 1, 0, ksize=3)
    sobel_y = cv2.Sobel(gray, cv2.CV_64F, 0, 1, ksize=3)
    gradient_magnitude = np.sqrt(sobel_x**2 + sobel_y**2)
    return np.mean(gradient_magnitude)

4. Brenner梯度法

1
2
3
4
5

def compute_brenner_gradient(image):
    gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
    shifted = np.roll(gray, -2, axis=1)
    diff = (gray - shifted) ** 2
    return np.sum(diff)

5. Sobel梯度与方差结合

1
2
3
4
5
6
7

def compute_sobel_variance(image):
    gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
    sobel_x = cv2.Sobel(gray, cv2.CV_64F, 1, 0, ksize=3)
    sobel_y = cv2.Sobel(gray, cv2.CV_64F, 0, 1, ksize=3)
    sobel_magnitude = np.sqrt(sobel_x**2 + sobel_y**2)
    variance = np.var(gray)
    return np.mean(sobel_magnitude) + variance

6. 拉普拉斯法（基于Laplacian算子）

1
2
3
4

def compute_laplacian(image):
    gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
    laplacian = cv2.Laplacian(gray, cv2.CV_64F)
    return np.var(laplacian)

需要将 compute_focus_measure(image) 替换为以上相应的函数以测试不同方法。

总结

本文介绍的六种焦点测量算子各有特点：局部方差法适合速度优先和高对比图像，熵法适合纹理丰富或低对比度图像，而Tenengrad、Brenner、Sobel+方差和拉普拉斯方法则更适用于多样化的自动对焦任务，尤其是基于梯度的算子在准确性和鲁棒性方面表现突出。

实际应用中，选择合适的焦点算子应综合考虑图像特性、计算资源和噪声环境。未来结合深度学习等新兴技术，有望进一步提升自动对焦的实时性和准确率。