Math Adventures with Python: An Illustrated Guide to Exploring Math with Code by Peter Farrell
这里介绍用Python来解决数学问题深化自己的计算思维,帮我自己成为数据格致家。
读这本书主要是想实现元胞自动机,这个以前很想实现,但是一直拖延到了现在才行动,哎!本来打算暑假更完的,但没空更,先挖坑,以后再填。
第一部分 搭上你的 Python 马车#
第 1 章 用 turtle 模块绘制多边形#
1.1Python的turtle模块
1.1.1导入turtle模块
1.1.2让小海龟动起来
1.1.3改变方向
1.2用循环使代码重复运行
1.2.1使用for循环
1.2.2运用for循环画一个正方形
1.3用函数创建快捷操作
1.4利用变量画出不同的图形
1.4.1在函数中使用变量
1.4.2变量错误
1.5等边三角形
1.5.1编写triangle()函数
1.5.2让变量变起来
第 2 章 用列表和循环把烦琐的算术变有趣#
2.1基本运算符
2.1.1变量运算
2.1.2用运算符编写函数average()
2.1.3注意运算顺序
2.1.4结合使用括号和运算符
2.2Python中的数据类型
2.2.1整数和浮点数
2.2.2字符串
2.2.3布尔类型
2.2.4查看数据类型
2.3用列表存储值
2.3.1向列表添加项
2.3.2列表的运算
2.3.3从列表中删除项
2.4在循环中使用列表
2.4.1使用列表索引访问单个项
2.4.2用enumerate()函数获取索引和值
2.4.3索引从0开始
2.4.4访问一系列列表项
2.4.5查找某项的索引
2.4.6字符串也有索引
2.5求和
2.5.1创建running_sum变量
2.5.2编写mySum()函数
2.6求一列数的平均值
第 3 章 用条件语句检验猜测#
3.1比较运算符
3.2用if和else语句做决定
3.3使用条件语句求因数
3.3.1编写factors.py程序
3.3.2海龟漫步
3.4制作一个猜数游戏
3.4.1制作一个随机数生成器
3.4.2读取用户输入
3.4.3将用户输入转换成整数
3.4.4用条件语句检查猜测是否正确
3.4.5用循环给予更多猜测机会
3.4.6猜数小提示
3.5计算平方根
3.5.1套用猜数游戏的逻辑
3.5.2编写squareRoot()函数
第二部分 奔向数学领域#
第 4 章 用代数学变换和存储数#
4.1解一次方程
4.1.1一次方程的解法公式
4.1.2编写equation()函数
4.1.3用print()替换return
4.2解更高次的方程
4.2.1用quad()函数解二次方程
4.2.2用plug()函数解三次方程
4.3用作图法解方程
4.3.1Processing入门
4.3.2制作你自己的作图工具
4.3.3绘制方程的图像
4.3.4用“猜测检验法”求根
4.3.5编写guess()函数
第 5 章 用几何学变换形状#
5.1画一个圆#
1
2
3
4
| def setup():
size(600,600)
def draw():
ellipse(200,0,50,50)
|
5.2用坐标指定位置#
计算机图形中坐标系和数学中坐标系不同
5.3变换函数平移和旋转#
1
2
3
4
5
6
7
| def setup():
size(600,600)
def draw():
translate(width/2,height/2)#不用具体数改变画布尺寸,移动坐标平面而非移动原点
#translate(200,200)
rotate(radians(20))#20度
rect(20,40,50,50)
|
画一圈圆
1
2
3
4
5
6
7
| def setup():
size(600,600)
def draw():
translate(width/2,height/2)
for i in range(12):
ellipse(200,0,50,50)
rotate(radians(360/12))
|
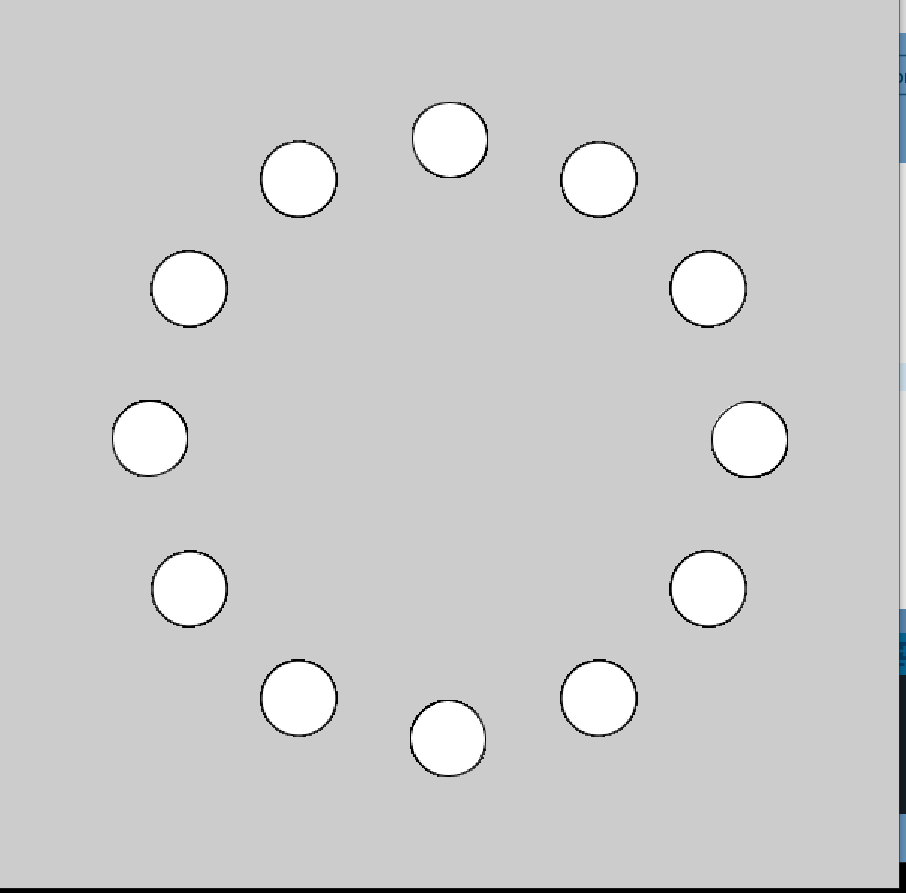
5.4使对象动画化#
5.4.1创建变量t#
1
2
3
4
5
6
7
8
9
10
11
12
| t = 0
def setup():
size(600,600)
def draw():
global t
background(255)#背景设置为白色
translate(width/2,height/2)
rotate(radians(t))
for i in range(12):
ellipse(200,0,50,50)
rotate(radians(360/12))
t +=0.1
|
5.4.2旋转各个正方形#
在processing中旋转中心是(0,0),我们在循环中先将其平移到每个正方形该在的位置,然后旋转,最后画出正方形。
1
2
3
4
5
6
7
8
9
10
11
12
| t = 0
def setup():
size(600,600)
def draw():
global t
background(255)#背景设置为白色
for i in range(12):
translate(200,0)
rotate(radians(t))
rect(0,0,50,50)
rotate(radians(360/12))
t +=0.1
|
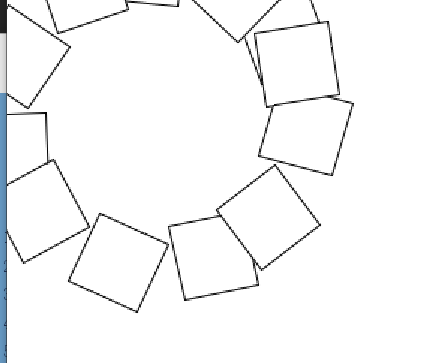
正方形不再绕画布中心旋转,而是整体在画布上不停移动。这是因为我们在不停的改变网格的位置和方向。在画完一个正方形后,我们需要在画下一个正方形之前将网格一会画布中心并转回之前的方向。
5.4.3 用pushMatrix()和popMatrix()保存方位#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| t = 0
def setup():
rectMode(CENTER)
size(600,600)
def draw():
global t
background(255)#背景设置为白色
# translate(width/2,height/2)
# rotate(radians(t))
for i in range(12):
pushMatrix()#保存当前方位
translate(200,500)
rotate(radians(t))
rect(0,0,50,50)
popMatrix()#回到保存的方位
rotate(radians(360/12))
t +=0.1
|
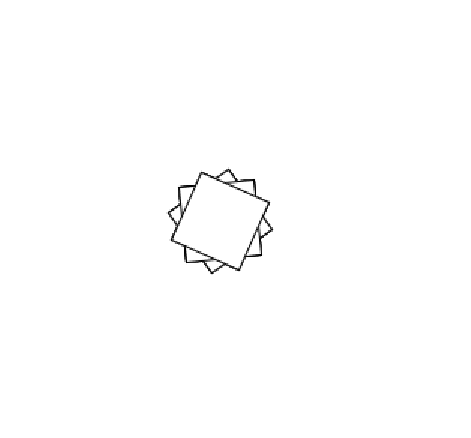
5.4.4 使正方形绕中心旋转#
在Setup()函数中加入rectMode(CENTER)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| t = 0
def setup():
rectMode(CENTER)
size(600,600)
def draw():
global t
background(255)#背景设置为白色
translate(width/2,height/2)
for i in range(12):
pushMatrix()#保存当前方位
rotate(radians(t*5))#转速增加到原来的五倍
rect(0,0,50,50)
popMatrix()#回到保存的方位
rotate(radians(360/12))
t +=0.1
|
5.6 制作一个可交互的彩虹网格#
5.5.1画出呈网格状排列的对象#
1
2
3
4
5
6
7
8
| def setup():
size(600,600)
def draw():
background(255)
for x in range(20):
for y in range(20):
rect(30*x,30*y,25,25)
|
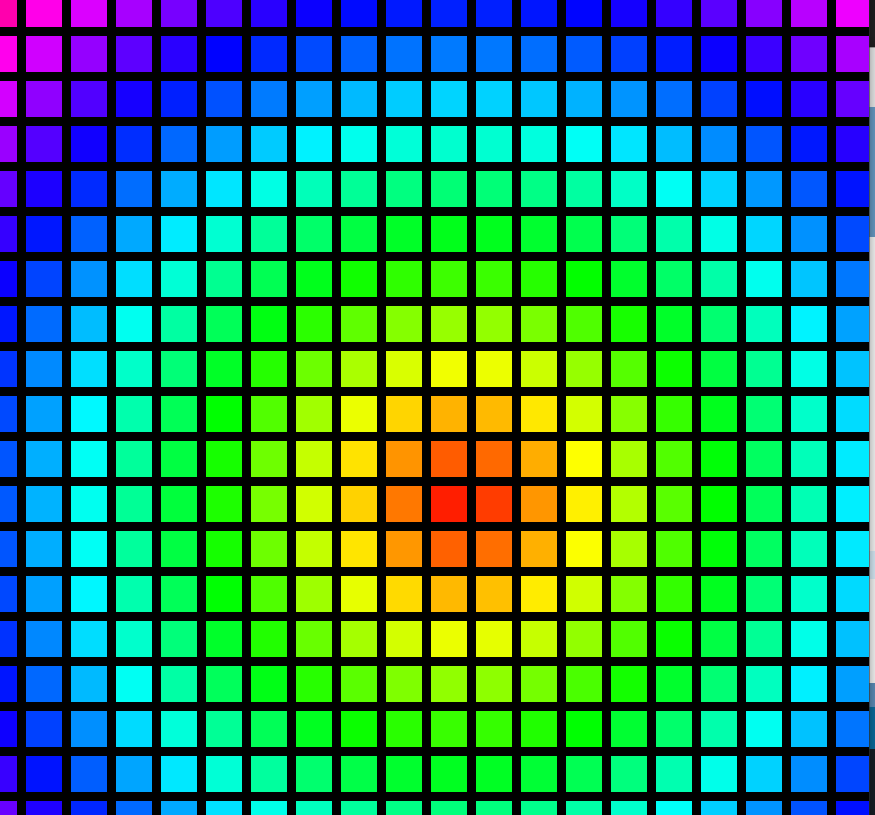
5.5.2 给对象涂上彩虹色#
colorMode()有RGB和HSB两种色彩模式。HSB指色相Hue、饱和度Saturation和明度Brightness
1
2
3
4
5
6
7
8
9
10
11
12
13
| def setup():
size(600,600)
rectMode(CENTER)
colorMode(HSB)
def draw():
background(0)#背景设置为黑色
translate(20,20)
for x in range(30):
for y in range(30):
distance = dist(30*x,30*y,mouseX,mouseY)#左上角坐标和鼠标距离
fill(0.5*distance,255,255)#只用更改第一个值,后面两个值可以一直设置为255
rect(30*x,30*y,25,25)
|
5.6 用三角形画出复杂的图案#
画一个旋转的三角形但不是等边三角形
1
2
3
4
5
6
7
8
9
10
11
12
| def setup():
size(600,600)
rectMode(CENTER)
t = 0
def draw():
global t
translate(width/2,height/2)
rotate(radians(t))
triangle(0,0,100,100,200,-200)#三个顶点坐标
t += 0.5
|
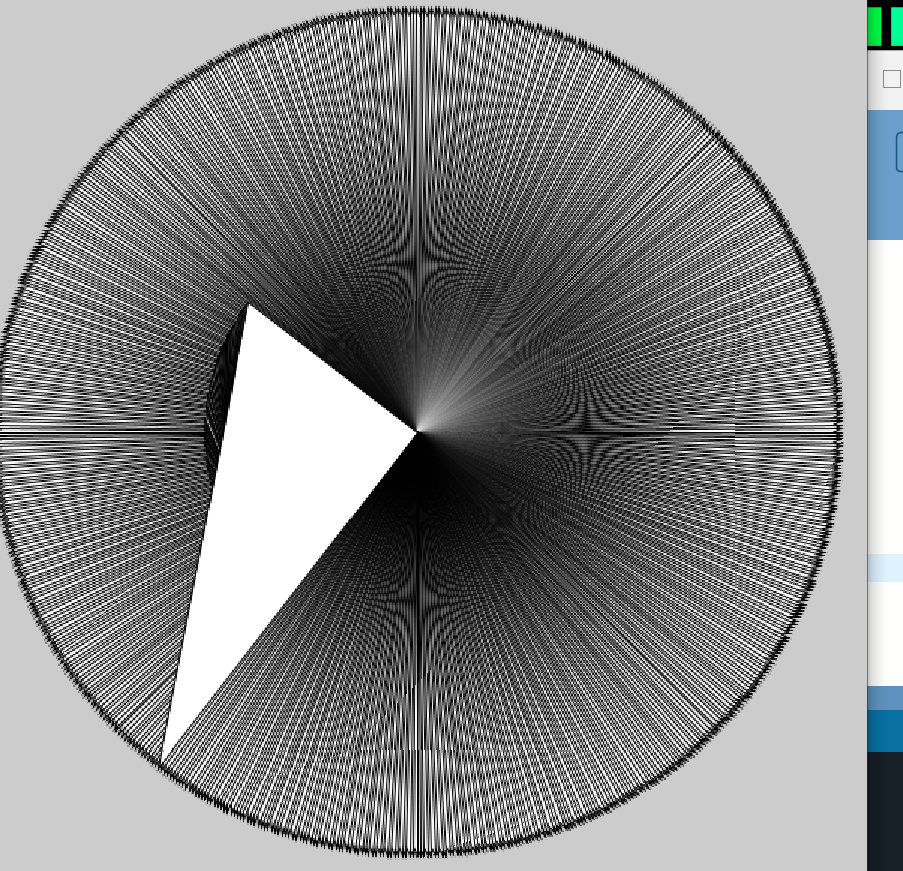
5.6.1 30-60-90三角形#
5.6.2 画一个等边三角形#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| def setup():
size(600,600)
rectMode(CENTER)
t = 0
def draw():
global t
translate(width/2,height/2)
rotate(radians(t))
tri(200)#画等边三角形
t += 0.5
def tri(length):
triangle(0,-length,-length*sqrt(3)/2,length/2,length*sqrt(3)/2,length/2)#以(0,0)为中心
|

5.6.3 画多个旋转的三角形#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| def setup():
size(600,600)
rectMode(CENTER)
t = 0
def draw():
global t
background(255)
translate(width/2,height/2)
for i in range(90):
#将三角形绕圆周等间距摆放
rotate(radians(360/90))
pushMatrix()#保存当前方位
#平移至圆周
translate(200,0)
#旋转一定角度
rotate(radians(t))
tri(100)#画等边三角形
popMatrix()#回到保存的方位
t += 0.5
def tri(length):
noFill()#设置三角形为透明
triangle(0,-length,-length*sqrt(3)/2,length/2,length*sqrt(3)/2,length/2)#以(0,0)为中心
|
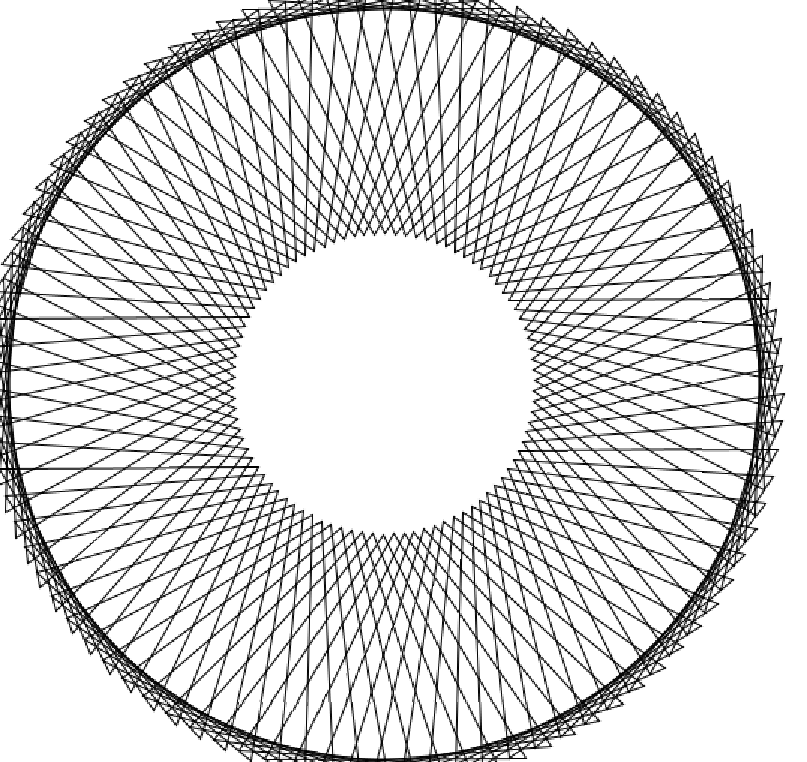
5.6.4 给旋转加上相位偏移#
引入相移(phase shift)改变三角形旋转的模式,它可以让每个三角形比上一个稍微慢一步,使草图呈现出波浪Wave或级联cascade效果。每个三角形都对应一个循环变量i,我们可以把i加入rotate(radians(t))中变成rotate(radians(t+i))。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| def setup():
size(600,600)
rectMode(CENTER)
t = 0
def draw():
global t
background(255)
translate(width/2,height/2)
for i in range(90):
#将三角形绕圆周等间距摆放
rotate(radians(360/90))
pushMatrix()#保存当前方位
#平移至圆周
translate(200,0)
#旋转一定角度
rotate(radians(t+i))
tri(100)#画等边三角形
popMatrix()#回到保存的方位
t += 0.5
def tri(length):
noFill()#设置三角形为透明
triangle(0,-length,-length*sqrt(3)/2,length/2,length*sqrt(3)/2,length/2)#以(0,0)为中心
|
效果:
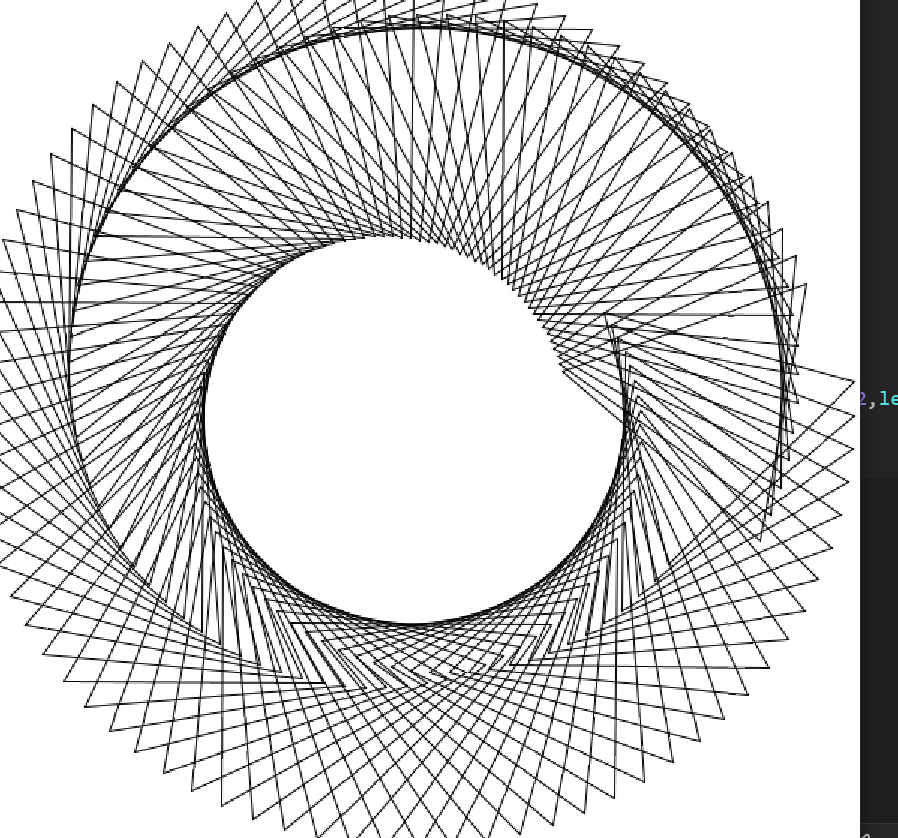
右边有一处中断是因为最后一个三角形的下一个三角形的相位应该是t+90,它和第一个三角形的相位差是90,而两个看起来相同的等边三角形的相位差应该是120的整数倍。可以把rotate(radians(t+i))改成rotate(radians(t+i*360/90))。
5.6.5 将图案画完#
将i乘以2来改变相移,增大相邻三角形之间的相位差。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| def setup():
size(600,600)
rectMode(CENTER)
t = 0
def draw():
global t
background(255)
translate(width/2,height/2)
for i in range(90):
#将三角形绕圆周等间距摆放
rotate(radians(360/90))
pushMatrix()#保存当前方位
#平移至圆周
translate(200,0)
#旋转一定角度
rotate(radians(t+2*i*360/90))
tri(100)#画等边三角形
popMatrix()#回到保存的方位
t += 0.5
def tri(length):
noFill()#设置三角形为透明
triangle(0,-length,-length*sqrt(3)/2,length/2,length*sqrt(3)/2,length/2)#以(0,0)为中心
|
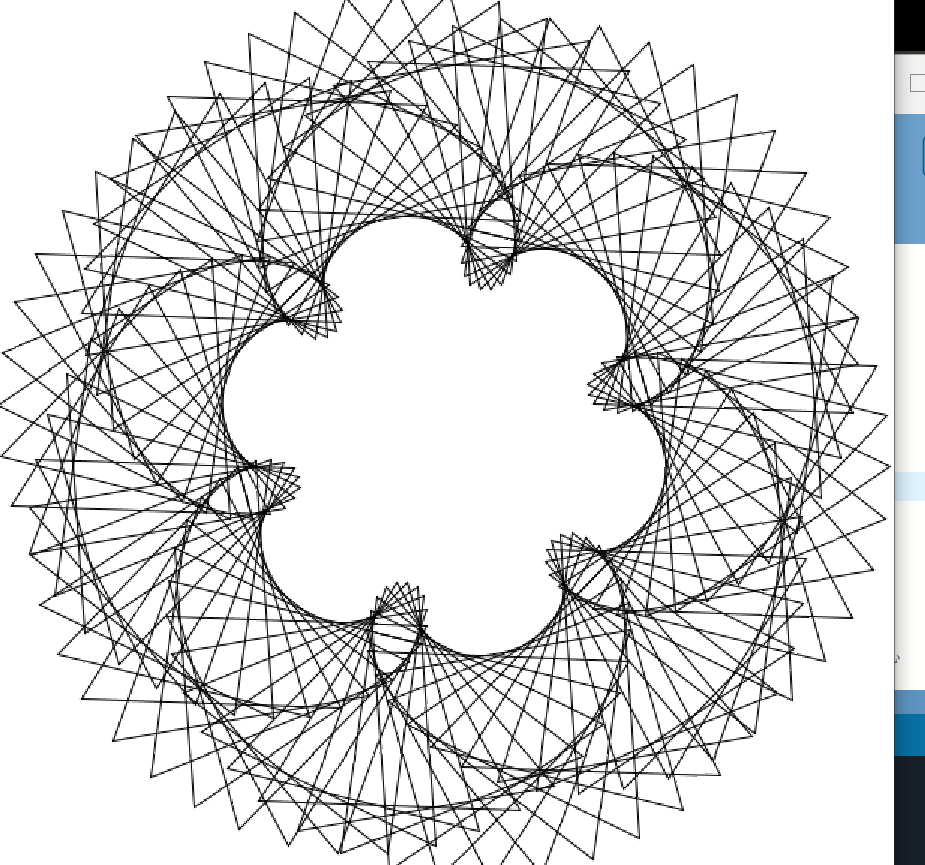
用stroke()函数可以给每个三角形上色
第 6 章 用三角学制造振荡#
6.1用三角学做旋转和振荡
6.2编写画多边形的函数
6.2.1用循环画一个正六边形
6.2.2画一个正三角形
6.3画正弦波
6.3.1圆过留痕
6.3.2使用Python内置的enumerate()函数
6.4编写万花尺程序
6.4.1画小圆
6.4.2旋转小圆
6.5画谐波图
6.5.1编写画谐波图的程序
6.5.2瞬间填好列表
6.5.3两个钟摆比一个强
第 7 章 复数#
7.1复数坐标系124
7.2将复数相加124
7.3将一个复数乘以i125
7.4将两个复数相乘126
7.5编写magnitude()函数127
7.6创建芒德布罗集128
7.6.1编写mandelbrot()函数130
7.6.2给芒德布罗集上色134
7.7创建茹利亚集135
第 8 章 将矩阵用于计算机图形和方程组#
8.1什么是矩阵138
8.2矩阵相加139
8.3矩阵相乘140
8.4矩阵乘法中的顺序很重要144
8.5画2D形状144
8.6变换矩阵147
8.7转置矩阵149
8.8实时旋转矩阵152
8.9制作3D形状154
8.10制作旋转矩阵155
8.11用矩阵解方程组159
8.11.1高斯消元法159
8.11.2编写gauss()函数161
第三部分 开辟你自己的道路#
第 9 章 用类构建对象#
9.1弹跳球程序170
9.1.1让小球动起来171
9.1.2让小球从墙上弹回172
9.1.3不用类创建多个小球173
9.1.4用类创建对象174
9.2“羊吃草”程序179
9.2.1编写表示小羊的类179
9.2.2让小羊四处走动.180
9.2.3添加能量属性181
9.2.4用类创建草182
9.2.5让草被吃掉后变成棕色185
9.2.6给每只小羊涂上随机的颜色187
9.2.7让小羊繁殖188
9.2.8让草再生189
9.2.9给予进化优势190
第 10 章 用递归制作分形#
10.1海岸线的长度194
10.1.1何为递归195
10.1.2编写factorial()函数195
10.1.3“种”一棵分形树196
10.2科赫雪花200
10.3谢尔宾斯基三角形205
10.4正方形分形207
10.5龙形曲线211
第 11 章 元胞自动机#
11.1创建一个元胞自动机217
11.1.1编写一个细胞类219
11.1.2调整细胞大小221
11.1.3让CA生长222
11.1.4将细胞放入一个矩阵223
11.1.5创建细胞列表224
11.2奇怪的Python列表225
11.2.1列表切片226
11.2.2让你的CA自动生长229
11.3玩玩“生命游戏”229
11.4初等元胞自动机232
第 12 章 用遗传算法解决问题#
12.1用遗传算法猜出句子239
12.1.1编写makeList()函数239
12.1.2测试makeList()函数240
12.1.3编写score()函数241
12.1.4编写mutate()函数241
12.1.5生成随机数242
12.2解决旅行商问题244
12.2.1使用遗传算法245
12.2.2编写calcLength()方法251
12.2.3测试calcLength()方法251
12.2.4随机路线252
12.2.5运用猜句程序的突变思想255
12.2.6突变列表中的两个数255
12.2.7通过交叉改进路线259








